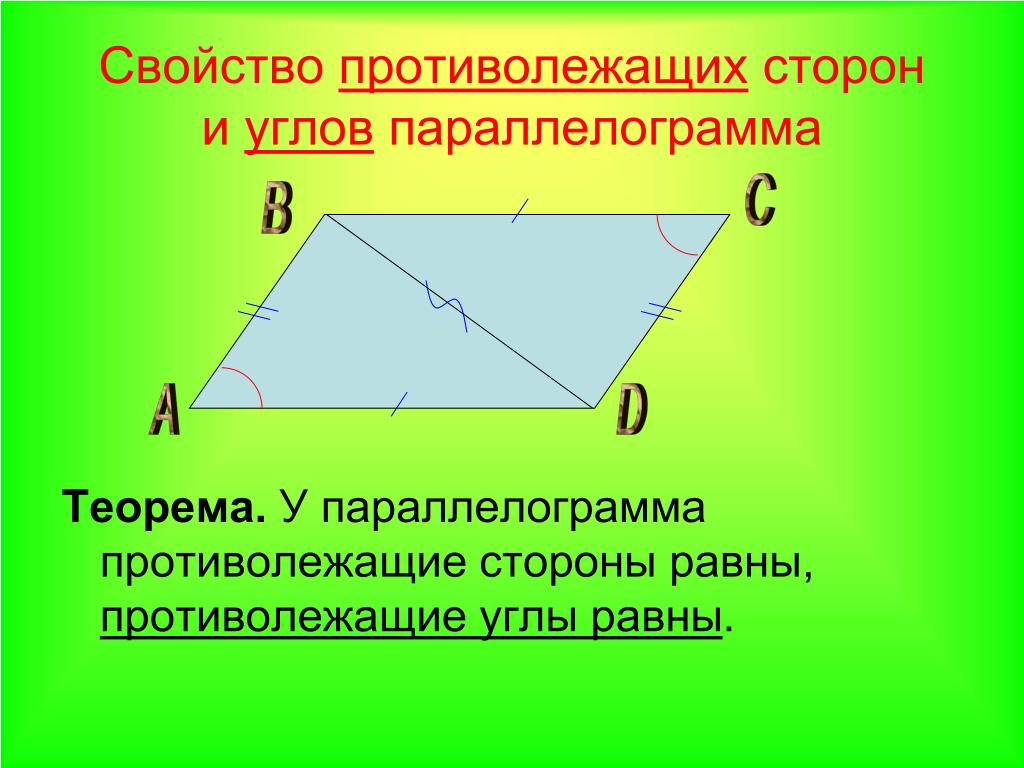
Углы параллелорамма
Получи беслпатные курсы подготовки к ЕГЭ и ОГЭ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-12-24
Углы параллелограмма. Здравствуйте! В этой публикации представлена группа заданий с параллелограммами. Требуется вычислить синус (косинус) заданного угла, сторону или высоту. Всё решение сводится к работе с прямоугольным треугольником. То есть вполне достаточно помнить определения тригонометрических функций и уметь применять их на практике. Задачи решаются в одно действие, многие ученики после построения эскиза, наверняка, смогут решить их устно.
Что ещё стоит отметить? Один факт (свойство синуса), который очень пригодится. Это то, что синусы смежных углов равны, подробнее об этом было написано в этой статье. Если озвучить кратко и простыми словами, то синусы углов сумма которых равна 1800 равны. Это видно и по формуле приведения:
*а также по тригонометрической окружности (при построении таких углов).
Как это применяется в задачах ниже? Как известно, сумма соседних углов параллелограмма равна 1800.
И если будет дан синус любого из углов, то это означает, что синусы соседних с ним углов имеют такое же значение.
Рассмотрим задачи:
27433.В параллелограмме ABCD высота, опущенная на сторону AB равна 4, AD=8. Найдите синус угла B.
Построим высоту:
Синус угла В равен синусу угла А, так как известно, что синусы смежных углов равны (указанные углы в сумме равны 180 градусам).
В прямоугольном треугольнике ADE:
Ответ: 0,5
27434. В параллелограмме ABCD высота, опущенная на сторону AB, равна 4, sinA=2/3. Найдите AD.
Построим указанную высоту:
В прямоугольном треугольнике ADE:
Ответ: 6
27435. В параллелограмме ABCD sinС=3/7. AD=21. Найдите высоту, опущенную на сторону AB.
Построим параллелограмм:
Угол С равен углу А. Рассмотрим прямоугольный треугольник ADE:
Ответ: 9
27436. В параллелограмме ABCD AB=3, AD=21, sinA=6/7.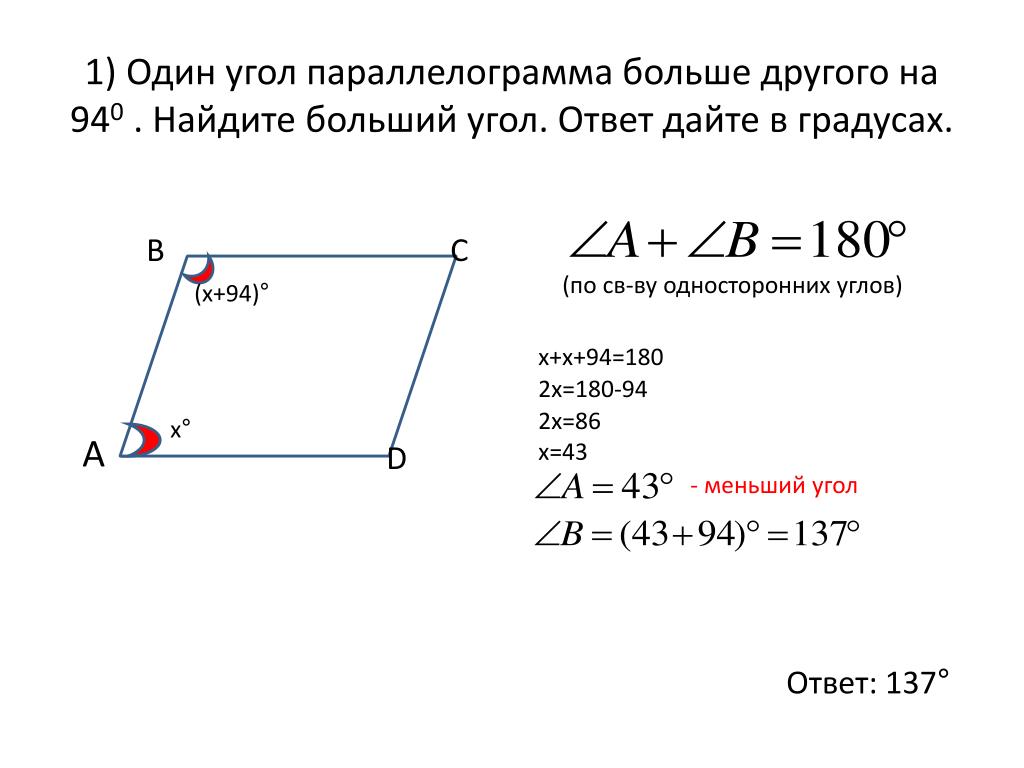
Найдите большую высоту параллелограмма.
Построим параллелограмм соблюдая соотношения сторон (АВ<AD):
Большей будет высота, которая проведена к меньшей стороне. Рассмотрим прямоугольный треугольник ADE:
Ответ: 18
27438. В параллелограмме ABCD cosA=(√51)/10. Найдите sinB.
Как уже сказано, синусы смежных углов равны. Для того, чтобы найти sinB, достаточно вычислить sinА. Из основного тригонометрического тождества следует, что:
Ответ: 0,7
27437. В параллелограмме ABCD sinA=(√21)/5. Найдите cosB.
*Посмотрите решение внимательно, есть важные нюансы.
Посмотреть решение
Этом всё. Есть ещё много задач с параллелограммами, их тоже рассмотрим, не пропустите. Успеха вам!
С уважением, Александр Крутицких.
Материалы принесли вам пользу? Расскажите о сайте в социальных сетях!
Категория: Четырёхугольники | ЕГЭ-№1ПараллелограммУглы
Подготовка к ОГЭ по математике.
Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Определение параллелограма и его свойства
1. Определение параллелограмма.
Если пару параллельных прямых пересечём другой парой параллельных прямых, то получим четырёхугольник, у которого противоположные стороны попарно параллельны.
В четырёхугольниках ABDС и ЕFNМ (рис. 224) ВD || АС и AB || СD;
ЕF || МN и ЕМ || FN.
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
2. Свойства параллелограмма.
Теорема. Диагональ параллелограмма делит его на два равных треугольника.
Пусть имеется параллелограмм ABDС (рис. 225), в котором AB || СD и АС || ВD.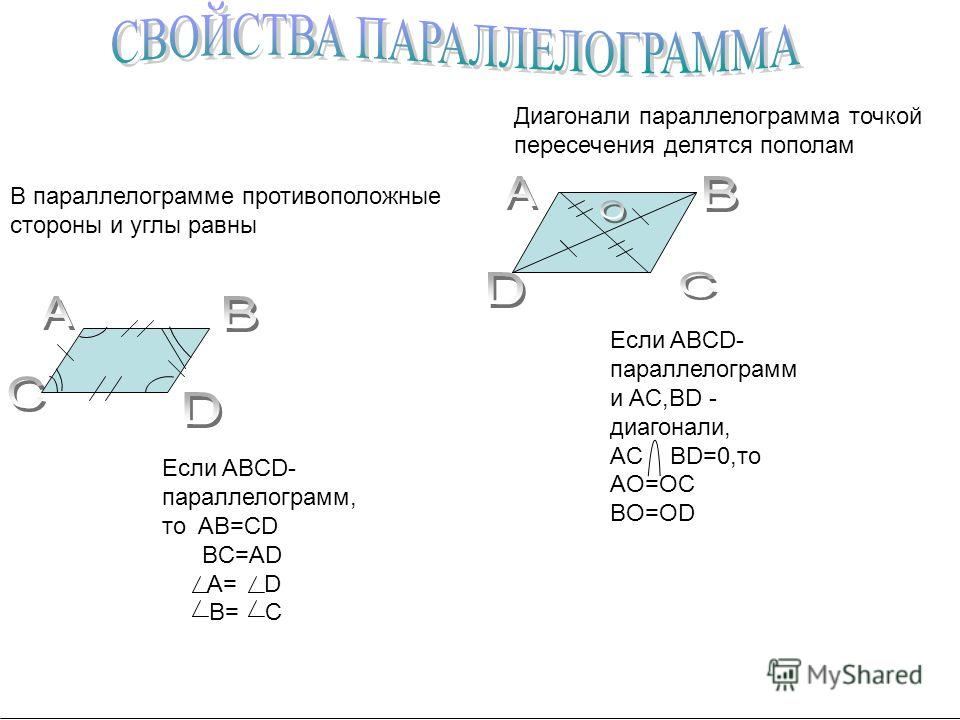
Требуется доказать, что диагональ делит его на два равных треугольника.
Проведём в параллелограмме ABDС диагональ СВ. Докажем, что \(\Delta\)CAB = \(\Delta\)СDВ.
Сторона СВ общая для этих треугольников; ∠ABC = ∠BCD, как внутренние накрест лежащие углы при параллельных AB и СD и секущей СВ; ∠ACB = ∠СВD, тоже как внутренние накрест лежащие углы при параллельных АС и ВD и секущей CB.
Отсюда \(\Delta\)CAB = \(\Delta\)СDВ.
Таким же путём можно доказать, что диагональ AD разделит параллелограмм на два равных треугольника АСD и ABD.
Следствия:
1. Противоположные углы параллелограмма равны между собой.
∠А = ∠D, это следует из равенства треугольников CAB и СDВ.
Аналогично и ∠С = ∠В.
2. Противоположные стороны параллелограмма равны между собой.
AB = СD и АС = ВD, так как это стороны равных треугольников и лежат против равных углов.
Теорема 2. Диагонали параллелограмма в точке их пересечения делятся пополам.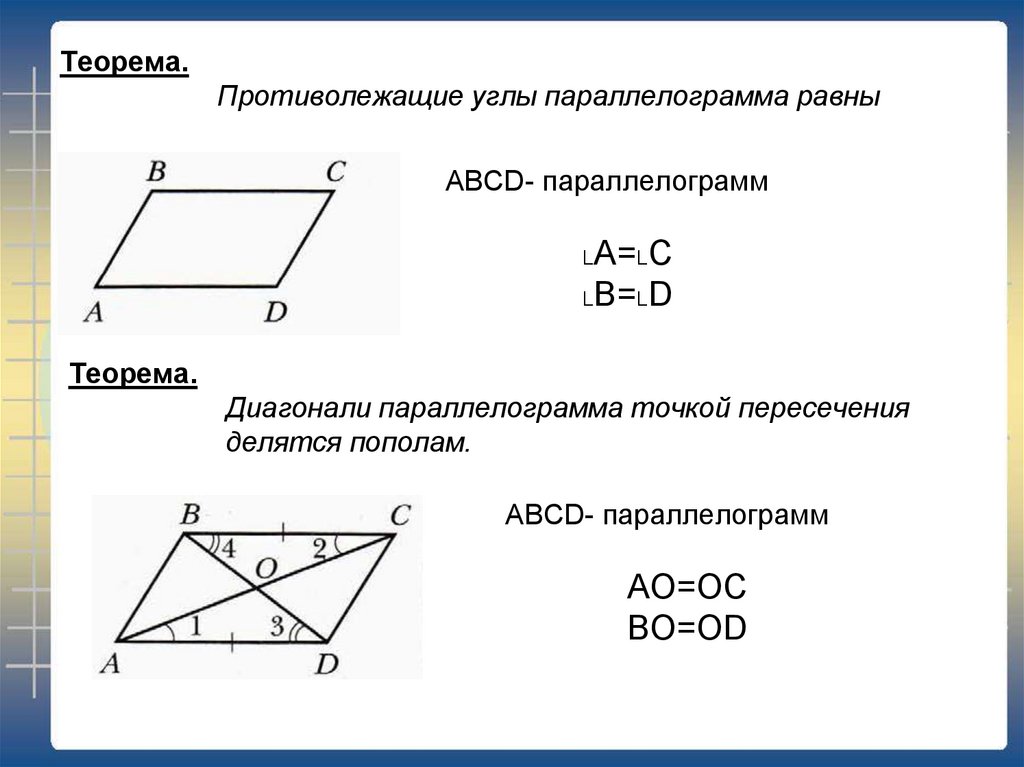
Пусть BC и AD — диагонали параллелограмма AВDС (рис. 226). Докажем, что АО = OD и СО = OB.
Для этого сравним какую-нибудь пару противоположно расположенных треугольников, например \(\Delta\)AOB и \(\Delta\)СОD.
В этих треугольниках AB = СD, как противоположные стороны параллелограмма;
∠1 = ∠2, как углы внутренние накрест лежащие при параллельных AB и СD и секущей AD;
∠3 = ∠4 по той же причине, так как AB || СD и СВ — их секущая.
Отсюда следует, что \(\Delta\)AOB = \(\Delta\)СОD. А в равных треугольниках против равных углов лежат равные стороны. Следовательно, АО = OD и СО = OB.
Теорема 3. Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
В параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC.
Треугольники равны, так как ∠1 = ∠4, ∠2 = ∠3 (накрест лежащие углы при параллельных прямых), а сторона АС общая.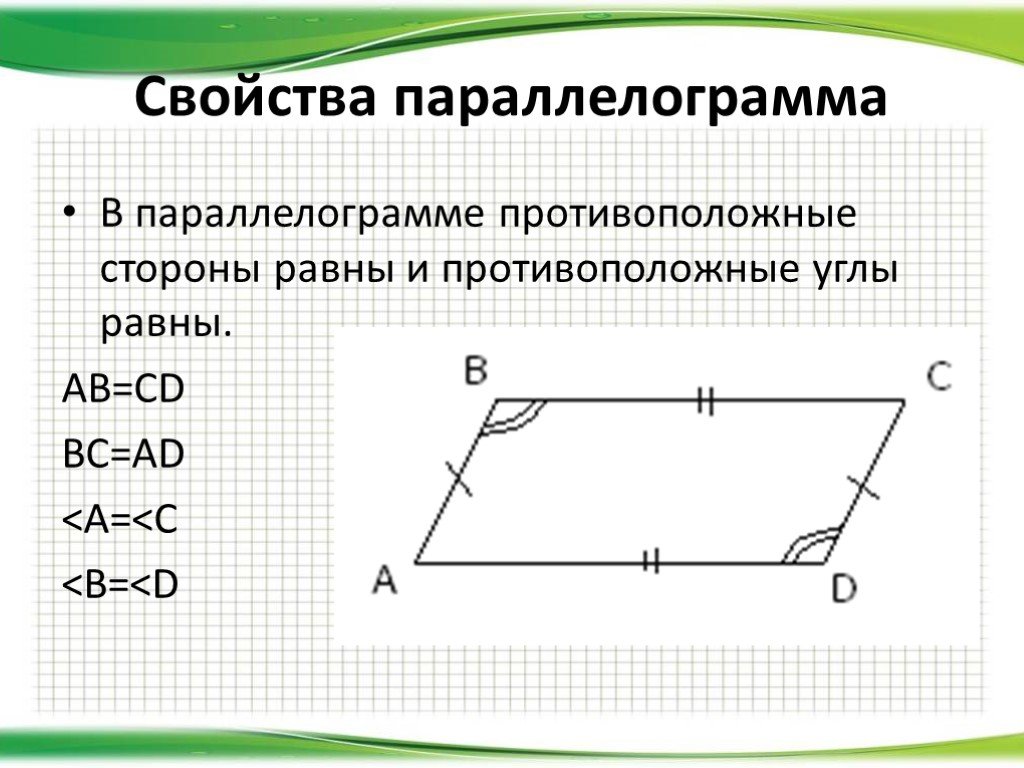
Из равенства \(\Delta\)ABC = \(\Delta\)ADC следует, что AB = CD, BC = AD, ∠B = ∠D.
Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых.
Видео-вопрос: Нахождение мер углов параллелограмма по заданному отношению между заданными углами
𝐴𝐵𝐶𝐷 — параллелограмм, а 𝑚∠𝐷𝐴𝐶 = 5𝑥°, 𝑚∠𝐵𝐴𝐶 = 3𝑥° и 𝑚∠𝐴𝐵𝐶 = 4𝑥°. Определить 𝑚∠𝐵𝐶𝐷 и 𝑚∠𝐴𝐷𝐶.
Стенограмма видео
𝐴𝐵𝐶𝐷 является параллелограммом, а мера угла 𝐷𝐴𝐶 равна пяти 𝑥 градусам, мера угла 𝐵𝐴𝐶 равна трем 𝑥 градусам, а мера угла 𝐴𝐵𝐶 равна четырем 𝑥 градусам. Определите меру угла 𝐵𝐶𝐷 и меру угла 𝐴𝐷𝐶.
Когда нам задают подобный вопрос, лучше всего начать с ввода информации об угле, которую нам дали. Угол 𝐷𝐴𝐶 равен пяти 𝑥 градусам, угол 𝐵𝐴𝐶 равен трем 𝑥 градусам, а угол 𝐴𝐵𝐶 равен четырем 𝑥 градусам. Нас просят найти два угла: угол 𝐵𝐶𝐷 и угол 𝐴𝐷𝐶.
Нам говорят, что 𝐴𝐵𝐶𝐷 — это параллелограмм, а это значит, что его противоположные стороны параллельны и конгруэнтны. Чтобы ответить на этот вопрос с помощью углов в параллелограмме, нам нужно вспомнить важный факт об углах в параллелограмме, а именно то, что противоположные углы в параллелограмме равны или конгруэнтны.
Таким образом, мы могли бы сразу же посмотреть на нашу диаграмму и увидеть, что угол при 𝐵 должен быть равен углу при 𝐷, который равен четырем 𝑥 градусам. Точно так же весь этот угол при 𝐷𝐴𝐵, который состоит из пяти 𝑥 градусов и трех 𝑥 градусов, будет равен этому углу при 𝐷𝐶𝐵, то есть он также равен восьми 𝑥 градусам. Глядя на диаграмму, мы видим, что нашли два неизвестных угла относительно 𝑥. Однако мы можем задаться вопросом, можем ли мы найти значение 𝑥 и дать эти ответы в виде числового значения.
На самом деле есть два разных способа найти значение 𝑥. Первый метод предполагает использование свойства параллелограмма, состоящего в том, что любые два последовательных угла в параллелограмме являются дополнительными, что означает, что их сумма составляет 180 градусов.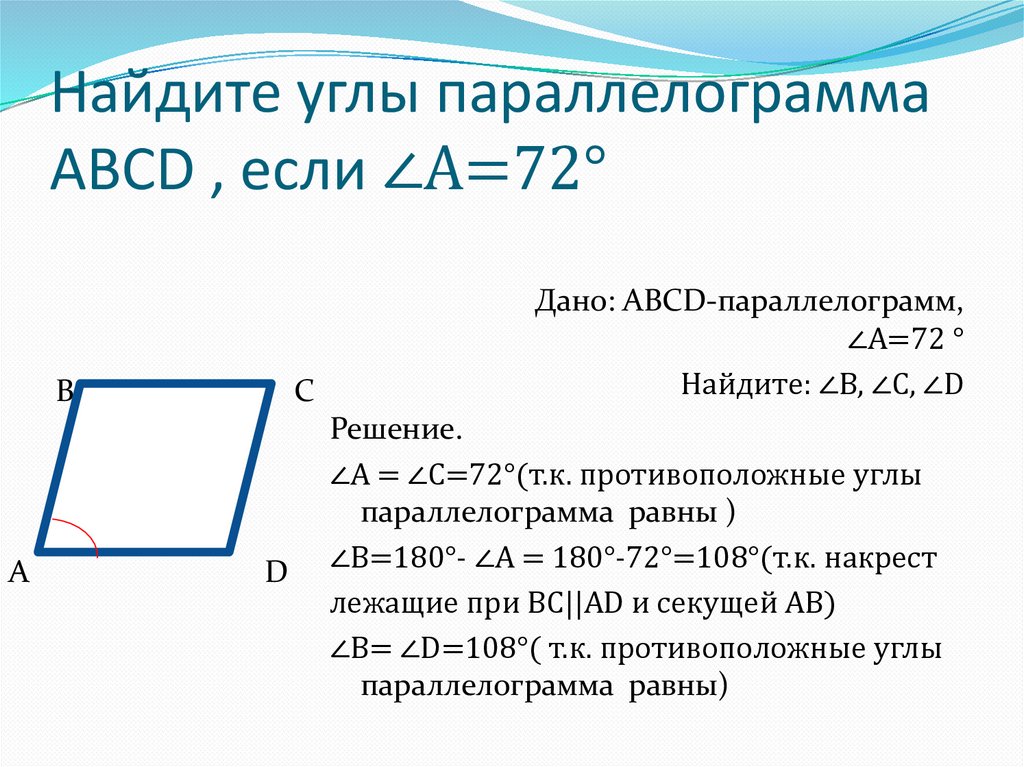
Альтернативный метод, который мы могли бы использовать, состоит в том, чтобы вспомнить, что сумма углов любого четырехугольника составляет 360 градусов. Затем мы могли бы добавить наши четыре угла, четыре 𝑥, восемь 𝑥, четыре 𝑥 и восемь 𝑥 градусов, и установить это равным 360 градусам. Упрощение даст нам 24𝑥 равно 360 градусам. Разделив на 24, мы снова получим, что 𝑥 равно 15 градусам. Но, конечно, нас не просили просто найти 𝑥. Нас попросили провести два измерения угла. Для угла 𝐵𝐶𝐷 мы установили, что это восемь 𝑥 градусов, и вычислили, что 𝑥 равно 15. Итак, вычисляем восемь умножить на 15. А это 120 градусов. Угол 𝐴𝐷𝐶 мы определили как четыре 𝑥 градуса, поэтому на этот раз мы умножаем четыре на 15, что равно 60 градусам.
Итак, у нас есть ответы для двух измерений угла: 120 градусов и 60 градусов.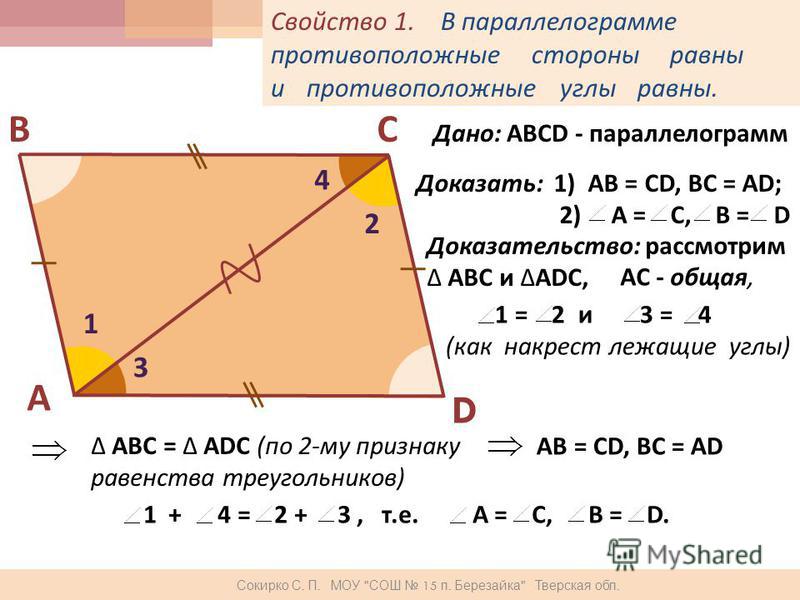
. Задача 1
Напомним, что параллелограмм имеет две пары последовательных и параллельных сторон. В результате углы внутри параллелограмма можно рассматривать как углы, образованные параллельными прямыми и секущей (соседние стороны действуют как секущие). По свойствам внутренних углов одной стороны эти углы в параллелограмме являются дополнительными, а противоположные углы равны.
Итак, чтобы решить переменные в параллелограмме, подставьте выражения углов (а) равными друг другу, если они противоположные углы, или (б) подставьте выражение, равное 180 — (выражение смежного угол).
противоположные стороны параллельно противоположные углы односторонние внутренние углы диагонали делить пополам последовательные углы
Вы можете использовать свойства параллелограмма, чтобы найти пропущенные переменные.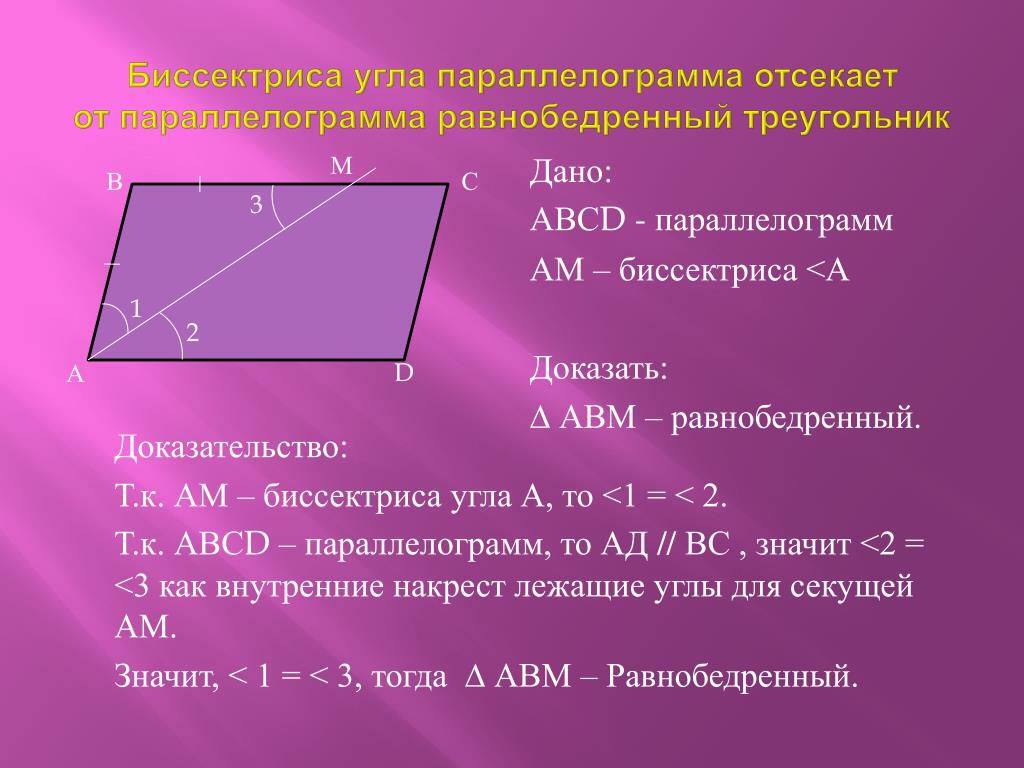
Итак, в этой задаче у нас есть две переменные, у нас есть x и у нас есть y, и они являются частью мер этих углов. Итак, начнем с нахождения x.
Ну, если я посмотрю на х, я увижу их в последовательных углах, и что я знаю о последовательных углах в параллелограмме? Что ж, если я посмотрю на эту диаграмму прямо здесь, я увижу, что последовательные углы — это внутренние углы одной и той же стороны двух параллельных прямых, поэтому они должны быть дополнительными.
Итак, что я могу сделать, так это сказать, что количество 6x плюс 10 плюс такой же внутренний угол, который равен 2x плюс 10, должно составлять 180 градусов. Таким образом, ключевым моментом здесь было понимание того, что у нас есть две параллельные линии, мы думали об этой стороне как о поперечной, поэтому, если вы хотите, вы можете нарисовать продолжение, поэтому эти две должны быть дополнительными. Итак, я собираюсь объединить 6 и 2x, и мы получим 8x, 10 и 10 равно 20, поэтому я собираюсь получить 180 с другой стороны.