Постановка транспортной задачи
Учреждение образования «Белорусская государственная
сельскохозяйственная академия»
Кафедра высшей математики
Методические указания
по изучению темы «Транспортная задача» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)
Горки, 2013
Транспортная задача
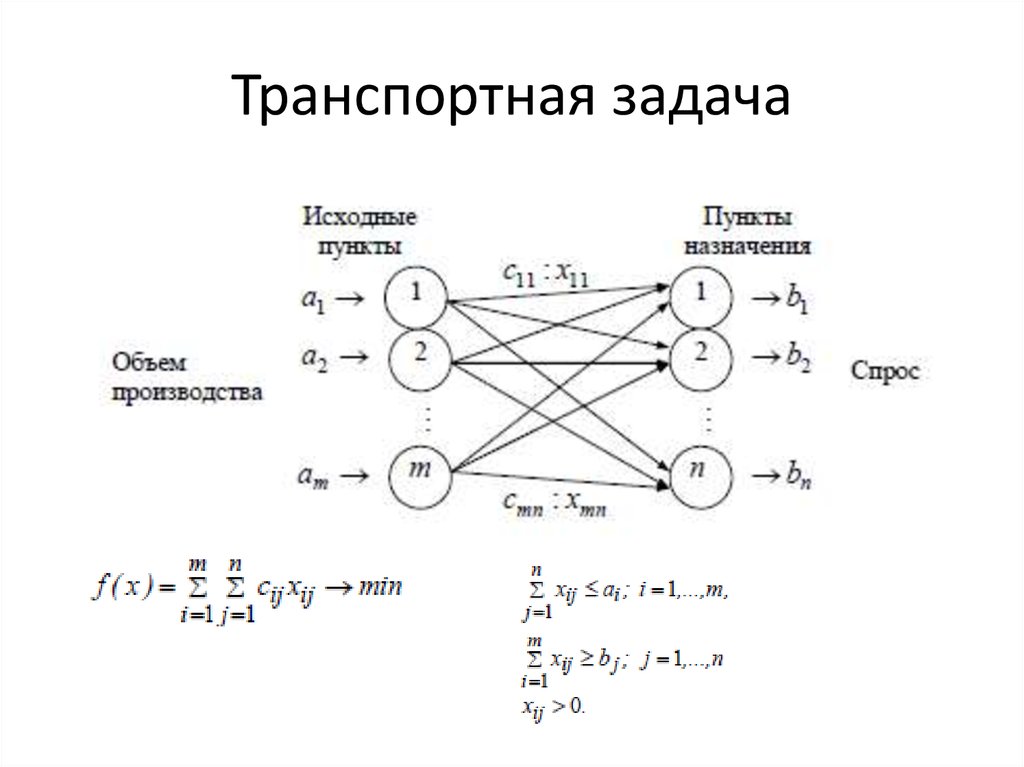
Транспортная задача является задачей линейного программирования. В общей постановке она выглядит следующим образом.
Имеется m пунктов отправления (поставщиков) с запасами единиц груза. Имеется n пунктов назначения (потребителей) с потребностями
.
Груз из пунктов отправления должен быть
доставлен в пункты назначения. Известны
транспортные издержки
,
связанные с перевозкой единицы груза
из пункта в пункт
.
Требуется составить такой план перевозок, при котором весь груз из пунктов отправления был бы доставлен потребителям и при этом спрос потребителей был бы удовлетворён, а транспортные издержки были минимальными.
Для разрешимости данной задачи необходимо и достаточно, чтобы сумма запасов была равна сумме потребностей всех пунктов, т.е. . Транспортная задача, в которой выполнено это условие, называется закрытой (или транспортной задачей с закрытой моделью).
Для наглядности транспортную задачу удобно представлять в виде таблицы, которую называют распределительной.
В таблице количество груза, перевозимого от поставщика к потребителю обозначено через .
Матрица называется матрицей тарифов, а числа – тарифами.
Поставщики | Потребители | Запасы груза | |||
… | |||||
… | |||||
… | |||||
… | … | … | … | … | … |
… | |||||
Потребность в грузе | … | ||||
Матрица называется планом
транспортной задачи. Здесь каждое число обозначает количество единиц груза,
который надо доставить от i-го
поставщика к j-му
потребителю. Матрицу Х называют ещё матрицей
перевозок.
Здесь каждое число обозначает количество единиц груза,
который надо доставить от i-го
поставщика к j-му
потребителю. Матрицу Х называют ещё матрицей
перевозок.
Общие суммарные затраты, связанные с перевозкой груза, можно представить в виде функции
.
Эта функция называется целевой функцией.
Кроме этого, переменные должны удовлетворять ограничениям по потребностям, по запасам и условиям неотрицательности. Всё это с учётом целевой функции можно записать в виде:
(1)
(2)
Условия (2) образуют систему ограничений. Любой план, удовлетворяющий этой системе, называется допустимым.
Таким образом, можно математически сформулировать транспортную задачу:
Даны система ограничений (2) и целевая функция (1).
 Требуется среди множества решений системы найти такой план перевозок, который минимизирует целевую функцию (1).
Требуется среди множества решений системы найти такой план перевозок, который минимизирует целевую функцию (1).Определение допустимого плана задачи
Правило «северо-западного угла». Суть данного правила состоит в следующем. Таблица заполняется, начиная с левого верхнего угла (северо-западного), двигаясь по строке вправо или по столбцу вниз в направлении правого нижнего угла.
Пример 1. Сельхозпредприятия ежедневно выделяют соответственно 30, 40 и 20 ц молока для снабжения пунктов . Стоимость перевозки и потребности пунктов даны в таблице.
Сельхоз- предприятия | Потребители | Наличие | |||
2 | 3 | 5 | 4 | 30 | |
3 | 2 | 4 | 1 | 40 | |
4 | 3 | 2 | 6 | 20 | |
Потребности | 20 | 25 | 35 | 10 | 90 |
Требуется
найти допустимый план задачи.
Решение. Найдём допустимый план задачи с помощью правила «северо-западного угла».
Сельхоз- предприятия | Потребители | Наличие | |||
2 20 | 3 10 | 5 | 4 | 30 | |
3 | 2 15 | 4 25 | 1 | 40 | |
4 | 3 | 2 10 | 6 10 | 20 | |
Потребности | 20 | 25 | 35 | 10 | 90 |
Затраты на перевозку составят
.
2.2. Правило «минимального элемента». Допустимый план, построенный по правилу «северо-западного угла», обычно оказывается далёким от оптимального. Поэтому в дальнейшем потребуется достаточно много преобразований для достижения оптимального плана. Сократить число таких преобразований позволяет правило «минимального элемента». Суть этого правила в следующем.
Заполнение таблицы начинается с клетки, которой соответствует наименьший элемент из всей матрицы тарифов. Затем остаток по столбцу или строке помещается в клетку того же столбца или строки, которым соответствует следующее по величине значение и т.д.
Пример 2. Решить предыдущий пример, используя правило «минимального элемента».
Решение.
Так как наименьшим элементом является
,
то заполнение таблицы начнём с этой
клетки. В клетку с элементом поместим требуемые для пункта
10
ц, затем в клетку с элементом
поместим
25 ц, а оставшиеся 5 ц – в клетку с элементом
. Таким образом, имеющиеся в наличии 40 ц
молока у сельхозпредприятия
распределены.
Аналогичным образом распределяем запасы
молока сельхозпредприятий и
.
Таким образом, имеющиеся в наличии 40 ц
молока у сельхозпредприятия
распределены.
Аналогичным образом распределяем запасы
молока сельхозпредприятий и
.
Сельхоз- предприятия | Потребители | Наличие | |||
2 15 | 3 | 5 15 | 4 | 30 | |
3 5 | 2 25 | 4 | 1 10 | 40 | |
3 | 2 20 | 6 | 20 | ||
Потребности | 20 | 25 | 35 | 10 | 90 |
Затраты на перевозку составят
.
Транспортная задача | это… Что такое Транспортная задача?
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.[1][2] Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки. Транспортная задача является по теории сложности вычислений NP-сложной и входит в класс сложности NP. Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).
Содержание
|
Постановка задачи
Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).
Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). Под названием транспортная задача ,определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, спец.метод решения транспортной задачи позволяет существенно упростить её решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок.
Под названием транспортная задача ,определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, спец.метод решения транспортной задачи позволяет существенно упростить её решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок.
История поиска методов решения
Проблема была впервые формализована французским математиком Гаспаром Монжем в 1781 году[3]. Основное продвижение было сделано на полях во время Великой Отечественной войны советским математиком и экономистом Леонидом Канторовичем[4]. Поэтому иногда эта проблема называется транспортной задачей Монжа — Канторовича.
Методы решения
Классическую транспортную задачу можно решить симплекс-методом, но в силу ряда особенностей её можно решить проще (для задач малой размерности).
Условия задачи располагают в таблице, вписывая в ячейки количество перевозимого груза из в груза , а в маленькие клетки — соответствующие тарифы .
Итерационное улучшение плана перевозок
Нахождение опорного плана
Требуется определить опорный план и путём последовательных операций найти оптимальное решение. Опорный план можно найти следующими методами: «северо-западного угла», «наименьшего элемента», двойного предпочтения и аппроксимации Фогеля.
Метод северо-западного угла (диагональный)
На каждом этапе максимально возможным числом заполняют левую верхнюю клетку оставшейся части таблицы. Заполнение таким образом, что полностью выносится груз из или полностью удовлетворяется потребность .
Метод наименьшего элемента
Одним из способов решения задачи является метод минимального (наименьшего) элемента. Его суть заключается в сведении к минимуму побочных перераспределений товаров между потребителями.
Алгоритм:
- Из таблицы стоимостей выбирают наименьшую стоимость и в клетку, которая ей соответствует, вписывают большее из чисел.
- Проверяются строки поставщиков на наличии строки с израсходованными запасами и столбцы потребителей на наличие столбца, потребности которого полностью удовлетворены.
 Такие столбцы и строки далее не рассматриваются.
Такие столбцы и строки далее не рассматриваются. - Если не все потребители удовлетворены и не все поставщики израсходовали товары, возврат к п. 1, в противном случае задача решена.
Итерации
После нахождения опорного плана перевозок, нужно применить один из алгоритмов его улучшения, приближения к оптимальному.
- Метод падающего камня (нем.)
- Метод потенциалов.
Решение с помощью теории графов
Рассматривается двудольный граф, в котором пункты производства находятся в верхней доле, а пункты потребления — в нижней. Пункты производства и потребления попарно соединяются рёбрами бесконечной пропускной способности и цены за единицу потока .
К верхней доле искусственно присоединяется исток. Пропускная способность рёбер из истока в каждый пункт производства равна запасу продукта в этом пункте. Цена за единицу потока у этих рёбер равна 0.
Аналогично к нижней доле присоединяется сток. Пропускная способность рёбер из каждого пункта потребления в сток равна потребности в продукте в этом пункте. Цена за единицу потока у этих рёбер тоже равна 0.
Пропускная способность рёбер из каждого пункта потребления в сток равна потребности в продукте в этом пункте. Цена за единицу потока у этих рёбер тоже равна 0.
Дальше решается задача нахождения максимального потока минимальной стоимости (mincost maxflow). Её решение аналогично нахождению максимального потока в алгоритме Форда — Фалкерсона. Только вместо кратчайшего дополняющего потока ищется самый дешёвый. Соответственно, в этой подзадаче используется не поиск в ширину, а алгоритм Беллмана — Форда. При возврате потока стоимость считается отрицательной.
Алгоритм «mincost maxflow» можно запускать и сразу — без нахождения опорного плана. Но в этом случае процесс решения будет несколько более долгим. Выполнение алгоритма «mincost maxflow» происходит не более чем за операций. ( — количество рёбер, — количество вершин.) При случайно подобраных данных обычно требуется гораздо меньше — порядка операций.
При решении несбалансированной транспортной задачи применяют приём, позволяющий сделать ее сбалансированной. Для этого вводят фиктивные пункты назначения или отправления. Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.
Для этого вводят фиктивные пункты назначения или отправления. Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.
Обобщения
Транспортная задача в сетевой постановке
В этом варианте пункты не делятся на пунктов отправления и пункты потребления, все пункты равноправны, но производство задается положительным числом, а потребление — отрицательным. Перевозки осуществляются по заданной сети, в которой дуги могут соединять любые пункты (включая производитель -> производитель, потребитель -> потребитель). Задача решается слегка измененным методом потенциалов, практически тем же, что и классическая постановка.
Транспортная задача с ограничениями пропускной способности
Вариант транспортной задачи в сетевой постановке, в котором задается максимальная пропускная способность некоторых дуг. Задача решается слегка усложненным методом потенциалов.
Многопродуктовая Транспортная задача
Вариант транспортной задачи, в которой присутствует несколько продуктов (пункты могут производить/потреблять несколько продуктов).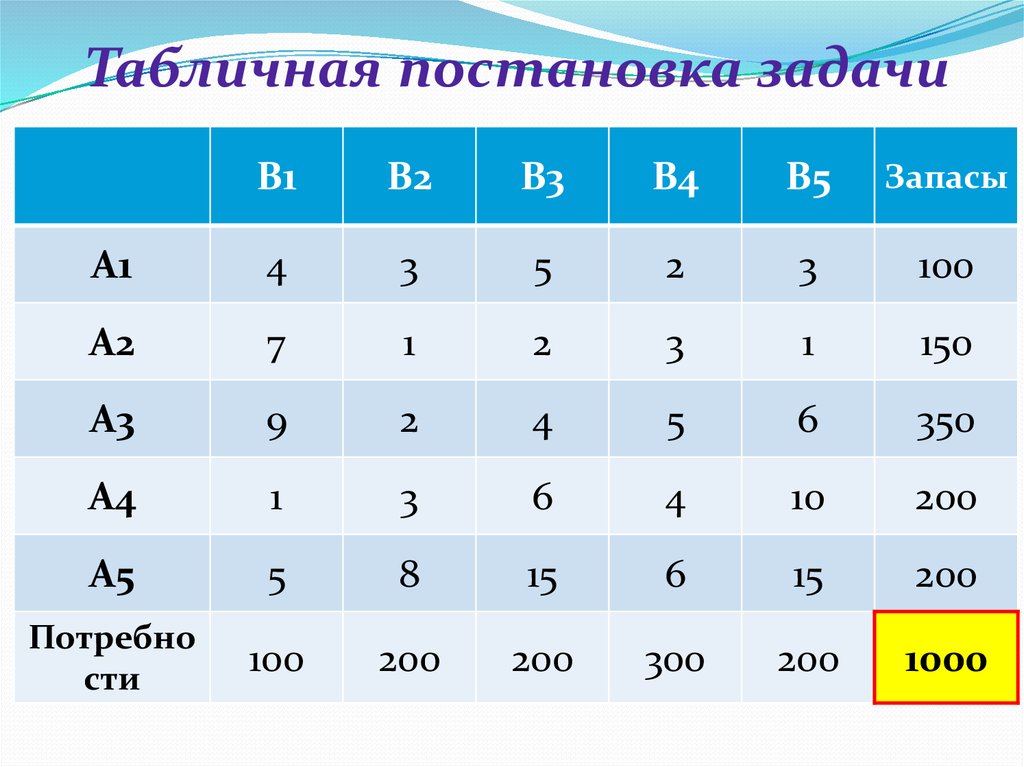 Для некоторых дуг задается ограничение на пропускную способность (без этого ограничения задача распадается на отдельные задачи по продуктам). Задача решается симплекс-методом (используется разложение Данцига-Вулфа, в качестве подзадач используются однопродуктовые транспортные задачи)
Для некоторых дуг задается ограничение на пропускную способность (без этого ограничения задача распадается на отдельные задачи по продуктам). Задача решается симплекс-методом (используется разложение Данцига-Вулфа, в качестве подзадач используются однопродуктовые транспортные задачи)
Примечания
- ↑ А. В. Кузнецов, Н. И. Холод, Л. С. Костевич. Руководство к решению задач по математическому программированию. — Минск: Высшая школа, 1978. — С. 110.
- ↑ Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5
- ↑ Monge G. Mémoire sur la théorie des déblais et de remblais. Histoire de l’Académie Royale des Sciences de Paris, avec les Mémoires de Mathématique et de Physique pour la même année, pages 666—704, 1781.
- ↑ Kantorovich L. On the translocation of masses // C.
 R. (Doklady) Acad. Sci. URSS (N. S.), 37:199-201, 1942.
R. (Doklady) Acad. Sci. URSS (N. S.), 37:199-201, 1942.
Ссылки
- Транспортная задача
- Алгоритмы нахождения максимального потока
- http://kb.mista.ru/article.php?id=859 Решение транспортной задачи в 1С:Предприятие 8.2
Определение проблемы — Департамент транспорта штата Колорадо
Перейти к содержимомуОпределение проблемы https://www.codot.gov/business/process-improvement-archive/self-service/tools/solve-guide/part4/problem-definition https://www.codot.gov/@@site-logo/siteLogo.png
Инструмент и почему он ценен
Четко определенная проблема является фокусом вашего проекта и должна быть написана ясным и лаконичным языком. Этот важный шаг помогает вам мобилизовать нужные ресурсы и работать над значимой проблемой, а не просто над раздражителем. Четко сформулированная постановка задачи — это первый шаг к успешному проекту, потому что четко сформулированная проблема — это наполовину решенная проблема!
Как применить
- Определить последствия, связанные с нерешением этой проблемы
- Подтвердите, что эта проблема уже существовала — это не единичный случай
- Напишите четкую и краткую формулировку проблемы, а не формулировку решения.

Хорошая постановка задачи:- Идентифицирует проблему
- Включает подтверждающие факты/данные
- Определяет влияние проблемы на организацию
- Знайте, где начинается и где заканчивается проблема — помните, что нельзя «кипятить океан»
- Для получения дополнительной помощи заполните контрольный список на следующей странице, чтобы убедиться, что у вас есть четко определенная проблема, связанная с моделью SOLVE.
Жемчужины и ловушки
Пример формулировки решения: Нам необходимо нанять больше FTE для работы в колл-центре из-за большого количества звонков
- Если в формулировке проблемы делается попытка решить несколько вопросов или проблем, позже это вызовет путаницу. и может быть индикатором того, что вы «кипятите океан».
- Если ваше описание проблемы содержит решение, то у вас увеличился короткий срок.
- Прыжок в проект без подтверждения проблемы может привести к пустой трате времени и ресурсов, особенно если это раздражает.

- Если вы не можете четко описать проблему, вам и другим будет сложно ее решить.
Контрольный список определения проблемы
Рассмотрите возможность использования приведенного ниже контрольного списка PROB для проверки формулировки проблемы.
Ваша постановка задачи соответствует?
P ain: Я знаю последствия нерешения проблемы (например, увеличение текучести кадров из-за сверхурочной работы, потеря финансирования).
R eal: Эта проблема не является аномалией; это было признано в прошлом рядом людей.
O bvious: Важность проблемы ясна всем, кто ее читает, даже если они не знакомы с ситуацией.
B ound: Я знаю, где проблема начинается и заканчивается.
Если вы сможете ответить на эти вопросы, то у вас есть прочная основа для перехода к Scope the Opportunity.
Примеры
- Плохо определенная проблема: выполнение контракта занимает целую вечность
- Четко определенная проблема: стандартный контракт проходит внутреннюю проверку и проверку в среднем в течение 150 дней, что приводит к жалобам почти от 25% наших поставщиков.

- Плохо определенная проблема: в этом месяце мне пришлось переписывать отчет о зачислении 5 раз. Четко определенная проблема: за последний год мы в среднем переписываем отчет о зачислении 4 раза в месяц, что требует дополнительных 15 часов (что заставляет меня искать другую работу).
Альберт Эйнштейн однажды сказал: «Если бы мне дали один час, чтобы спасти планету, я бы потратил 59 минут на определение проблемы и одну минуту на ее решение».
Четко определенная проблема часто имеет собственное решение, и это решение часто очевидно и прямолинейно. Правильно определяя проблемы, вы их создаете. Дуэйн
Оптимальная транспортная система: постановка задачи
Вы когда-нибудь ездили на поезде в День Благодарения?
Дорога домой начинается в 17:00?
Знаете ли вы кого-нибудь, кто не знает, как попасть на следующий прием к врачу или даже в продуктовый магазин?
Наверняка все мы сталкивались с этими проблемами, а если нет, то мы знаем кого-то, у кого они были. Вышеупомянутые проблемы обыденны, неудобны, а некоторые могут даже повлиять на самочувствие человека, но все они приемлемы при нынешнем состоянии общественного транспорта в нашей стране.
Вышеупомянутые проблемы обыденны, неудобны, а некоторые могут даже повлиять на самочувствие человека, но все они приемлемы при нынешнем состоянии общественного транспорта в нашей стране.
Что, если так быть не должно?
На первый взгляд, общественный транспорт ведет себя как классическая задача оптимизации. У нас есть определенный спрос (райдеры), у нас есть определенное количество ресурсов (транспортных средств), и нам нужно доставить каждого гонщика в указанное место назначения в течение определенного периода времени, предпочтительно преодолевая кратчайшее расстояние и используя наименьшее количество времени. Упрощенно, это очень похоже на классическую задачу коммивояжера.
Для тех из вас, кто не знаком с этой теорией, скажу, что это «задача теории графов, требующая наиболее эффективного (т.0052 п города. Общий метод решения неизвестен, и задача является NP-трудной» (Задача коммивояжера, 2019). С точки зрения непрофессионала, задача коммивояжёра требует решения проблемы посещения определённого количества мест только один раз, путешествуя по кратчайшему возможному расстоянию. Это стратегия выполнения поручений ленивого человека.
Это стратегия выполнения поручений ленивого человека.
Решение является NP-сложным (не может быть завершено за полиномиальное время) для этого алгоритма, но было показано, что решение разумно аппроксимируется эвристиками, такими как оптимизация муравьиной колонии, генетические алгоритмы, имитация отжига и другие решения для роевого интеллекта . Это те же самые алгоритмы, которые лежат в основе многих узнаваемых решений искусственного интеллекта, и они нацелены на то, чтобы приблизить поведение естественных систем.
Одним из примеров этого является теория, лежащая в основе алгоритмов оптимизации муравьиной колонии. Как следует из названия, алгоритмы оптимизации муравьиной колонии стремятся воспроизвести поисковое поведение муравьиной колонии. Муравьи используют петлю положительной обратной связи, чтобы сообщить остальной части колонии, какой путь ведет к лучшей пище. Разведчики бродят, оставляя за собой шлейф феромонов, которые действуют как хлебные крошки. Если муравей находит «решение» (в его случае — что-то съедобное), он повторяет свои шаги и оставляет более сильный след феромонов, чтобы другие муравьи могли прочитать его подпись и пройти его «успешный» путь к еде.
В оцифрованной версии реализован алгоритм поиска с несколькими итерациями (или муравьями). Каждый из оцифрованных муравьев записывает свой путь к успеху и силу своего решения, чтобы следующая итерация могла повторить наиболее успешные шаги и в конечном итоге приземлиться на локальном оптимуме или наилучшем возможном решении (насколько он может сказать). . По сути, у муравьев есть собственная совершенная транспортная система. Благодаря своему роевому интеллекту они могут каждый день находить почти идеальное решение своей проблемы с поиском еды, и ученые, работающие с данными, выяснили, как смоделировать такое поведение с помощью методов машинного обучения.
В этот момент вы можете подумать: «Окей, отлично, почему бы нам просто не использовать эту технику, чтобы починить наши транспортные системы, и покончить с этим?» Человеческое поведение и ожидания обычно не позволяют найти оптимальное решение. В конечном счете, поиск оптимального решения не является «справедливым» по отношению ко всем участникам системы, и она не помнит, как долго вы ждали.

 1 Итерационное улучшение плана перевозок
1 Итерационное улучшение плана перевозок Такие столбцы и строки далее не рассматриваются.
Такие столбцы и строки далее не рассматриваются.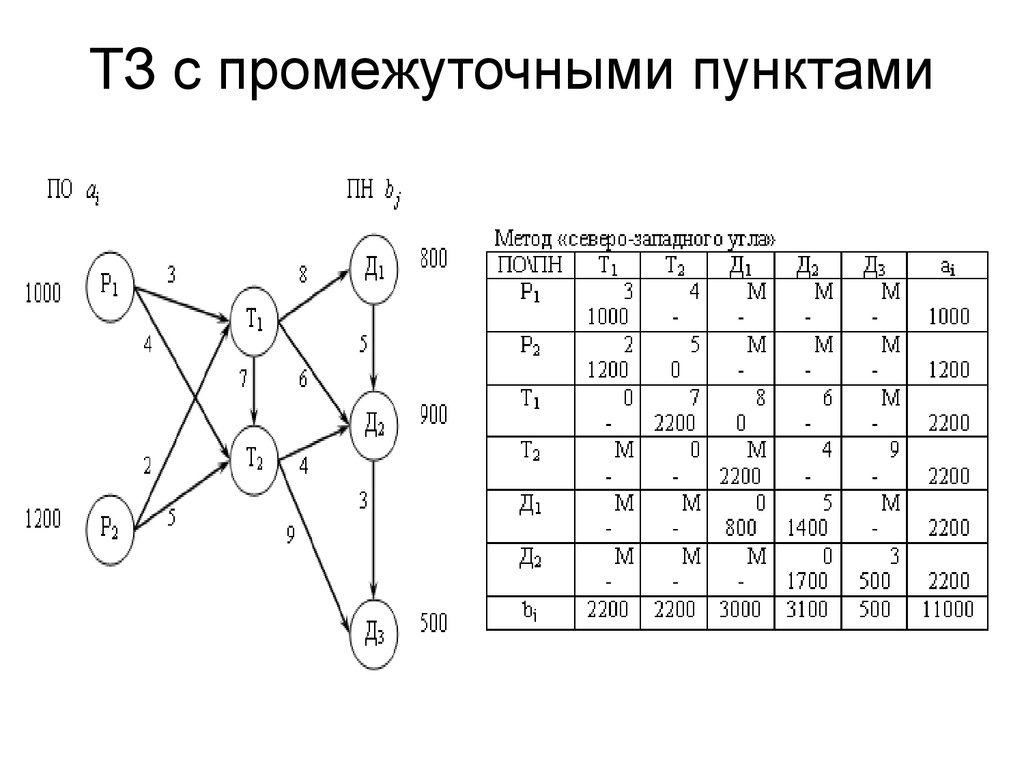 R. (Doklady) Acad. Sci. URSS (N. S.), 37:199-201, 1942.
R. (Doklady) Acad. Sci. URSS (N. S.), 37:199-201, 1942.