Как на калькуляторе посчитать экспоненту: Математика для блондинок: Экспонента на калькуляторе

alexxlab / / Разное

Содержание

Калькулятор (как пользоваться калькулятором) iPhone руководство (Айфон)


     

Использование калькулятора

Цифры и функции программы «Калькулятор» используются так же, как и в обычном калькуляторе. При нажатии кнопки добавления, вычитания, умножения или деления вокруг кнопки отображается белая окружность, напоминающая о том, какая операция будет выполнена. Поверните iPhone, чтобы перейти к расширенному научному калькулятору.

Стандартные функции памяти

• С; Нажмите для очистки отображаемого числа.

• МС: Нажмите для очистки памяти.

• /14+; Нажмите для добавления отображаемого числа к числу, хранящемуся в памяти. Если в памяти не хранится число, нажатие этой кнопки вызовет запоминание отображаемого числа в памяти.

• М-: Нажмите для вычитания отображаемого числа из числа, хранящегося в памяти.

• MR: Нажмите для замены отображаемого числа на число, хранящееся в памяти. Если вокруг этой кнопки отображается белая окружность, в памяти хранится какое-либо число.

При переключении между обычным и научным калькулятором сохраненное число остается в памяти.

Клавиши научного калькулятора

Поверните iPhone в горизонтальную ориентацию для отображения научного калькулятора.

2nd

(

Открывает выражение в скобках. Допускается вложение выражений.

) Закрывает выражение в скобках.

%

Вычисляет проценты, добавляет наценки и вычитает скидки. Для вычисления процента эту функцию следует использовать с клавишей умножения (х). Например, для вычисления 8 процентов от 500 введите 500 X 8 % =

(в результате получится 40).

Для добавления наценки или вычитания скидки эту функцию следует использовать с клавишами плюс (+) или минус (-). Например, для вычисления общей стоимости позиции стоимостью 500 долларов. США с учетом налога с продаж, равного 8 %, введите 500 + 8 % =

(в результате получится 540).

Возвращает обратное значение числа в десятичном формате.

Возводит число в квадрат.

Возводит число в куб.

Вычисляет факториал числа.

Вычисляет квадратный корень числа.

1/1спользуйте между значениями для вычисления корня степени х из у. Например,

log

Возвращает логарифм по основанию 10 введенного числа.

sin

Вычисляет синус числа.

Вычисляет арксинус числа. (Функция доступна после нажатия кнопки 2nd.)

cos

Вычисляет косинус числа.

Вычисляет арккосинус числа. (Функция доступна после нажатия кнопки 2nd. )

tan

Вычисляет тангенс числа.

Вычисляет арктангенс числа. (Функция доступна после нажатия кнопки 2nd.)

In

Вычисляет натуральный логарифм числа.

log2

Вычисляет логарифм по основанию 2. (Функция доступна после нажатия кнопки 2nd.)

sinh

Вычисляет гиперболический синус числа.

Вычисляет обратный гиперболический синус числа. (Функция доступна после нажатия кнопки 2nd.)

cosh

Вычисляет гиперболический косинус числа.

Вычисляет обратный гиперболический косинус числа. (Функция доступна после нажатия кнопки 2nd.)

tanh

Вычисляет гиперболический тангенс числа.

Вычисляет обратный гиперболический тангенс числа. (Функция доступна после нажатия кнопки 2nd. )

Нажмите после ввода значения для возведения константы е (2,718281828459045…) в степень, равную введенному значению.

Rad

1/1зменяется режим для задания тригонометрических функций в радианах.

Deg

1/1зменяется режим для задания тригонометрических функций в градусах.

EE

Оператор, который умножает текущее отображаемое число на 10 в степени следующего введенного числа.

Rand

Возвращает случайное число от 0 до 1.


Уравнение экспоненты онлайн калькулятор

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. {xln a}\]

Где можно решить уравнение с экспонентой онлайн?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Что такое Экспонента — Узнай Что Такое

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ..).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

  • через сумму ряда;
  • через формулу Муавра — Стирлинга;
  • другие.

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Джон Непер — шотландский математик (1550–1617 гг.)

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Леонард Эйлер — швейцарский математик (1707–1783 гг.)

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Узнайте также, что такое Число Пи, Натуральные числа и Логарифм.

Список функций доступных через калькулятор значений (Calculate)

Перечень основных функций с описанием и примерами

В списке содержащемся в окне инструмента Калькулятор значений (Calculate) входят не все функции, существует также некоторое количество других, в этот список не входящих.

Этот список приводит перечень функций, которые можно использовать с помощью Калькулятора значений, как содержащихся в его окне, так и дополнительных (например Replace).

Функции разбиты на следующие блоки:

  • Операции с числовыми значениями
  • Операции со строковыми значениями
  • Операции со значениями даты и времени
  • Таблица цветов
  • Константы конвертирования

У многих из приводимых функций есть ряд настраиваемых параметров.

Более подробную информацию и примеры можно получить в справочной системе Visual Basic for Applications, который присутствует в системе, если у вас установлен ArcGIS. Для получения подробной справки по каждой функции в ArcGIS yажмите Alt+F11 или выберите Tools\Macros\Visual Basic Editor. Откроется окно редактора VBA. Нажмите F1 и в появившейся справочной системе перейдите на закладку Index в поле ввода введие имя интересующей функции. Например, Abs Function.

»»Операции с числовыми значениями

Функция Действие Пример
Abs()

Возвращает абсолютное значение

 abs(-3.14) = 3.14
Atn()

Возвращает арктангенс

 4 * Atn(1) = Pi
Cos()

Возвращает косинус

 cos(0.27)
Exp()

Возвращает экспоненту

 exp(0.27)
Fix()

Возвращает целое число, округленное в меньшую сторону

 fix(-2.5) = -2
Int()

Возвращает целое число, округленное в большую сторону

 int(-2.5) = -3
Log()

Возвращает логарифм

 log(0.27)
Sin()

Возвращает синус

 sin(0. 27)
Sqr()

Возвращает квадратный корень

 sqr(0.27)
Tan()

Возвращает тангенс

 tan(0.27)

Операции с строковыми значениями

Функция Действие Пример
Asc()

Возвращает ANSI код символа

 asc(«s») = 115
Chr()

Возвращает символ соответствующий коду

 chr(115) = «s»
Format()

Возвращает значение в соответствии с инструкциями содержащимися в выражении, приведенное к некоторому формату

MyTime = #17:04:23#
Format(MyTime, «h:m:s») = «17:4:23»

IntStr()

Возвращает номер символа в строке с которого начинается исходная подстрока

 InStr(1,»test»,»e») = 2
Lcase()

Преобразует символы строки в строчные

 Lcase(«ПРивЕТ») = «привет»
Left()

Возвращает часть строки слева длинной N символов

 Left(«Привет»,3) = «При»
Len()

Возвращает длину строки

 Len(«Привет») = 6
Ltrim()

Удаляет пробелы в начале строки

 Ltrim(» Привет») = «Привет»
Mid()

Возвращает часть строки начиная с позиции «начало» и длиной N символов

 Mid(«Привет»,3,2) = «ве»
QBColor()

Возвращает представление кода RGB цвета с помощью [calculate-funclist. html#color кодовой таблицы цветов] 

 MyForm.BackColor = QBColor(ColorCode)
Right()

Возвращает часть строки справа длинной N символов

 Right(«Привет»,3) = «вет»
Rtrim()

Удаляет пробелы в конце строки

 Rtrim(«Привет «) = «Привет»
Space()

Строка из (число) пробелов

 Space(5) = »     »
StrConv()

Конвертирует строку в соответствии с [calculate-funclist.html#param задаными параметрами ]

 StrConv(«ABCDEFG», vbFromUnicode)
String()

Возвращает строку из N повторяющихся символов

 String(5,»A») = «AAAAA»
Trim()

Удаляет начальные и конечные пробелы

 Trim(» Привет «) = «Привет»
Ucase()

Преобразует символы строки в заглавные буквы

 Ucase(«ПРивЕТ «) = «ПРИВЕТ»

Заменяет подстроку в строке на другую строку

Replace(«ABC», «BC», «DC») = «ADC»

Операции со значениями даты и времени

Функция Действие Пример
Date()

Возвращает текущую дату

Date() = текущая дата

DateAdd()

Возвращает дату через определенный интервал времени относительно начального

DateAdd(«m», 5, «12. 10.1985″) = «12.03.1986»

DateDiff()

Возвращает разницу между двумя датами.

DateDiff(«d», Now, «12.10.1985») = -7358

DatePart()

Возвращает часть даты\времени

DatePart(«yyyy», «12.10.1985») = 1985

Now()

Возвращает текущую системную дату и время

Now() = текущая системная дата и время

»»Таблица цветов

Number Color Number Color
0 Black 8 Gray
1 Blue 9 Light Blue
2 Green 10 Light Green
3 Cyan 11 Light Cyan
4 Red 12 Light Red
5 Magenta 13 Light Magenta
6 Yellow 14 Light Yellow
7 White 15 Bright White

»»Константы конвертирования

Constant Value Description

vbUpperCase

1

Конвертирует символы строки в верхний регистр

vbLowerCase

2

Конвертирует символы строки в нижний регистр

vbProperCase

3

Конвертирует первый символ каждого слова строки в верхний регистр

vbWide

4

Конвертирует однобайтные символы строки в двухбайтные

vbNarrow

8

Конвертирует двухбайтные символы строки в однобайтные

vbKatakana

16

Конвертирует символы Хирагана строки в символы Катакана

vbHiragana

32

Конвертирует символы Хирагана строки в символы Катакана

vbUnicode

64

Конвертирует строку в Unicode используя кодовую страницу по умолчанию (недоступно на Macintosh)

vbFromUnicode

128

Конвертирует строку из Unicode в кодовую страницу по умолчанию (недоступно на Macintosh)

Если у вас есть замечания, предложения или иные пути решения обсуждаемых проблем — будем рады добавить недостающую информацию к этой статье.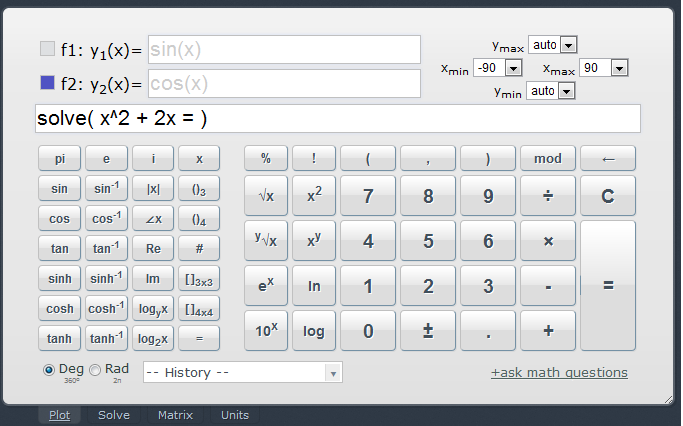

Калькулятор с квадратными скобками. Расчет значения экспоненциальной функции: онлайн калькулятор

Экспонента (число e) — иррациональное число, приблизительно равное 2,71828. Число e играет большую роль в дифференциальном и интегральном исчислениях и используется практически во всех научных сферах. Столь сухое математическое определение совершенно не раскрывает сути о физическом смысле экспоненты. Рассмотрим подробнее.

Смысл числа e

Число Пи представляет собой не просто иррациональное число, равное 3,1415, а одинаковое для всех случаев соотношение длины окружности к диаметру. Точно так же и число e имеет свой собственный смысл.

Экспонента — это базовое соотношение роста для всех растущих процессов. Любое число можно рассматривать как увеличенную единицу, любой квадрат — как масштабированный единичный квадрат, любой равносторонний треугольник — как увеличенный или уменьшенный правильный треугольник, ну а любой коэффициент роста можно представить в виде масштабированного коэффициента е. 100 000 = 2,71826

При бесконечном дроблении доллара прибыль будет увеличиваться на стотысячные знаки после запятой. Наши 2,71826 доллара прибыли будут стремиться к значению 2,718281828, что есть ничто иное как число Е.

И что все это значит?

Экспонента — это наибольший возможный результат стопроцентного непрерывного роста за конкретный период времени. Да, изначально нам обещают 100% прибыли, то есть всего $2, но каждый цент приносит свои дивиденды и по итогам у нас оказывается ровно $2,71828 прибыли. Число е – это максимум, который мы можем получить при разбиении прибыли на суммы бесконечно малых величин.

Это означает, что если при потенциальной стопроцентной прибыли мы вложим в бизнес $1, то получим $2,718 чистой прибыли. Если $2, то мы получим 2е чистой прибыли, а если $100, то наш профит составит 100е. Таким образом, e — это предельная константа, которая ограничивает процессы роста точно так же, как скорость света ограничивает передвижение информации в пространстве. −2 = 0,676

Заключение

Экспонента находит широкое применение в ситуациях, где что-либо непрерывно или дискретно растет. Вы можете использовать калькулятор возведения числа e в степень для подсчета результатов роста любых непрерывных процессов.

На калькуляторе, возьмите «инженерный» калькулятор , на котором можно вычислять значения математических функций. Ведите число , экспоненту которого необходимо посчитать. Затем просто нажмите на кнопку расчета экспоненты. На большинстве калькуляторов она выглядит как «ехр» или буква «е» с маленьким «иксом», расположенным немного выше и правее буквы «е». На индикаторе калькулятора сразу же появится результат (нажимать на кнопку «=» не нужно).

Для подсчета экспоненты на компьютере воспользуйтесь стандартным калькулятором ОС Windows. Для этого запустите программу «калькулятор» (нажмите кнопку «Пуск», затем «Выполнить», наберите в появившемся окошке «calc» и нажмите «Ок»). Если на клавиатуре виртуального калькулятора нет клавиш для вычисления математических функций, то переключите в инженерный режим (выберите пункт меню «Вид», а затем укажите на строке «Инженерный»).

Теперь наберите число, экспоненту которого нужно посчитать. Затем поставьте «галку» в окошке «Inv» и нажмите на кнопку вычисления натурального логарифма «ln». Обратите внимание, что после вычисления галочка в окошке «Inv» автоматически сбрасывается и ее необходимо выставлять снова. Не пользуйтесь для вычисления экспоненты кнопкой с надписью «ехр»! В калькуляторе Windows эта кнопка используется совершенно для других целей.

Существует три вида инженерных калькулятор ов: с обратной польской, арифметической и формульной записью. Бывают и такие калькуляторы, которые поддерживают переключения методов ввода выражений. Использование каждого из них имеет свои особенности.

Инструкция

Определите, какой метод ввода поддерживает ваш калькулятор . Если на нем отсутствует клавиша со знаком равенства, но есть клавиша со стрелкой, направленной вверх, перед вами — машинка с обратной польской записью. Наличие клавиши со знаком равенства говорит о том, что в приборе используется арифметический метод ввода. Наконец, если индикатор калькулятора, помимо сегментных знакомест, имеет еще и матричные, то аппарат рассчитан на формульную запись. В последнем случае, вместо знака равенства на соответствующей клавише может быть нанесено слово «EXE» или «Enter».

Чтобы произвести расчет на калькуляторе с обратной польской записью, необходимо вначале определить очередность выполнения действий. Делается это по общепринятым математическим правилам.Действия с двумя операндами выполняйте следующим образом. Введите первый операнд. Нажмите кнопку со стрелкой вверх, чтобы перенести его на один регистр стека вверх. Введите второй операнд, и лишь после этого нажмите на клавишу математического действия. На индикаторе отобразится результат вычисления.Для выполнения действия с одним операндом просто введите его, а затем нажмите на соответствующую этому действию кнопку.

На калькуляторе с арифметической записью действия с двумя операндами выполняйте так же, как на обычном калькуляторе. Действия же с одним операндом выполняйте так же, как на машинке с обратной польской записью.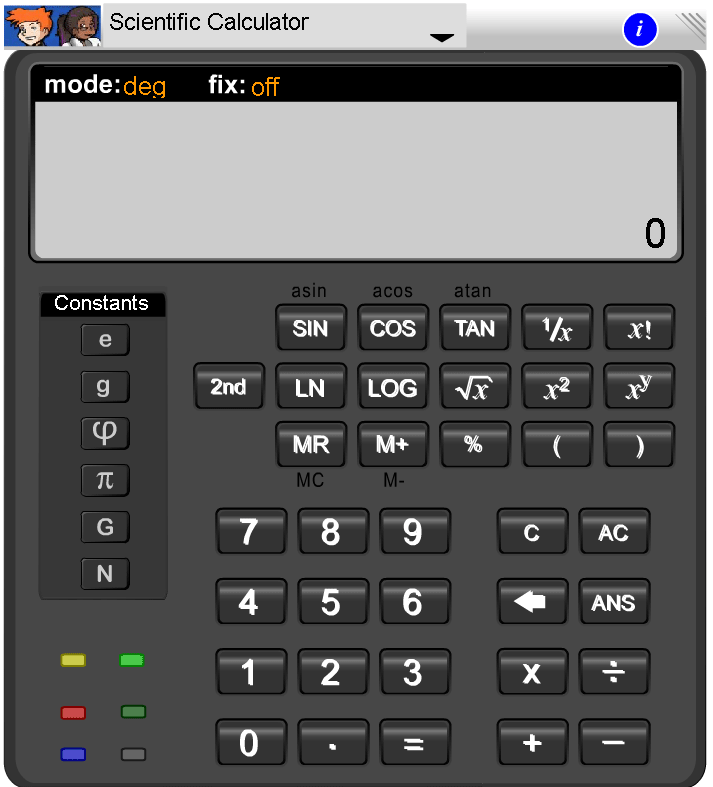 Если на клавиатуре присутствуют клавиши со скобками, необходимость в определении очередности вычислений отсутствует. Следует, однако, не допускать превышения уровня вложенности скобок, указанного в инструкции. При отсутствии инструкции определить этот уровень можно опытным путем, нажав клавишу с открывающей скобкой несколько раз и отметив, после которого по счету нажатия возникло сообщение об ошибке.

В калькулятор с формульной записью выражение вводят так же, как оно записывается на бумаге. Если поле ввода однострочное, формулы, содержащие дроби, преобразовывают в «одноэтажные» с помощью скобок и знака деления. При необходимости, введенное выражение можно откорректировать, пользуясь клавишами с горизонтальными стрелками, а также кнопками «Insert», «Backspace» и «Delete» (на разных калькуляторах их

Экспонентой в математике называется значение показательной функции. То есть, число «е», возведенное в степень «х». Значение числа «е» для приближенных расчетов можно принять равным 2,7.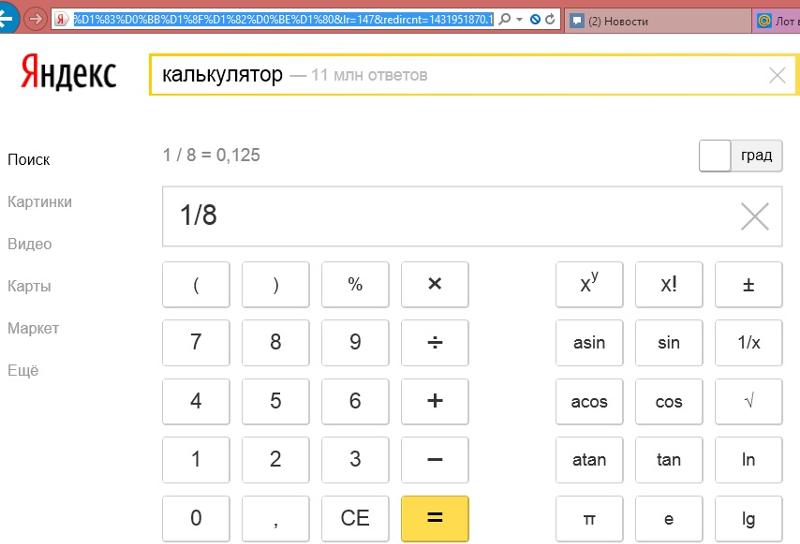 Однако, несмотря на простоту определения, без калькулятора или компьютера здесь не обойтись. Причем подсчет экспоненты на компьютере не так прост, как кажется.

Вам понадобится

калькулятор или компьютер

Спонсор размещения P&G Статьи по теме «Как посчитать экспоненту» Как находить стороны треугольника Как найти процент от числа Как найти угол между векторами

Инструкция

Чтобы посчитать экспоненту на калькуляторе, возьмите «инженерный» калькулятор, на котором можно вычислять значения математических функций. Ведите число, экспоненту которого необходимо посчитать. Затем просто нажмите на кнопку расчета экспоненты. На большинстве калькуляторов она выглядит как «ехр» или буква «е» с маленьким «иксом», расположенным немного выше и правее буквы «е». На индикаторе калькулятора сразу же появится результат (нажимать на кнопку «=» не нужно).

Для подсчета экспоненты на компьютере воспользуйтесь стандартным калькулятором ОС Windows. Для этого запустите программу «калькулятор» (нажмите кнопку «Пуск», затем «Выполнить», наберите в появившемся окошке «calc» и нажмите «Ок»). Если на клавиатуре виртуального калькулятора нет клавиш для вычисления математических функций, то переключите в инженерный режим (выберите пункт меню «Вид», а затем укажите на строке «Инженерный»).

Теперь наберите число, экспоненту которого нужно посчитать. Затем поставьте «галку» в окошке «Inv» и нажмите на кнопку вычисления натурального логарифма «ln». Обратите внимание, что после вычисления галочка в окошке «Inv» автоматически сбрасывается и ее необходимо выставлять снова. Не пользуйтесь для вычисления экспоненты кнопкой с надписью «ехр»! В калькуляторе Windows эта кнопка используется совершенно для других целей.

Как просто

Другие новости по теме:


Экспонента – это математическая функция, значение которой вычисляется по формуле «е» в степени «х». Значение числа «е» примерно равно 2,7. Если значения числа «х» — целые числа, то вычислить экспоненту можно и на листе бумаги. Но если показатель функции («х») принимает дробные или очень большие


Экономистам и техникам часто приходится высчитывать проценты от числа. Бухгалтерам нужно правильно посчитать налоги, банкирам – доходы (проценты) по вкладам, инженерам – допустимые отклонения параметров. Во всех подобных случаях необходимо считать проценты от какого-то известного значения. Вам


При решении технических задач иногда нужно посчитать куб числа. Под кубом в математике подразумевается число, возведенное в третью степень, то есть умноженное само на себя три раза. Проще всего это можно проделать при помощи инженерного калькулятора. Если же такого калькулятора нет, то можно

Как посчитать логарифм на калькуляторе

Логариифм числа b по основанию a определяется как показатель степени, в которую нужно построить основание a, дабы получить число b. Как водится, современные калькуляторы дозволяют посчитать логарифмы по основанию 10 и е, то есть десятичный (log) и настоящий (ln) логарифмы соответственно.

Вам понадобится

  • Калькулятор, базовые умения по математике.

Инструкция

1. Проверьте, может ли калькулятор считать логарифмы . Как водится это могут делать больше продвинутые версии либо инженерные калькуляторы. Дюже легко узнать может ли калькулятор считать логарифмы . Если может, то у него есть кнопки с надписью ln и log.

2. Позже того как вы удостоверитесь, что калькулятор разрешает считать логарифмы , включите его и введите число, логарифм которого хотите посчитать. Возможен, нужно обнаружить десятичный логарифм от числа 324. Наберите на калькуляторе 324.

3. После этого нажмите на кнопку “log”, если хотите обнаружить десятичный логарифм либо на кнопку “ln” – если естественный. Позже этого калькулятор произведет расчет и на экране высветится результат. В примере с числом 324, если посчитать десятичный логарифм, получится результат 2.5104, а если естественный, то 5.7807.

Степень числа разбирают в школе на уроках алгебры. 4= 4 096, то корень четвертой степени из 4 096 будет равен 8.

6. Если n = 2, тогда степень называют квадратом, если n = 3, степень называют кубом. Вычисление квадрата и куба из чисел первого десятка изготавливать довольно легко. Но с увеличением числа, возводимого в степень, и с увеличением самой степени, вычисления становятся трудоемкими. Для таких вычислении были разработаны особые таблицы. Также существуют особые инженерные и online калькуляторы, программные продукты. В качестве простейшего программного продукта для операций со степенями дозволено применять табличный редактор Excel.

Существует три вида инженерных калькуляторов: с обратной польской, арифметической и формульной записью. Бывают и такие калькуляторы, которые поддерживают переключения способов ввода выражений. Применение всякого из них имеет свои особенности.

Инструкция

1. Определите, какой способ ввода поддерживает ваш калькулятор. Если на нем отсутствует клавиша со знаком равенства, но есть клавиша со стрелкой, направленной вверх, перед вами – машинка с обратной польской записью. Присутствие клавиши со знаком равенства говорит о том, что в приборе применяется арифметический способ ввода. Наконец, если индикатор калькулятора, помимо сегментных знакомест, имеет еще и матричные, то агрегат рассчитан на формульную запись. В последнем случае, взамен знака равенства на соответствующей клавише может быть нанесено слово “EXE” либо “Enter”.

2. Дабы произвести расчет на калькуляторе с обратной польской записью, нужно сначала определить очередность выполнения действий. Делается это по общепризнанным математическим правилам.Действия с двумя операндами исполняйте дальнейшим образом. Введите 1-й операнд. Нажмите кнопку со стрелкой вверх, дабы перенести его на один регистр стека вверх. Введите 2-й операнд, и лишь позже этого нажмите на клавишу математического действия. На индикаторе отобразится итог вычисления.Для выполнения действия с одним операндом легко введите его, а после этого нажмите на соответствующую этому действию кнопку.

3. На калькуляторе с арифметической записью действия с двумя операндами исполняйте так же, как на обыкновенном калькуляторе. Действия же с одним операндом исполняйте так же, как на машинке с обратной польской записью.Если на клавиатуре присутствуют клавиши со скобками, надобность в определении очередности вычислений отсутствует. Следует, впрочем, не допускать превышения яруса вложенности скобок, указанного в инструкции. При отсутствии инструкции определить данный ярус дозволено опытным путем, нажав клавишу с открывающей скобкой несколько раз и подметив, позже которого по счету нажатия появилось сообщение об ошибке.

4. В калькулятор с формульной записью выражение вводят так же, как оно записывается на бумаге. Если поле ввода однострочное, формулы, содержащие дроби, преобразовывают в «одноэтажные» с поддержкой скобок и знака деления. При необходимости, введенное выражение дозволено скорректировать, пользуясь клавишами с горизонтальными стрелками, а также кнопками “Insert”, “Backspace” и “Delete” (на различных калькуляторах их наименования могут различаться). После этого нажимают клавишу “EXE” либо “Enter” и получают итог. Если данный итог требуется разместить в следующую формулу, пользуются клавишей “ANS”.

5. Во многих калькуляторах некоторые из клавиш способны исполнять больше одной функции. Примитивное нажатие клавиши соответствует выполнению той операции, наименование которой указано прямо на ней. Другие операции обозначены рядом с кнопкой тем либо другим цветом. Дабы принудить калькулятор исполнить такую функцию, следует вначале нажать регистровую клавишу, имеющую тот же цвет (она может именоваться “F”, “2ndF”, “S”), а после этого – кнопку, рядом с которой указана надобная вам операция.

Видео по теме

Из всеобщего ряда логарифмов два выделены особенно – это логарифм по основанию 10 (десятичный) и по основанию, равному числу “e” – константе, которую называют «числом Эйлера». Эта константа является числом иррациональным, то есть не имеет точного значения, а представляет собой безмерную дробь. Логарифм с таким основанием именуется естественным и имеет гораздо большее использование в интегральном и дифференциальном исчислении, чем десятичный логарифм.

Инструкция

1. Используйте онлайн-калькуляторы как особенно стремительный метод вычисления естественных логарифмов при наличии доступа в интернет. Таких сервисов довольно много в сети, но искать их через поисковые системы нет необходимости – некоторые из поисковиков и сами имеют вычислители с надобной функцией. Скажем, дозволено воспользоваться калькуляторами поисковых систем Google либо Nigma. Перейдя на основную страницу всякий из этих систем, введите в поле для поискового запроса запись необходимого вам математического действия. Скажем, для вычисления естественного логарифма числа 0,489 введите «ln 0.489». В качестве разделителя целой и дробной частей класснее применять точку, правда Nigma осознает верно и число с разделителем-запятой.

2. Задействуйте программный калькулятор, встроенный в операционную систему Windows, если доступ в интернет отсутствует. Открыть его дозволено через основное меню на кнопке «Пуск» (раздел «Все программы», подраздел «Типовые», сегмент «Служебные», пункт «Калькулятор») либо с подмогой диалога запуска программ, тот, что вызывается сочетанием клавиш WIN + R. В диалоге нужно ввести команду calc и щелкнуть кнопку «OK».

3. Переключите запущенный калькулятор в больше продвинутый режим. Если вы используете операционную систему Windows XP либо больше раннюю версию, то необходимый режим будет именоваться «инженерный», а в больше поздних версиях (Windows 7 и Windows Vista) – «ученый». Пункт с таким наименованием в всякий версии ОС размещен в раздел «Вид» меню калькулятора.

4. Используйте клавиатуру либо кнопки интерфейса на экране для ввода числа, естественный логарифм которого необходимо вычислить. После этого щелкните кнопку с меткой ln и программа посчитает и покажет итог вычисления.

На практике почаще каждого используются десятичные логарифмы, которые принято называть стандартными. Для их нахождения составлены особые таблицы, применяя которые дозволено обнаружить значение логарифма всякого позитивного числа с той либо другой точностью, заблаговременно приведя его к стандартному виду. Для решения большинства задач абсолютно довольны четырехзначные таблицы Брадиса с точностью до 0,0001, которые содержатся мантиссы десятичных логарифмов. Отзыв дозволено легко обнаружить по одному виду числа. Обращение с таблицами крайне примитивное.

Вам понадобится

  • – формула перехода от одного основания логарифма к иному;
  • – четырехзначные математические таблицы Брадиса.

Инструкция

1. Приведите логарифм к стандартному виду, если его основание не равно 10. Используйте формулу перехода от одного основания к иному.

2. Обнаружьте колляцию логарифма. Если число огромнее либо равно единице, то сосчитайте число цифр в целой части данного числа. Отнимите из этого числа единицу и получите значение колляции. Скажем, у логарифма числа 56,3 колляция равна 1. Если число является десятичной дробью, меньшей 1, то сосчитайте в ней число нулей до первой цифры, чудесной от нуля. Сделайте негативным подученное значение колляции. Скажем, у логарифма числа 0,0002 колляция равна -4.

3. Определите число для нахождения мантиссы как целое. Проигнорируйте в данном числе запятую, если она есть и отбросьте все нули, стоящие в конце числа. Расположение запятой в десятичном числе и последние нули никаким образом не влияют на величину мантиссы. Запишите образовавшееся целое число. Скажем, у логарифма числа 56,3 оно равно 563. В зависимости от того, сколько цифр содержится в этом числе, зависит алгорифм работы с четырехзначными таблицами. Существует три типа алгорифмов.

4. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее нахождения является трехзначным. Обнаружьте в четырехзначных математических таблицах Брадиса таблицу XIII «Мантиссы десятичных логарифмов». Перейдите на строчку, содержащую в первом столбце «N» эти две первые цифры числа, по которому ищется мантисса. Скажем, если имеем число 563, то ищите строчку, где в первом столбе стоит 56. После этого продвигайтесь по этой строчке вправо до ее пересечения со столбцом, номер которого совпадает с третьей цифрой начального числа. В нашем примере это столбец с номером 3. На пересечении обнаруженной строки и столбца находится значение мантиссы. Мантисса, обнаруженная по числу 563 равна 0,7505.

5. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее нахождения состоит из 2-х либо одной цифры. Припишите мысленно к этому числу такое число нулей, дабы оно стало трехзначным. Если число равно 56, то получается 560. Обнаружьте мантиссу по полученному трехзначному числу. Для этого исполните действия из шага 4. Мантисса по числу 560 равна 0,7482.

6. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее нахождения является четырехзначным. Обнаружьте мантиссу для числа, изображенного первыми тремя цифрами данного числа. Для этого исполните действия из шага 4. После этого передвигайтесь по горизонтальной строке от обнаруженной мантиссы в правую часть таблицы, расположенную за вертикальной толстой чертой и содержащей поправки на четвертую цифру. Обнаружьте в области поправок столбец с номером, совпадающим с четвертой цифрой числа. Прибавьте поправку, находящуюся на пересечении строки и столбца, к мантиссе, обнаруженной по трехзначному числу. Скажем, если число для нахождения мантиссы равно 5634, то мантисса по 563 равна 0,7505. Поправка по цифре 4 равна 3. Окончательный итог равен 0,7508.

7. Обнаружьте мантиссу логарифма, исполнив следующие действия, если число для ее содержит больше четырех цифр. Округлите число до четырех знаков так, дабы все цифры, начиная с пятой, были нулями. Отбросьте последние нули и обнаружьте мантиссу по четырехзначному числу. Для этого исполните действия из шага 7.

8.n)/n).Данный ряд дает значения ln(1 + x) для -1 < x ?1. Иными словами, так дозволено вычислить естественные логарифмы чисел от 0 (но не включая 0) до 2. Естественные логарифмы чисел за пределами этого ряда дозволено обнаружить путем суммирования обнаруженных, пользуясь тем, что логарифм произведения равен сумме логарифмов. В частности ln(2x) = ln(x) + ln (2).

9. Для утилитарных вычислений изредка бывает комфортно перейти от естественных логарифмов к десятичным. Всякий переход от одного основания логарифмов к иному совершается по формуле:logb(x) = loga(x)/loga(b).Таким образом, log10(x) = ln(x)/ln(10).

Знаменитый французский математик и звездочет XVIII-XIX столетий Пьер-Симон Лаплас утверждал, что изобретение логарифмов «продлило жизнь астрономам», ускорив процесс вычислений. И подлинно, взамен того, дабы умножать многозначные числа, довольно обнаружить по таблицам их логарифмы и сложить их.

Инструкция

1. Логарифм – один из элементов элементарной алгебры.log_a b = b. Простейшие правила логарифмов вещественных чисел: log_a a=1 и log_a 1=0. Основные формулы приведения: логарифм произведения – log_a (b*c) = log_a |b| + log_a |c|;логарифм частного – log_a (b/c) = log_a |b| – log_a |c|, где b и c – правильные.

4. Логарифмической функцией именуется логарифм переменного числа. Область значений такой функции – бесконечность, ограничения – основание правильное и не равно 1, причем функция повышается при основании огромнее 1 и убывает при основании от 0 до 1.

5. Логарифмическую функцию комплексного числа называют многозначной, так как для всякого комплексного числа существует логарифм. Это следует из определения комплексного числа, которое состоит из вещественной части и мнимой. И если для вещественной части логарифм определяется однозначно, то для мнимой неизменно имеется безмерное уйма решений. Для комплексных чисел применяются, в основном, естественные логарифмы, так как такие логарифмические функции связаны с числом е (экспонентой) и используются в тригонометрии.

6. Логарифмы находят использование не только в математике, но и в иных областях науки, скажем: физике, химии, астрономии, сейсмологии, истории и даже теории музыки (звуков).

7. 8-значные таблицы логарифмической функции наравне с тригонометрическими впервой опубликовал шотландский математик Джон Непер в 1614 году. В России особенно знамениты таблицы Брадиса, изданные впервой в 1921 году. В реальное же время для подсчета логарифмических и других функций применяются калькуляторы, следственно применение печатных таблиц ушло в прошлое.

Видео по теме

Полезный совет
Число е – экспонента, ее значение равно 2,7182818281828…. Существует вестимая мнемоническая фраза для запоминания: «Экспоненту помнить метод есть легкой: два и семь десятых, двукратно Лев Толстой», где «Лев Толстой» = «1828» (год рождения писателя).

Десятичным логарифмом называют функцию для вычисления неведомого показателя степени, в тот, что возводится число десять. Почаще мы имеем дело с этой функцией, как с комбинированный частью физических либо математических формул, но изредка доводится изготавливать и фактические вычисления. Если у вас есть вероятность пользоваться компьютером, то, разумеется, никаких сложностей с нахождением значения десятичного логарифма появиться не должно.

Инструкция

1. Воспользуйтесь, скажем, вычислительными вероятностями поисковой системы Google – при наличии доступа в интернет это, вероятно, самый стремительный из допустимых методов вычисления десятичных логарифмов. Процедура применения поисковика максимально примитивна – перейдите на его основную страницу, наберите lg и через пробел введите число, десятичный логарифм которого вас волнует. Google произведет расчет и отобразит на странице итог. Если взамен обозначения lg вы наберете «десятичный логарифм», то и такое указание математического действия будет верно осознано поисковой системой.

2. Используйте устанавливаемое совместно с операционной системой приложение, имитирующее калькулятор, если доступа в интернет нет. В ОС Windows ее дозволено вызвать с подмогой диалога запуска программ – нажмите сочетание клавиш win + r, наберите calc (имя файла этой программы без растяжения) и щелкните по кнопке OK. В основном меню ОС тоже есть ссылка на запуск этого приложения – ищите ее в сегменты «Типовые» подраздела «Служебные» из раздела «Все программы». Ссылка эта так и названа – «Калькулятор».

3. Нажмите сочетание клавиш alt + 2, дабы переключить приложение в «инженерный» режим. В больше ранних версиях Windows он назван «научным» – такую строку дозволено обнаружить в разделе «Вид» меню этой программы.

4. Введите число, десятичный логарифм которого вас волнует. Делать это дозволено как с клавиатуры, так и щелкая мышкой по соответствующим кнопкам в интерфейсе калькулятора на экране монитора. Обратите внимание, что тут для обозначения функции вычисления десятичного логарифма использована надпись log, а не привычное нам lg. Кликните по кнопке с символами log – калькулятор рассчитает и отобразит итог.

Видео по теме

Термин «логарифм » случился от 2-х греческих слов, одно из которых обозначает «число», а другое – «отношение». Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую нужно построить непрерывное значение (основание), дабы получить число, указанное под знаком логарифм а. Если основание равно математической константе, называемое числом “e”, то логарифм называют «естественным».

Вам понадобится

  • Доступ в интернет, Microsoft Office Excel либо калькулятор.

Инструкция

1. Воспользуйтесь во множестве представленными в интернете онлайн-калькуляторами – это, вероятно, самый стремительный и примитивный метод вычисления естественного логарифм а. Поиском соответствующего обслуживания вам заниматься не придется, потому что многие поисковые системы и сами имеют встроенные калькуляторы, абсолютно пригодные для работы с логарифм ами. Скажем, перейдите на основную страницу самого огромного сетевого поисковика – Google. Никаких кнопок для ввода значений и выбора функций тут не понадобится, примитивно наберите в поле ввода запроса необходимое математическое действие. Скажем, для вычисления логарифм а числа 457 по основанию “e” введите ln 457 – этого будет абсолютно довольно, дабы Google отобразил положительный результат с точностью до восьми знаков позже запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.

2. Используйте соответствующую встроенную функцию, если надобность вычисления значения естественного логарифм а появляется при работе с данными в знаменитом табличном редакторе Microsoft Office Excel. Эта функция тут вызывается с применением общепризнанного обозначения такого логарифм а в верхнем регистре – LN. Выделите ячейку, в которой должен быть отображен итог вычисления, и введите знак равенства – так в этом табличном редакторе обязаны начинаться записи в ячейках, содержащих формулы. После этого наберите наименование функции (LN) и в скобках укажите числовое значение, логарифм которого требуется вычислить – скажем, =LN(457). Позже того, как вы нажмете Enter, в этой ячейке таблицы отобразится итог вычисления естественного логарифм а.

3. Откройте программу-калькулятор, которая устанавливается совместно с операционной системой, если оба приведенных выше метода вам не подходят. Обнаружить соответствующую ссылку в ОС Windows 7 дозволено, если раскрыть основное меню щелчком по кнопке «Пуск», а после этого ввести «каль» в поле «Обнаружить программы и файлы». Ссылка с наименованием «Калькулятор» будет первой строкой в итоге поиска. В иных версиях ОС ее нужно искать в подразделе «Типовые» раздела «Все программы» основного меню. Переключите калькулятор в больше функциональный режим, нажав сочетание клавиш Alt + 2. После этого введите значение, настоящий логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит итог.

Видео по теме

Десятичный логарифм – это частный случай операции вычисления показателя степени, в которую нужно построить основание (в данном случае – десятку), дабы получить начальное число. Из всеобщего ряда оснований чести быть выделенными в независимую операцию сегодня считаются каждого два числа. Помимо десятки это математическая константа, называемая «числом e», которая является основанием естественного логарифм а. Вычисление логарифм ов, включая десятичные, на современном ярусе становления компьютерной техники и средств коммуникаций трудности не представляет.

Вам понадобится

  • ОС Windows, Microsoft Office Excel, доступ в интернет.

Инструкция

1. Рассчитайте десятичный логарифм во встроенном в операционную систему Windows калькуляторе. Дабы его запустить, кликните по кнопке «Пуск», наберите две буквы – «ка» – и нажмите клавишу Enter. Такой последовательностью действий вы принудите систему обнаружить приложения и файлы, начинающиеся с этих 2-х букв, и активировать первую строку списка итогов поиска – «Калькулятор».

2. Переключите приложение в «инженерный» вариант его интерфейса – нажмите комбинацию клавиш Alt + 2. Введите число, десятичный логарифм от которого требуется рассчитать, и кликните по четвертой слева кнопке в нижнем ряду интерфейса приложения – она помечена надписью log. На этом операция будет закончена, а итог отобразится в окошке калькулятора.

3. Дозволено рассчитать десятичный логарифм и с применением программы, которая почаще каждого используется для математических расчетов дома и в офисе – табличного редактора Microsoft Office Excel. Запустите приложение и перейдите на вкладку «Формулы» в меню редактора. В группе команд «Библиотека функций» раскройте выпадающий список «Математическое», щелкнув по средней пиктограмме в правой колонке кнопок этой группы. Из перечисленных функций выберите LOG10, и на экране появится форма с исключительным полем – «Число». Введите в него величину, из которой нужно извлечь десятичный логарифм , и нажмите кнопку OK. Итог отобразится в первой ячейке открытого листа электронной таблицы.

4. Дозволено обойтись вообще без вычислительных программ, а обратиться к поисковой системе Google. Данный поисковик имеет личный встроенный калькулятор, от вас понадобится лишь верно сформулировать запрос. Скажем, дабы вычислить десятичный логарифм числа 9,81 введите в поле поискового запроса log 9,81, нажмите кнопку отправки запроса и Google отобразит итог с точностью до девяти знаков позже запятой: log(9,81) = 0,991669007.

Видео по теме

Видео по теме

Обратите внимание!
Логарифм от числа, равного либо поменьше нуля, не существует и калькулятор в этом случае выдаст вам ошибку.

Полезный совет
Легко в уме дозволено посчитать логарифм единицы, он неизменно равен 0, а также логарифмы, которые являются степенью основания. Они легко будут равны этой степени.

Быстрое возведение чисел в квадрат без калькулятора

Сегодня мы научимся быстро без калькулятора возводить большие выражения в квадрат. Под большими я подразумеваю числа в пределах от десяти до ста.{2}}+n+(n+1) \\\end{align}\]

— аналогичная формула для чисел, больших на 1.

Надеюсь, данный прием сэкономит вам время на всех ответственных контрольных и экзаменах по математике. А у меня на этом все. До встречи!

Смотрите также:

  1. Что такое числовая дробь
  2. Задача B1 — время, числа и проценты
  3. Пробный ЕГЭ 2012. Вариант 7 (без производных)
  4. Специфика работы с логарифмами в задаче B15
  5. Задача C1: тригонометрия и показательная функция — 1 вариант

Как использовать экспоненты в научном калькуляторе

Научные калькуляторы обладают большей функциональностью, чем бизнес-калькуляторы, и одна вещь, которую они могут делать, что особенно полезно для ученых, — это вычислять экспоненты. На большинстве калькуляторов вы получаете доступ к этой функции, набирая основание, ключ экспоненты и, наконец, показатель степени. Хотя это соглашение, всегда полезно провести тест, потому что некоторые калькуляторы могут требовать, чтобы вы вводили числа в обратном порядке.

Scientific Vs.Бизнес-калькуляторы

Научные калькуляторы легко отличить от бизнес-калькуляторов благодаря множеству дополнительных функциональных клавиш. Если вы не уверены, есть ли у вас научный калькулятор, попробуйте этот расчет:

Введите (3 + 2 * 5 =) в указанном порядке. Научный калькулятор сначала автоматически произведет умножение и даст 13 в качестве ответа. Бизнес-калькулятор будет выполнять операции в том порядке, в котором вы их вводите и даете 25.

Вот лишь несколько функций научного калькулятора, которых вы не найдете в бизнес-калькуляторе:

  • Отрицание : Это клавиша, обозначаемая NEG или (-), превращает положительное число в отрицательное.Он отличается от клавиши вычитания.
  • Квадратный корень : Обозначается знаком квадратного корня, он автоматически отображает квадратный корень введенного вами числа.
  • Натуральный логарифм : Обозначается LN, эта клавиша отображает журнал и введенного вами числа. или заглавной E, увеличивает число y до любого показателя степени.5 =) Калькулятор должен отобразить число 100000, потому что оно равно 10 5 . Однако перед тем, как вы начнете составлять список вычислений, вам следует провести простой тест, чтобы убедиться, что ваш калькулятор не из тех, которые требуют, чтобы вы сначала вводили показатель степени.

    Введите число 2, нажмите кнопку экспоненты, затем введите 3. На дисплее должно отображаться 8. Если отображается 9, это потому, что калькулятор интерпретировал ввод как 3 2 вместо 2 3 . Это означает, что вам нужно ввести показатель степени перед основанием.ключ. Чтобы найти 10 5 , введите 10, затем клавишу y x , затем 5 и нажмите клавишу Enter или =.

    Показатели чтения

    Некоторые числа, например 265 миллиардов, содержат слишком много цифр для отображения на калькуляторе. Когда это происходит, калькулятор отображает число в экспоненциальном представлении, используя букву E для обозначения 10 в степени любого числа, следующего за ним. Например, 265 миллиардов отображается на научном калькуляторе как 2,65 E 11.

    Вы можете складывать, вычитать, умножать и делить большие числа так же, как и маленькие, и результаты будут отображаться в экспоненциальной нотации до тех пор, пока они продолжаются. чтобы отображалось слишком много цифр.

    2,65 E 8 + 5,78 E 7 = 3,23 E 8.

    2,65 E 8 / 5,78 E 7 = 4,58

    Как использовать экспоненты на калькуляторе iPhone и другие хитрости

    Если вы хотите узнать , как рассчитывать экспоненты на калькуляторе iPhone , у нас есть для вас хорошие новости.

    Интересно, что многие пользователи iPhone также сталкиваются с этими проблемами. Они не знают, как рассчитывать показатели на калькуляторе iPhone по умолчанию.

    Хорошая новость заключается в том, что калькулятор iPhone по умолчанию, безусловно, способен вычислять экспоненты.

    И в этом посте мы покажем вам, как сделайте это поэтапно. Кроме того, вы также научитесь печатать экспоненты в вашем iPhone.

    Как делать экспоненты на iPhone Калькулятор?

    Прежде всего, когда вы запускаете калькулятор iPhone на своем iPhone, вы видите обычный калькулятор. Но вы были бы удивлены, узнав, что на вашем iPhone есть научный калькулятор.

    И вам не нужно искать его, поскольку на самом деле это калькулятор по умолчанию.Чтобы найти научный калькулятор, вам сначала нужно включить функцию поворота экрана на вашем iPhone. Итак, давайте узнаем, как это сделать.

    Отключить блокировку книжной ориентации в iPhone

    Действия, которые необходимо выполнить

    • Получите доступ к «Центр управления» вашего iPhone, проведя пальцем по экрану.
    • Теперь, если значок «ориентация экрана» красный , тогда включена блокировка ориентации экрана.Это означает, что ваш iPhone не перейдет в альбомный режим автоматически, когда вы повернете телефон.
    • Таким образом, нажмите значок «Поворот экрана» в «Центре управления», и значок изменится на белый цвет . Кроме того, вы увидите уведомление над центром управления с сообщением «Блокировка портретной ориентации: выкл.»
    • Это означает, что если вы сейчас повернете телефон, экран превратится в альбомный режим

    Мы полагаем, что вы отключили портретную ориентацию блокировка ориентации на вашем iPhone.Плюс, если он уже был выключен, тогда вам хорошо идти.

    Как делать экспоненты на iPhone Калькулятор по умолчанию

    Действия, которые необходимо выполнить

    • Запустите приложение калькулятора на вашем iPhone
    • Как правило, в более новых версиях iOS вам нужно вывести центр управления, а затем нажать на значок «Калькулятор» оттуда, чтобы запустить приложение калькулятора
    • После того, как вы запустите приложение калькулятора, оно перейдет в портретный режим
    • Итак, просто поверните свой телефон в альбомный режим, и макет приложения калькулятора также изменится на альбомный режим
    • Теперь вы увидите много новых кнопок и параметров на калькуляторе.При такой ориентации он будет выглядеть как научный калькулятор.
    • Итак, если вы хотите возвести в квадрат любое число. Введите число и нажмите на калькуляторе кнопку ‘X 2 ’ . При этом калькулятор в мгновение ока покажет результат
    • аналогично, если вы хотите найти куб числа, вам нужно будет ввести это число и нажать на калькуляторе кнопку ‘X 3 ’ , чтобы найти результат
    • А что, если вы хотите найти более высокие показатели, чем квадрат или куб любого числа? Не беспокойтесь, есть способ
    • В этом случае введите базовое число, а затем нажмите на калькуляторе кнопку ‘X Y ’ .После этого нажмите на число, которое вы хотите использовать в качестве показателя степени или степени
    • Например, если вы хотите найти результат « 2 5 », , вам нужно сначала ввести «2» на калькуляторе. Затем нажмите кнопку « X Y » . После этого вам нужно нажать на кнопку «5». После этого нажмите на знак ‘=’ , чтобы увидеть результат

    Вот и все! Вот как вы делаете «возведение в степень» в калькуляторе iPhone.Однако есть и другой альтернативный метод. Вот как это выглядит…

    • Вы также можете использовать кнопку «EE» для ввода чисел в научные обозначения в калькуляторе iPhone. Он работает так же, как и символ экспоненты. Однако калькулятор не покажет это на экране как экспоненциальное представление, вместо него будет отображаться десятичная дробь
    • Для выполнения других сложных вычислений в приложении калькулятора iPhone вы можете использовать все другие научные функции, такие как ‘ 10 X , e X , 2√X , и другие
    • Вы также можете использовать Sin, Cos, Tan или логарифмические функции в калькуляторе iPhone

    Как набирать экспоненты на iPhone?

    Нет простых способов ввести экспоненты в текстовые поля iPhone.Скорее всего, можно скопировать и вставить уравнение из Интернета.

    Просто найдите символ экспоненты, который вы ищете. Просто скопируйте и вставьте его прямо в текстовое поле.

    Например, отсюда вы также можете скопировать символы экспоненты: 1234567890 . Не забудьте вставить с форматированием. После того, как вы вставили числа, вы можете удалить все ненужные числа, оставив только нужный.

    Заключительные мысли

    Если вы внимательно прочитали сообщение, теперь вы должны знать, как делать экспоненты в приложении калькулятора по умолчанию на iPhone.Теперь, в зависимости от версии iPhone или iOS, процесс или функциональность приложения-калькулятора вашего iPhone могут отличаться.

    Тем не менее, если вы используете более новую версию iOS, можно имитировать шаги, упомянутые выше.

    Опять же, если вы не можете сделать это с помощью калькулятора по умолчанию, вы можете установить любой другой сторонний научный калькулятор из App Store.

    Мы надеемся, что этот пост помог научиться делать экспоненты в калькуляторе iPhone.Если вы хотите узнать больше о менее известных хитростях и советах по поводу iPhone, вы также можете прочитать наш пост по этой теме.

    Как всегда, не забудьте поделиться этим сообщением с другими. И если вы есть какие-либо вопросы или предложения, вы можете сообщить нам об этом в разделе комментариев внизу!

    Экспоненциальная запись

    В науке мы имеем дело с числами, которые иногда очень велики или очень маленький.Когда вы занимаетесь математикой с помощью калькулятора, такие большие числа, но вы должны знать, как их использовать.

    Есть 60200000000000000000000 молекул в 18 граммах воды. Короче способ записать то же число — использовать экспоненциальную запись, чтобы показать все эти нули в виде числа в степени десяти:

    6,02 x 10 23 — более короткий способ представления всех эти молекулы. Такое число можно прочитать «Шесть целых ноль два раза. от десяти до двадцати третьего.«

    Небольшое число, например 0,0000000057, можно записать как 5,7 x 10 -9 . Такое число можно читать: «Пять целых семь десятков раз по десять с минусом. девять. «

    Как перейти с одного способа письма на другой?

    Ну, все дело в том, как перемещать десятичную точку. Написание 10 4 , например, означает, что вы пишете единицу, а затем перемещаете десятичную дробь точка четыре места. Поскольку показатель степени (4) является положительным числом, мы переместите десятичный знак вправо.На анимации ниже показано, как сделано:

    Обратите внимание, что анимация начинается с напоминания о том, что когда мы пишем « 1 », мы действительно пишем « 1. » но мы обычно не ставим десятичную точку. В конце анимации, десятичная точка находится на новом месте, но, опять же, мы не Напиши это. Обратите внимание, что всего четыре нуля. Это один из способов проверить, правильно ли вы все сделали.(10 4 , дает 4 нулей).

    А теперь попробуем наоборот. Что, если показатель степени отрицательное число? С номером 10 -4 , техника начинается так же — мы пишем цифру 1, помня, что после него стоит десятичная точка. Но тогда вместо перемещения десятичная точка вправо, перемещаем ее влево.

    Чтобы запомнить, в какую сторону двигаться (влево или вправо), запомните этот негативный экспоненты (например, -4 в примере) представляют собой очень маленькие числа — числа что меньше единицы.В результате они всегда будут начинаться с нуль. Положительные показатели (например, 4 в примере) дают числа больше одного.

    На научных калькуляторах иногда бывает сложно напечатать эти числа в.

    Но есть более быстрый способ, используя специальный кнопка, которая была разработана специально для экспоненциального обозначение.

    • Чтобы ввести 10 -4 , введите единицу * и затем нажмите x 10 x кнопка: Не можете найти эту кнопку на своем калькуляторе? Смотрите следующий коробка.
    • У вас должно получиться следующее:

    • Теперь введите четверку

    • Это число означает 1 x 10 4 , что совпадает с 10 4 .

    • Если ваш калькулятор работает так, вы можете пропустить следующий ящик.

    * Почему мы набрали 1, а не 10?

    • Давайте посмотрим, что будет, если мы попробуем десять.

    • Если вы нажмете =, вы получите

    • Это потому, что первый экран ( 10. 04 ) означает 10 x 10 4 . Этот номер такой же письмо 10 5 , что равно 100000.

    • Другое калькуляторы имеют « EXP » или кнопки « EE » на них для экспоненциального представления.Некоторые калькуляторы имеют кнопку которые можно нажимать напрямую, например, справа, у других эта функция доступна как двухклавишная операция.

    • На некоторых калькуляторах необходимо нажать команду 2nd (или кнопку Shift ) первый. Вот пример:

      + = « x 10 x »

    • На них выражение « x 10 x » является заменена буквой « E ».
    • Давайте возьмем такой пример, как 6,23 x 10 23 раз 4,11 .
    • Введите 6.23, затем кнопку EE, затем 23. После этого, введите 4,11 раза и нажмите Enter. Вот как это будет выглядеть на экран калькулятора:

    • Обратите внимание, как выражение « x 10 » заменена буквой « E ». Это сделано для экономии места на маленьком экране и во избежание путаницы с операции умножения.

    • Письмо « Е » помещен здесь, чтобы напомнить нам, что это число записано в « E xponential обозначение ».

      Для калькулятора: 6.23E23 равно 6,23 x 10 23 .

    • Ответ выше, 2.56E24 будет написано на вашей бумаге 2,56 x 10 24 .


    College Algebra
    Урок 42: Экспоненциальные функции

    Цели обучения


    После изучения этого руководства вы сможете:
    1. Используйте кнопки экспоненты и e на вашем калькулятор.
    2. Вычислить экспоненциальную функцию.
    3. График экспоненциальных функций.
    4. Расчет сложных процентов.

    Введение


    В этом уроке мы рассмотрим экспоненциальную функции. Перед тем, как начать, полезно ознакомиться с экспонентами в целом. это урок. Отличие этого руководства заключается в том, что ваша переменная x теперь является показателем степени, тогда как раньше переменная x была в вашей базе.Я не могу этого особо подчеркнуть, если ты не знакомы с основами экспонентов, которые вам нужны рассмотрение экспоненты, которые вы можете найти в Руководстве по 2: Целочисленные экспоненты. Одна вещь, которую мы рассмотрим в в этом разделе используются ваши экспоненты и клавиши e на вашем калькулятор. Поэтому убедитесь, что ваш калькулятор готов к работе. Так и будет также помочь вам с проблемами построения графиков. Скажем, мы посмотрим на эти экспоненциальные функции.

    Учебник


    Определение
    Экспоненциальная функция

    Функция f определяется

    где b > 0, b 1, а показатель степени x — любое действительное число, называется экспоненциальной функция.


    Снова обратите внимание, что переменная x в экспонента в отличие от основания, когда мы имеем дело с экспоненциальной функции.

    Также обратите внимание, что в этом определении основание b ограничено положительным числом, отличным от 1.




    Ключ экспоненты
    на калькуляторе

    Прежде чем мы перейдем к фактической экспоненте функции, я хотел чтобы убедиться, что все знают, как использовать ключ экспоненты на своем калькулятор. Поскольку существует много разных калькуляторов, я перейду более общие. На этом этапе вам нужно убедиться, что ты знать, как использовать ключ экспоненты, потому что мы будем его интенсивно использовать повсюду в этом, а также в следующем блоке.

    		 База поднята до ключ степени:
    ИЛИ

    Проверьте, есть ли у вас один из двух основных типов ключи экспоненты (у вас не будет обоих).Если у вас его нет, проверьте Другие. Если вы не видите ни того, ни другого, посмотрите справочное руководство, прилагаемое к в калькулятор, чтобы узнать, какой это ключ.




    База e

    e примерно 2.718281828 …


    Показательная функция с основанием e имеет вид называется естественной экспоненциальной функцией .

    e имеет значение (аналогично пи). e примерно 2,718281828 …

    Эта база используется в экономическом анализе и проблемах с участием естественных рост и распад.

    На этом этапе мы просто узнаем, как найти значение e возведено в степень с помощью калькулятора.



    Я хочу убедиться, что все знают, как использовать клавишу e на своем калькуляторе. Поскольку есть много разных калькуляторы Я рассмотрю наиболее распространенные.На этом этапе вам нужно убедитесь, что вы знаете, как использовать этот ключ, потому что мы быть используя его в большой степени.

    На калькуляторах есть два основных ключа e (у вас будет только один из них):

    e ключ и верхняя клавиша Caret:
    (2 клавиши)
    e и затем ^    		 e повышен до ключ степени:
    (1 ключ)

    Проверьте, есть ли у вас один из двух основных типов ключей e (у вас не будет обоих).Если у вас его нет, проверьте Другие. Если вы не видите ни того, ни другого, посмотрите справочное руководство, пришел с калькулятором, чтобы узнать, какой это ключ.

    Использование клавиши e с верхней клавишей каретки чаще всего встречается при построении графиков. калькуляторы но можно найти и на других типах калькуляторов.5. Если у вас есть 148.41316 …, вы правильно ввели. Если нет, попробуйте еще раз. Если вы все еще не можете найти его в справочном руководстве, которое прилагается к калькулятор.

    Ключ, который выглядит как это наиболее распространено в деловых и научных калькуляторах, но можно найти на другие типы калькуляторов.
    На большинстве деловых и научных калькуляторов функциональная клавиша e выглядит или очень похожа на нее. Так что проверьте этот ключ — обратите внимание, что разница между этим и приведенным выше в том, что у этого ключа есть Переменная экспонента, отображаемая на ключе — указанная выше клавиша имеет только e (нет экспонента. Если у вас есть этот ключ, давайте попрактикуемся, возьмем e и возведем его в 5-ю степень.В этой ситуации вы первый введите показатель степени, а затем активируйте свой ключ. Идите вперед и попробуйте, найдя e в 5-й степени. Введите 5 и нажмите. Вы должны были получить 148,41316 … в качестве ответа. Если нет, попробуйте очередной раз. Если вы все еще не можете найти его в справочном руководстве, которое прилагается к калькулятор.




    С помощью калькулятора,
    в целом

    Как упоминалось выше, существует множество различных типов калькуляторов там. Я хочу упомянуть несколько моментов о добавлении формулы.

    Графические калькуляторы:
    Большинство графических калькуляторов позволяют ввести всю формулу перед вы нажимаете ввод. Фактически, вы можете все это увидеть. если ты собираетесь подключить всю формулу за один раз, просто убедитесь, что вы осторожны. Обратите особое внимание на скобки В правильном месте.

    Деловые и научные калькуляторы:
    На большинстве деловых и научных калькуляторов вам нужно будет поставить формула частично по частям.Работайте наизнанку из скобка. ДО НЕ раунд, пока не дойдете до конца. По мере того, как вы идете шаг за шагом, не сотрите то, что у вас есть на экране калькулятора, но используйте это в следующем шаг, так что у вас будет полное десятичное число. Примеры набор вверх, чтобы показать вам, как собрать все вместе — шаг за шагом.

    Все калькуляторы:
    НЕ округляйте, пока не дойдете до окончательного ответа . Ты сможешь обратите внимание, что во многих примерах я ставлю точки после цифр, было бы продолжайте, если бы у меня было больше места на моем калькуляторе. Держать в помните, что в вашем калькуляторе может быть меньше или больше ячеек, чем в моем калькулятор делает — поэтому ваш калькулятор может дать немного другой ответ чем мой из-за округления. Хотя это должно быть очень близко.

    Убедитесь, что вы прошли через эти примеры с помощью калькулятора, чтобы убедиться, что вы вводите
    все нормально. Если ты возникли проблемы, проверьте справочник, прилагаемый к калькулятор или спросите об этом своего учителя математики.




    Пример 1 : приблизительное число, используя Калькулятор.Округлить до четырех знаков после запятой.


    Попробуйте это с помощью калькулятора и посмотрите, получите ли вы ответь, что я получил. Если вы этого не сделали, вернитесь к ключу e на калькуляторе , который есть у меня выше.


    Пример 2 : приблизительное число, используя Калькулятор.Округлить до четырех знаков после запятой.


    Попробуйте это с помощью калькулятора и посмотрите, получите ли вы ответь, что я получил. Если вы этого не сделали, вернитесь к ключу e на калькуляторе , который есть у меня выше.



    Построение графиков
    Экспоненциальные функции

    Шаг 1: Найдите заказанный пары.


    Я обнаружил, что лучший способ сделать это — это сделать то же самое каждый время. Другими словами, каждый раз вводите одни и те же значения для x , а затем найдите соответствующее значение y для данной функции.



    Это делается точно так же, как вы наносили точки, когда вы нарисовали линии и параболы.



    Основная кривая экспоненциальной функции выглядит например:


    ИЛИ ЖЕ




    Пример 3 : Постройте график функции.

    Обратите внимание, что основание = 4, а показатель степени — наша переменная x . Также обратите внимание, что это в основной форме, заданной определением выше, другими словами, на эту функцию не влияют никакие другие факторы.



    Я обнаружил, что лучший способ сделать это — это сделать то же самое каждый время.Другими словами, каждый раз вводите одни и те же значения для x , а затем найдите соответствующее значение y для данной функции.






    Пример 4 : Постройте график функции.

    Обратите внимание, что основание = 4, а показатель степени равен x — 1. Есть два внешних фактора, мы вычитаем 1 из нашего переменная x в экспоненте И мы добавляем 3 к нашей базе после того, как возводим ее в в показатель степени x — 1.



    Я обнаружил, что лучший способ сделать это — это сделать то же самое каждый время.Другими словами, каждый раз вводите одни и те же значения для x , а затем найдите соответствующее значение y для данной функции.






    Пример 5 : Постройте график функции.

    Обратите внимание, что основание = 1/4, а показатель степени — это наша переменная х . На этот раз есть два внешних фактора, мы умножаем наши базовый формируем на 4, а затем вычитаем 3.

    Будьте осторожны, используйте порядок операций при работа над проблемой как это. Нам нужно сначала разобраться с экспонентой, прежде чем мы умножать на 4.Очень заманчиво скрестить четверку снаружи с в 4 в знаменателе нашей базы. Но 4 в знаменателе — это заключен в () с присоединенной к нему экспонентой, поэтому мы должны иметь дело с участием это сначала, прежде чем задействовать 4 внешних.

    Давайте найдем пары заказов. Опять же, мы будем использовать то же самое входные значения для x мы использовали в примерах 3 и 4 и найти соответствующие выходные значения для этой экспоненциальной функции.



    Я обнаружил, что лучший способ сделать это — это сделать то же самое каждый время. Другими словами, каждый раз вводите одни и те же значения для x , а затем найдите соответствующее значение y для данной функции.





    Сложная сумма и проценты

    Сложный процент означает, что в конце каждого процентный период проценты, полученные за этот период, добавляются к предыдущему принципу ( инвестированная сумма), так что она тоже будет приносить проценты сверх следующих процентов период.Другими словами, это накопительные проценты.



    Сложные проценты
    Формула

    где,
    S = соединение или накопленная сумма
    P = Основная сумма (начиная значение)
    r = номинальная ставка (годовая % ставки)
    n = количество соединения периодов в год
    t = количество лет



    Обратите внимание, что эта формула может Выглядит иначе чем та, что из твоего учебника по математике.Иногда используется A для сложные или накопленные проценты вместо S .

    Также иногда r представляет собой периодическую скорость, где в по приведенной выше формуле это номинальная ставка. В этом типе формула вы не увидите, что r делится на n , но вам все равно нужно это сделать, если ваш r представляет собой периодическую ставку.Это просто не показано как часть формула.

    Только учтите, что как бы ни формула выглядит концепция та же.



    Пример 6 : Найдите а) количество соединения И б) сложный проценты за данную инвестицию и ставку.

    15000 долларов США на 14 лет из расчета 5% годовых ежемесячно.


    Обратите внимание, что шаги, показанные на примеры 6, 7, и 8 идут о том, как сделать это по частям в бизнесе или научный калькулятор. Если у вас есть графический калькулятор, вы можете выбрать делать это так (по частям) или вы можете вставить всю формулу и тогда нажмите Enter, чтобы получить окончательный ответ.

    Также обратите внимание, что разные калькуляторы круглые к разным разрядным значениям. Итак, когда вы кладете это в ваш калькулятор имейте в виду, что ваш может округлять до другого место, чем у меня, поэтому последняя цифра может немного отличаться от справа от десятичной дроби. Кроме того, не округляйте ничего, пока вы получите окончательный ответ.Например, если вы округлите до 2 десятичный места на первом этапе, тогда ваш окончательный ответ может быть неверным. Ты хотите максимально приблизиться к цифрам, поэтому выбирайте все ваш калькулятор даст вам, а затем округлится, когда вы напишете окончательный ответ.


    P = 15000
    r = 5% =.05
    t = 14
    n = ежемесячно = 12 раз в год



    * Подключаемые значения указаны выше в составную форму.

    * Найдите число внутри ( ) первая

    * Поднимите () до 168-я степень
    * Умножить


    Итак, сложная СУММА будет 30162 доллара.39

    Сумма соединения — это общая сумма, которая находится в учетная запись. Как как вы думаете, мы получим интерес ?? Что ж, у нас есть принцип что является начальным количеством, и у нас есть сложное количество, которое конечный результат. Похоже, если мы возьмем разницу между ними, то покажет нам, сколько процентов было заработано от начала до конца.Какие делать Вы думаете?

    Общая сумма — принцип: 30162,39 — 15000 = 15162,39

    Итак, наш сложный процент в размере составляет 15162,39 доллара.

    Ух ты, наши деньги удвоились, а потом еще немного — конечно составили 168 раз.




    Пример 7 : Найдите а) количество соединения И б) сложный проценты за данную инвестицию и ставку.

    20500 долл. США на 15 лет из расчета 7,5% годовых раз в полгода.


    P = 20500
    r = 7,5% = 0,075
    t = 15
    n = раз в полгода = 2 раза в год год.



    * Подключаемые значения указаны выше в составную форму.

    * Найдите число внутри ( ) первая

    * Поднимите () до 30-я степень
    * Умножить


    Таким образом, сложная СУММА составит 61858,16 долларов США

    Сумма соединения — это общая сумма, которая находится в учетная запись.Как как вы думаете, мы получим интерес ?? Что ж, у нас есть принцип что является начальным количеством, и у нас есть сложное количество, которое конечный результат. Похоже, если мы возьмем разницу между ними, то покажет нам, сколько процентов было заработано от начала до конца. Какие делать Вы думаете?

    Общая сумма — основная сумма: 61858.16 — 20500 = 41358.16

    Итак, наш сложный процент в размере составляет 41358,16 доллара.




    Соединение непрерывно
    Формула

    где,
    S = соединение или накопленная сумма
    P = Основная сумма (начиная значение)
    r = номинальная ставка (годовая % ставка)
    t = количество лет


    Непрерывное смешивание означает, что оно каждое мгновение времени.

    Обратите внимание, что эта формула может выглядеть в отличии от этого тот, что из твоего учебника по математике. Иногда A используется для сложный или накопленные проценты вместо S .

    Только учтите, что как бы ни формула выглядит концепция та же.




    Пример 8 : Найдите накопленную стоимость инвестиции из 5000 долларов, которые начисляются непрерывно в течение четырех лет под проценты показатель из 4.5%.

    P = 5000
    r = 4,5% = 0,045
    t = 4



    * Вставьте значения, указанные выше, в сложный форма.

    * Поднимите e до 18-я степень

    * Умножить


    Таким образом, накопленная или составная СУММА будет 5986 долларов.09



    Практические задачи


    Это практические задачи, которые помогут вам перейти на следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Math работает как и все в противном случае, если вы хотите добиться успеха в этом, вам нужно практиковать это. Даже лучшие спортсмены и музыканты получали помощь и много практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики.

    Чтобы получить от них максимальную отдачу, вы должны решить проблему на свой, а затем проверьте свой ответ, щелкнув ссылку для ответа / обсуждения для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые позволили найти этот ответ.

    Практические задачи 1a — 1b: Приблизительное число с помощью калькулятора. Округлить до четырех знаков после запятой.

    Практические задачи 2a — 2b: Постройте график заданной функции.

    Практические задачи 3a — 3b: Найдите а) количество соединения И б) соединение проценты за данную инвестицию и ставку.


    Практическая задача 4a: Найдите накопленное значение для данные инвестиции и оцените.



    Нужна дополнительная помощь по этим темам?



    Последний раз редактировал Ким Сьюард 21 марта 2011 г.
    Авторские права на все содержимое (C) 2002 — 2011, WTAMU и Kim Seward. Все права защищены.

    Калькулятор экспоненты — возвести значение в степень

    Введите основание и показатель степени, чтобы вычислить результат ниже.

    x =?

    Как вычислить экспоненту

    Показатель степени — это количество раз, когда базовое значение должно быть умножено само на себя. Чтобы вычислить число, возведенное в степень, умножьте это число на себя для каждого значения экспоненты.

    Таким образом, 5 2 — это то же самое, что 5 × 5, а 5 3 — то же самое, что 5 × 5 × 5.

    Вычисление показателя также иногда называют возведением числа в n-ю степень.

    Например, вычисляет результат 8 4 .

    8 4 = 8 × 8 × 8 × 8
    8 4 = 4096

    Таким образом, 8 4 , или 8 в 4-й степени, равно 8 умноженным на 8 умноженным на 8 умноженным на 8, что равно 4096.

    Как вычислить отрицательную экспоненту

    Что делать, если показатель степени отрицательный? Для отрицательной экспоненты, вместо того, чтобы умножать число на само число раз для экспоненты, вы делите число само на себя, начиная с 1.

    Итак, 5 -2 то же самое, что 1 ÷ 5 ÷ 5, а 5 -3 то же самое, что 1 ÷ 5 ÷ 5 ÷ 5.

    Отрицательные показатели часто выражаются как 1 по основанию с положительным показателем.

    5 -2 = 15 2

    Например, вычисляет результат 8 4 .

    8 -4 = 18 4
    8 -4 = 18 × 8 × 8 × 8
    8 -4 = 14096
    8 -4 = 0,000244140625

    Таким образом, 8 -4 равно 0,000244140625.

    Правила специальных экспонент

    Есть некоторые особые правила с показателями, которые важно помнить.

    Когда показатель степени равен 1, результат возведения основания в степень всегда будет равен основанию.

    а 1 = а

    Когда показатель степени равен 0, результат возведения основания в степень всегда будет равен 1.

    а 0 = 1

    Когда показатель степени равен 2, вы также можете сказать, что базовое значение возведено в квадрат. Когда показатель степени равен 3, можно сказать, что базовое значение находится в кубе.

    Калькулятор выше обработает эти частные случаи вместе с отрицательными показателями, чтобы найти ответ.

    Как сделать полномочия в калькуляторе ▷ ➡️ Creative Stop ▷ ➡️

    Как сделать полномочия на калькуляторе . Вам нужно запитать достаточно большие числа и вы хотите упростить свою работу с помощью калькулятора , но все еще не можете найти способ.) , (x y ) o (x для ) .

    Чтобы использовать их, все, что вам нужно сделать, это написать la base (Ex. 2 ), нажать клавишу, в которой находится символ повышения в степени, присутствующий в вашем калькуляторе (например, (x ) y ) ), а затем запишите степень (например, 5 ), за которой следует символ (=) .

    Поскольку каждый калькулятор может немного отличаться по конструкции от других, я предлагаю вам обратиться к руководству по эксплуатации в вашем приобретенном пакете, если вы не можете использовать функцию питания, которую я упомянул в строках выше.

    Если, с другой стороны, ваш калькулятор не содержит кнопки, предназначенной для функции возведения в степень, вам придется выполнить расчет «вручную», умножив базу мощности на количество раз, которое вы хотите увеличить.

    Например, если вы хотите поднять 2 5 , вам нужно умножить 2 x 2 x 2 x 2 x 2 , а затем нажать кнопку (=) , чтобы увидеть результат операции или еще лучше , вы можете использовать калькулятор на мобильных телефонах, планшетах и ​​ПК и использовать его, следуя инструкциям в следующих параграфах.) o (x y ) присутствует в раскрывающемся меню, которое открывается, снова нажмите символ стрелка , чтобы закрыть открытое меню, введите экспонент (пример 5 ) и нажмите кнопку (=) , чтобы увидеть результат операции.

    На многих устройствах Android калькулятор также поддерживает научное представление.

    Поднимите число на калькуляторе iOS

    Хотите увеличить число во встроенном калькуляторе в iOS ?

    Если у вас iPhone , запустите приложение Calculator и переведите мобильный телефон в альбомный режим.Если вы активировали блокировку поворота, войдите в центр управления iOS, проведя пальцем снизу вверх (или из верхнего правого угла, если у вас iPhone X), и нажмите кнопку, которая представляет собой закрытый замок , который на эта точка откроется.

    Как вы можете видеть, поворот iPhone по горизонтали вызовет научный калькулятор: чтобы возвести число в степень, введите базис (например, 2 ), нажмите кнопку x y введите показатель степени (Исх. 5 ) и нажмите оранжевую кнопку, которая представляет собой символ (=) .

    Если у вас есть iPad К сожалению, вы не можете использовать калькулятор iOS, как я показал вам на iPhone, поскольку Apple (по какой-то неизвестной нам причине) решила не делать его доступным на своем планшете, по крайней мере, в виде настоящее приложение.) введите показатель степени (Пример. 5 ) и, как по «волшебству», результат операции отобразится в поле НАИЛУЧШИЙ РЕЗУЛЬТАТ . Конечно, это можно сделать и с iPhone.

    Если встроенный калькулятор Spotlight вам не подходит, вы можете воспользоваться одним из многих калькуляторов iPad, доступных в App Store (например, Калькулятор или калькулятор Pro + для iPad), которые работают почти так же, как приложение Apple Calculator и также предлагают некоторые дополнительные функции, касающиеся настройки вашего дизайна.

    Поднимите число в калькуляторе Windows

    Если вы хотите узнать, как загрузить число в калькулятор Windows, , все, что вам нужно сделать, это запустить приложение Calculator , установить научное представление и использовать кнопку для увеличения числа.

    Чтобы продолжить, введите « калькулятор » в строке поиска Windows и щелкните первый соответствующий результат. Если вы используете калькулятор в Windows 10 , нажмите кнопку (≡) , расположенную в верхнем левом углу, и выберите опцию Scientific .

    Если вы используете калькулятор Windows 7 (или более ранние версии операционной системы Microsoft), щелкните меню вместо view и установите флажок рядом со статьей Scientific , чтобы отобразить команды научного калькулятора.

    На этом этапе, независимо от того, используете ли вы Windows 10 или Windows 7, введите число , которое вы хотите возвести в степень (например, 2 ), нажмите кнопку x y В калькуляторе введите показатель степени (например, 5 ) и, наконец, нажмите кнопку (=) , чтобы увидеть результат расчета.

    В качестве альтернативы вы можете возвести число в степень следующим образом: напишите основание на клавиатуре, нажмите клавиши Shift + (^) запишите показатель степени (Пример. 5 ) и нажмите на клавиатуре кнопку (=) или Enter.

    Поднимите число на калькуляторе macOS

    Используйте Mac , и вы хотели бы знать, как увеличить число в «стандартном» калькуляторе, встроенном в MacOS ? Все, что вам нужно сделать, это открыть калькулятор, включить научное представление и использовать кнопку, чтобы возвести число в степень.

    Итак, запустите приложение Calculator (вы можете найти его в Launchpad , что искать в focus ) и выберите пункт Scientific в меню view .), и более экспонента . Простая правда?

    Калькулятор экспоненты

    — Calculator Academy

    Калькулятор ниже может найти либо окончательное значение переменной x, возведенное в степень n, либо вычислить показатель степени n, учитывая переменную X и конечное значение y.

    Формула экспонентов

    Для вычисления показателя степени используется следующая формула.

    X n = Y

    • Где X и Y — переменные
    • n — показатель степени

    Определение экспоненты

    Показатель степени — это термин, используемый в алгебре для описания числа факторизации в алгебраическом уравнении, показанном выше.Факторинг — это процесс умножения числа на само себя несколько раз. Например, 2, увеличенное до коэффициента 2 (2 2 ), равно 2 * 2 = 4. Другой пример — 3, увеличенное до коэффициента 4, что равно 3 4 = 3 * 3 * 3. * 3 = 81. В этих задачах коэффициент, до которого возводится исходное число, часто называют показателем n.

    Как рассчитать показатель степени?

    Следующий пример аналогичен описанному в разделе выше. Этот пример будет следовать расчету с учетом переменной x и показателя n.

    1. Первый шаг — определить значения как X, так и n. В этом случае мы будем считать x = 5 и n = 3.
    2. Следующим шагом является создание факторного уравнения для решения относительно Y. Это уравнение должно выглядеть следующим образом: 5 3 = Y.
    3. Последний шаг — умножить 5 на себя 3 раза, поэтому 5 * 5 * 5 = 125.

    Этот следующий пример покажет вам, как вычислить экспоненту с учетом исходной переменной X и окончательного значения Y.

    1. В этом примере предположим, что X = 8 и Y = 64.
    2. Первый шаг — понять, что логарифм — это величина, обратная экспоненте. Следовательно, показатель степени можно вычислить, используя логарифм Y с основанием X.
    3. Наконец решите уравнение n = log8 (64) = 2.

    FAQ

    Что такое показатель степени?

    Показатель степени — это термин, используемый в алгебре для описания числа факторизации в алгебраическом уравнении, показанном выше.

    .

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *