Как найти асимптоты графика функции: Как найти асимптоты графика функции, примеры решений

2

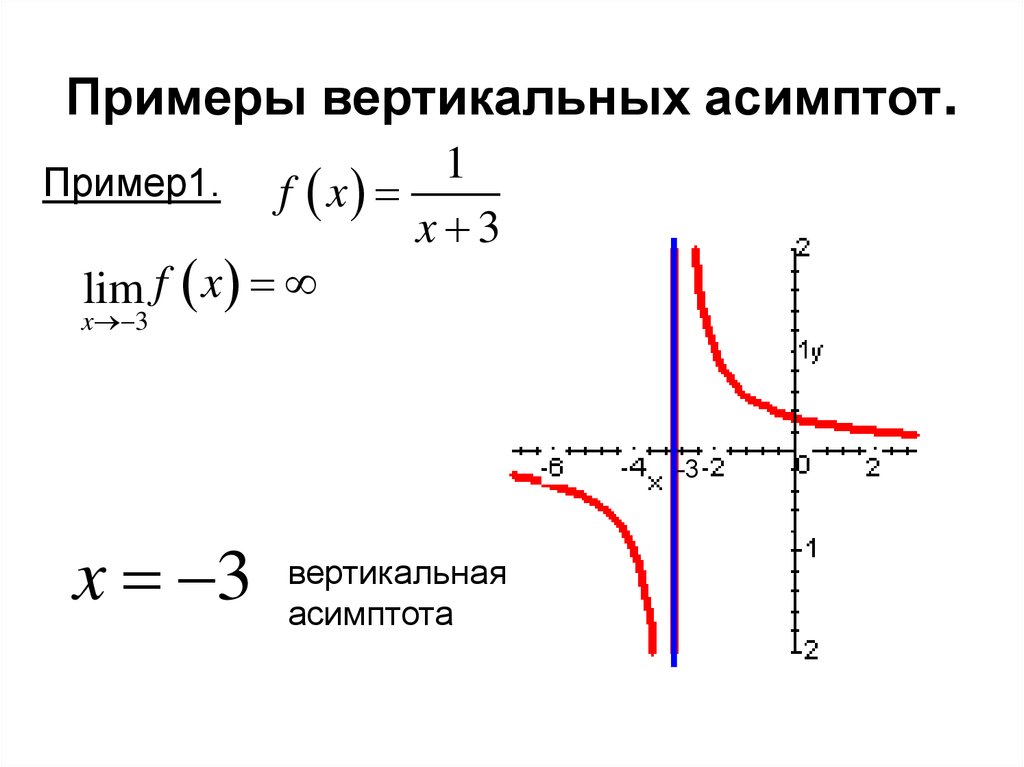
4.3.6. Асимптоты графика функции

а)Прямая х = а является вертикальной асимптотой графика функции у(х), если хотя бы один из односторонних пределов: обращается в бесконечность. Поэтому для отыскания вертикальных асимптот графика функции надо найти точки бесконечного разрыва данной функции, которые относятся к точкам разрыва 2-го рода.

Пример 34.Найти вертикальные асимптоты графика функции

Решение: Как отмечалось, данная функция не определена в точке . При этом

Поэтому прямая х = 1 является вертикальной асимптотой графика заданной функции.

б) График функции у(х) имеет наклонную асимптоту у = kx + b при , если существуют конечные пределы: Если хотя бы один из этих пределов не существует или бесконечен, то график функции не имеет наклонной асимптоты при .

(Если асимптота задана уравне­нием у = b, то ее называют горизонтальной).

Пример 35. Найти наклонные асимптоты графика функции

Решение: Найдем значения к и b для данной функции при

Аналогично находим, что при по-прежнему . Таким образом, график функции имеет одну и ту же наклонную асимптоту при ; это прямая у = х.

Чтобы составить достаточно полное представление о характере поведения функции и построить ее график, удобно проводить ее исследование по следующему плану:

1. Установить множество определения функции; при наличии точек разрыва найти в них односторонние пределы данной функции;

2.а) Найти точки пересечения графика функции с осями координат,

б) Отметить особенности графика заданной функции, не связанные с производными, например, симметрию, периодичность.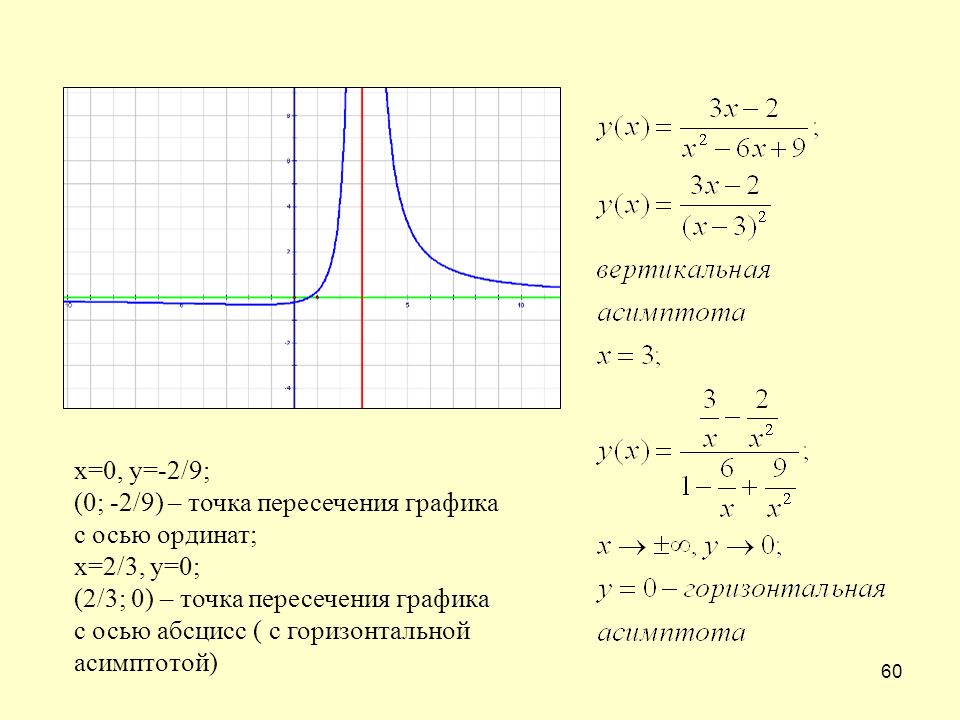

3. Установить промежутки возрастания и убывания функции, найти ее экстремумы.

4. Установить промежутки выпуклости и вогнутости график функции, найти точки перегиба.

5 Найти асимптоты графика функции.

Пример 36. Исследовать функцию

и сделать схематический чертеж ее графика.

Решение: Как отмечалось в примере 32, множество определения данной функции — вся числовая ось Ох, исключая точку График функции пересекается с осями координат в единственной точке 0(0,0). Функция не является ни четной, ни нечетной, поскольку и , поэтому график функции не обладает свойствами симметрии. Дальнейшее исследование этой функции фактически уже проведено в примерах 32 -35. По данным, полученным в этих примерах, сделан схематический чертеж графика заданной функции, который представлен на рис.13.

Пример 37. Исследовать функцию и сделать схематический чертеж ее графика.

Решение: 1. Множество определения данной функции — вся числовая ось Ох, кроме точки . Найдем односторонние пределы функции при . Предел слева так как и . При вычислении предела справа возникает неопределенность вида ; приводим ее к неопределенности вида

, к которой применяем правило Лопиталя:

2. а) Точки пересечения графика функции с осью Ох определяются из условия у = 0. В данном случае уравнение не имеет решений, так как х = 0 не входит в множество определения функции. Точки пересечения графика функции с осью Оу можно найти, положив х = 0. Для заданной функции это значение не входит в множество ее определения. Следовательно, график исследуемой функции не имеет точек пересечения с осями координат.

б) Поскольку , то функция не является ни четной, ни нечетной.

3. Находим

Производная у’ существует и конечна на всем множестве определения заданной функции . Поскольку точка разрыва первой производной х = 0 не принадлежит множеству определения функции, то все критические точки функции находим из условия: , или . Отсюда получаем .

Функция возрастает, если , то есть при и .

Функция убывает, если , в данном случае при Таким образом, при переходе через точку первая производная меняет знак с (-) на (+), то есть — точка минимума;

4. Находим

Вторая производная существует и конечна во всех точках множества определения данной функции. Тогда все точки перегиба находим из условия: у» =

0, то есть . Поскольку это уравнение не имеет решения, то точек перегиба нет. График функции — выпуклый, если у» < 0; в данном случае при х < 0. График функции вогнутый при x>0; > 0, где у» > 0.

3. Как было установлено в пункте 1, в точке х = 0 функция имеет бесконечный разрыв, поэтому прямая х = 0 является вертикальной асимптотой ее графика. Для определения наклонных асимптот найдем:

Значит, прямая у = x+1 является наклонной асимптотой графика функции при . Схематический чертеж графика функции приведен на рис.14.

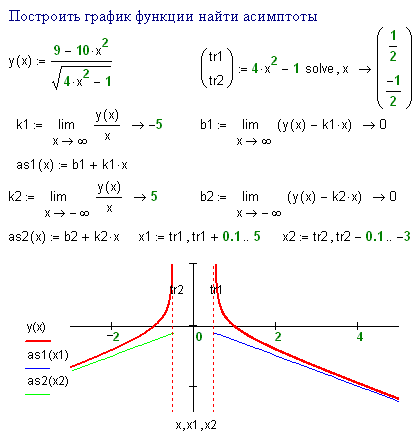
Пример 38. Исследовать функцию и сделать схематический чертеж графика.

Решение:

1). Данная функция определена на всей числовой

оси

2). Точки пересечения графика функции с осью Ох определяются из условия , откуда , а с осью — из условия , при этом . Данная функция — четная, поскольку , значит, ее график симметричен относительно оси .

3). . Первая производная обращается в бесконечность в точках х = 1, х = —1, в то время, как сама функция в этих точках определена. Значит, эти точки — критические для данной функции. Еще одна критическая точка определяется из условия у’ = 0; это х = 0. Функция убывает, если у’ < 0, то есть при и . Функция возрастает при у’ > 0, то есть при -1 < х < 0 и при х > 1. Таким образом, х = 0 -точка максимума, и — точки минимума данной функции; ; В точках х = -1 и

х = 1 данная функция имеет так называемый «острый» экстремум: касательная к графику функции в каждой из этих точек параллельна оси Оу.

4). . Вторая производная обращается в бесконечность при х = ±1, но эти точки не принадлежат множеству определения у’(х) и, следовательно, не являются критическими точками для первой производной. Значит, критические точки для нее определяем из условия у» = 0, откуда при то график у(х) в этих интервалах вогнутый, а в интервалах — график выпуклый, так как там у» < 0.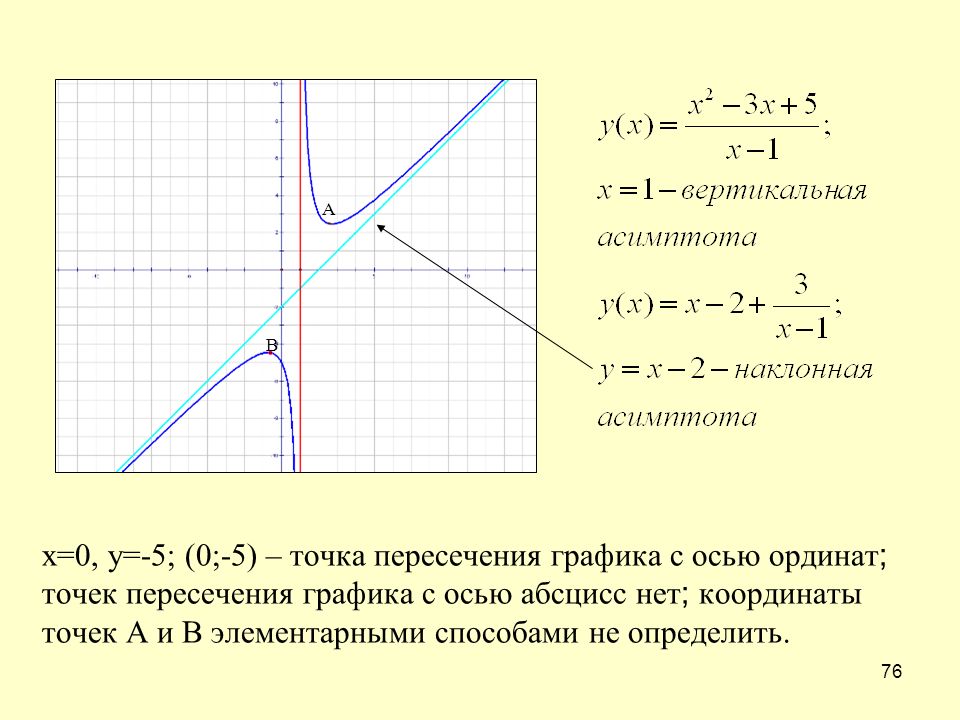

5). Поскольку функция определена на всей числовой оси Ox, то вертикальных асимптот у ее графика нет. Проверим наличие наклонных асимптот:

Таким образом, наклонные асимптоты также отсутствуют. На рис.15 схематически изображен график функции .

Error

Sorry, the requested file could not be found

More information about this error

Jump to… Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson.

Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.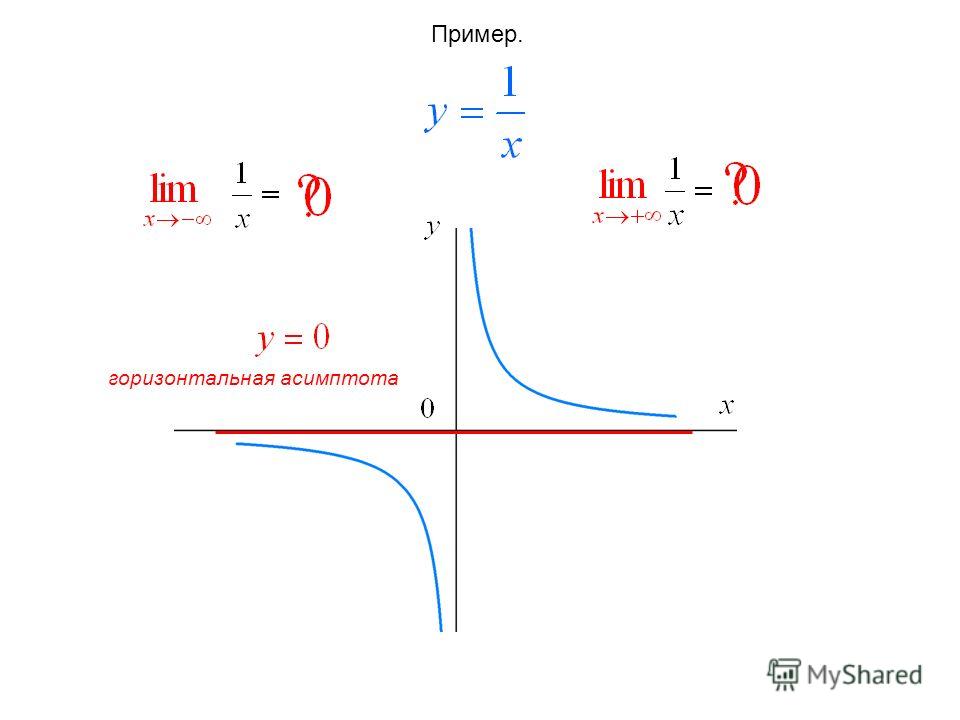 1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1. 2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2. 2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3. 5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)

Как найти вертикальные асимптоты

В математике асимптотой функции называется линия, к которой функция бесконечно приближается, но никогда не достигает. В более точных математических терминах асимптота кривой может быть определена как линия, расстояние между которой и кривой приближается к 0, поскольку одна или обе координаты x и y кривой стремятся к бесконечности. Другими словами, асимптота — это линия на графике, к которой функция будет приближаться все ближе и ближе, но никогда не достигнет ее.

Существует три основных вида асимптот; вертикальные, горизонтальные и наклонные; каждый определяется на основе их ориентации относительно плоскости координат. Вертикальные асимптоты являются наиболее распространенными и простыми для определения асимптотами. Вертикальная асимптота эквивалентна линии с неопределенным наклоном. Короче говоря, вертикальная асимптота рациональной функции расположена при значении x, которое устанавливает знаменатель этой рациональной функции в 0. Рациональная функция — это функция, которая выражается как частное двух полиномиальных уравнений. Например, график рациональной функции ƒ( x ) = 1/ x ² выглядит так:

Все графики, сгенерированные с помощью graphfree.com/>

Установка x равным 0 устанавливает знаменатель в рациональной функции ƒ( x ) = 1/ x ² до 0. Следовательно, эта функция имеет вертикальную асимптоту, расположенную на линии x=0. Вертикальные асимптоты уникальны тем, что один график может иметь несколько вертикальных асимптот. И наоборот, график может иметь только одну горизонтальную или одну наклонную асимптоту.

Концепция асимптоты

Поначалу кажется, что концепция асимптоты противоречит нашему повседневному опыту. Физические представления кривой на графике, такие как линии на листе бумаги или пиксели на экране компьютера, имеют конечную ширину. Продлив эти линии достаточно далеко, кривая, казалось бы, в конце концов встретится с асимптотической линией, или, по крайней мере, насколько может судить наше зрение. Следует помнить, что граф — это физическое представление идеализированных математических объектов. Идеализированная геометрическая линия имеет нулевую ширину, поэтому математическая линия может постоянно приближаться к чему-либо, но никогда не совпадать с ним.

В некотором смысле понятие «значение, к которому некоторое количество приближается, но никогда не достигает» можно рассматривать как восходящее к древнегреческим парадоксам, касающимся изменения, движения и непрерывности. Вот известный пример, приведенный Зеноном Элейским: великий атлет Ахиллес бежит стометровку. Чтобы пробежать 100 метров, он должен сначала преодолеть половину дистанции, поэтому он бежит 50 метров. Чтобы пробежать оставшиеся 50 метров, он должен сначала преодолеть половину этого расстояния, то есть 25 метров. Чтобы пройти оставшиеся 25 метров, он должен сначала преодолеть половину этого расстояния, то есть 12,5 метра. Чтобы пройти оставшиеся 12,5 метров, он должен сначала пройти половину этого расстояния, то есть 6,25 метра, и так далее, и тому подобное.

Экстраполяция этого рассуждения до бесконечности приводит нас к парадоксальному выводу, что Ахилл никогда  не пересечет финишную черту. Всегда будет — некоторое конечное расстояние, которое он должен пересечь первым, поэтому он никогда не достигнет финишной черты. Философы и математики веками ломали голову над парадоксами Зенона. Без ведома Зенона его парадоксы движения очень близки к отражению современной концепции математической асимптоты.

Определение вертикальной асимптоты

Первые формальные определения асимптоты возникли вместе с понятием предела в исчислении. Предел функции — это значение, к которому функция приближается, когда один из ее параметров стремится к бесконечности. Таким образом, функция имеет асимптоту как некоторое значение, такое что предел для уравнения при этом значении равен бесконечности.

Мы пока будем рассматривать только вертикальные асимптоты, так как они наиболее распространены и их легче всего определить. Вот общие условия для определения того, имеет ли функция вертикальную асимптоту: функция ƒ(x) имеет вертикальную асимптоту тогда и только тогда, когда существует некоторое x=a такое, что выход функции неограниченно возрастает по мере того, как x приближается к 9.0005 и . То есть функция имеет вертикальную асимптоту тогда и только тогда, когда существует некоторое x=a такое, что предел функции в точках и равен бесконечности.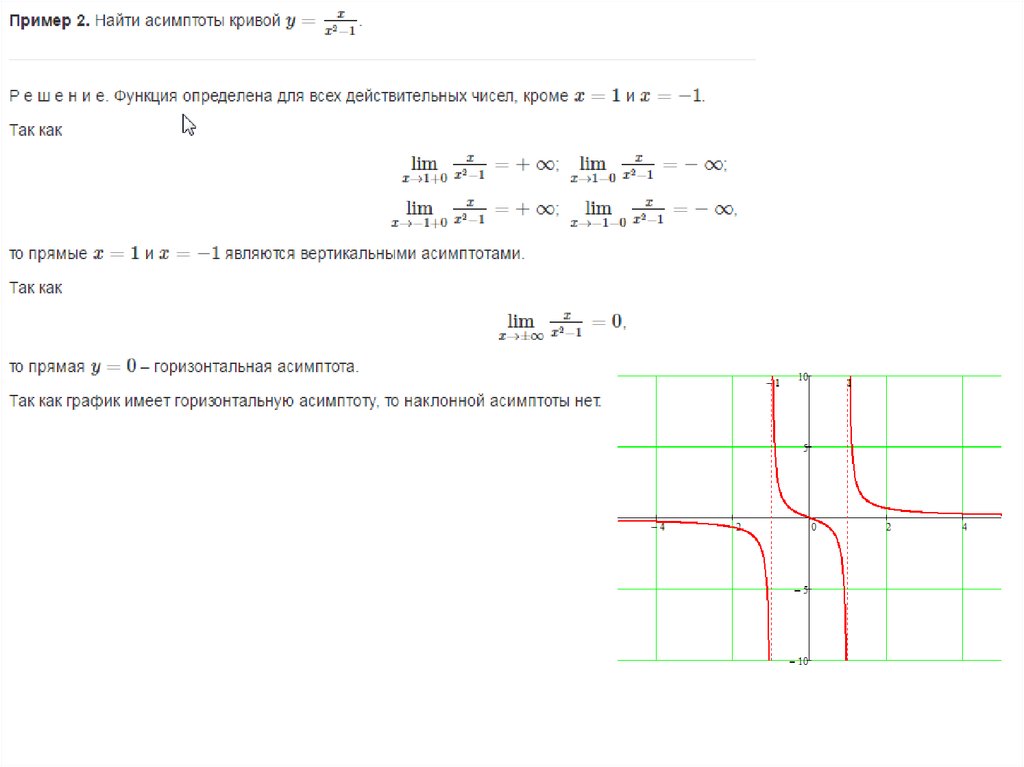

Последний абзац был полным, поэтому давайте рассмотрим простой пример, чтобы конкретизировать эту идею. Ниже приведен график функции ƒ(x) = 1/x:

Эта функция имеет форму обратной кривой. Обратите внимание на поведение функции, когда значение x приближается к 0 с обеих сторон. По мере того, как значение x становится все ближе и ближе к 0, функция начинает быстро неограниченно расти как в положительном, так и в отрицательном направлениях. Давайте посмотрим, что произойдет, когда мы начнем подставлять значения x, которые все ближе и ближе к 0, в функцию:

ƒ(1) = 1/1 = 1

ƒ(0,5) = 1/0,5 = 2

ƒ(0,25) = 1/0,25 = 4

ƒ(0,1) = 1/0,1 = 10

3

3

3 ƒ (0,01) = 1/0,01 = 100

ƒ (0,001) = 1/0,001 = 1000

ƒ (0,000001) = 1/0,000001 = 1 000 000

ƒ (0,00000001) = 1/0,0000000 = 100 000 000

Уведомление о том, что уведомление о том, что уведомление о том, что уведомление о том, что уведомление о том, что уведомление о том, что уведомление о том, чтобы когда x приближается к 0, выход функции становится сколь угодно большим в положительном направлении к бесконечности.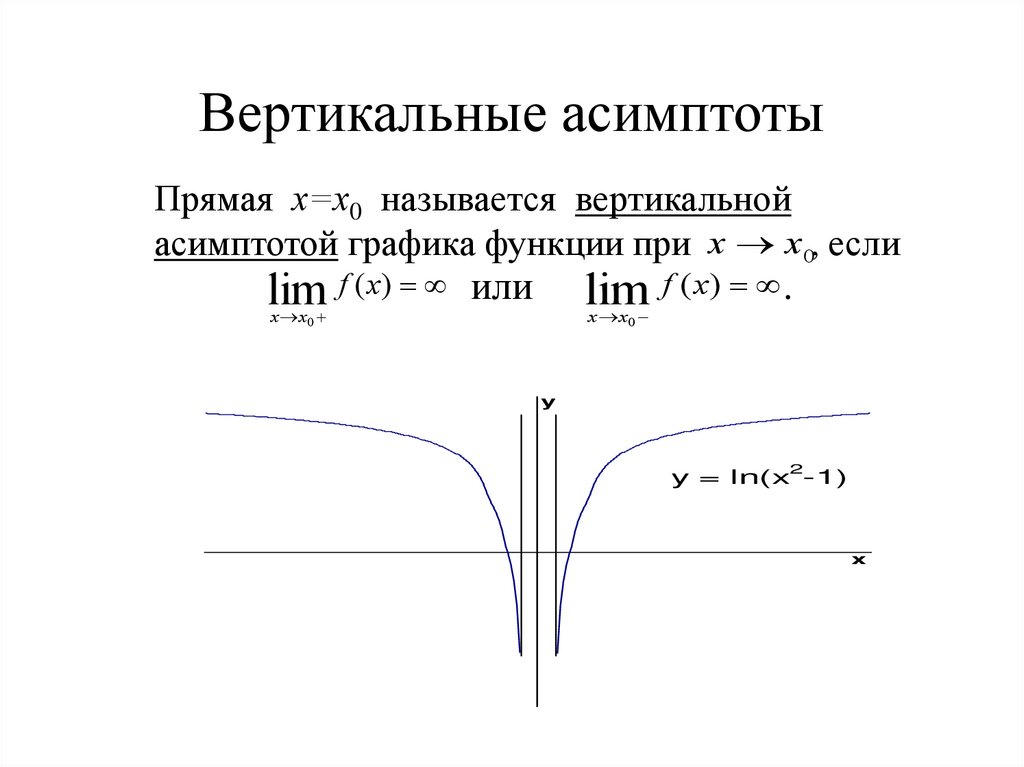 Самое главное, что функция никогда не пересечет линию при x = 0, потому что функция не определена для ƒ (0) (1/0 не определено в обычной арифметике). Точно так же, если приблизиться к 0 слева, значения равны 9.0003

ƒ(-0,5) = 1/-0,5 = -2

ƒ(-0,25) = 1/-0,25 = -4

ƒ(-0,1) = 1/-0,1 = -10

ƒ(- 0,01) = 1/-0,01 = -100

ƒ(-0,001) = 1/-0,001 = -1000

ƒ(-0,000001) = 1/-0,000001 = -1 000 000

1/-00 = 1/000000

-0,00000001 = -100 000 000

По мере того, как x приближается к 0 слева, выходной сигнал функции растет сколь угодно большим в отрицательном направлении к отрицательной бесконечности. Это двусторонняя асимптота, так как функция произвольно увеличивается в любом направлении при приближении к асимптоте с любой стороны. Некоторые функции приближаются к асимптоте только с одной стороны.

Как найти вертикальную асимптоту

Найти вертикальную асимптоту рациональной функции относительно просто. Все, что вам нужно сделать, это найти значение x, которое устанавливает знаменатель рациональной функции равным 0.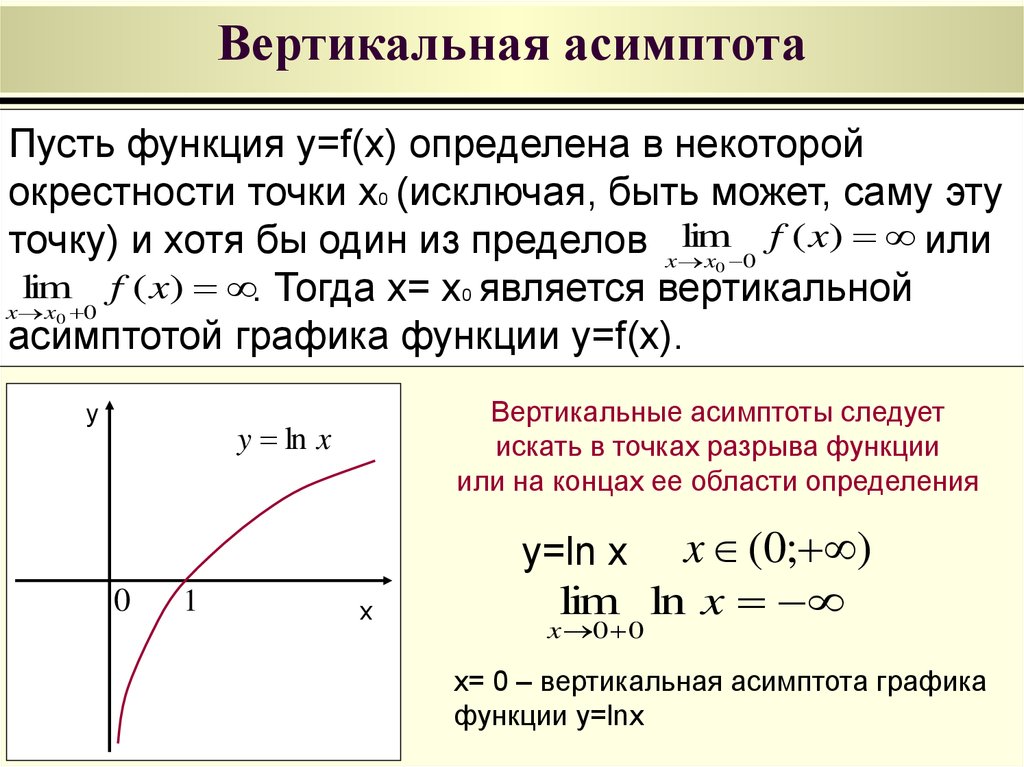 Вот простой пример:

Чему равна вертикальная асимптота функции ƒ(x) = (x+4)/3. (х-3) ?

Это просто. Все, что нам нужно сделать, это найти некоторое значение x, которое сделало бы знаменатель tern 3(x-3) равным 0. Мгновенное наблюдение подсказывает нам, что ответ равен 9.0087 х= 3 ; функция ƒ(x) = (x+4)/3(x-3) имеет вертикальную асимптоту при x=3.

Вместо прямого вычисления иногда может быть полезен график рациональной функции, позволяющий определить, имеет ли эта функция какие-либо асимптоты. График для функции ƒ(x) = (x+4)/(x-3) выглядит следующим образом:

Обратите внимание, как x приближается к 3 слева и справа, функция неограниченно растет в сторону отрицательной бесконечности и положительной бесконечности, соответственно. Простой взгляд на график не является доказательством того, что функция имеет вертикальную асимптоту, но может быть полезно начать поиск асимптоты.

Другие задачи с решениями

Давайте рассмотрим еще несколько задач, чтобы привыкнуть к нахождению вертикальных асимптот.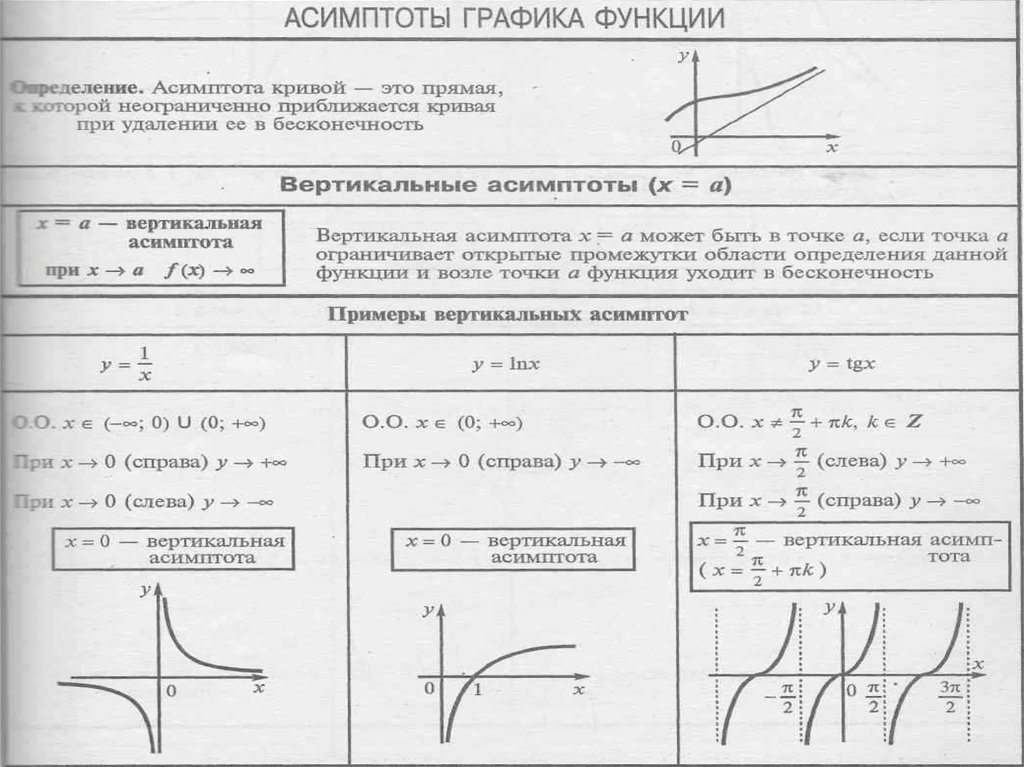

---

(1)

Какова вертикальная асимптота функции ƒ(x) = (x+2)/(x²+2x−8) ?

Решение:

Еще раз нам нужно найти значение x, при котором член в знаменателе равен 0. В этом случае член в знаменателе равен (x²+2x−8). Мы можем узнать значение x, которое устанавливает этот термин равным 0, путем факторизации. Факторинг (x²+2x−8) дает нам:

(x²+2x−8) = (x+4)(x-2)

Эта функция фактически имеет 2 значения x, которые устанавливают член знаменателя равным 0, x=-4 и x=2. Таким образом, функция ƒ(x) = (x+2)/(x²+2x−8) имеет 2 асимптоты, при -4 и 2. Графическое изображение этого уравнения дает нам:

Изобразив уравнение, мы можем увидеть, что функция имеет 2 вертикальные асимптоты, расположенные при значениях x -4 и 2.

(2)

Какова асимптота функции ƒ(x) = (x³−8)/(x²+9) ?

Решение:

Чтобы вычислить это, нам нужно установить знаменатель равным 0, поэтому:

x²+9 = 0

x² = -9

Упс! Это уравнение не имеет решения. Любое число в квадрате всегда больше 0, поэтому не существует такого значения x, что x² равно -9. Таким образом, не существует значения x, которое может установить знаменатель равным 0, поэтому функция ƒ(x) = (x+2)/(x²+2x−8) не имеет вертикальных асимптот!

(3)

Каковы асимптоты функции ƒ(x) = x/(x²+5x+6) ?

Решение:

Еще раз, мы можем решить это, разложив член знаменателя, чтобы найти значения x, которые устанавливают член равным 0. Разложение нижнего члена x²+5x+6 дает нам:

x²+ 5x+6 = (x+2)(x+3)

У этого многочлена есть два значения, которые приравняют его к 0, x=-2 и x=-3. Таким образом, функция ƒ(x) = x/(x²+5x+6) имеет две вертикальные асимптоты при x=-2 и x=-3. График этой функции дает нам:

Когда этот график приближается к -3 слева и -2 справа, функция приближается к отрицательной бесконечности. По мере приближения к -3 справа и -2 слева функция неограниченно растет до бесконечности. Расположение этих двух асимптот делит график на три отдельные части.

Таким образом, вертикальная асимптота — это вертикальная линия, к которой приближается некоторая функция, когда один из параметров функции стремится к бесконечности. Функция будет становиться все ближе и ближе к асимптоте, но никогда не коснется ее. Функция имеет вертикальную асимптоту тогда и только тогда, когда существует некоторое x=a такое, что предел функции при приближении к a равен положительной или отрицательной бесконечности. Можно определить вертикальные асимптоты рациональной функции, найдя значения x, при которых член знаменателя равен 0,9.0003

Видео с вопросами: набросок рациональной функции для нахождения асимптот

Стенограмма видео

Нарисуйте график функции 𝑓 𝑥 равно единице, деленной на 𝑥 плюс два минус один, а затем найдите горизонтальную асимптота 𝑓 из 𝑥. Найдите вертикальную асимптоту 𝑓 из 𝑥.

В этом вопросе нам дается функция 𝑓 от 𝑥, которая равна единице, деленной на 𝑥 плюс два минус один. И мы хотим определить как горизонтальная асимптота графика этой функции и вертикальная асимптота графика график этой функции. И нас просят сделать это построение графика функции. Итак, чтобы сделать это, давайте начнем с Глядя на график, который нас просят нарисовать, один делится на 𝑥 плюс два минус один. И один из способов сделать это — примечание 𝑓 из 𝑥 очень похоже на стандартную обратную функцию 𝑔 из 𝑥 равно к единице, разделенной на 𝑥. На самом деле, мы можем преобразовать обратную функцию на функцию 𝑓 от 𝑥, используя следующие преобразования.

Заметим, что 𝑔 из 𝑥 плюс два минус один равно 𝑓 из 𝑥. Мы находим эти значения непосредственно из заданная функция 𝑓 от 𝑥. Затем мы можем вспомнить, если мы добавим два к входные значения функции, затем мы собираемся перевести кривую по горизонтали на две единицы левее. Точно так же, если мы вычтем единицу из выходы функции, то мы переместим кривую по вертикали на единицу единица вниз. Поэтому мы можем начертить кривую 𝑦 равно 𝑓 из 𝑥, рисуя кривую 𝑦 равно единице над 𝑥, а затем применяя эти два преобразования.

Для этого начнем с вспоминая, чему график обратной функции 𝑦 равен единице над 𝑥 выглядит как. Его форма похожа на следующий. По мере приближения значений 𝑥 к ∞ выходы функции приближаются к нулю с положительного направления. И по мере приближения значений 𝑥 отрицательный ∞, выходы функции стремятся к нулю от отрицательного направление. 𝑥-ось является горизонтальной асимптота, как показано. Точно так же, как значения 𝑥 приближаются к нулю с положительного направления, выходы функции приближаются ∞. И по мере приближения значений 𝑥 ноль с отрицательного направления, выходы функции приближаются к отрицательному ∞.

Ось 𝑦 также является вертикальной асимптота функции. Мы хотим перевести график эта функция на две единицы влево и на одну единицу вниз. И самый простой способ сделать это сначала перевести его асимптоты. Конечно, вертикальный перевод вертикальная линия не изменит своего положения. Аналогично, горизонтальное перемещение горизонтальная линия не изменит своего положения. Так что нам нужно только перевести вертикальная асимптота на две единицы влево и горизонтальная асимптота на одну единицу вниз. Перевод строки 𝑥 равен нулю Две оставшиеся единицы дают нам строку 𝑥, равную минус двум, и переводя линия 𝑦 равна нулю на единицу вниз дает нам линию 𝑦 равна отрицательной один. Это будут асимптоты нашего функция 𝑓 из 𝑥.

Общий вид функции останется неизменным, потому что мы только переводим его по горизонтали и вертикально. Он все равно будет иметь ту же форму как обратную кривую. Однако, прежде чем мы зарисуем это кривой, может быть полезно определить такие вещи, как 𝑦- и 𝑥-перехваты кривой. кривой, чтобы определить ее ориентацию на плоскости. Мы можем найти 𝑦-перехват с помощью подставляя 𝑥 равно нулю в 𝑓 из 𝑥. Мы видим, что 𝑓, оцененное в нуле, равно половина минус один, что мы можем оценить как отрицательную половину. Итак, наша кривая 𝑦 равна 𝑓 𝑥 должен пересекать ось 𝑦 на отрицательной половине. На самом деле, этого достаточно, чтобы сейчас нарисуйте нашу кривую, так как мы знаем ее общую форму и 𝑦-перехват. Это дает нам следующее эскиз.

И стоит отметить, что мы смогли найти координаты 𝑥-перехвата, установив 𝑓 из 𝑥 равным нулю и решение. Мы получили бы это значение 𝑥 является отрицательным. Этот набросок теперь помогает нам обосновать почему горизонтальная асимптота и вертикальная асимптота функции являются линиями 𝑦 равно отрицательной единице, а 𝑥 равно отрицательной двойке соответственно. Поскольку мы просто переводим обратной кривой, мы просто переводим ее асимптоты. Таким образом, перевод обратной кривой одна единица вниз переведет его горизонтальную асимптоту на одну единицу вниз. У нас будет горизонталь асимптота 𝑦 равна отрицательной единице. Аналогичным образом, переводя обратная кривая на две единицы влево сдвинет свою вертикальную асимптоту на две единицы влево на прямую 𝑥 равно минус двум.

Таким образом, мы смогли сделать набросок график функции 𝑓 от 𝑥 равен единице, деленной на 𝑥 плюс два минус один и найти его горизонтальную и вертикальную асимптоты. Мы показали его горизонтальную асимптоту была ли прямая 𝑦 равна отрицательной единице, а ее вертикальная асимптота была прямой 𝑥 равно минус двум.

Асимптоты и производная | Преподавание исчисления

Что асимптота производной говорит вам о функции? Как на графике производной появляются асимптоты функции?

Один из моих самых читаемых постов — Reading the Derivative’s Graph, впервые опубликованный семь лет назад. Длинное название: «Вот график производной; расскажи мне о функции». Рассказывается, как быстро найти информацию о графике функции по графику производной. Недавно я получил вопрос от читателя, который спрашивал об асимптотах и ​​производных, теме, которую я не освещал в этом посте. Итак, я попытался найти взаимосвязь. Короткий ответ заключается в том, что асимптота производных мало что говорит вам о графике функции. (Возможно, поэтому эта идея никогда не проверялась на экзаменах AP по математическому анализу.)

Тем не менее, здесь есть чему поучиться. Возможно, вы сможете найти несколько вопросов, которые ваши студенты могут исследовать по этой теме. Вот что я определил.

Прежде чем мы начнем, вот два полезных, но редко используемых термина.

• Четная вертикальная асимптота — это функция, для которой функция неограниченно возрастает или убывает по обеим сторонам асимптоты. Другими словами, когда x приближается к a , функция приближается к бесконечности или отрицательной бесконечности с обеих сторон. Функция имеет четную вертикальную асимптоту на х = 2. (Рисунок 1)
• Нечетная вертикальная асимптота — это асимптота, для которой функция неограниченно возрастает с одной стороны и неограниченно убывает с другой. Функция имеет нечетную вертикальную асимптоту при 90 201 x = 90 202 2. (Рисунок 2). Точно так же функции тангенса, котангенса, секанса и косеканса имеют нечетные вертикальные асимптоты.

Рисунок 1: ЧЕТНАЯ вертикальная асимптота

Рисунок 2: Вертикальная асимптота ODD

Если функция имеет нечетную вертикальную асимптоту, то ее производная будет иметь четную вертикальную асимптоту. (Попросите учащихся объяснить, почему.)

Если функция имеет четную вертикальную асимптоту, то ее производная будет иметь нечетную вертикальную асимптоту. (Попросите учащихся объяснить, почему.)

T он делает вывод, что эти два утверждения ложны . То есть вертикальная асимптота производной не обязательно указывает на асимптоту функции. Загвоздка в непрерывности.

Непрерывные функции

Если производная существует при x = a, , то функция здесь непрерывна. Но, поскольку мы рассматриваем асимптоты производной, мы не можем знать только по производной, является ли функция непрерывной там, где производная имеет асимптоту.

Простой куспид — это ситуация, в которой в крайней точке график касается вертикальной линии. См. рис. 3. (Или можно сказать, что касательные с каждой стороны совпадают. Здесь мы ограничим обсуждение вертикальной касательной.) Непрерывная функция, имеющая точку возврата, будет показывать нечетную вертикальную асимптоту на графике своей производной. .

Пример   с вершиной в точке (2,1). (Рисунок 3).

Непрерывная функция, имеющая вертикальную касательную, а не точку возврата, имеет четную вертикальную асимптоту на графике производной. Например, при (2,0) (рис. 4).

Рисунок 3: Изгиб в точке (2,1)

Рисунок 4: вертикальная касательная.

Если вам дан график производной, и он показывает вертикальную асимптоту в x = a , и вы знаете, что функция там непрерывна, тогда

• нечетная вертикальная асимптота производной указывает точку возврата на графике функции. Это также будет экстремальным значением. (Попросите учащихся объяснить, почему.)
• четная вертикальная асимптота производной указывает на вертикальную касательную на графике функции, а не на экстремум. (Попросите учащихся объяснить, почему.)

Помимо этого, нет простого способа определить, в какой ситуации возникла асимптота производной.

Функции, которые не являются непрерывными

Если функция не является непрерывной при x = a , все становится намного сложнее.

• Если функция не непрерывна при x = a , то четная вертикальная асимптота производной   может указывать на нечетную вертикальную асимптоту на графике функции.

  No related posts.