Расчет пропорции формула: Как посчитать пропорцию — онлайн калькулятор

Содержание

Формула пропорции с неизвестным. Задачи на пропорции

С точки зрения математики, пропорцией является равенство двух отношений. Взаимозависимость характерна для всех частей пропорции, также как и их неизменный результат. Понять, как составить пропорцию можно, ознакомившись со свойствами и формулой пропорции. Чтобы разобраться с принципом решения пропорции, достаточным будет рассмотреть один пример. Только непосредственно решая пропорции, можно легко и быстро обучиться этим навыкам. А данная статья поможет читателю в этом.

Свойства пропорции и формула

Обращение пропорции. В случае, когда заданное равенство выглядит как 1a: 2b =3c: 4d, записывают 2b: 1a = 4d: 3c. (Причем 1a, 2b, 3c и 4d являются простыми числами, отличными от 0).
Перемножение заданных членов пропорции крест-накрест. В буквенном выражении это имеет такой вид: 1a: 2b = 3c: 4d, а запись 1a4d = 2b3c будет ему равносильна. Таким образом, произведение крайних частей любой пропорции (числа по краям равенства) всегда является равным произведению средних частей (чисел, расположенных посредине равенства).
При составлении пропорции может пригодиться и такое её свойство, как перестановка крайних и средних членов. Формулу равенства 1a: 2b = 3c: 4d, можно отобразить такими вариантами:
- 1a: 3c = 2b: 4d (когда переставляют средние члены пропорции).
- 4d: 2b = 3c: 1a (когда переставляют крайние члены пропорции).
Прекрасно помогает в решении пропорции её свойство увеличения и уменьшения. При 1a: 2b = 3c: 4d, записывают:
- (1a + 2b) : 2b = (3c + 4d) : 4d (равенство по увеличению пропорции).
- (1a – 2b) : 2b = (3c – 4d) : 4d (равенство по уменьшению пропорции).
Составить пропорцию можно сложением и вычитанием. Когда пропорция записана как 1a: 2b = 3c: 4d, тогда:
- (1a + 3с) : (2b + 4d) = 1a: 2b = 3c: 4d (пропорция составлена сложением).
- (1a – 3с) : (2b – 4d) = 1a: 2b = 3c: 4d (пропорция составлена вычитанием).
Также, при решении пропорции, содержащей дробные или большие числа, можно разделить или умножить оба её члена на одинаковое число. К примеру, составные части пропорции 70:40=320:60, можно записать так: 10*(7:4=32:6).
Вариант решения пропорции с процентами выглядит так. К примеру, записывают, 30=100%, 12=x. Теперь следует перемножить средние члены (12*100) и разделить на известный крайний (30). Таким образом, получается ответ: x=40%. Подобным способом можно при необходимости совершать перемножение известных крайних членов и делить их на заданное среднее число, получая искомый результат.

Если Вас интересует конкретная формула пропорции, то в самом простом и распространенном варианте пропорция представляет собой такое равенство (формулу): a/b = c/d, в нем a, b, c и d являются отличными от нуля четырьмя числами.

Задача 1 . Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги?

Решение. Пусть х см — толщина пачки бумаги из 500 листов. Двумя способами найдем толщину одного листа бумаги:

3,3: 300 или х: 500.

Так как листы бумаги одинаковые, то эти два отношения равны между собой. Получаем пропорцию (напоминание: пропорция — это равенство двух отношений

х=(3,3· 500): 300;

х=5,5. Ответ: пачка 500 листов бумаги имеет толщину 5,5 см .

Это классическое рассуждение и оформление решения задачи. Такие задачи часто включают в тестовые задания для выпускников, которые обычно записывают решение в таком виде:

или решают устно, рассуждая так: если 300 листов имеют толщину 3,3 см, то 100 листов имеют толщину в 3 раза меньшую. Делим 3,3 на 3, получаем 1,1 см. Это толщина 100 листовой пачки бумаги. Следовательно, 500 листов будут иметь толщину в 5 раз большую, поэтому, 1,1 см умножаем на 5 и получаем ответ: 5,5 см.

Разумеется, это оправдано, так как время тестирования выпускников и абитуриентов ограничено. Однако, на этом занятии мы будем рассуждать и записывать решение так, как положено это делать в 6 классе.

Задача 2. Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды?

Решение.

Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы.

5: 100 или х: 98. Получаем пропорцию:

5: 100 = х: 98.

х=(5· 98): 100;

х=4,9 Ответ: в 5кг арбуза содержится 4,9 кг воды .

Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти?

Решение.

Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти:

16,8: 21 или х: 35. Получаем пропорцию:

16,8: 21=х: 35.

Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (16,8 и 35 ) и делим на известный средний член (21 ). Сократим дробь на 7 .

Умножаем числитель и знаменатель дроби на 10 , чтобы в числителе и знаменателе были только натуральные числа.

Сокращаем дробь на 5 (5 и 10) и на 3 (168 и 3).

Ответ: 35 литров нефти имеют массу 28 кг.

После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?

Решение.

Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это:

х: 100 или 9: 18. Составляем пропорцию:

х: 100 = 9: 18.

Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100 и 9 ) и делим на известный крайний член (18 ). Сокращаем дробь.

Ответ : площадь всего поля 50 га.

Страница 1 из 1 1

Формула пропорций

Пропо́рция — это равенство двух отношений, когда a:b=c:d

отношение 1 : 10 равно отношению 7 : 70, что также можно записать в виде дроби: 1 10 = 7 70 читается как: «один относится к десяти так же, как семь относится к семидесяти»

Основные свойства пропорции

Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d , то a⋅d=b⋅c

1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7

Обращение пропорции: если a:b=c:d , то b:a=d:c

1 10 7 70 10 1 = 70 7

Перестановка средних членов: если a:b=c:d , то a:c=b:d

1 10 7 70 1 7 = 10 70

Перестановка крайних членов: если a:b=c:d , то d:b=c:a

1 10 7 70 70 10 = 7 1

Решение пропорции с одним неизвестным | Уравнение

1 : 10 = x : 70 или 1 10 = x 70

Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение

x = 1 ⋅ 70 10 = 7

Как посчитать пропорцию

Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?

Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток

Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?

Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей

Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и , и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.

Если говорить просто, то это овощи, приготовленные в воде по специальному рецепту. Я буду рассматривать два исходных компонента (овощной салат и воду) и готовый результат — борщ. Геометрически это можно представить как прямоугольник, в котором одна сторона обозначает салат, вторая сторона обозначает воду. Сумма этих двух сторон будет обозначать борщ. Диагональ и площадь такого «борщевого» прямоугольника являются чисто математическими понятиями и никогда не используются в рецептах приготовления борща.

Как салат и вода превращаются в борщ с точки зрения математики? Как сумма двух отрезков может превратиться в тригонометрию? Чтобы понять это, нам понадобятся линейные угловые функции.

В учебниках математики вы ничего не найдете о линейных угловых функциях. А ведь без них не может быть математики. Законы математики, как и законы природы, работают независимо от того, знаем мы о их существовании или нет.

Линейные угловые функции — это законы сложения. Посмотрите, как алгебра превращается в геометрию, а геометрия превращается в тригонометрию.

Можно ли обойтись без линейных угловых функций? Можно, ведь математики до сих пор без них обходятся. Хитрость математиков заключается в том, что они всегда рассказывают нам только о тех задачах, которые они сами умеют решать, и никогда не рассказывают о тех задачах, которые они решать не умеют. Смотрите. Если нам известен результат сложения и одно слагаемое, для поиска другого слагаемого мы используем вычитание. Всё. Других задач мы не знаем и решать не умеем. Что делать в том случае, если нам известен только результат сложения и не известны оба слагаемые? В этом случае результат сложения нужно разложить на два слагаемых при помощи линейных угловых функций. Дальше мы уже сами выбираем, каким может быть одно слагаемое, а линейные угловые функции показывают, каким должно быть второе слагаемое, чтобы результат сложения был именно таким, какой нам нужен. Таких пар слагаемых может быть бесконечное множество. В повседневной жизни мы прекрасно обходимся без разложения суммы, нам достаточно вычитания. А вот при научных исследованиях законов природы разложение суммы на слагаемые очень может пригодиться.

Ещё один закон сложения, о котором математики не любят говорить (ещё одна их хитрость), требует, чтобы слагаемые имели одинаковые единицы измерения. Для салата, воды и борща это могут быть единицы измерения веса, объема, стоимости или единицы измерения.

На рисунке показаны два уровня различий для математических . Первый уровень — это различия в области чисел, которые обозначены a , b , c . Это то, чем занимаются математики. Второй уровень — это различия в области единиц измерения, которые показаны в квадратных скобках и обозначены буквой U . Этим занимаются физики. Мы же можем понимать третий уровень — различия в области описываемых объектов. Разные объекты могут иметь одинаковое количество одинаковых единиц измерения. Насколько это важно, мы можем увидеть на примере тригонометрии борща. Если мы добавим нижние индексы к одинаковому обозначению единиц измерения разных объектов, мы сможем точно говорить, какая математическая величина описывает конкретный объект и как она изменяется с течением времени или в связи с нашими действиями. Буквой W я обозначу воду, буквой S обозначу салат и буквой B — борщ. Вот как будут выглядеть линейные угловые функции для борща.

Если мы возьмем какую-то часть воды и какую-то часть салата, вместе они превратятся в одну порцию борща. Здесь я предлагаю вам немного отвлечься от борща и вспомнить далекое детство. Помните, как нас учили складывать вместе зайчиков и уточек? Нужно было найти, сколько всего зверушек получится. Что же нас тогда учили делать? Нас учили отрывать единицы измерения от чисел и складывать числа. Да, одно любое число можно сложить с другим любым числом. Это прямой путь к аутизму современной математики — мы делаем непонятно что, непонятно зачем и очень плохо понимаем, как это относится к реальности, ведь из трех уровней различия математики оперируют только одним. Более правильно будет научиться переходить от одних единиц измерения к другим.

И зайчиков, и уточек, и зверушек можно посчитать в штуках. Одна общая единица измерения для разных объектов позволяет нам сложить их вместе. Это детский вариант задачи. Давайте посмотрим на похожую задачу для взрослых. Что получится, если сложить зайчиков и деньги? Здесь можно предложить два варианта решения.

Первый вариант . Определяем рыночную стоимость зайчиков и складываем её с имеющейся денежной суммой. Мы получили общую стоимость нашего богатства в денежном эквиваленте.

Второй вариант . Можно количество зайчиков сложить с количеством имеющихся у нас денежных купюр. Мы получим количество движимого имущества в штуках.

Как видите, один и тот же закон сложения позволяет получить разные результаты. Всё зависит от того, что именно мы хотим знать.

Но вернемся к нашему борщу. Теперь мы можем посмотреть, что будет происходить при разных значениях угла линейных угловых функций.

Угол равен нулю. У нас есть салат, но нет воды. Мы не можем приготовить борщ. Количество борща также равно нулю. Это совсем не значит, что ноль борща равен нулю воды. Ноль борща может быть и при нуле салата (прямой угол).

Лично для меня, это основное математическое доказательство того факта, что . Ноль не изменяет число при сложении. Это происходит потому, что само сложение невозможно, если есть только одно слагаемое и отсутствует второе слагаемое. Вы к этому можете относиться как угодно, но помните — все математические операции с нулем придумали сами математики, поэтому отбрасывайте свою логику и тупо зубрите определения, придуманные математиками: «деление на ноль невозможно», «любое число, умноженное на ноль, равняется нулю», «за выколом точки ноль» и прочий бред.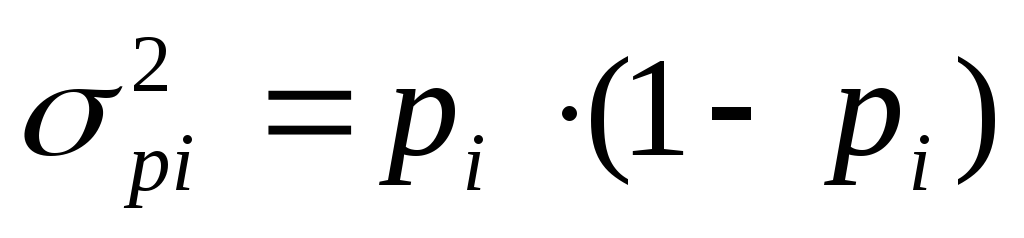 Достаточно один раз запомнить, что ноль не является числом, и у вас уже никогда не возникнет вопрос, является ноль натуральным числом или нет, потому что такой вопрос вообще лишается всякого смысла: как можно считать числом то, что числом не является. Это всё равно, что спрашивать, к какому цвету отнести невидимый цвет. Прибавлять ноль к числу — это то же самое, что красить краской, которой нет. Сухой кисточкой помахали и говорим всем, что » мы покрасили». Но я немного отвлекся.

Угол больше нуля, но меньше сорока пяти градусов. У нас много салата, но мало воды. В результате мы получим густой борщ.

Угол равен сорок пять градусов. Мы имеем в равных количествах воду и салат. Это идеальный борщ (да простят меня повара, это просто математика).

Угол больше сорока пяти градусов, но меньше девяноста градусов. У нас много воды и мало салата. Получится жидкий борщ.

Прямой угол. У нас есть вода. От салата остались только воспоминания, поскольку угол мы продолжаем измерять от линии, которая когда-то обозначала салат. Мы не можем приготовить борщ. Количество борща равно нулю. В таком случае, держитесь и пейте воду, пока она есть)))

Вот. Как-то так. Я могу здесь рассказать и другие истории, которые будут здесь более чем уместны.

Два друга имели свои доли в общем бизнесе. После убийства одного из них, всё досталось другому.

Появление математики на нашей планете.

Все эти истории на языке математики рассказаны при помощи линейных угловых функций. Как-нибудь в другой раз я покажу вам реальное место этих функций в структуре математики. А пока, вернемся к тригонометрии борща и рассмотрим проекции.

суббота, 26 октября 2019 г.

среда, 7 августа 2019 г.

Завершая разговор о , нужно рассмотреть бесконечное множество. Дало в том, что понятие «бесконечность» действует на математиков, как удав на кролика. Трепетный ужас перед бесконечностью лишает математиков здравого смысла. Вот пример:

Первоисточник находится . Альфа обозначает действительное число. Знак равенства в приведенных выражениях свидетельствует о том, что если к бесконечности прибавить число или бесконечность, ничего не изменится, в результате получится такая же бесконечность. Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:

Для наглядного доказательства своей правоты математики придумали много разных методов . Лично я смотрю на все эти методы, как на пляски шаманов с бубнами. По существу, все они сводятся к тому, что либо часть номеров не занята и в них заселяются новые гости, либо к тому, что часть посетителей вышвыривают в коридор, чтобы освободить место для гостей (очень даже по-человечески). Свой взгляд на подобные решения я изложил в форме фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Переселение бесконечного количества посетителей требует бесконечно много времени. После того, как мы освободили первую комнату для гостя, один из посетителей всегда будет идти по коридору из своего номера в соседний до скончания века. Конечно, фактор времени можно тупо игнорировать, но это уже будет из разряда «дуракам закон не писан». Всё зависит от того, чем мы занимаемся: подгоняем реальность под математические теории или наоборот.

Что же такое «бесконечная гостиница»? Бесконечная гостиница — это гостиница, в которой всегда есть любое количество свободных мест, независимо от того, сколько номеров занято. Если все номера в бесконечном коридоре «для посетителей» заняты, есть другой бесконечный коридор с номерами «для гостей». Таких коридоров будет бесконечное множество. При этом у «бесконечной гостиницы» бесконечное количество этажей в бесконечном количестве корпусов на бесконечном количестве планет в бесконечном количестве вселенных, созданных бесконечным количеством Богов. Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».

Логику своих рассуждений я вам продемонстрирую на примере бесконечного множества натуральных чисел. Для начала нужно ответить на очень простой вопрос: сколько множеств натуральных чисел существует — одно или много? Правильного ответа на это вопрос не существует, поскольку числа придумали мы сами, в Природе чисел не существует. Да, Природа отлично умеет считать, но для этого она использует другие математические инструменты, не привычные для нас. Как Природа считает, я вам расскажу в другой раз. Поскольку числа придумали мы, то мы сами будем решать, сколько множеств натуральных чисел существует. Рассмотрим оба варианта, как и подобает настоящим ученым.

Вариант первый. «Пусть нам дано» одно-единственное множество натуральных чисел, которое безмятежно лежит на полочке. Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:

Я записал действия в алгебраической системе обозначений и в системе обозначений, принятой в теории множеств, с детальным перечислением элементов множества. Нижний индекс указывает на то, что множество натуральных чисел у нас одно и единственное. Получается, что множество натуральных чисел останется неизменным только в том случае, если из него вычесть единицу и прибавить эту же единицу.

Вариант второй. У нас на полочке лежит много разных бесконечных множеств натуральных чисел. Подчеркиваю — РАЗНЫХ, не смотря на то, что они практически не отличимы. Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:

Нижние индексы «один» и «два» указывают на то, что эти элементы принадлежали разным множествам. Да, если к бесконечному множеству прибавить единицу, в результате получится тоже бесконечное множество, но оно не будет таким же, как первоначальное множество. Если к одному бесконечному множеству прибавить другое бесконечное множество, в результате получится новое бесконечное множество, состоящее из элементов первых двух множеств.

Множество натуральных чисел используется для счета так же, как линейка для измерений. Теперь представьте, что к линейке вы добавили один сантиметр. Это уже будет другая линейка, не равная первоначальной.

Вы можете принимать или не принимать мои рассуждения — это ваше личное дело. Но если когда-то вы столкнетесь с математическими проблемами, задумайтесь, не идете ли вы по тропе ложных рассуждений, протоптанной поколениями математиков. Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).

pozg.ru

воскресенье, 4 августа 2019 г.

Дописывал постскриптум к статье о и увидел в Википедии этот замечательный текст:

Читаем: «… богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приемов, лишенных общей системы и доказательной базы.»

Вау! Какие мы умные и как хорошо можем видеть недостатки других.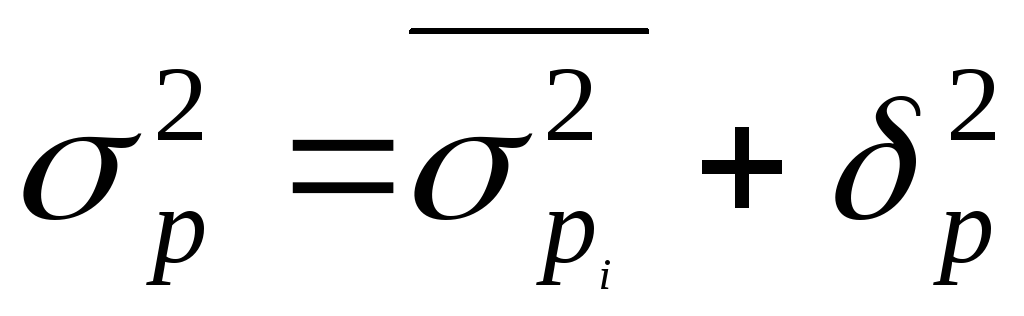 А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:

Богатая теоретическая основа современной математики не имеет целостного характера и сводится к набору разрозненных разделов, лишенных общей системы и доказательной базы.

За подтверждением своих слов я далеко ходить не буду — имеет язык и условные обозначения, отличные от языка и условных обозначений многих других разделов математики. Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.

суббота, 3 августа 2019 г.

Как разделить множество на подмножества? Для этого необходимо ввести новую единицу измерения, присутствующую у части элементов выбранного множества. Рассмотрим пример.

Пусть у нас есть множество А , состоящее из четырех человек. Сформировано это множество по признаку «люди» Обозначим элементы этого множества через букву а , нижний индекс с цифрой будет указывать на порядковый номер каждого человека в этом множестве. Введем новую единицу измерения «половой признак» и обозначим её буквой b . Поскольку половые признаки присущи всем людям, умножаем каждый элемент множества А на половой признак b . Обратите внимание, что теперь наше множество «люди» превратилось в множество «люди с половыми признаками». После этого мы можем разделить половые признаки на мужские bm и женские bw половые признаки. Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.

После умножения, сокращений и перегруппировок, мы получили два подмножества: подмножество мужчин Bm и подмножество женщин Bw . Приблизительно так же рассуждают математики, когда применяют теорию множеств на практике. Но в детали они нас не посвящают, а выдают готовый результат — «множество людей состоит из подмножества мужчин и подмножества женщин». Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в изложенных выше преобразованиях? Смею вас заверить, по сути преобразований сделано всё правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики. Что это такое? Как-нибудь в другой раз я вам об этом расскажу.

Что касается надмножеств, то объединить два множества в одно надмножество можно, подобрав единицу измерения, присутствующую у элементов этих двух множеств.

Как видите, единицы измерения и обычная математика превращают теорию множеств в пережиток прошлого. Признаком того, что с теорией множеств не всё в порядке, является то, что для теории множеств математики придумали собственный язык и собственные обозначения. Математики поступили так, как когда-то поступали шаманы. Только шаманы знают, как «правильно» применять их «знания». Этим «знаниям» они обучают нас.

В заключение, я хочу показать вам, как математики манипулируют с .

понедельник, 7 января 2019 г.

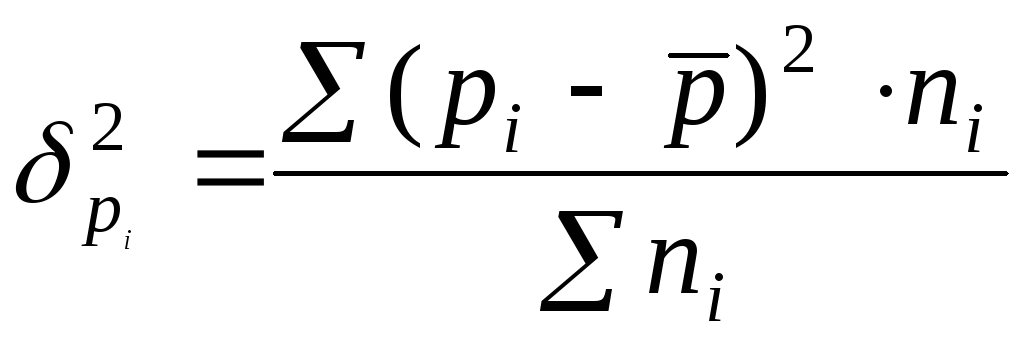
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:

Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.

Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса. .. » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.

С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.

Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».

Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:

За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.

Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.

Другая интересная апория Зенона повествует о летящей стреле:

Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.

В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Покажу процесс на примере. Отбираем «красное твердое в пупырышку» — это наше «целое». При этом мы видим, что эти штучки есть с бантиком, а есть без бантика. После этого мы отбираем часть «целого» и формируем множество «с бантиком». Вот так шаманы добывают себе корм, привязывая свою теорию множеств к реальности.

А теперь сделаем маленькую пакость. Возьмем «твердое в пупырышку с бантиком» и объединим эти «целые» по цветовому признаку, отобрав красные элементы. Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.

Этот простой пример показывает, что теория множеств совершенно бесполезна, когда речь заходит о реальности. В чем секрет? Мы сформировали множество «красное твердое в пупырышку с бантиком». Формирование происходило по четырем разным единицам измерения: цвет (красное), прочность (твердое), шероховатость (в пупырышку), украшения (с бантиком). Только совокупность единиц измерения позволяет адекватно описывать реальные объекты на языке математики . Вот как это выглядит.

Буква «а» с разными индексами обозначает разные единицы измерения. В скобках выделены единицы измерения, по которым выделяется «целое» на предварительном этапе. За скобки вынесена единица измерения, по которой формируется множество. Последняя строчка показывает окончательный результат — элемент множества. Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.

При помощи единиц измерения очень легко разбить одно или объединить несколько множеств в одно надмножество. Давайте более внимательно рассмотрим алгебру этого процесса.

§ 125. Понятие о пропорции.

Пропорцией называется равенство двух отношений. Вот примеры равенств, называемых пропорциями:

Примечание. Наименования величин в пропорциях не указаны.

Пропорции принято читать следующим образом: 2 так относится к 1 (единице), как 10 относится к 5 (первая пропорция). Можно читать иначе, например: 2 во столько раз больше 1, во сколько раз 10 больше 5. Третью пропорцию можно прочесть так: — 0,5 во столько раз меньше 2, во сколько раз 0,75 меньше 3.

Числа, входящие в пропорцию, называются членами пропорции . Значит, пропорция состоит из четырёх членов. Первый и последний члены, т. е. члены, стоящие по краям, называются крайними , а члены пропорции, находящиеся в середине, называются средними членами. Значит, в первой пропорции числа 2 и 5 будут крайними членами, а числа 1 и 10 — средними членами пропорции.

§ 126. Основное свойство пропорции.

Рассмотрим пропорцию:

Перемножим отдельно её крайние и средние члены. Произведение крайних 6 4 = 24, произведение средних 3 8 = 24.

Рассмотрим другую пропорцию: 10: 5 = 12: 6. Перемножим и здесь отдельно крайние и средние члены.

Произведение крайних 10 6 = 60, произведение средних 5 12 = 60.

Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних её членов.

В общем виде основное свойство пропорции записывается так: ad = bc .

Проверим его на нескольких пропорциях:

1) 12: 4 = 30: 10.

Пропорция эта верна, так как равны отношения, из которых она составлена. Вместе с тем, взяв произведение крайних членов пропорции (12 10) и произведение средних её членов (4 30), мы увидим, что они равны между собой, т. е.

12 10 = 4 30.

2) 1 / 2: 1 / 48 = 20: 5 / 6

Пропорция верна, в чём легко убедиться, упростив первое и второе отношения. Основное свойство пропорции примет вид:

1 / 2 5 / 6 = 1 / 48 20

Нетрудно убедиться в том, что если мы напишем такое равенство, у которого в левой части стоит произведение двух каких-нибудь чисел, а в правой части произведение двух других чисел, то из этих четырёх чисел можно составить пропорцию.

Пусть у нас имеется равенство, в которое входят четыре числа, попарно перемноженные:

эти четыре числа могут быть членами пропорции, которую нетрудно написать, если принять первое произведение за произведение крайних членов, а второе — за произведение средних. Изданного равенства можно составить, например, такую пропорцию:

Вообще, из равенства ad = bc можно получить следующие пропорции:

Проделайте самостоятельно следующее упражнение. Имея произведение двух пар чисел, напишите пропорцию, соответствующую каждому равенству:

а) 1 6 = 2 3;

б) 2 15 = б 5.

§ 127. Вычисление неизвестных членов пропорции.

Основное свойство пропорции позволяет вычислить любой из членов пропорции, если он неизвестен. Возьмём пропорцию:

х : 4 = 15: 3.

В этой пропорции неизвестен один крайний член. Мы знаем, что во всякой пропорции произведение крайних членов равно произведению средних членов. На этом основании мы можем написать:

x 3 = 4 15.

После умножения 4 на 15 мы можем переписать это равенство так:

х 3 = 60.

Рассмотрим это равенство. В нём первый сомножитель неизвестен, второй сомножитель известен и произведение известно. Мы знаем, что для нахождения неизвестного сомножителя достаточно произведение разделить на другой (известный) сомножитель. Тогда получится:

х = 60: 3, или х = 20.

Проверим найденный результат подстановкой числа 20 вместо х в данную пропорцию:

Пропорция верна.

Подумаем, какие действия нам пришлось выполнить для вычисления неизвестного крайнего члена пропорции. Из четырёх членов пропорции нам был неизвестен только один крайний; два средних и второй крайний были известны. Для нахождения крайнего члена пропорции мы сначала перемножили средние члены (4 и 15), а затем найденное произведение разделили на известный крайний член. Сейчас мы покажем, что действия не изменились бы, если бы искомый крайний член пропорции стоял не на первом месте, а на последнем. Возьмём пропорцию:

70: 10 = 21: х .

Запишем основное свойство пропорции: 70 х = 10 21.

Перемножив числа 10 и 21, перепишем равенство в таком виде:

70 х = 210.

Здесь неизвестен один сомножитель, для его вычисления достаточно произведение (210) разделить на другой сомножитель (70),

х = 210: 70; х = 3.

Таким образом, мы можем сказать, что каждый крайний член пропорции равен произведению средних, делённому на другой крайний.

Перейдём теперь к вычислению неизвестного среднего члена. Возьмём пропорцию:

30: х = 27: 9.

Напишем основное свойство пропорции:

30 9 = х 27.

Вычислим произведение 30 на 9 и переставим части последнего равенства:

х 27 = 270.

Найдём неизвестный сомножитель:

х = 270: 27, или х = 10.

Проверим подстановкой:

30: 10 = 27: 9. Пропорция верна.

Возьмём ещё одну пропорцию:

12: б = х : 8. Напишем основное свойство пропорции:

12 . 8 = 6 х . Перемножая 12 и 8 и переставляя части равенства, получим:

6 х = 96. Находим неизвестный сомножитель:

х = 96: 6, или х = 16.

Таким образом, каждый средний член пропорции равен произведению крайних, делённому на другой средний.

Найдите неизвестные члены следующих пропорций:

1) а : 3= 10:5; 3) 2: 1 / 2 = x : 5;

2) 8: b = 16: 4; 4) 4: 1 / 3 = 24: х .

Два последних правила в общем виде можно записать так:

1) Если пропорция имеет вид:

х: а = b: с , то

2) Если пропорция имеет вид:

а: х = b: с , то

§ 128. Упрощение пропорции и перестановка её членов.

В настоящем параграфе мы выведем правила, позволяющие упрощать пропорцию в том случае, когда в неё входят большие числа или дробные члены.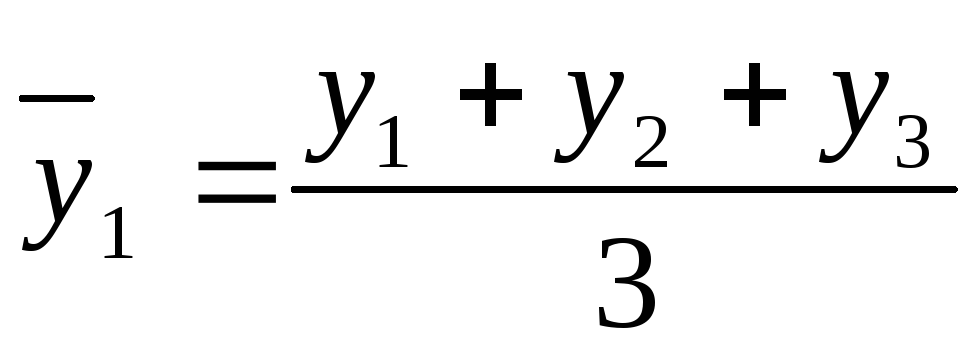 K числу преобразований, не нарушающих пропорцию, относятся следующие:

1. Одновременное увеличение или уменьшение обоих членов любого отношения в одинаковое число раз.

П р и м е р. 40: 10 = 60: 15.

Увеличив в 3 раза оба члена первого отношения, получим:

120:30 = 60: 15.

Пропорция не нарушилась.

Уменьшив в 5 раз оба члена второго отношения, получим:

Получили опять правильную пропорцию.

2. Одновременное увеличение или уменьшение обоих предыдущих или обоих последующих членов в одинаковое число раз.

Пример. 16:8 = 40:20.

Увеличим в 2 раза предыдущие члены обоих отношений:

Получили правильную пропорцию.

Уменьшим в 4 раза последующие члены обоих отношений:

Пропорция не нарушилась.

Два полученных вывода можно кратко высказать так: Пропорция не нарушится, если мы одновременно увеличим или уменьшим в одинаковое число раз любой крайний член пропорции и любой средний.

Например, уменьшив в 4 раза 1-й крайний и 2-й средний члены пропорции 16:8 = 40:20, получим:

3. Одновременное увеличение или уменьшение всех членов пропорции в одинаковое число раз. Пример. 36:12 = 60:20. Увеличим все четыре числа в 2 раза:

Пропорция не нарушилась. Уменьшим все четыре числа в 4 раза:

Пропорция верна.

Перечисленные преобразования дают возможность, во-первых, упрощать пропорции, а во-вторых, освобождать их от дробных членов. Приведём примеры.

1) Пусть имеется пропорция:

200: 25 = 56: x .

В ней членами первого отношения являются сравнительно большие числа, и если бы мы пожелали найти значение х , то нам пришлось бы выполнять вычисления над этими числами; но мы знаем, что пропорция не нарушится, если оба члена отношения разделить на одно и то же число. Разделим каждый из них на 25. Пропорция примет вид:

8:1 = 56: x .

Мы получили, таким образом, более удобную пропорцию, из которой х можно найти в уме:

2) Возьмём пропорцию:

2: 1 / 2 = 20: 5.

В этой пропорции есть дробный член (1 / 2), от которого можно освободиться. Для этого придётся умножить этот член, например, на 2. Но о д и н средний член пропорции мы не имеем права увеличивать; нужно вместе с ним увеличить какой-нибудь из крайних членов; тогда пропорция не нарушится (на основании первых двух пунктов). Увеличим первый из крайних членов

(2 2) : (2 1 / 2) = 20: 5, или 4: 1 = 20:5.

Увеличим второй крайний член:

2: (2 1 / 2) = 20: (2 5), или 2: 1 = 20: 10.

Рассмотрим ещё три примера на освобождение пропорции от дробных членов.

Пример 1. 1 / 4: 3 / 8 = 20:30.

Приведём дроби к общему знаменателю:

2 / 8: 3 / 8 = 20: 30.

Умножив на 8 оба члена первого отношения, получим:

Пример 2. 12: 15 / 14 = 16: 10 / 7 . Приведём дроби к общему знаменателю:

12: 15 / 14 = 16: 20 / 14

Умножим оба последующих члена на 14, получим: 12:15 = 16:20.

Пример 3. 1 / 2: 1 / 48 = 20: 5 / 6 .

Умножим все члены пропорции на 48:

24: 1 = 960: 40.

При решении задач, в которых встречаются какие-нибудь пропорции, часто приходится для разных целей переставлять члены пропорции. Рассмотрим, какие перестановки являются законными, т. е. не нарушающими пропорции. Возьмём пропорцию:

3: 5 = 12: 20. (1)

Переставив в ней крайние члены, получим:

20: 5 = 12:3. (2)

Переставим теперь средние члены:

3:12 = 5: 20. (3)

Переставим одновременно и крайние, и средние члены:

20: 12 = 5: 3. (4)

Все эти пропорции верны. Теперь поставим первое отношение на место второго, а второе — на место первого. Получится пропорция:

12: 20 = 3: 5. (5)

В этой пропорции мы сделаем те же перестановки, какие делали раньше, т. е. переставим сначала крайние члены, затем средние и, наконец, одновременно и крайние, и средние. Получатся ещё три пропорции, которые тоже будут справедливыми:

5: 20 = 3: 12. (6)

12: 3 = 20: 5. (7)

5: 3 = 20: 12. (8)

Итак, из одной данной пропорции путём перестановки можно получить ещё 7 пропорций, что вместе с данной составляет 8 пропорций.

Особенно легко обнаруживается справедливость всех этих пропорций при буквенной записи. Полученные выше 8 пропорций принимают вид:

а: b = с: d; c: d = a: b ;

d: b = с: a; b: d = a: c;

a: c = b: d; c: a = d: b;

d: c = b: a; b: a = d: c.

Легко видеть, что в каждой из этих пропорций основное свойство принимает вид:

ad = bc.

Таким образом, указанные перестановки не нарушают справедливости пропорции и ими можно пользоваться в случае надобности.

Как рассчитать процент в Google Таблицах

Содержание:

Выражение количества в процентах всегда помогает лучше понять пропорции. Это помогает нам лучше визуализировать количество в нашей голове и отлично подходит для сравнения. Неудивительно, что наиболее распространенные величины, такие как налог с продаж, скидки, банковские процентные ставки и т. д., обычно выражаются в процентах.

В этом уроке мы покажем вам, как использовать процентный формат Google Таблиц, чтобы упростить вам расчет и отображение процентов.

Что такое процент?

Термин процент или процент означает одну часть от ста. Вместо того, чтобы выражать соотношение в виде дроби случайного числа, мы обычно выражаем его в долях от ста.

Таким образом, мы получаем общий базовый уровень, помогающий нам четко видеть разницу в количественных пропорциях.

Зачем использовать процентное соотношение в Google Таблицах?

Процентный формат в таблицах Google — один из самых полезных числовых форматов.

Это помогает вам выражать значения в процентах, не только добавляя знак процента рядом с ним, но также преобразуя число в процентное значение.

Итак, если у вас есть дробное число, например, 0,15 в ячейке, форматирование его в процентном формате автоматически преобразует его в 15%.

Все, что вам нужно сделать, это выбрать ячейку и нажать кнопку «%» на панели инструментов Google Таблиц.Переходя к вопросу о том, почему мы используем проценты в таблицах Google, взгляните на изображения ниже:

Обратите внимание, что процент налога на добавленную стоимость форматируется по-разному для каждого листа. НДС отображается в виде доли от первого изображения, тогда как то же значение отображается в процентах во втором.

Согласитесь, вторую таблицу читать намного легче, чем первую.

Увидев, насколько полезно вычисление процентов, мы собираемся обсудить, как вы можете рассчитать проценты в различных практических ситуациях, например:

расчет процентной доли
расчет процента от общей суммы
расчет процентного изменения

Есть ряд других ситуаций, в которых может применяться процентное соотношение, но в этом уроке мы сосредоточимся только на этих трех.

Как рассчитать процент от пропорции

Первое применение процентов — это вычисление процентной доли. Другими словами, какая часть задачи принадлежит или не принадлежит определенной категории.

Например, в приведенной ниже таблице у нас есть цель продаж, выделенная для каждого сотрудника в столбце B, а продажи, сделанные ими, указаны в столбце C.

Допустим, мы хотим подсчитать, какой процент от поставленной цели достиг каждый человек.

Общая формула для этой ситуации:

Сделанные продажи / назначенная цель * 100

Чтобы применить эту общую формулу к вышеприведенному набору данных, нам нужно выполнить шаги, указанные ниже:

Выберите ячейку D2 (где будет отображаться результат первой строки).
Введите формулу = C2 / B2
Нажмите кнопку «Форматировать как процент» (%) на панели инструментов. Кроме того, вы можете перейти к Формат-> Число-> Процент в строке меню. Это преобразует результат формулы в процент и отобразит знак «%» рядом с результатом.
Вы должны увидеть результат во второй строке столбца D.
Перетащите маркер заполнения вниз, чтобы скопировать формулу в остальные ячейки столбца D.
Если вы видите, что результаты включают десятичные разряды, вы можете удалить десятичный разделитель, чтобы округлить процентное значение до ближайшего целого числа.

Теперь у вас есть список процентов продаж, сделанных каждым сотрудником. Вы обнаружите, что легче увидеть, кто был наиболее эффективным в достижении своих целей.

Как рассчитать процент от общей суммы

Затем давайте посмотрим на ситуацию, когда у нас есть продажи, сделанные каждым сотрудником (при условии, что все они имеют общую цель).

Мы хотим знать, какой процент от общего объема продаж сделал каждый сотрудник.

Общая формула для данного сотрудника будет:

Продажи, сделанные сотрудником / Всего продаж * 100

Общий объем продаж всех сотрудников можно рассчитать с помощью функции СУММ следующим образом:

= СУММ (B2: B6)

Сначала подсчитайте общий объем продаж. Для этого мы можем использовать функцию СУММ и отобразить результат в ячейке B7. Формула расчета итога будет = СУММ (B2: B6).
Затем выберите ячейку C2 (где будет отображаться результат первой строки).
Введите формулу = B2 / $ B $ 7
Нажмите кнопку «Форматировать как процент» (%) на панели инструментов. Кроме того, вы можете перейти к Формат-> Число-> Процент в строке меню. Это преобразует результат формулы в процент и отобразит знак «%» рядом с результатом.
Вы должны увидеть результат во второй строке столбца C.
Перетащите маркер заполнения вниз, чтобы скопировать формулу в остальные ячейки столбца C.
Если вы видите, что результаты включают десятичные разряды, вы можете удалить десятичный разделитель, чтобы округлить процентное значение до ближайшего целого числа.

Теперь у вас есть список процентов от общего объема продаж, совершенных каждым сотрудником.

Вы обнаружите, что легче увидеть, какой сотрудник внес наибольший или наименьший вклад в общий объем продаж. Вы даже можете использовать это, чтобы оценить их эффективность за определенный период времени.

Мы также рассмотрим подобную ситуацию в следующем разделе.

Объяснение формулы

Вы заметите, что мы использовали более или менее ту же базовую формулу, что и в предыдущем случае, но с очень небольшой разницей. Мы использовали абсолютную ссылку на общий объем продаж (ячейка B7).

Знак доллара ($) используется, чтобы указать, что ссылка является абсолютной, поэтому она не изменяется при копировании формулы в другие ячейки.

Мы делаем это, чтобы гарантировать, что каждое значение ячейки столбца B делится на одно и то же значение ячейки (в B7). Таким образом, каждый новый результат в столбце C будет рассчитываться на основе суммы в ячейке B7:

= B2 / $ B $ 7

Примечание: если мы просуммируем все проценты в столбце C, мы должны получить в сумме 100%, что, очевидно, имеет смысл.

Как рассчитать процентное изменение

Когда у вас есть процент продаж сотрудника, рассчитанный за каждый месяц или неделю, становится легко отслеживать их эффективность.

Вы можете легко увидеть, увеличивается или уменьшается их процент.

Давайте теперь рассмотрим ситуацию, когда у нас есть продажи, сделанные сотрудниками на 1-й и 2-й неделе.

Мы хотим знать, какое процентное изменение (улучшение или снижение) произошло в продажах каждого сотрудника.

Общая формула для этой ситуации:

(Новое значение - Старое значение) / Старое значение * 100

Выберите ячейку D2 (где будет отображаться результат первой строки).
Введите формулу = (C2-B2) / B2
Нажмите кнопку «Форматировать как процент» (%) на панели инструментов. Кроме того, вы можете перейти к Формат-> Число-> Процент в строке меню. Это преобразует результат формулы в процент и отобразит знак% рядом с результатом.
Вы должны увидеть результат во второй строке столбца D.
Перетащите маркер заполнения вниз, чтобы скопировать формулу в остальные ячейки столбца D.
Если вы видите, что результаты включают десятичные разряды, вы можете удалить десятичный разделитель, чтобы округлить процентное значение до ближайшего целого числа.

Теперь у вас есть список процентного увеличения / уменьшения продаж каждого сотрудника за недельный период.

Вы обнаружите, что легче увидеть, проанализировать, сравнить и отследить их работу в течение нескольких недель, месяцев или даже лет.

В этом руководстве мы показали вам, как рассчитывать проценты в Google Таблицах .

Мы согласны с тем, что существует множество других ситуаций, в которых необходимо вычислить процентное соотношение, но мы предполагаем, что этих трех примеров будет достаточно, чтобы дать вам общее представление о ваших возможностях благодаря функции «Форматировать как процент».

Мы рекомендуем вам применить это небольшое удобство к вашим повседневным потребностям в обработке данных и надеемся, что это поможет вам выполнять свою работу хотя бы на небольшой процент быстрее.

Как рассчитать процентное увеличение или уменьшение в Excel

Если вы боретесь с расчетом процентного увеличения или уменьшения в Microsoft Excel, это руководство расскажет вам об этом процессе.

Microsoft Excel отлично подходит как для базовых, так и для сложных расчетов, включая процентные различия. Если вам сложно рассчитать процентное увеличение или уменьшение на бумаге, Excel может сделать это за вас.

Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)

Если вы помните свою школьную математику, процесс вычисления процентов в Excel очень похож. Вот как использовать Excel для расчета процентного увеличения и уменьшения.

И выполнять другие процентные вычисления, такие как процентное отношение числа.

Расчет процентного увеличения в Excel

Процент увеличения включает в себя два числа. Основной математический подход для расчета процентного увеличения состоит в том, чтобы вычесть второе число из первого числа. Используя сумму этой цифры, разделите эту оставшуюся цифру на исходное число.

Пример, стоимость счета домашнего хозяйства стоит $ 100 в сентябре, но $ 125 в октябре. Чтобы рассчитать эту разницу, вы можете использовать формулу = СУММ (125-100) / 100 в Excel.

Если ваши цифры находятся в отдельных ячейках, вы можете заменить числа для ссылок на ячейки в своей формуле.

Например, если сумма счета за сентябрь находится в ячейке B4 и сумма счета за октябрь находится в камере B5, ваша альтернативная формула Excel будет = СУММ (B5-B4) / B4

Процентное увеличение в период с сентября по октябрь 25%с этой цифрой в виде десятичного числа (0,25) по умолчанию в Excel, используя формулу выше.

Если вы хотите отобразить этот показатель в процентах в Excel, вам нужно заменить форматирование для вашей ячейки.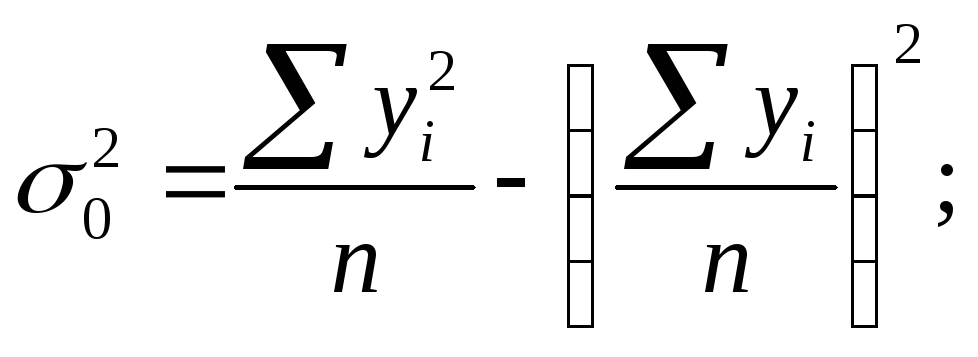 Выберите свою ячейку, затем нажмите Процент Стиль кнопка в Дом вкладка, под номер категория.

Вы также можете щелкнуть правой кнопкой мыши на вашей ячейке, нажмите Формат ячеек затем выберите Процентное соотношение от Категория -> Номер меню для достижения того же эффекта.

Расчет процентного снижения в Excel

Чтобы рассчитать процентное уменьшение между двумя числами, вы будете использовать расчет, идентичный процентному увеличению. Вы вычитаете второе число из первого, а затем делите его на первое число. Разница лишь в том, что первое число будет меньше второго.

Продолжая приведенный выше пример, если счет домохозяйства $ 125 в октябре, но возвращается $ 100 в ноябре вы использовали бы формулу = СУММ (100-125) / 125,

Использование ссылок на ячейки, если сумма счета за октябрь $ 125 находится в камере B4 и сумма счета за ноябрь $ 100 находится в камере B5, ваша формула Excel для процентного уменьшения будет = СУММ (В4-В5) / В5.

Разница между показателями за октябрь и ноябрь 20%, Excel отображает это как отрицательное десятичное число (-0,2) в клетках B7 и B8 над.

Установка типа номера ячейки в Процентное соотношение с использованием Кнопка «Стили в процентах» изменит десятичную цифру (-0,2) в процентах (-20%).

Расчет процента как пропорция

Excel также может помочь вам рассчитать процент как пропорцию. В этом разница между одним числом, как вашей полной цифрой, и меньшим числом. Это требует еще более простого математического расчета, чем процентное изменение.

Например, если у вас есть долг $ 100, и вы уже заплатили $ 50, то доля долга, который вы заплатили (и по совпадению все еще должны) 50%, Чтобы рассчитать это, вы просто разделить 50 на 100,

В Excel формула для расчета этого примера будет = 50/100, Используя ссылки на ячейки, где $ 100 находится в камере B3 и $ 50 находится в камере B4требуется формула = B4 / B3.

При этом используется только базовый оператор деления, чтобы получить результат в виде десятичного числа (0,5).

Преобразование этого типа номера ячейки в Процентное соотношение кликнув Домой> Кнопка Процент Стиль покажет правильную процентную цифру 50%.

Как рассчитать проценты числа

Расчет процента числа — это то, с чем вы столкнетесь в повседневной жизни. Хорошим примером будет предмет для продажи, где скидка составляет 20% применяется к первоначальной цене $ 200. Сотрудник магазина должен знать, что такое 20% от 200 долларов. Затем они могли бы вычесть это число из первоначальной цены, чтобы предоставить цену со скидкой.

Это требует еще одного простого математического вычисления в Excel. Знак умножения (*) и знак процента (%) используются здесь. Вычислить 20% от суммы $ 200, вы можете использовать либо = 20% * 200 или = 0,2 * 200 сделать расчет в Excel.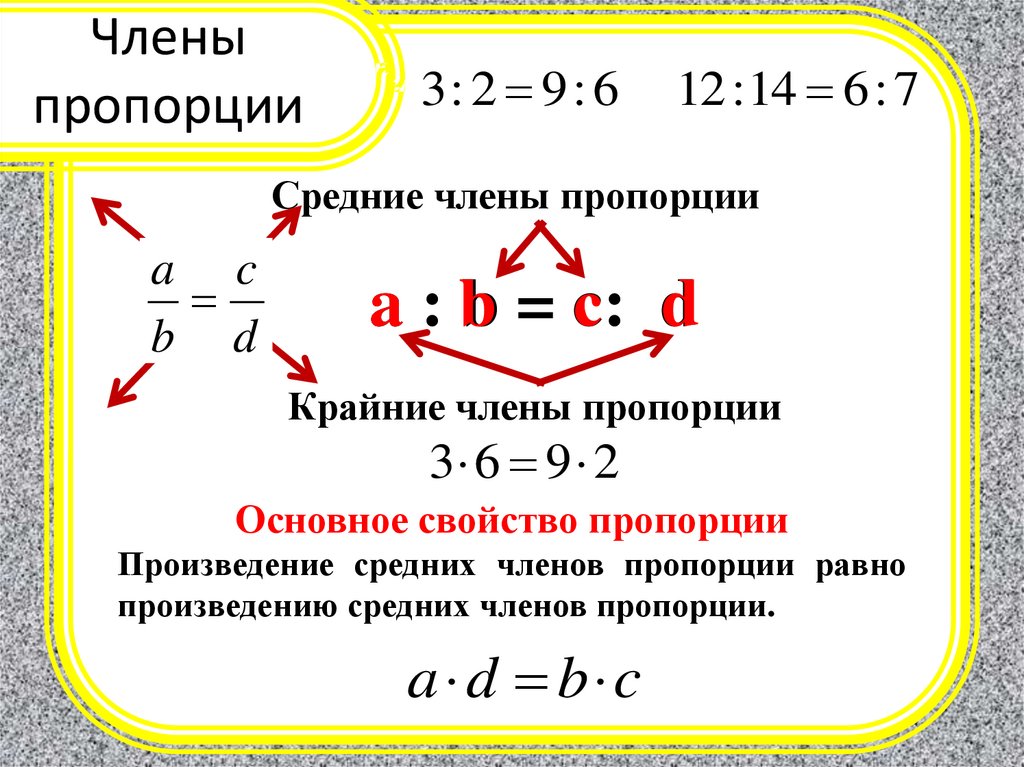

Использовать ссылки на ячейки, где 20% находится в клавише B4 и первоначальная цена $ 200 находится в клавише B5, вы можете использовать формулу = B4 * B5.

Результат тот же, используете ли вы 20%, 0.2 или отдельные ссылки на ячейки в вашей формуле.

20% от 200 долларов равно $ 40, как показано в ячейках От B6 до B8 над.

Использование Excel для сложных расчетов

Как показывает это руководство, Excel отлично подходит для простых вычислений, но он также обрабатывает и более сложные.

Расчеты с использованием таких функций, как функция VLOOKUP, упрощаются благодаря встроенному инструменту поиска функций.

Если вы новичок в Excel, воспользуйтесь советами Excel, которые должен знать каждый пользователь, для дальнейшего повышения производительности.

Оценка/Формула расчета среднего балла

Факультет сообщит об окончательных оценках в офис регистратора после представления оценок крайний срок в конце каждого семестра. Информация об оценках, включая академическую успеваемость учащегося не публикуются в академических записях студентов до конца семестра и не считаются официальными до тех пор, пока не будет завершена вся обработка в конце срока, обычно это происходит в течение трех рабочих дней после последнего дня выпускных экзаменов. Оценки за краткосрочные занятия можно просмотреть в записях академического консультирования студентов. если оценки были выставлены преподавателем.

В обязанности учащегося входит активный мониторинг баннерной сети и проверка их окончательные оценки после каждого семестра зачисления. Новые и возвращающиеся студенты получают учетные данные для входа в свою учетную запись почты Cat в начале семестра.

Оценка «Незавершенный» Указывает, что курсовая работа с номером 1000 и выше была завершена. удовлетворительный; но по неакадемическим причинам, не зависящим от студента, студент не смог выполнить все требования курса. Инструктор по курсу может поставить учащемуся неполную оценку («I»), и учащийся должен выполнить оставшиеся задание к концу следующего семестра зачисления убрать «Я». Без что касается зачисления, «I» должно быть удалено в течение одного календарного года. Если факультет Преподаватель не подал форму изменения оценки за курс, офис записи заменит неполную оценку оценкой «F» и пересчитает баллы учащегося. средний балл. Курс с неразрешенной оценкой «Незавершенный» не может быть повторен.

Сомнительные оценки

Если оценка кажется неправильной, учащийся должен немедленно уведомить об этом преподавателя. Окончательные оценки не будут изменены по истечении одного календарного года с назначенной даты и считаются частью постоянной академической успеваемости учащегося для EGSC. Ученики кто хочет обжаловать свою оценку, должен обратиться к политике учреждения для окончательного Разместите апелляцию об оценке курса на веб-странице Президента, посвященной политикам и процедурам, и заполните Форму апелляции об оценке.

Список декана (отличие или заслуга)

Студент со средним баллом за семестр 3,5 или выше за 15 или более часов Конечно, работа будет помещена в список чести декана за этот семестр.

Студент со средним семестровым баллом 3,5 или выше по крайней мере за 12 семестровых часов, но менее 15 семестровых часов курсовой работы будут помещены в список заслуг декана .

Учрежденческие кредит-часы не учитываются при определении чести или заслуг декана. Список. В этих расчетах используется только кредит степени.

Расчет среднего балла

Средний балл (GPA) рассчитывается путем умножения кредитов для каждого курса баллами, связанными с полученной оценкой, и суммой заработанных баллов для всех курсов, разделив общее количество баллов на количество кредитов, вы получите средний балл.

Следующие оценки были одобрены для использования Государственным колледжем Восточной Джорджии и включаются в определение среднего балла:

Статус	Марка	Баллы
Отлично	А	4
Хороший	Б	3
Среднее	С	2
Бедный	Д	1
Ошибка	F или WF	0
Удовлетворительно/пройдено	С	0
Неудовлетворительно/Неудовлетворительно	Ф	0

Следующие оценки были одобрены для использования Государственным колледжем Восточной Джорджии и , а не учитываются при определении среднего балла:

Марка	Описание
Я	Указывает, что учащийся не смог выполнить все требования для завершения курс по неакадемическим причинам, не зависящим от студентов; контроль.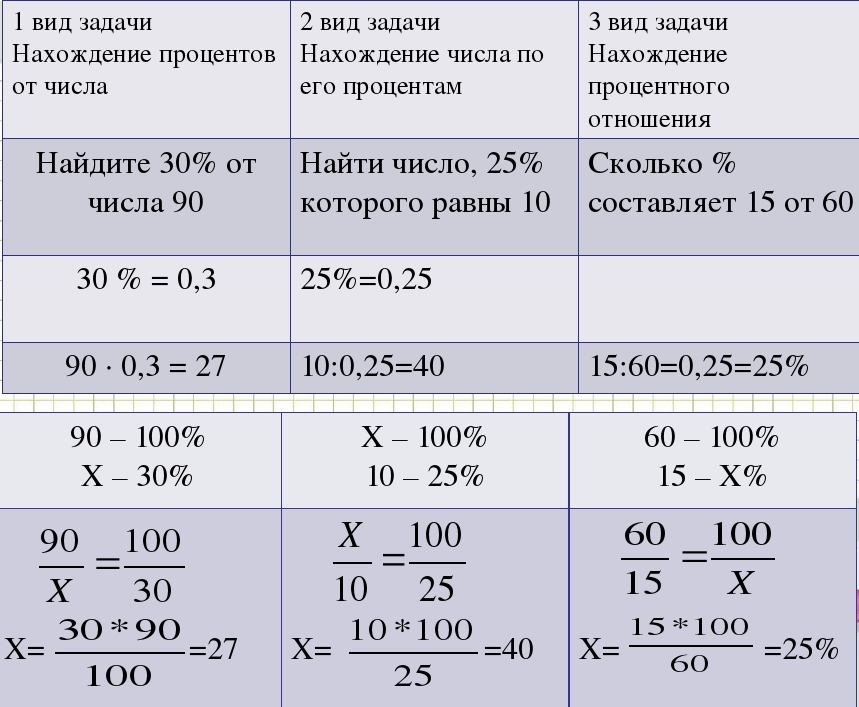 Неполный Если оценка (I) не будет удалена, в следующем семестре она будет преобразована в F.
ИП	Указывает, что учащийся не достиг компетенции, необходимой для завершения обучения. Курс поддержки обучения. Студент должен снова записаться на курс в следующих случаях: семестр.
К	Указывает зачет по экзамену по курсу по утвержденной экзаменационной программе (т.е. АП, КЛЕП и др.)
NR	Указывает, что за курс не выставлена оценка. Студент должен обратиться Инструктор немедленно.
Ш*	Указывает, что учащемуся было разрешено уйти без академического штрафа.
ВМ*	Указывает, что студент, зачисленный в вооруженные силы, получил приказ и должен уйти со всех классов. 100% возврат средств за обучение, оплаченное студенту.
С	Указывает на удовлетворительную или неудовлетворительную оценку
В	Указывает курс, выбранный Аудитом. Студенты не могут перевестись с аудита на зачет статус курса или наоборот.

*Оценка засчитывается в часы попыток

Об ИМТ для взрослых | Здоровый вес, питание и физическая активность

Калькулятор ИМТ для взрослых

Индекс массы тела (ИМТ) — это вес человека в килограммах, разделенный на квадрат роста в метрах. ИМТ — это недорогой и простой метод скрининга весовой категории — недостаточный вес, нормальный вес, избыточный вес и ожирение.

ИМТ не измеряет телесный жир напрямую, но ИМТ умеренно коррелирует с более прямыми измерениями телесного жира ^1,2,3 . Кроме того, ИМТ, по-видимому, так же сильно коррелирует с различными исходами обмена веществ и заболеваний, как и эти более прямые показатели ожирения ^4,5,6,7,8,9 .

Как используется ИМТ?
Каковы тенденции ИМТ для взрослых в США?
Почему ИМТ используется для измерения избыточного веса и ожирения?
Какие существуют другие способы оценки избыточной массы тела помимо ИМТ?
Как рассчитывается ИМТ?

Как интерпретируется ИМТ для взрослых?
Интерпретируется ли ИМТ для детей и подростков так же, как и для взрослых?
Насколько хорош ИМТ как индикатор ожирения?
Если спортсмен или другой человек с большой мускулатурой имеет ИМТ более 25, считается ли этот человек избыточным весом?
Каковы последствия ожирения для здоровья взрослых?

Как используется ИМТ?

ИМТ

может быть инструментом скрининга, но он не диагностирует полноту тела или здоровье человека. Чтобы определить, представляет ли ИМТ риск для здоровья, поставщик медицинских услуг проводит дополнительные оценки. Такие оценки включают измерение толщины кожной складки, оценку диеты, физической активности и семейный анамнез ¹⁰ .

К началу страницы

Каковы тенденции ИМТ для взрослых в США?

Распространенность ИМТ у взрослых больше или равна 30 кг/м ² (статус ожирения) значительно увеличился с 1970-х годов. Однако в последнее время эта тенденция выровнялась, за исключением пожилых женщин. Ожирение продолжает расти среди взрослых женщин в возрасте 60 лет и старше.

Чтобы узнать больше о тенденциях ожирения среди взрослых, посетите раздел Факты о ожирении среди взрослых.

К началу страницы

Почему ИМТ используется для измерения избыточного веса и ожирения?

Поскольку для расчета требуется только рост и вес, ИМТ является недорогим и простым инструментом. Чтобы увидеть формулу, основанную на килограммах и метрах или фунтах и дюймах, посетите страницу Как рассчитывается ИМТ?

К началу страницы

Какие существуют другие способы оценки избыточной массы тела помимо ИМТ?

Другие методы измерения жировых отложений включают измерение толщины кожной складки (калипером), подводное взвешивание, биоэлектрический импеданс, двухэнергетическую рентгеновскую абсорбциометрию (DXA) и изотопное разведение ^1,2,3 . Однако эти методы не всегда доступны, они либо дороги, либо требуют проведения высококвалифицированным персоналом. Кроме того, многие из этих методов может быть трудно стандартизировать для наблюдателей или машин, что усложняет сравнение между исследованиями и периодами времени.

К началу страницы

Как рассчитывается ИМТ?

ИМТ рассчитывается одинаково как для взрослых, так и для детей. Расчет производится по следующим формулам:

ИМТ рассчитывается одинаково как для взрослых, так и для детей. Расчет производится по следующим формулам:
Единицы измерения	Формула и расчет
Килограммы и метры (или сантиметры)	Формула: вес (кг) / [рост (м)] ² В метрической системе формулой для ИМТ является вес в килограммах, деленный на рост в метрах в квадрате. Поскольку рост обычно измеряется в сантиметрах, разделите рост в сантиметрах на 100, чтобы получить рост в метрах. Пример: Вес = 68 кг, Рост = 165 см (1,65 м) Расчет: 68 ÷ (1,65) ² = 24,98
Фунты и дюймы	Формула: вес (фунты) / [высота (дюймы)] ² x 703 Рассчитайте ИМТ, разделив вес в фунтах (фунтах) на рост в дюймах (дюймах) в квадрате и умножив на коэффициент преобразования 703. Пример: Вес = 150 фунтов, высота = 5 футов 5 дюймов (65 дюймов) Расчет: [150 ÷ (65) ² ] x 703 = 24,96

К началу страницы

Как интерпретируется ИМТ для взрослых?

Для взрослых 20 лет и старше ИМТ интерпретируется с использованием стандартных категорий весового статуса. Эти категории одинаковы для мужчин и женщин всех типов телосложения и возрастов.

Стандартные категории статуса веса, связанные с диапазонами ИМТ для взрослых, показаны в следующей таблице.
ИМТ	Статус веса
Ниже 18,5	Недостаточный вес
18,5 – 24,9	Здоровый вес
25,0 – 29,9	Избыточный вес
30,0 и выше	Ожирение

Например, вот диапазоны веса, соответствующие диапазоны ИМТ и категории веса для человека ростом 5 футов 9 дюймов. ″.

Начало страницы

Для детей и подростков интерпретация ИМТ зависит от возраста и пола. Для получения дополнительной информации об интерпретации для детей и подростков прочитайте – Что такое процентиль ИМТ и как его интерпретировать?

Интерпретируется ли ИМТ для детей и подростков так же, как и для взрослых?

ИМТ интерпретируется по-разному для детей и подростков, хотя он рассчитывается по той же формуле, что и ИМТ для взрослых. ИМТ детей и подростков должен быть привязан к возрасту и полу, поскольку количество жира в организме меняется с возрастом, а количество жира в организме различается у девочек и мальчиков. Диаграммы роста ИМТ к возрасту CDC учитывают эти различия и визуально отображают ИМТ в виде процентиля. Эти процентили были определены с использованием репрезентативных данных населения США в возрасте от 2 до 19 лет.-летки, собранные в различных обследованиях с 1963-65 по 1988-94 ¹¹ .

Ожирение среди детей в возрасте от 2 до 19 лет определяется как ИМТ, равный или превышающий 95 ^th процентиль детей того же возраста и пола в этой контрольной популяции с 1963 по 1994 год. Например, 10-летний мальчик среднего роста (56 дюймов) и весом 102 фунта будет иметь ИМТ 22,9 кг/м ² . Это поместит мальчика в 95 ^th процентилей по ИМТ, что означает, что его ИМТ больше, чем у 9.5% мальчиков того же возраста в этой референтной популяции — и он будет считаться страдающим ожирением.

Для получения дополнительной информации и доступа к диаграммам роста CDC

Для взрослых интерпретация ИМТ не зависит от пола или возраста. Узнайте больше об интерпретации ИМТ взрослых.

К началу страницы

Насколько хорош ИМТ как показатель полноты тела?

Корреляция между ИМТ и ожирением довольно сильная ^1,2,3,7 , но даже если два человека имеют одинаковый ИМТ, их уровень ожирения может различаться ¹² .

В целом,

При одинаковом ИМТ у женщин, как правило, больше жировых отложений, чем у мужчин.
При одинаковом ИМТ количество жира в организме может быть выше или ниже в зависимости от расовой/этнической группы ^13-15 .
При одинаковом ИМТ у пожилых людей в среднем больше жира, чем у молодых людей.
При одинаковом ИМТ у спортсменов меньше жира, чем у неспортсменов.

Точность ИМТ как индикатора жировых отложений также выше у лиц с более высокими уровнями ИМТ и жировых отложений ¹⁶ . В то время как человек с очень высоким ИМТ (например, 35 кг/м ² ), скорее всего, будет иметь высокий уровень жира в организме, относительно высокий ИМТ может быть результатом либо высокого содержания жира в организме, либо высокой мышечной массы тела (мышечной и кость). Обученный поставщик медицинских услуг должен провести соответствующую оценку состояния здоровья человека и оценить риски.

К началу страницы

Если спортсмен или другой человек с большой мускулатурой имеет ИМТ более 25, считается ли этот человек избыточным весом?

В соответствии с весовыми категориями ИМТ любой человек с ИМТ от 25 до 29,9 будет классифицирован как страдающий избыточным весом, а любой с ИМТ более 30 будет классифицирован как страдающий ожирением.

Тем не менее, у спортсменов может быть высокий ИМТ из-за увеличения мышечной массы, а не увеличения жировых отложений. В целом, человек с высоким ИМТ, скорее всего, будет иметь ожирение и будет считаться страдающим избыточным весом или ожирением, но это может не относиться к спортсменам. Обученный поставщик медицинских услуг должен провести соответствующую оценку состояния здоровья человека и оценить риски.

Начало страницы

Каковы последствия ожирения для здоровья взрослых?

Люди с ожирением подвержены повышенному риску многих заболеваний и состояний здоровья, включая следующие: ^{10, 17, 18}

Все причины смерти (смертность)
Высокое кровяное давление (гипертония)
Высокий уровень холестерина ЛПНП, низкий уровень холестерина ЛПВП или высокий уровень триглицеридов (дислипидемия)
Диабет 2 типа
Ишемическая болезнь сердца
Ход
Болезнь желчного пузыря
Остеоартрит (разрушение хряща и кости в суставе)
Апноэ во сне и проблемы с дыханием
Хроническое воспаление и повышенный окислительный стресс ^19,20
Некоторые виды рака (эндометрия, молочной железы, толстой кишки, почек, желчного пузыря и печени)
Низкое качество жизни
Психические заболевания, такие как клиническая депрессия, тревога и другие психические расстройства ^21,22
Боль в теле и трудности с физическим функционированием ²³

Для получения дополнительной информации об этих и других проблемах со здоровьем, связанных с ожирением, посетите веб-сайт Health Effects.

Начало страницы

¹ Гарроу, Дж.С. & Webster, J., 1985. Индекс Кетле (Вт/ч3) как показатель упитанности. Междунар. J. Obes ., 9(2), стр. 147–153.

² Фридман, Д.С., Хорлик, М. и Беренсон, Г.С., 2013. Сравнение уравнений Слотера для толщины кожной складки и ИМТ в прогнозировании уровня жира в организме и факторов риска сердечно-сосудистых заболеваний у детей. 900:15 утра. Дж. Клин. Нутр. , 98 (6), стр. 1417–24.

³ Wohlfahrt-Veje, C. et al., 2014. Телесный жир в детстве у 2647 здоровых датских детей: согласование ИМТ, окружности талии, кожных складок с двойной рентгеновской абсорбциометрией. евро. Дж. Клин. Нутр. , 68 (6), стр. 664–70.

⁴ Steinberger, J. et al., 2005. Сравнение измерений жировых отложений по ИМТ и кожным складкам с двухэнергетической рентгеновской абсорбциометрией и их связь с сердечно-сосудистыми факторами риска у подростков. Междунар. Дж. Обес. , 29 (11), стр. 1346–1352.

⁵ Sun, Q. et al., 2010. Сравнение двухэнергетических рентгеновских абсорбциометрических и антропометрических измерений ожирения по отношению к биологическим факторам, связанным с ожирением. утра. Дж. Эпидемиол. , 172 (12), стр. 1442–1454.

⁶ Лоулор, Д.А. и др., 2010. Связь между общим и центральным ожирением в детстве и его изменением с факторами риска сердечно-сосудистых заболеваний в подростковом возрасте: проспективное когортное исследование. BMJ , 341, p.c6224.

⁷ Флегаль, К.М. & Graubard, B.I., 2009. Оценки избыточной смертности, связанные с индексом массы тела и другими антропометрическими переменными. утра. Дж. Клин. Нутр. , 89 (4), стр. 1213–1219.

⁸ Фридман Д. С. и др., 2009 г. Связь индекса массы тела и толщины кожной складки с факторами риска сердечно-сосудистых заболеваний у детей: исследование сердца Богалусы. утра. Дж. Клин. Нутр ., 90(1), с.210–216.

⁹ Willett, K. et al., 2006. Сравнение биоэлектрического импеданса и ИМТ в прогнозировании заболеваний, связанных с ожирением. Обес. (Серебряный источник) , 14 (3), стр. 480–490.

¹⁰ НХЛБИ. 2013. Борьба с избыточным весом и ожирением у взрослых: систематический обзор данных от группы экспертов по ожирению [PDF – 5,98 МБ]

¹¹ Kuczmarski, R.J. et al., 2002. Диаграммы роста CDC за 2000 год для США: методы и разработка. Жизненный показатель здоровья . 11., 11(246), стр. 1–190.

¹² Прентис, А.М. & Джебб, С.А., 2001. Помимо индекса массы тела. Обес. Rev ., 2(3), стр. 141–7.

¹³ Вагнер, Д.Р. & Heyward, VH, 2000. Показатели состава тела у черных и белых: сравнительный обзор. утра. Дж. Клин. Нутр ., 71(6), стр.1392–1402.

¹⁴ Флегал, К.М. et al., 2010. Высокая степень ожирения и высокий индекс массы тела к возрасту у детей и подростков в США в целом и в разбивке по расово-этническим группам. 900:15 утра. Дж. Клин. Нутр ., 91(4), стр.1020–6.

¹⁵ Barba, C. et al., 2004. Соответствующий индекс массы тела для населения Азии и его последствия для политики и стратегий вмешательства. Ланцет , 363 (9403), стр. 157–163.

¹⁶ Брей, Г.А. и др., 2001. Оценка жировых отложений у полных и стройных 10-летних афроамериканцев и белых детей: Детское исследование Батон-Руж. утра. Дж. Клин. Нутр ., 73(4), с.687–702.

¹⁷ Клинические рекомендации по выявлению, оценке и лечению избыточного веса и ожирения у взрослых [PDF – 1,25 МБ].

¹⁸ Bhaskaran K, Douglas I, Forbes H, dos-Santos-Silva I, Leon DA, Smeeth L. Индекс массы тела и риск 22 конкретных видов рака: популяционное когортное исследование 5•24 миллионов Великобритании взрослые люди. Ланцет. 2014 30 августа; 384 (9945): 755-65. doi: 10.1016/S0140-6736(14)60892-8. Epub 2014 Aug 13.

¹⁹ Engstrom G, Hedblad B, Stavenow L, Lind P, Janzon L and Lingarde F. Чувствительные к воспалению белки плазмы связаны с увеличением веса в будущем. Диабет. август 2003 г.; 52(08): 2097-101.

²⁰ Marseglia L, Manti S, D’Angelo G, Nicotera A, Parisi E, DiRosa G, Gitto E, Arrigo T. Окислительный стресс при ожирении: критический компонент болезней человека. Международный журнал молекулярных наук. декабрь 2014 г.; 16(1):378-400.

²¹ Касен, Стефани и др. «Ожирение и психопатология у женщин: проспективное исследование за три десятилетия». Международный журнал ожирения 32.3 (2008): 558-566.

²² Луппино, Флориана С. и др. «Избыточный вес, ожирение и депрессия: систематический обзор и метаанализ продольных исследований». Архив общей психиатрии 67.3 (2010): 220-229.

²³ Хан Т. С. и др. «Качество жизни по отношению к избыточному весу и распределению жира в организме». Американский журнал общественного здравоохранения 88.12 (1998): 1814-1820.

Формула и расчет совокупного годового темпа роста (CAGR)

Что такое совокупный годовой темп роста (CAGR)?

Совокупный годовой темп роста (CAGR) — это норма прибыли (RoR), которая потребуется для того, чтобы инвестиции росли от начального баланса до конечного баланса, при условии, что прибыль реинвестируется в конце каждого периода жизненного цикла инвестиции. .

Основные выводы

Совокупный годовой темп роста (CAGR) является одним из наиболее точных способов расчета и определения доходности всего, что может расти или падать в цене с течением времени.
Измеряет сглаженную норму доходности.
Инвесторы могут сравнить CAGR двух или более альтернатив, чтобы оценить, насколько хорошо одна акция работает по сравнению с другими акциями в аналогичной группе или рыночному индексу. Таким образом,
CAGR — это хороший способ оценить эффективность различных инвестиций с течением времени или в сравнении с эталоном. 9{\frac{1}{n}}-1\times 100\\&\textbf{где:}\\&EV = \text{Конечное значение}\\&BV = \text{Начальное значение}\\&n = \text {Количество лет}\end{выровнено} CAGR=(BVEV)n1−1×100где:EV=Конечное значениеBV=Начальное значениеn=Количество лет
Чтобы рассчитать CAGR инвестиции:
1. Разделите стоимость инвестиции в конце периода на ее стоимость в начале этого периода.
2. Возведите результат в степень единицы, деленной на количество лет.
3. Вычтите единицу из последующего результата.
4. Умножьте на 100, чтобы преобразовать ответ в проценты.
Что CAGR может сказать вам
Совокупный годовой темп роста – это не реальная доходность, а репрезентативная цифра. По сути, это число, которое описывает скорость, с которой инвестиции росли бы, если бы они росли с одинаковой скоростью каждый год, а прибыль реинвестировалась бы в конце каждого года.
На самом деле такая производительность маловероятна. Однако CAGR можно использовать для сглаживания возвратов, чтобы их было легче понять по сравнению с альтернативными методами.
Пример использования CAGR
Представьте, что вы вложили 10 000 долларов в портфель с доходностью, описанной ниже:
- С 1 января 2018 г. по 1 января 2019 г. ваш портфель вырос до 13 000 долларов США (или 30% за первый год).
- На 1 января 2020 года портфель составлял 14 000 долларов США (или 7,69% с января 2019 года по январь 2020 года).
- На 1 января 2021 года портфель закончился с суммой в 19 000 долларов США (или 35,71% с января 2020 года по январь 2021 года).
Мы видим, что в годовом исчислении темпы роста инвестиционного портфеля в годовом исчислении сильно отличались, как показано в скобках. 9{\ гидроразрыва {1} {3}}-1 \ раз 100 = 23,86 \% CAGR = (10 000 долларов США 19 000 долларов США) 31−1 × 100 = 23,86%
CAGR в размере 23,86% за трехлетний инвестиционный период может помочь инвестору сравнить альтернативы для своего капитала или сделать прогнозы будущих значений. Например, представьте, что инвестор сравнивает эффективность двух некоррелированных инвестиций.
В любой конкретный год в течение периода одна инвестиция может расти, а другая падать. Это может иметь место при сравнении высокодоходных облигаций с акциями или инвестиций в недвижимость с развивающимися рынками. Использование CAGR сгладило бы годовой доход за период, чтобы было легче сравнивать два варианта.
В качестве другого примера предположим, что инвестор купил 55 акций Amazon.com (AMZN) в декабре 2017 года по цене 1180 долларов США за акцию, а общая сумма инвестиций составила 64 900 долларов США. Спустя три года, в декабре 2020 года, акции выросли до 3200 долларов за акцию, а инвестиции инвестора теперь составляют 176 000 долларов. Что такое CAGR?
Используя формулу CAGR, мы знаем, что нам нужно:
- Конечный баланс: 176 000 долл. США
- Начальный баланс: 64 900 долл. США
- Количество лет: 3 9(1/3)] — 1 = 39,5%.
  Дополнительные варианты использования CAGR
  CAGR можно использовать для расчета среднего роста одной инвестиции. Как мы видели в нашем примере выше, из-за волатильности рынка годовой рост инвестиций, вероятно, будет неустойчивым и неравномерным.
  Например, инвестиции могут увеличиться в цене на 8% в течение одного года, уменьшиться в цене на -2% в следующем году и увеличиться в цене на 5% в следующем. CAGR помогает сгладить доходность, когда ожидается, что темпы роста будут неустойчивыми и непостоянными.
  Сравнение инвестиций
  CAGR можно использовать для сравнения различных типов инвестиций друг с другом. Например, предположим, что в 2015 году инвестор разместил 10 000 долларов США на счете на пять лет с фиксированной годовой процентной ставкой 1 % и еще 10 000 долларов США во взаимный фонд акций. Норма прибыли в фонде акций будет неравномерной в течение следующих нескольких лет, поэтому сравнение между двумя инвестициями будет затруднено.
  Предположим, что в конце пятилетнего периода остаток на сберегательном счете составляет 10 510,10 долл., и, хотя другие инвестиции росли неравномерно, конечный остаток в фонде акций составил 15 348,52 долл. Использование CAGR для сравнения двух инвестиций может помочь инвестору понять разницу в доходах: 9{\ frac {1} {5}} — 1 \ умножить на 100 = 8,95 \% Фонд акций CAGR = (10 000 долларов США 15 348,52 долларов США) 51−1 × 100 = 8,95%
  На первый взгляд, фонд акций может показаться более выгодным вложением, поскольку его доходность почти в девять раз превышает доходность сберегательного счета. С другой стороны, одним из недостатков CAGR является то, что, сглаживая доходность, CAGR не может сказать инвестору, насколько волатильным или рискованным был фонд акций.
  Характеристики гусеницы
  CAGR также можно использовать для отслеживания эффективности различных бизнес-показателей одной или нескольких компаний наряду друг с другом. Например, за пятилетний период среднегодовой темп роста доли рынка крупных магазинов составил 1,82%, но среднегодовой темп роста удовлетворенности клиентов за тот же период составил -0,58%. Таким образом, сравнение среднегодовых темпов роста показателей внутри компании выявляет сильные и слабые стороны.
  Обнаружение слабых и сильных сторон
  Сравнение среднегодовых темпов роста деловой активности аналогичных компаний поможет оценить слабые и сильные стороны конкурентов. Например, CAGR удовлетворенности клиентов Big-Sale может показаться не таким низким по сравнению с CAGR удовлетворенности клиентов SuperFast Cable, составившим -6,31% за тот же период.
  Как инвесторы используют CAGR
  Понимание формулы, используемой для расчета CAGR, является введением во многие другие способы, которыми инвесторы оценивают прошлые доходы или оценивают будущие прибыли. Формулу можно алгебраически преобразовать в формулу, чтобы найти текущую или будущую стоимость денег или рассчитать пороговую норму прибыли. 9{\ frac {1} {18}} — 1 \ умножить на 100 = 6,90 \% Требуемая доходность = (15 000 долл. США 50 000 долларов ) 181−1 × 100 = 6,90%
  Эта версия формулы CAGR представляет собой просто переставленное уравнение текущей стоимости и будущей стоимости. Например, если инвестор знал, что ему нужно 50 000 долларов, и считал разумным ожидать 8% годового дохода от своих инвестиций, он мог использовать эту формулу, чтобы узнать, сколько ему нужно инвестировать для достижения своей цели.
  Изменение формулы CAGR
  Инвестиции редко делаются в первый день года, а затем продаются в последний день года. Представьте себе инвестора, который хочет оценить CAGR инвестиции в размере 10 000 долларов США, которая была введена 1 июня 2013 года и продана за 16 89 долларов США. 7.14 9 сентября 2018 г.
  Прежде чем можно будет выполнить расчет CAGR, инвестору необходимо знать дробный остаток периода владения. Они удерживали позицию в течение 213 дней в 2013 году, полного года в 2014, 2015, 2016 и 2017 годах и 251 дня в 2018 году. Эти инвестиции удерживались в течение 5,271 года, что рассчитывается следующим образом:
  - 2013 = 213 дней
  - 2014 = 365
  - 2015 = 365
  - 2016 = 365
  - 2017 = 365
  - 2 201896
  Общее количество дней, в течение которых удерживались инвестиции, составило 1 924 дня. Чтобы рассчитать количество лет, разделите общее количество дней на 365 (1924/365), что равно 5,271 года.
  Общее количество лет, в течение которых удерживались инвестиции, может быть помещено в знаменатель показателя степени в формуле CAGR следующим образом:
  Инвестиции CAGR знак равно ( $ 16 , 897,14 $ 10 , 000 ) 1 5.271 − 1 × 100 знак равно 10.46 % \text{CAGR инвестиций} =\, \left ( \frac{\$ 16,89{\ гидроразрыва {1} {5,271}} -1 \ умножить на 100 = 10,46 \% Инвестиции CAGR=(10 000 долларов США 16 897,14 )5,2711 −1 × 100 = 10,46%
  Плавное ограничение скорости роста
  Наиболее важным ограничением CAGR является то, что, поскольку он рассчитывает сглаженный темп роста за период, он игнорирует волатильность и подразумевает, что рост в течение этого времени был устойчивым. Доходы от инвестиций неравномерны во времени, за исключением облигаций, удерживаемых до погашения, депозитов и аналогичных инвестиций.
  Кроме того, CAGR не учитывает, когда инвестор добавляет средства в портфель или выводит средства из портфеля в течение измеряемого периода.
  Например, если у инвестора есть портфель на пять лет, и он вкладывает средства в портфель в течение пятилетнего периода, CAGR будет завышен. CAGR рассчитывал бы норму доходности на основе начального и конечного балансов за пять лет и, по сути, учитывал бы депонированные средства как часть годового темпа роста, что было бы неточным.
  Другие ограничения CAGR
  Помимо сглаженных темпов роста, CAGR имеет и другие ограничения. Второе ограничение при оценке инвестиций заключается в том, что независимо от того, насколько устойчивым был рост компании или инвестиций в прошлом, инвесторы не могут предполагать, что темпы роста останутся такими же в будущем. Чем короче временной интервал, использованный в анализе, тем меньше вероятность того, что реализованный CAGR будет соответствовать ожидаемому CAGR, если полагаться на исторические результаты.
  Третье ограничение CAGR — это ограничение представительства. Скажем, инвестиционный фонд стоил 100 000 долларов в 2016 году, 71 000 долларов в 2017 году, 44 000 долларов в 2018 году, 81 000 долларов в 2019 году и 126 000 долларов в 2020 году. будет технически правильно. Однако они упускают очень важную информацию об истории фонда, в том числе тот факт, что CAGR фонда за последние пять лет составлял скромные 4,73%.
  CAGR и IRR
  CAGR измеряет доходность инвестиций за определенный период времени. Внутренняя норма доходности (IRR) также измеряет эффективность инвестиций, но является более гибкой, чем CAGR.
  Наиболее важным отличием является то, что CAGR достаточно прост, чтобы его можно было рассчитать вручную. Напротив, более сложные инвестиции и проекты или те, которые имеют много различных притоков и оттоков денежных средств, лучше всего оценивать с помощью IRR. Чтобы вернуться к IRR, идеально подойдет финансовый калькулятор, Excel или система учета портфеля.
  Те, кто заинтересован в том, чтобы узнать больше о CAGR и других финансовых темах, могут захотеть записаться на один из лучших курсов по инвестированию, доступных в настоящее время.
  Что является примером совокупного годового темпа роста (CAGR)?
  CAGR — это показатель, используемый инвесторами для расчета скорости роста количества с течением времени. Слово «компаунд» означает тот факт, что CAGR учитывает эффект компаундирования или реинвестирования с течением времени. Например, предположим, что у вас есть компания, доход которой вырос с 3 до 30 миллионов долларов за 10 лет. В этом случае среднегодовой темп роста составит примерно 25,89.%.
  Что считается хорошим CAGR?
  То, что считается хорошим CAGR, зависит от контекста. Но, вообще говоря, инвесторы будут оценивать это, думая об альтернативных издержках, а также о рискованности инвестиций. Например, если компания выросла на 25% в отрасли со средним CAGR ближе к 30%, то ее результаты могут показаться блеклыми по сравнению с ней. Но если бы темпы роста в масштабах всей отрасли были ниже, например, 10% или 15%, то CAGR мог бы быть очень впечатляющим.
  Как правило, чем выше среднегодовой темп роста, тем лучше.
  В чем разница между CAGR и темпами роста?
  Основное различие между CAGR и темпами роста заключается в том, что CAGR предполагает, что темпы роста повторяются или «усугубляются» каждый год, в то время как традиционные темпы роста этого не делают. Многие инвесторы предпочитают CAGR, потому что он сглаживает волатильность годовых темпов роста. Например, даже высокодоходная и успешная компания, скорее всего, будет иметь несколько лет плохой работы в течение своей жизни. Эти неудачные годы могут оказать большое влияние на темпы роста в отдельные годы, но окажут относительно небольшое влияние на среднегодовой темп роста компании.
  Может ли CAGR быть отрицательным?
  Да. Отрицательный CAGR указывает на потери с течением времени, а не на прибыль.
  Что такое CAGR с поправкой на риск?
  Чтобы сравнить характеристики производительности и риска различных вариантов инвестирования, инвесторы могут использовать CAGR с поправкой на риск.
  No related posts.

Формула пропорции с неизвестным. Задачи на пропорции

Свойства пропорции и формула

Формула пропорций

Основные свойства пропорции

Решение пропорции с одним неизвестным | Уравнение

Как посчитать пропорцию

суббота, 26 октября 2019 г.

среда, 7 августа 2019 г.

воскресенье, 4 августа 2019 г.

суббота, 3 августа 2019 г.

понедельник, 7 января 2019 г.

Как рассчитать процент в Google Таблицах

Что такое процент?

Зачем использовать процентное соотношение в Google Таблицах?

Как рассчитать процент от пропорции

Как рассчитать процент от общей суммы

Объяснение формулы

Как рассчитать процентное изменение

Как рассчитать процентное увеличение или уменьшение в Excel

Расчет процентного увеличения в Excel

Расчет процентного снижения в Excel

Расчет процента как пропорция

Как рассчитать проценты числа

Использование Excel для сложных расчетов

Оценка/Формула расчета среднего балла

Сомнительные оценки

Список декана (отличие или заслуга)

Расчет среднего балла

Об ИМТ для взрослых | Здоровый вес, питание и физическая активность

Как используется ИМТ?

Каковы тенденции ИМТ для взрослых в США?

Почему ИМТ используется для измерения избыточного веса и ожирения?

Какие существуют другие способы оценки избыточной массы тела помимо ИМТ?

Как рассчитывается ИМТ?

Как интерпретируется ИМТ для взрослых?

Интерпретируется ли ИМТ для детей и подростков так же, как и для взрослых?

Насколько хорош ИМТ как показатель полноты тела?

Если спортсмен или другой человек с большой мускулатурой имеет ИМТ более 25, считается ли этот человек избыточным весом?

Каковы последствия ожирения для здоровья взрослых?

Формула и расчет совокупного годового темпа роста (CAGR)

Что такое совокупный годовой темп роста (CAGR)?

Основные выводы

Что CAGR может сказать вам

Пример использования CAGR

Дополнительные варианты использования CAGR

Сравнение инвестиций

Характеристики гусеницы

Обнаружение слабых и сильных сторон

Как инвесторы используют CAGR

Изменение формулы CAGR

Плавное ограничение скорости роста

Другие ограничения CAGR

CAGR и IRR

Что является примером совокупного годового темпа роста (CAGR)?

Что считается хорошим CAGR?

В чем разница между CAGR и темпами роста?

Может ли CAGR быть отрицательным?

Что такое CAGR с поправкой на риск?

Добавить комментарий Отменить ответ