Пересечение нескольких множеств в одну строчку
Сегодня на паре по программированию для журналистики данных мы столкнулись с такой задачей: есть список множеств, нужно найти пересечение их всех. Как это проще всего сделать в Python? Оказывается, у этой задачи есть решение в одну строчку.
Собственно, дело было так. Мы смотрели на данные по госзакупкам через API сайта clearspending.ru. Там у каждого контракта куча разных атрибутов. Как видно из следующих примеров, наборы атрибутов (в данном случае, ключей в словаре) у разных контрактов различаются. Мы хотели найти такие атрибуты, которые есть у всех контрактов.
In [2]:
import requests
# пример из документации
# https://github.com/idalab/clearspending-examples/wiki/Описание-API-Контракты
entrypoint = "http://openapi.clearspending.ru/restapi/v3/contracts/search/"
r = requests.get(entrypoint, {'customerregion': '05', 'sort':'-price'})
response = r.json()
contracts = response['contracts']['data']
In [3]:
contracts[0].keys()
Out[3]:
dict_keys(['finances', 'documentBase', 'versionNumber', 'mongo_id', 'suppliers', 'placingWayCode', 'contractUrl', 'foundation', 'products', 'scan', 'fileVersion', 'contractProcedure', 'economic_sectors', 'signDate', 'fz', 'currentContractStage', 'printFormUrl', 'price', 'protocolDate', 'number', 'regNum', 'currentContractStage_raw', 'loadId', 'attachments', 'customer', 'placing', 'regionCode', 'id', 'currency', 'singleCustomerReason', 'execution', 'publishDate', 'schemaVersion'])
In [4]:
contracts[1].keys()
Out[4]:
dict_keys(['signDate', 'versionNumber', 'mongo_id', 'finances', 'contractUrl', 'foundation', 'misuses', 'regionCode', 'fileVersion', 'documentBase', 'fz', 'currentContractStage', 'price', 'placing', 'number', 'products', 'publishDate', 'customer', 'regNum', 'suppliers', 'id', 'currency', 'execution', 'loadId'])
По такому поводу я рассказал про множества в Python (давно откладывал это — к слову не приходилось) и написал такой код.
In [5]:
fields = set(contracts[0])
# сделали множество из списка ключей первого контракта
# здесь словарь contracts[0] рассматривается как iterable
# а в этом случае он итерирует свои ключи
# поэтому .keys() дописывать не нужно
for contract in contracts[1:]:
fields.intersection_update(contract)
# пересечь множество fields с множеством, полученным из списка ключей
# очередного контракта и результат записать в fields
# иными словами, выкинуть из fields те элементы, которых нет в
# списке ключей очередного контракта
fields
Out[5]:
{'currency',
'customer',
'fileVersion',
'fz',
'id',
'loadId',
'mongo_id',
'number',
'price',
'products',
'publishDate',
'regNum',
'regionCode',
'versionNumber'}sum(). Должно, наверное, и для множеств быть что-то похожее? На паре тратить время на поиски не хотелось, но, придя домой, я всё же решил найти ответ на этот вопрос. Оказывается, есть очень просто решение!
Оказывается, есть очень просто решение!In [6]:
fields = set.intersection(*[set(contract) for contract in contracts]) fields
Out[6]:
{'currency',
'customer',
'fileVersion',
'fz',
'id',
'loadId',
'mongo_id',
'number',
'price',
'products',
'publishDate',
'regNum',
'regionCode',
'versionNumber'}Дело в том, что set.intersection() принимает на вход любое количество аргументов! С помощью спискового включения мы делаем список множеств, составленных из ключей каждого контракта, затем звёздочкой «распаковываем» этот список в набор аргументов set.intersection() — вжух — и всё готово!
Пожалуй, по сравнению с моим исходным подходом есть только один недостаток: по памяти это решение более требовательное, потому что сначала создаётся список, потом он передаётся функции. Причём из-за необходимости распаковывать элементы здесь бессмысленно заменять список на генератор — всё равно память придётся тратить. Впрочем, с практической точки зрения это скорее всего не принципиально.
UPD. После подсказки @rusorrow о том, что .keys() не нужен при создании множества, я подумал, что можно было бы сделать ещё короче: с помощью map — мне кажется, что так даже лучше — это, пожалуй, тот случай, когда map упрощает код по сравнению со списочными включениями.
In [7]:
set.intersection(*map(set, contracts))
Out[7]:
{'currency',
'customer',
'fileVersion',
'fz',
'id',
'loadId',
'mongo_id',
'number',
'price',
'products',
'publishDate',
'regNum',
'regionCode',
'versionNumber'}Tweet
Пересечение множеств
Этот урок объяснит, как найти пересечение множеств. Начнем с определения пересечения двух множеств.
Определение:
Для двух множеств A и B пересечением является множество, содержащее элементы или объекты, принадлежащие A и B одновременно.
Мы пишем A ∩ B
По сути, мы находим A ∩ B, ища все элементы A и B, которые являются общими. Далее разберем на примерах.
Далее разберем на примерах.
Пример #1 .
Чтобы упростить задачу, обратите внимание, что то, что у них есть общего, выделено жирным шрифтом.
Пусть A = { 1 апельсин , 1 ананас, 1 банан, 1 яблоко } и B = { 1 ложка, 1 апельсин , 1 нож, 1 вилка, 1 яблоко }
A= {1 апельсин, 1 яблоко}
Пример #2 .
Найдите пересечение A и B, а затем постройте диаграммы Венна.
А = { б , 1, 2, 4 , 6 } и B = { 4 , a, b , c, d, f }
A ∩ B = { 4, b }
4 9 Пример 3 .
A = { x / x число больше 4 и меньше 8 }
B = { x / x положительное число меньше 7 }
A = { 5 , 6 , 7 } и B = { 1, 2, 3, 4, 5 , 6 }
A ∩ B = { 5, 6 }
Или A ∩ B = { x / x число больше 4 и меньше чем 7 }
Пример #4 .
A = {x/x — страна в Азии}
B = {x/x — страна в Африке}
Поскольку в Азии и Африке нет одинаковых стран, пересечение пусто.
A ∩ B = { }
Пример №5 .
А = {#, %, &, *, $}
B = { }
Этот пример тонкий! Поскольку пустое множество входит в любое множество, оно также входит в A, хотя вы этого не видите.
Таким образом, пустое множество — это единственное, что общего между множествами A и B.
А ∩ В = { }
На самом деле, поскольку пустое множество включено в любое множество, пересечение пустого множества с любым множеством является пустым множеством.
Определение объединения трех множеств:
Пересечением трех множеств A, B и C называется множество, содержащее элементы или объекты, принадлежащие A, B и C одновременно.
Мы пишем A ∩ B ∩ C
По сути, мы находим A ∩ B ∩ C, ища все элементы, которые A, B и C имеют общие.
A = { # , 1, 2, 4 , 6}, B = { # , a, b, 4 , c} и C = A = { #
, %, &, * , $, 4 }A ∩ B ∩ C = { 4 , # }
На приведенном ниже графике показана заштрихованная область пересечения двух множеств
На приведенном ниже графике показана заштрихованная область пересечения трех множеств
На этом урок о пересечении множеств заканчивается. Если у вас есть какие-либо вопросы о пересечении множеств, я буду более чем счастлив ответить на них.
Если у вас есть какие-либо вопросы о пересечении множеств, я буду более чем счастлив ответить на них.
Пройди тест ниже, чтобы узнать, насколько хорошо ты умеешь находить пересечение множеств.
Треугольник 30-60-90
3 апреля, 23 17:08
Что такое треугольник 30-60-90? Определение, доказательство, площадь и простые примеры из реальной жизни.
Подробнее
Расчет условной вероятности с помощью таблицы непредвиденных обстоятельств
29, 23 марта 10:19
Научитесь рассчитывать условную вероятность с помощью таблицы непредвиденных обстоятельств. Эта таблица непредвиденных обстоятельств может помочь вам разобраться быстро и безболезненно.
Подробнее
Дискретная математика — Нахождение пересечения трех множеств
спросил
Изменено 2 года, 2 месяца назад
Просмотрено 6к раз
$\begingroup$
80 учащихся спросили, нравятся ли им математика, естественные науки или гуманитарные науки.
24 учащимся не нравился ни один из предметов, 9понравилась математика только , 16 нравились науки только , 9 нравились гуманитарные науки только , 12 нравились математика и гуманитарные науки, 7 любили математику и естественные науки и 9 любили гуманитарные и наука.
а) Сколько учеников любят все три предмета?
б) Сколько учеников любят математику или естествознание?
в) Сколько студентов не любят гуманитарные науки?
Вот диаграмма Венна, отображающая данную информацию:
а) нахождение пересечения множеств M, S и H
|M∩S∩H|=|M∪S∪H|−(|M|+|S|+|H|)+|M∩S|+|M∩H|+|S∩H|
-2 |M∩S∩H|= (80 — 24) — (9 + 16 + 9) — (12 + 7 + 9)
-2 |M∩S∩H|= 56 — 34 — 28
-2 |M∩S∩H|= 22 — 28
-2 |M∩S∩H|= -6
|M∩S∩H|= 3
Не могу б) или в) потому что, когда я говорю, что пересечение равно 3, все остальные числа на диаграмме Венна меняются (очевидно). Например, если пересечение равно 3, то количество людей, которым нравятся математика и естествознание, = 4 (7 — 3 ) и количество людей, которым нравятся математика и гуманитарные науки = 9 (12 — 3 ).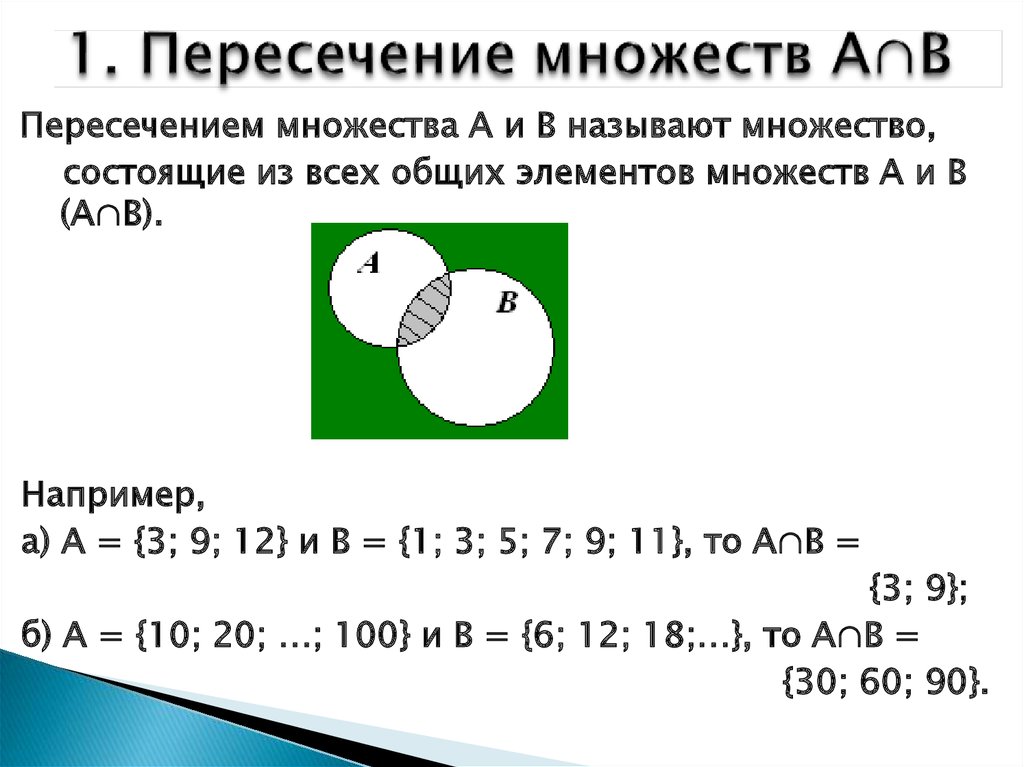 Но когда я складываю новые числа (3 + 9 + 4), я получаю 16, и я не могу сделать 9 — 16 (что равно -5, ОТРИЦАТЕЛЬНОЕ ЧИСЛО!!!). Может кто-нибудь, пожалуйста, дайте мне знать, что у меня есть сделано неправильно, и как, черт возьми, я должен вычислить пересечение трех наборов?! Любая помощь будет принята с благодарностью.
Но когда я складываю новые числа (3 + 9 + 4), я получаю 16, и я не могу сделать 9 — 16 (что равно -5, ОТРИЦАТЕЛЬНОЕ ЧИСЛО!!!). Может кто-нибудь, пожалуйста, дайте мне знать, что у меня есть сделано неправильно, и как, черт возьми, я должен вычислить пересечение трех наборов?! Любая помощь будет принята с благодарностью.
- дискретная математика
- элементарная теория множеств
$\endgroup$
$\begingroup$
Итак, ваша первая проблема заключается в том, что ваша диаграмма Венна не отображает данную информацию, как вы заметили в конце. Это сбивает вас с толку, несмотря на то, что ваше решение по существу правильное, хотя и несколько странно рассчитано (хотя я понятия не имею, почему вы пытаетесь вычислить 9–16 долларов: вам не нужно настраивать внешние значения, потому что они уже в ваша диаграмма Венна правильно; действительно, они даны в вопросе).
Обозначим количество учеников, которым нравятся все три предмета, $x$.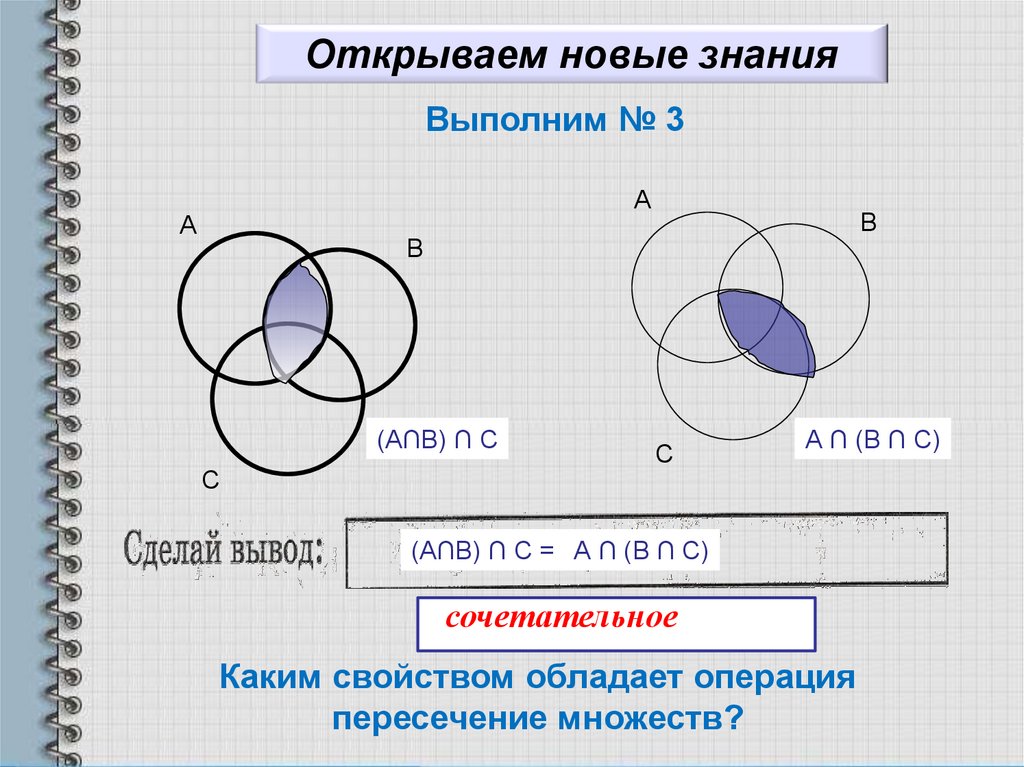 Тогда ваша реальная диаграмма Венна выглядит так:
Тогда ваша реальная диаграмма Венна выглядит так:
Теперь, суммируя все эти значения, мы видим, что 80 долларов = 24 + 9 + 16 + 9 + 7 — х + 9 — х + 12 — х + х = 86 — 2х$, и поэтому 2х долларов = 6 $ и $x = 3$. Таким образом, полная диаграмма Венна выглядит так:
Теперь мы можем решить вопросы, просто прочитав диаграмму.
$\endgroup$
1
$\begingroup$
Вы упускаете из виду, что 7$, которые любят математику и естественные науки, и 12$, которые любят математику и гуманитарные науки, и 9$$ кто любит гуманитарные науки и науки, ПЕРЕКРЫВАЮТ и каждая из этих групп включает тех, кому нравятся все три.
Вы предположили, что это все отдельные и каждая группа исключила те $?$, которым понравились все три.
====
Используйте это изображение вместо
Когда вы говорите $12$ как математика и гуманитарные науки, это двусмысленно относительно того, имеется ли в виду наличие $12$, которые любят математику, гуманитарные науки и не любят науку.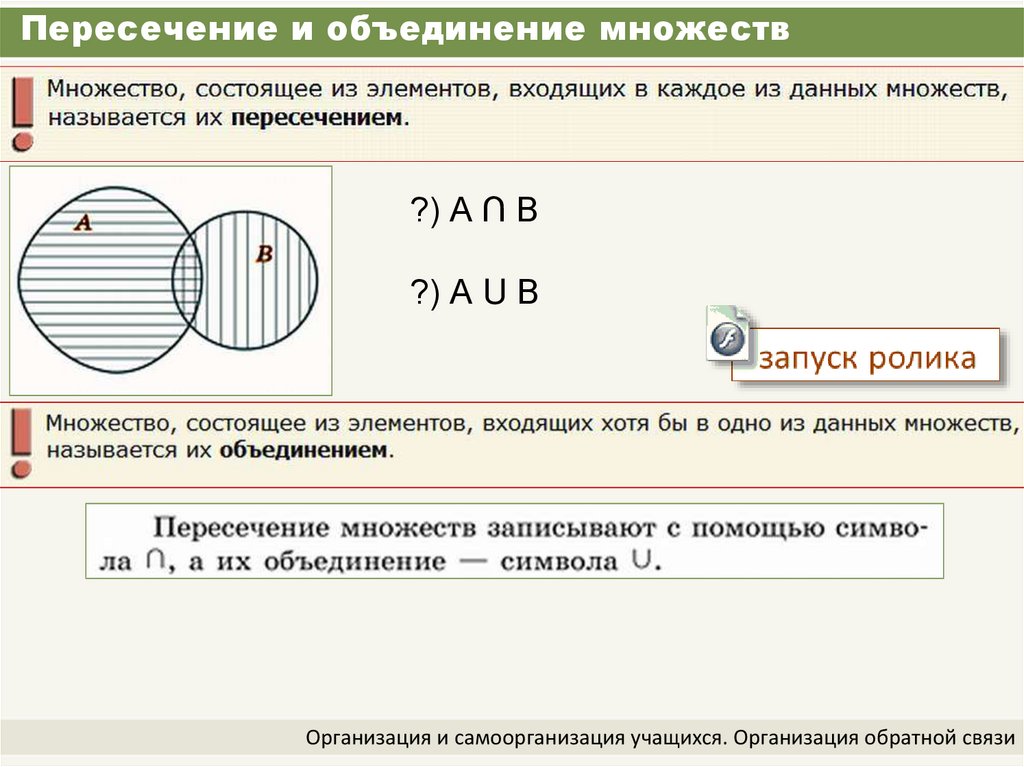 Или если есть 12$, которые любят математику и гуманитарные науки и могут любить или не любить науку.
Или если есть 12$, которые любят математику и гуманитарные науки и могут любить или не любить науку.
Если вы интерпретируете это первым способом, есть $12$, которые любят математику и гуманитарные науки, но не любят естественные науки, и используйте рисунок, который вы нарисовали, вы получите отрицательное число для тех, кто любит все три.
Но если вы интерпретируете это вторым способом (что является логическим, буквальным и математическим способом интерпретации этого; если вам говорят, что они любят математику и гуманитарные науки, это означает, что все, кто любит математику и гуманитарные науки, независимо от того, что еще они могут или может не нравиться) тогда, если есть $?$, которым нравятся все три, то есть $12$, которым нравятся математика и гуманитарные науки, а может и не нравиться наука; и есть $12-?$, которые любят математику и гуманитарные науки и не любят науку.
Другой способ просмотра:
Но здесь должно быть ясно, что области $7,12,9$ перекрываются.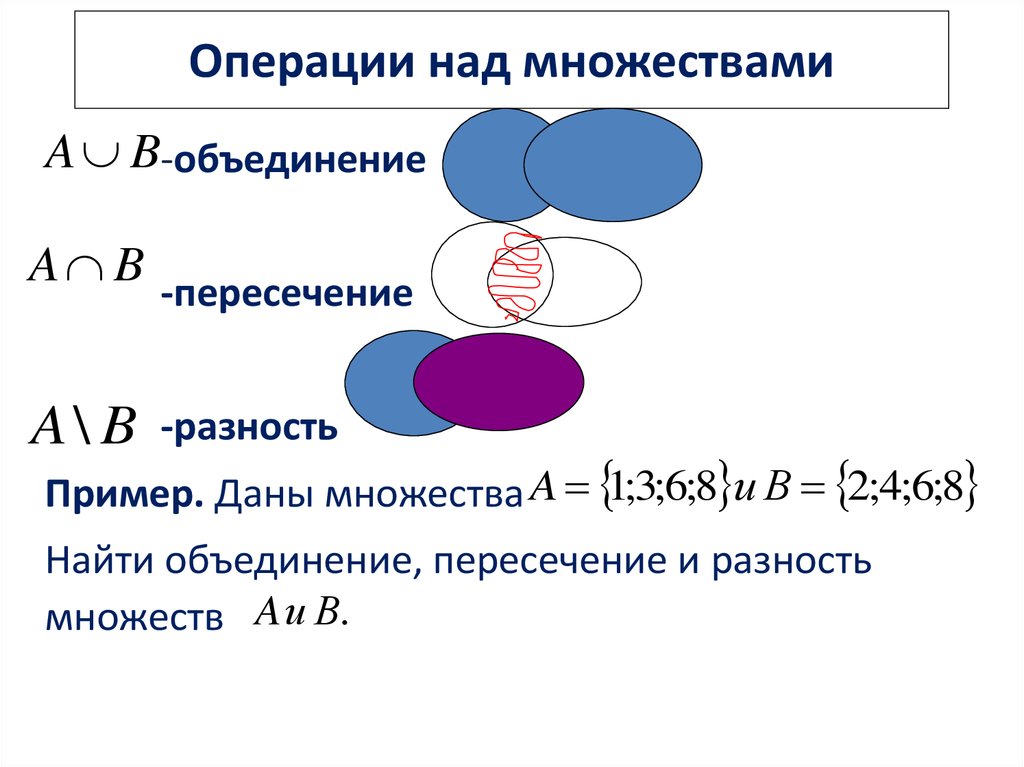

 keys()
keys()
 24
учащимся не нравился ни один из предметов, 9понравилась математика только , 16
нравились науки только , 9 нравились гуманитарные науки только , 12 нравились математика и
гуманитарные науки, 7 любили математику и естественные науки и 9 любили гуманитарные и
наука.
24
учащимся не нравился ни один из предметов, 9понравилась математика только , 16
нравились науки только , 9 нравились гуманитарные науки только , 12 нравились математика и
гуманитарные науки, 7 любили математику и естественные науки и 9 любили гуманитарные и
наука.