Определитель как решать: Определитель матрицы или просто определитель и его вычисление

Применение определителей 2 и 3 порядка в решении задач координатно – векторным методом (ЕГЭ)

ПРИМЕНЕНИЕ ОПРЕДЕЛИТЕЛЕЙ 2 И 3 ПОРЯДКА В РЕШЕНИИ ЗАДАЧ
№14 ЕГЭ ПО МАТЕМАТИКЕ КООРДИНАТНО – ВЕКТОРНЫМ МЕТОДОМ.
Выполнил: Каримов Н.Х.
учитель
МБОУ «Кутлушкинская средняя
общеобразовательная школа».
СОДЕРЖАНИЕ:
1. Введение.
2. Нахождение угла между плоскостями.
3. Нахождение угла между прямой и плоскостью.
4. Нахождение расстояния от точки до плоскости.
5. Заключение.
1. Введение.
Цель данной работы рассмотреть координатно – векторный метод решения
задач №14 из ЕГЭ по математике и показать возможность применения
определителей третьего порядка для нахождении уравнения плоскости.
Метод координат — весьма эффективный и универсальный способ нахождения
любых углов или расстояний между стереометрическими объектами в пространстве.
Данный метод решения заключается во введении (привязке к исследуемым
фигурам) декартовой системы координат, а затем – исчислении образующихся
векторов (их длин и углов между ними).

Преимущество координатного метода перед альтернативным решением
средствами дополнительных построений состоит в том, что удается
полностью отстраниться от чертежа и заниматься исключительно числами
(координатами).
2. Нахождение угла между плоскостями.
Величина двугранного угла измеряется
величиной соответствующего
линейного угла(рис.1.).
Чтобы построить линейный угол
двугранного угла, нужно взять на линии
пересечения плоскостей произвольную
точку, и в каждой плоскости провести к
этой точке луч перпендикулярно линии
пересечения плоскостей. Угол,
образованный этими лучами и есть
линейный угол двугранного угла:
Рис.1. Угол между плоскостями.
В высшей математике есть такое правило, которое позволит нам с легкостью
решать задания данного типа методом координат.
Угол между двумя плоскостями в пространстве равен модулю угла между
нормалями к этим плоскостям.
Таким образом, если мы найдем координаты вектора нормали, то
воспользовавшись формулой косинуса угла между векторами, известной из
школьного курса геометрии, найдем искомый угол.
n1 n2
cos
n1 n2
Нахождение координат вектора нормали.
Уравнение плоскости имеет вид
Ax By Cz D 0
В этом уравнении плоскости коэффициенты А, В, С – координаты вектора
нормали к плоскости (то есть вектора, перпендикулярного плоскости).
n{ A; B; C}
Рис.2. Нормаль к плоскости.
Нахождение уравнения плоскости через определитель.
Уравнение плоскости проходящей через точки M1 ( x1 ; y1 ; z1 ) M2 ( x2 ; y2 ; z2 )
M 3 ( x3 ; y3 ; z3 ) в координатной форме будет иметь вид:
x x1
y y1
z z1
x2 x1
y 2 y1
z 2 z1 0
x3 x1
y3 y1
z3 z1
Если совместить точку М1 с началом координат то определитель упроститься
x
y
z
x2
y2
z2 0
x3
y3
z3
Для составления уравнения плоскости можно использовать определитель
третьего порядка, который можно посчитать по формуле разложения по строке.
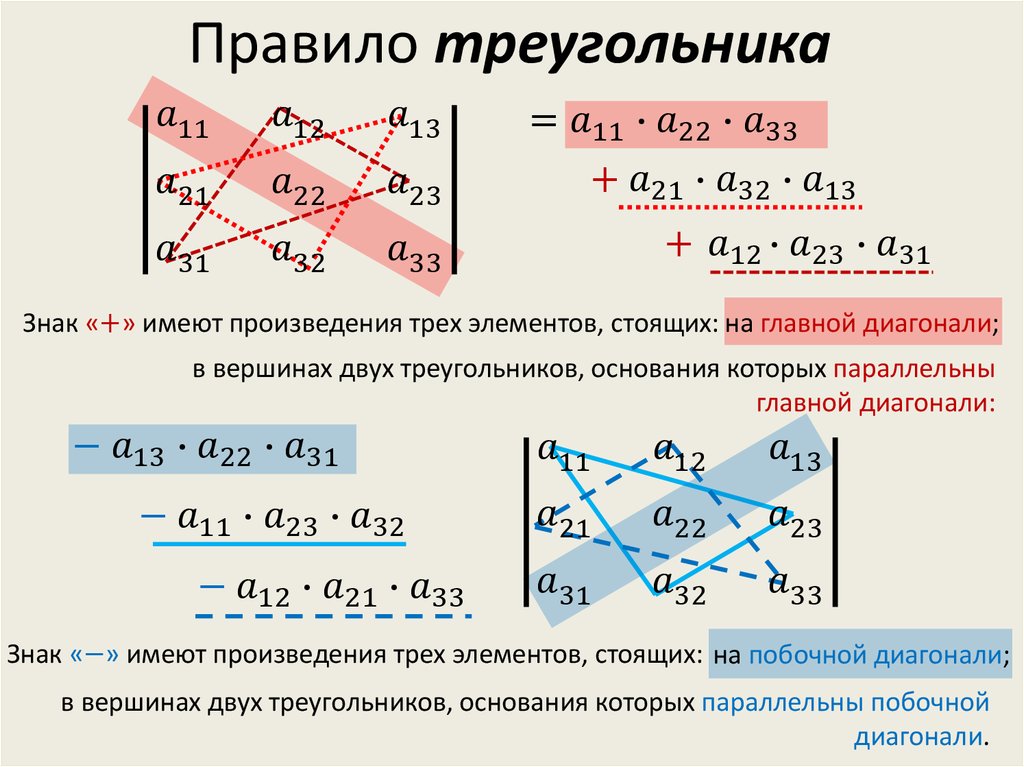
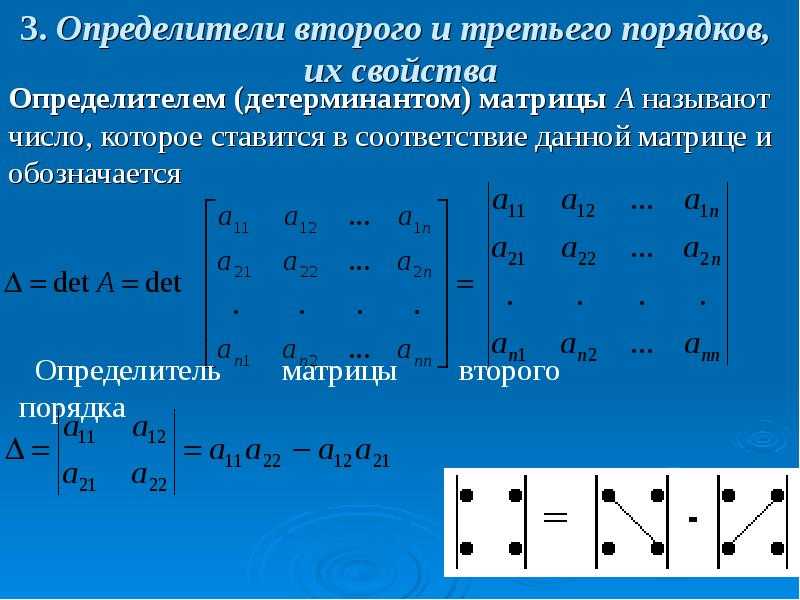
Нахождение определителя.
Определителем квадратной матрицы называется число, которое может быть
вычислено по элементам матрицы по формуле разложения по первой строке:
n
(-1) k 1a1k M 1k
k 1
где М1к – детерминант матрицы, полученной из исходной вычеркиванием
первой строки и k – го столбца.
Для матрицы второго порядка определитель вычисляется по формуле:
a11
a12
a21 a22
a11a22 a12a21
Для матрицы третьего порядка определитель вычисляется по формуле:
a11
a12
a13
a 21
a 22
a 23 a11 ( 1)1 1
a 31
a 32
a 33
a 22
a 23
a 32
a 33
a12 ( 1)1 2
a 21
a 23
a 31
a 33
a13 ( 1)1 3
a11 ( a 22 a 33 a 23a 32 ) a12 ( a 21a 33 a 23a 31 ) a13 ( a 21a 32 a 22 a 31 )
a 21
a 22
a 31
a 32
Пример нахождения уравнения плоскости и вектора нормали.
Заданы точки:
нормали.
x
y
z
0
1 0,5 x
1
0
1
A(0;0;0) , B (0;1;0,5)
1 0,5
0
1
y
0 0,5
1
1
z
,
C (1;0;1)
0 1
1 0
найдем уравнение плоскости и вектор
x (1 0) y (0 0,5) z (0 1) x 0,5 y z
x 0,5 y z 0 — уравнение плоскости проходящее через точки А, В, С.
Вектор нормали
n{1;0,5; 1}
Угол между нормалями в координатной форме.
После того, как мы нашли координаты векторов нормалей двух плоскостей, угол
между двумя пересекающимися плоскостями можно вычислить как угол между
нормалями по формуле:
cos
где n1{A1 ; B1 ; C1}
n2 {A2 ; B2 ; C2 }
A1 A2 B1 B2 C1C2
A , B C A B C
2
1
2
1
2
1
2
2
2
2
2
2
,
— вектор
нормали плоскости A1x B1y C1z D1 0
— вектор
нормали плоскости A2 x B2 y C2 z D2 0
Алгоритм решения задач на нахождение угла между плоскостями:
1. На рисунке изображаем указанные в задаче плоскости
2. Вписываем фигуру в систему координат
4. Находим уравнения заданных плоскостей
5. Находим координаты вектора нормали к плоскостям
6. Подставляем в формулу «косинус угла между плоскостями»
7. После чего (если требуется в задаче), зная косинус, находим значение
самого угла.
Для того, чтобы лучше понять алгоритм решения данных типов задач,
лучше рассмотреть решение самых простых из них.
Ниже будут приведены решения именно таких заданий.
Задача 2. 1.
В правильной треугольной призме , все ребра которой равны 1, найдите
косинус угла между плоскостями ACB1 и BA1C1 .
Решение
Впишем призму в декартову систему координат как показано на рис.3. Для
нахождения угла между заданными плоскостями нам необходимо найти
координаты векторов нормали к этим плоскостям.
1. Найдем уравнение плоскости ACB1 .
Найдем координаты точек, задающих
указанную плоскость: A(0;0;0) , B1 (1;0;1) ,
1 3
C( ;
;0).
2 2
Рис.3. Треугольная призма.
Найдем уравнение плоскости.
x
y
1
0
3
2
0,5
z
0
1 x 3
2
0
1
0
y
1
1
0,5 0
z
1
0
3
3
) y (0 0,5) z (
0)
3 x (0
2
2
2
0,5
3
3
x 0,5 y
z 0
2
2
Умножив каждое слагаемое на (-2) получим уравнение плоскости:
3x — y — 3z 0
n1{ 3; 1; 3}
n1
2
3 ( 1) 2 ( 3) 2 7
2. Найдем уравнение плоскости BA1C1 . Найдем координаты точек, задающих
1 3
указанную плоскость: A1 (0;0;1) , B(1;0;0) , C1 ( ; ;1)
2 2
Найдем уравнение плоскости.
x x1
y y1
z z1
x 2 x1
y 2 y1
z 2 z1 1 0
x3 x1
y 3 y1
z 3 z1
x
y
z -1
1
0
3
2
0,5
0
-1 x 3
2
0
1
0
x 0
y
0,5 0
1
1
0,5
0
Получили уравнение плоскости
n2 { 3;1; 3}
y 0
z 1
x
0 0 0 1 1
3
0 1 1 0,5
2
( z 1)
1
0,5
2
0
3
2
z -1
-1 0
0
0
3
3
3
x 0,5 y
z
0
3
2
2
2
2
3x y 3 3 0
n2
y
2
3 1 3 7
2
3. Найдем косинус угла между заданными плоскостями.
n n
A A B B C1C 2
cos 1 2 1 2 1 2
n1 n 2
n1 n 2
Ответ: cos
1
.
7
3 3 ( 1) 1 3 3
7 7
1
7
3. Нахождение угла между прямой и плоскостью.
Прежде чем переходить к алгоритму решения данного типа заданий вспомним,
что же является углом между прямой и плоскостью.
Углом между плоскостью и не перпендикулярной ей прямой называется угол
между этой прямой и её проекцией на данную плоскость (рис.4.).
Рис.4. Угол между прямой и плоскостью.
На прямой можем выделить вектор, и найти его координаты:
Нормаль можем провести к точке пересечения прямой
Вектор нормали будет иметь следующие координаты:
Тогда можем найти
n p
cos
n p
Из рисунка видно, что
Т.е получили
2
n p
sin
n p
,но нам нужен
значит
p{x 1 ; y1 ; z1}
и плоскости.
n{ A; B; C}
cos
cos cos(
2
) sin
A x1 B y1 C z1
A2 B 2 C 2 x12 y12 z12
Алгоритм решения задач на нахождение угла между прямой и
плоскостью:
1. На рисунке изображаем указанные в задаче прямую и плоскость (прямой
придаем направление, т.е. вектор)
2. Вписываем фигуру в систему координат
3. Находим координаты концов направляющего вектора.
4. Находим координаты вектора
5. Находим координаты вектора нормали к плоскости
6. Подставляем в формулу «синус угла между прямой и плоскостью»
7. После чего (если требуется в задаче), зная синус, находим значение
самого угла.
Задача 3.1.
В правильной четырехугольной пирамиде ABCD, все ребра которой равны 1,
найдите синус угла между прямой BE и плоскостью SAD, где — E середина
ребра SC .
Решение
Впишем правильную четырехугольную пирамиду ABCD, в декартову систему
координат как показано на рис. 5.
Рис.5. Правильная четырехугольная пирамида.
Для нахождения угла между заданной прямой и плоскостью нам необходимо
найти координаты вектора принадлежащего прямой BE и координаты нормали
плоскости SAD.
1. Найдем уравнение плоскости и координаты вектора нормали.
Найдем координаты точек, задающих указанную плоскость:
1 1 2
S( ; ;
)
2 2 2
x
y
z
0
1
0 x
0,5
2
2
0,5 0,5
1
A(0;0;0)
0
0
2 y
0,5
2
2
1
x z 0
2
2
D(0;1;0)
0
0
1
2
2
x(
0) y (0 0) z (0 0,5)
x 0,5z
2 z
0,5 0,5
2
2
2
2
1
n{ ;0; }
2
2
2
1
3
n ( ) 2 02 ( ) 2
2
2
2
2. Найдем координаты вектора
BE
т.к
3 3 2
B(1;0;0) E ( ; ; )
4 4 4
1 2
3 2
2 2
12
BE ( ) ( ) ( )
4
4
4
4
1 3 2
BE{ ; ; }
4 4 4
3. Найдем синус угла между прямой и плоскостью.
.
sin
A x 1 B y1 C z1
A B C x y z
2
Ответ:
2
2
2
sin
3
2
1
2
1
2
1
2
1
3
1
2
( ) 0 ( )
2
4
4
2 4
3 12
2
4
2 2
2
8
3
3
4
4. Нахождение расстояния от точки до плоскости.
Для начала выясним, что называется расстоянием от точки до плоскости.
Расстояние от точки до плоскости, не содержащей эту точку, есть длина
отрезка перпендикуляра, опущенного из этой точки на плоскость (рис.6.) .
Рис.6. Расстояние от точки до плоскости.
Итак, для того, чтобы найти расстояние от точки до плоскости нам необходимо
найти координаты точки, и координаты нормали данной плоскости. После чего
воспользоваться следующей формулой:
d
( x0 ; y 0 ; z 0 )
Ax0 By 0 Cz0 D
A2 B 2 C 2
— координаты заданной точки
Ax By Cz D 0
— уравнение плоскости
, где
Алгоритм решения задач на нахождение расстояния от точки
до плоскости:
1. На рисунке отмечаем указанные в задаче точку и плоскость.
2. Вписываем фигуру в систему координат.
3. Находим координаты точек (данной и трех точек плоскости).
4. Составляем уравнение плоскости .
5. Находим координаты вектора нормали плоскости.
6. Подставляем в формулу «расстояние от точки до плоскости»
Задача 4. 1.
В правильной шестиугольной призме АВ …F1 все ребра которой
равны 1, найдите расстояние от точки A до плоскости BFE1 .
Рис.7. Правильная шестиугольная призма.
Для нахождения расстояния между заданной точкой и плоскостью нам
необходимо найти координаты точки A и координаты нормали плоскости
BFE1.
1. Найдем уравнение плоскости BFE1. Найдем координаты точек, задающих
указанную плоскость:
B(1;0;0)
1 3
F ( ;
;0)
2 2
E1 (0; 3;1)
Воспользовавшись понятием определителя найдем уравнение плоскости.
x 1
1
— -1
2
0 1
y-0
z — 0 x 1
3
1
0 0 — 0 1
2
2
3 0 1 0
1
y
3
2
3
z
3
0 ( x 1) 2
3
1
1
y
2
1
1
0
1
1
z
2
1
1
0
1
3
1
3 3
3
3
3
1
0) y ( 1 0) z (
(
))
x
1 y 3z
2
2
2
2
2
2
2
Получили уравнение плоскости:
( x 1)(
3 x 3 y 2 3z 3 0
n{ 3;3; 2 3}
n ( 3 ) 2 32 ( 2 3 ) 2 24
3
2
3
2. ndet(B-A)$%, где n это размер матриц, значит это равенство выполняется только при четном n.

матрицы линейная-алгебра определитель

задан 11 Мар ’19 12:14

Orange
876●18
89% принятых

старыеновыеценные

Если бы умножали $%(A^T-B^T)(A+B)$%, то сразу получили бы желаемое. TB$%… то есть при нечётном $%n$% определитель из левой части равенства равен нулю… ссылка отвечен 11 Мар ’19 15:54 all_exist 55.7k●3●13

Ваш ответ

Если вы не нашли ответ, задайте вопрос.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Присоединяйтесь!

регистрация »

отмечен:

линейная-алгебра ×1,697
матрицы ×527
определитель ×119

задан
11 Мар ’19 12:14

показан
837 раз

обновлен
13 Ноя ’19 19:35

Связанные исследования

Связанные вопросы

Отслеживать вопрос

по почте:

Зарегистрировавшись, вы сможете подписаться на любые обновления

по RSS:

Ответы

Ответы и Комментарии

определителей и правило Крамера | безграничная алгебра |

Матрицы

Определители квадратных матриц 2 на 2

Определитель квадратной матрицы

2×22\times 22×2

 — это математическая конструкция, используемая при решении задач, которая находится по специальной формуле.

Цели обучения

Потренируйтесь находить определитель матрицы

2×22\times 22×2

Основные выводы

Ключевые моменты

Ключевые термины

• определитель : Уникальная скалярная функция над квадратными матрицами, которая является дистрибутивной при умножении матриц, полилинейна в строках и столбцах и принимает значение 1 для единичной матрицы. Его аббревиатура «

  det⁡\detdet

  ».

Что такое определитель?

Матрица часто используется для представления коэффициентов в системе линейных уравнений, и определитель может использоваться для решения этих уравнений. Использование определителей в исчислении включает определитель Якоби в правиле замены переменных для интегралов функций многих переменных. Детерминанты также используются для определения характеристического многочлена матрицы, что важно для задач на собственные значения в линейной алгебре. В аналитической геометрии определители выражают знаковые

ннн

-мерные объемы

ннн

-мерные параллелепипеды. Иногда определители используются просто как компактная запись для выражений, которые в противном случае было бы громоздко записывать.

Можно доказать, что любая матрица имеет единственную обратную, если ее определитель отличен от нуля. Также можно доказать различные другие теоремы, в том числе то, что определитель произведения матриц всегда равен произведению определителей; и определитель эрмитовой матрицы всегда действителен.

Определитель матрицы

[A][A][A]

обозначается как

det⁡(A)\det(A)det(A)

,

det⁡ A\det\ Adet A

, или

∣A∣\left | А \право |∣А∣

. В случае, когда элементы матрицы выписаны полностью, определитель обозначается путем окружения элементов матрицы вертикальными чертами вместо скобок или круглых скобок матрицы.

Например, определитель матрицы

[abde]\begin{bmatrix} a & b \\ d & e \end{bmatrix}[ad​be​]

пишется

∣abde∣\begin{vmatrix} a & b \\ d & e \end{vmatrix}∣

∣​ad​be​∣

∣​

.

Определитель матрицы 2 на 2

В линейной алгебре определитель — это значение, связанное с квадратной матрицей. Его можно вычислить из элементов матрицы с помощью специального арифметического выражения, показанного ниже:

Для

2×22 \times 22×2

матрица,

[abcd]\begin{bmatrix} a & b\\ c & d \end{bmatrix}[ac​bd​]

,

определитель

∣abcd∣\begin{vmatrix} a & b\\ c & d \end{vmatrix}∣

∣​ac​bd​∣

∣​

 определено как

ad-bcad-bcad-bc

.

Пример 1. Найдите определитель следующей матрицы:

[4−275]\displaystyle \begin{bmatrix} 4 & -2 \\ 7 & 5 \end{bmatrix}[47​−25​]

Определитель

∣4−275∣\begin{vmatrix} 4 & -2\\ 7 & 5 \end{vmatrix}∣

∣​47​−25​∣

∣​

равен:

(

4⋅5)−(−2⋅7)=20−(−14)=34\displaystyle \начать{выравнивать} (4 \cdot 5) — (-2 \cdot 7)&= 20 — (-14)\\ &=34 \end{align}(4⋅5)−(−2⋅7)​=20−(−14)=34​​

Кофакторы, миноры и дополнительные детерминанты

Кофактор записи

(i,j)(i,j)(i,j)

матрицы

AAA

— минор этой матрицы со знаком.

Цели обучения

Объясните, как использовать минорные матрицы и матрицы кофакторов для вычисления определителей

Ключевые выводы

Ключевые точки

Ключевые термины

• кофактор : Знаковый минор записи матрицы.
• младший : Определитель некоторой меньшей квадратной матрицы, вырезанной из матрицы

  AAA

  путем удаления одной или нескольких ее строк или столбцов.

Кофактор и минор: определения

Кофактор

В линейной алгебре кофактор (иногда называемый дополнением) описывает конкретную конструкцию, которая полезна для вычисления как определителя, так и обратной квадратной матрицы. В частности, кофактор записи

(i,j)(i,j)(i,j)

матрицы, также известной как

(i,j)(i,j)(i,j) Кофактор

этой матрицы является минорным знаком этой записи.

Кофактор 9{i+j}M_{ij}Cij​=(−1)i+jMij​

Незначительный

Чтобы узнать, что такое знаковый минор, нам нужно знать, что такое минор матрицы. В линейной алгебре минор матрицы

AAA

является определителем некоторой меньшей квадратной матрицы, вырезанной из

AAA

путем удаления одной или нескольких ее строк или столбцов. Миноры, полученные удалением всего одной строки и одного столбца из квадратных матриц (первые миноры), необходимы для вычисления матрицы кофакторов.

Let

AAA

BE

M × NM \ Times NM × N

и

KKK

Интеллект с

0 5 0 5 0 и

k≤nk \leq nk≤n

.

K × KK \ Times KK × K

MINATE

AAA

является детерминантом

K × KK \ Times KK × K

, полученная из

AAA

с помощью DELEDTING

.0005

m-km-km-k

строк и

n-kn-kn-k

столбцов.

Вычисление определителя

Определитель любой матрицы можно найти, используя ее знаковые миноры. Определитель — это сумма миноров со знаком любой строки или столбца матрицы, масштабированных по элементам в этой строке или столбце.

Расчет миноров

Следующие шаги используются, чтобы найти определитель данного минора матрицы A:

1. Выберите запись

   aija_{ij}aij​

   из матрицы.
2. Вычеркните записи, лежащие в соответствующей строке

   iii

   и столбце

   jjj

   .
3. Переписать матрицу без отмеченных элементов.
4. Получите определитель этой новой матрицы.

MijM_{ij}Mij​

называется второстепенным для записи

aija_{ij}aij​

.

Примечание: если

i+ji+ji+j

четное число, то кофактор совпадает с его минором:

Cij=MijC_{ij}=M_{ij}Cij​=Mij​

. В противном случае он равен аддитивной величине, обратной своему минору: 

Cij=-MijC_{ij}=-M_{ij}Cij​=-Mij​

Вычисление определителя

Мы найдем определитель следующей матрицы A, вычислив определители ее сомножителей для третьего, самого правого столбца, а затем умножив их на элементы этого столбца.

[147305−1911]\displaystyle \begin{bmatrix} 1 и 4 и 7\\ 3 & 0 & 5\\ -1& 9&11\\ \end{bmatrix}⎣

⎡​13−1​409​7511​⎦

⎤​

В качестве примера вычислим определитель минора

M23M_{23}M23​

5 , которая является определителем матрицы

2×22 \times 22×2

, образованной удалением

222

-й строки и

333

-го столбца. Черная точка представляет элемент, который мы удаляем.

∣14∙∙∙∙−19∙∣=∣14−19∣=(9−(−4))=13\displaystyle \начать{выравнивать} \begin{vmatrix} 1 & 4 & \bullet\\ \bullet& \bullet& \bullet\\ -1& 9&\bullet \end{vmatrix} &= \begin{vmatrix} 1 & 4\\ -1&9 \end{vmatrix}\\ &=(9-(-4))\\&=13 \end{align}∣

∣​1∙−1​4∙9​∙∙∙​∣

∣​​=∣

∣​1−1​49​∣

∣​=(9− (−4))=13​

Поскольку

i+j=5i+j=5 i+j=5

 является нечетным числом, кофактор является аддитивным, обратным его минору: 

−(13 )=−13-(13)=-13−(13)=−13

Умножаем это число на

a23=5a_{23}=5a23​=5

, что дает

−65-65−65

.

Тот же процесс проводится, чтобы найти детерминанты

C13C_ {13} C13

и

C33C_ {33} C33

, которые затем умножаются на

a13a_ {13} a13

8

88

8

8

8

8 и

a33a_{33}a33​

соответственно. Затем определитель находится путем суммирования всех этих значений:

det⁡A=a_13det⁡C_13+a_23det⁡C_23+a_33det⁡C_33=7⋅27−5⋅13+11⋅−12=−8\begin {align} \ det{A} &= a\text{\textunderscore}{13}\det{C\text{\textunderscore}{13}}+a\text{\textunderscore}{23}\det{C\text{\textunderscore {23}}+a\text{\textunderscore}{33}\det{C\text{\textunderscore}{33}} \\ &= 7\cdot27-5\cdot13+11\cdot-12 \\& =-8 \end{align}detA​=a_13detC_13+a_23detC_23+a_33detC_33=7⋅27−5⋅13+11⋅−12=−8​​

Правило Крамера

Правило Крамера использует определители для решения уравнения

Ax=bAx=bAx=b

, когда

AAA

является квадратной матрицей.

Цели обучения

Используйте правило Крамера для решения одной переменной в системе линейных уравнений

Ключевые выводы

Ключевые моменты

• Правило Крамера работает только с квадратными матрицами, которые имеют ненулевой определитель и единственное решение.
• Рассмотрим линейную систему

  {ax+by=ecx+dy=f\left\{\begin{matrix} ax+by & ={\color{Red}e}\\ cx+dy & ={\color{Red }f} \end{matrix}\right.{ax+bycx+dy​=e=f​

  , что в матричном формате равно

  [abcd][xy]=[ef]\begin{bmatrix}a&b\\c&d \end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}{\color{Red}e}\\{\color{Red}f}\end{bmatrix}[ac ​bd​][xy​]=[ef​]

  . Предположим, что определитель отличен от нуля. Затем

  xxx

   и

  yyy

   и находятся по правилу Крамера:

  x = ∣ebfd∣∣abcd∣=ed-bfad-bcx=\frac{\begin{vmatrix}{\color{Red}e}&b\\{\color{Red}f}&d\end{vmatrix}} {\ begin {vmatrix} a & b \\ c & d \ end {vmatrix}} = \ frac {{\ color {Red} e} db {\ color {Red} f}} {ad-bc} x = ∣

  ∣​ ac​bd​∣

  ∣​∣

  ∣​ef​bd​∣

  ∣​=ad-bced-bf​

    и

  y=∣aecf∣∣abcd∣=af-ecad-bcy= frac{\begin{vmatrix}a&{\color{Red}e}\\c&{\color{Red}f}\end{vmatrix}}{\begin{vmatrix}a&b\\c&d\end{vmatrix}}= \ frac {a {\ color {Red} f} — {\ color {Red} e} c} {ad-bc} y = ∣

  ∣​ac​bd​∣

  ∣​∣

  ∣​ac​ef​∣

  ∣​=ad-bcaf-ec​

  .
• Правило Крамера эффективно для решения небольших систем и может быть вычислено довольно быстро; однако по мере роста системы вычисление новых определителей может быть утомительным.

Ключевые термины

• определитель : Уникальная скалярная функция над квадратными матрицами, дистрибутивная при умножении матриц, полилинейная в строках и столбцах и принимающая значение

  111

  для единичной матрицы. Его аббревиатура «

  det⁡\detdet

  ».
• квадратная матрица : Матрица, имеющая такое же количество строк, как и столбцов.

«Правило Крамера» — это еще один способ решения системы линейных уравнений с матрицами. Он использует формулу для расчета решения системы с использованием определения определителей.

Правило Крамера:  Определение

Правило Крамера — это явная формула для решения системы линейных уравнений, в которой столько уравнений, сколько неизвестных, т. е. квадратная матрица, действительная, когда система имеет единственное решение. Он выражает решение через определители (квадратной) матрицы коэффициентов и матриц, полученных из нее путем замены одного столбца вектором правых частей уравнений.

Правило Крамера:  Формула

Правила для

2×22\times 22×2

 Матрица

Рассмотрим линейную систему:

[abcd][xy]=[ef]\displaystyle \begin{bmatrix}a&b\\c&d\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}{\color{Red}e}\\{\color{Red} f}\end{bmatrix}[ac​bd​][xy​]=[ef​]

Предположим, что определитель не равен нулю. Тогда

xxx

и

yyy

можно найти по правилу Крамера:

x=∣ebfd∣∣abcd∣=ed-bfad-bc\displaystyle x = \ frac {\ begin {vmatrix} {\ color {Red} e} & b \\ {\ color {Red} f} & d \ end {vmatrix}} {\ begin {vmatrix} a & b \\ c & d \ end {vmatrix }} = \ frac {{\ color {Red} e} db {\ color {Red} f}} {ad-bc} x = ∣

∣​ac​bd​∣

∣​∣

∣​ef​bd​∣

∣​=ad-bced-bf​

И:

∣daf=∣af=∣∣ec af-ecad-bc\displaystyle y = \ frac {\ begin {vmatrix} a & {\ color {Red} e} \\ c & {\ color {Red} f} \ end {vmatrix}} {\ begin {vmatrix} a & b \\ c & d \ end {vmatrix }} = \ frac {a {\ color {Red} f} — {\ color {Red} e} c} {ad-bc} y = ∣

∣​ac​bd​∣

∣​∣

∣​ac​ef​∣

∣​=ad-bcaf-ec​

Правила для

3×33 \times 33×3

 Matrix

Дано:

[abcdefghi][xyz]=[jkl]\displaystyle \begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix} \begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}{\color{Red}j}\\ {\color{Red}k}\\{\color{Red}l}\end{bmatrix}⎣

⎡​adg​beh​cfi​⎦

⎤​⎣

⎡​xyz​⎦

⎤ = ⎣

⎡ JKL ⎦

⎤

, затем значения

XXX

,

YYY

и

Zzz

можно найти следующим образом:

и

Zzz

можно найти следующим образом:

и

zzz

. 0005

x=∣jbckeflhi∣∣abcdefghi∣y=∣ajcdkfgli∣∣abcdefghi∣z=∣abjdekghl∣∣abcdefghi∣\displaystyle x=\frac{\begin{vmatrix}{\color{Red}j}&b&c\\{\color{Red}k}&e&f\\{\color{Red}l}&h&i\end{vmatrix}}{\begin {vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}} \четверка y = \ frac {\ begin {vmatrix} a & {\ color {Red} j} & c \\ d & {\ color {Red} k} & f \\ g & {\ color {Red} l} & i \ end {vmatrix}} {\ begin {vmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {vmatrix}} \четверка z = \ frac {\ begin {vmatrix} a & b & {\ color {Red} j} \\ d & e & {\ color {Red} k} \\ g & h & {\ color {Red} l} \ end {vmatrix}} {\ begin {vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}x=∣

∣​adg​beh​cfi​∣

∣​∣

∣​jkl​beh​cfi​∣

∣​​y=∣

∣​​​​​y=∣

∣​9adg​00 90 0 0 90 ∣

∣ adg jkl cfi ∣

∣ z = ∣

∣ adg beh cfi ∣

∣

∣ adg Beh jkl ∣

∣

Использование правила Крамера

Пример 1.

Решите систему с помощью правила Крамера:

{3x+2y=10−6x+4y=4\displaystyle \left\{\begin{matrix} 3x+2y & = 10\\ -6x+4y & = 4 \end{matrix}\right.{3x+2y−6x+4y​=10=4​

В матричном формате:

[32−64][xy]=[104]\displaystyle \begin{bmatrix}3&2\\-6&4\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}10\\4\end{bmatrix}[3−6​24 ​][xy​]=[104​]

x=∣ebfd∣∣abcd∣=ed-bfad-bc\displaystyle \начать{выравнивать} x&=\frac{\begin{vmatrix}{\color{Red}e}&b\\{\color{Red}f}&d\end{vmatrix}}{\begin{vmatrix}a&b\\c&d\end{vmatrix }}\\&=\frac{{\color{Red}e}db{\color{Red}f}}{ad-bc}\end{align}x​=∣

∣​ac​bd​∣

∣​∣

∣​ef​bd​∣

∣​=ad-bced-bf​​

x=∣10244∣∣32−64∣=10⋅4−2⋅4(3⋅ 4)−[2⋅(−6)]=3224=43\displaystyle \начать{выравнивать} x&=\frac{\begin{vmatrix}10&2\\4&4\end{vmatrix}}{\begin{vmatrix}3&2\\-6&4\end{vmatrix}}\\&=\frac{10\cdot 4-2 \cdot 4}{(3 \cdot 4) -[2 \cdot (-6)]}\\&=\frac{32}{24}=\frac{4}{3}\end{align}x​ =∣

∣​3−6​24​∣

∣​∣

∣​104​24​∣

∣​​=(3⋅4)−[2⋅(−6)]10⋅4 −2⋅4​=2432​=34​​

y=∣aecf∣∣abcd∣=af-ecad-bc\displaystyle \начать{выравнивать} y&=\frac{\begin{vmatrix}a&{\color{Red}e}\\c&{\color{Red}f}\end{vmatrix}}{\begin{vmatrix}a&b\\c&d\end{vmatrix }}\\ & = \ frac {a {\ color {Red} f} — {\ color {Red} e} c} {ad-bc} \end{выравнивание}y​=∣

∣​ac​bd​∣

∣​∣

∣​ac​ef​∣

∣​=ad-bcaf-ec​​

y=∣310−63∣64∣ ∣=(3⋅4)−[10⋅(−6)](3⋅4)−[2⋅(−6)]=7224=3\displaystyle \начать{выравнивать} y&=\frac{\begin{vmatrix}3&10\\-6&4\end{vmatrix}}{\begin{vmatrix}3&2\\-6&4\end{vmatrix}}\\ &=\frac{(3 \cdot 4)-[10 \cdot(-6)]}{(3 \cdot 4)-[2 \cdot (-6)]}\\ &=\фракция{72}{24}=3 \end{align}y​=∣

∣​3−6​24​∣

∣​∣

∣​3−6​104​∣

∣​​=(3⋅4)−[2 ⋅(−6)](3⋅4)−[10⋅(−6)]​=2472​=3​

Решение системы:

(43,3)(\frac{4}{3}, 3)(34​,3)

.

Лицензии и атрибуции

Контент под лицензией CC, совместно используемый ранее

• Курирование и доработка. Автор: : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права

Лицензионный контент CC, конкретное указание авторства

• Определяющее. Предоставлено : Википедия. Лицензия : CC BY-SA: определитель Attribution-ShareAlike
• . Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
• Незначительное (линейная алгебра). Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Кофактор (линейная алгебра). Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• несовершеннолетний. Предоставлено : Википедия. Лицензия : CC BY-SA: Кофактор Attribution-ShareAlike
• . Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
• Определяющее. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Правило Крамера. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• определитель. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
• квадратная матрица. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike

Предыдущая

Следующая

Детерминанты матрицы — Уроки Византа

Определитель матрицы
— это действительное число, связанное с квадратной матрицей. Определитель матрицы
содержит важную информацию о природе матрицы. Важно помнить
, что только квадратные матрицы имеют определители, чтобы не тратить время на попытки
найти определитель неквадратной матрицы.

Определитель матрицы A обозначается как

или со скобками как

Все размеры n x n имеют определители, но мы сосредоточимся только на определителях 9.0713 матриц размером 2 х 2 и 3 х 3

Дана матрица 2 x 2 A

определитель числа A равен

Дана матрица B размера 3 x 3

определитель числа B равен

Постарайтесь запомнить приведенные выше формулы или решить много практических задач, чтобы они
легко запомнить. Ниже приведены некоторые примеры:

Примеры определителей матрицы

Пример 1: Найти det M при условии, что

Решение:

Пример 2: Найдите определитель матрицы A , приведенной ниже:

Решение:

Викторина по детерминантам

1.

-335

2.

2

3.

-8

4.