Как найти площадь квадрата формула: Как найти площадь квадрата, формула

Площадь квадрата

К содержанию

Квадрат — это правильный четырёхугольник, у которого все стороны и углы равны между собой.
Площадь квадрата равна квадрату его стороны:

S = a²

Начнем с того случая, когда a = 1/n, где n является целым числом.
Возьмем квадрат со стороной 1 и разобьем его на n² равных квадратов так, как показано на рисунке 1.

Так как площадь большого квадрата равна единице, то площадь каждого маленького квадрата равна 1/n². Сторона каждого маленького квадрата равна 1/n, т. е. равна a. Итак,

S = 1/n² = (1/n)² = a².   (1)

Пусть теперь число aпредставляет собой конечную десятичную дробь, содержащую n знаков после запятой (в частности, число a может бать целым, и тогда n = 0). Тогда число m = a · 10ⁿ целое. Разобьем данный квадрат со стороной a на m

2 равных квадратов так, как показано на рисунке 2.

При этом каждая сторона данного квадрата разобьется на m равных частей, и, значит, сторона любого маленького квадрата равна

a/m = a / (a · 10ⁿ) = 1/10ⁿ.

По формуле (1) площадь маленького квадрата равна (1/10ⁿ)². Следовательно, площадь S данного квадрата равна

m² · (1/10ⁿ)² = (m/10ⁿ)² = ((a · 10ⁿ)/10ⁿ)² = a².

Наконец, пусть число a представляет собой бесконечную десятичную дробь. Рассмотрим число a_n, получаемое из a отбрасыванием всех десятичных знаков после запятой, начиная с (n + 1)-го. Так как число a отличается от a_n не более чем на 1/10ⁿ, то a

n ≤ a ≤ a_n + 1/10ⁿ, откуда

a_n² ≤ a² ≤ (a_n + 1/10ⁿ)².   (2)

Ясно, что площадь S данного квадрата заключена между площадью квадрата со стороной a_n и площадью квадрата со стороной a_n + 1/10ⁿ:

т. е. между a_n² и (a_n + 1/10ⁿ)²:

a_n² ≤ S ≤ (a_n + 1/10ⁿ)².   (3)

Будем неограниченно увеличивать число n. Тогда число 1/10ⁿ будет становиться сколь угодно малым, и, значит, число (a_n + 1/10ⁿ)² будет сколь угодно мало отличаться от числа a_n². Поэтому из неравенств

(2) и (3) следует, что число S сколь угодно мало отличается от числа a². Следовательно, эти числа равны: S = a², что и требовалось доказать.

Так же площадь квадрата можно найти с помощью следующих формул:

S = 4r²,
S = 2R²,

где r — радиус вписанной в квадрат окружности,
R — радиус описанной вокруг квадрата окружности.

Площадь треугольника Площадь параллелограмма Площадь ромба Площадь трапеции Площадь круга Площадь прямоугольника Площадь многоугольника

---

Другие заметки по алгебре и геометрии

Полезная информация?

как найти, формула, через диагональ

Содержание:

• Квадрат
• Нахождение площади квадрата
  • Через длину стороны
  • Через диагональ
  • Через радиус вписанной окружности
  • Через радиус описанной окружности
  • Через периметр

Содержание

• Квадрат
• Нахождение площади квадрата
  • Через длину стороны
  • Через диагональ
  • Через радиус вписанной окружности
  • Через радиус описанной окружности
  • Через периметр

Квадрат

Определение

Квадрат — геометрическая фигура, являющаяся правильным четырехугольником.

2}{16}\)

Источник: mnogoformul.ru

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Площадь квадрата — веб-формулы

Квадрат — это правильный многоугольник с четырьмя сторонами. У него четыре прямых угла и параллельные стороны. Чтобы вычислить площадь квадрата, умножьте основание само на себя, что может быть выражено как сторона × сторона. Если квадрат имеет основание длиной 8 дюймов, его площадь будет 8 × 8 = 64 квадратных дюйма.

Площадь квадрата определяется как:

A = a ²

где a = длина стороны

 

Периметр квадрата = 4a
Диагональ квадрата = (a)(sqrt(2)) или 1,414 (a)

 

Пример 1: Найдите площадь квадрата со стороной 15 м

Решение :

Площадь квадрата = a ² = 15 ² = 225 м ²

 

 

Пример 2: Вычислите площадь квадрата, если длина стороны квадрата 35 см.

Решение :

Площадь квадрата определяется как a × a.

Площадь = 35 × 35

Площадь = 1225см

 

 

Пример 3: Какова площадь квадратного поля, если его периметр равен 32 ярдам?

Решение :

 

Периметр квадратного поля = 32 ярда, а поскольку периметр квадрата равен P = 4s, где s — длина стороны. Мы можем легко определить длину, выделив s из приведенной выше формулы:

с = P/4 = 32 / 4 = 8 ярдов

 

Площадь квадратного поля = s × s

Подставляем значение s, имеем:

Площадь = 8 × 8 = 64 ярда ²

Следовательно, площадь квадратного поля равна 64 ярда ² .

 

 

Пример 4: Сторона квадратного парка равна 200 м. Какова будет стоимость газона по цене 0,5 доллара за кв. м?
Решение :

 

Нам нужно найти площадь парка, а затем умножить ее на стоимость м ² .

Площадь квадратного парка = сторона × сторона

A = с²

Подставьте значения и упростите.
А = 200 × 200
A = 40 000 м ²

Площадь озеленения = площадь парка = 40 000 кв.м.

Стоимость озеленения = площадь озеленения × ставка за квадратный метр.

Подставляем значения, которые получим:
Стоимость = 40 000 x 0,5 = 20 000 долларов США.

Таким образом, стоимость травяного покрова составляет 20 000 долларов.

 

 

Пример 5: Квадратный газон окружен дорожкой шириной 2 м вокруг него. Если площадь дорожки 160 кв м, найдите площадь газона.

Решение :

Дано: Квадратный газон окружен дорожкой шириной 2 м; площадь дорожки 160 кв.м.
Чтобы найти: Площадь газона.
(Подсказка: лужайка окружена дорожкой, т. е. дорожка проходит по внешнему краю лужайки. чтобы найти площадь лужайки, вычтите площадь дорожек из общей площади)
Пусть сторона газона равна y, тогда мы имеем:

Внешняя сторона, включая дорожку = сторона лужайки + ширина дорожки с обеих сторон.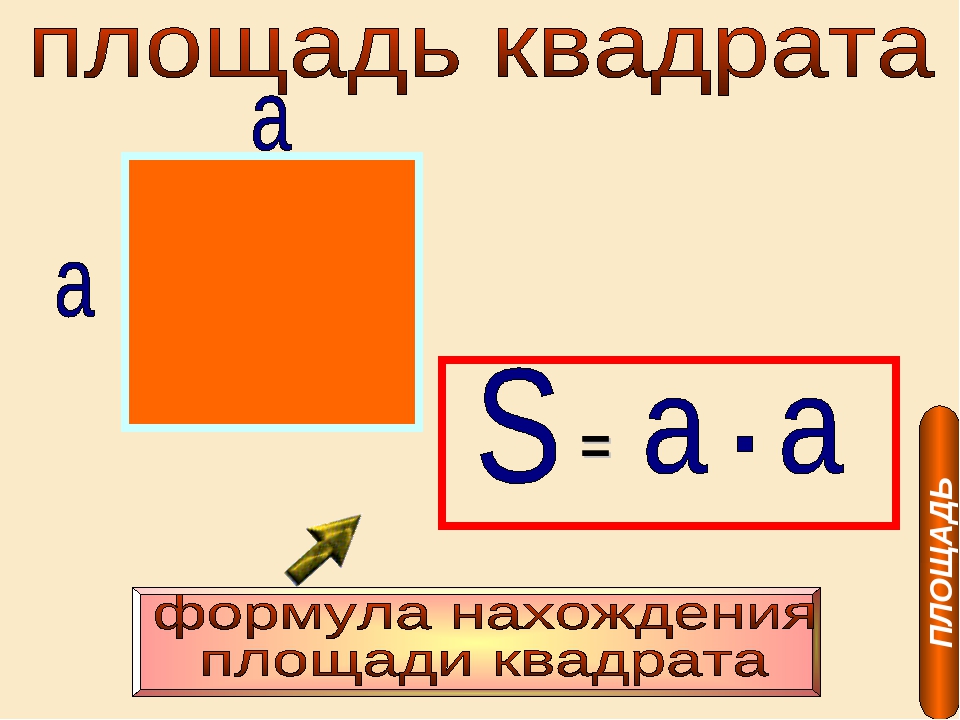

= у + (2 + 2)
= y + 4

Общая площадь, включая путь = (y + 4) × (y + 4).
= у² + 8у + 16 (и).
А площадь газона = (сторона)² = y × y = y² (ii).

Поскольку дана площадь пути (160 м ² ), мы имеем:
Площадь дорожки = Общая площадь, включая дорожку — площадь газона.
А = (i) — (ii).
Подставим данные значения в следующее уравнение, и, выделив y, мы сможем определить длину стороны газона:
160 = (y² + 8y + 16) — y²
160 = у² + 8у + 16 — у²
160 = у² — у² + 8у + 16
160 = 8 лет + 16
160 — 16 = 8 лет
144 = 8 лет
18 = у
Сторона газона = 18 м

Площадь газона = сторона × сторона

А = с²
А = 18 × 18
А = 324 м ²

Отсюда площадь газона = 324 м ²

.

Онлайн-калькулятор площади

Площадь квадрата — 2 метода

Содержание

Площадь двумерной фигуры (плоской фигуры) можно рассматривать как количество квадратных единиц, необходимых для заполнения квадрата. {2}$ и т. д. 9{\circ} \right)$. Квадрат — это особый вид прямоугольника (равносторонний) и особый вид параллелограмма (равносторонний и равноугольный).

Какова площадь квадрата?

Площадь квадрата – это мера занимаемой им площади или поверхности. Рассмотрим квадрат длины $6$ единиц, т. е. квадрат, у которого длина всех ребер (сторон) равна $6$ единиц.

Далее разделим этот квадрат на несколько маленьких квадратов со стороной $1$.

9{2}$.

Как вычислить площадь квадрата по сторонам?

Площадь квадрата равна квадрату его длины. Для нахождения площади квадрата используются следующие шаги:

Шаг 1: Запишите длину квадрата

Шаг 2: Подставьте значение длины квадрата в формулу

Шаг 4: Упростите выражение в формуле, чтобы получить площадь в квадратных единицах

Примеры

9{2}$

Количество плиток = $\frac {250000}{625} = 400$

Следовательно, чтобы покрыть квадратный двор длиной $5 м$, необходимо количество квадратных плиток длиной $25 см$, равное $400 $. {2}$ 9{2}$

Количество плиток = $\frac {25}{0,0625} = 400$

Следовательно, чтобы покрыть квадратный двор длиной $5 м$, необходимо количество квадратных плиток длиной $25 см$, равное $400 $.

10 Известные математики

Формула площади квадрата с использованием диагонали

Вы также можете найти площадь квадрата, если известна длина его диагонали. В этом случае вы используете теорему Пифагора, чтобы найти площадь квадрата.

Рассмотрим квадрат со стороной $s$ и диагональю $d$. 9{2}$.

Рекомендуемая литература

• Что такое длина? (с определением, единицами и преобразованием)
• Вес – определение, единица измерения и преобразование
• Что такое емкость (определение, единицы и примеры)
• Что такое время? (с определением, фактами и примерами)
• Что такое температура? (с определением и единицами измерения)
• Чтение календаря
• Периметр прямоугольника – определение, формула и примеры
• Периметр квадрата – определение, формула и примеры 9{2}$.

  No related posts.