Процент, Процентное соотношение
Процент (что означает «на сотню») это сравнение с 100.
Символ процента %. Так, например, 5 процентов записывается как 5%.
Предположим, что в комнате 4 человека.
50% это половина — 2 человека.
25% это четверть — 1 человек.
0% это ничего — 0 человек.
100% это целое — все 4 человека в комнате.
Если в комнату заходят ещё 4 человека, то их колличество становится 200%.
1% это $\frac{1}{100}$
Если всего есть 100 человек, то 1% из них это один человек.
Чтобы выразить математически число X как процент от Y вы делаете следующее:
$X : Y \times 100 = \frac{X}{Y} \times 100$
Пример: Сколько процентов от 160 составляет 80?
Решение:
$\frac{80}{160} \times 100 = 50\%$
Увеличение/Уменьшение процентного соотношения
Когда число увеличивается относительно другого числа, то величина увеличения представляется как:
Увеличение = Новое число — Старое число
Однако, когда число уменьшается относительно другого числа, то эту величину можно представить как:
Уменьшение = Старое число — Новое число
Увеличение или уменьшение числа всегда выражается на основании старого числа.
Поэтому:
%Увеличение = 100 ⋅ (Новое число — Старое число) ÷ Старое число
%Уменьшение = 100 ⋅ (Старое число — Новое число) ÷ Старое число
Например, у Вас было 80 почтовых марок и Вы начали в этом месяце собирать ещё пока общее количество почтовых марок достигло 120. Процентное увеличение числа марок, которые у Вас есть равно
$\frac{120 — 80}{80} \times 100 = 50\%$
Когда у Вас стало 120 марок, Вы и Ваш друг договорились обменять игру «Lego» на несколько из этих марок. Ваш друг взял несколько марок, которые ему понравились, и когда Вы подсчитали оставшиеся марки, то обнаружили, что у Вас осталось 100 марок. Процентное уменьшение числа марок может быть подсчитано как:
$\frac{120 — 100}{120} \times 100 = 16,67\%$
Калькулятор Процентов
| Что если % из ? | Результат: | |
| это какой процент от ? | Ответ: % | |
| это % от чего? | Ответ: | |
Как процентные соотношения помогают в реальной жизни
Есть два способа, как процентные соотношения помогают в решении наших каждодневных проблем:
1.
Мы сравниваем две разных величины, когда все величины соотносятся с одной и той же основной величиной равной 100. Чтобы объяснить это, давайте рассмотрим следующий пример:
Пример: Том открыл новую бакалейную лавку. За первый месяц он купил бакалеи за \$650 и продал за \$800, а во втором купил за \$800 и продал за \$1200. Надо рассчитать делает ли Том больше прибыли или нет.
Напрямую из этих чисел мы не можем сказать растёт доход Тома или нет, потому что расходы и выручка каждый месяц разные. Для того, чтобы решить эту задачу, нам нужно соотнести все значения к фиксированной основной величине равной 100. Давайте выразим процентное соотношение его доходов к расходам в первый месяц:
(800 — 650) ÷ 650 ⋅ 100 = 23,08%
Это значит, что если Том тратил \$100, то он делал прибыль в размере 23.08 в первый месяц.
Теперь давайте применим тоже самое ко второму месяцу:
(1200 — 800) ÷ 800 ⋅ 100 = 50%
Так, во втором месяце, если Том тратил \$100, то его доход был \$50(потому что \$100⋅50% = \$100⋅50÷100=\$50).
Теперь понятно,что доходы Тома растут.
2. Мы можем определять количество части большей величины, если известно процентное соотношение этой части. Чтобы объяснить это, давайте рассмотрим следующий пример:
Пример: Синди хочет купить 8 метров шланга для своего сада. Она пошла в магазин и обнаружила, что там есть катушка со шлангом длиной 30 метров. Однако, она заметила, что на катушке написано, что 60% уже продано. Она должна узнать хватит ли ей оставшегося шланга.
Решение:
В табличке сказано, что
$\frac{Продано\ длина}{Всего\ длина} \times 100 = 60\%$
$Продано\ длина = \frac{60 \times 30}{100} = 18м$
Поэтому остаток 30 — 18 = 12м, которого вполне достаточно Синди.
Примеры:
1. Райн любит собирать спортивные карточки с его любимыми игроками. У него есть 32 карточки с игроками бейсбола, 25 карточки с футболистами и 47 с баскетболистами. Каково процентное соотношение карточек каждого спорта в его коллекции?
Решение:
Общее количество карточек = 32 + 25 + 47 = 104
Процентное соотношение бейсбольных карточек = 32/104 x 100 = 30,8%
Процентное соотношение футбольных карточек = 25/104 x 100 = 24%
Процентное соотношение баскетбольных карточек = 47/104 x 100 = 45,2%
Обратите внимание, что если сложить все проценты, то получится 100%, что представляет общее количество карточек.
2. На уроке был математический тест. Тест состоял из 5 вопросов; за три из них давали по три 3 балла за каждый, а за осташиеся два — по четыре балла. Вам удалось правильно ответить на два вопроса по 3 балла и на один вопрос по 4 балла. Какое процентное соотношение баллов Вы получили за этот тест?
Решение:
Общее количество = 3×3 + 2×4 = 17 баллов
Полученные балы = 2×3 + 4 = 10 баллов
Процентное соотношение полученных баллов = 10/17 x 100 = 58,8%
3. Вы купили видео игру за \$40. Потом цены на эти игры подняли на 20%. Какова новая цена видео игры?
Решение:
Увеличение цены равно 40 x 20/100 = \$8
Новая цена равна 40 + 8 = \$48
высчитать процентное соотношение чисел
Вы искали высчитать процентное соотношение чисел? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить процентное соотношение, не
исключение.
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «высчитать процентное соотношение чисел».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как высчитать процентное соотношение чисел,вычислить процентное соотношение,как вывести процентное соотношение одного числа от другого,как высчитать процент из двух чисел,как высчитать процентное соотношение двух чисел,как высчитать процентное соотношение между числами,как вычислить процент между двумя числами,как вычислить процентное соотношение двух чисел,как вычислить процентное соотношение между числами,как вычислить соотношение в процентах,как из двух чисел высчитать процент,как найти процент между двумя числами,как найти процент от двух чисел,как найти процентное отношение,как найти процентное отношение двух чисел,как найти процентное соотношение двух чисел,как найти процентное соотношение одного числа от другого,как найти проценты от двух чисел,как найти соотношение двух чисел в процентах,как определить процентное соотношение,как определить процентное соотношение двух чисел,как от двух чисел узнать процент,как подсчитать процентное соотношение двух чисел,как посчитать в процентном соотношении,как посчитать отношение одного числа к другому,как посчитать процент от двух чисел,как посчитать процент отклонения одного числа от другого,как посчитать процентное соотношение двух чисел,как посчитать процентное соотношение двух чисел в процентах,как посчитать соотношение в процентах одного числа к другому,как посчитать соотношение одного числа к другому,как посчитать соотношение чисел,как рассчитать процентное соотношение между двумя числами,как рассчитать соотношение в процентах,как узнать процент от двух чисел,как узнать процентное соотношение между двумя числами,калькулятор процентного соотношения,калькулятор процентного соотношения чисел,калькулятор соотношения чисел,найти процентное соотношение двух чисел онлайн,нахождение процентного отношения двух чисел,отношение одного числа к другому в процентах,отношение одного числа к другому как посчитать,посчитать соотношение между двумя числами,процент между двумя числами как найти,процентное соотношение двух чисел онлайн,процентное соотношение двух чисел формула,процентное соотношение чисел,соотношение чисел в процентах,формула процентного соотношения,формула процентного соотношения двух чисел.
Где можно решить любую задачу по математике, а так же высчитать процентное соотношение чисел Онлайн?
Решить задачу высчитать процентное соотношение чисел вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Как рассчитать проценты — пустышки
Прослушать статью:Скачать аудио Оставляете ли вы чаевые в ресторане или выясняете, сколько стоит эта стильная обувь со скидкой, вам не обойтись без процентов.
Несмотря на то, что в Интернете есть множество процентных калькуляторов, полезно иметь возможность быстро посчитать в уме, чтобы рассчитать проценты без какой-либо цифровой помощи.
Что такое процент?
Слово процент происходит от слова процент. Если вы разделите слово «процент» на его корневые слова, вы увидите «процент» и «процент». Цент — это старое европейское слово французского, латинского и итальянского происхождения, означающее «сто». Таким образом, процент переводится непосредственно как «на сотню». Если у вас есть 87 процентов, вы буквально имеете 87 на 100. Если за последние 100 дней снег шел 13 раз, он шел в 13 процентах случаев.Как найти процент
Числа, которые вы будете преобразовывать в проценты, могут быть предоставлены вам в двух различных форматах: десятичном и дробном. Десятичный формат легче вычислить в процентах. Преобразовать десятичную дробь в проценты так же просто, как умножить ее на 100. Чтобы преобразовать 0,87 в проценты, просто умножьте 0,87 на 100.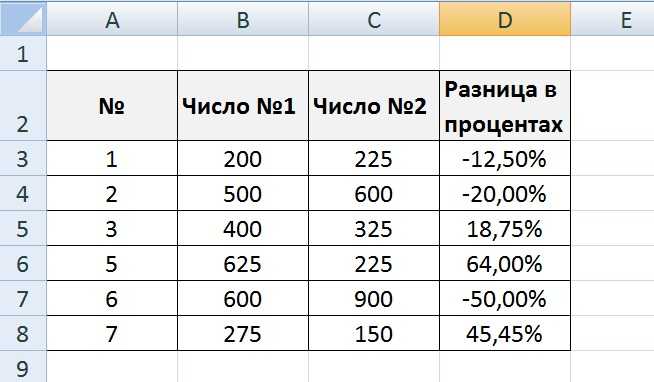
0,87 × 100 = 87, что дает нам 87 процентов.
Проценты часто обозначаются символом %. Вы можете представить свой ответ как 87% или 87% — оба варианта приемлемы.
Если вам дана дробь, преобразуйте ее в проценты, разделив верхнее число на нижнее. Если вам дано 13/100, вы должны разделить 13 на 100.13 ÷ 100 = 0,13
Затем выполните описанные выше шаги для преобразования десятичной дроби в проценты.
.13 × 100 = 13, что дает вам 13%.
Более сложная задача возникает, когда вам нужно знать процентное соотношение, когда вам дают числа, которые не так точно укладываются в 100.
В большинстве случаев вам будут давать проценты от определенного числа. Например, вы можете знать, что 40 процентов вашей зарплаты пойдет на налоги, и вы хотите узнать, сколько это денег.
Как рассчитать процент от определенного числа
Этот процесс является обратным тому, что вы делали ранее. Сначала преобразуйте процентное число в десятичное число. Затем вы делите свой процент на 100.
Таким образом, 40 процентов будут 40, разделенными на 100.40 ÷ 100 = 0,40
Затем, когда вы получите десятичную версию вашего процента, просто умножьте его на заданное число (в в этом случае сумма вашей зарплаты). Если ваша зарплата составляет 750 долларов, вы должны умножить 750 на 0,40.
750 × 0,40 = 300
Ваш ответ будет 300. Вы платите 300 долларов налогов.
Давайте попробуем другой пример. Вам нужно откладывать 25 процентов своей зарплаты в течение следующих 6 месяцев, чтобы заплатить за предстоящий отпуск. Если ваша зарплата составляет 1500 долларов, сколько вы должны откладывать?
Начните с преобразования 25 процентов в десятичную дробь.
25 ÷ 100 = 0,25
Теперь умножьте десятичную дробь на сумму вашей зарплаты, или 1500.
1500 × 0,25 = 375
Это означает, что вам нужно откладывать 375 долларов с каждой зарплаты.
Об этой статье
Эту статью можно найти в категории:
- Базовая математика,
Нахождение процентов — Как найти проценты
Главная
90 052Узнать
Потребительская математика
- Процент
- Простые проценты
- Виды простых процентов
- Расчет простых процентов
- Расчет общей суммы простых процентов
- Простой расчет процентного времени
- Расчет основного долга для простых процентов
- Сложные проценты
- Расчет сложных процентов
- Вычисление сложного принципала
- Расчет сложной процентной ставки
- Расчет времени
Слово процентов означает одну сотую.
Процент — это число или отношение в виде дроби от 100. За числом в процентах всегда следует символ процента (%) . Ниже приведены примеры процентов:
`5%,10%,33 1/3%«,67,5%,100%`
Процент применяется в разных областях. Он обычно используется в бухгалтерском учете и финансах, таких как процентные ставки, прибыль, продажи и налогообложение. Ряд школ и университетов использовали проценты для выражения оценок учащихся. Вероятности, факты о питании и загрузка процесса представлены в процентах.
Процент – это результат умножения определенного числа на процент. В большинстве случаев проценты меньше, чем число, поскольку процент
является частью числа или количества.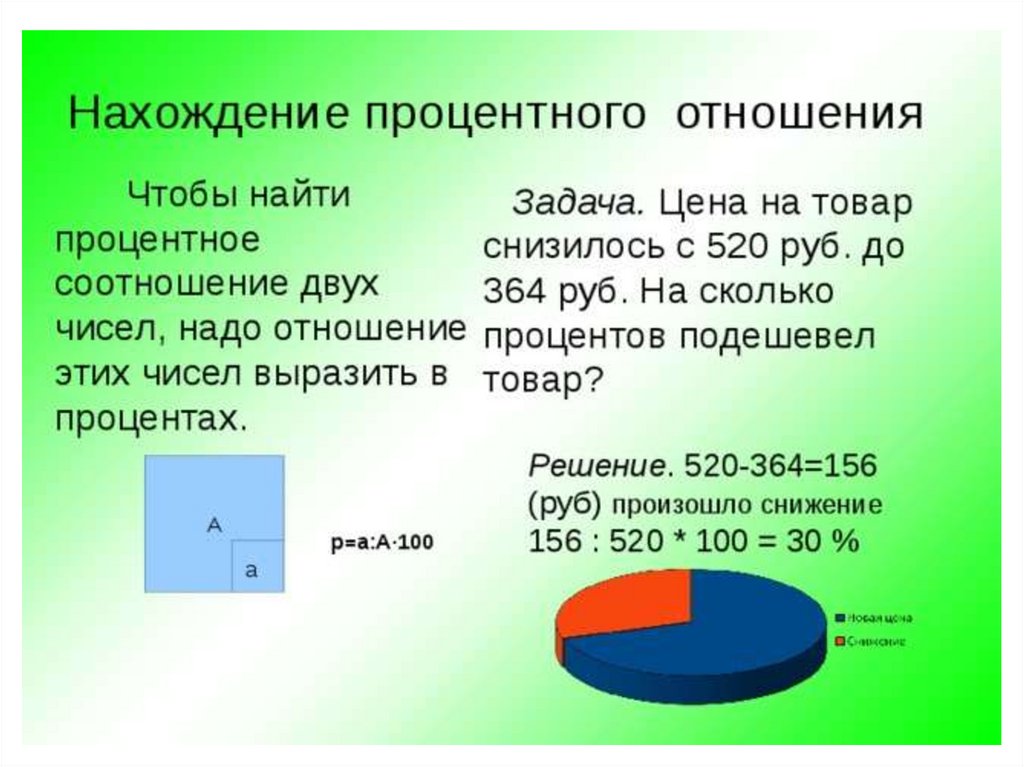
Но бывают случаи, что процент больше числа. Это произойдет, если процент больше 100%.
Короче говоря, процент — это определенный процент от числа.
В большинстве случаев за количеством следует фраза «процент».
Например;
70% от 50 равно 35.
В этом выражении 50 — это количество, 35 — это процент, а 70% — это процент.
Пример 3:
Пример 4:
Чтобы найти процент от числа, разделите процент на количество, затем умножьте произведение на 100. Поставьте символ процента (%) после конечного произведения.
Если процент больше количества, это означает, что процент больше 100%. Процент является фактором увеличения значения количества.
Пример 5:
Пример 6:
Пример 7:
Для получения процентов необходимо преобразовать проценты в десятичную форму, прежде чем умножать их на количество.
Ниже приведены шаги преобразования процентов в десятичные числа:
1.
Не обращайте внимания на символ процента (%).
2. Переместите запятую на два знака влево.
Пример 8:
Пример 9:
Пример 10:
Десятичные дроби легко преобразовать в проценты: просто переместите десятичную точку на две позиции вправо, а затем поставьте символ процента (%).
Пример 11:
Пример 12:
Иногда преобразование процентов в дроби является более простым способом получения процентов. Дроби предпочтительнее использовать, чем десятичные дроби, если десятичная дробь имеет много цифр. Это делает умножение более удобным, поскольку для упрощения процента используется только факторизация.
Вот шаги преобразования процентов в дроби:
1. Не обращайте внимания на символ процента (%).
2. Разделите процент на 100. Если числитель имеет цифры справа от десятичной точки, перемещайте десятичную точку, пока числитель не станет целым числом.
Переместите десятичную точку знаменателя (равную 100) на то же количество знаков после запятой, на которое переместилась десятичная точка числителя.
3. Сократить до минимума.
Пример 13:
Пример 14:
Пример 15:
При преобразовании дробей в проценты проще и удобнее сначала преобразовать дробь в десятичную, а затем преобразовать десятичную в проценты.
Вот этапы преобразования дробей в проценты:
1. Разделить числитель дроби на знаменатель. Результат в десятичной форме.
2. Умножьте десятичную форму на 100.
3. Поместите символ процента (%) после последней цифры процента.
В случае смешанных номеров;
1. Примените шаги, описанные выше, только для правильной части смешанного числа.
2. Умножьте целое число смешанной дроби на 100.
3. Сложите произведение (целое число, умноженное на 100) и десятичную форму правильной дроби.
4. Поместите символ процента (%) после последней цифры процента.
Пример 16:
Пример 17:
Пример 18:
Существуют некоторые неверные представления об использовании слов процент и процент. Два слова имеют
процента относится к определенному числу.
Например;
Бернадетт правильно ответила на 90 процентов тестовых вопросов.
Она набрала 90% (процентов) в тесте.
Процент — это результат умножения числа на процент. Он обозначает часть и в основном описывается как более низкий или более высокий.
Например;
Бернадетт набрала высокий балл в тесте.
Она набрала 90/100 баллов по тесту.
Обычно слово «процент» стоит после определенного числа, и обычно это целые или счетные числа. Он обычно не используется в предложениях, так как всегда заменяется символом процента (%). Слово «процент» стоит перед дробью или после прилагательного (например, высокий, низкий, большой, маленький).