Чему равен косинус угла между векторами?
Чему равен косинус угла между векторами?
Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
Как найти косинус угла между векторами в трехмерном пространстве?
Косинус угла между векторами (cos а) равняется отношению скалярного произведения векторов a и b на произведение модулей векторов |a| и |b|. Скалярное произведение рассчитывается как сумма произведений соответствующих координат. Модуль вектора равен корню квадратному из суммы квадратов координат вектора.
Как найти значение косинуса угла?
Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Что такое косинус острого угла?
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. 2 x (один плюс катангенс квадрат икс равно 1 к синусу квадрат икс).
2 x (один плюс катангенс квадрат икс равно 1 к синусу квадрат икс).
Чему равен котангенс 60 градусов?
| значение угла α (градусов) | значение угла α в радианах | ctg (котангенс) |
|---|---|---|
| 60 | π/3 | 0,5774 |
| 65 | 13π/36 | 0,4663 |
| 70 | 7π/18 | 0,3640 |
| 75 | 5π/12 | 0,2679 |
Чему равен угол 60 градусов?
Таблица СИНУСОВ для углов от 0° до 360° градусов
| Угол в градусах | Sin (Синус) | ||||||
|---|---|---|---|---|---|---|---|
| 59° | 0.Чему равен Котангенс пи на 2?ctg (п / 2) = 0. Более опытные в тригонометрии довольно часто используют тригонометрическую окружность (также часто ее называют тригонометрическим кругом). Чему равен косинус угла в 60 градусов?сos (60°) = cos (π/3) = 1/2. Чему равен косинус угла в 120 градусов?Как найти значения тригонометрических функций для угла 120 градусов
Чему будет равен косинус 90 градусов?сos (90°) = cos (π/2) = 0. Что значит синус?Синус угла – это отношение дальнего от угла катета к гипотенузе. Косинус – отношение ближнего к гипотенузе. Тангенс угла – это отношение дальнего от угла катета к ближнему. Котангенс – наоборот. Что такое синус простыми словами?Синус угла – отношение противолежащего катета к гипотенузе; Косинус угла – отношение прилежащего катета к гипотенузе; … Котангенс угла – отношение прилежащего катета к противолежащему. Для чего нужен синус?Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности. … Остальным синусы и косинусы не нужны вообще! В повседневной жизни большинство людей почти никогда их не используют. Как работает синус?Длина катета, противолежащего углу, равна ординате точки A1(x,y) A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
|
Элементы высшей математики
Элементы высшей математики
ОглавлениеПРЕДИСЛОВИЕЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ § 1. Ось § 2. Вектор § 3. Направленные углы § 4. Проекция вектора с оси на ось § 5. Векторные цепи § 6. Цепи углов § 7. Проекции вектора на две взаимно перпендикулярные оси § 8. Угол между двумя лекторами. Условия параллельности и перпендикулярности S 9. Упражнения и контрольные вопросы Глава 2. КООРДИНАТЫ § 1. Метод координат § 2. Основные задачи, решаемые методом координат § 3. Упражнения Глава 3. ФУНКЦИИ § 1. Переменные в постоянные § 2. Понятие о функциональной зависимости § 3. Классификация математических функций § 4. Обзор и графическое изображение простейших функции одного аргумента § 5. Обратные функции § 6. Понятие об уравнении линии § 7. Упражнения Глава 4. ПРЯМАЯ § 1. Уравнение прямой, проходящей через данную точку § 2.  Общее уравнение прямой Общее уравнение прямой§ 3. Частные случаи § 4. Переход к уравнению с угловым коэффициентом § 5. Построение прямой § 6. Определение угла между двумя прямыми § 7. Условие совпадения прямых § 8 Пересечение прямых § 9. Расстояние от точки до прямой § 10. Другой подход к выводу уравнения прямой § 11. Прямая, проходящая через две точки § 12. Уравнение прямой в отрезках на осях § 13. Задачи на прямую линию Глава 5. ПРОСТЕЙШИЕ КРИВЫЕ. ПРЕОБРАЗОВАНИЕ КООРДИНАТ § 1. Окружность § 2. Эллипс. Построение посредством нитн. Зависимость между полуосями и полуфокусным расстоянием § 3. Построение эллипса по точкам § 4. Уравнение эллипса § 5. Связь эллипса с окружностью § 6. Директрисы эллипса § 7. Гипербола. Построение посредством нити § 8. Построение гиперболы по точкам § 10. Асимптоты. Геометрическое значение b § 11. Директрисы гиперболы § 12. Парабола. Построение по точкам § 13.  Уравнение параболы Уравнение параболы§ 14. Преобразование координат § 15. Пример на упрощение уравнения кривой путем параллельного переноса осей § 16. Поворот осей § 17. Общий случай § 18. Полярные координаты § 19. Спираль Архимеда § 20. Логарифмическая спираль § 21. Примеры на составление полярных уравнений кривых § 22. Выражение прямоугольных координат через полярные § 23. Уравнение лемнискаты § 24. Параметрическое задание линий § 25. Построение графика § 26. Циклоида § 27. Упражнения Глава 6. ВЕКТОРЫ, ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ § 1. Оси, векторы, углы § 2. Проекции § 3. Проекции на три взаимно перпендикулярные оси. Длина вектора через проекции § 4. Простейшие зависимости, содержащие величину вектора, проекции и направляющие косинусы § 5. Проекция вектора на оси. Косинус угла между двумя векторами. Скалярное произведение векторов § 6. Координаты § 7. Выражение проекций вектора через координаты конца и начала § 8.  Выражение длины вектора через координаты концов. Расстояние между двумя точками Выражение длины вектора через координаты концов. Расстояние между двумя точками§ 9. Деление отрезка в данном отношении § 10. График уравнения с двумя переменными § 11. Поверхность как след, образуемый перемещением некоторой деформируемой плоской кривой § 12. Цилиндрические поверхности § 13. Обратная задача. Уравнение шаровой поверхности § 14. Уравнение плоскости, проходящей через данную точку § 15. Общее уравнение плоскости § 16. Частные случаи § 17. Выяснение расположения плоскости относительно осей § 18. Угол между плоскостями. Условие параллельности. Условие перпендикулярности § 19. Условие совпадения плоскостей § 21. Прямая как пересечение двух плоскостей § 22. Прямая, проходящая через данную точку § 23. Прямая, проходящая через две точки § 24. Переход от системы уравнений прямой в общем виде к системе в виде пропорций § 25. Угол между прямыми. Условие параллельности. Условие перпендикулярности § 26.  Угол между прямой и плоскостью. Условие параллельности и перпендикулярности Угол между прямой и плоскостью. Условие параллельности и перпендикулярности§ 27. Простейшие поверхности. Эллипсоид § 28. Другие простейшие поверхности § 29. Кривая в пространстве как пересечение двух поверхностей § 30. Параметрические уравнения § 31. Винтовая линия § 32. Параметрические уравнения в механике § 33. Переход от параметрического представления к общему и обратно § 34. Преобразование координат § 35. Упражнения ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ § 1. Бесконечно малые § 2. Понятие предела переменной величины § 3. Понятие бесконечно большой § 4. Свойства бесконечно малых § 5. Основные свойства пределов § 6. Предел непрерывной функции § 7. Геометрическое истолкование непрерывности § 8. Свойство непрерывной функции § 9. Предел функции, зависящей от нескольких переменных § 10. Особые случаи разыскания предела § 11. Замечательный тригонометрический предел § 12. Признак существования предела § 13.  x. x.§ 9. Производные произведения и частного. Производные tg x и ctg x. § 10. Производные обратных тригонометрических функций § 11. Сводка основных формул § 12. Дифференциал § 13. Основные формулы для дифференциалов § 14. Высшие производные § 15. Высшие дифференциалы § 16. Дифференцирование неявных функций § 17. Дифференцирование функций, заданных параметрическим способом § 18. Преобразование дифференциалов к новой переменной Глава 3. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ § 1. Непрерывность первой производной § 2. Возрастание и убывание функций. Максимум и минимум § 3. Приложение к построению графиков § 4. Наибольшее и наименьшее значения функции § 5. Прикладные задачи на наибольшее и наименьшее значения § 6. Направление выпуклости, точки перегиба § 7. Приложение к построению графиков § 8. Построение графиков разрывных функций § 9. Признак максимума и минимума, основанный на исследовании знака первой производной § 10.  Признак максимума и минимума, основанный на исследовании знака второй и высших производных Признак максимума и минимума, основанный на исследовании знака второй и высших производных§ 11. Асимптоты § 12. Дифференциал дуги § 13. Направляющие косинусы касательной § 14. Радиус кривизны, центр кривизны § 15. Дифференциал дуги и направляющие косинусы касательной для кривой в пространстве § 16. Упражнения Глава 4. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ § 1. Функции многих переменных. Область определения. Непрерывность § 2. Частные производные и полный дифференциал § 3. Частные производные и полный дифференциал сложной функции многих переменных § 4. Дифференцирование неявных функций § 5. Частные производные и полные дифференциалы высшего порядка § 6. Упражнения ЧАСТЬ ТРЕТЬЯ. ОСНОВЫ ТЕОРИИ ЧИСЕЛ Глава 1. ТЕОРИЯ ДЕЛИМОСТИ § 2. Общий наибольший делитель § 3. Общее наименьшее кратное § 4. Простые числа § 5. Единственность разложения на простые сомножители § 6. Непрерывные дроби и их связь с алгоритмом Евклида Вопросы к главе 1 Глава 2.  ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ§ 1. Функции [x] и {x} § 2. Мультипликативные функции § 3. Число делителей и сумма делителей § 5. Функция Эйлера Вопросы к главе II Глава 3. СРАВНЕНИЯ § 2. Свойства сравнений, подобные свойствам равенств § 3. Дальнейшие свойства сравнений § 4. Полная система вычетов § 5. Приведенная система вычетов § 6. Теоремы Эйлера и Ферма Вопросы к главе 3 Глава 4. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ § 2. Сравнения первой степени § 3. Система сравнений первой степени § 4. Сравнения любой степени по простому модулю § 5. Сравнения любой степени по составному модулю Вопросы к главе 4 Глава 5. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ § 2. Символ Лежандра § 3. Символ Якоби § 4. Случай составного модуля Вопросы к главе 5 Глава 6. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ § 2. Первообразные корни по модулям § 3. Разыскание первообразных корней по модулям § 4. Индексы по модулям § 5.  a a§ 7. Индексы по любому составному модулю Вопросы к главе 6 Глава 7. ХАРАКТЕРЫ § 2. Важнейшие свойства характеров Вопросы к главе 7 РЕШЕНИЯ ВОПРОСОВ Решения к главе 2 Решения к главе 3 Решения к главе 4 Решения к главе 5 Решения к главе 6 ОТВЕТЫ К ЧИСЛЕННЫМ ПРИМЕРАМ |
. Можем ли мы использовать «векторное произведение», чтобы найти угол между двумя векторами?
Задавать вопрос
спросил
Изменено 4 года, 1 месяц назад
Просмотрено 2к раз
$\begingroup$
Имеются два вектора: $A = (\hat i + j + k)$ и $B = (\hat i — \hat j — \hat k)$, где $\hat i$, $\hat j $ и $\hat k$ — единичные векторы вдоль осей $x$, $y$ и $z$ соответственно. Нам нужно найти угол между этими двумя векторами. Конечно, лучший способ сделать это — использовать «скалярное произведение». Скалярное произведение этих двух векторов дает $(-1)$, что равно $3\cos\theta$
\начать{выравнивать}
\ подразумевает && -1 & = 3\cos \тета \\
\ подразумевает && \ тета & = \ arccos (-1/3) = 109° \quad \text{(приблизительно)}
\end{align}
Нам нужно найти угол между этими двумя векторами. Конечно, лучший способ сделать это — использовать «скалярное произведение». Скалярное произведение этих двух векторов дает $(-1)$, что равно $3\cos\theta$
\начать{выравнивать}
\ подразумевает && -1 & = 3\cos \тета \\
\ подразумевает && \ тета & = \ arccos (-1/3) = 109° \quad \text{(приблизительно)}
\end{align}
Теперь, если я использую векторное произведение, я получаю $A \times B = (2\hat j — 2\hat k)$, поэтому $|A \times B| = \sqrt{8}$, что равно $3\sin\theta$.
\начать{выравнивание} \ подразумевает && \sqrt{8} & = 3\sin \theta \\ \подразумевает && \theta & = \arcsin (\sqrt{8}/3) = 70,5° \quad \text{(приблизительно)} \end{align}
Почему эти два угла не равны? Разве они не должны быть равны?
- векторы
- геометрия
$\endgroup$
4
$\begingroup$
Ваш аргумент о перекрестном произведении ошибочен, потому что арксинус не может различить углы в интервале $[0,90°]$ и углы в интервале $[90°,180°]$.
Правильный угол получается из аргумента скалярного произведения, $\arccos(-1/3) \приблизительно 109°$, и вы должны быть в состоянии проверить (по крайней мере численно), что этот угол удовлетворяет $$ \sin\mathopen{}\left(\arccos(-1/3)\right)\mathclose{} «=» \ гидроразрыва {\ sqrt {8}} {3} = \frac{||A\times B||}{||A|| \, ||В||}. $$
Арксинус, с другой стороны, всегда ограничивается получением углов в интервале $[-90°,90°]$, что означает, что он отражает $109,5°$ около отметки $90°$ для получения $70,5°$, которые вы наблюдаете.
Из-за этого ограничения ваш метод векторного произведения ненадежен, и его не следует использовать для вычисления углов между векторами.
$\endgroup$
$\begingroup$
Я бы посоветовал использовать оба
$$ \| А \раз В\| = \| А \| \| Б \| \sin \тета $$ $$ А \cdot В = \| А \| \| Б \| \cos \тета $$
или
$$ \tan \theta = \frac{ \| A \times B \|}{A \cdot B} $$
и в вычислительном отношении использовать функцию atan2(dy,dx)
Angle = atan2( cross(A,B), dot(A,B)) = atan2( 2*sqrt(2),-1 ) = 1,910633r = 109,47122°
Проблема с вычислением только $\sin(\theta)$ заключается в том, что ответ может быть только между $[- \tfrac{\pi}{2} \ldots \tfrac{\pi}{2} )$.
Хотя приведенное выше также имеет ту же область, что и вычисление $\cos(\theta)$ для $[0 \ldots \pi)$, это может быть быстрее в вычислительном отношении, поскольку величина векторов никогда не вычисляется (избегая двух sqrt() ) вызовов.
$\endgroup$
3
$\begingroup$
На самом деле ни синуса, ни косинуса недостаточно, чтобы найти ориентированный угол. Косинус (скалярное произведение) дает угол знаку. Синус необходимо иметь знак. Поэтому в принципе следует использовать как векторное, так и скалярное произведение.
$\endgroup$
2
Как найти угол и модуль вектора
В физике иногда нужно найти угол и модуль вектора, а не компоненты. Чтобы найти величину, вы используете теорему Пифагора. И найти
И найти
вы используете функцию арктангенса (или арксинус или косинус).
Например, предположим, что вы ищете отель, который находится в 20 милях к востоку, а затем в 20 милях к северу. Каков угол (измеренный с востока) от вашего нынешнего местоположения в направлении отеля и как далеко находится отель? Вы можете записать эту задачу в векторной записи, например:
Шаг 1: (20, 0)
Шаг 2: (0, 20)
При сложении этих векторов вы получите следующий результат:
(20, 0) + (0, 20) = (20, 20)
Результирующий вектор равен (20, 20). Это один из способов задать вектор — использовать его компоненты. Но эта проблема не требует результатов с точки зрения компонентов. Вопрос хочет знать угол и расстояние до отеля.
Использование угла, созданного вектором, чтобы добраться до отеля.
Другими словами, глядя на рисунок выше, проблема спрашивает:
Если вы знаете вертикальную и горизонтальную составляющие вектора, найти модуль вектора не так сложно, потому что вам просто нужно найти гипотенузу прямоугольного треугольника.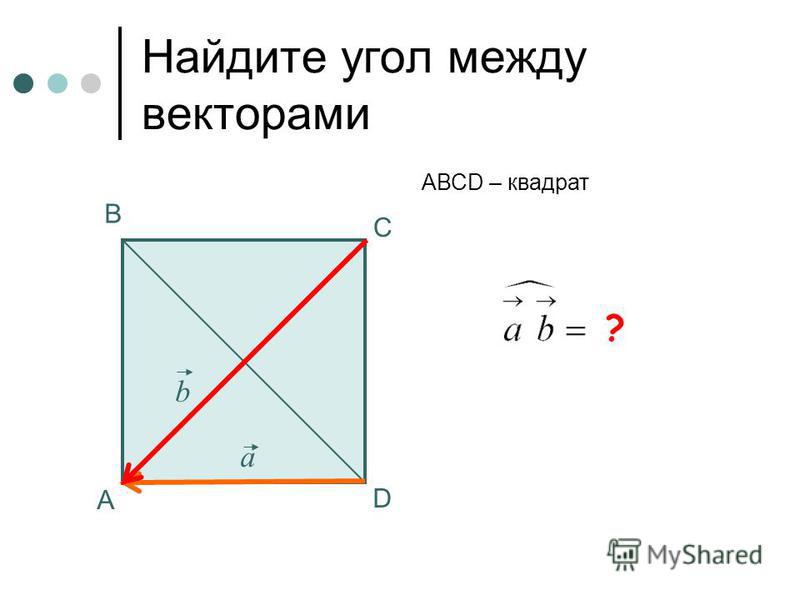 Вы можете использовать теорему Пифагора ( x 2 + y 2 = ч 2 ), решенную для ч :
Вы можете использовать теорему Пифагора ( x 2 + y 2 = ч 2 ), решенную для ч :
Подстановка чисел дает
Имейте в виду, что когда вы знаете горизонтальную и вертикальную составляющие вектора, вы можете использовать тангенс для нахождения угла, потому что
Все, что вам нужно сделать, это взять арктангенс y / x :
Предположим, вы проезжаете 20 миль на восток и 20 миль на север. Вот как вы находите
угол между вашим исходным положением и вашим конечным положением:
Итак, отель находится примерно в 28 милях под углом 45 градусов.
Будьте осторожны при вычислениях с арктангенсами, потому что углы, отличающиеся на 180 градусов, имеют одинаковый тангенс. Когда вы берете арктангенс, вам может понадобиться добавить или вычесть 180 градусов, чтобы получить фактический угол, который вы хотите. Кнопка арктангенса на вашем калькуляторе всегда даст вам угол между 90 градусов и –90 градусов. Если ваш угол не находится в этом диапазоне, вам нужно добавить или вычесть 180 градусов.
Если ваш угол не находится в этом диапазоне, вам нужно добавить или вычесть 180 градусов.
Для этого примера ответ 45 градусов должен быть правильным. Но представьте себе ситуацию, в которой вам нужно прибавить или вычесть 180 градусов: предположим, вы идете в направлении, противоположном отелю. Вы проходите 20 миль на запад и 20 миль на юг ( x = -20 миль, y = -20 миль), поэтому, если вы используете тот же метод для определения угла, вы получите следующее:
Вы получаете тот же ответ для угла, даже если вы идете в совершенно противоположном направлении, как раньше! Дело в том, что тангенсы углов, отличающихся на 180 градусов, равны. Но если вы посмотрите на компоненты вектора ( x = -20 миль, y = -20 миль), они оба отрицательны, поэтому угол должен быть между -90 градусами и -180 градусами. Если вы вычтете 180 градусов из вашего ответа в 45 градусов, вы получите -135 градусов, что является вашим фактическим углом, измеренным от положительной оси x по часовой стрелке.


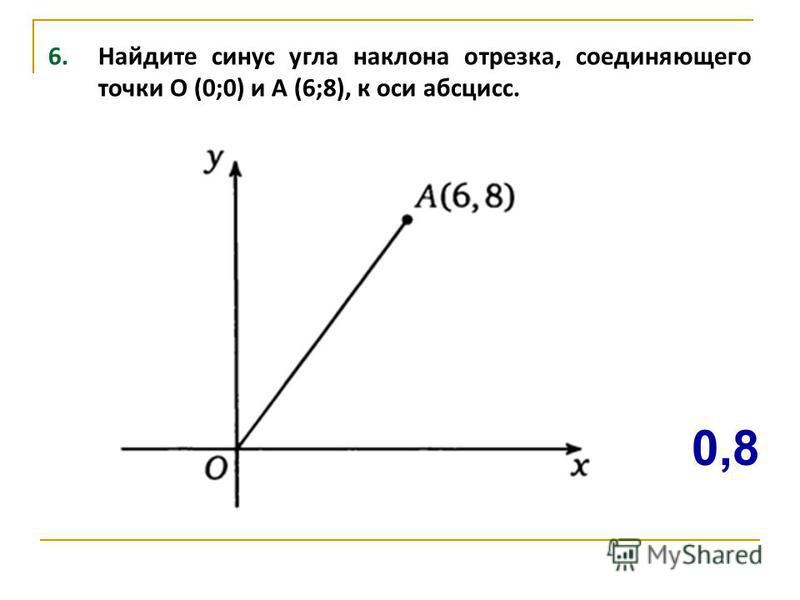 В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.