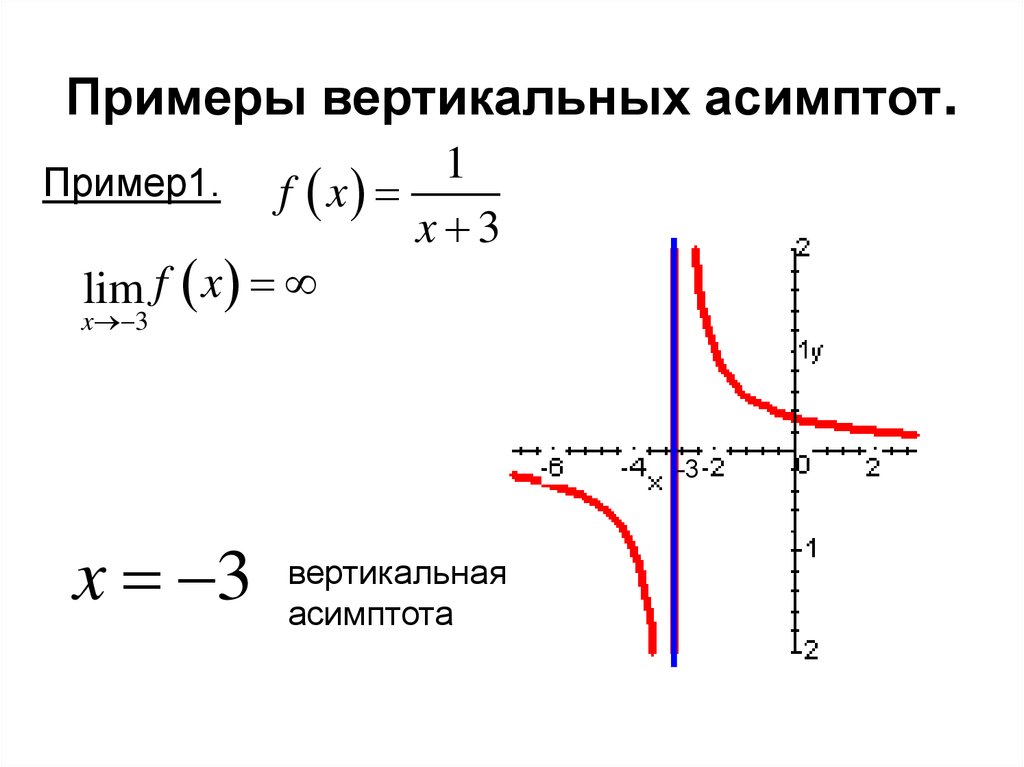
как найти наклонную, горизонтальную и вертикальную, примеры решения
Что такое асимптота — понятие и определение
Определение
Асимптота графика функции у=f (x) представляет собой прямую L, максимально приближающеюся к графику функции, точка которого стремится к бесконечности, то есть неограниченно удаляется от начала координат по кривой. Расстояние между этой точкой функции у=f(x) и асимптотой L стремится к нулю.
На рисунке приведены примеры асимптот графиков функций.
Источник: pnu.edu.ruНа рисунке слева продемонстрирована кривая, которая приближается к асимптоте и остается с одной стороны по отношению к ней.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На рисунке справа представлена кривая (график функции), которая пресекает асимптоту бесконечное множество раз с разных сторон
Асимптоты графика функции, основные виды
Асимптоты делятся на три вида: 
У разных функции в наличии может быть различное количество асимптот:
- Парабола и синусоида не имеют асимптот.
- Экспоненциальная и логарифмическая функции имеют 1 асимптоту.
- Арктангенс и арккотангенс — две.
- Тангенс и котангенс — бесконечное количество.
- Гипербола имеет горизонтальную и вертикальную асимптоты.
Приведем пример нахождения асимптот гиперболы.
Определение
Гипербола — геометрическое место расположения точек, от которых абсолютная величина разности растояний до двух фокусов (заданных точек), является постоянной и меньшей, чем расстояние между самими фокусами.
Определение
Асимптоты гиперболы — прямые, которые тесто связаны с ней и определяются уравнениями \(y=\frac bax\) и \(-y=\frac bax\).
При \(x\rightarrow+\infty\) разность ординат асимптоты и гиперболы будет \(\delta\rightarrow0\). {1/x}=\infty\)
{1/x}=\infty\)
Наклонные асимптоты
Если в определении асимптоты присутствует +∞ или —∞, то она относится либо к горизонтальной, либо к наклонной.
Асимптота графика функции у=f(x) является наклонной, если эту функцию можно представить в виде f(x)=kx+b+а(х). При этом должно выполняться условие: \(a(x)\rightarrow0\) при \\(x\rightarrow+\infty\). Прямая будет иметь вид y=kx+b.
Прямая у=kx+b будет наклонной асимптотой при \(x\rightarrow+\infty\) и \(x\rightarrow-\infty\), если существуют пределы:
\(\lim_{x\rightarrow+\infty}\frac{f(x)}x=k\)
\(\lim_{x\rightarrow+\infty}\left[f(x)-kx\right]=b\)
Если k=0, то наклонная асимптота превращается в горизонтальную.
Применение правила Лопиталя
Правило Лопиталя применяется, когда границы не определены, например, 0/0 или ∞/∞:
\(\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\left\{\frac00\right\}\) или \(\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\left\{\frac\infty\infty\right\}\)
Если функции можно дифференцировать, и они относятся к окрестностям точки x=a, тогда наклонную асимптоту необходимо искать по формуле:
\(\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}\)
Производная может применяться многократно для получения константы в числителе или знаменателе. 2})=1\)
2})=1\)
\(b=\lim_{x\rightarrow\infty}(y-kx)=\lim_{x\rightarrow\infty}(x+\frac1x-x)=\lim_{x\rightarrow\infty}\frac1x=0\)
Прямая у=х — наклонная асимптота графика данной функции.
Пример 2
Имеется функция \(y=\frac{\left|x\right|(x-1)}{x+1}.\)
Рассмотрим два варианта:
x>0 и x<0.
Если x>0, то
\(k_1=\lim_{x\rightarrow+\infty}\frac yx=\lim_{x\rightarrow+\infty}\frac{\left|x\right|(x-1)}{x(x+1)}=\lim_{x\rightarrow+\infty}\frac{x(x-1)}{x(x+1)}=1\)
\(b_1=\lim_{x\rightarrow+\infty}(y-k_1x)=\lim_{x\rightarrow+\infty}\left(\frac{\left|x\right|(x-1)}{x(x+1)}-x\right)=\lim_{x\rightarrow+\infty}\frac{x(x-1)-x(x+1)}{x+1}=-2\)
То есть правая ветвь кривой имеет наклонную асимптоту в виде прямой у=х-2.
Если x<0, то
\(k_2=\lim_{x\rightarrow-\infty}\frac yx=\lim_{x\rightarrow-\infty}\frac{\left|x\right|(x-1)}{x(x+1)}=\lim_{x\rightarrow-\infty}\frac{(-x)(x-1)}{x(x+1)}=-1\)
\(b_2=\lim_{x\rightarrow-\infty}(y-k_2x)=\lim_{x\rightarrow-\infty}\left(\frac{\left|x\right|(x-1)}{x+1}+x\right)=\lim_{x\rightarrow-\infty}\frac{(-x)(x-1)+x(x+1)}{x+1}=2\)
То есть левая ветвь кривой имеет наклонную асимптоту в виде прямой у=-х+2.
то y=0 — горизонтальная асимптота графика функции при \(x\rightarrow+\infty\).
Как найти асимптоты кривых
Часто задание на нахождение асимптот функции встречается в курсе математического анализа, в частности при решении задач на тему исследования функции. Для того, чтобы успешно ответить на вопрос: как найти асимптоты функции? необходимо уметь вычислять пределы, понимать что они собой представляют, знать основные методы решения пределов. Если всё это вы умеете на должном уровне, тогда найти асимптоты для вас не будет проблемой. Итак, что такое асимптота? Асимптота это линия, к которой бесконечно приближается ветвь графика функции. Чтобы было наглядно, посмотрите на изображения представленные ниже.
Обратите внимание, что соприкосновения между асимптотой и графиками нет, и не должно быть. Асимптота бесконечно приближается к графику функции. Давайте рассмотрим какие виды асимптоты функции бывают и как их находить, но о последнем будет рассказано далее.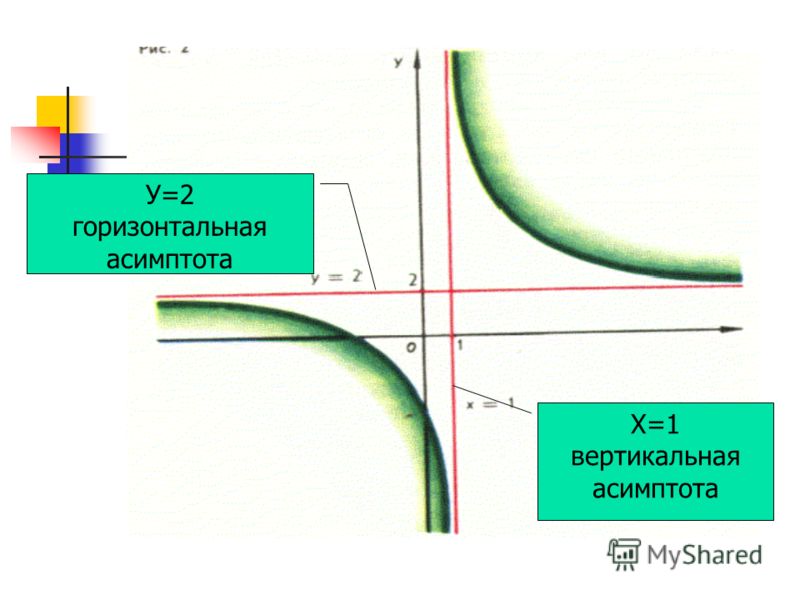
Из таблицы узнаем, что асимптоты у функции бывают трех видов: вертикальные, горизонтальные, наклонные. Каждую найти асимптоту функции нужно по своему. Для этого нужны лимиты. Сколько бывает асимптот всего у функции? Ответ: ни одной, одна, две, три. и бесконечно много. У каждой функции по разному.
Вертикальные асимптоты
Чтобы найти данный вид асимптот необходимо найти область определения заданной функции и отметить точки разрыва. В этих точках предел функции будет равен бесконечности, а это значит, что функция в этой точке бесконечно приближается к линии асимптоты.
Горизонтальные асимптоты
Необходимо устремить аргумент лимита функции к бесконечности. Если предел существует и равен числу, то горизонтальная асимптота будет найдена и равна $ y=y_0 $ как показано во втором столбце таблицы
Наклонные асимптоты
Наклонная асимптота представляется в виде $ y = kx+b $. Где $ k $ — это коэффициент наклона асимптоты. Сначала находится коэффициент $ k $, затем $ b $. Если какой либо из них равен $ infty $, тогда наклонной асимптоты нет. А если $ b = 0 $, то получаем горизонтальную асимптоту. Так что для экономии времени лучше сразу находить наклонную асимптоту, а горизонтальная проявится сама собой в случае её существования.
Если какой либо из них равен $ infty $, тогда наклонной асимптоты нет. А если $ b = 0 $, то получаем горизонтальную асимптоту. Так что для экономии времени лучше сразу находить наклонную асимптоту, а горизонтальная проявится сама собой в случае её существования.
Примеры решений
| Пример 1 |
| Найти все асимптоты графика функции $$ f(x) = frac<5x> <3x+2>$$ |
| Решение |
| Ответ |
| $$ y = frac<5> <3>$$ |
| Пример 2 |
| Найти все асимптоты графика функции $ f(x) = frac<1> <1-x>$ |
| Решение |
| Решение |
| Ответ |
| $$ y = 0 $$ |
Если в задачах даются элементарные функции, то заранее известно сколько и есть ли асимптоты. Например, у параболы, кубической параболы, синусоиды вообще нет никаких. У графиков функций таких как логарифмическая или экспоненциальная есть по одной. А у функций тангенса и котангенса бесчисленное множество асимптот, но арктангенс и арккатангенс имеет по две штуки.
Во всех приведенных примерах пределы вычислялись с помощью правило Лопиталя, которое очень ускоряет процесс вычисления и создает меньше ошибок.
Определение. Прямая называется асимптотой кривой, если расстояние от переменной точки M кривой до этой прямой при удалении точки M в бесконечность стремиться к нулю.
Асимптоты бывают вертикальными, они показывают поведение функции в окрестности особой точки, когда , и наклонными, дающими представление о поведении функции при .
Если особая точка, уравнение вертикальной асимптоты .
Теорема. Кривая имеет наклонную асимптоту при , уравнение которой , если принимают конечное значение и .
Доказательство. Из определения асимптоты следует , где бесконечно малая при , то есть . Остается определить параметры уравнения асимптоты. Для этого вычислим , . Итак, если оба предела существуют и конечны, параметры прямой и определены, причем точки этой прямой бесконечно сближаются с точками кривой при .
Пример. . Ясно, что — уравнение вертикальной асимптоты.
Определим ,
.
Наклонная асимптота при имеет уравнение .
Исследование функции, построение ее графика
I. Исследование самой функции. Необходимо установить
1) Область определения функции, ее особые точки, вертикальные асимптоты.
2) Точки пересечения кривой с осями координат
3) Функция четная, нечетная или общего вида
4) Функция периодическая или не периодическая
II. Исследование производной функции. Необходимо определить
Необходимо определить
1) Точки максимума и минимума функции
2) Интервалы возрастания и убывания функции
III. Исследование второй производной
1) Точки перегиба
2) Интервалы выпуклости и вогнутости функции
IV. Исследование поведения функции при . Наклонные асимптоты.
В качестве примера рассмотрим функцию
1. Область существования функции – вся числовая ось, то есть . Следовательно, у этой кривой нет особых точек, нет и вертикальных асимптот.
2. Кривая пересекает оси координат в начале координат. Следовательно, первая характерная точка графика .
3. Кривая нечетная: , следовательно, она симметричная относительно начала координат.
4. Функция непериодическая.
II. 1. Определим первую производную , приравниваем ее нулю, откуда получаем еще две характерные (критические) точки , , координаты этих точек на плоскости , . Рассмотрим первую из этих точек , левее ее производная , правее , следовательно, это точка минимума функции.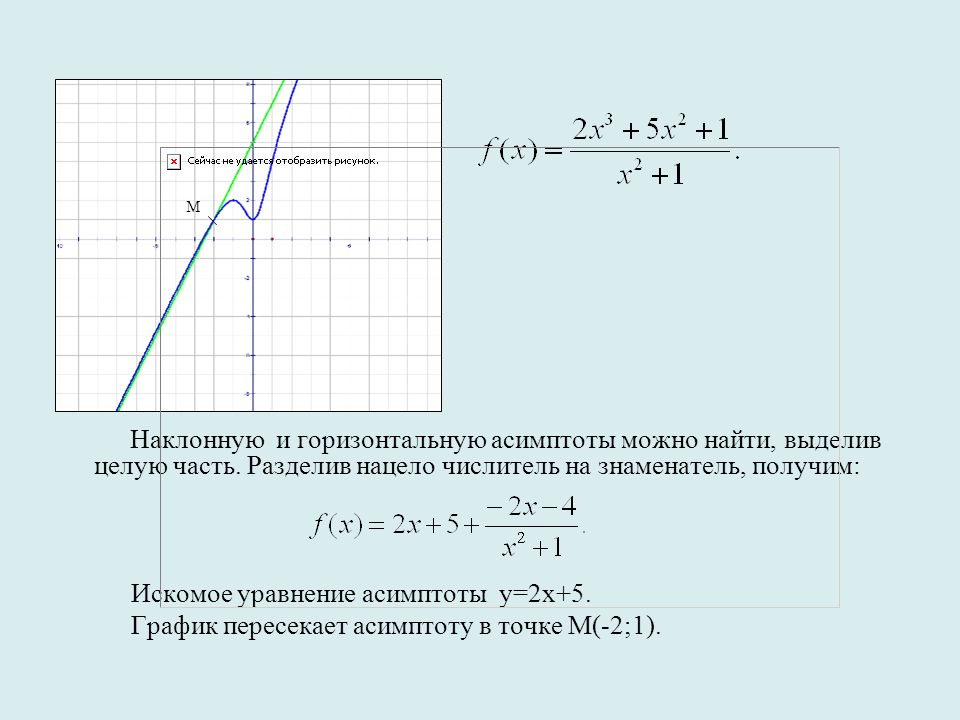
2. Знак первой производной определяется выражением , следовательно, она положительна на интервале , в остальных областях она отрицательна. Итак, функция убывает на интервале , возрастает на интервале , затем опять убывает на .
III. 1. Определяем вторую производную функции:
.
Приравниваем производную нулю и получаем еще три характерные точки функции, одна из которых уже известна. Две другие и . На координатной плоскости они имеют координаты , . Знак второй производной определяется ее числителем. Левее точки она отрицательна, правее . Следовательно, это точка перегиба. Левее точки имеем , правее ., еще одна точка перегиба. Левее точки получаем , правее , третья точка перегиба.
2. Поскольку других точек, в которых вторая производная меняет знак у функции нет, можно утверждать, что на интервале кривая выпуклая, на интервале кривая вогнутая, на интервале кривая опять выпуклая и, наконец, на интервале — вогнутая.
IY. Определяем наклонные асимптоты кривой, уравнение асимптоты , причем
,
,
Поскольку уравнение асимптоты , асимптотой функции является ось .
В итоге график функции имеет вид
На рисунке отчетливо наблюдаются точки максимума и минимума функции и три точки перегиба. Видим также, что кривая «прижимается» к оси при , стремящемся как к плюс, так и к минус бесконечности, следовательно, асимптота единая.
Рассмотрим пример при другом оформлении результата. Пусть . Область существования данной функции – вся числовая ось, кроме точки . Функция непериодическая (нет тригонометрических функций), общего вида (не четная, не нечетная).
Определим вначале все характерные точки графика, то есть точки пересечения с осями координат, особые точки, точки максимума и минимума, точки перегиба. Для этого вычислим первую и вторую производные
,
.
Исследуя функцию и ее производные, устанавливаем, что имеется одна особая точка и еще три характерных точки , , .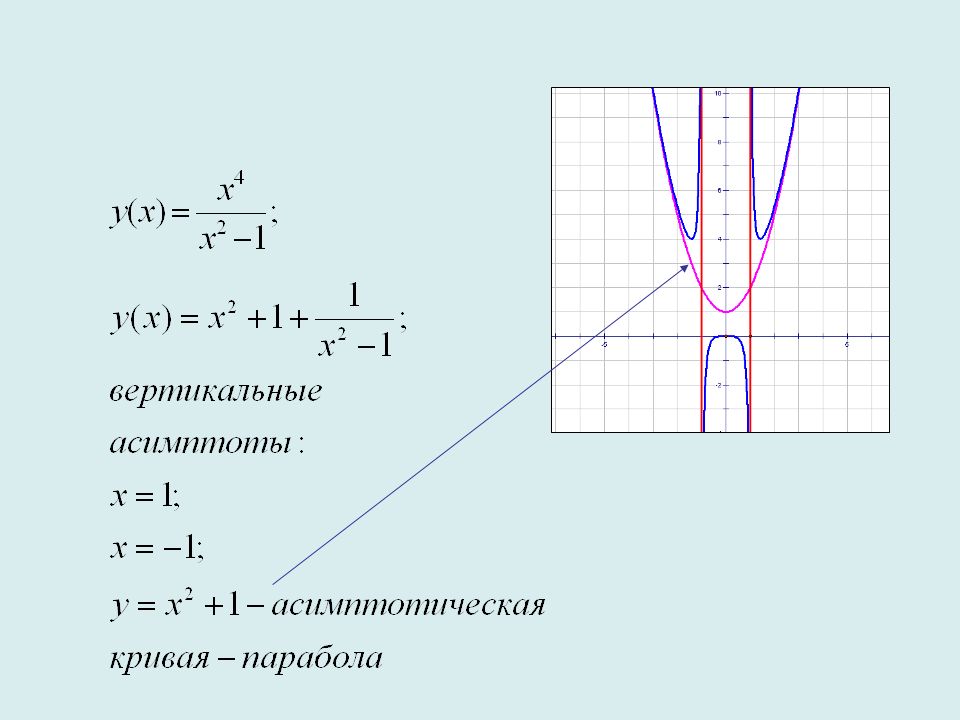
| -2 | -1 | ||||||||
| 0 | н.с. | >0 | |||||||
| 0 | >0 | н.с. | 0 | >0 | >0 | >0 | н.с. | >0 | |
| Примеч. | , убыв., выпукл. | Т. Пер. | , убыв., вогн. | Min | , возр., вогн. | , возр., вогн. | Н.с. | , убыв., вогн. |
В таблице собрана вся информация о функции, примечания позволяют проще построить ее график.
Определим наклонную асимптоту кривой , причем
,
.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 — | 7302 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Литература: [3], гл. V, § 10
Прямая называется асимптотой кривой y = f (x), если расстояние от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность от начала координат (рис. 1.7).
Различают вертикальные и наклонные асимптоты. Вертикальная асимптота имеет уравнение вида x = x0 и является прямой, параллельной оси Оy. Наклонная асимптота имеет уравнение вида y = k x + b. В частном случае при k = 0 асимптота называется горизонтальной, так как ее уравнение y = b есть прямая, параллельная оси Ох.
Вертикальные асимптоты.
Пусть дана кривая y = f (x). Для нахождения вертикальной асимптоты этой кривой находят точки ее бесконечного разрыва (точки разрыва второго рода).
Для нахождения вертикальной асимптоты этой кривой находят точки ее бесконечного разрыва (точки разрыва второго рода).
и ,
то прямая x = x0 ─ вертикальная асимптота кривой y = f (x) (рис. 1.8).
Наклонные и горизонтальные асимптоты.
Пусть задана кривая y = f (x). Для нахождения наклонной асимптоты, уравнение которой y = k x + b, находят коэффициенты k и b, вычисляя пределы: ,. Эти пределы вычисляются отдельно для случаеви. Если хотя бы один из пределов для вычисленияk и b равен ∞ или не существует, то кривая наклонных и горизонтальных асимптот не имеет.
В частном случае, когда k = 0, а b ─ конечное число, кривая имеет горизонтальную асимптоту, уравнение которой y = b.
Пример. Найти асимптоты кривой .
Решение. Функция определена на всем множестве действительных чиселR, кроме точки x = 1.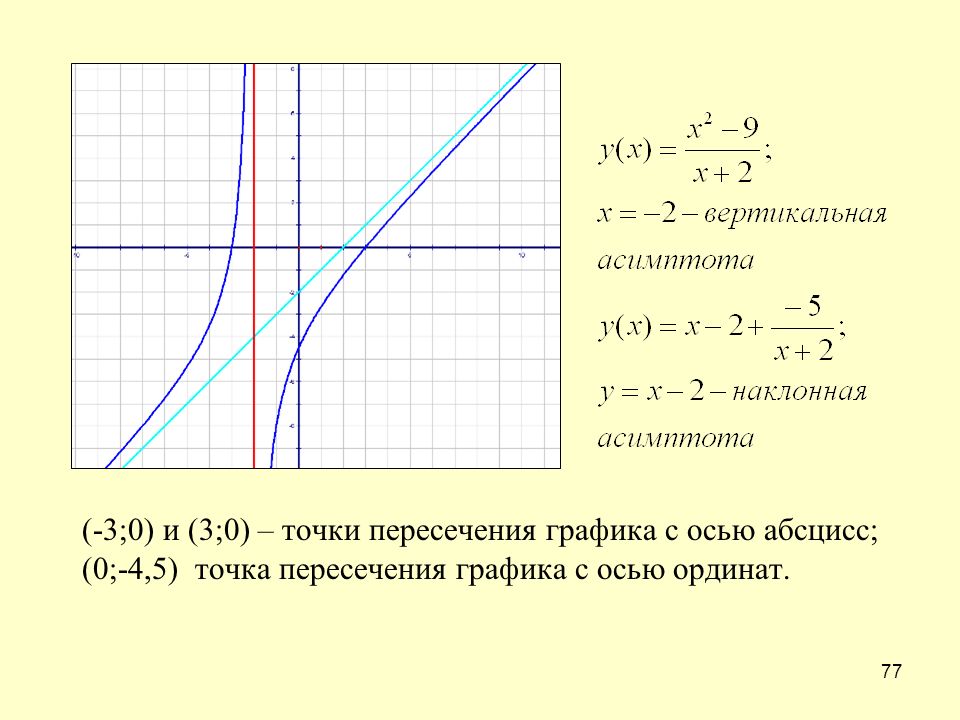 Определим характер разрыва, для чего вычислим пределы функции при x → 1 слева (x 1):
Определим характер разрыва, для чего вычислим пределы функции при x → 1 слева (x 1):
, .
Так как один из пределов бесконечен, то x = 1 является точкой разрыва второго рода, и, следовательно, кривая имеет вертикальную асимптоту x = 1.
Определим, имеет ли кривая наклонную или горизонтальную асимптоту. Для этого вычисляем соответствующие пределы:
, Уравнение асимптотыy = k x + b принимает вид y = 1 (горизонтальная асимптота).
хематический график функции представлен на рис. 1.9.
1.14. Схема полного исследования функции и построение ее графика
Литература: [3], гл. V, § 11
1. Находим область определения функции.
2. Устанавливаем четность, нечетность функции, периодичность. Находим характерные точки, например, точки пересечения с осями координат.
3.Находим точки разрыва функции, определяем их характер. При наличии точек разрыва второго рода (точек бесконечного разрыва) устанавливаем наличие вертикальных асимптот графика функции.
4. Находим производную функции, критические точки, промежутки монотонности, точки экстремума и значения функции в этих точках.
5. Находим вторую производную функции, интервалы выпуклости и вогнутости кривой и точки перегиба графика функции.
6.Устанавливаем наличие у исследуемой кривой наклонных и горизонтальных асимптот.
7. По полученным данным строим график функции.
Замечание. Если функция является четной или нечетной, то исследование проводят не на всей числовой оси, а на промежутке [0, +∞). Затем график продолжают симметрично относительно оси ординат на промежуток (-∞, 0), если функция четная, и относительно центра системы координат, если функция нечетная.
Если функция периодическая, то ее график строят для одного периода, а затем периодически продолжают на всю числовую ось.
Пример. Провести полное исследование функции и построить ее график.
1. Функция определена и непрерывна на всей числовой оси, кроме точек x = ± 2.
2. Функция нечетная, так как для нее выполняется условие . Поэтому достаточно провести исследование на промежутке [0, +∞).
3. В промежутке [0, +∞) имеется одна точка разрыва x = 2. Исследуем характер точки разрыва, для чего вычислим следующие пределы:
,
Так как односторонние пределы бесконечные, то прямая x = 2 является вертикальной асимптотой.
4. Находим первую производную:
.
Находим критические точки на промежутке [0, +∞): ,. В точкепроизводная не существует, но эта точка не является критической, так как функция в ней не определена.
5. Находим вторую производную:
.
Вторая производная на промежутке [0, +∞) обращается в ноль в точке x1 = 0 и не существует в точке x3 = 2, которая не входит в область определения функции.
По полученным данным строим таблицу:
(2, )
Вертикальная асимптота графика. Как найти асимптоты графика функции
Ни одной, одна, две, три,… или бесконечно много.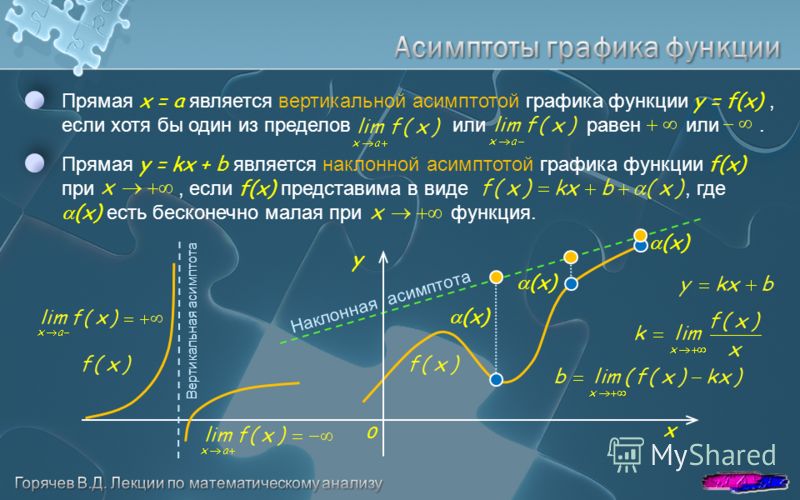 За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса — бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса — бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Что значит найти асимптоты графика функции?
Это значит выяснить их уравнения, ну и начертить прямые линии, если того требует условие задачи. Процесс предполагает нахождение пределов функции.
Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.
Примечание: обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой — зависит от контекста.
Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один из односторонних пределов бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова — любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат.
Из вышесказанного также следует очевидный факт: если функция непрерывна на, то вертикальные асимптоты отсутствуют. На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
Обратное утверждение в общем случае неверно: так, функция не определена на всей числовой прямой, однако совершенно обделена асимптотами.
Наклонные асимптоты графика функции
Наклонные (как частный случай — горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при, а график арктангенса при — двумя такими асимптотами, причём различными.
Поэтому график функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при, а график арктангенса при — двумя такими асимптотами, причём различными.
Асимптотой графика функции y = f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
На рисунке 3.10. приведены графические примеры вертикальной , горизонтальных и наклонной асимптот.
Нахождение асимптот графика основано на следующих трех теоремах.
Теорема о вертикальной асимптоте. Пусть функция у = f(х) определена в некоторой окрестности точки x 0 (исключая, возможно, саму эту точку) и хотя бы один из односторонних пределов функции равен бесконечности, т.е. Тогда прямая x = x 0 является вертикальной асимптотой графика функции у = f(х).
Очевидно, что прямая х = х 0 не может быть вертикальной асимптотой, если функция непрерывна в точке х 0 , так как в этом случае . Следовательно, вертикальные асимптоты следует искать в точках разрыва функции или на концах ее области определения.
Следовательно, вертикальные асимптоты следует искать в точках разрыва функции или на концах ее области определения.
Теорема о горизонтальной асимптоте. Пусть функция у = f(х) определена при достаточно больших х и существует конечный предел функции . Тогда прямая у = b есть горизонтальная асимптота графика функции.
Замечание. Если конечен только один из пределов , то функция имеет соответственно левостороннюю либо правостороннюю горизонтальную асимптоту.
В том случае, если , функция может иметь наклонную асимптоту.
Теорема о наклонной асимптоте. Пусть функция у = f(х) определена при достаточно больших х и существуют конечные пределы . Тогда прямая y = kx + b является наклонной асимптотой графика функции.
Без доказательства.
Наклонная асимптота, так же, как и горизонтальная, может быть правосторонней или левосторонней, если в базе соответствующих пределов стоит бесконечность определенного знака.
Исследование функций и построение их графиков обычно включает следующие этапы:
1. Найти область определения функции.
Найти область определения функции.
2. Исследовать функцию на четность-нечетность.
3. Найти вертикальные асимптоты, исследовав точки разрыва и поведение функции на границах области определения, если они конечны.
4. Найти горизонтальные или наклонные асимптоты, исследовав поведение функции в бесконечности.
Определение . Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точкиграфика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат .
По способам их отыскания выделяют три вида асимптот: вертикальные , горизонтальные, наклонные.
Очевидно, горизонтальные являются частными случаями наклонных (при ).
Нахождение асимптот графика функции основано на следующих утверждениях.
Теорема
1 . Пусть
функция
определена хотя бы в некоторой
полуокрестности точкии хотя бы один из ее односторонних
пределов в этой точке бесконечен, т. е.
равенили.
Тогда прямаяявляется вертикальной асимптотой
графика функции .
е.
равенили.
Тогда прямаяявляется вертикальной асимптотой
графика функции .
Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).
Теорема 2 . Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции. Тогда прямаяесть горизонтальная асимптота графика функции.
Может случиться, что , а, причеми- конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов или, то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.
Теорема 3 . Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределыи. Тогда прямаяявляется наклонной асимптотой графика функции .
Заметим,
что если хотя бы один из указанных
пределов бесконечен, то наклонной
асимптоты нет.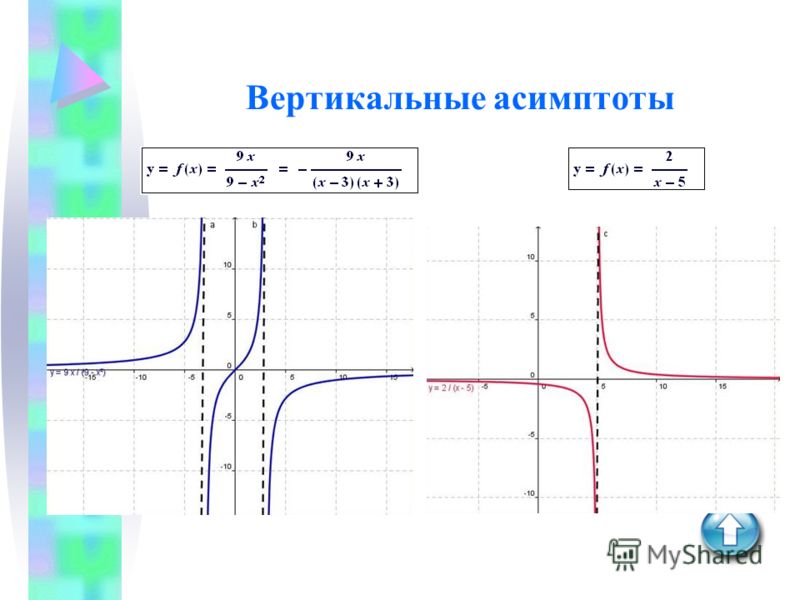
Наклонная асимптота так же, как и горизонтальная, может быть односторонней.
Пример . Найдите все асимптоты графика функции .
Решение .
Функция определена при . Найдем ее односторонние пределы в точках.
Так как и(два других односторонних предела можно уже не находить), то прямыеиявляются вертикальными асимптотами графика функции.
Вычислим
(применим правило Лопиталя) =.
Значит, прямая — горизонтальная асимптота.
Так как горизонтальная асимптота существует, то наклонные уже не ищем (их нет).
Ответ : график имеет две вертикальные асимптоты и одну горизонтальную.
Общие исследование функции y = f (x ).
Область
определения функции. Найти ее область определения D (f )
. Если это не слишком сложно, то полезно
найти также область значений E (f )
. (Однако, во многих случаях, вопрос
нахождения E (f )
откладывается до нахождения экстремумов
функции.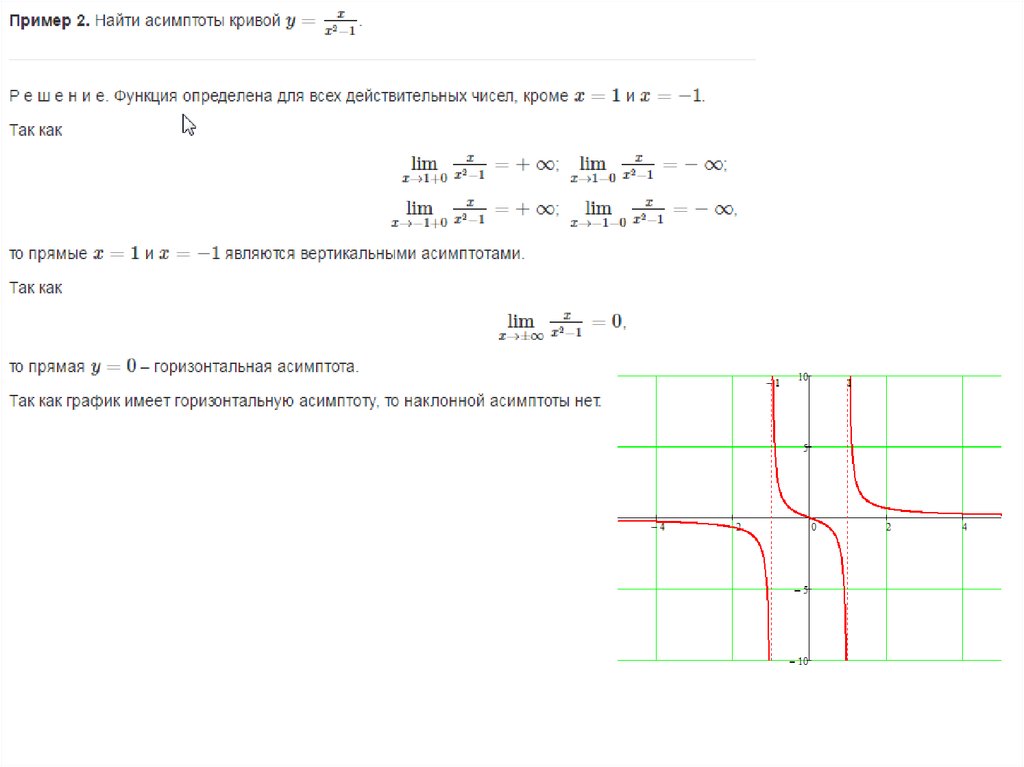 )
)
Особые свойства функции. Выяснить общие свойства функции: четность, нечетность, периодичность и т.п. Не любая функция обладает такими свойствами, как четность либо нечетность. Функция заведомо не является ни четной, ни нечетной, если ее область определения несимметрична относительно точки 0 на оси Ox . Точно так же, у любой периодической функции область определения состоит либо из всей вещественной оси, либо из объединения периодически повторяющихся систем промежутков.
Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определенияD (f ), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.
Наклонные
и горизонтальные асимптоты. Если область определения D (f )
вклоючает в себя лучи вида (a;+)
или (−;b),
то можно попытаться найти наклонные
асимптоты (или горизонтальные асимптоты)
при x+или x−соответственно, т. е. найти limxf(x).Наклонные
асимптоты : y = kx + b, где
k=limx+xf(x)
и b=limx+(f(x)−x).Горизонтальны
асимптоты : y = b, где
limxf(x)=b.
е. найти limxf(x).Наклонные
асимптоты : y = kx + b, где
k=limx+xf(x)
и b=limx+(f(x)−x).Горизонтальны
асимптоты : y = b, где
limxf(x)=b.
Нахождение точек пересечения графика с осями . Нахождение точки пересечения графика с осью Oy . Для этого нужно вычислить значение f (0). Найти также точки пересечения графика с осью Ox , для чего найти корни уравнения f (x ) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближунно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.
Нахождение
точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти
характерные точки графика, которые не
были упомянуты в предыдущих пунктах.
Например, если функция имеет наклонную
асимптоту, то можно попытаться выяснить,
нет ли точек пересечения графика с этой
асимптотой.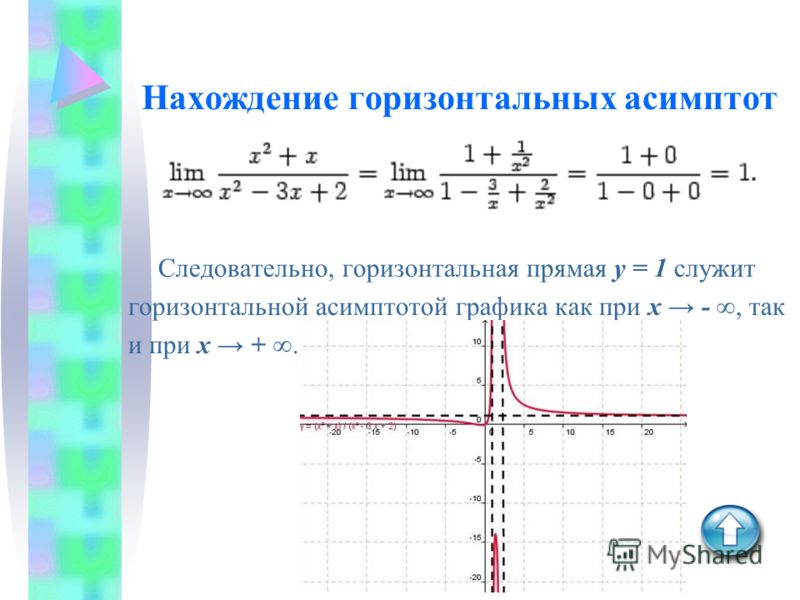
Нахождение интервалов выпуклости и вогнутости . Это делается с помощью исследования знака второй производной f(x). Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции. Найдя f(x) , мы решаем неравенство f(x)0. На каждом из интервалов решения функция будет выпуклой вниз. Решая обратное неравенство f(x)0, мы находим интервалы, на которых функция выпукла вверх (то есть вогнута). Определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).
Асимптотой графика функции y = f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
На рисунке 3. 10. приведены графические примеры вертикальной , горизонтальных и наклонной асимптот.
10. приведены графические примеры вертикальной , горизонтальных и наклонной асимптот.
Нахождение асимптот графика основано на следующих трех теоремах.
Теорема о вертикальной асимптоте. Пусть функция у = f(х) определена в некоторой окрестности точки x 0 (исключая, возможно, саму эту точку) и хотя бы один из односторонних пределов функции равен бесконечности, т.е. Тогда прямая x = x 0 является вертикальной асимптотой графика функции у = f(х).
Очевидно, что прямая х = х 0 не может быть вертикальной асимптотой, если функция непрерывна в точке х 0 , так как в этом случае . Следовательно, вертикальные асимптоты следует искать в точках разрыва функции или на концах ее области определения.
Теорема о горизонтальной асимптоте. Пусть функция у = f(х) определена при достаточно больших х и существует конечный предел функции . Тогда прямая у = b есть горизонтальная асимптота графика функции.
Замечание. Если конечен только один из пределов , то функция имеет соответственно левостороннюю либо правостороннюю горизонтальную асимптоту.
В том случае, если , функция может иметь наклонную асимптоту.
Теорема о наклонной асимптоте. Пусть функция у = f(х) определена при достаточно больших х и существуют конечные пределы . Тогда прямая y = kx + b является наклонной асимптотой графика функции.
Без доказательства.
Наклонная асимптота, так же, как и горизонтальная, может быть правосторонней или левосторонней, если в базе соответствующих пределов стоит бесконечность определенного знака.
Исследование функций и построение их графиков обычно включает следующие этапы:
1. Найти область определения функции.
2. Исследовать функцию на четность-нечетность.
3. Найти вертикальные асимптоты, исследовав точки разрыва и поведение функции на границах области определения, если они конечны.
4. Найти горизонтальные или наклонные асимптоты, исследовав поведение функции в бесконечности.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости функции и точки перегиба.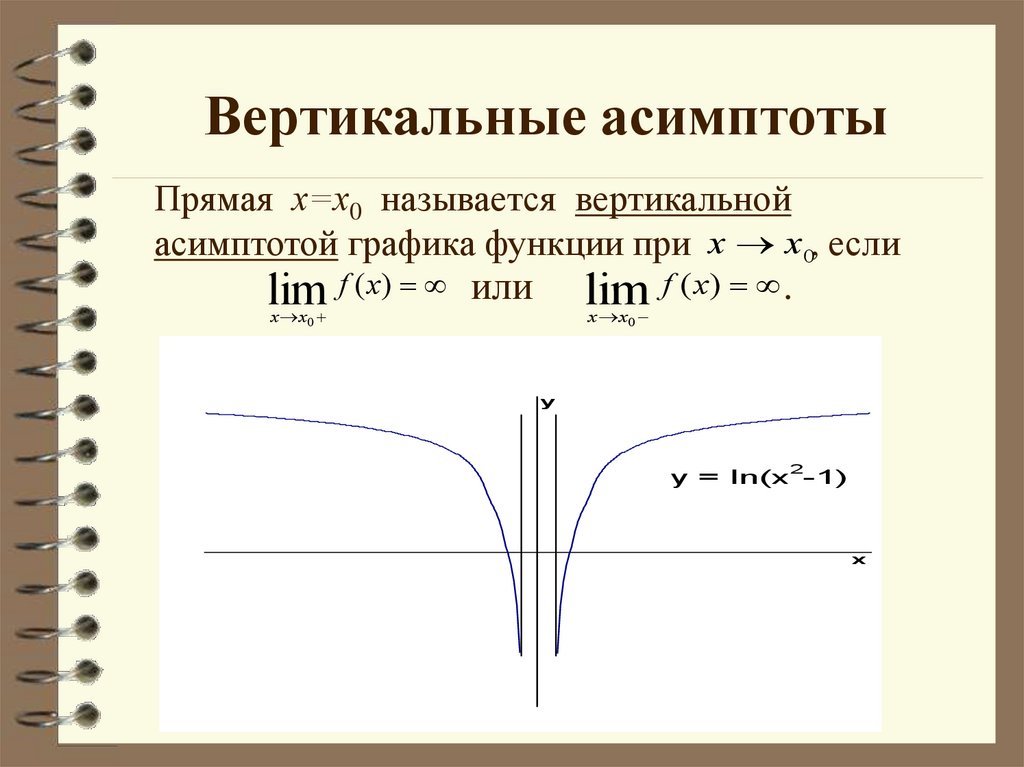
7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Дифференциал функции
Можно доказать, что если функция имеет при некоторой базе предел, равный конечному числу, то ее можно представить в виде суммы этого числа и бесконечно малой величины при той же базе (и наоборот): .
Применим это теорему к дифференцируемой функции: .
Таким образом, приращение функции Dу состоит из двух слагаемых: 1) линейного относительно Dх, т.е. f `(x)Dх; 2) нелинейного относительно Dх, т.е. a(Dx)Dх. При этом, так как , это второе слагаемое представляет собой бесконечно малую более высокого порядка, чем Dх (при стремлении Dх к нулю оно стремится к нулю еще быстрее).
Дифференциалом функции называется главная, линейная относительно Dх часть приращения функции, равная произведению производной на приращение независимой переменной dy = f `(x)Dх.
Найдем дифференциал функции у = х.
Так как dy = f `(x)Dх = x`Dх = Dх, то dx = Dх, т. е. дифференциал независимой переменной равен приращению этой переменной.
е. дифференциал независимой переменной равен приращению этой переменной.
Поэтому формулу для дифференциала функции можно записать в виде dy = f `(x)dх. Именно поэтому одно из обозначений производной представляет собой дробь dy/dх.
Геометрический смысл дифференциала проиллюстрирован
рисунком 3.11. Возьмем на графике функции y = f(x) произвольную точку М(х, у). Дадим аргументу х приращение Dх. Тогда функция y = f(x) получит приращение Dy = f(x + Dх) — f(x). Проведем касательную к графику функции в точке М, которая образует угол a с положительным направлением оси абсцисс, т.е. f `(x) = tg a. Из прямоугольного треугольника MKN
KN = MN*tg a = Dх*tg a = f `(x)Dх = dy.
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда х получает приращение Dх.
Свойства дифференциала в основном аналогичны свойствам производной:
3. d(u ± v) = du ± dv.
4. d(uv) = v du + u dv.
5. d(u/v) = (v du — u dv)/v 2 .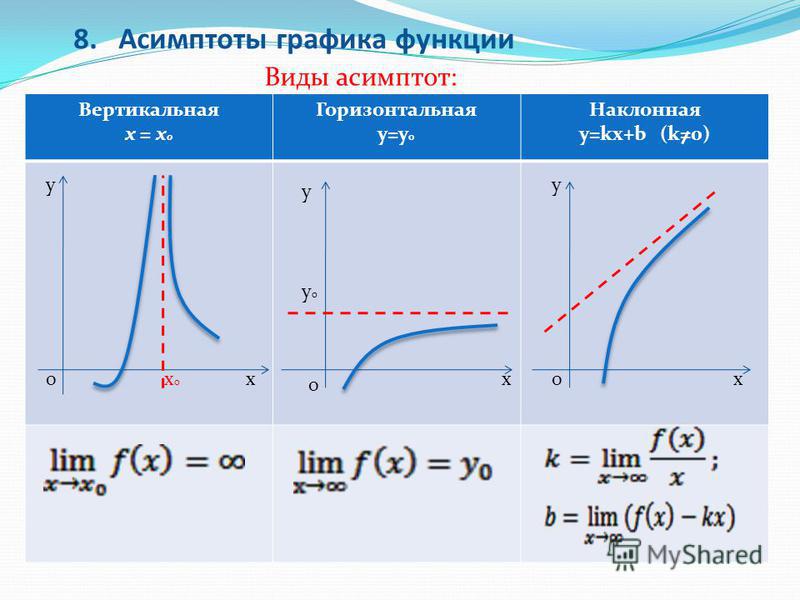
Однако, существует важное свойство дифференциала функции, которым не обладает ее производная – это инвариантность формы дифференциала .
Из определения дифференциала для функции y = f(x) дифференциал dy = f `(x)dх. Если эта функция y является сложной, т.е. y = f(u), где u = j(х), то y = f и f `(x) = f `(u)*u`. Тогда dy = f `(u)*u`dх. Но для функции
u = j(х) дифференциал du = u`dх. Отсюда dy = f `(u)*du.
Сравнивая между собой равенства dy = f `(x)dх и dy = f `(u)*du, убедимся, что формула дифференциала не изменяется, если вместо функции от независимой переменной х рассматривать функцию от зависимой переменной u. Это свойство дифференциала и получило название инвариантности (т.е. неизменности) формы (или формулы) дифференциала.
Однако в этих двух формулах все же есть различие: в первой из них дифференциал независимой переменной равен приращению этой переменной, т.е. dx = Dx, а во в торой дифференциал функции du есть лишь линейная часть приращения этой функции Du и только при малых Dх du » Du.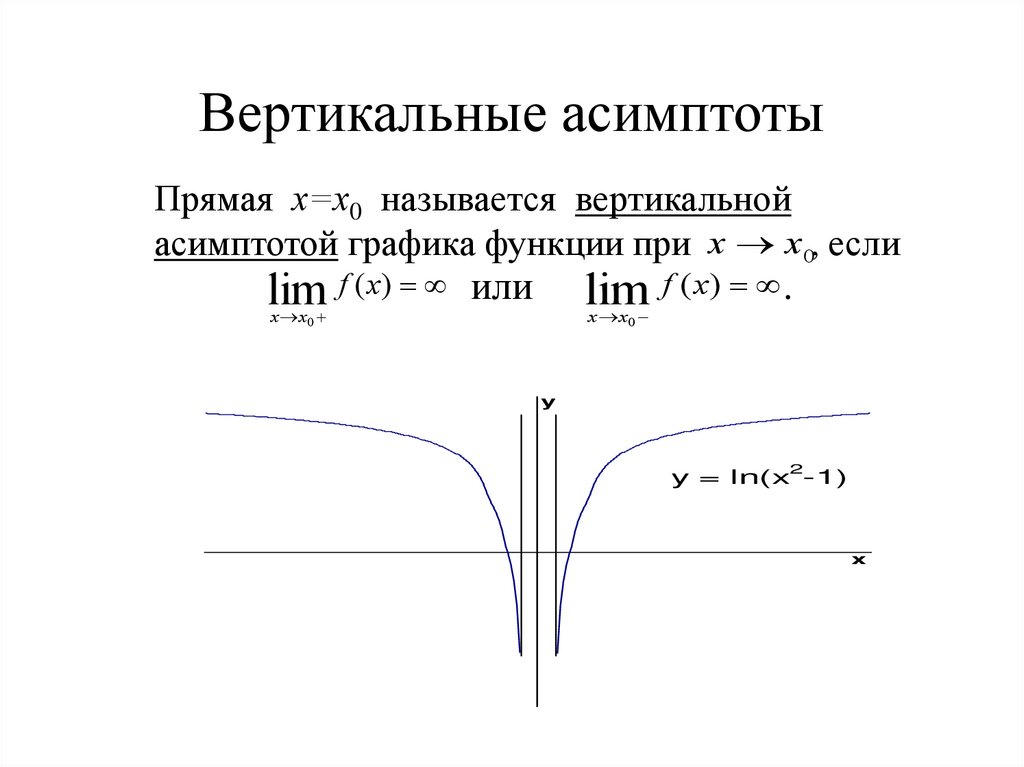
Во многих случаях построение графика функции облегчается, если предварительно построить асимптоты кривой.
Определение 1. Асимптотами называются такие прямые , к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты
Определение . Прямая x = a является вертикальной асимптотой графика функции , если точка x = a является точкой разрыва второго рода для этой функции.
Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f (x ) , если выполняется хотя бы одно из условий:
При этом функция f (x )
может быть вообще не определена соответственно при x ≥ a и x ≤ a .
Замечание:
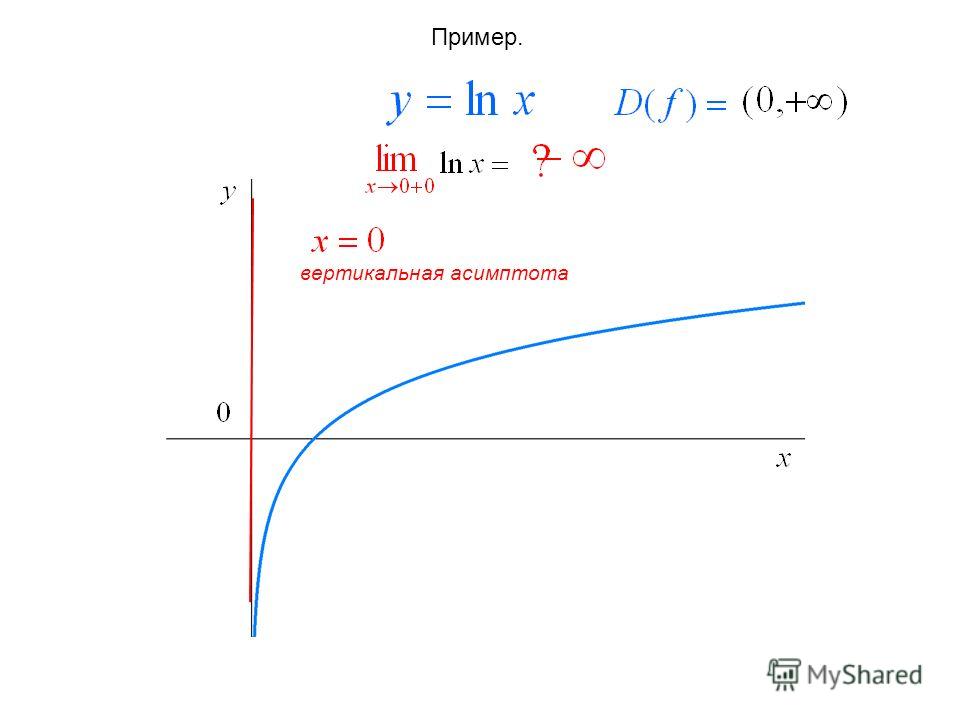
Пример 1. График функции y =lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
(рис. сверху).
самостоятельно, а затем посмотреть решения
Пример 2. Найти асимптоты графика функции .
Пример 3. Найти асимптоты графика функции
Горизонтальные асимптоты
Если (предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b ), то y = b – горизонтальная асимптота кривой y = f (x ) (правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности, и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).
Пример 5. График функции
при a > 1
имеет левую горизонтальную
асимпототу y = 0
(т.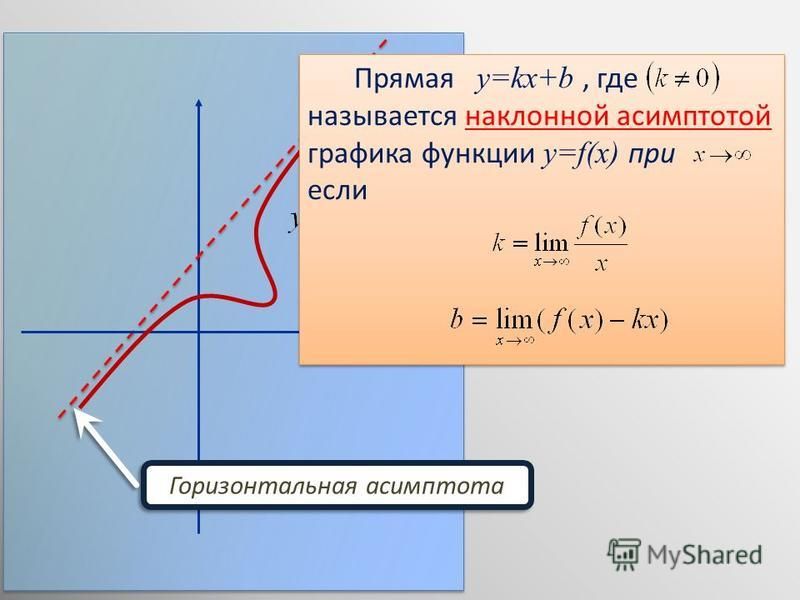 е.
совпадающую с осью Ox ), так как предел функции при стремлении «икса»
к минус бесконечности равен нулю:
е.
совпадающую с осью Ox ), так как предел функции при стремлении «икса»
к минус бесконечности равен нулю:
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении «икса» к плюс бесконечности равен бесконечности:
Наклонные асимптоты
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны
осям координат, поэтому для их построения нам требовалось лишь определённое число — точка на оси
абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше —
угловой коэффициент k , который показывает угол наклона прямой, и свободный член b , который показывает,
насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию,
а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение
прямой с угловым коэффициентом . Существование наклонной асимптоты определяется следующей теоремой,
на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f (x ) имела асимптоту y = kx + b , необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:
(1)
(2)
Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус
бесконечности прямая y = kx + b является двусторонней асимптотой кривой.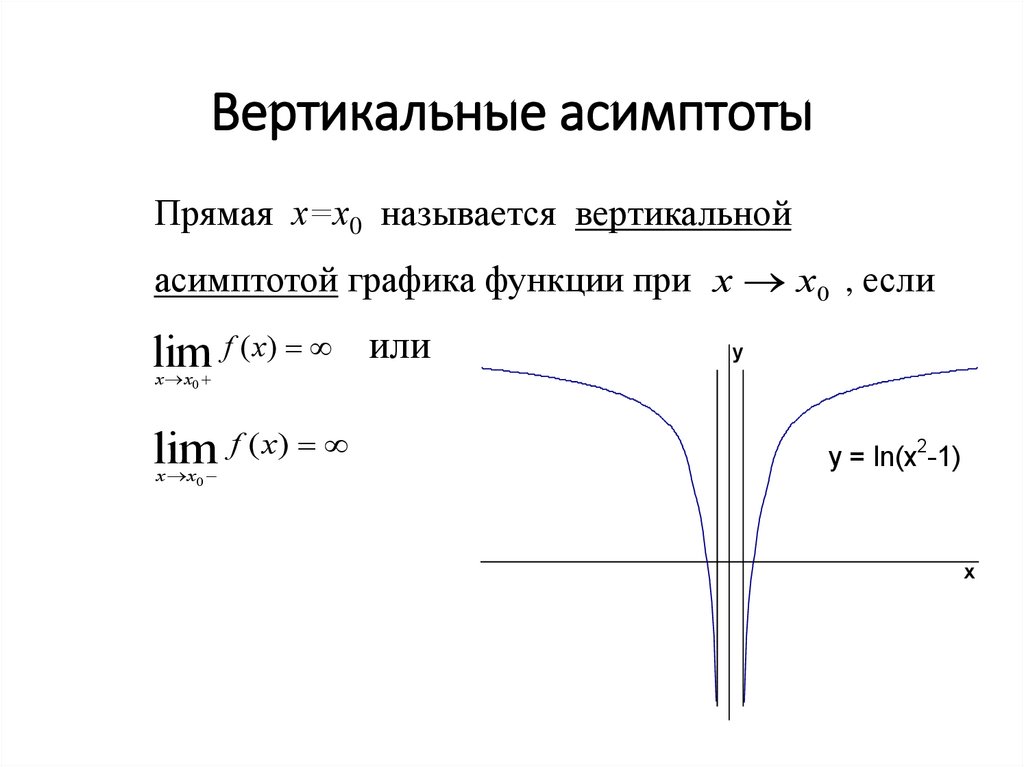
Если хотя бы один из пределов, определяющих асимптоту y = kx + b , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0 .
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0 , т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0 – вертикальная асимптота графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2
и b = 0
. Прямая y = 2x является двусторонней
наклонной асимптотой графика данной функции (рис. внутри примера).
Прямая y = 2x является двусторонней
наклонной асимптотой графика данной функции (рис. внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1 . Вычислим односторонние пределы и определим вид разрыва:
Заключение: x = −1 — точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.
Ищем наклонные асимптоты. Так как данная функция — дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой — наклонной асимптоты:
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:
y = −3x + 5 .
На рисунке график функции обозначен бордовым цветом, а асимптоты — чёрным.
Пример 8. Найти асимптоты графика функции
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:
Ищем наклонные асимптоты:
.
Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .
Пример 9. Найти асимптоты графика функции
Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения функции. Функция определена, когда выполняется неравенство и при этом . Знак переменной x совпадает со знаком . Поэтому рассмотрим эквивалентное неравенство . Из этого получаем область определения функции: . Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как функция определена при x = 0 .
Рассмотрим правосторонний предел при (левосторонний предел не существует):
.
Точка x = 2 — точка разрыва второго рода, поэтому прямая x = 2 — вертикальная асимптота графика данной функции.
Ищем наклонные асимптоты:
Итак, y = x + 1
—
наклонная асимптота графика данной функции при . Ищем наклонную асимптоту при :
Ищем наклонную асимптоту при :
Итак, y = −x − 1 — наклонная асимптота при .
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при .
Рецепты
Как найти вертикальную асимптоту функции? — Блог Магуш
By Shaun Ault on 13 января 2017 г. в AP
В этой статье мы поговорим о страшном слове на букву А, асимптоте . По моему опыту, студенты часто зацикливаются на термине и могут полагать, что такие проблемы невозможны. Но при наличии твердого понимания концепций и нескольких алгебраических приемов в вашем наборе инструментов не так уж сложно найти вертикальные асимптоты функции.
Типы асимптот
Существует три типа асимптот: горизонтальная, вертикальная и наклонная.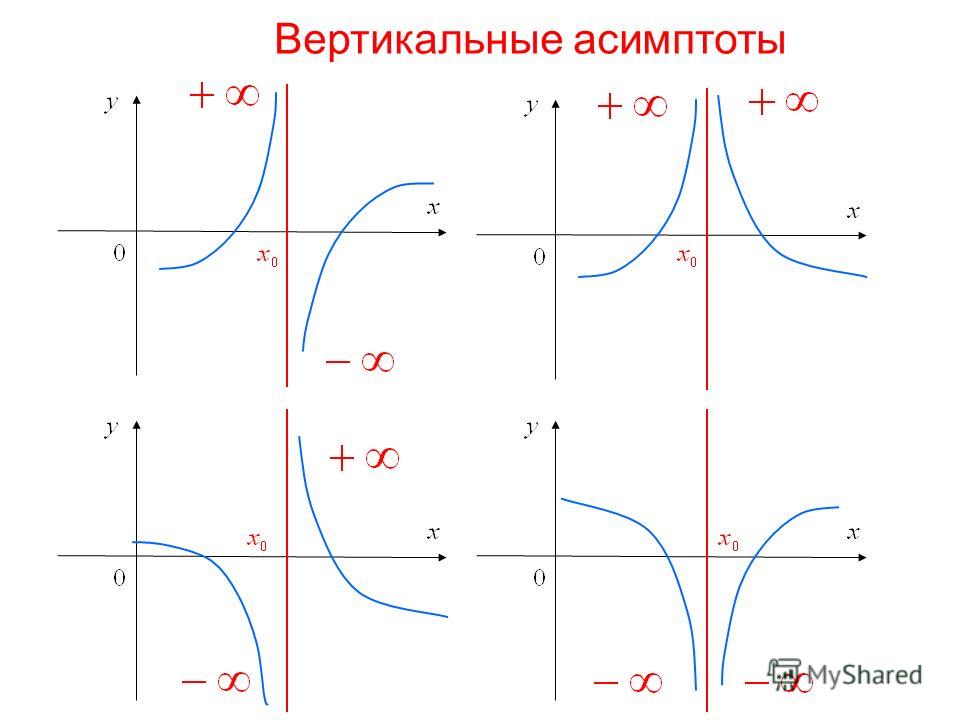 Эта статья посвящена вертикальным асимптотам. Горизонтальные асимптоты обсуждаются в другом месте, а наклонные асимптоты редко можно увидеть на экзамене AP (дополнительную информацию о наклонных или наклонных асимптотах см. в этой статье и в этом полезном видео).
Эта статья посвящена вертикальным асимптотам. Горизонтальные асимптоты обсуждаются в другом месте, а наклонные асимптоты редко можно увидеть на экзамене AP (дополнительную информацию о наклонных или наклонных асимптотах см. в этой статье и в этом полезном видео).
Вертикальные асимптоты
Вертикальная асимптота (или VA для краткости) для функции представляет собой вертикальную линию x = k показывает, где функция f(x) становится неограниченной. Другими словами, y значения функции становятся сколь угодно большими в положительном смысле ( y → ∞) или отрицательном смысле ( y → -∞), когда x приближается к k либо слева или справа.
Вертикальная асимптота подобна «кирпичной стене», которую функция не может пересечь. Представьте, что вы летите в самолете и впереди видите огромную гору. Если вы не можете обойти гору направо или налево, что бы вы сделали? Вероятно, вы бы взлетели вверх, чтобы не задеть его. Теперь представьте, что гора вертикальна и бесконечно высока. Тогда вы можете вечно лететь вверх, чтобы не столкнуться с ним, и все равно никогда не перелететь через гору!
Теперь представьте, что гора вертикальна и бесконечно высока. Тогда вы можете вечно лететь вверх, чтобы не столкнуться с ним, и все равно никогда не перелететь через гору!
Функция может иметь любое количество вертикальных асимптот или вообще не иметь их. Некоторые функции даже имеют бесконечно много VA. График, показанный ниже, имеет вертикальные асимптоты x = -3 и x = 1,
.Поскольку определение включает в себя переменные, приближающиеся к фиксированным значениям, не должно вызывать удивления то, что пределы должны быть каким-то образом задействованы. Точное определение вертикальной асимптоты выглядит следующим образом. Мы говорим, что x = k есть ВА для функции f(x) , если левый или правый предел x = k бесконечен:
Нахождение вертикальных асимптот
Существует два основных способа нахождения вертикальных асимптот для задач на экзамене AP Calculus AB: графически (из самого графика) и аналитически (из уравнения для функции). Мы поговорим об обоих.
Мы поговорим об обоих.
Определение вертикальных асимптот по графику
Если дан график, то искать разрывы в графике. Если кажется, что ветвь функции поворачивается к вертикали, то вы, вероятно, смотрите на VA. Это помогает нарисовать вертикальную линию на x — значение, где, по вашему мнению, должна быть асимптота (см. график, показанный выше). Обратите внимание: если часть графика действительно касается вашей вертикальной линии, то эта линия не является асимптотой.
Определение вертикальных асимптот из уравнения
Если вам нужно найти вертикальные асимптоты на экзамене AP, вам, скорее всего, не дадут график. Поэтому вам нужно знать, что искать в уравнении самой функции. Спросите себя, где эта функция имеет бесконечный предел? Мы увидим, как это применимо к двум разным видам функций, рациональным функциям и тригонометрическим функциям.
Вертикальные асимптоты в рациональных функциях
Если ваша функция рациональна, то есть если f(x) имеет вид дроби, f(x) = p(x) / q(x) , в котором оба p (x) и q(x) являются полиномами, то мы выполняем следующие два шага:
1.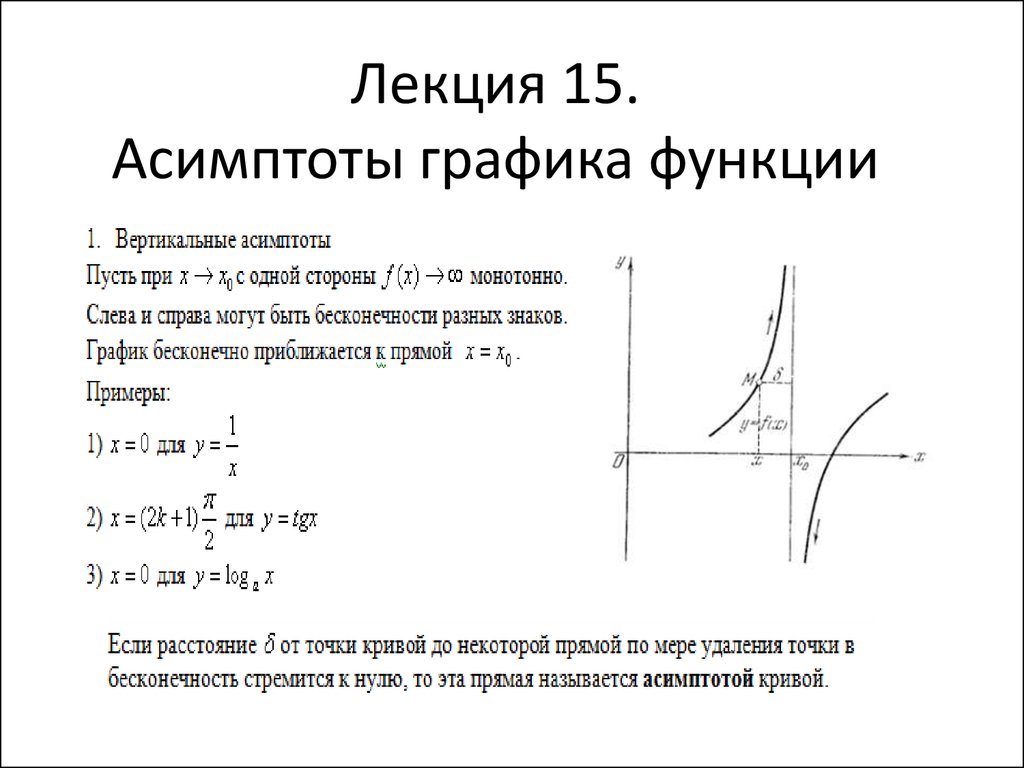 Разложить на множители числитель (вверху) и знаменатель (внизу). Это очень важно, потому что если какие-либо факторы в конечном итоге сокращаются, то они не будут способствовать каким-либо вертикальным асимптотам.
Разложить на множители числитель (вверху) и знаменатель (внизу). Это очень важно, потому что если какие-либо факторы в конечном итоге сокращаются, то они не будут способствовать каким-либо вертикальным асимптотам.
2. Как только ваша рациональная функция полностью редуцирована, посмотрите на множители в знаменателе. Если есть коэффициент, включающий (x – a) , то x = a является VA. Если есть множитель, включающий (x + a) , то x = – a является ВА. Обратите внимание, что оба раза знак кажется противоположным (точно так же, как при решении факторизованного многочлена, который был установлен равным нулю).
Практика нахождения вертикальных асимптот
Давайте посмотрим, как работает наш метод. Найдите вертикальные асимптоты каждой функции.
Решения:
(a) Первый фактор и отмена.
Поскольку множитель х – 5 отменен, он не влияет на окончательный ответ. Внизу осталось только x + 5, а это значит, что есть один VA с x = -5.
Внизу осталось только x + 5, а это значит, что есть один VA с x = -5.
(б) На этот раз после факторинга аннулирования нет.
Находим две вертикальные асимптоты, х = 0 и х = -2.
Вертикальные асимптоты тригонометрических функций
Метод факторинга применим только к рациональным функциям. Однако многие другие типы функций имеют вертикальные асимптоты. Возможно, наиболее важными примерами являются тригонометрические функции. Из шести стандартных триггерных функций четыре имеют вертикальные асимптоты: tan x , cot x , sec x и csc x . На самом деле у каждой из этих четырех функций их бесконечно много!
Например, f(x) = кроватка x имеет VA при каждом целом кратном π. Другими словами, x = n π есть ВА для каждого n = 0, ±1, ±2, ±3, …
Использование графического калькулятора
Более общие функции могут быть сложнее взломать. Если вы работаете над разделом экзамена, который позволяет использовать графический калькулятор, то вы можете просто построить график функции и попытаться определить разрывы в графике, на которых y -значения становятся неограниченными. Некоторые калькуляторы, такие как TI-84, даже имеют опцию под названием для обнаружения асимптот , которая автоматически отображает ВА в виде графика. Однако будьте осторожны; если окно просмотра слишком маленькое, вы можете пропустить VA.
Если вы работаете над разделом экзамена, который позволяет использовать графический калькулятор, то вы можете просто построить график функции и попытаться определить разрывы в графике, на которых y -значения становятся неограниченными. Некоторые калькуляторы, такие как TI-84, даже имеют опцию под названием для обнаружения асимптот , которая автоматически отображает ВА в виде графика. Однако будьте осторожны; если окно просмотра слишком маленькое, вы можете пропустить VA.
Заключение
Асимптоты — это просто определенные линии, которые говорят нам о поведении функций. Вертикальная асимптота показывает, где функция имеет бесконечный предел (неограниченные и -значения). Важно уметь находить ДС на заданном графике, а также находить их аналитически из уравнения функции. Ваш графический калькулятор также может помочь. Потратив немного времени и практики, эти методы можно легко освоить, и поэтому вертикальные асимптоты не должны быть «кирпичной стеной», которая мешает вам далеко продвинуться на экзамене AP по математическому анализу!
Гарантированно улучшите свой результат SAT или ACT.
 Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!
Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!Автор
Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!
Расчет AP
← Предыдущий
Следующий →
Мы настоятельно рекомендуем учащимся помогать друг другу и отвечать на комментарии других учащихся, если это возможно!
Если вы являетесь студентом Premium Magoosh и хотели бы более персонализированного обслуживания от наших инструкторов, вы можете использовать вкладку «Справка» на панели управления Magoosh. Спасибо!
исчисление — Нахождение вертикальной асимптоты заданной функции
Вопрос
Изменено 8 лет, 11 месяцев назад
Просмотрено 3к раз
$\begingroup$
Для любой функции как найти ее вертикальную асимптоту? Я знаю, что для рациональных чисел я могу сделать это, приравняв знаменатель к 0. Вот и все. Просто соберите исключения для $x$ упорядоченным образом. Когда исключение является границей, как в данном случае, оно обычно будет асимптотой. $\endgroup$ $\begingroup$ Нельзя ли просто повернуть ось (для общего алгоритма). В любом уравнении, если вы поменяете значения x и y , вы получите своего рода повернутую ось. Я имею в виду, что поменяйте местами x и y в приведенном выше уравнении, затем получите y через x в новом уравнении, а затем используйте те же методы, которые вы использовали бы для алгоритмов для горизонтальной оси? Дайте мне знать, ясно это или нет. (Предполагая, что вновь полученное уравнение может быть определено в заданном интервале) $\endgroup$ 1 $\begingroup$ Зависит от типа функции. Итак, в этом случае, когда у вас есть $y=\ln(f(x))=\ln(1-\ln(x))$, вы хотите найти $a$ такое, что $1-\ln(x )\к 0+$ как $x\к а$ (возможно, только справа или слева). Сможете ли вы найти такой $a$? $\ln$ также обладает тем свойством, что $\lim\limits_{x\to+\infty}\ln(x)=+\infty$, поэтому $\ln(f(x))$ перейдет в $ +\infty$, где $f(x)\to+\infty$. Для $f(x)=1-\ln(x)$ это происходит там, где и имеют свою вертикальную асимптоту, потому что при $x\to0+$ $1-\ln(x)\to +\infty$. Ответ и комментарий указывают на то, что неплохо было бы найти домен и проверить его границы. Это верно, но вообще не даст вертикальных асимптот; это зависит от конкретных свойств задействованных функций. $\endgroup$ $\begingroup$ Я бы рассмотрел производную вашей функции. Обратите внимание, что хотя производная не существует в точке асимптоты, по сторонам от точки асимптоты значение производной стремится к $\pm \infty $. Это означает, что нужно искать точки, в которых знаменатель производной равен $0$. В вашем случае производная: $$\cfrac{-1}{1-\ln(x)}\cdot \cfrac{1}{x}.$$ Вы видите, где производная переходит в $\pm \infty$? Как указал @JonasMeyer, есть и другие критические точки, в которых производная может перейти в $\pm \infty$. Чтобы избежать их, проверяйте, что функция не определена в точке, где производная переходит в $\pm \infty$, поскольку как в вертикальных касательных, так и в точках возврата функция определена. http://math.uchicago.edu/~vipul/teaching-0910/152/infinitycuspsasymptotes.pdf $\endgroup$ 3 Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Обязательно, но не отображается Электронная почта Требуется, но не отображается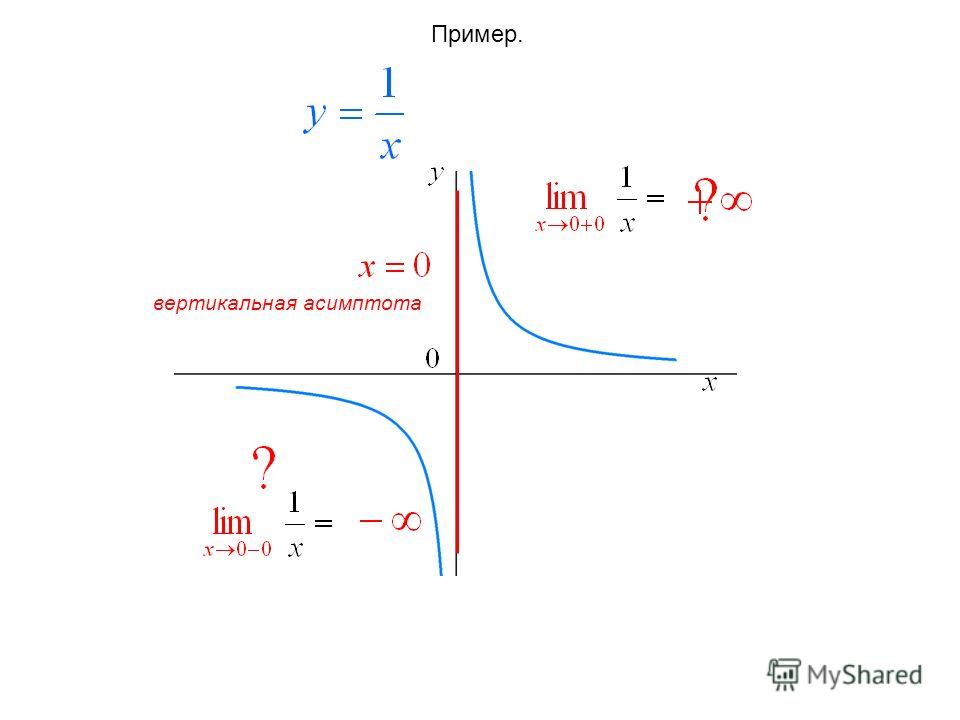 1 \Rightarrow x < e.$$
Итак, теперь $x=e$ — еще одна вертикальная асимптота, и $x
1 \Rightarrow x < e.$$
Итак, теперь $x=e$ — еще одна вертикальная асимптота, и $x Здесь предполагается, что вы знаете, вычисляете или ищете, что $y=\ln(x)$ имеет вертикальную асимптоту в точке $x=0$, где $\lim\limits_{x\to0+}\ln(x)= -\infty$. Таким образом, если что-то еще находится внутри $\ln$, $y=\ln(f(x))$, тогда будет вертикальная асимптота, когда то, что находится внутри, идет к $0$ справа: где $f(x)\ до 0+$.
Здесь предполагается, что вы знаете, вычисляете или ищете, что $y=\ln(x)$ имеет вертикальную асимптоту в точке $x=0$, где $\lim\limits_{x\to0+}\ln(x)= -\infty$. Таким образом, если что-то еще находится внутри $\ln$, $y=\ln(f(x))$, тогда будет вертикальная асимптота, когда то, что находится внутри, идет к $0$ справа: где $f(x)\ до 0+$. Это работает для этой проблемы.
Это работает для этой проблемы. Твой ответ
Зарегистрируйтесь или войдите в систему
Опубликовать как гость
Опубликовать как гость
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
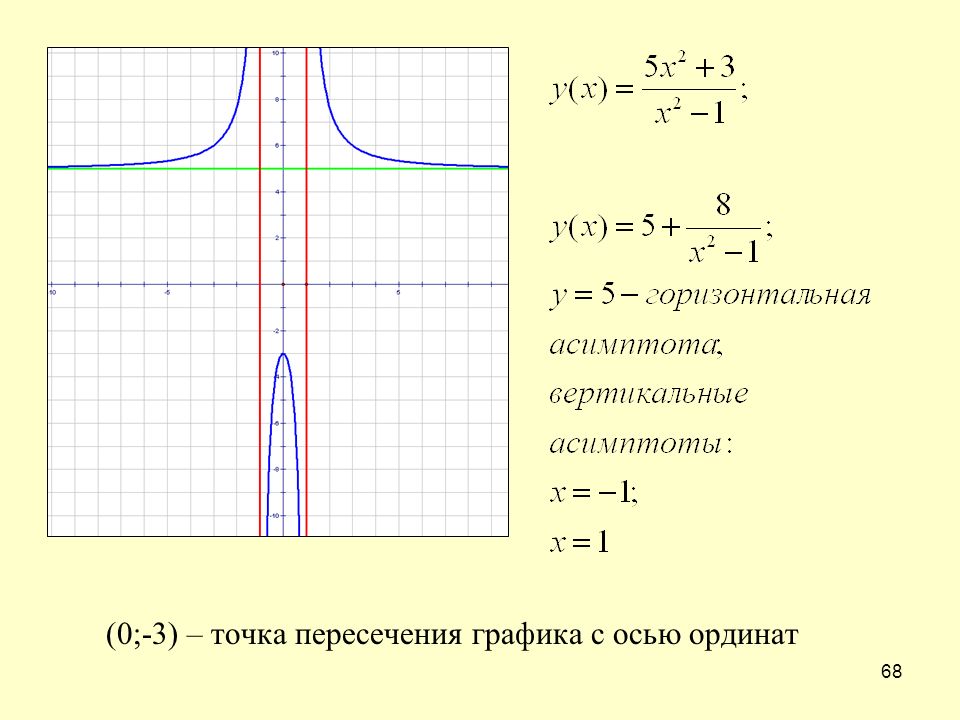
.
Определите вертикальную и горизонтальную асимптоты | Колледж Алгебра |
Глядя на график рациональной функции, мы можем исследовать ее локальное поведение и легко увидеть, существуют ли асимптоты. Возможно, мы даже сможем приблизительно определить их местонахождение. Однако даже без графика мы можем определить, имеет ли данная рациональная функция какие-либо асимптоты, и вычислить их расположение.
Вертикальные асимптоты
Вертикальные асимптоты рациональной функции могут быть найдены путем изучения факторов знаменателя, которые не являются общими с факторами в числителе. Вертикальные асимптоты возникают в нулях таких факторов.
Как сделать: по заданной рациональной функции определите любые вертикальные асимптоты ее графика.
- Разложите числитель и знаменатель на множители.
- Обратите внимание на любые ограничения в домене функции.

- Сократите выражение, сократив общие множители в числителе и знаменателе. 9{2}}{\left(2+x\right)\left(1-x\right)}\qquad \end{cases}{k(x)=2−x−x25+2×2 =(2+x )(1−x)5+2×2
Чтобы найти вертикальные асимптоты, мы определяем, где эта функция будет неопределенной, приравнивая знаменатель к нулю:
{(2+x)(1−x)=0 x=−2,1\begin{cases}\left(2+x\right)\left(1-x\right)=0\qquad \\ \text{ }x=-2,1\qquad \end{ case}{(2+x)(1−x)=0 x=−2,1
Ни
x=−2x=-2x=−2
ни
x=1x=1x=1
— это нули числителя, поэтому два значения обозначают две вертикальные асимптоты. Рисунок 9{2}-2x — 3}f(x)=x2−2x−3×2−1
можно переписать, разложив числитель и знаменатель на множители.f(x)=(x+1)(x−1)(x+1)(x−3)f\left(x\right)=\frac{\left(x+1\right)\left( х — 1 \ вправо) {\ влево (х + 1 \ вправо) \ влево (х — 3 \ вправо)} f (х) = (х + 1) (х-3) (х + 1) (х- 1)
Обратите внимание, что
x+1x+1x+1
является общим множителем числителя и знаменателя. Нуль этого коэффициента,
Нуль этого коэффициента,x=-1x=-1x=-1
, является местоположением удаляемого разрыва. Заметьте также, чтоx−3x — 3x−3
не является множителем ни в числителе, ни в знаменателе. Нуль этого фактора,x=3x=3x=3
, является вертикальной асимптотой.Рисунок 10
A Общее примечание: устранимые разрывы рациональных функций для множителя в знаменателе, общего с множителем в числителе. Мы факторизируем числитель и знаменатель и проверяем наличие общих множителей. Если мы их находим, мы устанавливаем общий множитель равным 0 и решаем. Это место устранимого разрыва. Это верно, если кратность этого множителя больше или равна кратности в знаменателе. Если кратность этого множителя больше в знаменателе, то при этом значении все же имеется асимптота. 9{2}-4}k(x)=x2−4x−2
.
Решение
Разложите числитель и знаменатель на множители.
k(x)=x−2(x−2)(x+2)k\left(x\right)=\frac{x — 2}{\left(x — 2\right)\left(x +2\right)}k(x)=(x−2)(x+2)x−2
Обратите внимание, что в числителе и знаменателе есть общий множитель,
x−2x — 2x−2
.
 Ноль для этого коэффициента равен
Ноль для этого коэффициента равенx=2x=2x=2
. Это место устранимого разрыва.
Обратите внимание, что в знаменателе есть множитель, которого нет в числителе,
х+2х+2х+2
. Ноль для этого коэффициента равен
x=−2x=-2x=−2
. Вертикальная асимптота равна
x=-2x=-2x=-2
. Рис. 11 иметь дырку.
Попробуйте 5
Найдите вертикальные асимптоты и устранимые разрывы графика числа 9{2}+5x}f(x)=x3−6×2+5xx2−25
. Решение
Горизонтальные асимптоты
В то время как вертикальные асимптоты описывают поведение графика, когда выход становится очень большим или очень маленьким, горизонтальные асимптоты помогают описать поведение графика, когда вход становится очень большим или очень маленьким.
 Напомним, что поведение конца многочлена будет отражать поведение старшего члена. Точно так же конечное поведение рациональной функции будет отражать отношение старших членов функций числителя и знаменателя. 9{2}}=\frac{4}{x}f(x)≈x24x=x4
Напомним, что поведение конца многочлена будет отражать поведение старшего члена. Точно так же конечное поведение рациональной функции будет отражать отношение старших членов функций числителя и знаменателя. 9{2}}=\frac{4}{x}f(x)≈x24x=x4. Это говорит нам о том, что при неограниченном увеличении или уменьшении входных данных эта функция будет вести себя аналогично функции
g(x)=4xg\left(x\right)=\frac{4}{x}g(x) =x4
, и выходные значения будут приближаться к нулю, что приведет к горизонтальной асимптоте при y = 0. Обратите внимание, что этот график пересекает горизонтальную асимптоту.
. x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne{0}\text{, где степень}p< \text{степень q}f(x)=q(x)p(x),q(x)=0, где степень p<степень q 9{2}}{x}=3xf(x)≈x3x2=3x
. Это говорит нам о том, что при неограниченном увеличении или уменьшении входных данных эта функция будет вести себя аналогично функции
g(x)=3xg\left(x\right)=3xg(x)=3x
.
 По мере того, как входы становятся большими, выходы будут расти, а не выравниваться, поэтому этот график не имеет горизонтальной асимптоты. Однако график
По мере того, как входы становятся большими, выходы будут расти, а не выравниваться, поэтому этот график не имеет горизонтальной асимптоты. Однако графикg(x)=3xg\left(x\right)=3xg(x)=3x
выглядит как диагональная линия, и поскольку f будет вести себя аналогично g 9{2}-2x+1}{x — 1}x−13×2−2x+1
. Частное равно
3x+13x+13x+1
, а остаток равен 2. Наклонная асимптота представляет собой график прямой
g(x)=3x+1g\left(x\right)=3x+ 1g(x)=3x+1
.
Рис. 13. Наклонная асимптота при
f(x)=p(x)q(x),q(x)≠0f\left(x\right)=\frac{p\left(x\right) )}{q\left(x\right)},q\left(x\right)\ne 0f(x)=q(x)p(x),q(x)=0
, где степень
p> степень q по 1p>\text{ степень }q\text{ по }1p> степень q по 1
.

Случай 3: Если степень знаменателя = степени числителя, существует горизонтальная асимптота в точке
y=anbny=\frac{{a}_{n}}{{b}_{n} }y=bnan
, где
an{a}_{n}an
и
bn{b}_{n}bn
— старшие коэффициенты
p( x)p\left(x\right)p(x)
и
q(x)q\left(x\right)q(x)
для
f(x)=p(x)q (x),q(x)≠0f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ ne 0f(x)=q(x)p(x),q(x)=0 9{2}}=3f(x)≈x23x2=3
. Это говорит нам о том, что по мере увеличения входных данных эта функция будет вести себя как функция
g(x)=3g\left(x\right)=3g(x)=3
, которая представляет собой горизонтальную линию. Как
x→±∞,f(x)→3x\to \pm \infty ,f\left(x\right)\to 3x→±∞,f(x)→3
, что приводит к горизонтальной асимптоте при y = 3.
 Обратите внимание, что этот график пересекает горизонтальную асимптоту.
Обратите внимание, что этот график пересекает горизонтальную асимптоту.Рис. 14. Горизонтальная асимптота при
f(x)=p(x)q(x),q(x)≠0, где степень p=степень qf\left(x\right)=\frac{p\left(x\right)}{q \left(x\right)},q\left(x\right)\ne 0\text{где степень }p=\text{степень }qf(x)=q(x)p(x), q(x)=0, где степень p=степень q
.
Обратите внимание, что хотя график рациональной функции никогда не пересекает вертикальную асимптоту , график может пересекать или не пересекать горизонтальную или наклонную асимптоту. Кроме того, хотя график рациональной функции может иметь много вертикальных асимптот, график будет иметь не более одной горизонтальной (или наклонной) асимптоты. 9{4}f(x)≈x3x5=3×4
,
конечное поведение графика будет похоже на поведение четного многочлена с положительным старшим коэффициентом.
x→±∞,f(x)→∞x\to \pm \infty , f\left(x\right)\to \infty x→±∞,f(x)→∞
A Общее примечание: Горизонтальные асимптоты рациональных функций
Горизонтальную асимптоту рациональной функции можно определить, глядя на степени числителя и знаменателя.

- Степень числителя меньше степени знаменателя: горизонтальная асимптота при y = 0,
- Степень числителя больше степени знаменателя на единицу : нет горизонтальной асимптоты; наклонная асимптота.
- Степень числителя равна степени знаменателя: горизонтальная асимптота при отношении старших коэффициентов.
Пример 7. Определение горизонтальной и наклонной асимптот
Для следующих функций определите горизонтальную или наклонную асимптоту. 9{3}-8}k(x)=x3−8×2+4x
: Степень
p=2
Степень
q=3q =3q=3
, так что существует горизонтальная асимптота y = 0.
Пример 8. Определение горизонтальных асимптот
Ранее в задаче о концентрации сахара мы создали уравнение
C(t)=5+t100 +10tC\left(t\right)=\frac{5+t}{100+10t}C(t)=100+10t5+t
.

Найдите горизонтальную асимптоту и интерпретируйте ее в контексте задачи.
Решение
И числитель, и знаменатель линейны (степень 1). Поскольку степени равны, у отношения старших коэффициентов будет горизонтальная асимптота. В числителе старший член равен t с коэффициентом 1. В знаменателе старший член равен 10 t с коэффициентом 10. Горизонтальная асимптота будет при соотношении этих величин:
t→∞ ,C(t)→110t\to \infty , C\left(t\right)\to \frac{1}{10}t→∞,C(t)→101
Горизонтальная асимптота этой функции будет равна
y=110y=\frac{1}{10}y=101
.
Это говорит нам о том, что по мере увеличения значений t значения C приблизятся к
110\frac{1}{10}101
. В контексте это означает, что с течением времени концентрация сахара в резервуаре будет приближаться к одной десятой фунта сахара на галлон воды или
110\frac{1}{10}101
фунтов на галлон.

Пример 9. Определение горизонтальной и вертикальной асимптот
Найдите горизонтальную и вертикальную асимптоты функции
f(x)=(x−2)(x+3)(x−1)(x+2)(x −5) f \ влево (х \ вправо) = \ гидроразрыва {\ влево (х — 2 \ вправо) \ влево (х + 3 \ вправо)} {\ влево (х — 1 \ вправо) \ влево (х + 2 \right)\left(x — 5\right)}f(x)=(x−1)(x+2)(x−5)(x−2)(x+3)
Решение
Первый , заметим, что эта функция не имеет общих сомножителей, поэтому потенциальных устранимых разрывов нет.
Функция будет иметь вертикальные асимптоты, когда знаменатель равен нулю, в результате чего функция будет неопределенной. Знаменатель будет равен нулю при
x=1,−2 и 5x=1,-2,\text{и }5x=1,−2 и 5
, что указывает на вертикальные асимптоты для этих значений.
Числитель имеет степень 2, а знаменатель имеет степень 3. Поскольку степень знаменателя больше степени числителя, знаменатель будет расти быстрее, чем числитель, в результате чего выходные данные будут стремиться к нулю по мере увеличения входных данных.
 большой, и поэтому
большой, и поэтомуx→±∞,f(x)→0x\to \pm \infty , f\left(x\right)\to 0x→±∞,f(x)→0
. Эта функция будет иметь горизонтальную асимптоту на уровне
у=0у=0у=0
.
. е \ влево (х \ вправо) = \ гидроразрыва {\ влево (2x — 1 \ вправо) \ влево (2x + 1 \ вправо)} {\ влево (х — 2 \ вправо) \ влево (х + 3 \ вправо) }f(x)=(x−2)(x+3)(2x−1)(2x+1)
Решение
A Общее примечание: пересечения рациональных функций
рациональная функция будет иметь y -пересечение, когда вход равен нулю, если функция определена в нуле. Рациональная функция не будет иметь y -перехват, если функция не определена в нуле.
Аналогично, рациональная функция будет иметь x -перехватов на входах, которые приводят к нулю на выходе.
 Поскольку дробь равна нулю только тогда, когда числитель равен нулю, x -отрезков может произойти только тогда, когда числитель рациональной функции равен нулю.
Поскольку дробь равна нулю только тогда, когда числитель равен нулю, x -отрезков может произойти только тогда, когда числитель рациональной функции равен нулю.Пример 10. Нахождение точек пересечения рациональной функции
Найдите точки пересечения
f(x)=(x−2)(x+3)(x−1)(x+2)(x−5) е \ влево (х \ вправо) = \ гидроразрыва {\ влево (х — 2 \ вправо) \ влево (х + 3 \ вправо)} {\ влево (х — 1 \ вправо) \ влево (х + 2 \ вправо) \left(x — 5\right)}f(x)=(x−1)(x+2)(x−5)(x−2)(x+3)
.
Решение
Мы можем найти y -отрезок, оценивая функцию в нуле
{f(0)=(0−2)(0+3)(0−1)(0+2)(0 −5) =−610 =−35 =−0,6\begin{cases}f\left(0\right)=\frac{\left(0 — 2\right)\left(0+3\right)}{\ влево(0 — 1\вправо)\влево(0+2\вправо)\влево(0 — 5\вправо)}\qquad \\ \text{ }=\frac{-6}{10}\qquad \\ \ text{ }=-\frac{3}{5}\qquad \\ \text{ }=-0.
 6\qquad \end{case}⎩
6\qquad \end{case}⎩⎨
⎧f(0)=(0−1)( 0+2)(0−5)(0−2)(0+3)=10−6=−53=−0,6
Перехваты x будут происходить, когда функция равна нулю:
{0=(x−2)(x+3)(x−1)(x+2)(x−5)Это ноль, когда числитель равен нулю.0=(x−2)(x+3)x=2,−3\begin{case} 0=\frac{\left(x — 2\right)\left(x+3) \right)}{\left(x — 1\right)\left(x+2\right)\left(x — 5\right)}\qquad & \text{Это ноль, когда числитель равен нулю}.\ qquad \\ 0=\left(x — 2\right)\left(x+3\right)\qquad & \qquad \\ x=2, -3\qquad & \qquad \end{cases}⎩
⎨
⎧0=(x−1)(x+2)(x−5)(x−2)(x+3)0=(x−2)(x+3)x=2,−3 Это ноль, когда числитель равен нулю.
y -отрезок равен
(0,−0,6)\left(0,-0,6\right)(0,−0,6)
, x -отрезок равен
(2,0) \влево(2,0\вправо)(2,0)
и
(-3,0)\влево(-3,0\вправо)(-3,0)
.


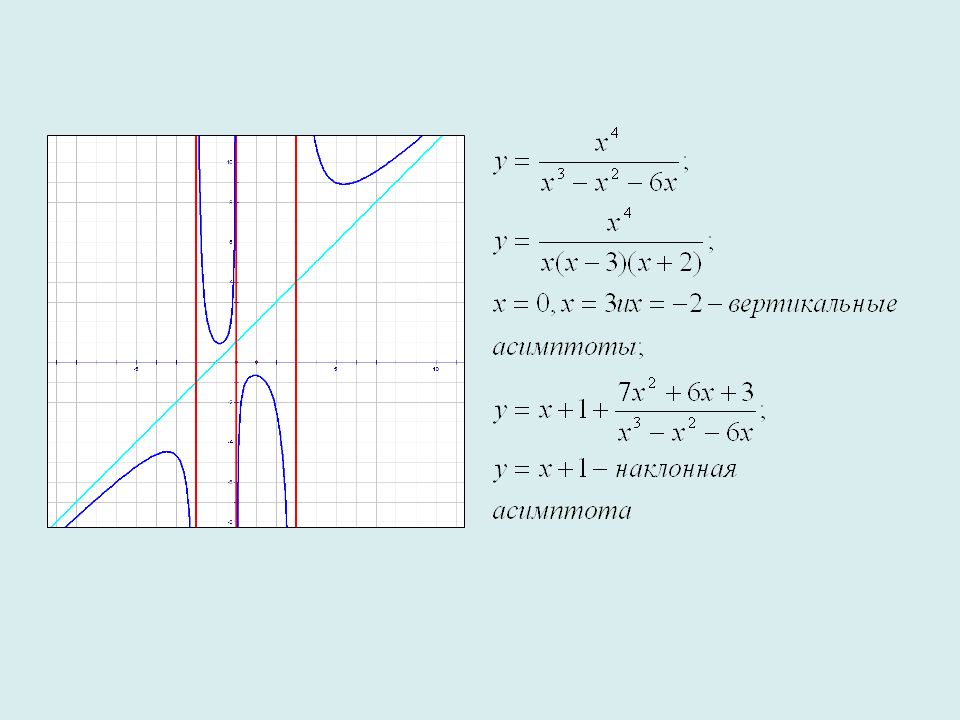
 <-x>$
<-x>$
 Нуль этого коэффициента,
Нуль этого коэффициента, Ноль для этого коэффициента равен
Ноль для этого коэффициента равен Напомним, что поведение конца многочлена будет отражать поведение старшего члена. Точно так же конечное поведение рациональной функции будет отражать отношение старших членов функций числителя и знаменателя. 9{2}}=\frac{4}{x}f(x)≈x24x=x4
Напомним, что поведение конца многочлена будет отражать поведение старшего члена. Точно так же конечное поведение рациональной функции будет отражать отношение старших членов функций числителя и знаменателя. 9{2}}=\frac{4}{x}f(x)≈x24x=x4 По мере того, как входы становятся большими, выходы будут расти, а не выравниваться, поэтому этот график не имеет горизонтальной асимптоты. Однако график
По мере того, как входы становятся большими, выходы будут расти, а не выравниваться, поэтому этот график не имеет горизонтальной асимптоты. Однако график
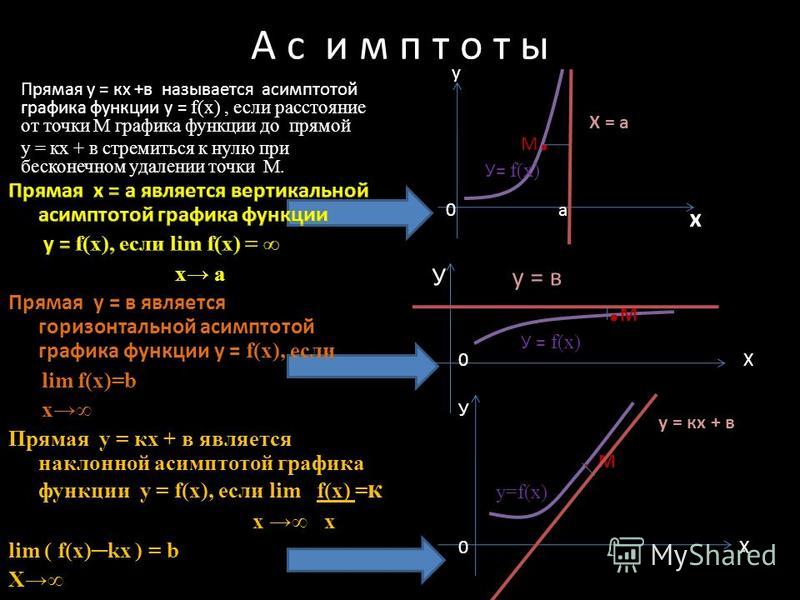 Обратите внимание, что этот график пересекает горизонтальную асимптоту.
Обратите внимание, что этот график пересекает горизонтальную асимптоту.
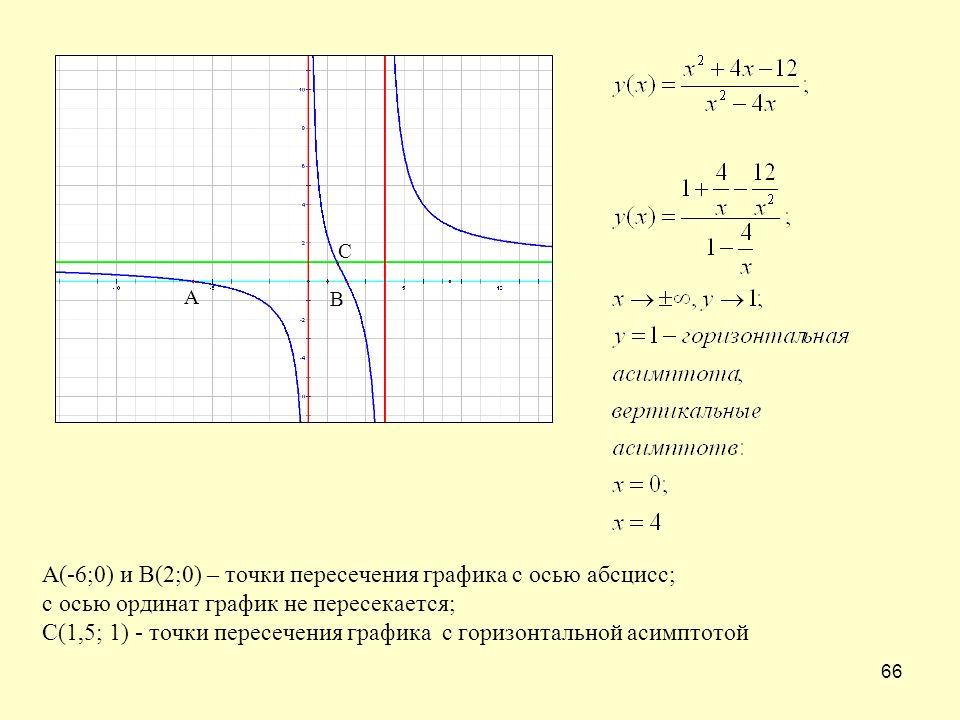

 большой, и поэтому
большой, и поэтому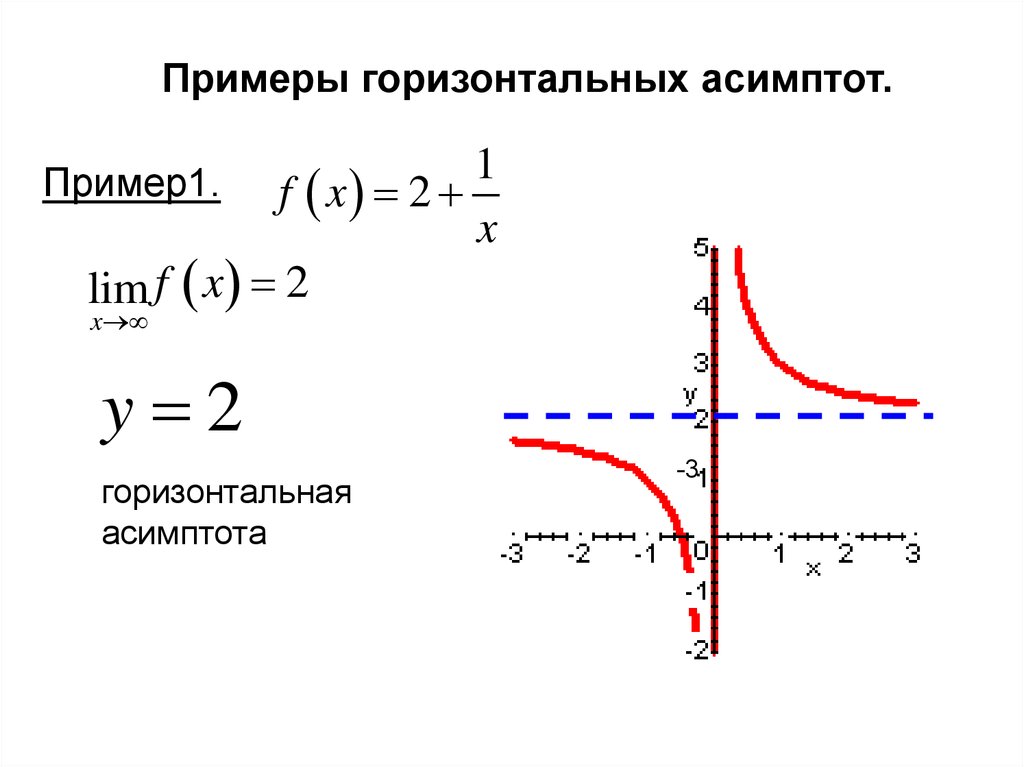 Поскольку дробь равна нулю только тогда, когда числитель равен нулю, x -отрезков может произойти только тогда, когда числитель рациональной функции равен нулю.
Поскольку дробь равна нулю только тогда, когда числитель равен нулю, x -отрезков может произойти только тогда, когда числитель рациональной функции равен нулю.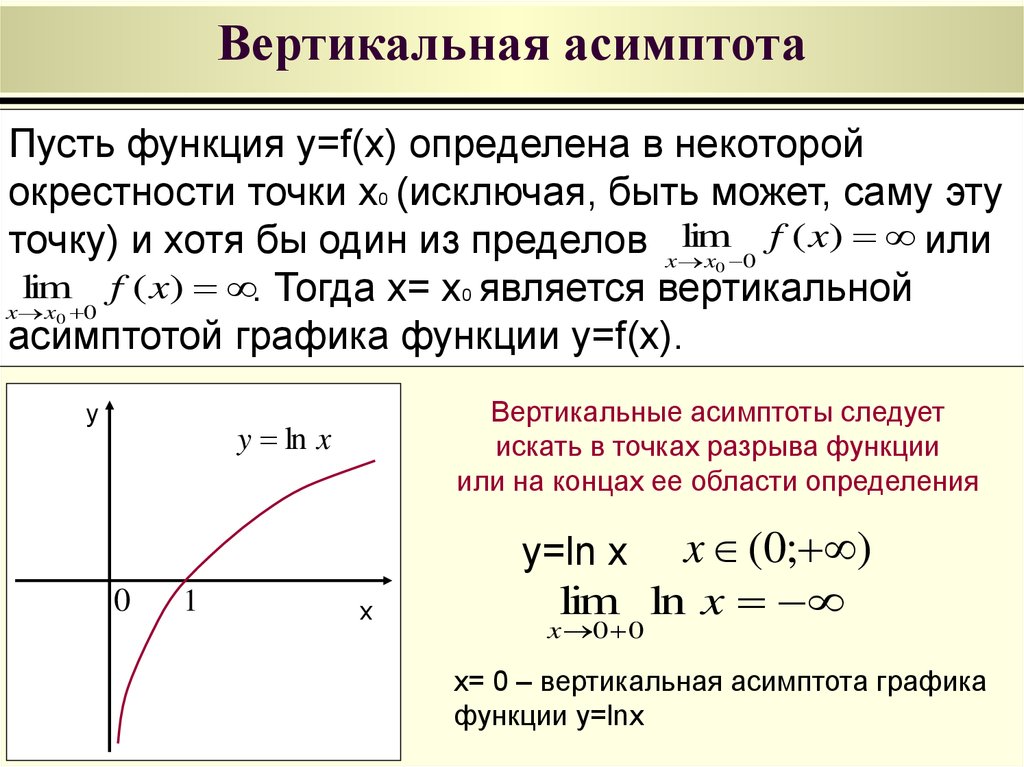 6\qquad \end{case}⎩
6\qquad \end{case}⎩