Сторона параллелограмма: онлайн-калькулятор, формулы и примеры
Параллелограммом называют четырёхугольный многоугольник, две соседние стороны которого равны и параллельны противоположным. Помимо этого, есть ещё несколько важных условий определения фигуры как параллелограмма:
- В месте пересечения диагонали делятся пополам, а точка, в которой пересекаются диагонали, является одновременно центром этих двух отрезков. При этом она всегда лежит внутри фигуры.
- Любая диагональ данного четырёхугольника разделяет его на одинаковые треугольники, так как проходит из одной вершины к противоположной, то есть по центру четырёхугольника.
- Сумма квадратов сторон равна сумме квадратов диагоналей.
- Углы фигуры, расположенные друг напротив друга, попарно равны. Это условие вытекает из
утверждения, что параллельные стороны фигуры равны.

- Сумма двух односторонних углов равна 180°. Это условие напрямую связано с теоремой о двух параллельных прямых и секущей. И действительно, если рассматривать две противоположные и третью между ними стороны параллелограмма как две параллельные прямые и секущую, то можно заметить, что углы, принадлежащие одной стороне, будут соответствовать односторонним углам, сумма которых, согласно теореме, равна 180°.
Только при выполнении всех условий четырёхугольный многоугольник будет считаться параллелограммом.
- Длинная сторона параллелограмма через две диагонали и острый угол между ними
- Длинная сторона параллелограмма через две диагонали и тупой угол между ними
- Короткая сторона параллелограмма через две диагонали и острый угол между ними
- Короткая сторона параллелограмма через две диагонали и тупой угол между ними
- Сторона параллелограмма через две диагонали и другую известную сторону
- Сторона параллелограмма через высоту и синус угла
- Сторона параллелограмма через площадь и высоту
Нахождение длинной стороны через две диагонали и острый угол между ними
Длинную сторону параллелограмма можно найти, зная обе диагонали и острый угол между ними, по формуле:
a = (√(D² + d² — 2 (D * d) * cosα)) / 2
где D – длинная диагональ, d – короткая диагональ, α — острый угол между диагоналями.
Длин. диагональ (D):
ммсмдмм
Кор. диагональ (d):
ммсмдмм
Угол (α):
градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Допустим, дан параллелограмм, у которого диагонали 7 и 4 см, а угол между ними 68º. Тогда, согласно формуле, сторона будет равна: a = (√(7² + 4² — 2 (7 * 4) * cos68º)) / 2 = 3,317 см. Ответ: 3,317 см.
Нахождение короткой стороны через две диагонали и острый угол между ними
Можно вычислить и короткую сторону по формуле:
b = (√(D² + d² + 2 (D * d) * cosα)) / 2
где D – длинная диагональ, d – короткая диагональ, α — острый угол между диагоналями.
Длин. диагональ (D):
ммсмдмм
Кор. диагональ (d):
ммсмдмм
Угол (α):градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Теперь необходимо найти другую сторону параллелограмма. Данные останутся те
же, что и в прошлой задаче, но в уравнении поменяется знак, так как по отношению к углу поменялась
сторона, которую надо найти. Сторона b будет равна: b = (√(7² + 4² + 2 (7 * 4) * cos68º)) / 2 = 4.64.
Ответ: 4,64 см.
Теперь необходимо найти другую сторону параллелограмма. Данные останутся те
же, что и в прошлой задаче, но в уравнении поменяется знак, так как по отношению к углу поменялась
сторона, которую надо найти. Сторона b будет равна: b = (√(7² + 4² + 2 (7 * 4) * cos68º)) / 2 = 4.64.
Ответ: 4,64 см.
Нахождение длинной стороны через две диагонали и тупой угол между ними
Стороны параллелограмма можно найти, зная диагонали и тупой угол между ними. Для этого нужно использовать следующую формулу:
a = (√(D² + d² + 2 (D * d) * cosβ)) / 2
где D – длинная диагональ, d – короткая диагональ, β — тупой угол между диагоналями.
Длин. диагональ (D):
ммсмдмм
Кор. диагональ (d):
ммсмдмм
Угол (β):
градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Рассмотрим нахождение сторон всё того же параллелограмма с диагоналями 7 и 4
см. Однако на этот раз возьмём между диагоналями другой угол: β=112º. В таком случае для стороны a
минус меняется на плюс, а сама сторона равна: a = (√(7² + 4² + 2 (7 * 4) * cos112º)) / 2 = 3.914
Рассмотрим нахождение сторон всё того же параллелограмма с диагоналями 7 и 4
см. Однако на этот раз возьмём между диагоналями другой угол: β=112º. В таком случае для стороны a
минус меняется на плюс, а сама сторона равна: a = (√(7² + 4² + 2 (7 * 4) * cos112º)) / 2 = 3.914
Нахождение короткой стороны через две диагонали и тупой угол между ними
Аналогично можно найти и короткую сторону, зная диагонали и тупой угол между ними:
b = (√(D² + d² — 2 (D * d) * cosβ)) / 2
где D – длинная диагональ, d – короткая диагональ, β — тупой угол между диагоналями.
Длин. диагональ (D):
ммсмдмм
Кор. диагональ (d):
ммсмдмм
Угол (β):
градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Для стороны b так же изменится знак в формуле, но наоборот: плюс на минус. Тогда
получается: b = (√(7² + 4² — 2 (7 * 4) * cos112)) / 2 = 4,64 см. Ответ совпал с ответом второй
задачи, все опять решено верно, а сторона в воображаемом параллелограмме действительно равна 4,64
см.
Для стороны b так же изменится знак в формуле, но наоборот: плюс на минус. Тогда
получается: b = (√(7² + 4² — 2 (7 * 4) * cos112)) / 2 = 4,64 см. Ответ совпал с ответом второй
задачи, все опять решено верно, а сторона в воображаемом параллелограмме действительно равна 4,64
см.
Нахождение стороны параллелограмма через диагонали и другую сторону
Как и в случае с прошлыми пунктами, существуют формула, которая позволяет найти сторону параллелограмма с использованием диагоналей и известной стороны. Вот она:
a = √(D² + d² — 2b² / 2)
где D, d — диагонали, b — сторона.
Диагональ (D):
ммсмдмм
Диагональ (d):
ммсмдмм
Сторона (b):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Выводится данная формулы из первого следствия теоремы косинусов.
Пример. Используем для следующих задач другой параллелограмм. Эта фигура будет с диагоналями 9 и 5 см и стороной 6 см. Тогда другая сторона данного параллелограмма равна: a = √(9² + 5² — 2 * 6² / 2) = 4,1 см. Ответ: 4,1 см.
Для проверки ответа можем решить обратную задачу, при которой нам не известна сторона b, но известна сторона a = 4,1 см. По обратной формуле получается b = √(9² + 5² — 2 * 4,1² / 2) = 6 см. Ответ совпадает с изначальными данными первой задачи. А значит и этот воображаемый параллелограмм действительно существует.
Нахождение стороны через синус угла и высоту
Высота – это отрезок, опущенный перпендикулярно из вершины фигуры на противоположную сторону. Есть
несколько интересных свойств у неё. Например, высоты, проведенные из острых углов, будут всегда
лежать вне фигуры, в то время как высоты из тупых углов всегда лежат внутри. Если из одного угла
опустить две высоты, то между ними образуется угол, равный смежному углу параллелограмма. Равными
будут те высоты, что заключены между параллельными сторонами четырёхугольника. Найти сторону
параллелограмма через эту величину достаточно просто, по формуле:
Если из одного угла
опустить две высоты, то между ними образуется угол, равный смежному углу параллелограмма. Равными
будут те высоты, что заключены между параллельными сторонами четырёхугольника. Найти сторону
параллелограмма через эту величину достаточно просто, по формуле:
a = h / sinα
где: h — высота параллелограмма, sin α — угол.
Высота (h):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Стоит заметить, что высота должна быть опущена не к искомой стороне, а к соседней. При этом для формулы сойдет синус любого известного угла параллелограмма.
Пример. Найти сторону параллелограмма, если высота, опущенная на соседнюю сторону
равна 10 см, а острый угол — 30º.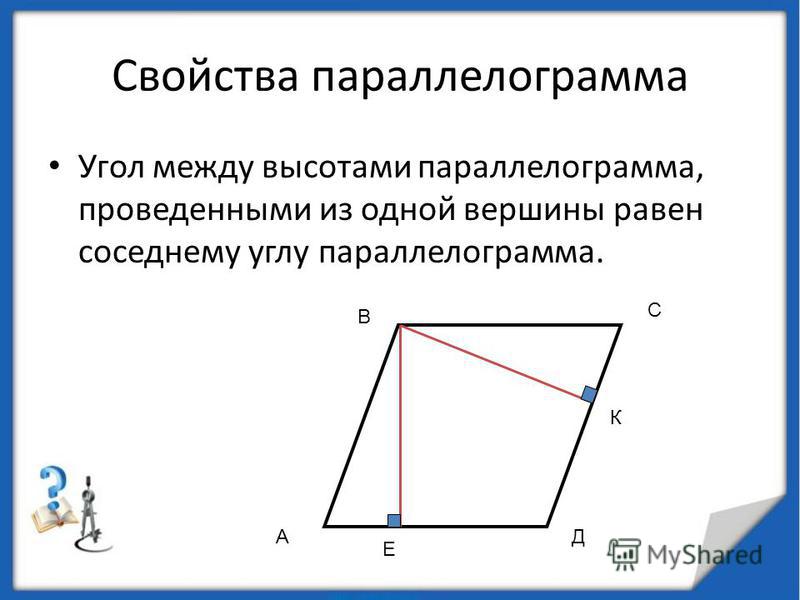 Решение: a=10 / 0,5 = 20 см
Решение: a=10 / 0,5 = 20 см
Нахождение стороны через площадь и высоту
Более подробно о площади и высоте параллелограмма рассказано в пунктах выше. В этом достаточно легко вывести единственную формулу, по которой можно найти сторону. Если площадь является произведением стороны на высоту, то сторона будет равна отношению площади к высоте:
a = S / h
где S — площадь параллелограмма, h — высота.
Площадь (S):
мм²см²дм²м²
Высота (h):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Причем не имеет значения, к какой стороне опущена высота: к искомой или соседней.
Пример. Найти сторону параллелограмма, если его площадь равна 20 см, а высота, опущенная на одну из сторон — 5 см. Решение: a = 20 / 5 = 4 см.
Фигура кажется сложной для восприятия из-за того, что её нельзя постоянно наблюдать где-то в
повседневной жизни. Однако всё становится проще, если вспомнить, что есть более известные широкой
публике частные случаи параллелограмма. Их-то человек обычно наблюдает ежедневно. Это ромб,
прямоугольник и квадрат. Причем последний, хоть и наиболее известен, является и наиболее
интересным.
Однако всё становится проще, если вспомнить, что есть более известные широкой
публике частные случаи параллелограмма. Их-то человек обычно наблюдает ежедневно. Это ромб,
прямоугольник и квадрат. Причем последний, хоть и наиболее известен, является и наиболее
интересным.
Ромб считается частным случаем, потому что представляет собой параллелограмм, диагонали которого в
точке пересечения образуют прямой угол. Прямоугольник является частным случаем, потому что это
параллелограмм, у которого все углы прямые. У квадрата же положение ещё интереснее, так как его
можно назвать не только частным случаем параллелограмма, но и прямоугольника, и ромба. Квадрат – это
комбо трёх предыдущих определений. Можно даже сказать, что квадрат одновременно является особенным
случаем и для параллелограмма, и для прямоугольника, и для ромба. Все его стороны равны,
противоположные стороны параллельны. Все углы являются прямыми, даже образующиеся при пересечении
диагоналей, которые к тому же делятся пополам в точке пересечения.
Все углы являются прямыми, даже образующиеся при пересечении
диагоналей, которые к тому же делятся пополам в точке пересечения.
Как найти меньшую сторону параллелограмма: найдите меньшую сторону параллелограмма если высоты параллелограмма равны 6 см и 16 см а — ЭкоДом: Дом своими руками
Содержание
Как найти стороны параллелограмма
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Формулы длины сторон через диагонали и угол между ними.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):
Формулы сторон параллелограмма через диагонали и сторону, (a, b):
Формулы сторон параллелограмма , (a, b):
2. Формулы длины сторон параллелограмма через высоту.
Формулы длины сторон параллелограмма через высоту.
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
α, β — углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):
3. Дополнительные, интересные формулы параллелограмма:
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол между диагоналями
Формула суммы квадратов диагоналей:
Формула разности квадратов сторон:
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Задачи по школьной математике.

Параллелограмм
Сторона параллелограмма втрое больше другой его стороны. Найдите стороны параллелограмма, если его периметр равен 24.

 Найдите отношение площадей квадрата и четырехугольника EFLN.
Найдите отношение площадей квадрата и четырехугольника EFLN. Найдите стороны параллелограмма.
Найдите стороны параллелограмма.Высота параллелограмма, проведенная из вершины тупого угла, равна 2 и делит сторону параллелограмма пополам. Острый угол параллелограмма равен 30◦. Найдите диагональ, проведенную из вершины тупого угла, и углы, которые она образует со сторонами.
Диагонали параллелограмма ABCD пересекаются в точке O. Периметр параллелограмма равен 12, а разность периметров треугольников BOC и COD равна 2. Найдите стороны параллелограмма.
Сторона BC параллелограмма ABCD вдвое больше стороны AB. Биссектрисы углов A и B пересекают прямую CD в точках M и N, причем MN = 12. Найдите стороны параллелограмма.
Угол при вершине A ромба ABCD равен 20◦. Точки M и N — основания перпендикуляров, опущенных из вершины B на стороны AD и CD. Найдите углы треугольника BMN.
Докажите, что точки попарного пересечения биссектрис всех четырех углов параллелограмма являются вершинами прямоугольника.
Докажите, что отрезок, соединяющий середины противоположных сторон параллелограмма, проходит через его центр.
На сторонах AB и CD прямоугольника ABCD взяты точки K и M так, что AKCM является ромбом. Диагональ AC составляет со стороной AB угол 30◦. Найдите сторону ромба, если наибольшая сторона прямоугольника ABCD равна 3.
|
Обозначения в формулах эквивалентны обозначениям на рисунках, а именно: а — стороны, параллелограмма, параллельные друг другу b — боковые стороны параллелограмма h — высота параллелограмма d — диагональ параллелограмма S — площадь параллелограмма α — острый угол при основании параллелограмма Высота параллелограмма равна соотношению площади к основанию (Формула 1) Высота параллелограмма равна произведению боковой стороны на синус угла при основании (Формула 2) Соотношение оснований параллелограмма равно обратно пропорциональному соотношению высот, опущенных на соответствующие стороны (Формула 3) Высоты параллелограмма, опущенные из одной вершины, образуют угол, равный углу параллелограмма при соседней вершине (Рисунок 2) Высота параллелограмма равна, корню из разности квадрата боковой стороны и квадрата длины отрезка, образующего прямоугольный треугольник, другими сторонами которого являются боковая сторона и высота (Формула 4) Высота параллелограмма равна корню из разности квадрата диагонали, из которой опущена высота и квадрата длины отрезка между точкой, из которой проведена диагональ и точкой пересечения высоты и основания (Формула 5) | Позначення у формулах еквівалентні позначенням на малюнках, а саме:
а — сторони, паралелограма, паралельні один одному b — бічні сторони паралелограма h — висота паралелограма d — дiагональ паралелограма S — площа паралелограма α — гострий кут при основі паралелограма Висота паралелограма дорівнює співвідношенню площі до підстави (Формула 1) Висота паралелограма дорівнює твору бічної сторони на синус кута при його основі (Формула 2) Співвідношення підстав паралелограма дорівнює обернено пропорційному співвідношенню висот, опущених на відповідні сторони (Формула 3) Висоти паралелограма, опущені з однієї вершини, утворюють кут, рівний куту паралелограма при сусідній вершині (Малюнок 2) Висота паралелограма рівна, корню з різниці квадрата бічної сторони і квадрата довжини відрізка, створюючого прямокутний трикутник, іншими сторонами якого є бічна сторона і висота (Формула 4) Висота паралелограма дорівнює корню з різниці квадрата діагоналі, з якої опущена висота і квадрата довжини відрізка між точкою, з якої проведена діагональ і точкою пересічення висоти і основання (Формула 5) |
Площадь параллелограмма, треугольника и трапеции — урок.
Геометрия, 8 класс.
Площадь параллелограмма
Необходимо определить, что такое высота параллелограмма.
Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону. Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.
Высота \(BE\), проведённая между длинными сторонами, короче высоты \(BF\), проведённой между короткими сторонами.
Так как стороны ромба одинаковы, то высоты ромба также одинаковы: \(BE = BF\).
Площадь произвольного параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
Проведём высоты из двух вершин \(B\) и \(C\) к стороне \(AD\) .
Прямоугольные треугольники \(ABE\) и \(DCF\) равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
Параллелограмм \(ABCD\) и прямоугольник \(EBCF\) — равновеликие, так как состоят из равных фигур:
SABCD=SABE+SEBCD;SEBCF=SEBCD+SDCF.
Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
SEBCF=BE⋅BC;SABCD=BE⋅BC=BE⋅AD.
Если обозначить сторону через \(a\), высоту — через \(h\), то:
Sп−гр=a⋅h.
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
Площадь ромба
Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.
SABCD=4⋅SABO=4⋅BO⋅AO2=2⋅BO⋅AO.
Формула определения площади ромба:
Sромба=d1⋅d22.
Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.
Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали:
Sквадрата=d22.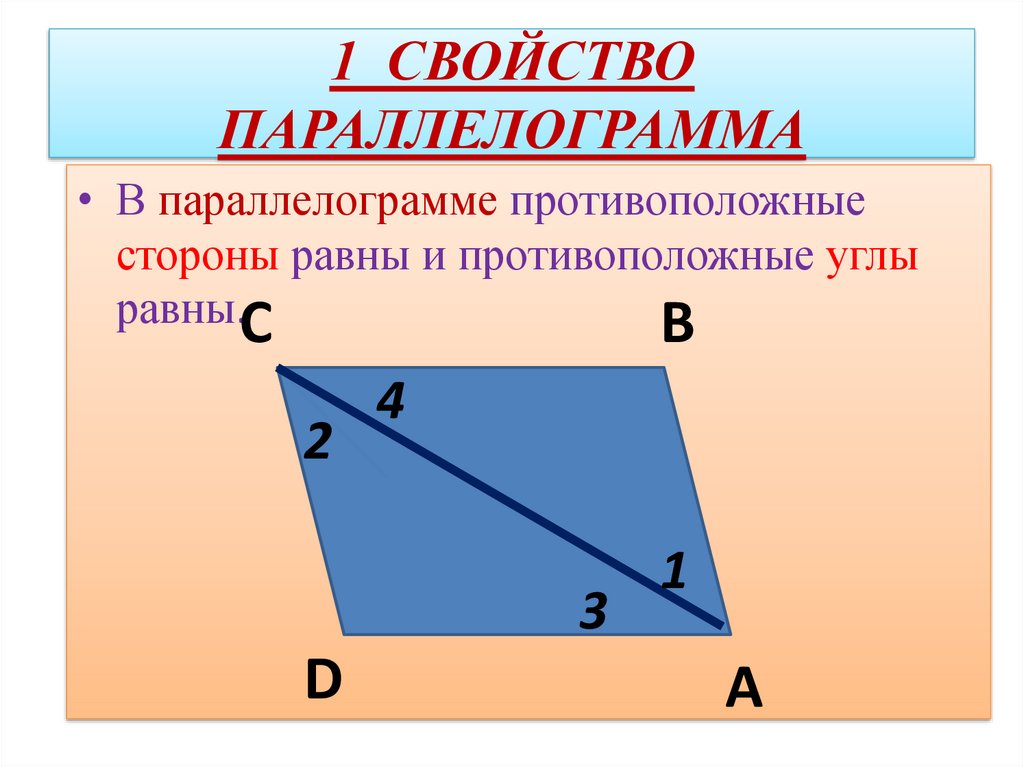
Площадь произвольного треугольника
Так как диагональ параллелограмма делит его на два равных треугольника, то площадь треугольника равна половине площади параллелограмма.
Sтреуг=aha2, где \(h\) — высота (на рисунке — \(BE\)), проведённая к стороне \(a\) (на рисунке — \(AD\)).
Для определения площади треугольника можно использовать любую сторону и высоту, проведённую к этой стороне.
Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.
SΔ=pp−ap−bp−c;p=a+b+c2
— формула Герона, где \(a\), \(b\) и \(c\) — стороны треугольника, \(p\) — полупериметр треугольника.
Площадь прямоугольного треугольника
Так как катеты прямоугольного треугольника взаимно перпендикулярны, то один катет может быть высотой, а другой катет — стороной, к которой проведена высота. Получаем формулу:
S=a⋅b2, где \(a\) и \(b\) — катеты.
Для прямоугольного треугольника также можно применять формулы площади произвольного треугольника.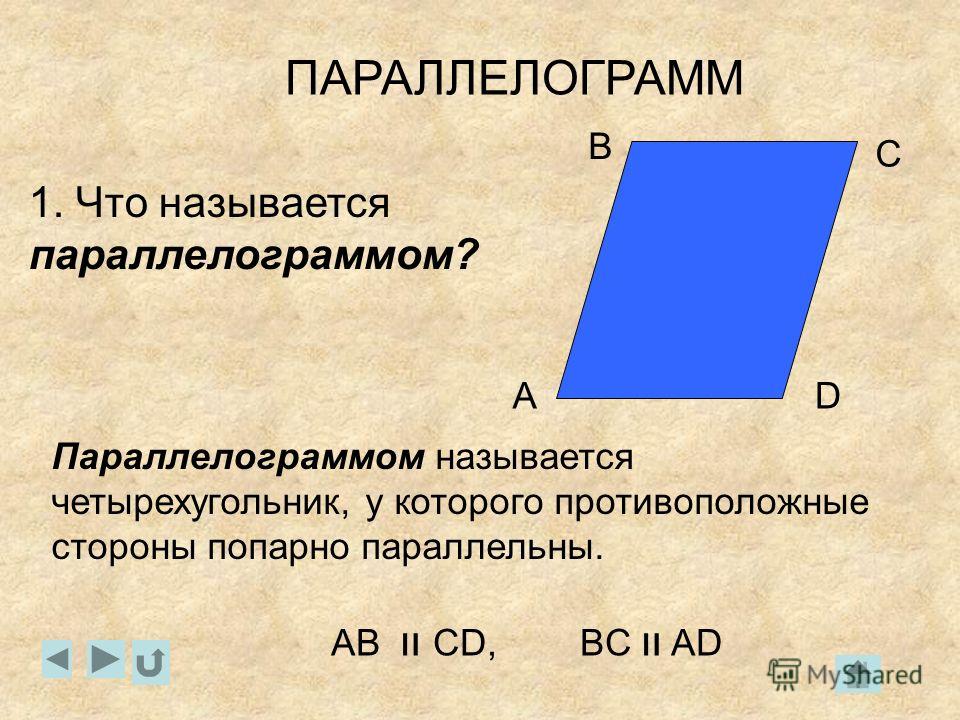
Пример:
1. вычислим площадь треугольника со сторонами \(17\) см, \(39\) см, \(44\) см.
Решение:
p=17+39+442=50;SΔ=50⋅50−17⋅50−39⋅50−44=50⋅33⋅11⋅6==25⋅2⋅3⋅11⋅11⋅2⋅3=5⋅2⋅3⋅11=330см2.
Чтобы легче было вычислить корень, необходимо не перемножать все числа, а раскладывать их на множители: a⋅a=a.
Формулу Герона можно использовать для вычисления высоты треугольника.
Пример:
2. вычислим меньшую высоту треугольника, стороны которого равны \(15\) см, \(13\) см, \(4\) см.
Решение:
используем две формулы вычисления площади: SΔ=aha2 и SΔ=pp−ap−bp−c.
Меньшая высота в треугольнике — та, которая проведена к большей стороне, поэтому \(a =\) \(15\) см.
SΔ=pp−ap−bp−c=16⋅1⋅3⋅12=24см2.
Составляем уравнение:
15⋅h4=24⋅215⋅h=48;h=4815=3,2(см).
Иногда формула Герона используется для вычисления площади параллелограмма, если даны стороны параллелограмма и его диагональ.
Пример:
3. дан параллелограмм со сторонами \(17\) см и \(39\) см, длина диагонали равна \(44\) см. Вычислим площадь параллелограмма.
Решение:
диагональ делит параллелограмм на два равных треугольника. Используем результат, полученный в первом примере:
Sпараллелограмма=2⋅SΔ=2⋅330=660(см2).
Площадь трапеции
Трапеция имеет одну пару параллельных сторон, следовательно, имеет одну высоту — перпендикуляр, проведённый между параллельными сторонами.
Чаще всего высоту трапеции проводят из вершин или через точку пересечения диагоналей.
Площадь трапеции определим как сумму площадей треугольников, на которые трапецию делит диагональ.
SABCD=SABD+SDBC;SABCD=AD⋅BE2+BC⋅DF2=AD⋅BE2+BC⋅BE2==AD+BC⋅BE2.
Если обозначить параллельные стороны (основания) трапеции через \(a\) и \(b\), высоту через \(h\), то:
Sтрап=a+b2⋅h.
Обрати внимание!
Важные следствия:
1. если высоты треугольников равны, то их площади относятся как длины оснований.
2. Если основания треугольников равны, то их площади относятся как длины высот.
3. Если высоты треугольников равны и их основания равны, то они равновелики, например, медиана делит треугольник на две равновеликие части.
Задания В5. Параллелограмм | Подготовка к ЕГЭ по математике
В этой статье работаем с Задачами №3 ЕГЭ по математике, которые связаны с параллелограммом.
Смотрите в других статьях разбор Задачи №3, в которых фигурирует:
– треугольник;
– прямоугольник;
– ромб;
– произвольный четырехугольник;
– трапеция;
– многоугольник;
– круг;
– векторы;
– координатная плоскость;
Задача 1. Найдите площадь параллелограмма, изображенного на рисунке.
Решение: + показать
Задача 2. Найдите площадь параллелограмма, если две его стороны равны 25 и 20, а угол между ними равен 30˚.
Решение: + показать
Задача 3. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Решение: + показать
Задача 4. Стороны параллелограмма равны 8 и 16. Высота, опущенная на первую сторону, равна 12. Найдите высоту, опущенную на вторую сторону параллелограмма.
Решение: + показать
Так как согласно формуле площади параллелограмма , то
Откуда
Ответ: 6.
Задача 5. Периметр параллелограмма равен 38. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.
Решение: + показать
Пусть меньшая сторона параллелограмма равна , тогда большая сторона равна согласно условию.
Периметр параллелограмма – сумма длин всех сторон, при этом противоположные стороны параллелограмма равны.
Поэтому
Ответ: 8.
Задача 6. Боковая сторона равнобедренного треугольника равна 26. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.
Решение: + показать
Задача 7. Площадь параллелограмма равна 116. Найдите площадь параллелограмма , вершинами которого являются середины сторон данного параллелограмма.
Решение: + показать
Задача 8. Площадь параллелограмма равна 180. Точка — середина стороны . Найдите площадь треугольника .
Решение: + показать
Вы можете пройти тест «Задачи №3. Параллелограмм»
Параллелограмм. Свойства, площадь и признаки
Параллелограмм — это четырехугольник, имеющий две пары параллельных сторон.
Свойства параллелограмма:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Диагонали параллелограмма в точке пересечения делятся пополам.

Давайте посмотрим, как свойства параллелограмма применяются в решении задач ЕГЭ.
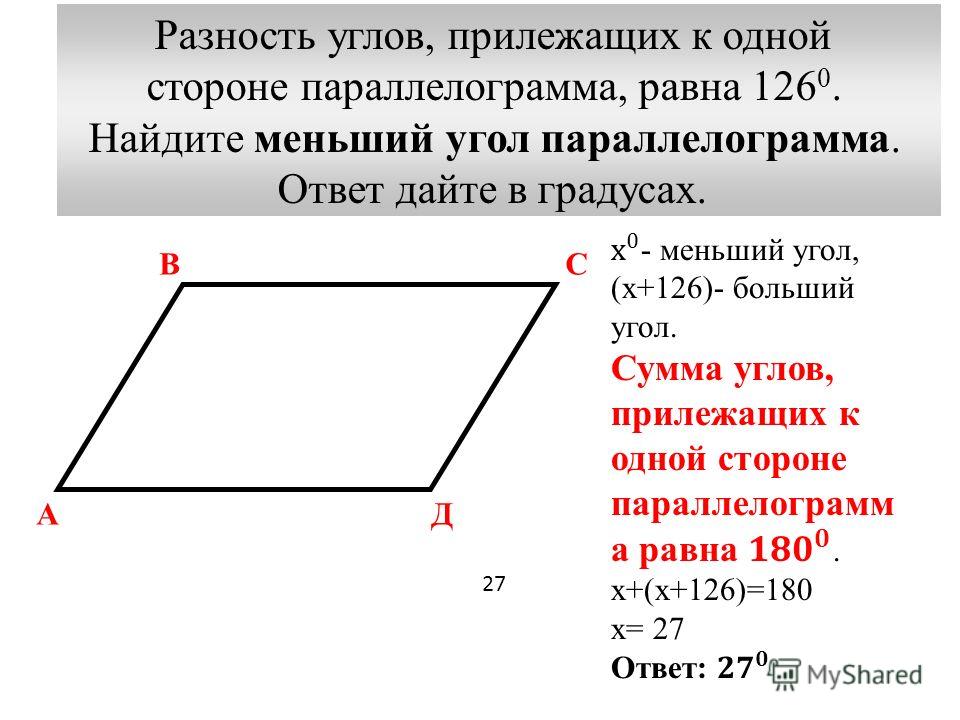
1. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Пусть и — биссектрисы углов параллелограмма, прилежащих к стороне . Сумма углов и равна . Углы и — половинки углов и . Значит, сумма углов и равна градусов. Из треугольника находим, что угол — прямой.
Ответ: .
Биссектрисы углов параллелограмма, прилежащих к одной стороне, — перпендикулярны.
Легко доказывается и другое свойство биссектрис параллелограмма:
Биссектрисы противоположных углов параллелограмма — параллельны.
Ты нашел то, что искал? Поделись с друзьями!
2. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна . Найдите его большую сторону.
Найдем на этом рисунке накрест лежащие углы. Мы уже рассказывали, что это такое.
Углы и , а также и — накрест лежащие. Накрест лежащие углы равны. Значит, угол равен углу , а угол — углу .
Получаем, что треугольники и — равнобедренные, то есть , а . Тогда .
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Запишем формулы площади параллелограмма:
, где — основание параллелограмма, — его высота.
, где и — стороны параллелограмма, — угол между ними.
И еще одна формула.
, где и — диагонали параллелограмма, — угол между ними.
3 формулы площади параллелограмма — онлайн калькулятор расчета
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Площадь параллелограмма через сторону и высоту вычисляется по формуле:
- a — сторона параллелограмма.
- h — высота.
Формула площади параллелограмма через стороны и угол между ними:
- a — сторона параллелограмма.

- b — сторона параллелограмма.
- α — угол между сторонами.
Для быстрого расчета площади параллелограмма воспользуйтесь онлайн калькулятором:
Формула площади параллелограмма через диагонали параллелограмма и угол между ними
- d и D — диагонали параллелограмма.
- α — угол между диагоналями.
Онлайн расчет:
Оцени статью
Оценить
Средняя оценка / 5. Количество голосов:
Спасибо, помогите другим — напишите комментарий, добавьте информации к статье.
Или поделись статьей
Видим, что вы не нашли ответ на свой вопрос.
Помогите улучшить статью.
Напишите комментарий, что можно добавить к статье, какой информации не хватает.
Отправить
Спасибо за ваши отзыв!
Как найти длину стороны параллелограмма
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.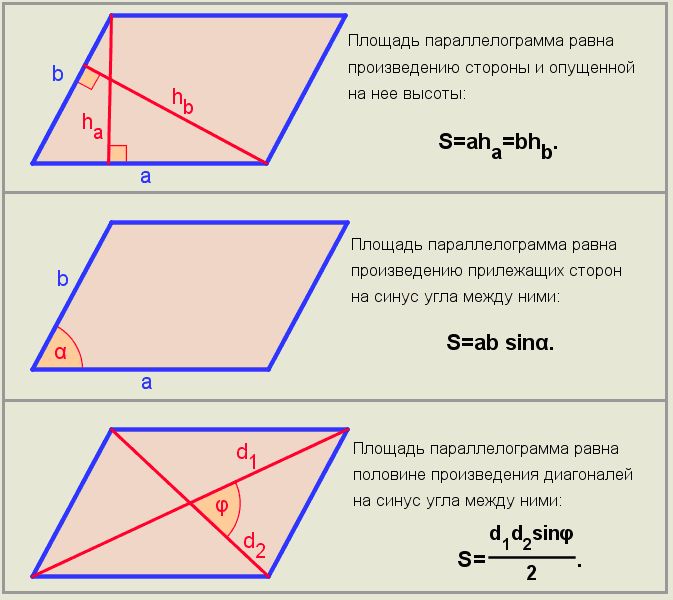 Таким образом, если вы не уверены, что контент находится
Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как найти длину диагонали параллелограмма
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects. org.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Геометрия
— Может ли параллелограмм иметь целые числа для всех четырех сторон и обеих диагоналей?
Ваша догадка неверна. Существует непрямоугольный не ромбовидный параллелограмм с целой стороной и длиной диагонали:
Предположим, что параллелограмм — это $ ABCD $, где $ AB = a $, $ AD = b $ и $ BD = c $. 2 $$
2 $$
Чтобы удовлетворить неравенствам треугольника, выберем
$$ \ color {blue} {a = 2r-s \ qquad b = 2s + r \ qquad c = 2 (r + s) — (rs) \ qquad d = 2 (rs) + (r + s)} $ $
Гарантируется, что они образуют непрямоугольный не ромбовидный целочисленный параллелограмм с заданными ограничениями на $ r $ и $ s $. Тот, что изображен вверху этого ответа, соответствует $ (r, s) = (5,2) $, а самый маленький экземпляр (тот, у которого длина сторон 4 и 7) соответствует $ (r, s) = (3, 2) $.
Площадь параллелограмма с учетом диагоналей и стороны
Основная формула для вычисления площади параллелограмма — это длина одной стороны, умноженная на высоту параллелограмма с этой стороны.
Но что нам делать, если у нас нет этих измерений (сторона, высота)? Что, если вместо этого нам будет представлена длина одной стороны и длина обеих диагоналей?
Давайте посмотрим, как мы можем вычислить площадь параллелограмма в этом случае в следующей задаче.
Задача
У параллелограмма длина стороны 13 единиц и длина диагонали 24 единицы и 10 единиц.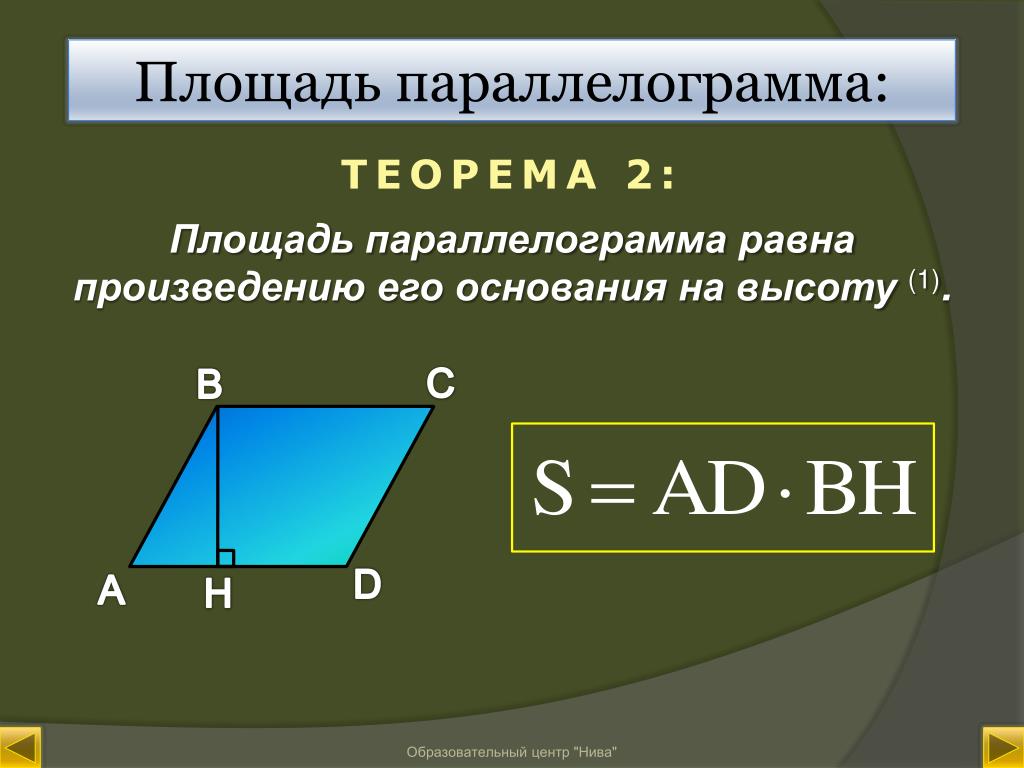 Найдите его область.
Найдите его область.
Стратегия
Есть два способа начать думать об этой проблеме, и оба приведут нас к одной и той же точке и решению.
Поскольку у нас есть обе диагонали, мы можем начать с размышлений о свойствах диагоналей в параллелограммах — они делят друг друга пополам. Итак, если у нас есть диагонали в 24 и 10 единиц, они делят друг друга пополам на сегменты по 12 единиц и 5 единиц соответственно:
Итак, теперь у нас есть треугольник со сторонами 5, 12 и 13 — тройка Пифагора, что означает треугольник. представляет собой прямоугольный треугольник, и мы можем легко вычислить его площадь как ножку x ножку / 2 или 5×12 / 2 = 30.
Но если m∠AOB = 90 °, то m∠AOD = 90 °, поскольку AOB и ∠AOD представляют собой линейную пару, которая в сумме дает 180 °.Треугольники ΔAOB и ΔAOD тогда конгруэнтны (по бокам-углам-сторонам), как и треугольники ΔAOB и ΔCOB (также по бокам-углам-бокам). Итак, у нас есть 4 треугольника площадью 30, составляющих площадь параллелограмма, площадь которого, таким образом, равна 4×30 = 120.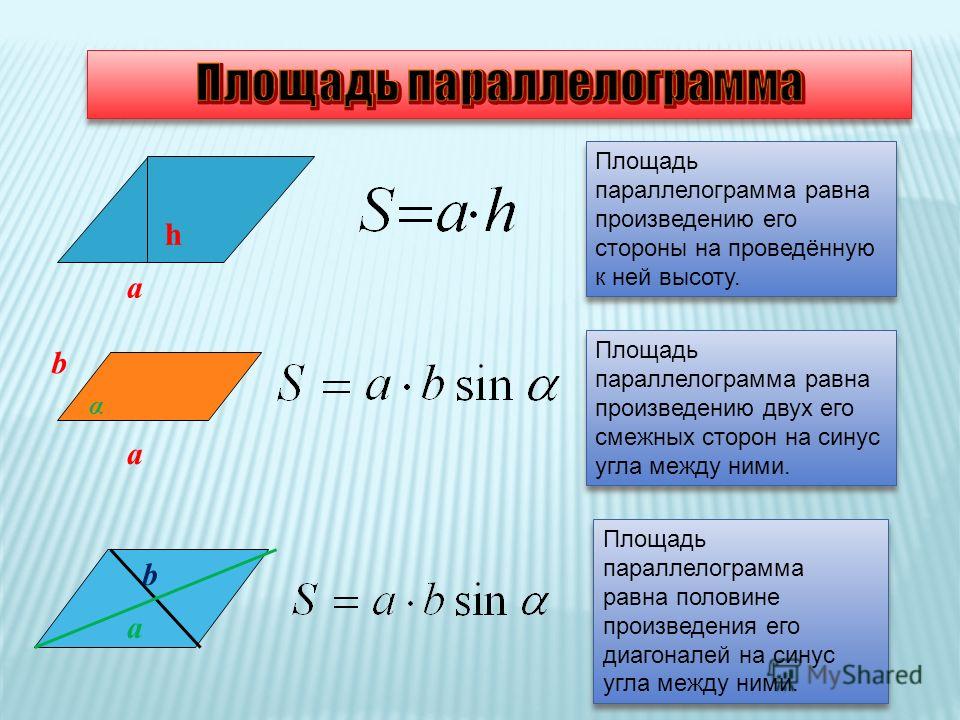
Другой способ осмыслить проблему — вспомнить, что если параллелограмм представляет собой ромб, то его площадь равна произведению диагоналей, разделенных на два. Это потому, что ромб также является воздушным змеем, и мы показали, что площадь воздушного змея равна половине произведения его диагоналей.
Итак, если мы докажем, что параллелограмм является ромбом, мы можем использовать это напрямую. Мы можем перейти к доказательству того, что этот параллелограмм действительно является ромбом, используя тот факт, что если диагонали параллелограмма перпендикулярны, это ромб — и мы показали выше, что эти диагонали действительно перпендикулярны.
Таким образом, площадь параллелограмма равна (диагональ x диагональ / 2), или 24×10 / 2 = 120, как указано выше.
Решение
(1) AC = 24 // Дано
(2) BD = 10 // Дано
(3) AO = OC = 12 // Диагонали параллелограмма делят друг друга пополам
(4) BO = OD = 5 // Диагонали параллелограмма делят друг друга пополам
(5) AB = 13 // Дано
(6) m∠AOB = 90 ° // (3), (4), (5), обратное теореме Пифагора ( 5,12,13 — тройка Пифагора)
(7) AC⊥DB // (6), определение перпендикулярных прямых
(8) ABCD — ромб // параллелограмм с перпендикулярными диагоналями — ромб
(9) Площадь ABCD = | AC | · | DB | / 2 // Площадь ромба — произведение диагоналей, разделенных на два
(10) Площадь ABCD = 24 · 10/2 = 120 квадратных единиц // (1), (2), (9)
Итак, в этом случае у нас есть диагонали и сторона параллелограмма, которые образуют пифагорову тройку. Это упрощает расчет площади параллелограмма. Но как насчет других параллелограммов, у которых диагонали не перпендикулярны?
Это упрощает расчет площади параллелограмма. Но как насчет других параллелограммов, у которых диагонали не перпендикулярны?
Оказывается, мы можем определить площадь параллелограмма и для этих случаев. Нам просто нужно будет использовать еще немного вычислений, известных как формула Герона для площади треугольника, который не является прямоугольным.
Видео с вопросом: Определение длины стороны параллелограмма по подобию треугольников
Стенограмма видео
Учитывая, что 𝐴𝐵𝐶𝐷 — параллелограмм, 𝐵 — середина отрезка 𝐴𝐹, 𝐶𝐸
равно восьми сантиметрам, 𝐷𝐸 равно 16 сантиметрам, а 𝐶𝑋 равно 11
в сантиметрах найдите длину отрезка 𝐴𝐷.
В этом вопросе нам сначала говорят, что 𝐴𝐵𝐶𝐷 — параллелограмм. Это четырехугольник в верхней части рисунка. Одно из основных свойств параллелограммов, о которых мы должны помнить, заключается в том, что
противоположные стороны параллельны. На рисунке это будет означать, что прямая 𝐷𝐴 параллельна прямой 𝐶𝐵 и прямой 𝐶𝐷.
параллельно 𝐵𝐴. Следующее, что нам говорят, — это то, что 𝐵 — это середина отрезка прямой. И нам даны размеры: 𝐶𝐴 — восемь сантиметров, 𝐷𝐴 — 16.
Следующее, что нам говорят, — это то, что 𝐵 — это середина отрезка прямой. И нам даны размеры: 𝐶𝐴 — восемь сантиметров, 𝐷𝐴 — 16.
сантиметры, а 𝐶𝑋 равно 11 сантиметрам, поэтому мы можем заполнить эти измерения
на диаграмму.
Вопрос просит нас найти длину этого отрезка 𝐴𝐷. Чтобы разобраться с этим, мы должны вспомнить еще один важный факт об обратном.
стороны параллелограмма. Мы знаем, что они параллельны, но мы также должны помнить, что противоположные стороны
конгруэнтный. Это означает, что они одинаковой длины. Следовательно, если нам нужна длина стороны, противоположной 𝐴𝐷, длина линии
отрезок 𝐶𝐵, то мы бы знали, что он будет такой же длины.Указанная здесь длина 11 сантиметров относится только к отрезку линии.
𝐶𝑋, а не на весь отрезок 𝐶𝐵. Итак, давайте посмотрим, есть ли способ, которым мы можем вычислить этот отрезок линии 𝑋𝐵.
Рассмотрим эти два треугольника. У нас есть меньший треугольник 𝐶𝐸𝑋 и больший треугольник. Затем мы могли бы спросить себя, похожи ли эти два треугольника. Это означает, что они будут той же формы, но разного размера. Один из способов доказать сходство в треугольниках — использовать критерий AA в
Это означает, что они будут той же формы, но разного размера. Один из способов доказать сходство в треугольниках — использовать критерий AA в
что мы видим, если существуют две пары соответствующих пар конгруэнтных углов.Итак, давайте посмотрим на углы в этих треугольниках. Давайте посмотрим на этот угол 𝐸𝑋𝐶 и посмотрим, будет ли угол равный этому
один. Что ж, на самом деле было бы. Есть вертикально противоположный угол, угол 𝐵𝑋𝐹. Таким образом, эти два угла будут равны по размеру.
Теперь посмотрим на угол 𝐸𝐶𝑋. Если учесть, что у нас есть параллельные прямые и, то трансверсаль прямой
𝐶𝐵 даст нам равный угол. Можно сказать, что угол 𝐶𝐵𝐹 равен углу, потому что у нас есть альтернативные
углы.Как мы показали, есть две пары соответствующих углов, равных, тогда
мы показали, что правило AA выполняется. Это означает, что наши два треугольника 𝐶𝐸𝑋 и 𝐵𝐹𝑋 действительно похожи. Итак, давайте вернемся к причине, по которой мы хотели проверить, что эти два треугольника были
аналогично, и это нужно для определения длины отрезка 𝑋𝐵.
В этих похожих треугольниках они будут иметь одинаковую пропорцию между каждой длиной на
меньший треугольник равняется каждой длине большего треугольника.Мы могли бы также подумать об этом с точки зрения нахождения масштабного коэффициента. Чтобы найти этот масштабный коэффициент, нам нужна соответствующая пара длин на
меньший треугольник и на больший треугольник. Теперь нам не дается длина этого отрезка 𝐵𝐹, но мы можем его обработать.
получиться относительно просто. Поскольку нам говорят, что 𝐵 — это середина, тогда длина линии
отрезок 𝐵𝐹 будет такой же, как длина этого отрезка.
Используя тот факт, что в параллелограмме противоположные стороны параллельны и совпадают,
тогда длина 𝐴𝐵 будет равна сумме восьми сантиметров и 16
сантиметры. А это 24 сантиметра. Итак, 𝐵𝐹 тоже 24 сантиметра. Теперь у нас есть пара соответствующих сторон в меньшем треугольнике и в большем треугольнике.
треугольник, который позволит нам вычислить масштабный коэффициент.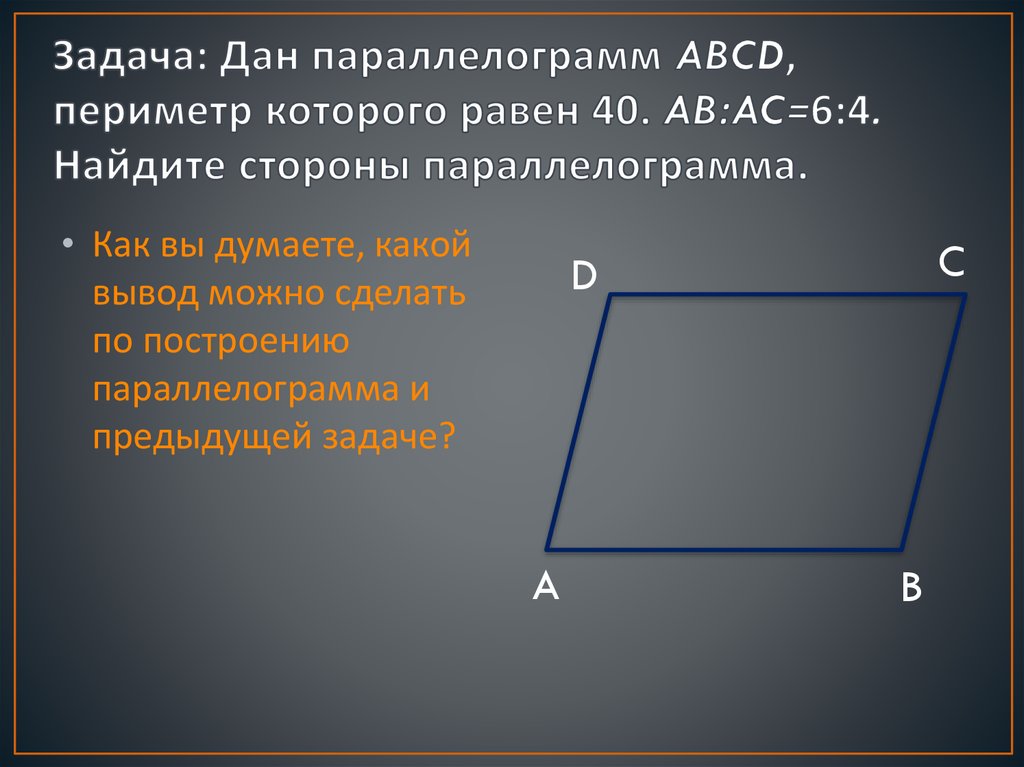 Если 𝐶𝐴 равно восьми сантиметрам, а 𝐵𝐹 — 24 сантиметра, то масштабный коэффициент должен
Если 𝐶𝐴 равно восьми сантиметрам, а 𝐵𝐹 — 24 сантиметра, то масштабный коэффициент должен
быть три. Это означает, что каждую длину меньшего треугольника можно умножить на три, чтобы получить
соответствующей длины на большем треугольнике.
Мы помним, что мы пытаемся найти эту длину отрезка 𝐵𝑋, поэтому
сторона меньшего треугольника соответствовала бы этой длине? Это будет отрезок 𝐶𝑋.Поэтому мы можем взять 𝐶𝑋 из 11 сантиметров и умножить его на масштабный коэффициент
три, чтобы получить длину 33 сантиметра. И, наконец, после всей этой работы мы готовы рассчитать длину
отрезка 𝐴𝐷. Помня, что параллелограмм имеет равные противоположные стороны, мы добавляем 11
сантиметра и 33 сантиметра, что дает нам окончательный ответ, что длина
отрезок 𝐴𝐷 составляет 44 сантиметра.
Parallelogram — математическое определение слова
Parallelogram — математическое определение слова — Math Open Reference
Попробуйте это Перетащите оранжевые точки на каждую вершину
, чтобы изменить форму параллелограмма. Обратите внимание, как противоположные стороны остаются параллельными.
Обратите внимание, как противоположные стороны остаются параллельными.
Параллелограмм — это
четырехугольник с противоположными сторонами
параллельно.
Но есть различные тесты, которые можно применить, чтобы увидеть, является ли что-то параллелограммом.
Это «родитель» некоторых других четырехугольников,
которые получаются добавлением различного рода ограничений:
- Прямоугольник — это параллелограмм, но все четыре внутренних угла фиксированы под углом 90 °
- Ромб — это параллелограмм, у которого все четыре стороны равны по длине
- Квадрат — это параллелограмм, но все стороны равны по длине и
внутренние углы 90 °
Четырехугольник является параллелограммом, если:
- Обе пары противоположных сторон параллельны. (По определению). Или же:
- Обе пары противоположных сторон равны. Если они совпадают, они также должны быть параллельны. Или же:
- Одна пара противоположных сторон равны и параллельны.
 Тогда другая пара также должна быть параллельна.
Тогда другая пара также должна быть параллельна.
Свойства параллелограмма
Эти факты и свойства верны для параллелограммов и форм-потомков: квадрата, прямоугольника и ромба.
| База | Базой можно считать любую сторону.Выбирайте любой понравившийся. Если используется для расчета площади (см. Ниже), необходимо использовать соответствующую высоту. На рисунке выше выбрана одна из четырех возможных баз и соответствующая высота. |
| Высота (высота) | Высота (или высота) параллелограмма — это расстояние по перпендикуляру. от основания на противоположную сторону (которую, возможно, придется удлинить). На рисунке выше показана высота, соответствующая базовому CD. |
| Площадь | Площадь параллелограмма можно найти, умножив основание на соответствующую высоту.См. Также Площадь параллелограмма |
| Периметр | Расстояние вокруг параллелограмма. Сумма его сторон. См. Также Периметр параллелограмма Сумма его сторон. См. Также Периметр параллелограмма |
| Напротив сторон | Противоположные стороны конгруэнтные (равные по длине) и параллельно. Изменяя форму параллелограмма вверху страницы, обратите внимание на то, что противоположные стороны всегда имеют одинаковую длину. |
| Диагонали | Каждая диагональ разрезает другую диагональ на две равные части, как показано на рисунке ниже.Видеть Диагонали параллелограмма для интерактивной демонстрации этого. |
| Интерьер Уголки | Противоположные углы равны, как видно ниже. Последовательные углы всегда являются дополнительными (добавить к 180 °) Подробнее об этих свойствах см. |
Параллелограмм вписанный в любой четырехугольник
Если вы найдете
средние точки
каждой стороны любого
четырехугольник
затем свяжите их последовательно линиями, результат всегда будет
параллелограмм.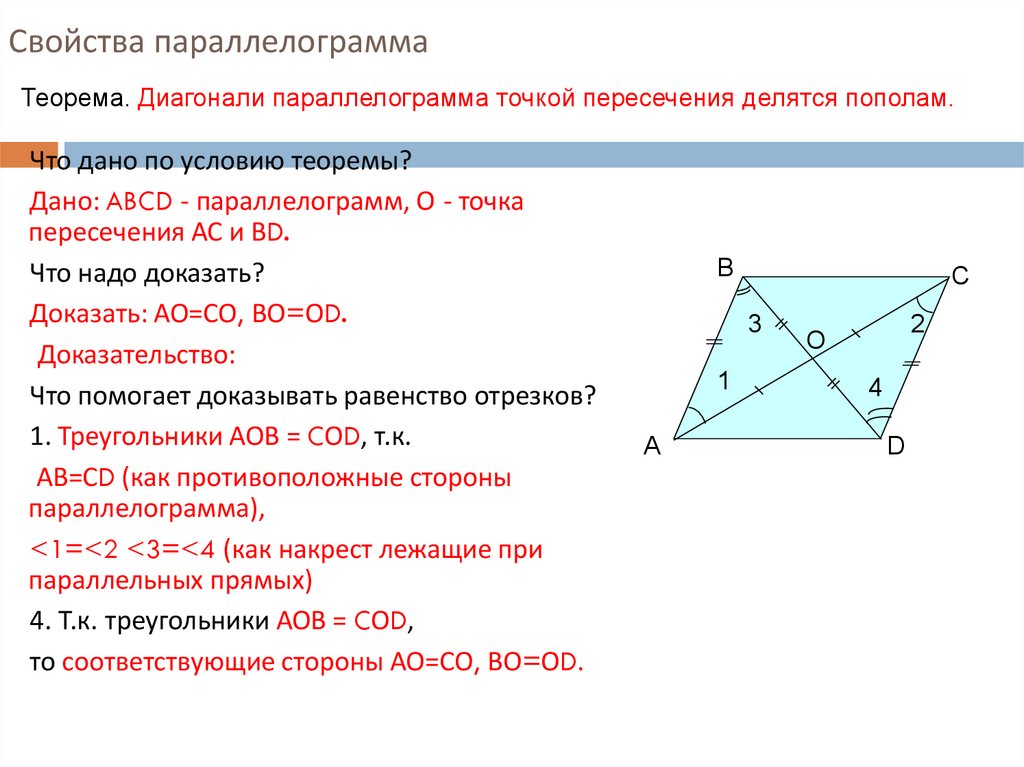
Сначала это может показаться нелогичным, но посмотрите
Параллелограмм вписан в любой четырехугольник
для оживленного исследования этого факта.
Другие темы полигонов
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные многоугольники
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
1.2.2: Основания и высоты параллелограммов
Давайте еще немного исследуем область параллелограммов.
Упражнение \ (\ PageIndex {1} \): параллелограмм и его прямоугольники
Елена и Тайлер находили площадь этого параллелограмма:
Рисунок \ (\ PageIndex {1} \)
Переместите ползунок, чтобы увидеть, как Тайлер это сделал:
Переместите ползунок, чтобы увидеть, как это сделала Елена:
Как совпадают две стратегии определения площади параллелограмма? Чем они разные?
Резюме
- Мы можем выбрать любую из четырех сторон параллелограмма в качестве основания .
 И сторона (сегмент), и его длина (размер) называются основанием.
И сторона (сегмент), и его длина (размер) называются основанием. - Если мы проведем любой перпендикулярный сегмент от точки на основании до противоположной стороны параллелограмма, этот сегмент всегда будет иметь одинаковую длину. Мы называем это значение высотой . Существует бесконечно много сегментов, которые могут представлять высоту!
Рисунок \ (\ PageIndex {6} \): 2 копии одного и того же параллелограмма. Слева база = 6 единиц. Соответствующая высота = 4 единицы. Справа база = 5 единиц.Соответствующая высота = 4,8 единицы. Для обоих показаны 3 разных сегмента, обозначающих высоту.
Вот две копии одного и того же параллелограмма. Слева сторона, являющаяся основанием, имеет длину 6 единиц. Соответствующая высота — 4 единицы. Справа сторона, являющаяся основанием, имеет длину 5 единиц. Соответствующая высота составляет 4,8 единицы. Для обоих показаны три разных сегмента, обозначающих высоту. Мы могли бы привлечь гораздо больше!
Независимо от того, какая сторона выбрана в качестве основания, площадь параллелограмма является произведением этого основания и соответствующей ему высоты. Мы можем это проверить:
Мы можем это проверить:
\ (4 \ times 6 = 24 \ qquad \ text {и} \ qquad 4.8 \ times 5 = 24 \)
Мы можем понять, почему это так, разложив параллелограммы на прямоугольники.
Рисунок \ (\ PageIndex {7} \)
Обратите внимание, что длины сторон каждого прямоугольника являются основанием и высотой параллелограмма. Несмотря на то, что два прямоугольника имеют разные длины сторон, произведения длин сторон равны, поэтому они имеют одинаковую площадь! И оба прямоугольника имеют ту же площадь, что и параллелограмм.
Мы часто используем буквы вместо цифр. Если \ (b \) — основание параллелограмма (в единицах), а \ (h \) — соответствующая высота (в единицах), то площадь параллелограмма (в квадратных единицах) является произведением этих двух чисел. \ (b \ cdot h \)
Обратите внимание, что мы пишем символ умножения с маленькой точки вместо символа \ (\ times \). Это сделано для того, чтобы мы не запутались, означает ли \ (\ times \) умножение или буква \ (x \) заменяет число.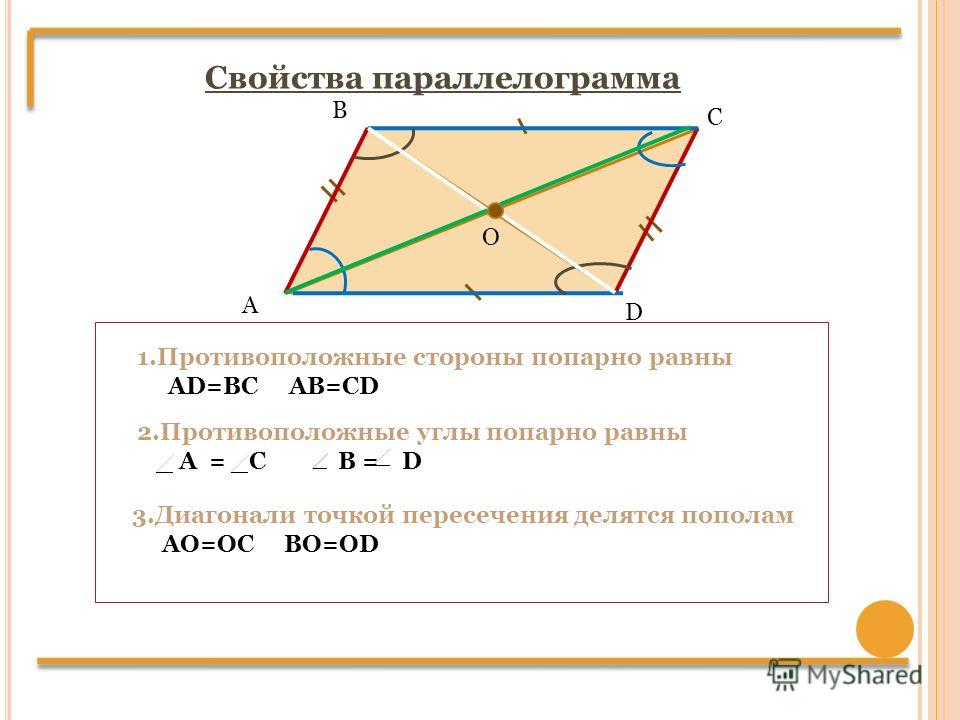
В старшей школе вы сможете доказать, что отрезок перпендикуляра от точки на одной стороне параллелограмма до противоположной стороны всегда будет иметь одинаковую длину.
Рисунок \ (\ PageIndex {8} \)
. Легче всего это увидеть, если нарисовать параллелограмм на миллиметровой бумаге. А пока мы будем использовать это как факт.
Глоссарий
Определение: основание (параллелограмма или треугольника)
В качестве основы фигуры мы можем выбрать любую сторону параллелограмма или треугольника.Иногда мы используем слово base для обозначения длины этой стороны.
Рисунок \ (\ PageIndex {9} \)
Определение: высота (параллелограмма или треугольника)
Высота — это кратчайшее расстояние от основания фигуры до противоположной стороны (для параллелограмма) или противоположной вершины (для треугольника).
Мы можем показать высоту более чем в одном месте, но она всегда будет перпендикулярна выбранному основанию.
Рисунок \ (\ PageIndex {10} \)
Определение: параллелограмм
Параллелограмм — это четырехугольник, у которого две пары параллельных сторон.
Вот два примера параллелограммов.
Рисунок \ (\ PageIndex {11} \): два параллелограмма с указанными углами и длинами сторон. Слева верхняя и нижняя стороны = 5 шт. Левая и правая стороны = 4,24 единицы. Верхний левый и нижний правый углы = 135 градусов. Правый верхний и левый нижний углы = 45 градусов. Справа верхняя и нижняя стороны = 9,34 единицы. Левая и правая стороны = 4 шт. Верхний левый и нижний правый углы = 27,2 градуса. Правый верхний и левый нижний углы = 152,8 градуса.
Определение: Четырехугольник
Четырехугольник — это тип многоугольника с 4 сторонами. Прямоугольник — это пример четырехугольника. Пятиугольник — это не четырехугольник, потому что у него 5 сторон.
.
Как найти стороны параллелограмма? – Обзоры Вики
Отсюда, как найти четвертую сторону параллелограмма? Мы знаем, что противоположные стороны параллелограмма равны между собой. Итак, АВ=CD и ВС=AD. х=9 и у=4. Следовательно, четвертая вершина (9,4).
Итак, АВ=CD и ВС=AD. х=9 и у=4. Следовательно, четвертая вершина (9,4).
Дополнительно Что является основанием параллелограмма? В параллелограмме термин «основание» относится к длина одной стороны и «высота» длины перпендикулярного отрезка между этой стороной и противоположной стороной. Любая сторона параллелограмма может быть основанием.
Какова длина параллелограмма?
Параллелограмм – это плоская фигура, у которой противоположные стороны параллельны и равный по длине. Угол A и угол B в сумме дают 180°, поэтому они являются дополнительными углами. ПРИМЕЧАНИЕ. Квадраты, прямоугольники и ромбы — все это параллелограммы!
Как найти стороны параллелограмма с диагоналями? р2+q2=2(а2+б2)
p и q — длины диагоналей соответственно. х и у — стороны параллелограмма.
х и у — стороны параллелограмма.
Как узнать, какая сторона является основанием? База может быть с любой стороны, а не только нарисованный внизу. Для расчета площади необходимо использовать высоту под прямым углом к выбранной базе. Выбирайте любую удобную сторону в качестве основы. В равнобедренном треугольнике за основу обычно принимается неравная сторона.
Чему равны основание и высота параллелограмма?
Высота параллелограмма. Измерение высоты параллелограмма — это расстояние между противоположными сторонами параллелограмма. … The база определяется как одна из двух выбранных противоположных сторон.
Также Является ли прямоугольник параллелограммом? Это всегда так. Квадраты — это четырехугольники с 4 равными сторонами и 4 прямыми углами, а также у них есть два набора параллельных сторон. Параллелограммы — это четырехугольники с двумя наборами параллельных сторон. … Параллелограмм — это прямоугольник.
Как найти вершины параллелограмма?
Пусть точки (4, 5) (7, 6) (4, 3) (1, 2) представляют собой точки A, B, C и D. Противоположные стороны четырехугольника, образованного данными четырьмя точками, равны. Также диагонали не равны. Следовательно, данные точки образуют параллелограмм.
Противоположные стороны четырехугольника, образованного данными четырьмя точками, равны. Также диагонали не равны. Следовательно, данные точки образуют параллелограмм.
Вершины параллелограмма равны? Параллелограмм (координатная геометрия) Четырехугольник, у которого обе пары противоположных сторон параллельны и конгруэнтны, положение которого на координатной плоскости определяется координатами четыре вершины (углы). … У него все те же свойства, что и у знакомого параллелограмма: противоположные стороны параллельны и конгруэнтны.
Какая диагональ у параллелограмма?
Диагонали параллелограмма равны соединительные отрезки прямых между противоположными вершинами параллелограмма. Используя эту формулу, мы можем определить длину диагоналей, только используя длину сторон и любой из известных углов.
Какая форма представляет собой параллелограмм?
Параллелограмм — это четырехугольник с 2 парами параллельных сторон. На этих фигурах стороны одного цвета параллельны друг другу. Фигура с четырьмя сторонами одинаковой длины. Фигура имеет два набора параллельных сторон и не имеет прямых углов.
Фигура с четырьмя сторонами одинаковой длины. Фигура имеет два набора параллельных сторон и не имеет прямых углов.
Как найти стороны и углы параллелограмма? Это также можно рассчитать по формуле S = (n — 2) × 180 °, где ‘n’ представляет количество сторон в многоугольнике. Здесь «n» = 4. Следовательно, сумма внутренних углов параллелограмма = S = (4 − 2) × 180° = (4 − 2) × 180° = 2 × 180° = 360°.
Чему равны противоположные стороны параллелограмма?
Противоположные стороны параллелограмм равны. Диагонали параллелограмма делят друг друга пополам.
Как найти площадь параллелограмма по сторонам и диагоналям? Площадь параллелограмма можно вычислить, если известны диагонали и угол их пересечения. Формула дается как, площадь = ½ × d1 × d2 sin(x), где «d1» и «d2» — длины диагоналей параллелограмма, а «x» — угол между ними.
Что такое основание треугольника или параллелограмма?
Глоссарий. Мы можем выбрать любая сторона параллелограмма или треугольник, который будет основанием фигуры. Иногда мы используем слово «база» для обозначения длины этой стороны. Высота — это кратчайшее расстояние от основания фигуры до противоположной стороны (для параллелограмма) или противоположной вершины (для треугольника).
Какая сторона является основанием треугольника? Основание – это сторона треугольника, которую считают нижняя, а высота треугольника — это перпендикулярная линия, опущенная на его основание из вершины, противоположной основанию.
Какая сторона является основанием прямоугольного треугольника?
Основание и высота прямоугольного треугольника равны всегда стороны, прилегающие к прямому углу, а гипотенуза — самая длинная сторона.
Может ли любая сторона параллелограмма быть основанием? Любая сторона параллелограмма может быть основанный. Высота может быть нарисована под любым углом к стороне, выбранной в качестве основы.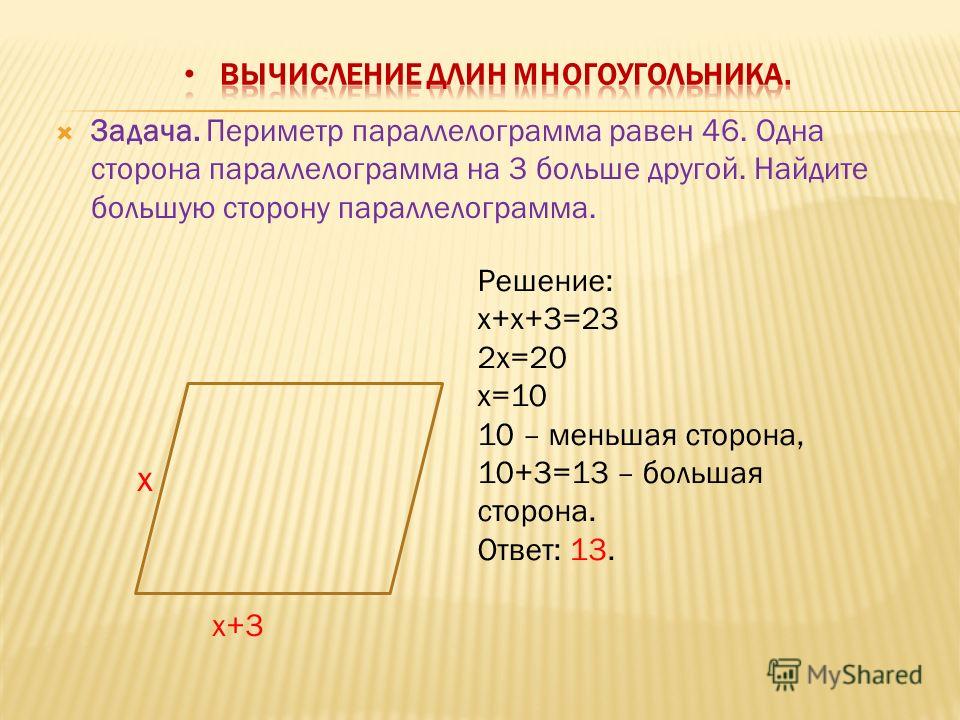 Основание и соответствующая ему высота должны быть перпендикулярны друг другу.
Основание и соответствующая ему высота должны быть перпендикулярны друг другу.
Какая из них является высотой параллелограмма?
Высота параллелограмма равна расстояние по перпендикуляру между основанием и стороной, параллельной основанию параллелограмма.
Как найти длину стороны параллелограмма
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
ACT Math Help » Геометрия » Плоская геометрия » Четырехугольники » Параллелограммы » Как найти длину стороны параллелограмма
Параллелограмм , и .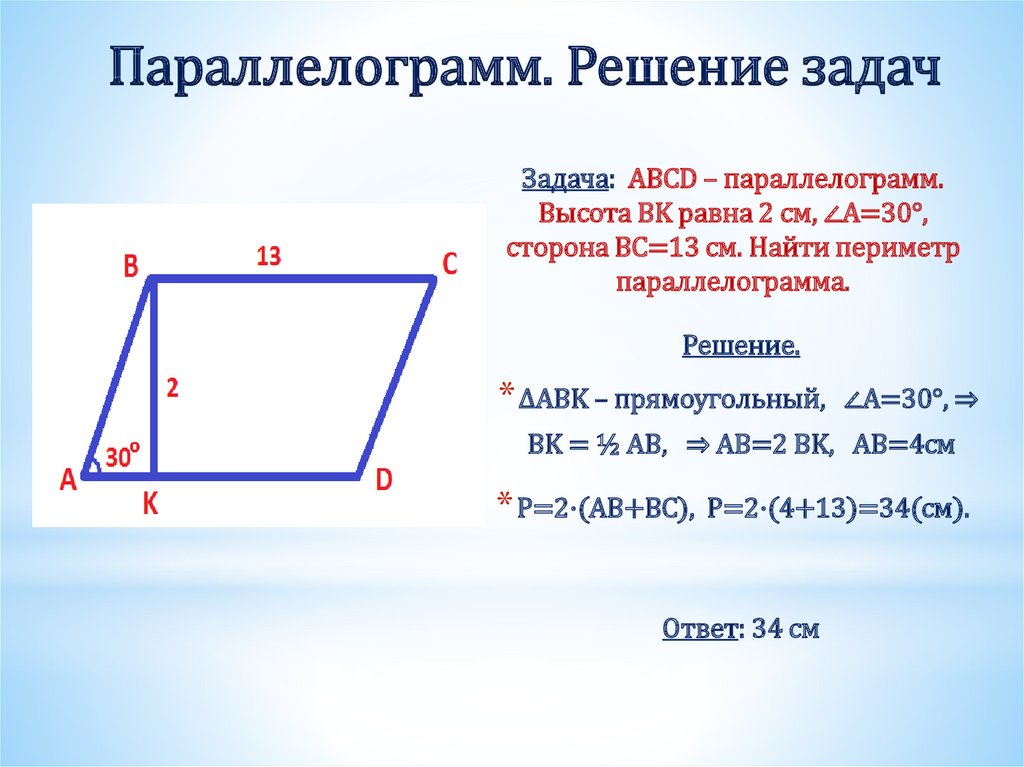 Находить .
Находить .
Возможные ответы:
Недостаточно информации для решения проблемы.
Правильный ответ:
Пояснение:
В параллелограмме противоположные стороны равны. Таким образом,
Сообщить об ошибке
В параллелограмме , и . Находить .
Возможные ответы:
Недостаточно информации для решения проблемы.
Правильный ответ:
Пояснение:
В параллелограмме противоположные стороны равны.
Сообщить об ошибке
Параллелограмм имеет площадь . Если , найдите .
Возможные ответы:
Недостаточно информации для решения проблемы.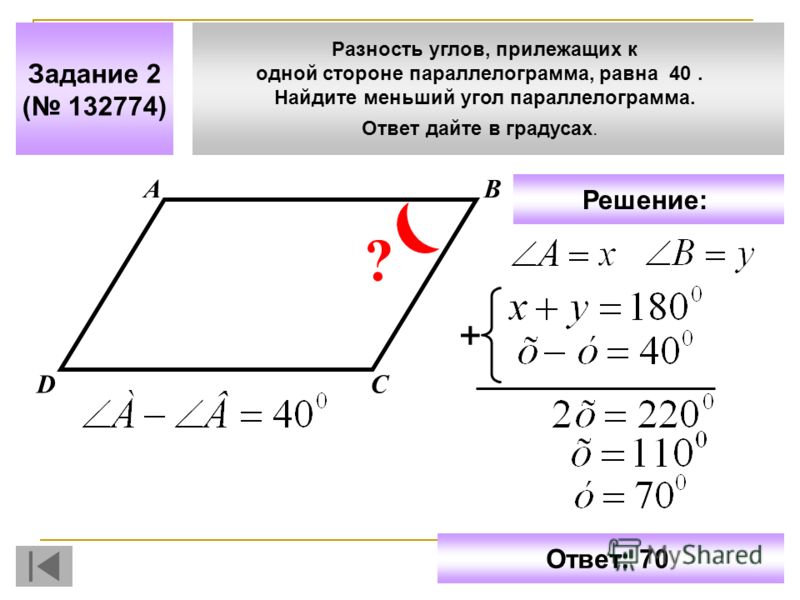
Правильный ответ:
Объяснение:
Площадь параллелограмма определяется как:
В этой задаче высота определяется как , а площадь . Оба и являются базами.
Сообщить об ошибке
является параллелограммом. Находить .
Возможные ответы:
Недостаточно информации для решения проблемы.
Правильный ответ:
Объяснение:
это гипотенуза прямоугольного треугольника, образованного, когда мы рисуем высоту параллелограмма. Поскольку это прямоугольный треугольник, мы можем использовать SOH CAH TOA для нахождения . Что касается , мы знаем противоположную сторону треугольника и ищем гипотенузу. Таким образом, мы можем использовать функцию синуса для решения .
Таким образом, мы можем использовать функцию синуса для решения .
Сообщить об ошибке
Найдите длину основания параллелограмма высотой и площадью .
Возможные ответы:
Правильный ответ:
Объяснение:
Формула площади параллелограмма:
Подставив данные значения, мы получим:
Сообщить об ошибке
– параллелограмм площадью . Находить .
Возможные ответы:
Недостаточно информации для решения проблемы.
Правильный ответ:
Объяснение:
Чтобы найти , мы должны сначала найти . Формула площади параллелограмма:
Формула площади параллелограмма:
Нам дана площадь и основание.
Теперь мы можем использовать тригонометрию для решения . Что касается , мы знаем противоположную сторону прямоугольного треугольника и ищем гипотенузу. Таким образом, мы можем использовать функцию синуса.
Сообщить об ошибке.
Посмотреть ACT Репетиторы по математике
Мехак
Сертифицированный преподаватель
Университет Гуру Нанак Дев, бакалавр наук, химия. Университет Гуру Нанак Дев, магистр химии.
Просмотр ACT Репетиторы по математике
Чарльз
Сертифицированный репетитор
Университет Северной Алабамы, бакалавр наук, химия. Университет Вандербильта, доктор философии, органическая химия.
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Учитесь по концепции
Вопрос Видео: Нахождение длины стороны параллелограмма по подобию треугольников
Стенограмма видео
Учитывая, что 𝐴𝐵𝐶𝐷 — параллелограмм, 𝐵 — середина отрезка 𝐴𝐹, 𝐶𝐸
равно восьми сантиметрам, 𝐷𝐸 равно 16 сантиметрам, а 𝐶𝑋 равно 11
см, найдите длину отрезка 𝐴𝐷.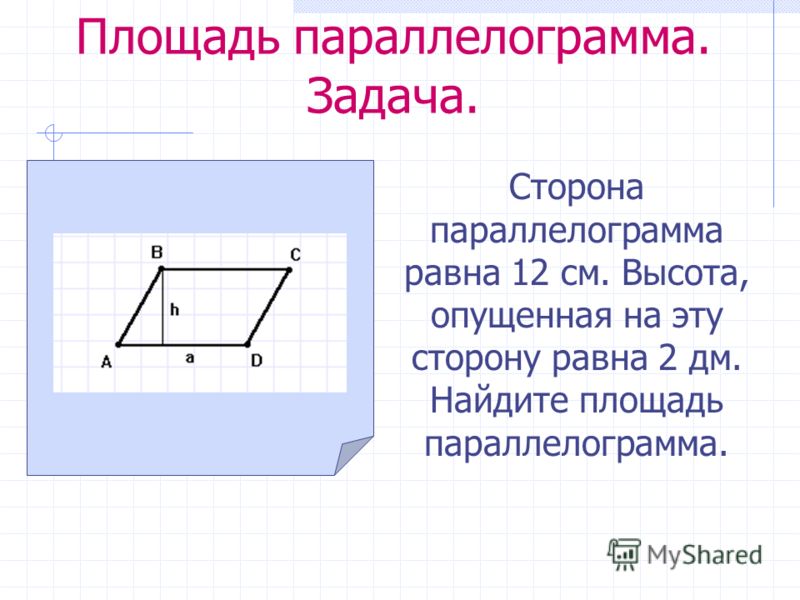
В этом вопросе нам сначала говорят, что 𝐴𝐵𝐶𝐷 — параллелограмм. Это четырехугольник в верхней части этой фигуры. Одно из основных свойств, которое мы должны помнить о параллелограммах, заключается в том, что противоположные стороны параллельны. На рисунке это будет означать, что линия 𝐷𝐴 параллельна линии 𝐶𝐵 и линии 𝐶𝐷 параллелен 𝐵𝐴. Следующее, что нам говорят, это то, что 𝐵 — это середина отрезка 𝐴𝐹. И нам даны измерения, что 𝐶𝐴 это восемь сантиметров, 𝐷𝐴 это 16 сантиметров, а 𝐶𝑋 равно 11 сантиметрам, поэтому мы можем заполнить эти измерения на схему.
Вопрос просит нас найти длину этого отрезка 𝐴𝐷. Чтобы разобраться в этом, нам следует вспомнить еще один важный факт об обратном.
стороны в параллелограмме. Мы знаем, что они параллельны, но мы также должны помнить, что противоположные стороны
конгруэнтный. Это значит, что они одинаковой длины. Следовательно, если нам нужна длина стороны, противоположной 𝐴𝐷, длина линии
отрезок 𝐶𝐵, то мы знали бы, что он будет такой же длины. Приведенная здесь длина 11 сантиметров относится только к отрезку линии.
𝐶𝑋, а не всему отрезку 𝐶𝐵. Итак, давайте посмотрим, есть ли способ вычислить этот отрезок 𝑋𝐵.
Приведенная здесь длина 11 сантиметров относится только к отрезку линии.
𝐶𝑋, а не всему отрезку 𝐶𝐵. Итак, давайте посмотрим, есть ли способ вычислить этот отрезок 𝑋𝐵.
Давайте рассмотрим эти два треугольника. У нас есть меньший треугольник 𝐶𝐸𝑋 и больший треугольник 𝐵𝐹𝑋. Затем мы могли бы спросить себя, подобны ли эти два треугольника. Это означает, что они будут одинаковой формы, но разного размера. Один из способов, которым мы можем доказать подобие в треугольниках, — это использовать критерий АА в что мы видим, если есть две пары соответствующих пар углов конгруэнтны. Итак, давайте проверим углы в этих треугольниках. Давайте посмотрим на этот угол 𝐸𝑋𝐶 и посмотрим, есть ли угол, равный этому один. Ну, на самом деле, было бы. Есть вертикально противоположный угол, угол 𝐵𝑋𝐹. Таким образом, эти два угла будут равны по величине.
Теперь посмотрим на угол 𝐸𝐶𝑋. Если учесть, что у нас есть параллельные прямые 𝐷𝐶 и 𝐴𝐹, то секущая
𝐶𝐵 даст нам равный угол.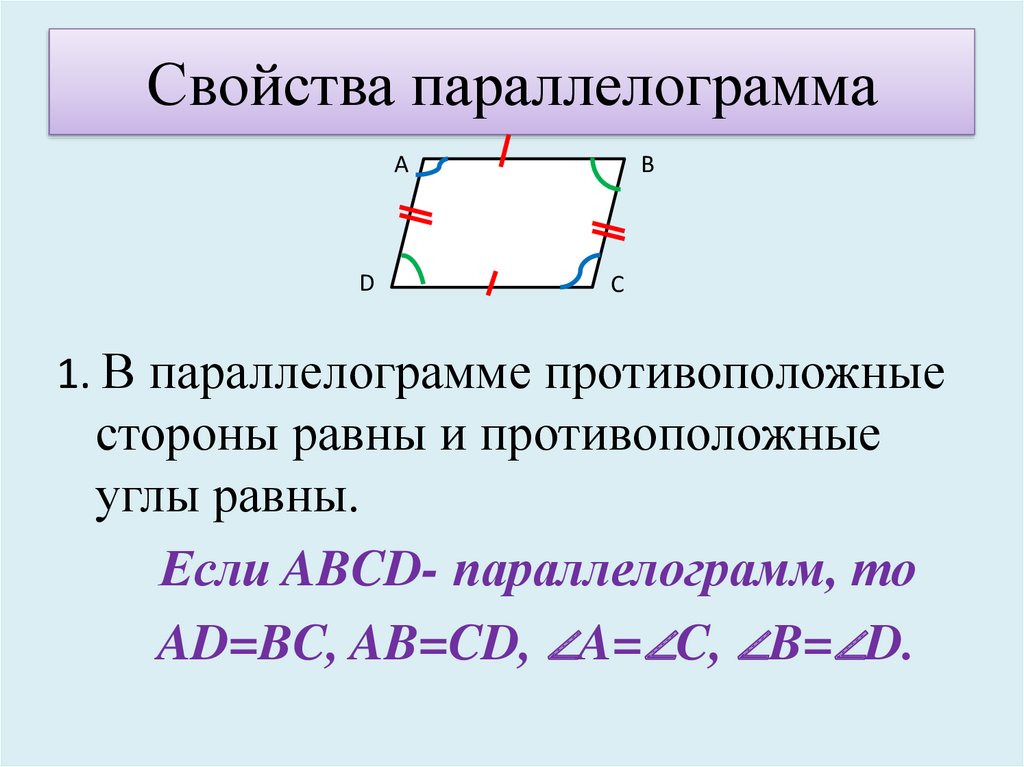 Мы можем сказать, что угол 𝐶𝐵𝐹 равен углу 𝐴𝐶𝑋, потому что у нас есть альтернативные
углы. Поскольку мы показали, что существуют две пары соответствующих углов, равных, то
мы показали, что правило АА выполняется. Это означает, что наши два треугольника, 𝐶𝐸𝑋 и 𝐵𝐹𝑋, действительно подобны. Итак, вернемся к причине, по которой мы хотели проверить, что эти два треугольника
аналогично, и это нужно, чтобы найти длину отрезка 𝑋𝐵.
Мы можем сказать, что угол 𝐶𝐵𝐹 равен углу 𝐴𝐶𝑋, потому что у нас есть альтернативные
углы. Поскольку мы показали, что существуют две пары соответствующих углов, равных, то
мы показали, что правило АА выполняется. Это означает, что наши два треугольника, 𝐶𝐸𝑋 и 𝐵𝐹𝑋, действительно подобны. Итак, вернемся к причине, по которой мы хотели проверить, что эти два треугольника
аналогично, и это нужно, чтобы найти длину отрезка 𝑋𝐵.
В этих подобных треугольниках они будут иметь одинаковую пропорцию между каждой длиной на
меньшего треугольника к каждой длине большего треугольника. Мы могли бы также думать об этом с точки зрения нахождения коэффициента масштабирования. Чтобы найти этот масштабный коэффициент, нам нужна соответствующая пара длин на
меньшем треугольнике и на большем треугольнике. Теперь нам не известна длина этого отрезка 𝐵𝐹, но мы на самом деле можем его вычислить.
выходит относительно просто.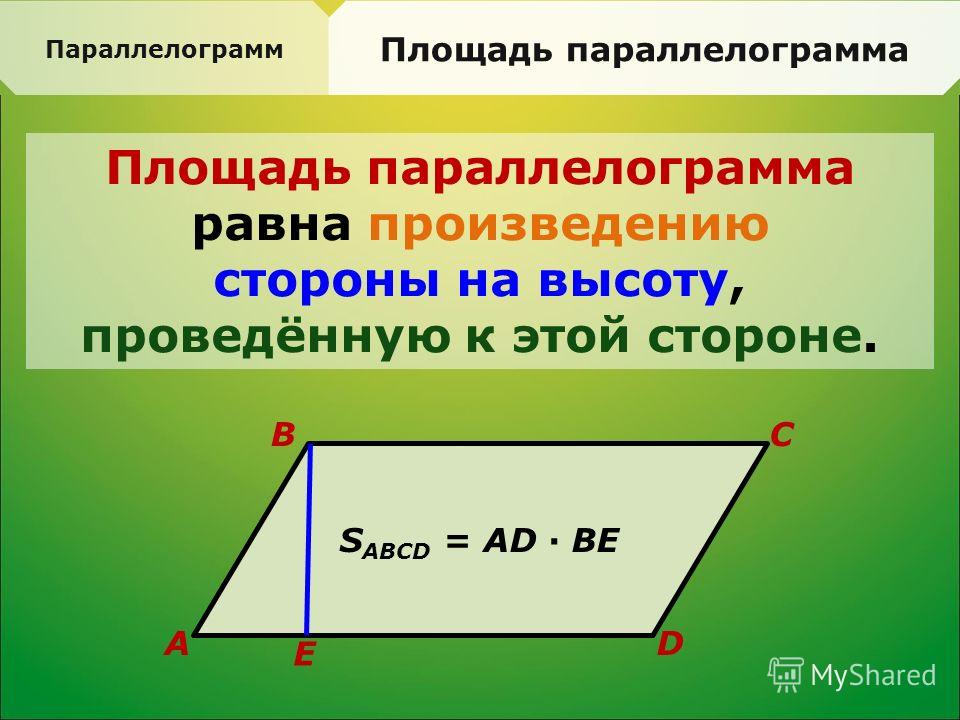 Поскольку нам сказали, что 𝐵 — это середина 𝐴𝐹, то длина линии
отрезок 𝐵𝐹 будет такой же, как длина этого отрезка 𝐴𝐵.
Поскольку нам сказали, что 𝐵 — это середина 𝐴𝐹, то длина линии
отрезок 𝐵𝐹 будет такой же, как длина этого отрезка 𝐴𝐵.
Используя тот факт, что в параллелограмме противоположные стороны параллельны и конгруэнтны, то длина 𝐴𝐵 будет равна сумме восьми сантиметров и 16 сантиметры. А это 24 сантиметра. Итак, 𝐵𝐹 тоже 24 сантиметра. Теперь у нас есть пара соответствующих сторон в меньшем треугольнике и в большем. треугольник, который позволил бы нам определить коэффициент масштабирования. Если 𝐶𝐴 равно восьми сантиметрам, а 𝐵𝐹 равно 24 сантиметрам, то масштабный коэффициент должен быть три. Это означает, что каждую длину меньшего треугольника можно умножить на три, чтобы получить соответствующую длину на большем треугольнике.
Мы помним, что пытаемся найти эту длину отрезка 𝐵𝑋, так что
сторона меньшего треугольника будет соответствовать этой длине? Это будет вот этот, отрезок 𝐶𝑋. Поэтому мы можем взять 𝐶𝑋, равное 11 сантиметрам, и умножить его на масштабный коэффициент
три, чтобы получить длину 33 сантиметра. И, наконец, после всей этой работы мы почти готовы вычислить длину
отрезка 𝐴𝐷. Вспоминая, что у параллелограмма противоположные стороны конгруэнтны, прибавляем 11.
сантиметров и 33 сантиметра, что дает нам окончательный ответ, что длина
Отрезок 𝐴𝐷 равен 44 сантиметрам.
Поэтому мы можем взять 𝐶𝑋, равное 11 сантиметрам, и умножить его на масштабный коэффициент
три, чтобы получить длину 33 сантиметра. И, наконец, после всей этой работы мы почти готовы вычислить длину
отрезка 𝐴𝐷. Вспоминая, что у параллелограмма противоположные стороны конгруэнтны, прибавляем 11.
сантиметров и 33 сантиметра, что дает нам окончательный ответ, что длина
Отрезок 𝐴𝐷 равен 44 сантиметрам.
Решатель геометрических задач — Параллелограмм
Решатель геометрических задач
Параллелограмм
| параллелограмм |
Они дают треки, некоторые задачи могут быть решены автоматически, числовые значения не имеют значения в различных примерах.
Дорожка 1
Длина основания параллелограмма 20 см, высота 15 см. Вычислите площадь параллелограмма.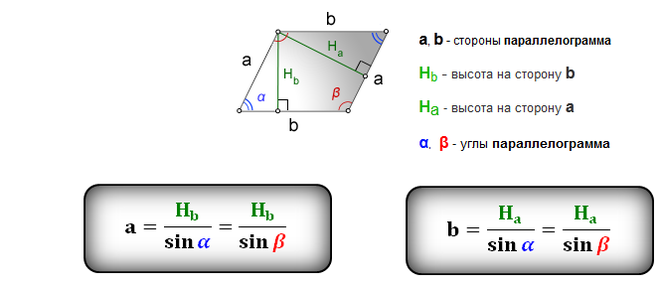
Дорожка 2
Длина основания параллелограмма 20 см , а площадь 300 см . Вычислите высоту параллелограмма.
Дорожка 3
Высота параллелограмма 15 см , а площадь 300 см . Вычисляет основание параллелограмма.
Дорожка 4
Угол параллелограмма равен 120 . Вычислите размер остальных трех углов.
Дорожка 5
Высота параллелограмма равна тройке основания; их сумма равна 60 см. Вычислите площадь параллелограмма.
Дорожка 6
Две последовательные стороны параллелограмма составляют одну из трех пятых другой, и их разница составляет 150 сантиметров. Вычислите периметр параллелограмма.
Дорожка 7
Параллелограмм и треугольник эквивалентны. Гипотенуза треугольника равна 50 см, а короткие стороны соответственно 3/5 и 4/5 гипотенузы. Вычислите высоту параллелограмма, зная, что его основание равно гипотенузе, удвоенной высоте треугольника.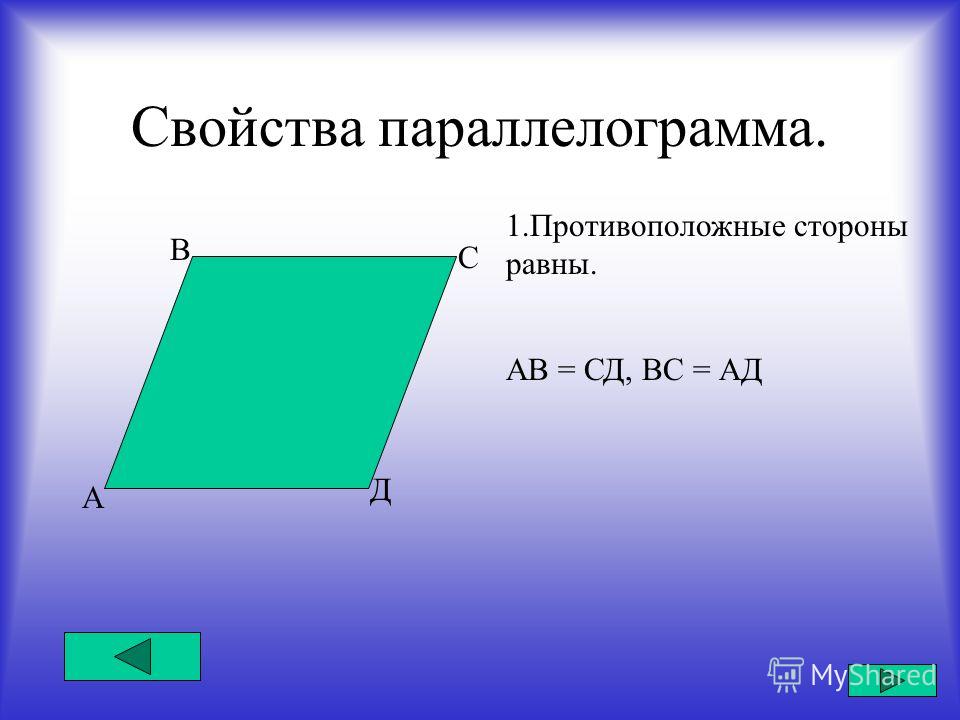
Дорожка 8
Периметр параллелограмма равен 128 см , а его площадь равна 1440 см . Зная, что две последовательные стороны составляют одну 3/5 другой, вычисляет площадь прямоугольника, имеющего размеры, конгруэнтные двум высотам параллелограмма.
Направляющая 9
Параллелограмм имеет площадь 1500 см , а основание составляет 5/3 высоты относительно него. Вычислите меру основания и высоту относительно него.
Путь 10
Площадь параллелограмма 3150 м, сумма двух высот 105 м и одна из них составляет 3/4 другой. Вычислите периметр параллелограмма.
Дорожка 11
Периметр параллелограмма равен 400 см, а одна сторона равна 3/5 его ряда. Вычислите периметр и площадь равностороннего треугольника с длиной стороны, равной большей стороне параллелограмма.
Дорожка 12
Разница между двумя соседними сторонами параллелограмма составляет 10 см. Вычислите длину сторон, зная, что периметр равен 120 см.
Вычислите длину сторон, зная, что периметр равен 120 см.
Дорожка 13
Параллелограмм имеет основание 60 дм, высоту 30 дм, угол 45 градусов. Вычислите периметр и площадь.
Дорожка 14
В параллелограмме разность амплитуд двух углов, примыкающих к одной стороне, равна 2920\’30\». Вычислите величину каждого угла.
Дорожка 15
В параллелограмме диагональ и нижняя наклонная сторона перпендикулярны друг другу. Нижняя диагональ 24 см, а косая сторона 18 см. Вычислите периметр и площадь параллелограмма.
Дорожка 16
Вычислите площадь параллелограмма, зная, что высота равна 3/5 основания, а их разность составляет 20 см.
Дорожка 17
Вычислите площадь параллелограмма, зная, что размер 15 см и высота 3/5 относительного основания.
Дорожка 18
Вычислите площадь параллелограмма, зная, что сумма основания и высоты равна 80 дм, а основание составляет 5/3 высоты.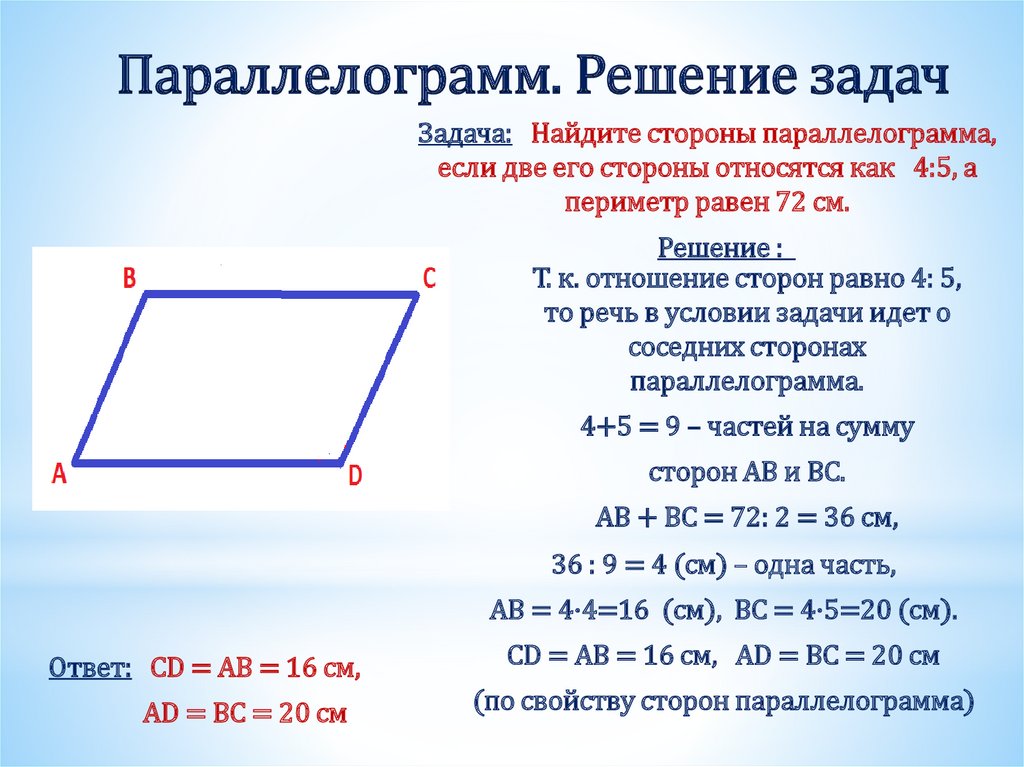
Путь 19
Зная, что основание параллелограмма равно 50 м, а его высота равна его 3/5, вычисляет площадь параллелограмма.
Дорожка 20
Вычислите размер периметра параллелограмма площадью 1200 см, зная, что его высоты равны 50 см и 30 см.
Дорожка 21
Сторона квадрата равна большей стороне параллелограмма с периметром 160 см и стороной, равной 5/3 его ряда. Вычислите периметр квадрата.
Дорожка 22
Основание параллелограмма равно 30 дм и 3/5 части, относящейся к нему. Вычисляет площадь.
Дорожка 23
Две высоты параллелограмма 30,4 см и 24 см . Зная, что сторона наименьшей высоты имеет длину 38 см, вычислите меру другой стороны и периметр.
Дорожка 24
В параллелограмме одна сторона составляет 3/5 его ряда. Зная, что его периметр равен 4/7 периметра параллелограмма с длинными сторонами соответственно 100 см и 40 см, вычисляет протяженность сторон первого параллелограмма
Путь 25
160 см и одна сторона составляет 3/5 своего ряда.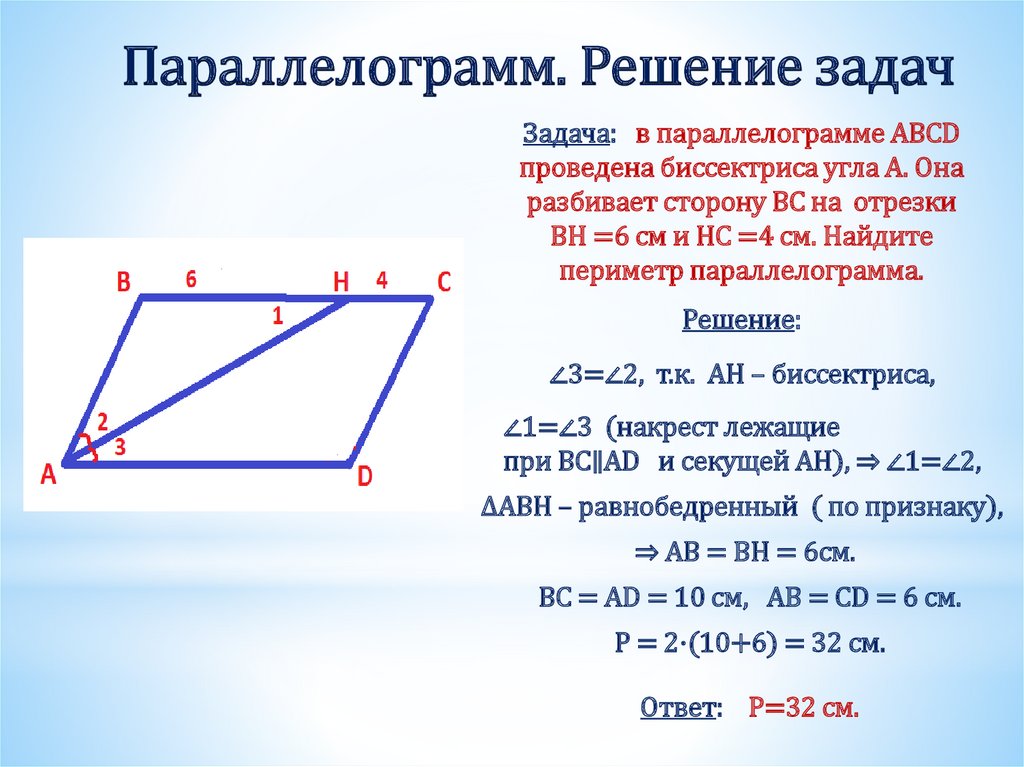 Вычислите две стороны.
Вычислите две стороны.
Дорожка 26
Площадь параллелограмма 800 см, острый угол А равен 45, а высота DH на стороне АВ равна 10 см. Вычисляет длины сторон, периметр и другие высоты параллелограмма.
Дорожка 27
Периметр параллелограмма равен 260 см, а одна сторона равна 5/8 другой. Зная, что высота относительно большей стороны равна 48 см, можно вычислить площадь и протяженность малой диагонали параллелограмма.
Дорожка 28
Одна сторона параллелограмма равна 50 см, а относительная высота равна 20 см. Вычислите меру другой стороны и периметра, зная, что высота, к которой она относится, равна 25 см.
Дорожка 29
Вычислите высоту прямоугольного участка площадью 1000 см, зная, что две последовательные стороны равны 50 см и 40 см.
Дорожка 30
Две последовательные стороны параллелограмма равны 40 см и 50 см . Если относительная высота до большей стороны равна 20 см, как мера относительной высоты до второй стороны?
Если относительная высота до большей стороны равна 20 см, как мера относительной высоты до второй стороны?
Направляющая 31
Меньшая сторона параллелограмма с периметром 160 см равна 30 см. Вычислите его площадь, зная, что высота по большей стороне равна 20 см
Дорожка 32
Площадь ромба равна 864 см, а диагональ равна 4/3 другого. Вычислите площадь параллелограмма, основание и высота которого соответственно равны 25/24 и 15/24 наибольшей диагонали ромба, периметр квадрата равен 16/15 параллелограмма.
Путь 33
Периметр параллелограмма равен 220 м, одна сторона равна 50 м, а его высота равна его 3/5. Вычислите:
площадь параллелограмма ;
измерение высоты с другой стороны;
периметр квадрата равен 9/15 части параллелограмма;
периметр прямоугольника высотой 20 м, эквивалентного двойному параллелограмму.
Направляющая 34
В параллелограмме ABCD высота и нижняя диагональ равны 24 см и 30 см соответственно.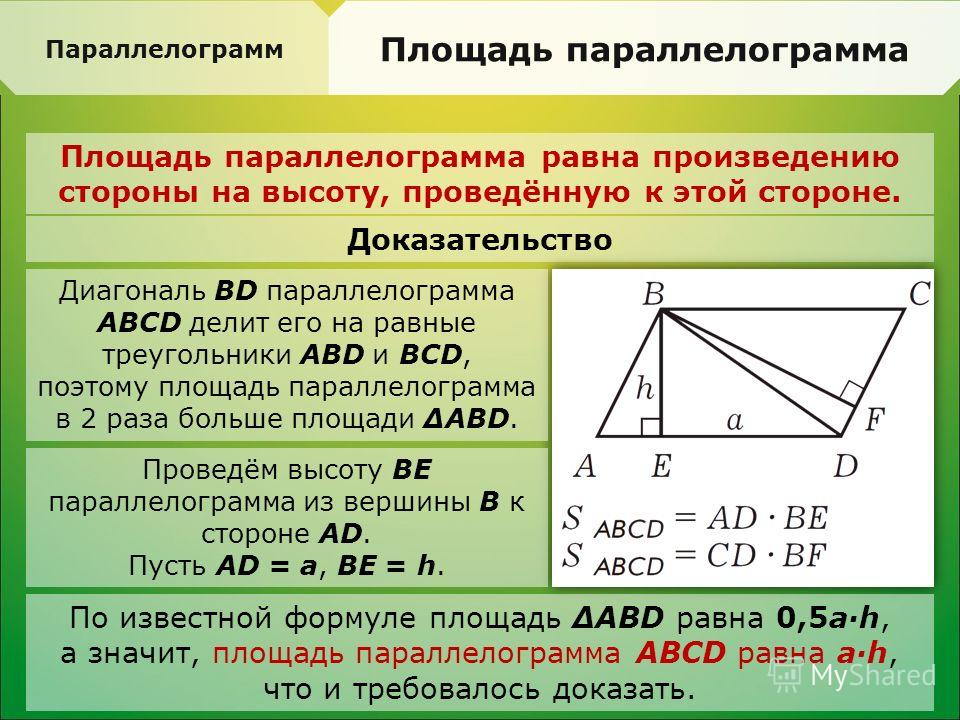 Зная, что каждый острый угол равен 30, вычислите периметр и площадь параллелограмма.
Зная, что каждый острый угол равен 30, вычислите периметр и площадь параллелограмма.
Дорожка 35
Вычисляет длину нижней диагонали и длину ее проекции на основе параллелограмма, зная, что первая из них перпендикулярна наклонной стороне, что периметр параллелограмма равен 96 см и что основание больше стороны 12 см.
Дорожка 36
Вычисляет периметр квадрата, эквивалентного параллелограмму с периметром 210 см, наклонной стороной 25 см и высотой 20 см.
Дорожка 37
Параллелограмм и треугольник имеют длинные основания 50 см и 40 см соответственно. Если две фигуры имеют одинаковую площадь и высота параллелограмма равна 30 см, вычисляется высота треугольника.
Путь 38
В параллелограмме основание в три раза больше высоты относительно него, а площадь равна 7500 м , сторона квадрата равна удвоенной разнице между основанием и высотой параллелограмма вычислить периметр и площадь кв.
Дорожка 39
Параллелограмм имеет основание 40 см и высоту 3/5 основания . Вычислите периметр прямоугольника, конгруэнтного параллелограмму, зная, что его основание вдвое больше основания параллелограмма.
Дорожка 40
Параллелограмм имеет основание 40 см и высоту 3/5 основания. Вычислите периметр прямоугольника, подобного параллелограмму, зная, что его основание равно 50 см.
Дорожка 41
Основание параллелограмма равно 40 см, а наклонная сторона равна 20 см. Вычислите периметр.
Дорожка 42
Параллелограмм имеет основание 40 см и площадь 800 см . Вычислите высоту.
Дорожка 43
Параллелограмм имеет высоту 20 см и площадь 800 см . Вычисляет базу.
Дорожка 44
Периметр параллелограмма 260 см, а наклонная сторона 50 см. Вычисляет базу.
Дорожка 45
Периметр параллелограмма 260 см, а основание 80 см.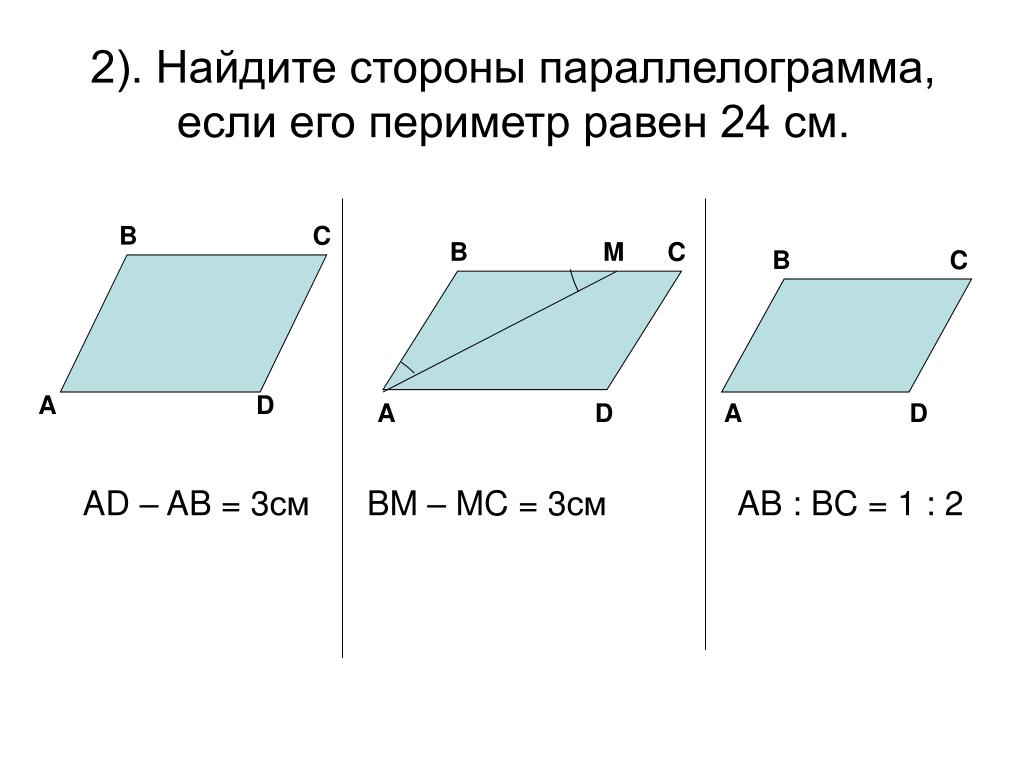



 Тогда другая пара также должна быть параллельна.
Тогда другая пара также должна быть параллельна.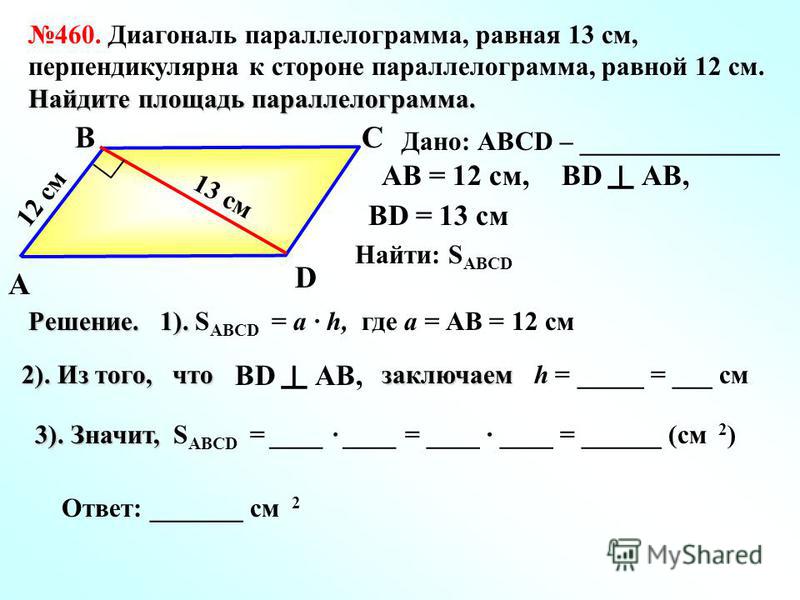 И сторона (сегмент), и его длина (размер) называются основанием.
И сторона (сегмент), и его длина (размер) называются основанием.