Даны комплексные числа z1=2+3i и z2=3-2i. Бесплатный доступ к контрольной работе
Даны комплексные числа z1=2+3i и z2=3-2i.docЗарегистрируйся в два клика и получи неограниченный доступ к материалам, а также промокод на новый заказ в Автор24. Это бесплатно.
Условие
Даны комплексные числа z1=2+3i и z2=3-2i. Вычислить z1+z2, z1-z2, z1∙z2, z1∙z2,z1z2, z1+z22.
Решение
Z1+z2=2+3i+3-2i=5+i; z1-z2=2+3i-3-2i=-1+5i; z1∙z2=2+3i∙3-2i=2∙3+3i∙3-2i∙2-2i∙3i= =6+9i-4i-6∙-1=12+5i; z1∙z2=2+3i∙3+2i=2∙3+3i∙3+2i∙2+2i∙3i= =6+9i+4i+6∙-1=13i; z1z2=2+3i3-2i=2+3i∙3+2i3-2i∙3+2i=13i32-2i2=13i9—4=13i13=i; z1+z22=5+i2=52+2∙5∙i+i2=25+10∙i-1=24+10i.
Зарегистрируйся, чтобы продолжить изучение работы
и получи доступ ко всей экосистеме Автор24
Больше контрольных работ по высшей математике:
Все Контрольные работы по высшей математике
Закажи контрольную работу
Наш проект является банком работ по всем школьным и студенческим предметам. Если вы не хотите
тратить
время на написание работ по ненужным предметам или ищете шаблон для своей работы —
он есть у нас.
Если вы не хотите
тратить
время на написание работ по ненужным предметам или ищете шаблон для своей работы —
он есть у нас.
Не нашел ответ на свой вопрос?
Опиши, с чем тебе нужна помощь. Эксперты Автор24 бесплатно ответят тебе в течение часа
Выбери предметАвиационная и ракетно-космическая техникаАвтоматизация технологических процессовАвтоматика и управлениеАгрохимия и агропочвоведениеАктерское мастерствоАнализ хозяйственной деятельностиАнглийский языкАнтикризисное управлениеАрхеологияАрхитектура и строительствоАстрономияБазы данныхБанковское делоБезопасность жизнедеятельностиБиблиотечно-информационная деятельностьБизнес-планированиеБиологияБиотехнологияБухгалтерский учет и аудитВетеринарияВнешнеэкономическая деятельностьВодные биоресурсы и аквакультураВоенное делоВоспроизводство и переработка лесных ресурсовВысшая математикаГеографияГеодезияГеологияГеометрияГидравликаГидрометеорологияГостиничное делоГосударственное и муниципальное управлениеДеловой этикетДеньгиДетали машинДизайнДокументоведение и архивоведениеЕстествознаниеЖелезнодорожный транспортЖурналистикаЗемлеустройство и кадастрИздательское делоИнвестицииИнженерные сети и оборудованиеИнновационный менеджментИнформатикаИнформационная безопасностьИнформационные технологииИскусствоИсторияКартография и геоинформатикаКитайский языкКонфликтологияКраеведениеКредитКриминалистикаКулинарияКультурологияЛитератураЛогикаЛогистикаМаркетингМатериаловедениеМашиностроениеМедицинаМеждународные отношенияМеждународные рынкиМенеджментМенеджмент организацииМеталлургияМетрологияМеханикаМикро-, макроэкономикаМикропроцессорная техникаМорская техникаМузыкаНалогиНаноинженерияНачертательная геометрияНемецкий языкНефтегазовое делоОрганизационное развитиеПарикмахерское искусствоПедагогикаПожарная безопасностьПолиграфияПолитологияПочвоведениеПраво и юриспруденцияПриборостроение и оптотехникаПриродообустройство и водопользованиеПрограммированиеПроизводственный маркетинг и менеджментПромышленный маркетинг и менеджментПроцессы и аппаратыПсихологияРабота на компьютереРадиофизикаРежиссураРеклама и PRРелигияРусский языкРынок ценных бумагСадоводствоСварка и сварочное производствоСвязи с общественностьюСельское и рыбное хозяйствоСервисСопротивление материаловСоциальная работаСоциологияСтандартизацияСтатистикаСтрановедениеСтратегический менеджментСтрахованиеТаможенное делоТеатроведениеТекстильная промышленностьТелевидениеТеоретическая механикаТеория вероятностейТеория игрТеория машин и механизмовТеория управленияТеплоэнергетика и теплотехникаТехнологические машины и оборудованиеТехнология продовольственных продуктов и товаровТовароведениеТорговое делоТранспортные средстваТуризмУправление качествомУправление персоналомУправление проектамиФармацияФизикаФизическая культураФилософияФинансовый менеджментФинансыФранцузский языкХимияХирургияХолодильная техникаЦенообразование и оценка бизнесаЧертежиЧерчениеЭкологияЭконометрикаЭкономикаЭкономика предприятияЭкономика трудаЭкономическая теорияЭкономический анализЭлектроника, электротехника, радиотехникаЭнергетическое машиностроениеЭтикаЯдерная энергетика и теплофизикаЯдерные физика и технологииЯзыки (переводы)Языкознание и филологияEVIEWSSPSSSTATAДругоеТвой вопрос отправлен
Скоро мы пришлем ответ экпертов Автор24 тебе на почту
Помощь эксперта
Нужна помощь по теме или написание схожей работы?
Свяжись напрямую с автором и обсуди заказ.
5
svetakha
Высшая математика 691 заказ
Отправить письмо схожим авторам, которые сейчас на сайте
Регистрация прошла успешно!
Теперь вам доступен полный фрагмент работы, а также
открыт доступ ко всем сервисам
экосистемы
Введи почту
Зарегистрируйся через почту и получи неограниченный доступ к материалам. Это бесплатно.
Читать тексты на сайте можно без ограничений. Однако для копирования и использования работ нужно зарегистрироваться в экосистеме Автор24. Это бесплатно.404 Cтраница не найдена
Размер:
AAA
Изображения
Вкл. Выкл.
Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «КОМПЛЕКСНЫЕ ЧИСЛА» в 11 классе | Тест по алгебре (11 класс) на тему:
Опубликовано 24. 03.2015 — 9:44 — БУРМИСТРОВА ЕЛЕНА ЮРЬЕВНА
03.2015 — 9:44 — БУРМИСТРОВА ЕЛЕНА ЮРЬЕВНА
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «КОМПЛЕКСНЫЕ ЧИСЛА»
Скачать:
Реклама
Подтяните оценки и знания с репетитором Учи.ру
За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Вводный урок бесплатно, онлайн, 30 минут
Записаться >
Предварительный просмотр:
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «КОМПЛЕКСНЫЕ ЧИСЛА» ВАРИАНТ 1
Вычислите: а); б) ; в) ; г) ; д) ; е) .
а) -3; б) -i; в) 1 + i; г).
z=.
а) ; б) | КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «КОМПЛЕКСНЫЕ ЧИСЛА» ВАРИАНТ 2
Вычислите: а); б) ; в) ; г) ; д) ; е) .
а) -4; б) i; в) 1- i; г).
.
а) ; б) |
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «КОМПЛЕКСНЫЕ ЧИСЛА» ВАРИАНТ 1
Вычислите: а); б) ; в) ; г) ; д) ; е) .
а) -3; б) -i; в) 1 + i; г).
z=.
а) ; б) | КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «КОМПЛЕКСНЫЕ ЧИСЛА» ВАРИАНТ 2
Вычислите: а); б) ; в) ; г) ; д) ; е) .
а) -4; б) i; в) 1- i; г).
.
а) ; б) |
По теме: методические разработки, презентации и конспекты
Контрольная работа по теме «Модуль числа. Действия с рациональными числами» (6 класс)
Контрольная работа по теме «Модуль числа. Действия с рациональными числами» (6 класс)…
Контрольная работа по теме «Комплексные числа» 11 класс. профильный уровень
Контрльная работа по теме «комплексные числа» для профильного 11 класса. …
…
контрольная работа по теме «Смешанные числа» 5 класс
контрольная работа 2 варианта…
Презентация: 5 класс.Подготовка к контрольной работе по теме «Натуральные числа»
Зубарева И.И. Математика 5 класс: учебник для учащихся общеобразовательных учреждений.Мнемозина,2013. Презентация: Подготовка к контрольной работе по теме «Натуральные числа» .г.Нижний Новгород МБОУ С…
Контрольная работа по теме «Комплексные числа»
Контрольная работа представлена в двух вариантах для учащихся 10 класса по теме «Комплексные числа»….
Контрольная работа по теме «Действительные числа» в форме ЭГЕ, алгебра и начала анализа, 10-й класс.
Контрольная работа по теме «Действительные числа» в форме ЭГЕ, алгебра и начала анализа, 10-й класс.Подготовка к ЕГЭ….
Контрольная работа по теме «Натуральные числа» (5 класс): подготовка, проведение, проверка
В материале предложены задания для подготовки, проведения и проверки контрольной работы «Натуральные числа» (5 класс). ..
..
Поделиться:
Операции — веб-формулы
Алгебраические операции над комплексными числами
При выполнении операций с комплексными числами мы можем поступать так же, как в алгебре действительных чисел, заменяя i 2 на -1, когда это встречается.
1. Добавление комплексных чисел
(a+bi) + (c+di) = (a+c) + (b+d)i
Пример:
z1 = 3 — 4i и z2 = -2 + 2i
z1 + z2 = (3 + (-2)) + (-4 + 2)i = 1 -2i
2. Вычитание комплексных чисел
(a+bi) — (c+di) = (a-c)+ (b-d)i
Пример:
z1 = 3 — 4i и z2 = -2 + 2i
z1 — z2 = (3 — (-2)) — (-4 — 2)i = 5 +6i
3. Умножение комплексных чисел
Умножение комплексных чисел
(a+bi)(c+di) = ac+bci+adi+bdi 2
= (ac-bd)+(ad+bc)i
Пример:
z1 = 3 — 4i и z2 = -2 + 2i
z1 ∙ z2 = (3 ∙ (-2)) + (-4 ∙ (-2))i + (3 ∙ 2)i + (-4 ∙ 2)i 2 = -6 + 14i -8i 2
4. Деление комплексных чисел
(a+bi)/(c+di)=(a+bi)/(c+di)×(c-di)/(c-di)
=(ac-adi+bci-bdi 2 )/(c 2 -d 2 i 2 )
=(ac+bd+(bc-ad)i)/(c 2 -d 2 i 2 )
=(ac+bd)/(c 2 +d 2 )+(bc-ad)/(c 2 +d 2 ) я
Пример:
z1 = 3 — 4i и z2 = -2 + 2i
z1 / z2 = (3 ∙ (-2) + (-4 ∙ 2))/((-2) 2 + 2 2 ) + (-4 ∙ (-2) — 3 ∙ 2)/( (-2) 2 + 2 2 )i = -14/8 + (2/8)i = -7/4 + i/4
Неравенства в мнимых числах не определены. Как например z >0, 4 + zi < 2+4i не имеют смысла в комплексных числах.
Как например z >0, 4 + zi < 2+4i не имеют смысла в комплексных числах.
В действительных числах, если a 2 + b 2 =0 , то a=b=0 ; однако в комплексных числах,
z 1 2 + z 2 2 не означает z 1 = 902 0 0 0 2
Комплексное сопряжение: комплексное сопряжение а + би есть а — би . Важность комплексно-сопряженного числа заключается в том, что произведение комплексного числа на его сопряженное является действительным числом.
(а + bi)(a − bi) = (a + b )
Аддитивная идентичность: Аддитивная идентичность — это комплексное число, представляющее понятие нуля для сложения комплексных чисел: 0 + 0i .
(а + би) + (0 + 0и) = а + би
Мультипликативная идентичность: Мультипликативная идентичность — это комплексное число, которое представляет понятие единицы для умножения комплексных чисел на 1+0i.
(а + би)(1+ 0i) = а + би
Пример 1 : Упростить (2 √(-9) -3 )(3√(-16) — 1)
(2 √(-9) -3 )(3√(-16) — 1)
=(2 · 3i — 3)(3 · 4 i — 1)
=(6i — 3)(12i — 1)
= 72i 2 – 36i – 6i + 3
= -69 – 42i Пример 3
Мы должны уменьшить знаменатель и числитель, умножив числитель и знаменатель на комплексное число 10+2i.
Используйте формулу (a+ b) (a-b) = a 2 — b 2 , чтобы уменьшить знаменатели. Используйте формулу (a+b) 2 = a 2 +2ab+ b 2 , чтобы уменьшить числители.
Сложите и возведите в квадрат члены, чтобы получить значения.
В комплексных числах значение i 2 равно -1.
Подставьте значение i 2 в приведенное выше уравнение, чтобы уменьшить знаменатели.
Пример 4 : Найдите произведение комплексных чисел 1+ i и √ 3- i в полярной форме.
Решение : Мы можем легко найти, что полярная форма 1+ i и √ 3- i соответственно,
Мы знаем, что z 1 z 2 = r 1 r 2 ( cos (θ 1 + θ 2 ) + i sin (θ 1 + θ 1 + θ 2 2 90) 9,04 2 90 Эта формула говорит, что для умножения двух комплексных чисел нам нужно умножить модули и сложить аргументы. Следовательно, умножая 1+ на и √ 3- на по указанному выше правилу, мы получим:
Пример 5 : Упростить i 64,002 .
Решение: i 64 002 = i 64 000 + 2 = i 4 · 16 000 + 2 = i 2
6 = –6youtube.com/v/6xEO4BeawzA&hl=en_US&fs=1&color1=0x006699&color2=0x54abd6″ allowfullscreen=»true» allowscriptaccess=»always»>
Для комплексных чисел z1 = 2 + 3i и z2 = 4 — 5i значение (z1 + z2)2 равно — Sarthaks eConnect
← Предыдущий вопрос Следующий вопрос →
спросил в комплексных числах по Анкитакаруан (46,0 тыс. баллов)закрыто Анкитакаруан
Для комплексных чисел z 1 = 2 + 3i и z 2 = 4 — 5i, значение (z 1 + z 2 ) 2 равно
1. 32 — 24и
2. -32 — 24и
3. 32 + 24i
4. -32 + 24i
- математика
- комплексных чисел
1 Ответ
0 голосов
ответил по Синдхусай (30,0 тыс. баллов)
баллов) выбрано Анкитакаруан
Лучший ответ
Правильный ответ — вариант 1: 32–24i 92-2\times6\times2i\)
= 36 — 4 — 24i
= 32 — 24i
← Предыдущий вопрос Следующий вопрос →
Похожие вопросы
Если z1 = \(\rm 2\sqrt{5} + 5i\) и z2 = \(\rm \sqrt{5} + i\), то найти квадрант, в котором (z1 — z2) лежит
спросил 27 фев в комплексных числах по Ведантк (30,0 тыс. баллов)
- математика
- комплексных чисел
Рассмотрим следующие утверждения 1. Сумма двух комплексных чисел всегда является комплексным числом. 2. Для любых двух комплексных чисел z1 и z2: z1 + z2 ≠ z
спросил 1 марта в комплексных числах по Рохитпатил (54,5 тыс. баллов)
- математика
- комплексных чисел
Найдите arg(z1z2z3), если известно, что arg(z1) = \(\pi\over3\), arg(z2) = \(\pi\over4\) и arg(z3) = \(\ pi\over6\) для комплексного числа z1, z
спросил
1 марта
в комплексных числах
по
Рохитпатил
(54,5 тыс. {2}}\) = 0 и arg(z1) — arg( z2) = 2π, то найдите arg(z2)
{2}}\) = 0 и arg(z1) — arg( z2) = 2π, то найдите arg(z2)
спросил 27 фев в комплексных числах по Ведантк (30,0 тыс. баллов)
- математика
- комплексных чисел
На комплексной плоскости точки A и B находятся в точках z1 = 5 – 2i и z2 = 1 + i. Если P(z) движется так, что |z – z1| = 2|z – z2|, то максимальная площадь ΔPAB i
спросил 24 фев в комплексных числах по АвнеешВерма (30,0 тыс. баллов)
- математика
- комплексных чисел
Категории
- Все категории
- JEE (28,1к)
- NEET (8,5к)
- Наука (740к)
- Математика
(240к)
- Система счисления (9,7к)
- Множества, отношения и функции (5,5к)
- Алгебра
(35,3к)
- Алгебраические выражения (2,2к)
- Полиномы (2,5к)
- Линейные уравнения (4.1к)
- Квадратные уравнения (3,5к)
- Арифметическая прогрессия (2,6к)
- Геометрические прогрессии (485)
- Биномиальная теорема (1,9к)
- Перестановки (873)
- Комбинации (411)
- Комплексные числа (1,5к)
- Матрицы (3,5к)
- Детерминанты (1,9к)
- Математическая индукция (543)
- Линейные неравенства (356)
- Экспоненты (803)
- Квадраты и квадратные корни (748)
- Кубы и кубические корни (254)
- Факторизация (871)
- Расстояние, время и скорость (877)
- Логарифм (1,1к)
- Коммерческая математика (7,4к)
- Координатная геометрия (10,0 к)
- Геометрия (11,7к)
- Тригонометрия (10,7к)
- Измерение (6,8к)
- Статистика (4,8к)
- Вероятность (5,3к)
- Векторы (2,8к)
- Исчисление (19,6к)
- Линейное программирование (904)
- Статистика (2,8к)
- Наука об окружающей среде (3,6к)
- Биотехнология (536)
- коммерция (62,1к)
- Электроника (3,7к)
- Компьютер (15,6к)
- Искусственный интеллект (ИИ) (1,4к)
- Информационные технологии (13,2к)
- Программирование
(8.
 6к)
6к) - Политическая наука (6,4к)
- Домашняя наука (4.0k)
- Психология (3,3к)
- Социология (5,5к)
- Английский (57,6к)
- хинди (20,3к)
- Способность (23,7к)
- Рассуждение (14,6к)
- ГК (25,7к)
- Олимпиада (527)
- Советы по навыкам (72)
- CBSE (710)
- РБСЭ (49,1к)
- Общий (56,9к)
- МСБШСЭ (1,8к)
- Совет Тамилнаду (59,3к)
- Совет Кералы (24,5к)
[PDF] Глава 1 Комплексные числа Охваченные результаты:
Глава 1
Комплексные числа Охваченные результаты: E1 E2 E3 E9
ценит творчество, мощь и полезность математики для решения широкого круга задач выбирает подходящие стратегии построения аргументов и доказательств как в конкретных, так и в абстрактных условиях использует взаимосвязь между алгебраическими и геометрические представления комплексных чисел и конических сечений передают абстрактные идеи и отношения с использованием соответствующих обозначений и логических аргументов
ge s
1. 1 Арифметика комплексных чисел и решение квадратных уравнений Потребность в комплексных числах более полная система счисления. Первоначально нужны были только числа для счета (1, 2, 3, …). Позже люди обнаружили потребность в нуле и в отрицательных числах, что дало нам множество целых чисел. Дроби и десятичные дроби дали нам множество рациональных чисел. С такими числами, как 2 и π, был разработан набор иррациональных чисел. Рациональные и иррациональные вместе образуют множество действительных чисел. Эти системы счисления были разработаны математиками для решения новых и различных возникающих проблем. Например, для решения различных типов уравнений требуются различные типы чисел. Используя только целые числа, мы можем решить такие уравнения, как x + 5 = 2, но мы не можем решить 5x = 2. Для этого нам нужны рациональные числа. Чтобы решить x2 = 5, нам нужны иррациональные числа. Есть и другие уравнения, которые нельзя решить, используя какие-либо действительные числа. Простейший пример: x2 + 1 = 0.
1 Арифметика комплексных чисел и решение квадратных уравнений Потребность в комплексных числах более полная система счисления. Первоначально нужны были только числа для счета (1, 2, 3, …). Позже люди обнаружили потребность в нуле и в отрицательных числах, что дало нам множество целых чисел. Дроби и десятичные дроби дали нам множество рациональных чисел. С такими числами, как 2 и π, был разработан набор иррациональных чисел. Рациональные и иррациональные вместе образуют множество действительных чисел. Эти системы счисления были разработаны математиками для решения новых и различных возникающих проблем. Например, для решения различных типов уравнений требуются различные типы чисел. Используя только целые числа, мы можем решить такие уравнения, как x + 5 = 2, но мы не можем решить 5x = 2. Для этого нам нужны рациональные числа. Чтобы решить x2 = 5, нам нужны иррациональные числа. Есть и другие уравнения, которые нельзя решить, используя какие-либо действительные числа. Простейший пример: x2 + 1 = 0. Однако это уравнение можно решить, определив число i такое, что i2 = -1: x2 + 1 = 0, т. е. x2 − i2 = 0 , где i2 = −1 (x − i) (x + i) = 0 (разность двух квадратов) ∴ x = i или x = −i
Однако это уравнение можно решить, определив число i такое, что i2 = -1: x2 + 1 = 0, т. е. x2 − i2 = 0 , где i2 = −1 (x − i) (x + i) = 0 (разность двух квадратов) ∴ x = i или x = −i
Пример 1
Решите квадратное уравнение x2 − 4x + 13 = 0.
Решение
Обратите внимание, что дискриминант ∆ = b2 − 4ac = 16 − 52 = −36. Следовательно, квадратное уравнение не имеет действительных корней, а парабола y = x2 − 4x + 13 находится полностью над осью x. Однако мы можем найти решения, используя комплексные числа, которые имеют форму a + bi, где a и b – действительные числа.
Глава 1 Комплексные числа
NSME2_SB_01.indd 1
1 30/07/13 14:10
Метод 1 Использование квадратичной формулы
Метод 2 Завершение квадрата
2
x2 — 4x + 13 = 0
x — 4x + 13 = 0
x2 — 4x + 4 + 9 = 0 0009
2 x = -b ± b — 4ac 2a x = 4 ± -36 2 x = 2 ± 3 -1 x = 2 ± 3i
(x — 2)2 = -9 x — 2 = ±3i x = 2 ± 3i
Комплексная система счисления
m pl
e
pa
ge s
Любое число z вида x + iy, где x и y — действительные числа, называется комплексным числом. x — действительная часть z, обозначаемая Re (z) = x, а y называется мнимой частью z (хотя она не является буквально «воображаемой» в обычном смысле этого слова), обозначается Im (z) = у. (Обратите внимание, что мы используем одну букву z для обозначения комплексного числа x + iy, чтобы подчеркнуть, что x + iy — это одно число, несмотря на то, что оно записано как сумма двух частей.) Если мнимая часть z равна нулю, т. е. y = 0, то z чисто вещественное. Это означает, что множество действительных чисел является подмножеством множества комплексных чисел. Если действительная часть z равна нулю, т. е. x = 0, то z является чисто мнимым, т.е. 3i или −i. Следующие определения относятся к комплексным числам. Равенство Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны их мнимые части: a + bi = c + di тогда и только тогда, когда a = c и b = d Сложение и вычитание Если z = z1 ± z2, где z1 = x1 + iy1 и z2 = x2 + iy2, то z = (x1 + x2) ± i(y1 + y2).
x — действительная часть z, обозначаемая Re (z) = x, а y называется мнимой частью z (хотя она не является буквально «воображаемой» в обычном смысле этого слова), обозначается Im (z) = у. (Обратите внимание, что мы используем одну букву z для обозначения комплексного числа x + iy, чтобы подчеркнуть, что x + iy — это одно число, несмотря на то, что оно записано как сумма двух частей.) Если мнимая часть z равна нулю, т. е. y = 0, то z чисто вещественное. Это означает, что множество действительных чисел является подмножеством множества комплексных чисел. Если действительная часть z равна нулю, т. е. x = 0, то z является чисто мнимым, т.е. 3i или −i. Следующие определения относятся к комплексным числам. Равенство Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны их мнимые части: a + bi = c + di тогда и только тогда, когда a = c и b = d Сложение и вычитание Если z = z1 ± z2, где z1 = x1 + iy1 и z2 = x2 + iy2, то z = (x1 + x2) ± i(y1 + y2).
Sa
Умножение Если z = z1 × z2, где z1 = x1 + iy1 и z2 = x2 + iy2, то: z = (x1 + iy1)(x2 + iy2) = x1x2 + i2y1y2 + ix1y2 + ix2y1 = ( x1x2 − y1y2) +i(x1y2 + x2y1)
Сопряжение комплексного числа Если z = x + iy, то сопряжение z равно z = x − iy. (Это похоже на сопряжение surd.) Обратите внимание, что произведение комплексного числа и его сопряжения является действительным числом: z z = (x + iy)(x — iy) = x2 — i2y2 = x2 + y2 Деление z Чтобы вычислить деление z = 1, умножьте числитель и знаменатель на сопряженное z2. Это реализует z2 в знаменателе, т. е. делает знаменатель действительным. Это похоже на то, как мы рационализируем знаменатель при делении сурдов.
(Это похоже на сопряжение surd.) Обратите внимание, что произведение комплексного числа и его сопряжения является действительным числом: z z = (x + iy)(x — iy) = x2 — i2y2 = x2 + y2 Деление z Чтобы вычислить деление z = 1, умножьте числитель и знаменатель на сопряженное z2. Это реализует z2 в знаменателе, т. е. делает знаменатель действительным. Это похоже на то, как мы рационализируем знаменатель при делении сурдов.
Пример 2 Если z1 = 2 + 3i и z2 = −1 + 4i, найти: (a) z1 + z2 (b) z1 − z2 (c) z1 × z2 (d) z 2 z 2 (e) z12
2
(f) z1 ÷ z2
Новое расширение 2 для старшеклассников по математике для 12-го года обучения
NSME2_SB_01.indd 2
30/07/13 14:10
+ 3Решение (a) + (−1 + 4i) = 1 + 7i (б) z1 − z2 = 2 + 3i − (−1 + 4i) = 3 − i
(в) z1 × z2 = (2 + 3i)(−1 + 4i) = −2 + 8i − 3i + 12i2 = −2 + 5i − 12 = −14 + 5i (d) z 2 z 2 = (−1 + 4i)(−1 − 4i) = (−1)2 − 16i2 = 1 + 16 = 17
(д) z12 = (2 + 3i)2 = 4 + 12i + 9i2 = 4 + 12i — 9 = -5 + 12i z (2 + 3i) (-1 — 4i) -2 — 8i — 3i — 12i 2 −2 − 11i + 12 10 − 11i 10 11 (f) 1 = 2 + 3i = × = = = = − i z 2 −1 + 4i (−1 + 4i) (−1 − 4i) 1 + 16 17 17 17 1 − 16i 2
Пример 3
Выразите z3 + 64 как произведение трех линейных множителей. Отсюда найдите три кубических корня из −64.
Отсюда найдите три кубических корня из −64.
Решение
z3 + 64 = (z + 4)(z2 − 4z + 16) = (z + 4)(z − 4z + 4 + 12) 2
2
= (z + 4)(( z − 2) − 12i ) 2
ge s
(сумма двух кубов)
2
(заполнить квадрат)
(построить разность двух квадратов) 2
= (z + 4)(z − 2 − 2 3i)( z − 2 + 2 3i)
pa
= (z + 4)((z − 2) − (2 3i) )
Кубические корни из −64 получаются из z + 4 = 0, z − 2 − 2 3i = 0, z − 2 + 2 3i = 0,
e
∴ Корни равны −4, 2 − 2 3i и 2 + 2 3i.
Квадратные корни комплексного числа
Пример 4
m pl
Общий метод нахождения квадратных корней комплексного числа проиллюстрирован в следующем примере.
Решение
Sa
Найдите квадратный корень из 3 + 4i.
Пусть z = x + iy, где x, y вещественные, такие, что z2 = 3 + 4i: (x + iy)2 = 3 + 4i
(x2 − y2) + 2xyi = 3 + 4i и мнимые части левой и правой сторон: x2 − y2 = 3 [1] 2xy = 4 [2] Из [2] y = 2 , затем подставить в [1]: x 2 − 42 = 3 x x x4 − 3×2 − 4 = 0 (x2 − 4)( x2 + 1) = 0 x2 = 4 или x2 = −1 Но x действительно ∴ x = ±2 — единственные решения. Подставив это в [2]: y = ±1 Таким образом, квадратные корни из 3 + 4i равны 2 + i и -2 − i, что можно записать как ±(2 + i). 92=a, затем введите b=4, а затем введите 2*x*y=b. Это построит две прямоугольные гиперболы с точками пересечения (2, 1) и (-2, -1). (Обратите внимание на связь с примером 4: точки пересечения дают квадратные корни из a + ib = 3 + 4i.) 2 В строке ввода введите a=5, а затем b=-6. Точки пересечения новых гипербол дадут квадратные корни из 5 − 6i. 3 Продолжайте изменять значения a и b, чтобы посмотреть, что произойдет. (Вы можете использовать «ползунки» инструмента Slider для значений a и b.)
Подставив это в [2]: y = ±1 Таким образом, квадратные корни из 3 + 4i равны 2 + i и -2 − i, что можно записать как ±(2 + i). 92=a, затем введите b=4, а затем введите 2*x*y=b. Это построит две прямоугольные гиперболы с точками пересечения (2, 1) и (-2, -1). (Обратите внимание на связь с примером 4: точки пересечения дают квадратные корни из a + ib = 3 + 4i.) 2 В строке ввода введите a=5, а затем b=-6. Точки пересечения новых гипербол дадут квадратные корни из 5 − 6i. 3 Продолжайте изменять значения a и b, чтобы посмотреть, что произойдет. (Вы можете использовать «ползунки» инструмента Slider для значений a и b.)
a=2
для создания
4 Можете ли вы проверить, что каждое ненулевое комплексное число имеет два квадратных корня?
1 i5 = … A 1 B −1
C i D −i
2 Решите следующие уравнения. (a) x2 + 9 = 0 (b) x2 + 25 = 0 2 (d) −x + 2x − 5 = 0 (e) x2 = 4x − 20 3 Упростим: (a) (3 + 5i) + (7 − 2i)
(c) x2 + 2x + 17 = 0 (f) −2×2 + 2x − 13 = 0
e
квадратные уравнения
pa
ge s
Арифметика комплексных чисел. решение
решение
(б) (4 + 7и) — (-2 + 9и)
(в) (5 + 2и)(3 — 4и) (г) (7 + 3и)(7 — 3и)
m pl
1 2 + 3i 3i + 2 (k) −8 + 3i − 2 + 3i (l) 5 + 9i 8 + 5i (j) (i) 2 + 5i 2 − 5i 2 − 4i 4 − 3i −2 − 4i 1 + 2i (e) (2 − 5i)2 (f) i17 (g) ( 3 + 2i)( 3 − 2i)
4 Если z = 5 − 2i, найти: (a) z−1
Sa
(б) z (в) z z
2 (г) z2 (д) (z — z )
(е)
5 Если z1 = 3 + i и z2 = 2 — 3i, найти:
(а) (z1 − z2)2 (б) z1 × z 2 (в) z1z 2 (г)
6 Найдите действительные числа x и y такие, что: (a) (x + iy)(2 − 3i) = −13i (b) (1 + i)x + (2 − 3i)y = 10
(h )
(
)
2
z −1 z −i z1 − z 2 z1 + z 2
z−2 =1+i 7 Решить уравнение: (a) 2z − 1 = (4 − i)2 (b) z 8 Найдите линейные множители следующих выражений. (а) z2 + 9 (б) z2 + 36 (в) (z − 3)2 + 16 (г) (2z + 3)2 + 8 (д) z2 + 2z + 26 (е) z2 − 6z + 20 (g) 2z2 + 2z + 4 (h) z3 + 1000
9 Найдите квадратные корни из следующего: корни −8 + 6i. (b) Следовательно, решите 2z2 + (1 − i)z + (1 − i) = 0. (c) Используйте свой ответ на (b), чтобы убедиться, что результаты для суммы корней и для произведения корней a квадратное уравнение верно, когда коэффициенты и корни являются комплексными числами.
(c) Используйте свой ответ на (b), чтобы убедиться, что результаты для суммы корней и для произведения корней a квадратное уравнение верно, когда коэффициенты и корни являются комплексными числами.
4
Новое расширение 2 для старшеклассников по математике для 12-го года обучения
NSME2_SB_01.indd 4
30/07/13 14:10
11 Решите следующие квадратные уравнения. (а) z2 — (3 — 2i)z + (1 — 3i) = 0 (б) z2 — z + (4 + 2i) = 0 2 (в) z — (2 + 2i)z + (-1 + 2i) = 0 (d) z2 − (3 + i)z + (2 − 3i) = 0 12 (a) Покажите, что 3 − i является корнем уравнения z3 − ( 3 − i)z2 + 9z − 9 3 + 9i = 0. (b) Найдите два других решения уравнения. (c) Используйте свой ответ на (b), чтобы проверить, что результаты для суммы корней, для суммы произведений пар корней и для произведения корней кубического уравнения верны, когда коэффициенты и корни являются комплексными числами . 13 Если z1 = x1 + iy1 и z2 = x2 + iy2, покажите, что следующие уравнения верны. (а) z1 + z1 = 2 × Re(z1) (б) z1 − z1 = 2 × Im(z1) × i (в) z1 + z 2 = z1 + z 2 (г) z1 − z 2 = z1 − z 2 (e) z1 × z 2 = z1 × z 2
14 Пусть z = a + ib, где a, b действительны. Докажите, что всегда существует два квадратных корня из z, за исключением случаев, когда a = b = 0.
Докажите, что всегда существует два квадратных корня из z, за исключением случаев, когда a = b = 0.
ge s
15 (a) Выразите z3 + 125 как произведение трех линейных множителей. Пусть w — один из невещественных комплексных корней уравнения z3 + 125 = 0. (b) Покажите, что w2 = 5w — 25. (c) Следовательно, упростите (5w — 25)3.
pa
1.2 Геометрическое представление комплексного числа в виде точки Мнимая ось y
P(x + yi) y
m pl
e
Поскольку комплексное число z = x + iy состоит из двух частей, его можно рассматривать как упорядоченную пару (x, y), поэтому комплексные числа можно представить в виде точек на плоскости. Любое комплексное число z = x + iy может быть представлено точкой P с координатами (x, y) на числовой плоскости, в которой ось x является «действительной» осью, а ось y — «мнимой» осью. Это декартово представление комплексных чисел называется диаграммой Аргана в честь французского математика Жана-Робера Аргана (1768–1822). Числовая плоскость, на которую нанесены диаграммы Аргана, называется плоскостью комплексных чисел.
Числовая плоскость, на которую нанесены диаграммы Аргана, называется плоскостью комплексных чисел.
x
O
Реальная ось
x
Пример 5
SA
Геометрическое добавление и вычитание сложных чисел
, если Z1 = 5 + 2i и z2 = 1 + 3i, показать z1 + z2 и z1, если z1 = 5 + 2i и z2 = 1. − z2 на диаграмме Аргана.
Решение Алгебраически z1 + z2 = 6 + 5i и z1 − z2 = 4 − i.
На диаграмме Аргана точки P, Q и R представляют z1, z2 и z1 + z2 соответственно. Обратите внимание на расположение R, чтобы завершить параллелограмм OPRQ.
На диаграмме также показаны точки Q′ и S, представляющие −z2 и z1 − z2 соответственно. Обратите внимание, что z1 − z2 было вычислено как z1 + (−z2). S завершает параллелограмм OPSQ’.
y 6 5 4 3 2
R z1 + z2 Q z2
Pz 1
1 –2 –1–1O –2 –z2–3 Q’ –4
1
2 90
5 6 z1 – z2
7
8 x
Глава 1 Комплексные числа
NSME2_SB_01. indd 5
indd 5
5 30/07/13 14:10
Геометрическое представление умножения на i Пример 6
Если z = 4 + 3i, покажите iz, i2z и i3z на диаграмме Аргана.
Решение
iz Q
2
3
Алгебраически: iz = -3 + 4i, i z = -4 — 3i и i z = 3 — 4i. Диаграмма Аргана показывает, что каждое умножение на i вызывает поворот точки z против часовой стрелки вокруг начала координат на π (90 °). 2
z P
1 –6 –5 –4 –3 –2 –1–1O –2 R –3 i2z –4 –5 –6
1
2
3
4
5
6 x
S I3Z
GE S
Разведка технологии
Y 6 5 4 3 2
Умножение I
1 В новом окне окна, окно, окно New Geogebra, окон щелкните правой кнопкой мыши в любом месте графического представления, чтобы открыть всплывающее меню, и выберите «Сетка», чтобы включить сетку.
pa
2 В строке ввода введите комплексное число, например 3+2i. Это должно отображаться как z1 в представлениях Графика и Алгебра. (Если нет, начните заново и введите z_1=3+2i.) 3 Чтобы умножить комплексное число z1 на i, теперь вы можете ввести i*z_1 в строке ввода. Продукт должен отображаться как z2. чтобы создать круг через z1 и его кратные i. Где
(Если нет, начните заново и введите z_1=3+2i.) 3 Чтобы умножить комплексное число z1 на i, теперь вы можете ввести i*z_1 в строке ввода. Продукт должен отображаться как z2. чтобы создать круг через z1 и его кратные i. Где
m pl
5 Использовать инструмент Окружность через три точки центр круга?
e
4 Теперь снова умножьте этот результат z2 на i, введя i*z_2 в строке ввода. Новый результат должен появиться как z3.
6 Создайте следующий множитель, введя i*z_3 в строке ввода. Новый результат z4 на круге? 7 Используйте инструмент Move tool
, чтобы переместить исходную точку z1. Что ты заметил?
Sa
8 Создайте следующий множитель, введя i*z_4 в строке ввода. Где новый результат z5? 9Какой вывод вы делаете об умножении чисел на i? Напишите заключение со ссылкой на угол поворота.
Геометрическое представление сопряженных элементов Точки, представляющие пару комплексно-сопряженных чисел, являются отражением действительной оси. (Это связано с тем, что число и его комплексное сопряжение совпадают, за исключением того, что мнимая часть изменилась с отрицательной на положительную или наоборот.)
(Это связано с тем, что число и его комплексное сопряжение совпадают, за исключением того, что мнимая часть изменилась с отрицательной на положительную или наоборот.)
Исследование технологии Сопряжение z Чтобы показать сопряжение комплексного числа в GeoGebra, вы можно использовать инструмент «Отразить объект в линии», чтобы отразить комплексное число по оси x. (Щелкните точку комплексного числа, а затем щелкните ось X.)
Форма комплексного числа в виде аргумента модуля Точка P на диаграмме Аргана может быть расположена в декартовых координатах (т. его модуль (во множественном числе «модули») и его аргумент — это расстояние: от начала координат O до P. • Аргумент — это угол, под которым луч OP наклонен к положительному направлению действительной оси. В частности, мы определяем модуль z как mod z = z = x + iy = x 2 + y 2 = r
y P
Из этого определения и диаграммы следует, что x = r cos θ и y = r sin θ.
г = |г|
Следовательно, для любого комплексного числа: z = x + iy = r cos θ + ir sin θ = r(cos θ + i sin θ ) Когда комплексное число выражается в виде r(cos θ + i sin θ ) , говорят, что он находится в форме mod-arg. Можно использовать сокращение r cis θ.
Можно использовать сокращение r cis θ.
z = x + iy y
θ O
x
x
Тогда аргумент z = x + iy определяется как arg z = θ такой, что x = r cos θ и y = r≀s Очевидно, , бесконечное количество значений θ возможно для любого комплексного числа z, полученного путем сложения или вычитания кратных 2π (или 360 °). Следовательно:
Результаты всегда должны выдаваться с использованием главного аргумента. Примечание: arg 0 не определен.
Запишите каждое из следующих значений в форме mod-arg. (a) 1 + 3i
(b) −1 + 3i
Решение
pa
Пример 7
ge s
Определим главный аргумент как θ такое, что −π
2 (c) − 3i
(г) 1 − 3i
y
(а) z = 12 + ( 3 ) = 2 2
1 + √3i
θ2
θ91 901
–1 – √3i
Sa
x
θ3
m pl
–1 + √3i
e
Всегда полезно показывать комплексные числа на диаграмме Argand.
θ4
1 – √3i
2 cos θ = 1 и 2 sin θ = 3, поэтому θ — угол первого квадранта. ∴ arg z = θ = π 3 ∴ 1 + 3i = 2 cis π 3
∴ arg z = θ = π 3 ∴ 1 + 3i = 2 cis π 3
(б) z =
2
2 cos θ = −1 и 2 sin θ = 3, поэтому квадрантный угол θ является . ∴ arg z = θ = 2π 3 ∴ −1 + 3i = 2 cis 2π 3
(c) z =
(−1)2 + ( 3 ) = 2
(−1)2 + (− 3 ) = 2 2
2 cos θ = −1 и 2 sin θ = −3 , поэтому θ — угол третьего квадранта. ∴ arg z = θ = − 2π (Обратите внимание на использование главного аргумента.) 3 2π ∴ -1 − 3i = 2 cis − 3
( )
2 (d) z = 1 + ( − 3 ) = 2 2
2 cos θ = 1 и 2 sin θ = − 3, поэтому θ — угол четвертого квадранта. ∴ arg z = θ = − π (опять же, обратите внимание на использование главного аргумента.) 3 π ∴ 1 − 3i = 2 cis − 3
( )
Глава 1 Комплексные числа
NSME2_SB_01.indd 7
7 30/07/13 14:10
2 Результат z × z = z
Этот полезный результат можно доказать следующим образом. Пусть z = x + iy, так что z = x − iy. ∴ LHS = (x + iy)(x − iy) = x2 + y2 = RHS
Произведения в форме mod–arg Пусть z1 = r1(cos q1 + i sin q1) и z2 = r2(cos q2 + i sin q2 ). Затем z1 × z2 = r1r2 (cos q1 + i sin q1) (cos q2 + i sin q2)
Затем z1 × z2 = r1r2 (cos q1 + i sin q1) (cos q2 + i sin q2)
= r1r2 (cos q1 cos q2 — sin q1 sin q2 + i sin q1 cos q2 + i cos q1 sin q2)
= r1r2(cos (q1 + q2) + i sin (q1 + q2)) = r1r2 cis (q1 + q2)
Это комплексное число в форме mod–arg с модулем r1r2 и аргументом (q1 + q2) . ∴ z1 z 2 = z1 × z 2
пример 8
ge s
Также обратите внимание, что arg z1 + arg z2 — это одно из значений arg (z1z2), но не обязательно главное значение (возможно, нам придется добавить или вычесть число, кратное 2π, чтобы получить главный аргумент. )
)
( (
)
m pl
Решение
e
3 3 4 4 5 π Отсюда находим точное значение cos 12
(
))
z1 × z2 = 2 2 cos 2π + 3π + i sin 2π + 3π 3 4 3 4 17 π 17 π + i sin = 2 2 cos (в форме mod-arg, но без использования главного аргумента) 12 12 = 2 2 2 cos −7π + i sin −7π (вычитая 2π, чтобы найти главный аргумент) 12 12 Чтобы найти z1 × z2 в декартовой форме:
(
))
SA
((
(
) ()
(
)
)
z1 = 2 cos 2π + i sin 2π = 2 — 1 + I 3 =. −1 + 3i 3 3 2 2 z2 = 2 cos 3π + i sin 3π = 2 ⎛− 1 + 1 i⎞ = −1 + i 4 4 ⎝ 2 2 ⎠ ∴ z1 × z2 = (−1 + 3i)( − 1 + i) = (1 − 3) + (−1 − 3)i Итак, 2 2 cos −7π + i sin −7π = (1 − 3) + (−1 − 3)i в декартовой форме 12 12
−1 + 3i 3 3 2 2 z2 = 2 cos 3π + i sin 3π = 2 ⎛− 1 + 1 i⎞ = −1 + i 4 4 ⎝ 2 2 ⎠ ∴ z1 × z2 = (−1 + 3i)( − 1 + i) = (1 − 3) + (−1 − 3)i Итак, 2 2 cos −7π + i sin −7π = (1 − 3) + (−1 − 3)i в декартовой форме 12 12
Приравнивание действительных частей (поскольку мы пытаемся доказать результат, включающий cos 5π ): 12 −7 π 1 − 3 −7 π = 2 2 cos = 1 − 3 ∴ cos 12 12 2 2 −7 π 7 π 5 π = cos = − cos Но cos (поскольку cos x – четная функция и cos (π − θ ) = −cos θ ) 12 12 12 ∴ − cos 5π = 1 − 3, поэтому cos 5π = 3 − 1 = 6 − 2 12 12 4 2 2 2 2
8
Новое расширение 2 для старшеклассников по математике для 12-го года обучения
NSME2_SB_01.indd 8
30/07/13 14:10
Исследование технологии Умножение комплексных чисел Рассмотрим умножение комплексных чисел z1 + 2i = 3 и z2 = 1 + 3i. 1 В новом окне GeoGebra щелкните правой кнопкой мыши в любом месте графического представления, чтобы открыть всплывающее меню, и выберите «Сетка», чтобы включить сетку. 2 На панели ввода постройте график, введя 3+2i, а затем 1+3i. Они должны отображаться как z1 и z2 в представлениях Графика и Алгебра. (Если нет, начните заново и введите z_1=3+2i, затем z_2=1+3i.) 3 Чтобы умножить комплексные числа z1 и z2, введите z_1*z_2 в строке ввода. Продукт должен отображаться в представлении «Алгебра» как z3 = -3 + 11i, но вам может потребоваться уменьшить масштаб, чтобы увидеть эту точку в представлении «Графика». Теперь вы можете использовать GeoGebra для геометрической интерпретации продукта. 4 Добавьте начало координат в виде точки, введя O=(0,0) в строке ввода. Затем используйте инструмент «Вектор между двумя точками», чтобы создать векторы от начала координат О до точек z1, z2 и z3. 5 Вычислите длину каждого вектора, найдя модуль каждого из комплексных чисел. Чтобы найти модуль для числа z1, введите abs(z_1) в строке ввода и так далее для z2 и z3. Они должны отображаться в представлении «Алгебра» как числа a, b и c.
Они должны отображаться как z1 и z2 в представлениях Графика и Алгебра. (Если нет, начните заново и введите z_1=3+2i, затем z_2=1+3i.) 3 Чтобы умножить комплексные числа z1 и z2, введите z_1*z_2 в строке ввода. Продукт должен отображаться в представлении «Алгебра» как z3 = -3 + 11i, но вам может потребоваться уменьшить масштаб, чтобы увидеть эту точку в представлении «Графика». Теперь вы можете использовать GeoGebra для геометрической интерпретации продукта. 4 Добавьте начало координат в виде точки, введя O=(0,0) в строке ввода. Затем используйте инструмент «Вектор между двумя точками», чтобы создать векторы от начала координат О до точек z1, z2 и z3. 5 Вычислите длину каждого вектора, найдя модуль каждого из комплексных чисел. Чтобы найти модуль для числа z1, введите abs(z_1) в строке ввода и так далее для z2 и z3. Они должны отображаться в представлении «Алгебра» как числа a, b и c.
ge s
6 Теперь вы можете умножить длины векторов на z1 и z2 (т. е. модули z1 и z2), умножив их значения a и b.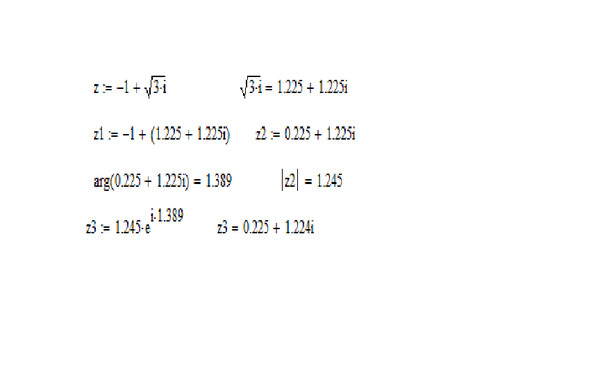 Для этого введите a*b в строке ввода. Что вы заметили в результате (отображаемом в представлении алгебры как d )? Это показывает, что: z1z 2 = z1 × z 2
Для этого введите a*b в строке ввода. Что вы заметили в результате (отображаемом в представлении алгебры как d )? Это показывает, что: z1z 2 = z1 × z 2
pa
GeoGebra также можно использовать для исследования соотношений между углами, образуемыми с положительной осью x (т. е. аргументами). 7 Чтобы измерить углы, сделанные с положительной осью x, вам сначала нужно создать точку на положительной оси x для измерения. Эта точка может быть где угодно на положительной оси X. Используйте инструмент «Новая точка» A или введите координаты соответствующей точки в строке ввода, например. А=(4,0).
e
8 Измерьте угол, который каждый вектор (до z1, z2 и z3) образует с осью X, используя инструмент Угол, щелкнув (по порядку) точку
z3
m pl
10
Sa
A, затем исходная точка O, а затем точка z1, z2 или z3. Результаты должны отображаться в представлении алгебры как α, β и γ. Из этого вы должны быть в состоянии подтвердить, что α + β = γ. Можете ли вы интерпретировать этот результат с точки зрения аргументов z1, z2 и произведения z3? 9Представьте произведение z3 через его модуль и аргумент. Чем полезно понимание комплексных чисел в форме mod-arg?
Можете ли вы интерпретировать этот результат с точки зрения аргументов z1, z2 и произведения z3? 9Представьте произведение z3 через его модуль и аргумент. Чем полезно понимание комплексных чисел в форме mod-arg?
Y 12
8 6
γ = 1,84 RAD 4 2 –4
–3 –2
–1 O
Z2
β = 1,25 RAD Z1 α = 0,59 RAD A
1
2
3
4
x
Частные в форме mod–arg Пусть z1 = r1(cos q1 + i sin q1) и z2 = r2(cos q2 + i sin q2). z r (cos θ1 + i sin θ1) Тогда 1 = 1 z 2 r2 (cos θ 2 + i sin θ 2 ) r (cos θ1 + i sin θ1) (cos θ 2 − i sin θ 2 ) = 1 × r2 ( cos θ 2 + я sin θ 2 ) (cos θ 2 — я sin θ 2 ) =
(
2
2
R2 (cos θ 2 + sin θ 2) r1 = cos (θ1 — θ 2) + i sin (θ1 — θ 2) r2
(
=
)
r1 (cos θ1 cos θ 2 + sin θ1 sin θ 2 ) + i (sin θ1 cos θ 2 − cos θ1 sin θ 2 )
)
r1 цис θ − θ 2 ) r2 ( 1
90 Комплексное число в форме mod–arg с модулемr1 и аргументом (q1 — q2) r2
Глава 1 Комплексные числа
NSME2_SB_01. indd 9
indd 9
9 30/07/13 14:10
∴
z z1 = 1 z2 z2
z Также обратите внимание, что arg z1 − arg z2 является одним значением arg 1 , но не обязательно главным значением. (Возможно, нам придется прибавить z2 или вычесть число, кратное 2π, чтобы найти главный аргумент.) Модуль частного — это частное модулей. Аргумент частного есть разность аргументов.
Пример 9
z1 в форме mod–arg. z2
Решение
(
)
(
z1 = 2 cos π + i sin π and z2 = 2 cos −π + i sin −π 4 4 6 6 z ∴ 1 = 2 cis π − −π = 2 cos 5π + i sin 5π z2 2 4 6 2 12 12
(
)
(
)
)
PA
Два специальных результатах
GE S
, если Z1 = 1 + I и Z2 = 3 — I, найдите
1. Если z = r(cos θ + i sin θ ), то сопряженное z = r cis (−θ )
1 = 1 cis(−θ ) z r
2 Если z = r(cos θ + i sin θ, то
е
Этот второй результат можно доказать следующим образом:
Метод 2 1 = 1 × z = z = r цис (−θ ) = 1 цис (−θ ) z z z z2 r r2
m pl
Метод 1 1 = 1cis0 = 1 cis (0 − θ ) = 1 cis (−θ ) z r cisθ r r
Sa
Степени, использующие форму mod-arg
Теорема де Муавра (названа в честь французского математика Абрахама де Муавра (1667–1754)) утверждает: Если z = r(cos θ + i sin θ ) и n — целое число, то zn = rn(cos nθ + i sin nθ ) Вы докажете эту теорему в вопросе 15 упражнения 1. 2 ниже.
2 ниже.
Пример 10 Если z = 1 + i, выразить z-10 в декартовой форме (x + iy).
Решение
(
)
z = 1 cos π + i sin π 4 4 2 −10 ∴ z-10 = ⎛ 1 ⎞ cos −10π + i sin −10π 4 4 ⎝ 2⎠
((
= 32 cos -π + i sin −π 2 2 = −32i
10
)
)
Новая старшая математическая расширение 2 для года для годы 12
NSME2_SB_01.indd 10
30/07/07/07/ 13 14:10
Пример 11
(
)
(
)
Пусть z1 = 2 cos π + i sin π, z2 = 2 cos −π + i sin −π. 4 4 3 3
n
⎛z ⎞ (a) Найдите наименьшее натуральное число n, для которого ⎜ 1 ⎟ является действительным числом. ⎝ z2 ⎠ z13 (b) Если z = 5, найти z в декартовой форме. z2
Решение
z13 (б) z = 5 z2
(а) arg z1 = π и arg z2 = − π 3 4 ⎛z ⎞ ∴ arg ⎜ 2 ⎟ ⎟ = π ⎠ 3
=
n
n
n
=
((
(
= =
)
)
)
= 1+I
PA
⎛Z ⎛z 1 ⎟ является ⎝ z2 ⎠ ⎝ z2 ⎠ целым числом, кратным π, потому что это делает аргумент нулевым (поэтому мнимая часть равна нулю). n = 12 — это наименьшее положительное значение n, при котором это происходит.
n = 12 — это наименьшее положительное значение n, при котором это происходит.
(
ge s
⎛z ⎞ ∴ arg ⎜ 1 ⎟ = 7nπ 12 ⎝ z2 ⎠
23 (cos π + i sin π ) 2 ) 2 cos −9 cos −5π4 + i sin4 −5π + i sin 9π 4 4 π π 2 cos + i sin 4 4 2⎛ 1 +i 1 ⎞ ⎝ 2 2⎠ 5
e
Геометрическое представление произведений с участием комплексных чисел — консолидация и обобщение
Sa
m pl
Умножение комплексного числа z на действительное число k: • arg (kz) = arg k + arg z Если k положительное действительное число, то arg k = 0, поэтому arg (kz) = arg z. Если k — отрицательное действительное число, то arg k = π, поэтому arg (kz) = π + arg z = π + arg z − 2π = −(π − arg z). (Обратите внимание, что 2π вычитается, чтобы найти главный аргумент.) • kz = k × z, т. е. существует масштабирование с коэффициентом k. Если k — отрицательное действительное число, то направление от начала координат O до точки, представляющей kz, противоположно в направлении от O до точки, представляющей z.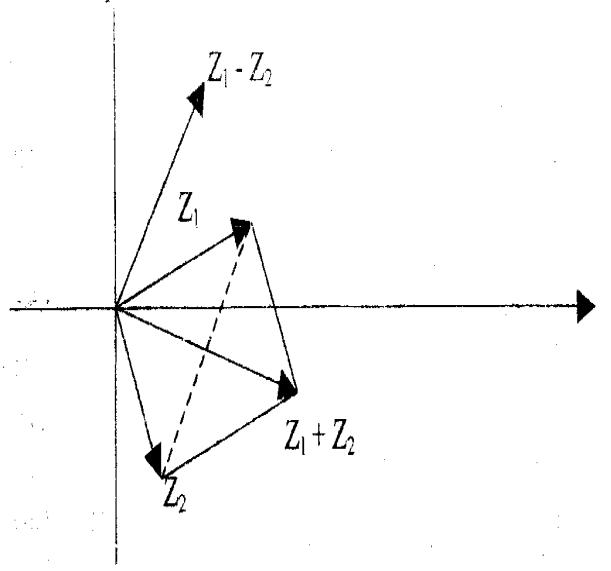 Умножение комплексного числа z на i: • arg (iz) = arg i + arg z = π + arg z 2 • iz = i × z = z при i = 1 • Следовательно, умножение на i вызывает поворот против часовой стрелки на π вокруг начало координат O без изменения модуля. Умножение комплексного числа z на ki, где k — действительное число: • Это объединяет два приведенных выше случая. • Поверните на π против часовой стрелки вокруг O, а затем масштабируйте с коэффициентом k, не забывая также изменить направление 2, если k отрицательное. Умножение комплексного числа z на другое комплексное число r(cos θ + i sin θ ): • arg (z × r cis θ ) = arg z + arg (r cis θ ) = arg z + q • z × r cis θ = z × r cis θ = z × r • Чтобы умножить на r cis θ, поверните на θ против часовой стрелки вокруг O и затем масштабируйте с коэффициентом r. Глава 1 Комплексные числа
Умножение комплексного числа z на i: • arg (iz) = arg i + arg z = π + arg z 2 • iz = i × z = z при i = 1 • Следовательно, умножение на i вызывает поворот против часовой стрелки на π вокруг начало координат O без изменения модуля. Умножение комплексного числа z на ki, где k — действительное число: • Это объединяет два приведенных выше случая. • Поверните на π против часовой стрелки вокруг O, а затем масштабируйте с коэффициентом k, не забывая также изменить направление 2, если k отрицательное. Умножение комплексного числа z на другое комплексное число r(cos θ + i sin θ ): • arg (z × r cis θ ) = arg z + arg (r cis θ ) = arg z + q • z × r cis θ = z × r cis θ = z × r • Чтобы умножить на r cis θ, поверните на θ против часовой стрелки вокруг O и затем масштабируйте с коэффициентом r. Глава 1 Комплексные числа
NSME2_SB_01.indd 11
11 30/07/13 14:10
y
Пример 12 На диаграмме Аргана справа показан единичный круг, а также точки, представляющие комплексные числа z1 и z2. (a) z = z1 и (b) z = z2, отметить точки A, B, C, D, E, Для F, G представляют z , 2z, -z, iz, − 1 iz , z2 и (1 + 3и)з. 2
(a) z = z1 и (b) z = z2, отметить точки A, B, C, D, E, Для F, G представляют z , 2z, -z, iz, − 1 iz , z2 и (1 + 3и)з. 2
1
Решение
A: z – это отражение z на действительной оси –1 B: 2z – это z, масштабированное с коэффициентом 2 C: −z – это z, масштабированное с коэффициентом –1 (т.е. обратно через O) D: iz повернута на z на π против часовой стрелки вокруг O 2 E: − 1 iz масштабируется по iz с коэффициентом − 1 2 2 2 2 F: z имеет модуль, равный (mod z), и аргумент, который равно 2 × arg z G: 1 + 3i = 2 cis π , поэтому (1 + 3i)z находится путем поворота 3 против часовой стрелки на π и последующего удвоения модуля. 3 года (а) (б)
B
–1
x
1
m pl
A
y
B
1 z2
G –1
D
O F A C
E 1
x
–1
SA
–1
E
E
Z1
C
x
1
GE S
F
D 1
–1
O
9999999999999999999999999999999999999999999999999999999999999999999999999999999999999–1 ГО
z1
z2
Пример 13. Пусть OABC — квадрат на диаграмме Аргана, где O — начало координат. Точки A и C представляют собой комплексные числа z и iz соответственно. (a) Найдите комплексное число, представленное буквой B. (b) Теперь квадрат повернут против часовой стрелки на 45° вокруг точки O, образуя OA′B′C′. Найдите комплексные числа, представленные A′, B′ и C′. (c) E — точка пересечения диагоналей квадрата OA′B′C′. Какое комплексное число представляет E?
Пусть OABC — квадрат на диаграмме Аргана, где O — начало координат. Точки A и C представляют собой комплексные числа z и iz соответственно. (a) Найдите комплексное число, представленное буквой B. (b) Теперь квадрат повернут против часовой стрелки на 45° вокруг точки O, образуя OA′B′C′. Найдите комплексные числа, представленные A′, B′ и C′. (c) E — точка пересечения диагоналей квадрата OA′B′C′. Какое комплексное число представляет E?
12
Новое расширение 2 для старшеклассников по математике для 12-х классов
NSME2_SB_01.INDD 12
30/07/13 2:10
Решение (A) B представляет Z + IZ (завершение параллелограммы представляет сумму)
B
Y
B A ′
B ′
Y
B A ′
B
Y
B A ′
B
Y
B A ‘ C E C’
A
O
Следовательно, A’ представляет z × 1 (cos 45° + i sin 45°) = z (1 + i) 2 B′ представляет (z + iz) × 1(cos 45° + i sin 45°) 2 = z (1 + i) = z × 2i = 2 iz 2 2
Способ 2 В квадрате длина диагонали в 2 раза больше длины стороны.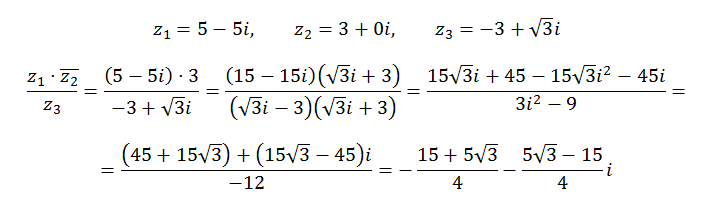 Кроме того, диагонали наклонены под углом 45° к сторонам. Следовательно, когда A повернута на 45° к A′, A′ является точкой на диагонали OB, которая равна 1 от O. 2 Таким образом, A′ представляет число 1 × (z + iz) 2 = z (1 + i) 2 B′ – точка на продолжении OC, такая что OB′ = 2 × OC. Следовательно, B′ представляет собой 2 × iz = 2 iz
Кроме того, диагонали наклонены под углом 45° к сторонам. Следовательно, когда A повернута на 45° к A′, A′ является точкой на диагонали OB, которая равна 1 от O. 2 Таким образом, A′ представляет число 1 × (z + iz) 2 = z (1 + i) 2 B′ – точка на продолжении OC, такая что OB′ = 2 × OC. Следовательно, B′ представляет собой 2 × iz = 2 iz
ge s
(b) Метод 1 A’ образуется путем поворота A против часовой стрелки на 45° вокруг O. × 1(cos 45° + i sin 45°) = z (−1 + i) 2 (c) Диагонали квадрата делят друг друга пополам, поэтому E является серединой OB′. Следовательно, E представляет: 1 × 2 iz 2
Упражнение 1.2 Геометрическое представление комплексного числа в виде точки
1 Если z = 2 + i и w = -3 − 4i, представьте каждое из следующих чисел на комплексной плоскости. 1 (a) z (b) z (c) z z (d) 3z (e) −2z (f) (g) z + w z 2 (h) −w (i) z − w (j) z (k) Re(z) (l) Im(z)
( ( (
Sa
))
2 Если z = 2 cos −2π + i sin −2π , то z4 = … 3 3 −2π + i sin −2π B 16 cos 2π + i sin 2π A 16 cos 3 3 3 3 4π + i sin 4π π π C 16 cos + i sin D 16 cos 3 3 3 3
)
( (
) )
3 Если z = z, то arg z = … π C 0 D 0 или π A π B 2 4 Выразите каждое из следующих чисел в форме mod–arg.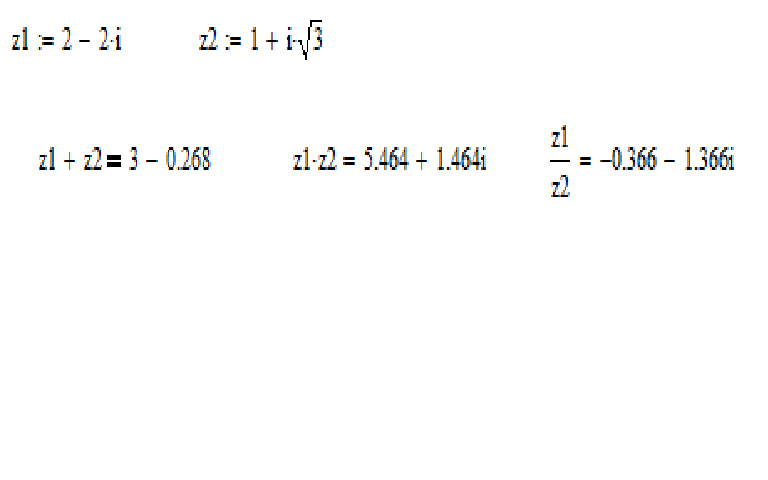 (Приведите аргумент в радианах и в точной форме.)
(Приведите аргумент в радианах и в точной форме.)
(a) 2 − 2i (b) − 3 + i (f) −3 − 3i (g) 2 3 − 2i
(c) −6 − 6i (з) 2 + 2i
(d) 4i (e) −4
5 Преобразуйте каждое из следующих чисел в декартову форму. π π −π + i sin −π (a) 4 cos + i sin (b) 8 cos 3 3 4 4 3 π 3 π −2 π (c) 6 cos + i sin (d) 2 cos + i sin − 2π 4 4 3 3
((
)
)
((
)
)
Глава 1 Комплексные номера
NSME2_SB_01.indd 13
13 30/07/13 2:10 PM
. 6 Для каждого из следующих значений найдите zw и z в форме mod-arg. w π π π π π π π (a) z = 4 cos + i sin , w = 4 cos + i sin (b) z = 5 cos + i sin , w = 3 cos + i sin 3 3 6 6 2 2 4 4 −3π + i sin −3π , w = 2 cos π + i sin π (c) z = 2 cos 4 4 4 4 7 Если z = x + iy, докажите следующее. 2 2 z = 2Re(z ) (a) z = z (b) z z = z (c) z + z 8 На диаграмме Аргана отметьте точки A, B и C для представления комплексных чисел z, w и z + w . Дайте геометрическое объяснение, чтобы показать, что z + w ≤ z + w .
(
)
(
()
9 Найдите следующую в картезианской форме.
(
)
5
(
)
)
(
(
)
)
(
(
)
))
(
)
8
3π + I sin 3π ⎤ (b) ⎡ 2 cos −3π + i sin −3π ⎤ (c) (3 + i) 6 (a) ⎡2 cos ⎢ ⎣ ⎢⎣ 10 10 ⎥⎦ 4 4 ⎥⎦ 1 -3 (d) (1 -i) 5 (e) (3 -i) 4 (f) 5 (г) (−4 -4 3i) (2 3 + 2и)
(1 + i)3 ( 3 + i)6 (j) (1 − i)4 (1 − i)8
ge s
(h) (1 − i)3(2 + 2i)4 (i)
m pl
Sa
()
e
pa
10 (а) 25(cos 2θ + i sin 2θ ) (б) 5(sin θ − i cos θ ) (в) 1 (cos θ − i sin θ ) 5 11 Если z = r(cos θ + i sin θ ) , покажите, что 2 z 2 действительно. z +r 12 OABC — квадрат на диаграмме Аргана. O представляет 0, A представляет собой -4 + 2i, B представляет собой z, C представляет собой w, а D представляет собой точку, где встречаются диагонали квадрата. Обратите внимание, что есть два квадрата, которые удовлетворяют этим требованиям. Для каждого квадрата найдите: (a) комплексные числа, представленные C и D в декартовой форме w . (b) значение arg z 13 Пусть z = 3 + i и w = z × (cos θ + i sin θ ), где −π 0. (b) Найдите значение arg (z + w). 14 На диаграмме Аргана OABC представляет собой прямоугольник. Длина ОС в два раза больше длины ОА. Вершина A соответствует комплексному числу z. Найдите комплексное число, представленное D, точкой пересечения диагоналей OB и AC. 15 (a) Если z = cos θ + i sin θ, докажите по индукции, что zn = cos nθ + i sin nθ для всех натуральных чисел n. (Это доказательство теоремы Муавра для натуральных чисел.) 1 (b) Записав z −n = n , завершите доказательство теоремы Муавра для целых отрицательных чисел. z 16 Используйте теорему де Муавра, чтобы доказать, что сопряженная степень равна степени сопряженной, т. е. пусть z = r(cos θ + i sin θ ) и докажите, что z n = (z ) . 17 Мы уже доказали (ранее и в вопросе 16), что: • z + z = 2Re(z ) и z − z = 2Im(z ) × i • сопряженная сумма равна сумме сопряженных • сопряжение разности равно разности сопряженных • сопряжение произведения равно произведению сопряженных • сопряжение частного равно частному сопряженных • сопряжение степени равно сила сопряжения.
Для каждого квадрата найдите: (a) комплексные числа, представленные C и D в декартовой форме w . (b) значение arg z 13 Пусть z = 3 + i и w = z × (cos θ + i sin θ ), где −π 0. (b) Найдите значение arg (z + w). 14 На диаграмме Аргана OABC представляет собой прямоугольник. Длина ОС в два раза больше длины ОА. Вершина A соответствует комплексному числу z. Найдите комплексное число, представленное D, точкой пересечения диагоналей OB и AC. 15 (a) Если z = cos θ + i sin θ, докажите по индукции, что zn = cos nθ + i sin nθ для всех натуральных чисел n. (Это доказательство теоремы Муавра для натуральных чисел.) 1 (b) Записав z −n = n , завершите доказательство теоремы Муавра для целых отрицательных чисел. z 16 Используйте теорему де Муавра, чтобы доказать, что сопряженная степень равна степени сопряженной, т. е. пусть z = r(cos θ + i sin θ ) и докажите, что z n = (z ) . 17 Мы уже доказали (ранее и в вопросе 16), что: • z + z = 2Re(z ) и z − z = 2Im(z ) × i • сопряженная сумма равна сумме сопряженных • сопряжение разности равно разности сопряженных • сопряжение произведения равно произведению сопряженных • сопряжение частного равно частному сопряженных • сопряжение степени равно сила сопряжения.




 6к)
6к)