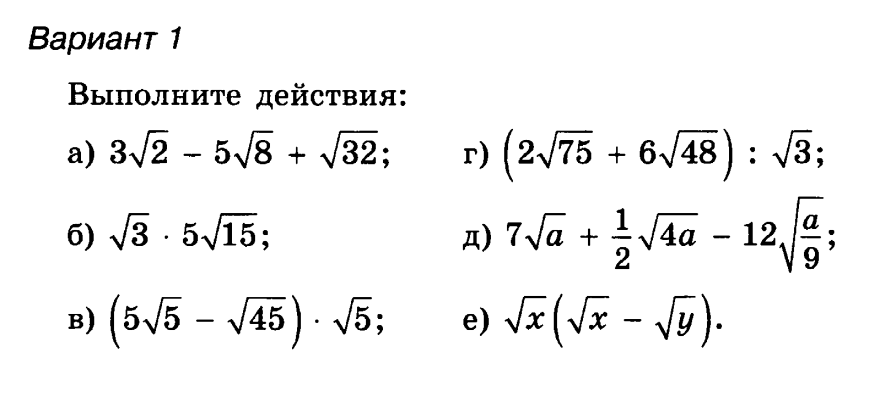Как найти значение выражения с корнями 9 класс огэ: Нахождение значения алгебраического выражения. Задание 8. Основной государственный экзамен 9 класс, Математика: уроки, тесты, задания.

Преобразование выражений, содержащих знак корня

Вопросы занятия:

·  вспомнить основные понятия, связанные с квадратными корнями;

·  вспомнить свойства арифметического квадратного корня;

· рассмотреть, какие преобразования можно выполнять в выражениях, содержащих знак корня.

Материал урока

Стоит напомнить, что квадратным корнем из числа 𝑎 называют такое число 𝑏, квадрат которого равен 𝑎 ().

Например, числа 8 и –8 квадратные корни из числа 64, так как  и .

Из любого неотрицательного действительного числа существует квадратный корень.

Квадратный корень из отрицательного числа не существует.

Если  – квадратный корень из числа а, то  также является квадратным корнем из числа а, и других квадратных корней из числа а нет.

Также вы помните, что арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен

а и обозначается он так:

Например,

Знак  называется знаком арифметического квадратного корня.

Выражение, стоящее под знаком корня, называется подкоренным выражением.

Извлечь квадратный корень из числа а – это значит найти значение выражения .

Выражение  при  не имеет смысла.

Не путайте квадратный корень и арифметический квадратный корень из числа.

Запись  читают «квадратный корень из а». Слово «арифметический» при чтении опускают.

Значок  всегда означает «арифметический квадратный корень из числа».

Из определения квадратного корня следует тождество:

Например,

Напомним, что над выражениями, содержащими квадратные корни можно выполнять ряд преобразований. К таким преобразованиям относят: преобразования корней из произведения, дроби и степени

; умножение и деление корней; вынесение множителя за знак корня, внесение множителя под знак корня и избавление от иррациональности в знаменателе.

Теперь стоит повторить свойства арифметического квадратного корня и их применения.

Итак, первое свойство: если  и , то .

Чтобы извлечь квадратный корень из произведения неотрицательных чисел, можно извлечь его из каждого сомножителя отдельно и результаты перемножить.

Следует помнить, что это свойство распространяется и на тот случай, когда подкоренное выражение представляет собой произведение трёх, четырёх и т.д. неотрицательных множителей.

Например, если , , , то .

Сделаем вывод:

корень из неотрицательных множителей равен произведению корней из этих множителей.

Верно и обратное утверждение: произведение корней из неотрицательных чисел равно корню из произведения этих чисел.

Задание.

Вычислить значение выражения:

а) ;                                        б) .

Первое выражение: . Воспользуемся свойством корня из произведения. Тогда корень из произведения этих чисел можно записать произведением корней, т.е. произведением . Найдём значения каждого из корней. В результате получим,

Следующее выражение: . Воспользуемся свойством корня из произведения. Тогда произведение этих корней равно корню из произведения . Затем представим подкоренное выражение в виде множителей, каждый из которых является квадратом целого числа. Тогда произведение значений каждого корня равно:

Следующее свойство: если  и , то .

Чтобы извлечь квадратный корень из дроби, можно извлечь корень отдельно из числителя и знаменателя и первый результат разделить на второй.

Сделаем вывод: корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, делённому на корень из знаменателя.

Верно и обратное утверждение: частное корней равно корню из частного этих чисел.

Задание.

Вычислить значение выражения:

а);                                                      б) .

Первое выражение: . Найдём его значение. Представим подкоренное выражение в виде неправильной дроби. Получим,

Следующее выражение: . Воспользуемся свойством корня из дроби. Тогда получим,

Перейдём к следующему свойству: при любом значении а верно равенство: .

Равенство  является тождеством. Это тождество применяется при извлечении квадратного корня из степени с чётным показателем.

Чтобы извлечь корень из степени с чётным показателем, достаточно представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством: .

Задание.

Найти значение выражения:

а) ;                           б) ;                     в) .

Первое выражение: . Видим, в подкоренном выражении записана чётная степень. Применим свойство корня из степени с чётным показателем. Тогда, получим,

Следующее выражение: . Как и в предыдущем  выражении под корнем имеем чётную степень. Значит, можем воспользоваться свойством корня из чётной степени. Тогда получим,

И последнее выражение: . Перепишем подкоренное выражение, как . Теперь в подкоренном выражении имеем чётную степень. По свойству корня из степени с чётным показателем получим,

А теперь давайте перейдём к таким преобразованиям выражений, содержащих квадратные корни, как вынесение множителя из-под знака корня и внесение множителя под знак корня.

Итак, если  и , то .

Такое преобразование называют вынесением множителя из-под знака корня.

Задание.

Вынесите множитель из-под знака корня:

а) ;                                                            б) .

Первое выражение: . Представим подкоренное выражение в виде произведения 16 и 2. Число 16 – это, в свою очередь, 4

2. Тогда получим,

Следующее выражение: . Аналогично предыдущему примеру, подкоренное выражение представим в виде произведения 4 и 17. Упростим произведение. В итоге получим,

Если  и , то .

Если  и , то .

Такое преобразование называют внесением множителя под знак корня.

Задание.

Внесите множитель под знак корня:

а) ;                                                            б) .

Первое выражение: . Представим число 5 в виде арифметического квадратного корня. Выполним умножение, применяя свойство корня из произведения. Получим,

Следующее выражение: . Число 0,3 представим в виде произведения  и 0,3. Затем число 0,3 представим в виде корня. Воспользуемся свойством корня из произведения. Посчитаем. Получим,

Очень важное место в преобразовании выражений, содержащих квадратные корни, занимает избавление от иррациональности в знаменателе или числителе дроби.

Если , то .

Такое преобразование называют избавлением от иррациональности в знаменателе дроби.

Задание.

Избавиться от иррациональности в знаменателе дроби:

а) ;                         б) ;                     в) .

Первое выражение: . Чтобы избавиться от иррациональности в знаменателе дроби, нам пригодится основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то значение дроби не изменится. Т.е. чтобы избавиться от корня в знаменателе дроби мы можем числитель и знаменатель дроби умножить на этот корень. Умножим числитель и знаменатель нашей дроби на . Упростим числитель и знаменатель дроби. Получим,

Следующее выражение. Умножим числитель и знаменатель дроби на . Упростим. В итоге получим,

Следующее выражение немного посложнее: . Но не стоит сразу пугаться! Чтобы избавиться от иррациональности в данной дроби, нам следует обратиться к формуле разности квадратов. Для применения этой формулы нам нужно умножить числитель и знаменатель дроби на выражение . Сворачивая знаменатель по формуле разности квадратов, получим,

Посмотрите, мы избавились от иррациональности в знаменателе. Выражение  называют сопряжённым выражением по отношению к выражению . Поэтому очень часто вместо того чтобы говорить умножим числитель и знаменатель на сумму или разность тех или иных выражений, говорят просто «умножим на сопряжённое выражение знаменателю (числителю)».

А теперь давайте рассмотрим задания на преобразование выражений, которые содержат квадратные корни.

Задание.

Упростить выражение:

.

Рассмотрим выражение: . Каждое подкоренное выражение представим в виде произведения, таким образом, чтобы хотя бы один из множителей являлся квадратом натурального числа. Затем воспользуемся свойством корня из произведения. Теперь применим свойство корня из степени с чётным показателем. Упростим получившееся выражение. Обратите внимание, все слагаемые в нашем примере имеют корни с одинаковыми подкоренными выражениями. И отличаются лишь коэффициентами, записанными перед ними. Корни, которые имеют одинаковые подкоренные выражения, являются подобными слагаемыми. Чтобы привести подобные слагаемые достаточно сложить их коэффициенты и умножить на одинаковое выражение, содержащее корень. Приведём подобные слагаемые в нашем примере. Получим,

Задание.

Преобразовать выражение:

.

Воспользуемся формулой квадрата суммы. Упростим это выражение. Воспользуемся следствием из определения квадратного корня. Затем применим свойство корня из произведения. Приведём подобные. В итоге получим,

Задание.

Сократить дроби:

а) ;                                                        б) .

Рассмотрим первую дробь: . Напомним, что для выполнения сокращения дроби необходимо разложить выражения (в числителе или знаменателе) на множители. Для этого используют вынесение общего множителя за скобки или же применяют формулы сокращённого умножения. В нашем случае в числителе дроби число 7 можно представить, как . Тогда вынесем общий множитель  за скобку. Смотрите, дробь можно сократить на выражение . После сокращения получим,

Теперь перейдём ко второй дроби: . Заметим, что в числителе  можно представить, как , а 2, как . Тогда числитель данной дроби можно разложить по формуле разности квадратов двух выражений. Сократим дробь на выражение . В результате получим,

Итоги урока

На этом уроке поговорили о «преобразовании выражений, содержащих знак корня». Вспомнили основные понятия, связанные с квадратными корнями. Поговорили о свойствах арифметического квадратного корня. А затем рассмотрели, какие преобразования можно выполнять в выражениях, содержащих знак корня.

Иррациональные выражения — что это, определение и ответ

Иррациональные выражения – это выражения, содержащие в себе корни различных чисел. {2}} = \left| a \right|\)

8. \(\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}\)

ПОДОБНЫЕ РАДИКАЛЫ:

Корни могут называть радикалами, а подобные радикалы – это корни из одинаковых чисел. Чтобы сложить подобные радикалы, нужно вынести повторяющийся радикал как общий множитель. Например:

\(\sqrt{2} + 5\sqrt{3}\ –\ 2\sqrt{3}\ –3\sqrt{2} = (5\sqrt{3}\ –\ 2\sqrt{3}) + (\sqrt{2}\ –\ 3\sqrt{2}) = (5\ –2)\sqrt{3} + (1\ –3)\sqrt{2} = 3\sqrt{3}\ –\ 2\sqrt{2}\)

МЕТОДОМ РАЗЛОЖЕНИЯ ПОДКОРЕННОГО ВЫРАЖЕНИЯ НА МНОЖИТЕЛИ:

По свойству корней мы знаем, что

\(\sqrt{\text{ab}} = \sqrt{a} \bullet \sqrt{b}\)

Поэтому при упрощении иррациональных выражений используется метод разложения на множители.

Например:

\(\sqrt{18} + \sqrt{32} = \sqrt{9 \bullet 2} + \sqrt{16 \bullet 2} = \sqrt{9} \bullet \sqrt{2} + \sqrt{16} \bullet \sqrt{2}\)

Корни из 9 и из 16 легко извлекаются:

\(\sqrt{9} \bullet \sqrt{2} + \sqrt{16} \bullet \sqrt{2} = 3\sqrt{2} + 4\sqrt{2} = 7\sqrt{2}\)

ПРИМЕНЕНИЕ ФСУ ДЛЯ УПРОЩЕНИЯ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ:

1. {2} = 49\ –\ 5 = 44\)

Из-за того, что в разности квадратов оба выражения возводятся в квадрат, корень второй степени уходит.

ДРОБНЫЕ ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ:

1. Рассмотрим выражение:

\(\frac{3\sqrt{8}}{\sqrt{2}}\)

Упростить его можно двумя способами.

• 1 Способ:

Домножим дробь на иррациональное выражение в знаменателе:

\(\frac{3\sqrt{8}}{\sqrt{2}} = \frac{3\sqrt{8} \bullet \sqrt{2}}{\sqrt{2} \bullet \sqrt{2}}\)

Произведение двух корней можно занести под один корень:

\(\frac{3\sqrt{8 \bullet 2}}{\sqrt{2 \bullet 2}} = \frac{3\sqrt{16}}{\sqrt{4}} = \frac{3 \bullet 4}{2} = 6\)

Ответ: 6.

• 2 Способ:

Внесем частное двух корней под один корень:

\(\frac{3\sqrt{8}}{\sqrt{2}} = 3\sqrt{\frac{8}{2}}\)

Числа внутри корня можно сократить:

\(3\sqrt{\frac{8}{2}} = 3\sqrt{4} = 3 \bullet 2 = 6\)

Ответ: 6. {2}} = \frac{(\sqrt{a}\ –\ 3\sqrt{b})(\sqrt{a} + 3\sqrt{b})}{(\sqrt{a}\ –\ 3\sqrt{b})(\sqrt{a}\ –\ 3\sqrt{b})}\)

2. Сократим одинаковые скобки в числителе и в знаменателе:

\(\frac{(\sqrt{a}\ –\ 3\sqrt{b})(\sqrt{a} + 3\sqrt{b})}{(\sqrt{a}\ –\ 3\sqrt{b})(\sqrt{a}\ –\ 3\sqrt{b})} = \frac{\sqrt{a} + 3\sqrt{b}}{\sqrt{a}\ –\ 3\sqrt{b}}\)

3. Теперь подставим в выражение значения a и b:

\(\frac{\sqrt{a} + 3\sqrt{b}}{\sqrt{a}\ –\ 3\sqrt{b}} = \frac{\sqrt{8} + 3\sqrt{2}}{\sqrt{8}\ –\ 3\sqrt{2}}\)

4. Разложим \(\sqrt{8}\) на множители:

\(\frac{\sqrt{8} + 3\sqrt{2}}{\sqrt{8}\ –\ 3\sqrt{2}} = \frac{\sqrt{4 \bullet 2} + 3\sqrt{2}}{\sqrt{4 \bullet 2}\ –\ 3\sqrt{2}} = \frac{2\sqrt{2} + 3\sqrt{2}}{2\sqrt{2}\ –\ 3\sqrt{2}} = \frac{5\sqrt{2}}{–\sqrt{2}} = \ –5\)

Ответ: \(–5\).

ПРИБЛИЖЕННЫЕ ЗНАЧЕНИЯ КОРНЕЙ:

Приближенное значение корня:

Можно найти приближенное значение любого корня. Для этого предполагают, между какими числами корень может находиться.

Например:

\(\sqrt{30}\)

Округлим \(\sqrt{30}\) до целого. Представим его как число, заключенное между какими-то натуральными числами. Мы знаем, что ближайшие значения квадратов для 30 – это 25 (квадрат 5) и 36 (квадрат 6):

\(\sqrt{25} < \sqrt{30} < \sqrt{36}\)

\(5 < \sqrt{30} < 6\)

Значит округление \(\sqrt{30}\) в сторону 5 – это округление с недостатком, а в сторону 6 – округление с избытком. Значит целое значение \(\sqrt{30} = 5\).

Подберем значение \(\sqrt{30}\) до десятых. Найдем квадраты чисел 5,1, 5,2, 5,3 и т.д., пока не найдем два значения, между которыми заключено число 30.

\(\sqrt{29,16} < \sqrt{30} < \sqrt{30,25}\)

\(5,4 < \sqrt{30} < 5,5\)

Теперь мы знаем, что число \(\sqrt{30}\) = 5,4 до десятков. Таким образом можно найти приближенное значение корня до любого разряда.

СРАВНЕНИЕ КОРНЯ С ЧИСЛОМ:

Чтобы сравнить корень и число, нужно возвести оба числа в квадрат:

\(a > b \Longleftrightarrow a^{2} > b^{2} \Longleftrightarrow \sqrt{a} > \sqrt{b}\)

Сравнить:

\(\sqrt{98}\ и\ 9\)

1. {2}\)

\(98\ и\ 81\)

2. Определим знак неравенства между этими числами. Для их корней знак будет таким же:

\(98 > 81\)

\(\sqrt{98} > 9\)

Если корень сравнивают с отрицательным числом, то возводить оба числа в квадрат не нужно. Любой корень всегда будет больше отрицательного числа, т.к. любое положительное число больше отрицательного:

\(\sqrt{a}\ и\ b,\ при\ b < 0\)

\(a > 0\ по\ определению\ корня\)

\(b < 0 < \sqrt{a}\)

\(b < \sqrt{a}\)

Квадратный корень — Формула, Примеры

Квадратный корень из числа — это операция, обратная возведению числа в квадрат. Квадрат числа — это значение, которое получается, когда мы умножаем число само на себя, а квадратный корень из числа получается путем нахождения числа, которое при возведении в квадрат дает исходное число.

Если «а» — это квадратный корень из «b», это означает, что a × a = b. Квадрат любого числа всегда является положительным числом, поэтому каждое число имеет два квадратных корня, один из которых имеет положительное значение, а другой — отрицательное. Например, и 2, и -2 являются квадратными корнями из 4. Однако в большинстве случаев только положительное значение записывается как квадратный корень из числа.

1.	Что такое квадратный корень?
2.	Как найти квадратный корень?
3.	Таблица квадратного корня
4.	Формула квадратного корня
5.	Упрощение квадратного корня
6.	Квадратный корень из отрицательного числа
7.	Квадрат числа
8.	Как найти квадрат числа?
9.	Квадраты и квадратные корни
10.	Часто задаваемые вопросы о Square Root

Что такое квадратный корень?

Квадратный корень из числа — это такой множитель числа, который при умножении на себя дает исходное число. Квадраты и квадратные корни являются специальными показателями. Рассмотрим число 9. Когда 3 умножается само на себя, в результате получается 9. Это можно записать как 3 × 3 или 3 ² . Здесь показатель степени равен 2, и мы называем его квадратом. Теперь, когда показатель степени равен 1/2, он относится к квадратному корню из числа. Например, √n = n ^1/2 , где n — целое положительное число.

Квадратный корень Определение

Квадратный корень из числа равен степени 1/2 этого числа. Другими словами, это число, произведение которого само по себе дает исходное число. Он представлен с помощью символа «√». Символ квадратного корня называется радикалом, тогда как число под символом квадратного корня называется радикалом.

Как найти квадратный корень?

Чтобы найти квадратный корень числа, мы просто смотрим, возводя в квадрат, какое число даст фактическое число. Очень легко найти квадратный корень из числа, являющегося полным квадратом. Совершенные квадраты — это положительные числа, которые можно представить как произведение числа самого на себя. Другими словами, совершенные квадраты — это числа, которые выражаются как значение степени 2 любого целого числа. Мы можем использовать четыре метода, чтобы найти квадратный корень из чисел и эти методы следующие:

• Метод повторного вычитания
• Метод простой факторизации
• Метод оценки
• Метод длинного деления

Следует отметить, что первые три метода удобно использовать для полных квадратов, а четвертый метод, т. е. метод деления в длину, можно использовать для любого числа, независимо от того, является оно полным квадратом или нет.

Метод многократного вычитания квадратного корня

Это очень простой метод. Мы вычитаем последовательные нечетные числа из числа, для которого мы находим квадратный корень, пока не достигнем 0. Количество раз, которое мы вычитаем, является квадратным корнем данного числа. Этот метод работает только для совершенных квадратных чисел. Найдем квадратный корень из 16, используя этот метод.

1. 16 — 1 = 15
2. 15 — 3 =12
3. 12 — 5 = 7
4. 7- 7 = 0

Вы можете заметить, что мы вычли 4 раза. Таким образом, √16 = 4 ·

Извлечение квадратного корня с помощью метода факторизации простых чисел

Факторизация любого числа простыми числами означает представление этого числа как произведения простых чисел. Чтобы найти квадратный корень данного числа с помощью метода простой факторизации, мы следуем шагам, приведенным ниже:

• Шаг 1: Разделите данное число на его простые множители.
• Шаг 2: Сформируйте пары факторов так, чтобы оба фактора в каждой паре были равны.
• Шаг 3: Возьмите один множитель из пары.
• Шаг 4: Найдите произведение множителей, полученных путем взятия одного множителя из каждой пары.
• Шаг 5: Этот продукт представляет собой квадратный корень из заданного числа.

Найдем квадратный корень из 144 этим методом.

Этот метод работает, когда заданное число является числом в идеальном квадрате.

Извлечение квадратного корня с помощью метода оценки

Оценка и аппроксимация относятся к разумному предположению фактического значения, чтобы сделать расчеты более простыми и реалистичными. Этот метод помогает в оценке и аппроксимации квадратного корня из заданного числа. Воспользуемся этим методом, чтобы найти √15. Найдите ближайшее к 15,9 число в форме идеального квадрата.а 16 — числа с совершенным квадратом, ближайшие к 15. Мы знаем, что √16 = 4 и √9 = 3. Отсюда следует, что √15 лежит между 3 и 4. Теперь нам нужно посмотреть, ближе ли √15 к 3 или 4. Рассмотрим 3,5 и 4. Так как 3,5 ² = 12,25 и 4 ² = 16. Таким образом, √15 лежит между 3,5 и 4 и ближе к 4.

Найдем квадраты 3,8 и 3,9. Так как 3,8 ² = 14,44 и 3,9 ² = 15,21. Это означает, что √15 находится между 3,8 и 3,9. Мы можем повторить процесс и проверить между 3,85 и 3,9.. Мы можем заметить, что √15 = 3,872.

Это очень долгий и трудоемкий процесс.

Вычисление квадратного корня методом деления в длину

Деление в длину — это метод деления больших чисел на этапы или части, разбивающий задачу деления на последовательность более простых шагов. С помощью этого метода мы можем найти точный квадратный корень из любого заданного числа. Давайте разберемся с процессом нахождения квадратного корня методом деления в длину на примере. Найдем квадратный корень из 180.

• Шаг 1: Поместите черту над каждой парой цифр числа, начиная с разряда единиц (крайняя правая сторона). У нас будет две пары, т.е. 1 и 80
• Шаг 2: Мы делим самое левое число на наибольшее число, квадрат которого меньше или равен числу в самой левой паре.

Шаг 3: Опустите число под следующей чертой справа от остатка. Прибавьте к делителю последнюю цифру частного. Справа от полученной суммы найдите подходящее число, которое вместе с результатом суммы образует новый делитель для нового делимого, переносимого вниз.

Шаг 4: Новое число в частном будет иметь то же число, которое было выбрано в делителе. Условие то же — либо меньше, либо равно дивиденду.

Шаг 5: Теперь мы продолжим этот процесс дальше, используя десятичную точку и добавляя нули попарно к остатку.

Шаг 6: Полученное частное будет квадратным корнем числа. Здесь квадратный корень из 180 приблизительно равен 13,4 и больше знаков после запятой можно получить, повторив тот же процесс следующим образом.

Таблица квадратного корня

Таблица квадратного корня состоит из чисел и их квадратных корней. Также полезно находить квадраты чисел. Вот список квадратных корней из совершенных квадратных чисел и некоторых несовершенных квадратных чисел от 1 до 10.

Число	Квадратный корень
1	1
2	1,414
3	1,732
4	2
5	2,236
6	2,449
7	2,646
8	2,828
9	3
10	3,162

Числа, не являющиеся полными квадратами, являются иррациональными числами.

Формула квадратного корня

Квадратный корень числа имеет показатель степени 1/2. Формула квадратного корня используется для нахождения квадратного корня из числа. Мы знаем формулу экспоненты: \(\sqrt[\text{n}]{x}\) = x ^1/n . Когда n = 2, мы называем это квадратным корнем. Мы можем использовать любой из вышеперечисленных методов для нахождения квадратного корня, например, разложение на простые множители и так далее. 9 ^1/2 = √9 = √(3×3) = 3. Итак, формула для записи квадратного корня числа: √x= x ^1/2 .

Упрощение квадратного корня

Чтобы упростить квадратный корень, нам нужно найти простую факторизацию данного числа. Если фактор не имеет пары, сохраните их под символом квадратного корня, в противном случае извлеките одно число из квадратного корня из каждой пары. Например: √12 = \(\sqrt{2 \times 2\times3}\) = 2√3. Это связано с тем, что правило упрощения квадратного корня таково: √xy = √(x × y), где x и y — положительные целые числа.

Для дробей также действует аналогичное правило: √x/√y = √(x/y). Например: √50/√10 = √(50/10)= √5

Квадратный корень из отрицательного числа

Квадратный корень из отрицательного числа не может быть действительным числом, поскольку квадрат является либо положительным числом, либо нулем. Но у комплексных чисел есть решения квадратного корня из отрицательного числа. Главный квадратный корень -x равен: √(-x)= i√x. Здесь i — квадратный корень из -1.

Например: возьмем квадратное число, например 16. Теперь давайте посмотрим на квадратный корень из -16. Настоящего квадратного корня из -16 не существует. √(-16)= √16 × √(-1) = 4i (как √(-1)= i), где i представлено как квадратный корень из -1. Итак, 4i — это квадратный корень из -16.

Квадрат числа

Любое число, возведенное в степень два (y ² ), называется квадратом основания. Итак, 5 ² или 25 называется квадратом числа 5, а 8 ² или 64 — квадратом числа 8. Мы можем легко найти квадрат числа, умножив число два раза. Например, 5 ² = 5 × 5 = 25 и 8 ² = 8 × 8 = 64. Когда мы находим квадрат целого числа, полученное число представляет собой полный квадрат. Некоторые из идеальных квадратов, которые у нас есть, это 4, 9., 16, 25, 36, 49, 64 и так далее. Квадрат числа всегда положительное число.

☛Также проверьте:

• Квадрат от 1 до 50
• Квадрат от 1 до 30
• Квадрат от 1 до 20
• Квадрат от 1 до 25
• Квадраты от 1 до 100
• Квадрат от 1 до 40

Как найти квадрат числа?

Квадрат числа можно найти, умножив число само на себя. Для однозначных чисел мы можем использовать таблицы умножения, чтобы найти квадрат, а в случае двух или более двузначных чисел мы выполняем умножение числа само по себе, чтобы получить ответ. Например, 9× 9 = 81, где 81 — это квадрат 9. Аналогично, 3 × 3 = 9, где 9 — это квадрат 3.

Квадрат числа записывается путем возведения в степень числа 2. Например, квадрат 3 записывается как 3 ² и читается как «3 в квадрате». Вот несколько примеров:

• 4 ² = 4 × 4 = 16
• (-6) ² = -6 × -6 = 36
• (5/3) ² = 5/3 × 5/3 = 25/9

Квадраты и квадратные корни

Существует очень сильная связь между квадратами и квадратными корнями, поскольку каждый из них является обратным отношением другого. т. е. если x ² = y, то x = √y. Его можно просто запомнить так:

• Когда «квадрат» удаляется из одной части уравнения, мы получаем квадратный корень с другой стороны. Например, 4 ² = 16 означает, что 4 = √16. Это также известно как «извлечение квадратного корня с обеих сторон».
• Когда «квадратный корень» удаляется из одной части уравнения, мы получаем квадрат с другой стороны. Например, √25 = 5 означает, что 25 = 5· ² . Это также известно как «квадрат с обеих сторон»

Эта логика помогает решать многие уравнения в алгебре. Рассмотрим следующий пример:

Пример: Решите уравнение √(2x + 3) = 10.

Решение:

Возведение в квадрат обеих частей уравнения приведет к сокращению квадратного корня слева сторона.

2x + 3 = 10 ²

2x + 3 = 100

2x = 97

x = 97/2 = 48,5

Вот еще различия между квадратами и квадратными корнями.

9)

	Квадраты	Квадратные корни
Определение	Произведение числа, умноженного само на себя.	Это число, которое при умножении само на себя дает исходное число.
Пример	7 2 = 49	Квадратный корень (√)
Результат	Положительный всегда.	Может быть как положительным, так и отрицательным.
Домен	Набор всех действительных чисел	Набор всех неотрицательных действительных чисел.
Обратный	Обратное значение квадрата равно квадратному корню.	Обратное значение квадратного корня равно квадратному.

☛ Статьи по теме

• Калькулятор уравнения квадратного корня
• Рабочие листы по квадратным корням

Квадратный корень из чисел

Cuemath — одна из ведущих мировых обучающих платформ по математике, которая предлагает онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

Часто задаваемые вопросы о квадратном корне

Что такое квадратный корень в математике?

квадратный корень из числа — это число, которое при умножении само на себя дает действительное число. Например, 2 — это квадратный корень из 4, и это выражается как √4 = 2. Это означает, что если 2 умножить на 2, получится 4, и это можно проверить как 2 × 2 = 4.

☛ Проверить :

• Квадратный корень от 1 до 10
• Квадратный корень от 1 до 20
• Квадратный корень от 1 до 25
• Квадратный корень от 1 до 30
• Квадратный корень от 1 до 50
• Квадратный корень от 1 до 100

Как вычислить квадратный корень из числа?

Очень легко найти квадратный корень из числа, которое является полным квадратом. Например, 9 — это полный квадрат, 9 = 3 × 3. Итак, 3 — это квадратный корень из 9, и это можно выразить как √9 = 3. Квадратный корень из любого числа, как правило, можно найти, используя любым из четырех способов, приведенных ниже:

• Метод повторного вычитания
• Метод простой факторизации
• Метод оценки и приближения
• Метод длинного деления

Может ли квадратный корень быть отрицательным?

Да, квадратный корень из числа может быть отрицательным. Фактически, все совершенные квадраты, такие как 4, 9, 25, 36 и т. д., имеют два квадратных корня, один из которых является положительным значением, а другой — отрицательным. Например, квадратные корни из 4 равны -2 и 2. Чтобы убедиться в этом, мы можем увидеть, что (-2) × (-2) = 4. Точно так же квадратные корни из 9равны 3 и -3.

Как найти квадратный корень из десятичного числа?

Квадратный корень из десятичного числа можно найти с помощью метода оценки или метода деления в большую сторону. В случае десятичных чисел мы делаем пары целых частей числа и дробных частей отдельно. И затем, мы выполняем процесс деления в длинную точно так же, как и любое другое целое число.

Что такое символ квадратного корня?

Символ, который используется для обозначения квадратного корня, называется подкоренным знаком ‘√ ‘. Термин, написанный внутри подкоренного знака, называется подкоренным.

Как умножить два значения квадратного корня?

Допустим, у нас есть два числа a и b. Сначала найдем квадратный корень из чисел a и b. Затем, после нахождения квадратного корня, мы умножаем значение квадратного корня вместе. Поясним это на практической иллюстрации. Например, умножьте √4 × √16. Квадратный корень из 4 равен 2 (√4 = 2), а квадратный корень из 16 равен 4 (√16 = 4). Теперь мы умножим значение квадратного корня из 4 и 16, т. е. 2 × 4 = 8. Вместо этого мы можем применить свойство квадратных корней, √a × √b = √ab.

Что такое формула для вычисления квадратного корня числа?

Квадратный корень из любого числа можно выразить по формуле: √y = y ^½ . Другими словами, если показатель степени числа равен 1/2, это означает, что нам нужно найти квадратный корень из числа.

Что такое квадрат и квадратный корень числа?

Квадрат числа — это произведение, которое получается при умножении числа само на себя. Например, 6 × 6 = 36. Здесь 36 — это квадрат 6. Квадратный корень числа — это множитель числа, и когда он умножается сам на себя, получается исходное число. Теперь, если мы хотим найти квадратный корень из 36, то есть √36, мы получим ответ как √36 = 6. Следовательно, мы можем видеть, что квадрат и квадратный корень числа являются обратными операциями каждого другой.

Какой метод используется для нахождения квадратного корня из неполных квадратных чисел?

В математике несовершенным или несовершенным квадратным числом считается число, квадратный корень которого не может быть найден как целое число или как дробь целых чисел. Квадратный корень из несовершенного квадратного числа можно вычислить, используя метод деления в длинную сторону.

Как найти квадратный корень на калькуляторе?

Чтобы найти значение квадратного корня любого числа на калькуляторе, нам просто нужно ввести число, для которого мы хотим получить квадратный корень, а затем вставить символ квадратного корня √ в калькулятор. Например, если нам нужно найти квадратный корень из 81, мы должны ввести 81 в калькулятор, а затем нажать символ √, чтобы получить его квадратный корень. Мы получим √81 = 9.

☛ Проверить:

• Калькулятор квадратного корня
• Калькулятор квадратного корня дроби
• Добавление калькулятора квадратных корней
• Калькулятор умножения квадратных корней
• Упрощение калькулятора квадратных корней

Каковы применения формулы квадратного корня?

Существуют различные применения формулы квадратного корня:

• Формула квадратного корня в основном используется в алгебре и геометрии.
• Помогает найти корни квадратного уравнения.
• Широко используется инженерами.

Что означает квадрат числа?

Произведение, которое получается при умножении числа само на себя, — это квадрат числа. Например, 5 × 5 = 25. Здесь 25 — это квадрат 5, и это также можно записать как 5 ² = 25.

Как вычислить квадратный корень из отрицательного числа?

Обратите внимание, что квадратный корень из отрицательного числа не является действительным числом. Это мнимое число. Например, √(-4) = √(-1) × √4 = i (2) = 2i, где ‘i’ известно как «йота», а i ² = -1 (или) i = √(-1).

Почему квадрат отрицательного числа положительный?

Квадрат отрицательного числа положителен, потому что при умножении двух отрицательных чисел всегда получается положительное число. Например, (-4) × (-4) = 16.

what-is-the-cube-root-of-mc010-1-jpg — Googlesuche

AlleBilderBücherNewsMapsVideosShopping

suchoptionen

корень 512m12n15 Кто-нибудь может мне помочь?

brainly. com › Математика › Средняя школа

Ответ: Пошаговое объяснение: кубический корень – это, по сути, преобразование в степень. Кроме того, есть имущество, которое есть.

Ähnliche Fragen

Как найти кубический корень из 1331?

Чему равен кубический корень из 512 м?

Что такое кубический корень из 100?

Калькулятор кубического корня

www.calculatorsoup.com › Алгебра

Используйте этот калькулятор для нахождения кубического корня из положительных или отрицательных чисел. Для числа x кубический корень из x — это число a такое, что a3 = x.

Кубические корни 1-10 Карточки — Quizlet

quizlet.com › Кубические корни-1-10-флэш-карточки

Bewertung 4,4

(24)

Изучайте с помощью карточек и запоминайте термины как 1, 8, 27 и больше. … 1. кубический корень из 1. 8. кубический корень из 2. 27. кубический корень из 3.

Что такое кубический корень из mc010 1 jpg (FF5XTY)

nxwd. kintzelfoto.de

Что это кубический корень mc010 1 jpg Войдите в свой веб-интерфейс pfSense, перейдите в Брандмауэр/Псевдонимы и нажмите Добавить. Войдите в свой pfSense Web …

Онлайн-калькулятор кубического корня

www.cuemath.com › калькуляторы › вычисление кубического корня…

Воспользуйтесь онлайн-калькулятором кубического корня Cuemath и найдите кубический корень всего одним щелчком мыши. Попробуйте свои силы в нашем онлайн-калькуляторе кубического корня …

в кубе в математическом определении

rygks.hopfnei.de › …

Определение кубического корня (Иллюстрированный математический словарь) В некоторых случаях, особенно когда число… Что такое кубический корень из mc010 1 jpg — OPAM.

найти все действительные кубические корни каждого числа . … 1.3: Квадратные и кубические корни из действительных чисел …

Math is — i-Novative

nrwnu.i-novative-shop.de › важные-вопросы-для.