Числа π и e
Все знают геометрический смысл числа π — это длина окружности с единичным диаметром:
А вот смысл другой важной константы, e, имеет свойство быстро забываться. То есть, не знаю, как вам, а мне каждый раз стоит усилий вспомнить, чем же так замечательно это число, равное 2,7182818284590… (значение я, однако, по памяти записал). Поэтому я решил написать заметку, чтобы больше из памяти не вылетало.
Число e по определению — предел функции y = (1 + 1 / x)x при x → ∞:
| x | y | |
| 1 | (1 + 1 / 1)1 | = 2 |
| 2 | (1 + 1 / 2)2 | = 2,25 |
| 3 | (1 + 1 / 3)3 | = 2,3703703702… |
| 10 | (1 + 1 / 10)10 | = 2,5937424601. |
| 100 | (1 + 1 / 100)100 | = 2,7048138294… |
| 1000 | (1 + 1 / 1000)1000 | = 2,7169239322… |
| ∞ | lim× → ∞ | = 2,7182818284590… |
Это определение, к сожалению, не наглядно. Непонятно, чем замечателен этот предел (несмотря на то, что он называется «вторым замечательным»). Подумаешь, взяли какую-то неуклюжую функцию, посчитали предел. У другой функции другой будет.
Но число e почему-то всплывает в целой куче самых разных ситуаций в математике.
Для меня главный смысл числа e раскрывается в поведении другой, куда более интересной функции, y = kx. Эта функция обладает уникальным свойством при k = e, которое можно показать графически так:
В точке 0 функция принимает значение e0 = 1. Если провести касательную в точке x
= 0, то она пройдёт к оси абсцисс под углом с тангенсом 1 (в жёлтом треугольнике отношение противолежащего катета 1 к прилежащему 1 равно 1).
В точке 1 функция принимает значение e1 = e. Если провести касательную в точке x = 1, то она пройдёт под углом с тангенсом e (в зелёном треугольнике отношение противолежащего катета e к прилежащему 1 равно e). В точке 2 значение e2 функции снова совпадает с тангенсом угла наклона касательной к ней. Из-за этого, заодно, сами касательные пересекают ось абсцисс ровно в точках −1, 0, 1, 2 и т. д.Среди всех функций y = kx (например, 2x, 10x, πx и т. д.), функция ex — единственная обладает такой красотой, что тангенс угла её наклона в каждой её точке совпадает со значением самой функции. Значит по определению значение этой функции в каждой точке совпадает со значением её производной в этой точке: (
.. нужно возводить в разные степени, чтобы получилась такая картинка.Именно в этом, на мой вкус, состоит его смысл.
Числа π и e входят в мою любимую формулу — формулу Эйлера, которая связывает 5 самых главных констант — ноль, единицу, мнимую единицу i и, собственно, числа π и е:
eiπ + 1 = 0
Почему число 2,7182818284590… в комплексной степени 3,1415926535…i вдруг равно минус единице? Ответ на этот вопрос выходит за рамки заметки и мог бы составить содержание небольшой книги, которая потребует некоторого начального понимания тригонометрии, пределов и рядов.
Меня всегда поражала красота этой формулы. Возможно, в математике есть и более удивительные факты, но для моего уровня (тройка в физико-математическом лицее и пятёрка за комплексный анализ в универе) это самое главное чудо.
Икс\). X может быть любым числом или значением степени по вашему выбору, а e — показателем степени. Этот калькулятор также отображает простое решение для улучшения вашего понимания.
Продолжайте читать, чтобы узнать, чему равно e и как вычислить e. Тем не менее, начните с некоторых основ. Что такое Е в математике? E до x — одна из самых значимых констант в области математики. Мы не можем записать значение e в виде дроби, и оно имеет неизмеримое количество знаков после запятой. В арифметике оно известно как число Эйлера или натуральное число. 9n\) по мере того, как n приближается к бесконечности, и мы можем вычислить его как сумму бесконечного ряда.
Вы можете использовать этот бесплатный онлайн-калькулятор логарифмов, который поможет рассчитать логи и обратный логарифм по любой системе счисления.
Что означает E в калькуляторе (от e до x)?На дисплее калькулятора буква e представляет собой степень числа 10, за которой следует другое число. Это число будет известно как значение показателя степени. Например, электронный калькулятор может отображать число 25 триллионов как:
- 5e13.
В этом примере \(13\) — показатель степени \(10\), а \(2,5\) — показатель степени.
Для удобства онлайн-калькулятор экспоненты позволяет решать операции экспоненты, а также находить значение любого положительного или отрицательного целого числа, возведенного в n-ю степень.
Как рассчитать от Е до Х?Существует множество способов вычислить от е до х, но нет ни одного метода, от которого мы могли бы полностью зависеть в точности нашего ответа. Причина в том, что e иррационально и его цифры повторяются без ограничений. Хотя мы можем определить это следующим образом:
- Значение e = \( 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + … и т. д.\) .
- В этом примере знак «!» представляет факториалы
- Мы добавим первые несколько до: \(1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 = 2,71666…\)
Эйлер также использовал эту технику для вычисления e с точностью до 18 знаков после запятой. Тем не менее, вы можете попробовать электронный калькулятор, чтобы избежать этой суеты!
График E of X: Это может быть сложно изобразить, потому что все его значения y будут десятичными приближениями.
Следовательно, вы должны округлить эти значения, чтобы легко построить график. График e of x выглядит следующим образом:
| нет | (1 + 1/н) | |
| 1 | 2.00000 | |
| 2 | 2,25000 | |
| 5 | 2,48832 | |
| 10 | 2,59374 | |
| 100 | 2.70481 | |
| 1000 | 2,71692 | |
| 10 000 | 2,71815 | |
| 100 000 | 2,71827 9х | Число Эйлера |
| и 1 | 2,71828 | |
| и 2 | 7.38906 | |
| и 3 | 20.08554 | |
| и 4 | 54.59815 | |
| и 5 | 148. 41316 | |
| и 6 9Икс\). Калькулятор рассчитает:
Калькулятор позволяет производить неограниченное количество вычислений бесплатно. Часто задаваемые вопросы: Что такое E Infinity Value? E значение бесконечности будет равно нулю. Причина в том, что когда мы умножаем постоянное число на бесконечность, ответ будет равен нулю. Бесконечное значение E означает, что мы должны повышать e с очень высокой скоростью, поэтому это приведет к очень большому числу. Так что в качестве вывода можно сказать, что е, возведенное в бесконечность мощности, есть бесконечность. Однако дело обстоит иначе, если у нас есть определенное число. Например, e в степени 1 будет равно \( 2,718282……\) и т. Математик по имени Леонард Эйлер открыл число e и вычислил его значение с точностью до 23 знаков после запятой. Определенные свойства числа e сделали его «натуральным» числом в качестве логарифмического основания. Может ли E в степени равняться 0?Рассматривается как функция действительных чисел и имеет бесконечную область определения и диапазон, равный 0, ∞. Таким образом, он принимает только положительные значения, а 0 — единственное значение, которое ex не может принимать. Эти два номера не связаны. π было открыто в начале геометрии, тогда как e — относительно новое понятие, связанное с теорией пределов и функциональным анализом. Wind-up Context: С помощью этого бесплатного калькулятора e люди могут определить значение e, возведенное в степень x, за долю секунды. Как видите, значение E равно бесконечности, следовательно, его ручные вычисления могут быть сложными, довольно хлопотными и занимать много времени. Из источника Википедии: Стандартное нормальное распределение, Расстройства, Задачи оптимального планирования. Из источника Popular Mechanics: постоянная Эйлера, кто открыл постоянную Эйлера? Использование константы Эйлера для расчета сложных процентов. Из источника Aops Online: число Эйлера, число Эйлера как основание логарифмов и экспоненциальных функций, число Эйлера и исчисление, число Эйлера и исчисление.
Что такое число e?
Вам когда-нибудь было интересно, почему число e так популярно в математике? Число Эйлера, представляющее собой бесконечно длинное десятичное число, близкое к 2,71828, естественным образом появляется в удивительно широком диапазоне условий. Это число впервые появилось в 1683 году, когда Якоб Бернулли, преподаватель Базельского университета, изучал сложные проценты. Он хотел выяснить, что произойдет, если банк начислит проценты по кредиту в 1 доллар со 100-процентной годовой процентной ставкой бесконечное количество раз в год. Число, которое он нашел, было e . Уравнение выглядит так: Математик Леонард Эйлер дал e свое имя в 1731 году. С тех пор e был обнаружен в таких условиях, как вероятность, статистика, инженерия, биология, термодинамика и физика. «Представьте, что 100 человек идут на вечеринку, и все они вешают свои пальто на вешалку», — говорит По-Шен Лох, профессор математики в Университете Карнеги-Меллона, Popular Mechanics . «И когда они закончили, хозяин просто подходит к вешалке и вручает пальто каждому наугад. Число также появляется на кривых нормального распределения, которые можно найти в статистике случайных величин, которые складываются. Общее уравнение для кривой нормального распределения: Wikimedia Commons Число e , возведенное в степень, появляется в научных и инженерных уравнениях для датирования углерода, пружинного демпфирования, изменения температуры, роста бактерий и многого другого. «Датирование по углероду-14 имеет экспоненциальный спад», — говорит Синпин Сунь, выдающийся профессор математического факультета Университета штата Миссури.0296 Популярная механика . «Когда мы находим кость динозавра и говорим, что ей 614 миллионов лет, в то время вокруг никого не было. Откуда мы знаем, что этой кости был миллион лет? Мы используем датирование по углероду-14. Сан говорит, что уравнение для этого: Хотите верьте, хотите нет, но замедляющаяся пружина, которая демпфируется при отскоке, подчиняется аналогичному уравнению. «Если мы позволим блоку [с пружиной] колебаться в какой-то жидкости, он будет колебаться вперед и назад с немного меньшей амплитудой каждый раз», — объясняет Зак Стар, создатель одноименного образовательного канала STEM на YouTube, в видео о число и . «Огибающая этого уравнения, которая как бы сжимает его до нуля, имеет уравнение экспоненциального распада, которое включает e в некоторое отрицательное постоянное время». Охлаждающийся пирог, извлеченный из духовки, также соответствует приведенному выше уравнению. Константа C o — начальная температура. ✅ Стань умнее
|
д.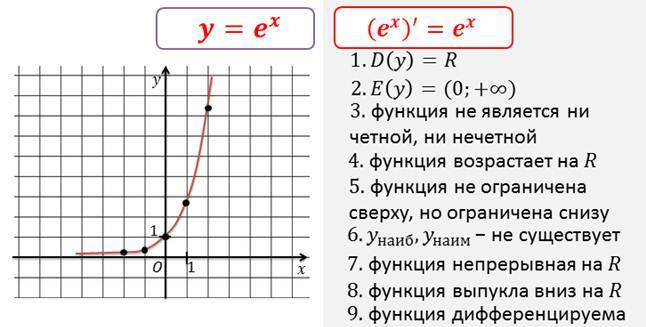
Поэтому не стесняйтесь использовать этот инструмент в образовательных и обучающих целях, поскольку вы поддерживаете экономию своего времени и усилий.
Математики называют это «естественным» отчасти потому, что оно встречается очень часто.
Каков шанс, что никому не вернут свою вещь? Получается, что шанс идет к 1/ e , так как этим занимается все больше и больше людей».
В течение жизни динозавра углерод-14 остается постоянным. Когда динозавр умирает… кость со временем начинает терять углерод-14».
