Как определить матрицу: Матрицы: определение и основные понятия.

alexxlab / / Разное

4.1.1 Матрицы и определители. Основные понятия

Исторически понятия матрицы и определителя появились в связи с изучением систем линейных уравнений. Мы же начнем изучение линейной алгебры с этих двух понятий, а затем покажем, каким образом можно использовать матричный аппарат для решения других задач.

Определение. Матрицей размера называется прямоугольная таблица, составленная из чисел ( строк, столбцов).

Обозначаются матрицы

, ,

Или кратко: , или одной буквой, например .

В частности, когда , матрица состоит из одной строки и называется матрицей – строкой. Если же , а , то получаем одностолбцовую матрицу, которую называют матрицей-столбцом.

Числа называются элементами матрицы.

Вообще, элементы матрицы могут быть произвольной природы, однако в данном разделе рассматриваются числовые матрицы.

Если , то матрицу называют квадратной матрицей порядка .

Определение. Перестановку чисел , когда большее число стоит раньше (левее) меньшего, назовем инверсией или беспорядком.

Число инверсий в перестановке обозначается .

Например, (Слагаемые в сумме показывают, сколько инверсий образуют числа в исходной перестановке).

Определение. Определителем Квадратной матрицы -го порядка называется алгебраическая сумма слагаемых, в каждом из которых сомножителей, взятых по одному и только по одному из каждой строки и каждого столбца, причем каждое слагаемое имеет множитель , где – число инверсий в перестановке верхних индексов (индексов строк), – число инверсий в перестановке нижних индексов (индексов столбцов). Число называется порядком определителя.

Для обозначения определителя используются символы:

Замечание 1. Определитель – число, поэтому, когда говорят о строках и столбцах определителя, то под этим понимают строки и столбцы соответствующей матрицы.

Замечание 2. Если верхние (нижние) индексы расположить в порядке возрастания (что достигается перестановкой сомножителей), то для определения знака каждого слагаемого в определителе достаточно сосчитать число инверсий только среди нижних (верхних) индексов.

Пример 1. Какое из слагаемых: a) , b) , c) , d) входит в качестве слагаемого в определитель 4-го порядка и с каким знаком?

Решение. Произведения b) и d) не могут войти в качестве слагаемых в определитель 4-го порядка, так как в b) присутствуют два элемента из второго столбца (должно быть по одному), а из четвертого столбца нет ни одного элемента; произведение d) имеет пять сомножителей, а у определителя 4-ого порядка четыре cтроки и четыре столбца. Два других произведения входят в качестве слагаемого в определитель 4-ого порядка, так как каждая строка и каждый столбец представлены единственным элементом, причем а) входит со знаком плюс, а с) со знаком минус. Действительно, расположим, допустим, нижние индексы по порядку , и сосчитаем , . Перед слагаемым а) будет множитель , а перед с) множитель , которые и определяют знак.

Можно было бы не наводить порядок среди индексов, тогда для слагаемого а) нужно сосчитать , и поставить перед ним знак , для слагаемого с) считаем , и ставим знак .

Пример 2. Выбрать значения и так, чтобы произведение входило в определитель пятого порядка со знаком минус.

Решение. По верхним индексам видим, что в произведении первая, третья и пятая строки представлены каждая своим элементом, а вторая и четвертая – нет. Следовательно, и должны принимать значения или . Имеется две возможности: 1) , или 2) , . Исследуем знак слагаемого в каждой ситуации. Для этого расположим индексы столбцов по порядку и найдем , . Итак, исследуемое слагаемое войдет в определитель пятого порядка со знаком минус, если положить , .

Определение. Матрица , полученная из матрицы заменой строк столбцами с теми же номерами и наоборот, называется транспонированной по отношению к .

.

Определители обладают рядом свойств, которые лежат в основе практических способов их вычисления.

Свойство 1. Определитель квадратной транспонированной матрицы равен определителю исходной матрицы.

Отсюда следует, что строки и столбцы определителя равноправны, т. е. любое свойство определителя, доказанное для строк, справедливо и для столбцов и наоборот.

Свойство 2. При перестановке любых двух строк определитель меняет знак.

Свойство 3. Определитель, имеющий две одинаковые строки, равен нулю.

Свойство 4.

 Общий множитель всех элементов некоторой строки определителя можно выносить за знак определителя.

Свойство 5. Определитель, содержащий две пропорциональные строки, равен нулю.

Свойство 6. Если все элементы некоторой строки определителя равны нулю, то определитель равен нулю.

Свойство 7. Определитель не изменится, если к элементам одной из его строк прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

< Предыдущая   Следующая >

Какая матрица в телевизоре? Как определить

Эта статья является в некоторой степени руководством по определению типа матриц экрана телевизора самостоятельно. Данный метод относится не только к матрицам TV, но и к матрицам мониторов, ноутбуков и других устройств, в которых применена ЖК-матрица. Метод фотографирования, о котором будет рассказано ниже, не единственный, но он более доступный, надежный и бесплатный для того, чтобы проверить, какой тип матрицы в телевизоре используется.

Лучшая матрица

Производитель телевизоров обычно не сообщает тип используемой матрицы для каждой конкретной модели. Маркетологи считают, что точная информация может «отвести» от покупки, если у потребителя есть предубеждение против какого-то определённого типа матриц.

Хотя нужно ясно понимать, что будь у одного из видов ЖК-панелей явное преимущество перед другими, то именно этот вид и использовался бы всеми брендами. Однако дисперсия основных характеристик матриц, влияющих на качество изображения, невелика. Поэтому производители, что называется, находятся в вечном поиске чаши Грааля.

Так, например, тип матрицы IPS имеет самые широкие углы обзора и естественные цвета, но страдает низкой контрастностью. VA-матрица, напротив, имеет отличный контраст, но не допускает качественного просмотра ТВ под углом. TN-матрица, применяемая чаще в мониторах, нежели в телевизорах, имеет качество изображения гораздо ниже, чем две вышеперечисленные панели.

Однако она обладает самым низким временем задержки, что очень ценно для компьютерных игр. Кроме того, себестоимость при ее производстве гораздо ниже, чем у VA и IPS. Можно, конечно, было бы назвать лучшей матрицу OLED (Organic Light Emitting Diode), у которой бесконечный контраст и с углами обзора всё в порядке…

Однако ее себестоимость намного дороже. Кроме того, OLED-матрица сильнее подвержена риску «ожога», чем ЖК. А поскольку нет однозначного ответа на вопрос: «Какой тип матрицы лучше», то самый лучший способ – определить матрицу самому.

Можно узнать тип матрицы по ее признакам?

Определить тип матрицы по ее признакам конечно же можно. Мы только что описали признаки основных матриц, применяемых в телевизорах. Каждая из них имеет свои модификации (PLS, SVA и так далее). Однако есть большой шанс ошибиться. Магазины, продающие телевизоры, работают в основном днем при хорошем освещении.

Поэтому заметить в такое время слабый контраст IPS-матрицы скорее всего не удастся. Кроме того, дорогие телевизоры оснащены локальным затемнением, которое несколько выправляет этот недостаток контраста. Тип матрицы VA может «выдать» себя недостаточными углами обзора. На сегодняшний день дорогие модели уже начали оснащать технологиями, которые заметно расширяют углы обзора.

Есть вариант перед покупкой найти технические характеристики интересующей вас модели. Однако мы уже не раз сталкивались со случаями, когда производитель выпускал телевизор с одной LED-матрицей, а менее чем через полгода заменял ее на другую. При этом в характеристиках появлялось сразу 2 типа матриц. При покупке в интернете это явный кот в мешке, но придя в магазин, вид матрицы можно проверить.

Есть вариант спросить у поддержки, но иногда она тоже не дает прямого ответа. Когда однажды поддержке был задан такой вопрос: «В телевизорах серии UK7550 какая матрица установлена — RGB или RGBW?», то ответ был следующим.

«К сожалению, производитель матриц не раскрывает особенности и конструкции, установленных в телевизорах 2018 года. Приносим извинения за данное неудобство. В этом случае Вы можете самостоятельно определить наличие или отсутствие белого субпикселя в структуре матрицы с помощью увеличительного стекла или специального окуляра при осмотре техники в магазине пред покупкой».

Сразу поясним, что увеличительное стекло или специальный окуляр должен быть немалой кратности. Приобретение такой оптики только для того, чтобы проверить тип матрицы раз в 10 лет, будет совсем нерентабельным. В нашем случае нужен обычный смартфон с видеокамерой средних характеристик. Процесс проверки матрицы опубликован чуть ниже.

Метод фотографирования

Описываемый метод известен многим. Однако постоянные вопросы в комментариях типа: «Какая матрица стоит в телевизоре» подвигли написать эту статью. Кроме того, мы сделали пару собственных изображений матриц VA и IPS. Эти снимки заметно отличаются от тех «лабораторных» фото, которые выложены в интернете.

Начнем с того, что нам нужно сделать макросъемку белого фона при включенном телевизоре. Самый надежный способ — иметь этот фон у себя на флешке. Можно просто сфотографировать фрагмент белого листа бумаги, чтобы не было теней. Еще лучше — создать самим этот фон в графическом редакторе или просто скачать файл, который находится ниже.

Идем с флешкой и своим смартфоном в магазин. Просим продавца воспроизвести файл с флешки. Каким бы капризным не был бы плеер, встроенный в телевизор, файл с расширением .jpg воспроизведется однозначно. Теперь надо перевести камеру смартфона в режим фотоаппарата и просто сфотографировать в режиме макросъемки небольшой участок матрицы.

Приближаем объектив камеры смартфона на минимальное расстояние к матрице. То есть, подносим смартфон примерно на расстояние 5 сантиметров к матрице экрана и начинаем его приближать / отдалять пока не произойдет фокусировка, и вы отчетливо на экране смартфона увидите сетку.

В зависимости от характеристик камеры мобильного телефона это расстояние составляет от 3-х до 12 сантиметров. Качество снимка будет зависеть и от того, насколько у вас дрожали руки при нажатии на кнопку. В результате должен получится примерно вот такой снимок, как внизу.

Теперь следует найти этот снимок в смартфоне, воспроизвести его и увеличивать (раздвигать пальцами) до тех пор, пока не появится такая структура, как на рисунке ниже.

Это матрица VA, применяемая в телевизоре Sony XF9005. На следующей картинке размещен аналогичный снимок.

Однако при его увеличении мы видим совсем другую структуру. Это матрица IPS, применяемая в телевизорах LG. Снимок не идеальный, и оттенки цветов тоже далеко не идеальны. Но при снимке матрицы с обычного смартфона все выглядит именно так. Главное — смотреть на структуру матрицы.

Как узнать матрицу RGBW

Стоит заметить и то, что в отличие от матриц Samsung, матрицы LG делятся на две главные категории: RGB матрица и RGBW матрица. Последняя имеет белый субпиксель в своей структуре. Это не особо сильно сказывается на качестве изображения, но позволяет сократить себестоимость панели примерно на 20 — 25 процентов.

В результате отзывы пользователей примерно такие: «Я бы не хотел покупать телевизор с дисплеем RGBW». О структуре этой панели писалось ранее на сайте UltraHD.su в статье RGBW и RGB отличия. https://ultrahd.su/video/rgbw-rgb-otlichiya.html К сожалению, нам не удалось на этот момент найти телевизор, в котором используется матрица дисплея RGBW, чтобы сделать собственный снимок.

В идеальном варианте структура IPS RGBW выглядит так, как показано на рисунке внизу. То есть при увеличении надо искать наличие / отсутствие дополнительного субпикселя белого цвета.

Матрицы TN и PLS

В заключение добавим еще пару структур матриц, которые чаще всего (кроме вышеперечисленных) используются в мониторах нежели в телевизорах. На левом рисунке размещены два типа матрицы TN. На правом — тип матрицы PLS.

А с какой матрицей купить телевизор собираетесь вы? (Комментарии внизу под статьей).

https://ultrahd.su/video/uznat-matricu-televizora. htmlКакая матрица в телевизоре? Как определить

4K Ultra HDВидеовидеоЭта статья является в некоторой степени руководством по определению типа матриц экрана телевизора самостоятельно. Данный метод относится не только к матрицам TV, но и к матрицам мониторов, ноутбуков и других устройств, в которых применена ЖК-матрица. Метод фотографирования, о котором будет рассказано ниже, не единственный, но он более доступный, надежный…4K Ultra HD SubscriberUltraHD

Определители квадратных матриц



Определители квадратных матриц 
   Math Task
       
 
1.Определители квадратных матриц.
2.Свойства определителей.

 

    
     
  1 2 3 4 5 6 7 8 9  
     
   

1.

Определители квадратных матриц.

   Как известно из раздела матричной алгебры, матрицы получили широкое распрастранение в экономике. Для того, чтобы как-то характеризовать матрицу, а также решать различные задачи с использованием матриц, в математике введено понятие определитель матрицы. Т.е. определитель матрицы — это число, характеризующее матрицу (параметр). Для каждой квадратной матрицы можно рассчитать число по ее элементам по определенной формуле, которое будет ее характеризовать.

  
 

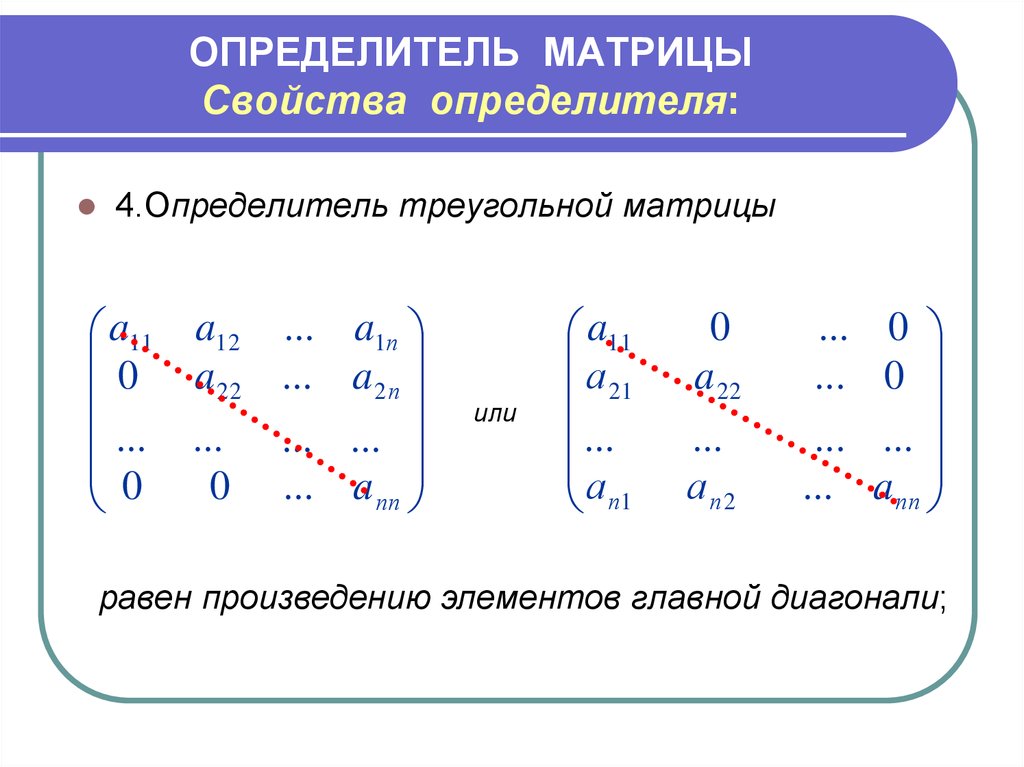
   Для матрицы первого порядка определитель равен элементу а11.

    
 

   Для матрицы второго порядка определитель равен разности произведений элементов матрицы, рассчитанный по формуле:

    
 

   Для матрицы третьего порядка определитель равен числу, рассчитанному по формуле:

    
 

    Определители квадратных матриц можно вычислить и другим способом: с помощью разложения элементов матрицы по строке. Для того, чтобы использовать такой способ, предварительно рассчитывают миноры и алгебраические дополнения. Минором Mij элемента аij называется определитель n-1 порядка, а алгебраическое дополнение это произведение Аij = (-1)i+j Mij

    
     

Таким образом, определитель третьего порядка можно разложить по элементам первой строки так:

    

2.Свойства определителей.

  
 

1. При транспонировании определитель не меняется.

2. Если поменять местами любые две строки (столбца) матрицы, то определитель поменяет знак на противоположный.

3. Для любой матрицы, определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

4. Определитель равен нулю, если матрица содержит две одинаковые строки (столбца).

5. Определитель равен нулю, если все элементы какой-либо строки (столбца) равны нулю.

6. Если суммировать произведения элементов любой строки (столбца) на алгебраические дополнения элементов любой другой строки (столбца), то определитель равен нулю.

7. Общий множитель любой строки (столбца) можно вынести за знак определителя.

  
 
 
         
   

Репетитор: Васильев Алексей Александрович

  
 
 

Предметы: математика, физика, информатика, экономика, программирование.

  2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты.

  
     
 
 
 

Пример.

    
   
         
   
     
  1 2 3 4 5 6 7 8 9  
 
 
     
 

 
     
     
  www. mathtask.ru  
     
     

Матрица Python и введение в NumPy

В этой статье мы узнаем о матрицах Python с использованием вложенных списков и пакета NumPy.

Матрица — это двумерная структура данных, в которой числа расположены в строках и столбцах. Например:

Эта матрица представляет собой матрицу 3×4 (произносится как «три на четыре»), поскольку она имеет 3 строки и 4 столбца.

Python Matrix

Python не имеет встроенного типа для матриц. Однако мы можем рассматривать список списка как матрицу. Например:

 А = [[1, 4, 5],
    [-5, 8, 9]]

Мы можем рассматривать этот список как матрицу, имеющую 2 строки и 3 столбца.

Обязательно изучите списки Python, прежде чем продолжить эту статью.

Давайте посмотрим, как работать с вложенным списком.

 А = [[1, 4, 5, 12],
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]]
печать("А=", А)
print("A[1] =", A[1]) # 2-я строка
print("A[1][2] =", A[1][2]) # 3-й элемент 2-й строки
print("A[0][-1] =", A[0][-1]) # Последний элемент 1-й строки
столбец = []; # пустой список
для строки в A:
  столбец.добавлять (строка [2])
print("3-й столбец =", столбец)

Когда мы запустим программу, вывод будет:

  А = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]]
А[1] = [-5, 8, 9, 0]
А[1][2] = 9
А[0][-1] = 12
3-й столбец = [5, 9, 11]

Вот еще несколько примеров, связанных с матрицами Python с использованием вложенных списков.

  • Добавить две матрицы
  • Транспонировать матрицу
  • Умножить две матрицы

Использование вложенных списков в качестве матрицы подходит для простых вычислительных задач, однако есть лучший способ работы с матрицами в Python с использованием пакета NumPy.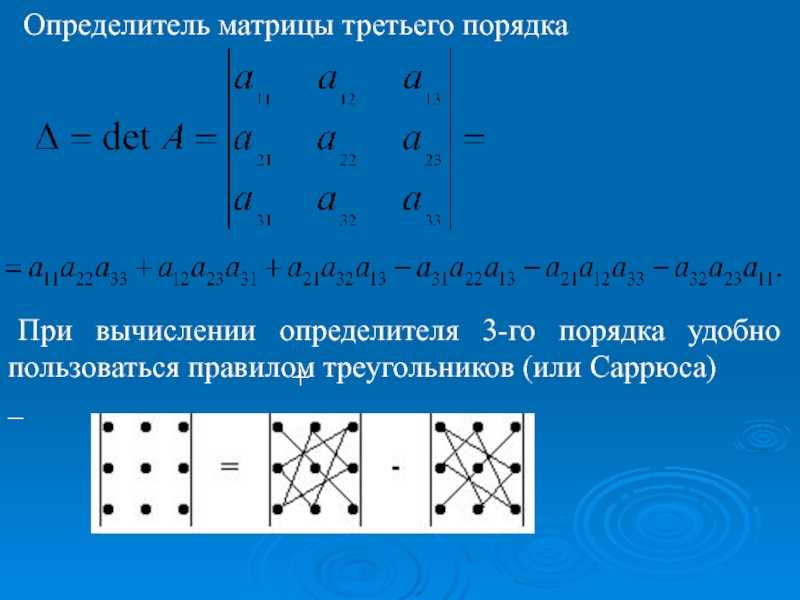

NumPy Array

NumPy — это пакет для научных вычислений, поддерживающий мощные объекты N-мерного массива. Прежде чем вы сможете использовать NumPy, вам необходимо установить его. Для получения дополнительной информации,

  • Посетите: Как установить NumPy?
  • Если вы используете Windows, загрузите и установите дистрибутив Python anaconda. Он поставляется с NumPy и несколькими другими пакетами, связанными с наукой о данных и машинным обучением.

После установки NumPy его можно импортировать и использовать.

NumPy предоставляет многомерный массив чисел (который на самом деле является объектом). Возьмем пример:

 импортировать numpy как np
а = np.массив ([1, 2, 3])
print(a) # Вывод: [1, 2, 3]
print(type(a)) # Вывод:

Как видите, класс массива NumPy называется ndarray .

Как создать массив NumPy?

Существует несколько способов создания массивов NumPy.

1. Массив целых, вещественных и комплексных чисел 

 импортировать numpy как np
A = np.массив ([[1, 2, 3], [3, 4, 5]])
печать(А)
A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой
печать(А)
A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив комплексных чисел
печать(А)

Когда вы запустите программу, вывод будет:

  [[1 2 3]
 [3 4 5]]
[[1.1 2. 3. ]
 [3. 4. 5. ]]
[[1.+0.j 2.+0.j 3.+0.j]
 [3.+0.к 4.+0.к 5.+0.к]]

2. Массив нулей и единиц 

 импортировать numpy как np
zeors_array = np.zeros ((2, 3))
печать (zeors_array)
'''
 Выход:
 [[0. 0. 0.]
  [0. 0. 0.]]
'''
one_array = np.ones( (1, 5), dtype=np.int32 ) // указание dtype
print(ones_array) # Вывод: [[1 1 1 1 1]]

Здесь мы указали dtype до 32 бит (4 байта). Следовательно, этот массив может принимать значения от -2 -31 до 2 -31 -1 .

3. Использование arange() и shape() 

 импортировать numpy как np
A = np.arange(4)
печать('А =', А)
B = np.arange(12).reshape(2, 6)
печать('В =', В)
'''
Выход:
А = [0 1 2 3]
В = [[ 0 1 2 3 4 5]
 [ 6 7 8 9 10 11]]
'''

Узнайте больше о других способах создания массива NumPy.

Операции с матрицами

Выше мы привели 3 примера: сложение двух матриц, умножение двух матриц и транспонирование матрицы. Раньше мы использовали вложенные списки для написания этих программ. Давайте посмотрим, как мы можем выполнить ту же задачу, используя массив NumPy.

Добавление двух матриц

Мы используем оператор + для добавления соответствующих элементов двух матриц NumPy.

 импортировать numpy как np
A = np.массив ([[2, 4], [5, -6]])
B = np.массив([[9, -3], [3, 6]])
C = A + B # поэлементное сложение
печать(С)
'''
Выход:
[[11 1]
 [ 8 0]]
 '''

Умножение двух матриц

Чтобы умножить две матрицы, мы используем метод dot() .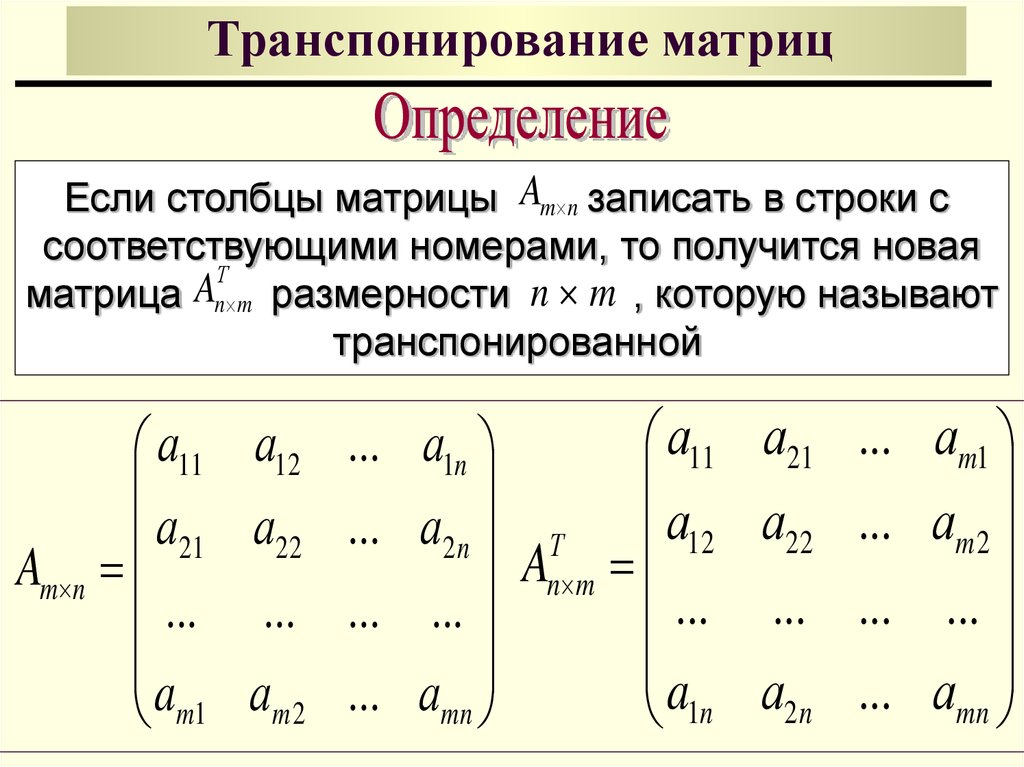 Узнайте больше о том, как работает numpy.dot.

Примечание: * используется для умножения массивов (умножения соответствующих элементов двух массивов), а не умножения матриц.

 импортировать numpy как np
A = np.массив ([[3, 6, 7], [5, -3, 0]])
B = np.массив ([[1, 1], [2, 1], [3, -3]])
С = А. точка (В)
печать(С)
'''
Выход:
[[ 36 -12]
 [-1 2]]
'''

Транспонирование матрицы

Мы используем numpy.transpose для вычисления транспонирования матрицы.

 импортировать numpy как np
A = np.массив ([[1, 1], [2, 1], [3, -3]])
печать (A.transpose())
'''
Выход:
[[ 1 2 3]
 [ 1 1 -3]]
'''

Как видите, NumPy значительно облегчил нашу задачу.

Доступ к элементам матрицы, строкам и столбцам

Доступ к элементам матрицы

Подобно спискам, мы можем получить доступ к элементам матрицы, используя индекс. Начнем с одномерного массива NumPy.

 импортировать numpy как np
А = np. массив ([2, 4, 6, 8, 10])
print("A[0] =", A[0]) # Первый элемент
print("A[2] =", A[2]) # Третий элемент
print("A[-1] =", A[-1]) # Последний элемент

Когда вы запустите программу, вывод будет:

  А[0] = 2
А[2] = 6
А[-1] = 10

Теперь давайте посмотрим, как мы можем получить доступ к элементам двумерного массива (который в основном является матрицей).

 импортировать numpy как np
A = np.массив([[1, 4, 5, 12],
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]])
# Первый элемент первой строки
печать("А[0][0] =", А[0][0])
# Третий элемент второй строки
печать("А[1][2] =", А[1][2])
# Последний элемент последней строки
print("А[-1][-1] =", А[-1][-1])

Когда мы запустим программу, вывод будет:

  А[0][0] = 1
А[1][2] = 9
А[-1][-1] = 19

Доступ к строкам матрицы 

 импорт numpy как np
A = np.массив([[1, 4, 5, 12],
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (в данном случае 3-я строка)

Когда мы запустим программу, вывод будет:

  А[0] = [1, 4, 5, 12]
А[2] = [-6, 7, 11, 19]
А[-1] = [-6, 7, 11, 19]

Доступ к столбцам матрицы 

 импорт numpy как np
A = np. массив([[1, 4, 5, 12],
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]])
print("A[:,0] =",A[:,0]) # Первый столбец
print("A[:,3] =", A[:,3]) # Четвертый столбец
print("A[:,-1] =", A[:,-1]) # Последний столбец (в данном случае 4-й столбец)

Когда мы запустим программу, вывод будет:

  А[:,0] = [ 1 -5 -6]
А[:,3] = [12 0 19]
А[:,-1] = [12 0 19]

Если вы не знаете, как работает приведенный выше код, прочтите раздел о нарезке матрицы в этой статье.

Нарезка матрицы

Нарезка одномерного массива NumPy аналогична списку. Если вы не знаете, как работает нарезка для списка, посетите статью Понимание нотации срезов в Python.

Возьмем пример:

 импортировать numpy как np
буквы = np.array([1, 3, 5, 7, 9, 7, 5])
# элементы с 3-го по 5-й
print(letters[2:5]) # Вывод: [5, 7, 9]
# элементы с 1-го по 4-й
print(letters[:-5]) # Вывод: [1, 3]
# от 6-го до последнего элемента
print(letters[5:]) # Вывод:[7, 5]
# от 1-го до последнего элемента
print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5]
# обращение списка
print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]

Теперь давайте посмотрим, как мы можем разрезать матрицу.

 импортировать numpy как np
A = np.массив([[1, 4, 5, 12, 14],
    [-5, 8, 9, 0, 17],
    [-6, 7, 11, 19, 21]])
print(A[:2, :4]) # две строки, четыре столбца
''' Выход:
[[ 1 4 5 12]
 [-5 8 9 0]]
'''
print(A[:1,]) # первая строка, все столбцы
''' Выход:
[[ 1 4 5 12 14]]
'''
print(A[:,2]) # все строки, второй столбец
''' Выход:
[ 5 9 11 ]
'''
print(A[:, 2:5]) # все строки, с третьего по пятый столбец
'''Выход:
[[ 5 12 14]
 [ 9 0 17 ]
 [11 19 21]]
'''

Как видите, использование NumPy (вместо вложенных списков) значительно упрощает работу с матрицами, и мы даже не коснулись основ. Мы предлагаем вам подробно изучить пакет NumPy, особенно если вы пытаетесь использовать Python для обработки и анализа данных.

Ресурсы NumPy, которые могут оказаться полезными:

  • Учебное пособие по NumPy
  • Ссылка NumPy

Матрица Определение и значение | Dictionary.com

  • Лучшие определения
  • Викторина
  • Связанный контент
  • Примеры
  • Британский
  • Научный

Показывает уровень сложности слова.

[ мей-трикс, ма- ]

/ ˈmeɪ trɪks, ˈmæ- /

Сохрани это слово!

См. синонимы для: матрица / матрицы на Thesaurus.com

Показывает уровень оценки в зависимости от сложности слова.

существительное, множественное число ma·tri·ces [mey-tri-seez, ma-], /ˈmeɪ trɪˌsiz, ˈmæ-/, ma·trix·es.

что-то, что составляет место или точку, из которой что-то еще возникает, принимает форму или развивается: Греко-римский мир был матрицей для западной цивилизации.

Анатомия. формирующая часть, как кориум под ногтем.

Биология.

  1. межклеточное вещество ткани.
  2. измельченное вещество.

Петрология. мелкозернистая часть породы, в которой заключены более крупные кристаллы или обломки породы.

мелкий материал, такой как цемент, в который вкраплены куски более крупного материала, такого как заполнитель.

Горное дело. пустошь.

Металлургия. кристаллическая фаза в сплаве, в которую внедрены другие фазы.

Печать. форма для отливки шрифтов.

мастер (по умолчанию 20).

Цифровая технология сетка, образованная перпендикулярными пересечениями, которые определяют потенциальное пространство, которое может быть заполнено, например, пикселями на экране, чернилами в матричной печати или материалом в 3D-печати.

(в прессе или штамповочном станке) многокомпонентный штамп или перфорированный блок, на который помещается формуемый материал.

Математика. прямоугольный массив чисел, алгебраических символов или математических функций, особенно когда такие массивы складываются и умножаются по определенным правилам.

Языкознание. прямоугольное отображение признаков, характеризующих набор языковых элементов, особенно фонем, обычно представляемых в виде набора столбцов со знаками плюс или минус, указывающими наличие или отсутствие каждого признака для каждого элемента.

Также называется ведущим. форма, изготовленная методом гальванопластики из записи диска, из которой можно штамповать другие диски.

Архаичный. матка.

ВИКТОРИНА

Сыграем ли мы «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?

Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!

Вопрос 1 из 6

Какая форма обычно используется с другими глаголами для выражения намерения?

Происхождение матрицы

1325–75; Среднеанглийское matris, матрица<латинское mātrix, самка животного, предназначенная для разведения (позднелатынь: регистр, первоначально таких зверей), родительский стебель (растений), производное от māter, мать

Слова рядом с матрицей

матрилокальный, супружеский, супружеский, супружеский виноград , матрипосталь, матрица, матрица штрих-кода, матричная механика, матричный принтер, матрица предложение

Dictionary.com Полный текст На основе Random House Unabridged Dictionary, © Random House, Inc. 2022

Слова, относящиеся к матрице

отливка, ковка, форма, сетка, модель, форма, происхождение, узор, источник, матка

Как использовать матрицу в предложение

  • Матрица аккумуляторов и трансмиссии также влияет на производительность.

    Электрический Mustang Mach-E от Ford — важный шаг в будущее|Дэн Карни|12 февраля 2021 г.|Popular-Science

  • Ни предложения де Блазио, ни матрица не ограничат текущую свободу действий полиции Нью-Йорка в отношении дисциплины.

    Городской совет Нью-Йорка предлагает радикальные реформы полиции Нью-Йорка|Эрик Умански и Хоакин Сапиен|1 февраля 2021 г.|ProPublica

  • Широко разрекламированное руководство по штрафам, известное как матрица дисциплины, было введено всего несколько дней назад полицией Нью-Йорка. .

    Все еще не могу дышать|Тофер Сандерс, ProPublica и Йоав Гонен, ГОРОД, видео Лукаса Уолдрона, ProPublica|21 января 2021 г.|ProPublica

  • Quanta также исследовала силу теории представлений, которая показывает связи, соединяющие сложные объекты, называемые группами, с гораздо более простой концепцией матриц.

    Год математики и информатики|Билл Эндрюс|23 декабря 2020 г.|Журнал Quanta

  • Многие матрицы имеют измерение, называемое определителем, которое представляет собой единственное значение, вычисляемое с использованием чисел в матрице.

    Неожиданное путешествие математика по физическому миру|Кевин Хартнетт|16 декабря 2020 г.|Журнал Quanta

  • Итак, мы стащили «Матрицу», и фильм, который они нам дали после, назывался «10 вещей, которые я ненавижу в тебе».

    Джозеф Гордон-Левитт о «Городе грехов» и о том, почему он считает себя мужчиной-феминисткой|Марлоу Стерн|14 августа 2014 г.|DAILY BEAST

  • Был новаторский создатель научно-фантастической франшизы «Матрица».

    Жаловаться, как будто это 1999 год: «Бойцовский клуб», «Красота по-американски» и бунт беспилотников | Артур Чу | 3 июня 2014 г. | DAILY BEAST

  • OnTheFly (бесплатно) – это приложение поисковой системы основано на программном обеспечении ITA Matrix, которое принадлежит Google.

    Лучшие приложения для путешествий для дорожных воинов|Мэттью Кепнес|27 мая 2014 г.|DAILY BEAST

  • Это ультиматум, направленный на поиск цели в дезориентирующей матрице асимметричной войны.

    История и логика военных ультиматумов, от Суэца до Крыма|Джейкоб Сигел|4 марта 2014|DAILY BEAST

  • Разве это не достаточно удивительно для Каку, что он вынужден прибегать к отсылкам к «Звездному пути» и обсуждениям Матрицы? ?

    Что произойдет с нашим разумом в будущем?|Роберт Херритт|2 марта 2014 г. |DAILY BEAST

  • Матрица или штамп помещается в силовой пресс, а пластинки прессуются из материала, используемого для изготовления звукозаписей. .

    Чудесная книга знаний|Разное

  • Надгробие под западным окном показывает матрицу того, что когда-то было великолепной латунью.

    Соборы Белла: Соборная церковь Карлайла|C. Кинг Элей

  • В довершение всего, Маргарет носила в кружеве на шее большую брошь из бирюзовой матрицы, которая подходила к ее глазам.

    Дом бабочек|Мэри Э. Уилкинс Фриман

  • Любая среда оставляет печать своей матрицы на индивидууме, формирующемся в ней.

    Смысл разделения мыслей|Марк Ирвин Клифтон

  • Это формировало матрицу, в которую заливали расплавленный металл, чтобы сделать стереотипную пластину или штамп для печати.

    Mark Twain, биография, 1835-1910, полное | или матрицы

    вещество, ситуация или среда, в которой что-либо берет свое начало, принимает форму или заключено в них

    анатомия толстая ткань в основании ногтя, из которой развивается ноготь на руке или ноге

    межклеточное вещество кости , хрящи, соединительная ткань и др.

    1. горная порода, в которую встроены окаменелости, галька и т. д.
    2. материал, в который заключен минерал; пустая порода

    печать

    1. металлическая форма для литья типа
    2. папье-маше или пластиковая форма, отпечатанная из формы и используемая для создания стереотипов . Его получают электроосаждением на шаблоне

      слой перфорированного материала, помещаемый под заготовку в пресс или штамповочную машину, на которую действует пуансон

      металлургия

      1. фасонный катод, используемый в гальванопластике
      2. металл, составляющий основную часть сплава
      3. мягкий металл в подшипнике скольжения, в который внедрены твердые частицы поверхностного металла композитный материал, такой как пластик в армированном волокном пластике

        представляет собой прямоугольный массив элементов, расположенных в строках и столбцах, используемый для облегчения решения таких задач, как преобразование координат. Обычно указывается в скобках: (a d b e c f) Определитель сравнения (по определению 3)

        лингвистика главное предложение сложного предложения

        вычисление прямоугольного массива элементов схемы, обычно используемых для генерации одного набора сигналов из другого животное, используемое для разведения, от матери-матери

        Collins English Dictionary — Complete & Unabridged 2012 Digital Edition © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Издатели 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012.

        Геология Минеральные зерна породы, в которых заключены окаменелости.

        Биология Компонент ткани животного или растения, находящийся вне клеток. Костные клетки встроены в матрицу из коллагеновых волокон и минеральных солей. Соединительная ткань состоит из клеток и внеклеточных волокон в жидкости, называемой основным веществом. Также называется внеклеточным матриксом

        Математика Прямоугольный массив числовых или алгебраических величин, подлежащих математическим операциям.

        Анатомия Формирующие клетки или ткань ногтя, ногтя на ноге или зуба.

        Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены. Определение

        в кембриджском словаре английского языка

        Примеры матрицы

        матрицы

        Механические требования также были важны, потому что после полимеризации матрица должна была быть стабильной.

        Из Phys.Org