Как посчитать минор 3 порядка: Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.

Алгебраические дополнения онлайн

Определение. Если в определителе n-го порядка вычеркнуть i строку и j столбец, то оставшийся определитель (n-1)-го порядка называется минором данного элемента a_i^j и обозначается M_i^j. Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Главным минором k-го порядка матрицы А называется определитель, составленный из элементов, расположенных на пересечении ее k строк и k столбцов с одинаковыми номерами.
Угловым минором k-го порядка матрицы А называется определитель, составленный из элементов, расположенных на пересечении ее первых k строк и первых k столбцов.

Определение. Алгебраическим дополнением элемента a_i^j определителя

D называется его минор, взятый со знаком (-1)^i+j.
Алгебраическое дополнение элемента a_i^j обозначается через A_i^j. Следовательно, A_i^j = (-1)^i+jM_i^j.

• Ввод данных
• Видеоинструкция

Размерность матрицы 2345678910

Пример №1. Дан определитель . Найти минор и алгебраическое дополнение элемента a₂¹ (выделен пунктиром).
Решение. Вычеркивая в определителе первую строку и второй столбец, на пересечении которых находится элемент a₂¹, получим . Тогда A₂¹ = (-1)¹⁺²M₂¹ = -14.
Теорема. Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения, т.е.

D=ai01·Ai01+ai02·Ai02+ . .. + ai0n·Ai0n  (*)
где i₀ – фиксировано.
Выражение (*) называют разложением определителя D по элементам строки с номером i₀.
Вычисление определителя n-го порядка сводится к вычислению одного определителя (n-1)-го порядка, для чего в какой–либо строке (или столбце) получают (n-1) нулей, а затем разлагают определитель по этой строке, пользуясь формулой (*).

Пример №2. Покажем нахождение алгебраических дополнений на примере определения обратной матрицы:

Решение находим с помощью калькулятора. Найдем главный определитель.
∆ = 0.73 ∙(0.72  ∙0.92 -(-0.17 ∙(-0.15  )))-(-0.19  ∙(-0.07  ∙0.92 -(-0.17 ∙(-0.12  ))))+(-0.12 ∙(-0.07  ∙(-0.15 )-0.72  ∙(-0.12  ))) = 0.437197
Транспонированная матрица

Алгебраические дополнения

∆_1,1 = (0. 72  ∙0.92 -(-0.15  ∙(-0.17 ))) = 0.6369

∆_1,2 = -(-0.07  ∙0.92 -(-0.12  ∙(-0.17 ))) = 0.0848

∆_1,3 = (-0.07  ∙(-0.15  )-(-0.12  ∙0.72  )) = 0.0969

∆_2,1 = -(-0.19  ∙0.92 -(-0.15  ∙(-0.12 ))) = 0.1928

∆_2,2 = (0.73 ∙0.92 -(-0.12  ∙(-0.12 ))) = 0.6572

∆_2,3 = -(0.73 ∙(-0.15  )-(-0.12  ∙(-0.19  ))) = 0.1323

∆_3,1 = (-0.19  ∙(-0.17 )-0.72  ∙(-0.12 )) = 0.1187

∆_3,2 = -(0.73 ∙(-0.17 )-(-0.07  ∙(-0.12 ))) = 0.1325

∆_3,3 = (0.73 ∙0.72  -(-0.07  ∙(-0.19  ))) = 0.5123
Обратная матрица

Пример №3. Алгебраическое дополнение также используется при определении количества остовных деревьев в графе.

Ранг матрицы методом окаймляющих миноров

Для того что бы вычислить ранг матрицы можно применить метод окаймляющих миноров или метод Гаусса. Рассмотрим метод Гаусса или метод элементарных преобразований.

Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.

Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.

Алгоритм нахождения ранга матрицы методом окаймляющих миноров:

1. Минор M k-того порядка не равен нулю.
2. Если окаймляющие миноры для минора M (k+1)-го порядка, составить невозможно (т.е. матрица содержит k строк или k столбцов), то ранг матрицы равен k. Если окаймляющие миноры существуют и все равны нулю, то ранг равен k. Если среди окаймляющих миноров есть хотя бы один, не равный нулю, то пробуем составить новый минор k+2 и т.д.

Разберем алгоритм более подробно. Сначала рассмотрим миноры первого (элементы матрицы) порядка матрицы A.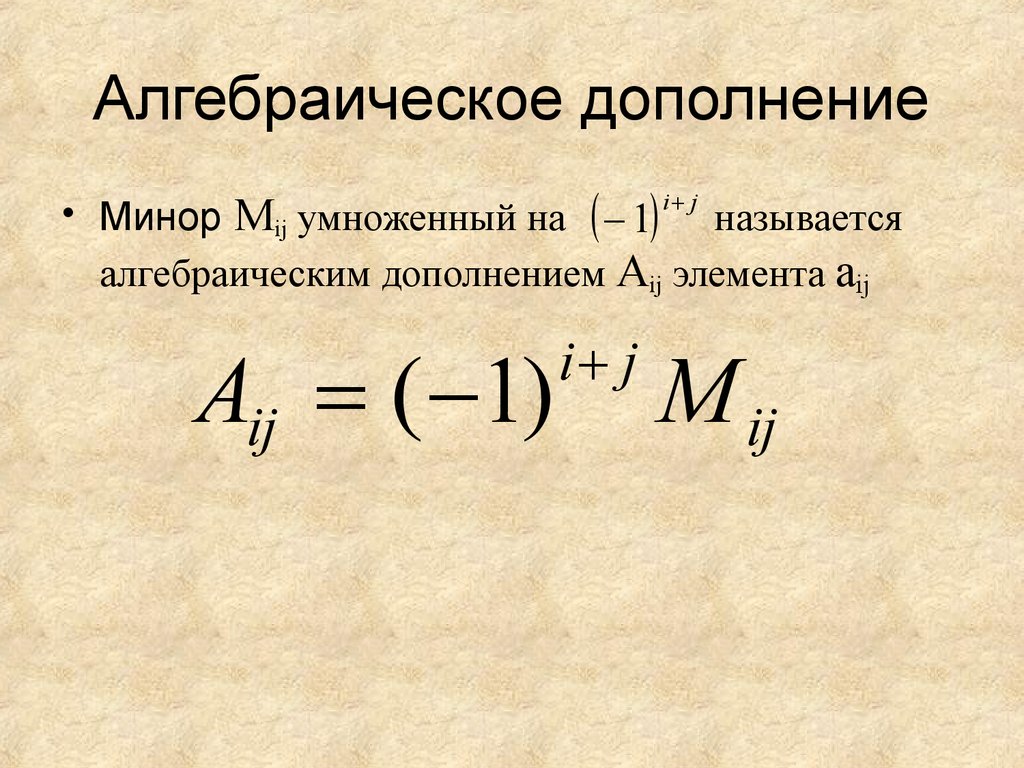 Если все они равны нулю, то rangA = 0. Если есть миноры первого порядка (элементы матрицы) не равные нулю M₁ ≠ 0, то ранг rangA ≥ 1.

Проверим есть ли окаймляющие миноры для минора M₁. Если такие миноры есть, то они буду миноры второго порядка. Если все миноры окаймляющие минор

M₁ равны нулю, то rangA = 1. Если есть хоть один минор второго порядка не равные нулю M₂ ≠ 0, то ранг rangA ≥ 2.

Проверим есть ли окаймляющие миноры для минора M₂. Если такие миноры есть, то они буду миноры третьего порядка. Если все миноры окаймляющие минор M₂ равны нулю, то rangA = 2. Если есть хоть один минор третьего порядка не равные нулю M₃ ≠ 0, то ранг rangA ≥ 3.

Проверим есть ли окаймляющие миноры для минора M₃. Если такие миноры есть, то они буду миноры четвертого порядка. Если все миноры окаймляющие минор M₃ равны нулю, то rangA = 3.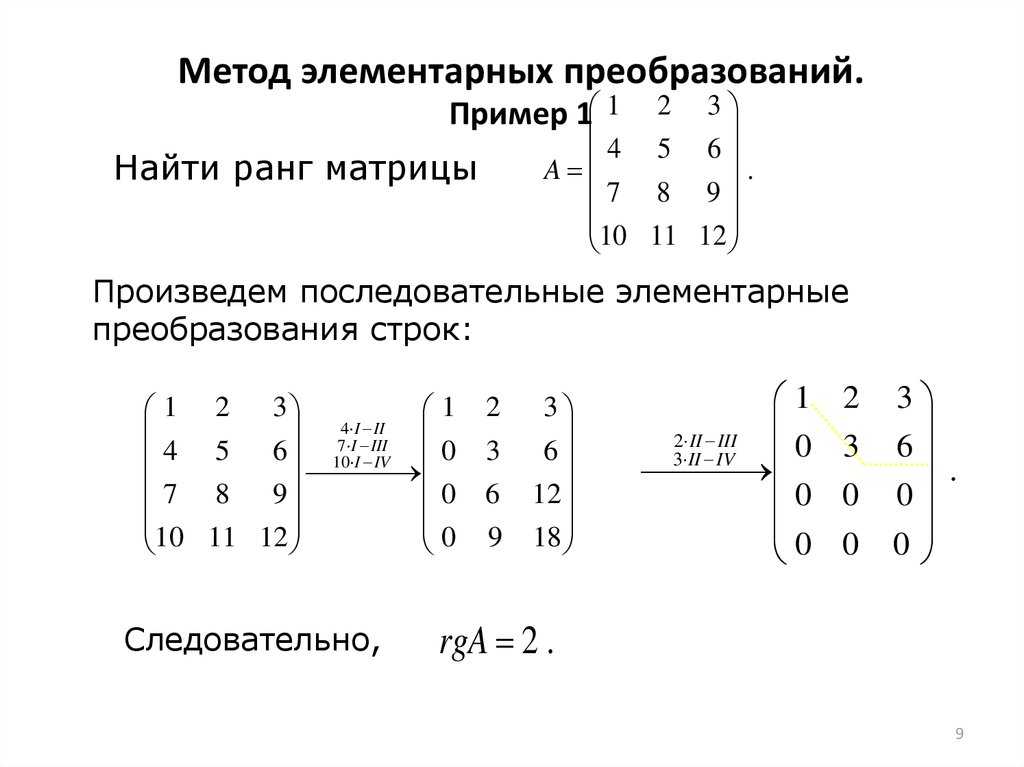 Если есть хоть один минор четвертого порядка не равные нулю M₄ ≠ 0, то ранг rangA ≥ 4

.

Проверяем есть ли окаймляющий минор для минора M₄, и так далее. Алгоритм прекращается, если на каком-то этапе окаймляющие миноры равны нулю или окаймляющий минор нельзя получить (в матрице «закончились» строки или столбцы). Порядок не нулевого минора, который получилось составить будет рангом матрицы.

Пример

Рассмотрим данный метод на примере. Дана матрицы 4х5:

У данной матрице ранг не может быть больше 4. Так же у этой матрице есть не нулевые элементы (минор первого порядка), значит ранг матрицы ≥ 1.

Составим минор 2-ого порядка. Начнем с угла.

Найдем определитель данного минора.

Так определитель равен нулю, составим другой минор.

Найдем определитель данного минора.

Определить данного минора равен -2. Значит ранг матрицы ≥ 2.

Если данный минор был равен 0, то составили бы другие миноры. До конца бы составили все миноры по 1 и второй строке. Потом по 1 и 3 строке, по 2 и 3 строке, по 2 и 4 строке, пока не нашли бы минор не равный 0, например:

Если все миноры второго порядка равны 0, то ранг матрицы был бы равен 1. Решение можно было бы остановить.

Продолжим поиска ранга матрицы. Составим минор 3-го порядка.

Найдем определитель этого минора.

Минор получился не нулевой. значит ранг матрицы ≥ 3.

Если бы данный минор был нулевым, то нужно было бы составить другие миноры. Например:

Если все миноры третьего порядка равны 0, то ранг матрицы был бы равен 2. Решение можно было бы остановить.

Продолжим поиска ранга матрицы. Составим минор 4-го порядка.

Найдем определитель этого минора.

Определитель минора получился равный 0. Построим другой минор.

Найдем определитель этого минора.

Минор получился равным 0.

Построить минор 5-го порядка не получится, для этого нет строки в данной матрицы. Последний минор не равный нулю был 3-го порядка, значит ранг матрицы равен 3.

Другой материал по теме

Миноры матрицы 3×3

• Математические сомнения
• Матрицы
• Несовершеннолетние

Определитель квадратной подматрицы второго порядка при выходе из строки и столбца элемента называется минором этого элемента в квадратной матрице третьего порядка.

Квадратная матрица три на три содержит девять элементов, расположенных в трех строках и трех столбцах. При вычислении младшего элемента остальные записи в этой строке и столбце не учитываются. Он образует квадратную матрицу два на два с оставшимися элементами, и определитель этой матрицы называется минором соответствующего элемента. Таким образом, для девяти элементов матрицы порядка $3$ можно вычислить девять миноров.

$D$ $\,=\,$ $\begin{bmatrix} d_{11} & d_{12} & d_{13} \\ d_{21} & d_{22} & d_{23} \\ d_{31} & d_{32} & d_{33} \\ \end{bmatrix}$

Теперь научимся находить минор каждого элемента матрицы $D$ порядка $3 \times 3$ . Для нахождения миноров элементов в матрице порядка $3$ необходимы знания по нахождению определителя матрицы второго порядка.

Миноры для элементов первой строки

Посмотрите на элементы первой строки матрицы $D$. Элементы $d_{11}$, $d_{12}$ и $d_{13}$ — это элементы первой строки матрицы $D$. Их миноры обозначаются $M_{11}$, $M_{12}$ и $M_{13}$ соответственно. Теперь давайте узнаем, как найти минор каждого элемента в первой матрице $3 \times 3$.

Младший элемент записи в первой строке и первом столбце

Запись $d_{11}$ является элементом первой строки и первого столбца. Оставьте элементы в первой строке и записи в первом столбце. Остальные элементы образуют квадратную матрицу порядка $2$.

Затем найдите определитель матрицы для вычисления минора элемента $d_{11}$, который в матричной алгебре обозначается как $M_{11}$.

$M_{11}$ $\,=\,$ $\begin{vmatrix} d_{22} & d_{23} \\ d_{32} & d_{33} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{11}$ $\,=\,$ $d_{22} \times d_{33}\,-\,d_{23} \times d_{32 }$

Минор записи в первой строке и втором столбце

Элемент $d_{12}$ является записью в первой строке и втором столбце. Оставьте записи в первой строке и записи во втором столбце. Оставшиеся элементы образуют квадратную матрицу порядка $2\times 2$.

Теперь вычислите определитель матрицы для нахождения минора элемента $d_{12}$, который в математике обозначается как $M_{12}$.

$M_{12}$ $\,=\,$ $\begin{vmatrix} d_{21} & d_{23} \\ d_{31} & d_{33} \\ \end{vmatrix}$

$\следовательно\,\,\,$ $M_{12}$ $\,=\,$ $d_{21} \times d_{33}\,-\,d_{23} \times d_{31} $

Минор записи в первой строке и третьем столбце

Запись $d_{13}$ является элементом в первой строке и третьем столбце. Оставьте элементы в первой строке и записи в третьем столбце. Оставшиеся элементы образуют квадратную матрицу второго порядка.

Теперь найдите определитель матрицы для оценки минора элемента $d_{13}$, который в матрицах просто представляется как $M_{13}$.

$M_{13}$ $\,=\,$ $\begin{vmatrix} d_{21} & d_{22} \\ d_{31} & d_{32} \\ \end{vmatrix}$

$\следовательно\,\,\,$ $M_{13}$ $\,=\,$ $d_{21} \times d_{32}\,-\,d_{22} \times d_{31} $

Миноры для элементов второй строки

Сосредоточьтесь на элементах второй строки матрицы $D$. Элементы $d_{21}$, $d_{22}$ и $d_{23}$ являются элементами второй строки матрицы $D$. Миноры этих элементов представлены $M_{21}$, $M_{22}$ и $M_{23}$ соответственно. Теперь давайте узнаем, как найти минор каждой записи во второй строке матрицы третьего порядка.

Минор записи во второй строке и первом столбце

Элемент $d_{21}$ является записью во второй строке и первом столбце. Оставьте элементы во второй строке и элементы в первом столбце. По остальным элементам он образует матрицу порядка $2\times 2$.

Теперь найдите определитель матрицы для вычисления минора элемента $d_{21}$, который обозначается $M_{21}$ в этой матричной алгебре.

$M_{21}$ $\,=\,$ $\begin{vmatrix} d_{12} & d_{13} \\ d_{32} & d_{33} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{21}$ $\,=\,$ $d_{12} \times d_{33}\,-\,d_{13} \times d_{32 }$

Минор записи во второй строке и втором столбце

Элемент $d_{22}$ является элементом второй строки и второго столбца. Записями во второй строке и записями во втором столбце пренебречь. Оставшиеся элементы образуют квадратную матрицу второго порядка.

Затем оцените определитель матрицы, чтобы найти минор элемента $d_{22}$. В математике это обозначается как $M_{22}$.

$M_{22}$ $\,=\,$ $\begin{vmatrix} d_{11} & d_{13} \\ d_{31} & d_{33} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{22}$ $\,=\,$ $d_{11} \times d_{33}\,-\,d_{13} \times d_{31} $

Минор записи во второй строке и третьем столбце

Запись $d_{23}$ является элементом во второй строке и третьем столбце. Теперь оставьте элементы во второй строке и записи в третьем столбце. Таким образом, из остальных элементов получается квадратная матрица порядка $2\times 2$.

Найдите определитель матрицы, чтобы найти минор элемента $d_{23}$ и обозначается $M_{23}$ просто в матрицах.

$M_{23}$ $\,=\,$ $\begin{vmatrix} d_{11} & d_{12} \\ d_{31} & d_{32} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{23}$ $\,=\,$ $d_{11} \times d_{32}\,-\,d_{12} \times d_{31} $

Миноры для элементов третьей строки

Наконец, сосредоточимся на элементах третьей строки матрицы $D$. Элементы $d_{31}$, $d_{32}$ и $d_{33}$ являются элементами третьей строки матрицы $D$. Миноры этих записей обозначаются $M_{31}$, $M_{32}$ и $M_{33}$ соответственно. Теперь давайте узнаем, как оценить младшие из них в третьей строке матрицы.

Второстепенная запись в третьей строке и первом столбце

Элемент $d_{31}$ — это элемент в третьей строке и первом столбце. Оставьте записи в третьей строке и записи в первом столбце. Из оставшихся элементов он образует квадратную матрицу размером $2 \times 2$.

Затем найдите определитель матрицы для вычисления минора элемента $d_{31}$, который в матричной алгебре обозначается как $M_{31}$.

$M_{31}$ $\,=\,$ $\begin{vmatrix} d_{12} & d_{13} \\ d_{22} & d_{23} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{31}$ $\,=\,$ $d_{12} \times d_{23}\,-\,d_{13} \times d_{22 }$

Минор записи в третьей строке и втором столбце

Элемент $d_{32}$ является записью в третьей строке и втором столбце. Не учитывать записи в третьей строке и записи во втором столбце. По остальным элементам образует квадратную матрицу порядка $2\times 2$.

Теперь вычислим определитель матрицы для вычисления минора элемента $d_{32}$, который в математике обозначается как $M_{32}$.

$M_{32}$ $\,=\,$ $\begin{vmatrix} d_{11} & d_{13} \\ d_{21} & d_{23} \\ \end{vmatrix}$

$\следовательно\,\,\,$ $M_{32}$ $\,=\,$ $d_{11} \times d_{23}\,-\,d_{13} \times d_{21} $

Минор записи в третьей строке и третьем столбце

Запись $d_{33}$ является элементом в третьей строке и третьем столбце. Оставьте элементы в третьей строке и записи в третьем столбце. Остальные элементы образуют квадратную матрицу второго порядка.

Теперь вычислите определитель матрицы, чтобы вычислить минор элемента $d_{33}$, и он представлен как $M_{33}$ просто в матрицах.

$M_{33}$ $\,=\,$ $\begin{vmatrix} d_{11} & d_{12} \\ d_{21} & d_{22} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{33}$ $\,=\,$ $d_{11} \times d_{22}\,-\,d_{12} \times d_{21} $

Миноры и кофакторы: расширение по ряду

Вернуться к Указатель уроков  | Делайте уроки в заказе | Подходит для печати страница Несовершеннолетние и кофакторы: введение;   Расширение вдоль строки (стр. 1 из 3) Нахождение определителя из 22 матрица проста: вы просто делаете перекрестное умножение и вычитаете: Процесс на 33 матрицы, хотя и немного более запутанные, все же довольно просты: вы добавляете повторы первого и второго столбцов до конца определителя, умножать по всем диагоналям, а складывать и вычитать в соответствии с правило: Но для 44-х и более крупные определители, вы должны вернуться к меньшим 22 и 33 детерминанты с помощью вещей, называемых «минорами» и «кофакторами». «Несовершеннолетний» определитель квадратной матрицы, образованной удалением одной строки и одной столбец из некоторой большей квадратной матрицы. Так как рядов много столбцы в исходной матрице, вы можете сделать из нее множество миноров. Эти второстепенные помечаются в соответствии с удаленными строкой и столбцом. Так что если вы должны были пойти, скажем, в a 2,4 запись из некоторой матрицы А и вычеркните строку и столбец, которые проходят через эту запись (т. если убрать второй строку и четвертый столбец матрицы), определитель новой (и меньшей) матрицы называется «младшим М 2,4 «. Как только вы найдете несовершеннолетнего M i, j , вы берете индекс имени несовершеннолетнего (« i, Дж » часть) и добавьте два числа и и j . Какой бы результат вы ни получили от этого сложения, сделайте это значение силой на 1, так что вы получите «+1» или «1», в зависимости от того, или + j четное или странный. Затем умножьте это на минор M i, j . Это дает ты «кофактор» A я, j . То есть: (1) i+j М я, к =  А я, к Вы еще не закончили. Да, есть еще. Чтобы найти определитель матрицы А , вам нужно выбрать строку или столбец матрицы, найти все кофакторы для этой строки или столбца умножьте каждый кофактор на его элемент матрицы и затем добавьте все значения, которые вы получили. Авторские права Элизабет Стапель 2006-2011 Все права защищены Хорошо, да; что вероятно не имело большого смысла. Вот другой способ сказать это: У вас есть матрица А . Вам нужно найти его определитель. Слишком большой, чтобы найти более простые методы, так что вам придется найти его, «раскрываясь вдоль строка или столбец». Ваш первый шаг в этом «расширение» будет выбирать строку или столбец. Скажем, вы выберите третий ряд. Для каждой записи в в третьей строке вы найдете кофактор этой записи и умножите вход по его кофактору. То есть для 3,1 запись А , вы найдете кофактор A 3,1 , а затем вы умножите кофактор на 3,1 запись: ( а 3,1 )( А 3,1 ). Для записи 3,2 , вы найдете кофактор A 3,2 , и умножить: ( на 3,2 )( на 3,2 ). И так далее. Тогда вы сложите все из этих продуктов: ( a 3,1 )( A 3,1 ) + ( а 3,2 )( А 3,2 ) + ( а 3,3 )( А 3,3 ) + . … Полученная сумма равна значение определителя матрицы A . (Вышеупомянутый беспорядок, почему никто делает определители вручную, если этого можно избежать: есть только , поэтому требуется много подверженной ошибкам бессмысленной рутинной работы.) Странный факт: это не независимо от того, какую строку или столбец вы используете для расширения; вы получите одинаковое значение независимо. Но эта гибкость может быть полезной. Найдите определитель следующей матрицы, разложив (а) по первой строке и (б) по третьему столбцу. (c) Сравните результаты каждого расширения. (a) Для расширения вдоль первая строка, мне нужно найти миноры, а затем кофакторы первой строки записи: а 1,1 , а 1,2 , а 1,3 , и а 1,4 . М 1,1 М 1,2 М 1,3 М 1,4 М 1,1 = 0 М 1,2 = 0 М 1,3 = 3 М 1,4 = 0 А 1,1 = (1) 1+1 М 1,1   = (1) 2 (0) = 0           А 1,2 = (1) 1+2 М 1,2   = (1) 3 (0) = 0           А 1,3 = (1) 1+3 М 1,3 = (1) 4 (3) = 3           А 1,4 = (1) 1+4 М 1,4   = (1) 5 (0) = 0           Итак, определитель эта матрица: дет( А ) = a 1,1 A 1,1 + a 1,2 A 1,2 + 1,3 А 1,3 + 1,4 А 1,4 7 знак равно 1(0) + 3(0) + (2)(3) + 1(0) знак равно 6 Теперь мне нужно расширить вниз столбец. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт