Урок алгебры в 9 классе по теме «График функции y = ax2 + bx + c».
Учитель | Малакмадзе Татьяна Леонидовна | |||
Предмет | Алгебра | |||
УМК | УМК Алгебра. Дорофеев Г.В. и др. (7-9). | |||
Класс | 9 класс. | |||
Тема урока | График функции y = ax2 + bx + c. | |||
№ урока по теме | Глава 2. Квадратичная функция (21 час): урок №12. Тема «График функции y = ax2 + bx + c»: урок №1. | |||
Тип урока | Урок рефлексии. | |||
Цель урока | Деятельностная: формировать у учеников способность к рефлексии коррекционно-контрольного типа, научить школьников находить причину своих затруднений, самостоятельно строить алгоритм действий по устранению затруднений, научить самоанализу действий и способам нахождения разрешения конфликта. Содержательная: закрепить усвоенные знания, понятия, способы действия и скорректировать их при необходимости. | |||
Задачи урока | Предметные: развивать умение работать с учебным математическим текстом, точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить логические обоснования, доказательства математических утверждений; овладение языком алгебры; систематизировать знания о графике квадратичной функции и его свойствах. Метапредметные: развивать умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учебе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности; осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований; умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; формулировать, аргументировать и отстаивать свое мнение; развивать смысловое чтение; умение оценивать правильность выполнения учебной задачи, собственные возможности ее решения. Личностные: формирование умения наблюдать, анализировать, сравнивать, делать выводы; осуществление контроля и самоконтроля; развитие умения преодолевать трудности для достижения намеченной цели; воспитывать культуру работы в группе. | |||
Межпредметные связи | Физика (баллистическое движение, движение тела под действием силы тяжести), информатика (построение графика квадратичной функции в различных программах), при просмотре видеофрагментов — иностранный язык (английский). | |||
Методы и формы обучения | Групповая, фронтальная. | |||
Используемые технологии | Технология развития критического мышления, информационные, здоровьесберегающие. | |||
Приемы ТРКМ | «Мозговой штурм»; «Ромашка вопросов»; «ЗХУ»; «Эстафета»; «Кто быстрее». | |||
Оборудование/ресурсное обеспечение урока: | Компьютер, мультимедийный проектор, учебник. Игра «Кто хочет стать миллионером?». URL: https://learningapps.org/4919238 Соответствие квадратичных функций и их свойств. URL: https://learningapps.org/4226780 | |||
Этап урока | Задачи этапа | УУД | Деятельность | |
учителя | обучающихся | |||
1. момент. (2 мин.) | Создать благоприятный психологический настрой на работу. | Коммуникативные: планирование учебного сотрудничества со сверстниками. Личностные: психологическая готовность учеников к уроку, самоопределение. | Приветствует обучающихся, проверяет готовность к уроку, создает эмоциональный настрой. | Приветствуют учителя. Приветствуют друг друга, используя метод активного обучения «Поздоровайся локтями». Проверяют наличие учебного материала на столах, организуют свое рабочее место. |
2. Актуализация знаний и формулирование темы и целей урока. (8 мин.) | Актуализация опорных знаний и способов действий. | Познавательные: структурирование знаний, рефлексия способов и условий действий, контроль и оценка процесса и результатов деятельности. Регулятивные: развитие умения формулировать тему и цель урока в соответствии с задачами и нормами русского языка. Коммуникативные: ориентация на партнера по общению, умение слушать собеседника, умение аргументировать свое мнение, убеждать и уступать. Личностные: развитие логического мышления. | Организует актуализацию имеющихся знаний о графике квадратичной функции. Задание: Выберите верный ответ. (Игра «Кто хочет стать миллионером?»). URL: https://learningapps.org/4919238 Постановка проблемы. Артур Кларк: «Мало знать, надо и применять. Мало очень хотеть, надо и делать!» Как слова писателя-фантаста связаны с тем, что мы будем делать на уроке? Предлагает отметить начальный уровень знаний по теме «График функции y=ax2+bx+c» на лесенке достижений; определить цели обучающихся на уроке. Заполнить 1 и 2 столбик таблицы «ЗХУ». Опрос выборочно о целях обучающихся. | Отвечают на вопросы задания и слушают ответы одноклассников. Формулируют тему урока. Ставят цели урока. Заполняют 1 и 2 столбик таблицы «ЗХУ». |
3.Выявление индивидуальных затруднений в реализации нового знания и умения. (7 мин. | Проанализировать причины затруднений в реализации нового знания и умения. | Познавательные: структурирование знаний, рефлексия способов и условий действий, контроль и оценка процесса и результатов деятельности. Регулятивные: коррекция умения. Коммуникативные: ориентация на партнера по общению, умение слушать собеседника, умение аргументировать свое мнение, убеждать и уступать. Личностные: развитие логического мышления. | Отвечает на вопросы, анализирует ошибки. Организует устную работу («Ромашка вопросов»). | Задают вопросы. Вносят исправления. Работают с листом диагностики. |
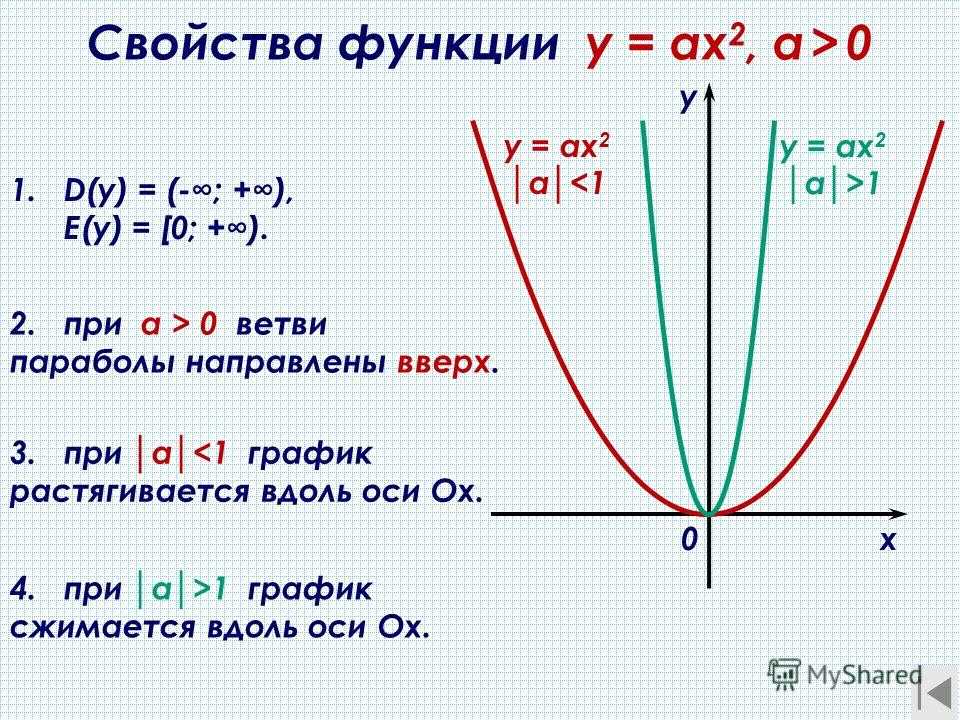
«Ромашка вопросов» От чего зависит направление ветвей параболы? (От знака старшего коэффициента (коэффициента a). Ветви параболы направлены вверх при a>0, вниз при a<0.) Чтобы построить график функции y=ax2+q, нужно… (перенести параболу y=ax2 влево вдоль оси Ох на отрезок длины p, если p>0, или вправо на отрезок длины , если p<0.) Чтобы построить график функции y=a(x+p) 2, нужно… (перенести параболу y=ax2 влево вдоль оси Ох на отрезок длины p, если p>0, или вправо на отрезок длины , если p<0. Какие способы вы знаете для определения знака коэффициента b? (1. Теорема Виета; 2. Формулы для нахождения координат вершины параболы.) Что такое «нули функции»? (Нули функции — это значения аргумента, при которых функция равна нулю.) Как найти нули функции? (Решить квадратное уравнение.) | ||||
4. Реализация на практике выбранного плана, стратегии по разрешению проблемы. (5 мин.) | Организовать деятельность по применению ранее полученных знаний. | Познавательные: структурирование знаний, коррекция способов и условий действий. Регулятивные: планирование своей деятельности для решения поставленной задачи, контроль полученного результата, коррекция полученного результата. Личностные: развитие внимания, зрительной и слуховой памяти, возможность самостоятельно осуществлять деятельность обучения. Коммуникативные: умение работать в группах, развитие диалогической речи. | Организует работу по выполнению заданий, отвечает на вопросы («Эстафета»). Фронтальная форма работы. | Выполняют задания, отвечают и слушают ответы одноклассников, контролируют правильность ответов, анализируют, задают вопросы. |
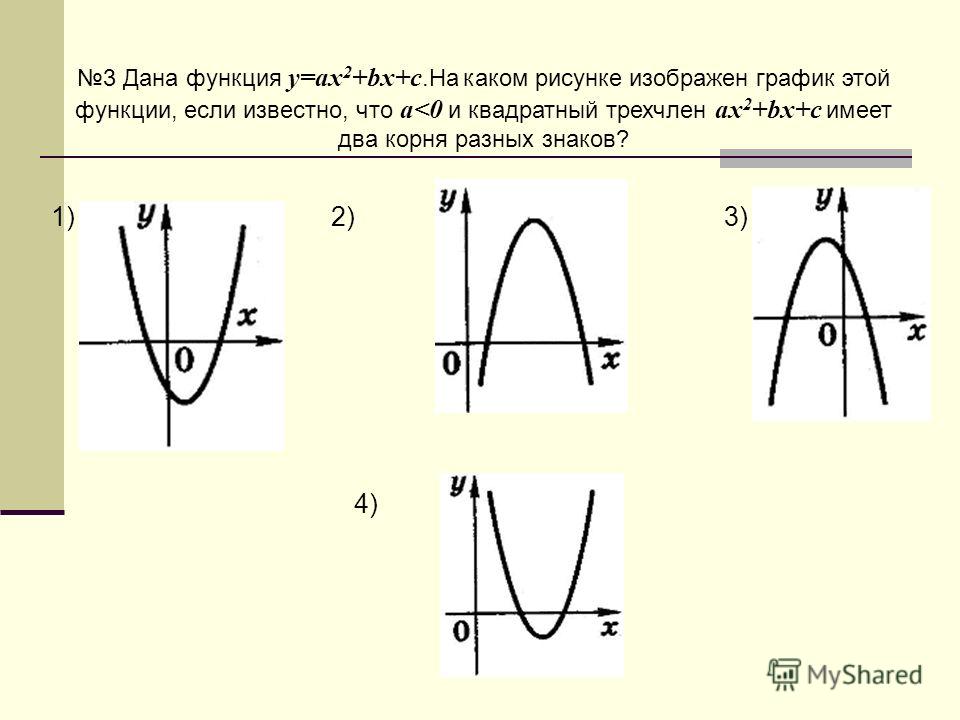
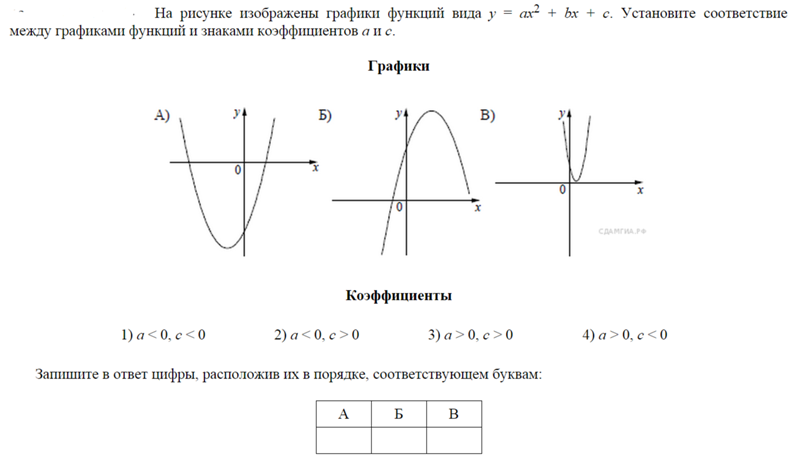
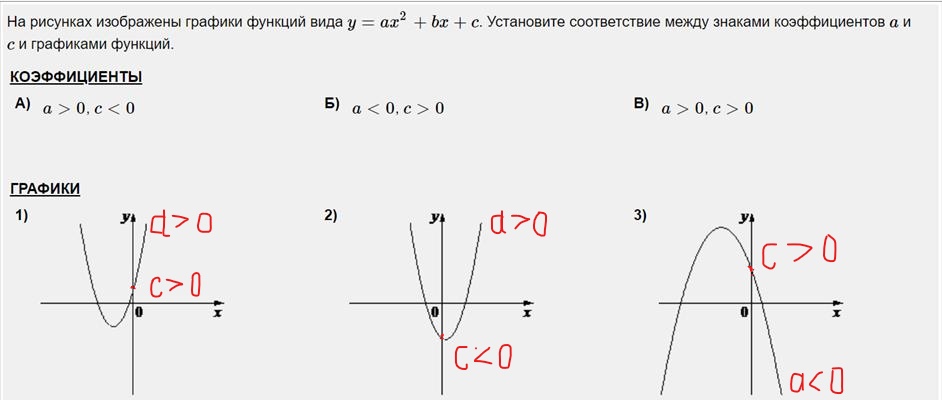
Ответ: а) 2 корня, а>0; б) нет корней, а>0; в) 2 корня, а<0; г) нет корней, а<0; д) 1 корень, а>0; е) 1 корень, а<0. | ||||
5. Динамическая пауза. (3 мин.) | Организовать физическую и психологическую разгрузку. | Коммуникативные: Взаимодействие с партнером по общению. | Проводит интеллектуальную физкультминутку. Демонстрация видеоролика «Парабола». | Выполняют упражнения для снятия физического и психического напряжения. Смотрят видеоролик. |
6. Обобщение и систематизация знаний. Осуществление самостоятельной работы и самопроверки. Тренировочные упражнения. (12 мин.) | Повторить свойства графика квадратичной функции. Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков. | Познавательные: структурирование знаний, коррекция способов и условий действий. Регулятивные: планирование своей деятельности для решения поставленной задачи, контроль полученного результата, коррекция полученного результата, его оценка. Личностные: развитие внимания, зрительной и слуховой памяти, возможность самостоятельно осуществлять деятельность обучения. Коммуникативные: умение работать в группах, развитие диалогической речи. | Организует деятельность по применению полученных знаний: распределяет учащихся по вариантам, отслеживает прохождение тестов, организует проверку, оказывает индивидуальную помощь. Соответствие квадратичных функций и их свойств. URL: https://learningapps.org/4226780 | Решают разноуровневые задачи на свойства графика квадратичной функции, сверяют свои результаты с предложенными, анализируют, задают вопросы. |
Карточка 2. «Зеленый» уровень. №1. Ответ:
№2. Ответ:
№3. . . Ответ:
№4. Ответ:
Карточка 2. «Желтый» уровень. №1. Найдите нули функции y = x2 ‒ 7x +10. Ответ:
№2. Ответ:
№3. Ответ:
Карточка 2. «Красный» уровень. №1. Ответ:
№2.
Ответ:
|
8. | Дать информацию и инструктаж по домашнему заданию. | Личностные: формирование навыков самоорганизации. | Осуществляет показ видеоролика «Квадратичная функция в жизни» при наличии резерва времени. (3 мин) Демонстрирует соответствующий слайд презентации и комментирует домашнее задание, отвечает на вопросы. | Слушают, задают вопросы, записывают задание в дневник. |
Квадратичная функция в окружающем мире. График квадратичной функции подковообразной формы называется параболой. Параболы весьма широко распространены в окружающем мире. (На фото: арка Парабола в Сент-Луисе, штат Миссури, США; скалы Братья (Парабола), Саяны; римские акведуки (водопровод древних римлян)). Многие проблемы нашего мира могут быть решены с помощью квадратичных функций. Один тип проблем (вопросов) касается объектов, находящихся под действием силы тяжести. Их траектории являются параболами, потому что то, что подброшено вверх, в конце концов, обязательно упадет вниз. Запущенные объекты, такие как ракеты, снаряды, пушечные ядра, предметы, которые бросаются как баскетбольные мячи, предметы, которые пинают, как футбольные мячи, и предметы, пущенные из рогатки подобно злобным птичкам навстречу цели, — все совершают параболическое движение. Анализ графика в каждом случае позволяет ответить на важные вопросы, такие как… Какой была максимальная высота подъема объекта? Как далеко от точки старта предмет ударится о землю? Как долго объект был в полете? И так много ещё! А теперь найдите несколько парабол в вашей жизни! | ||||
П. Дополнительно: № 281, 282. Подготовить сообщение «Парабола в нашей жизни». | ||||
9. Рефлексия. (5 мин.) | Дать качественную оценку работы класса и отдельных обучающихся. | Познавательные: Построение речевого высказывания в устной форме, контроль и оценка процесса и результатов деятельности. Регулятивные: контроль и оценка своей деятельности в рамках урока. Коммуникативные: умение слушать и вступать в диалог, формулирование и аргументация своего мнения. Личностные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности. | Организует рефлексию и самооценку учениками собственной учебной деятельности на уроке. | Соотносят цель и результаты своей учебной деятельности и фиксируют степень их соответствия. |
Квадратичная функция — Графики функций
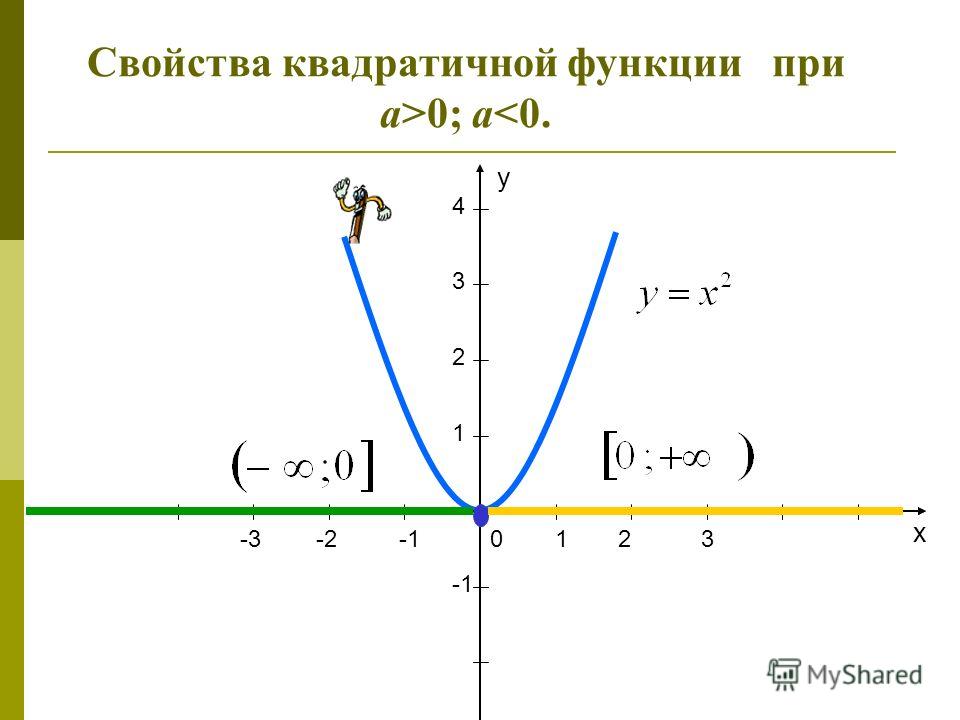
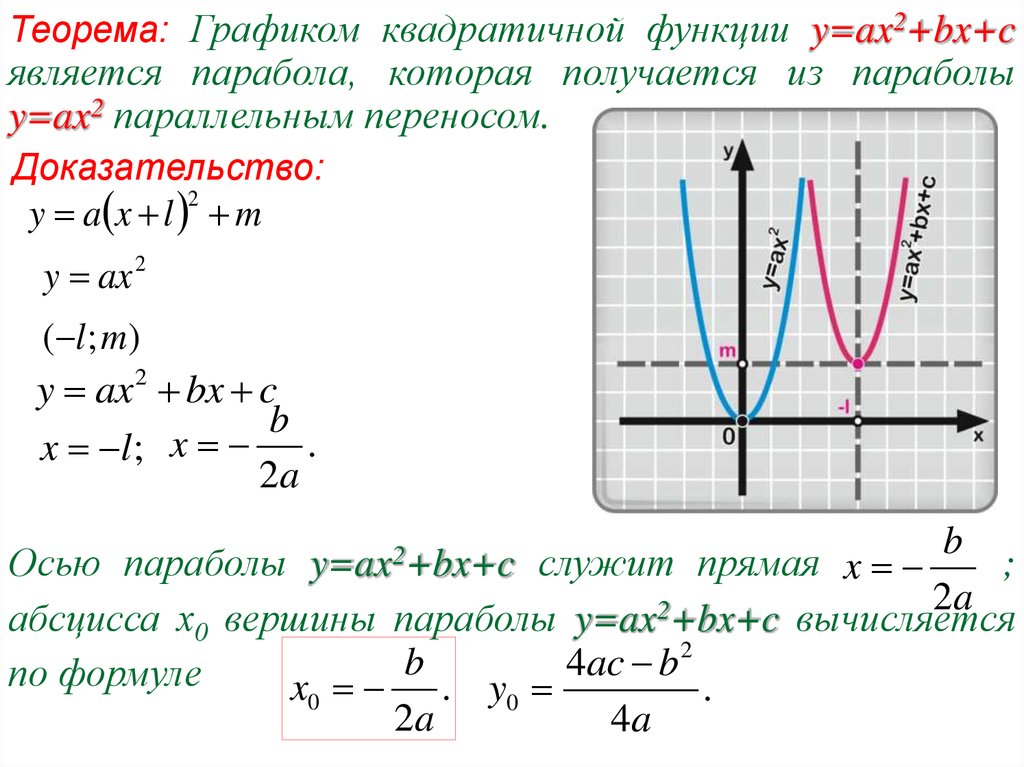
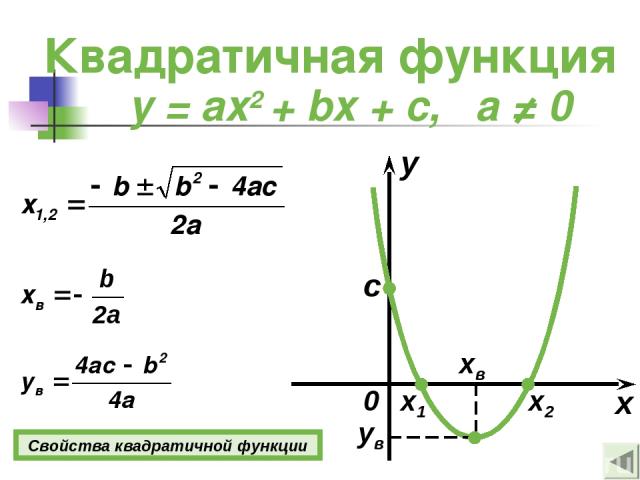
•Квадратичной функцией называется функция вида y=ax2+bx+c, где a,b,c — числа, причем a≠0. Чтобы построить график функции y=x2 составим таблицу значений и построим график, используя полученные точки: Внимание! Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как график функции y=x2 при любых значениях остальных коэффициентов. Итак: Второй этап построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью ОХ. Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции y=f(x) с осью ОХ, нужно решить уравнение f(x)=0. В случае квадратичной функции y=ax2+bx+c нужно решить квадратное уравнение ax2+bx+c=0. В процессе решения квадратного уравнения мы находим дискриминант: D=b2-4ac, который определяет число корней квадратного уравнения. И здесь возможны три случая: 2. Если D=0 ,то уравнение ax2+bx+c=0 имеет одно решение, и, следовательно, парабола y=ax2+bx+c имеет одну точку пересечения с осью ОХ. 3.Если D>0, то уравнение ax2+bx+c=0 имеет два решения, и, следовательно, парабола y=ax2+bx+c имеет две точки пересечения с осью ОХ: , Значит, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции. Следующий важный этап построения графика квадратичной функции – координаты вершины параболы:
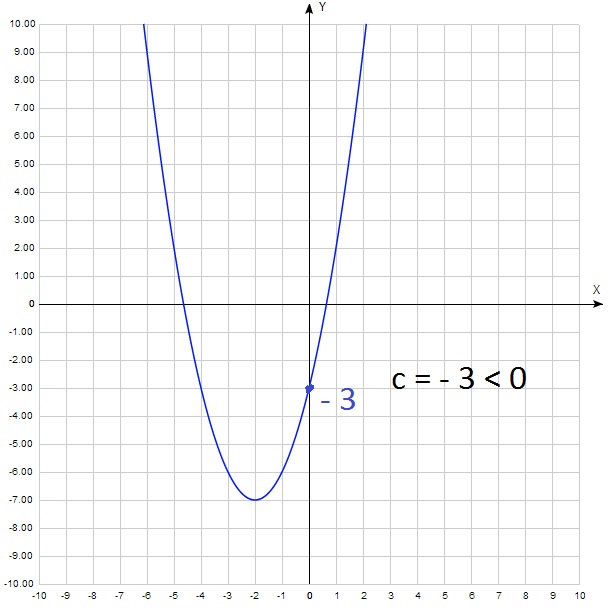
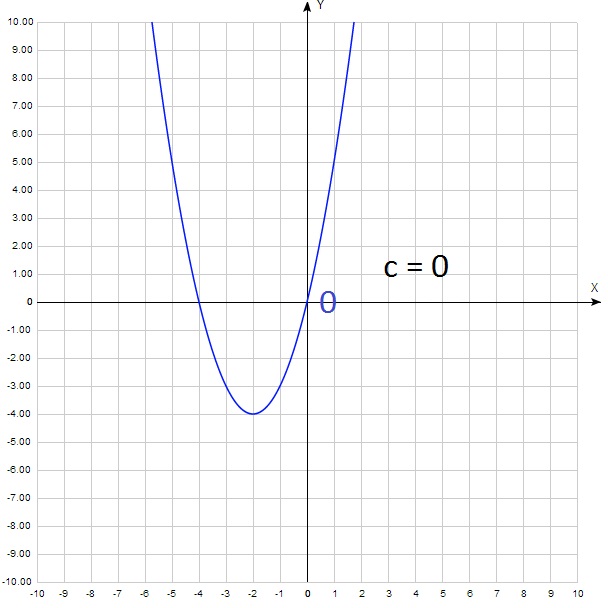
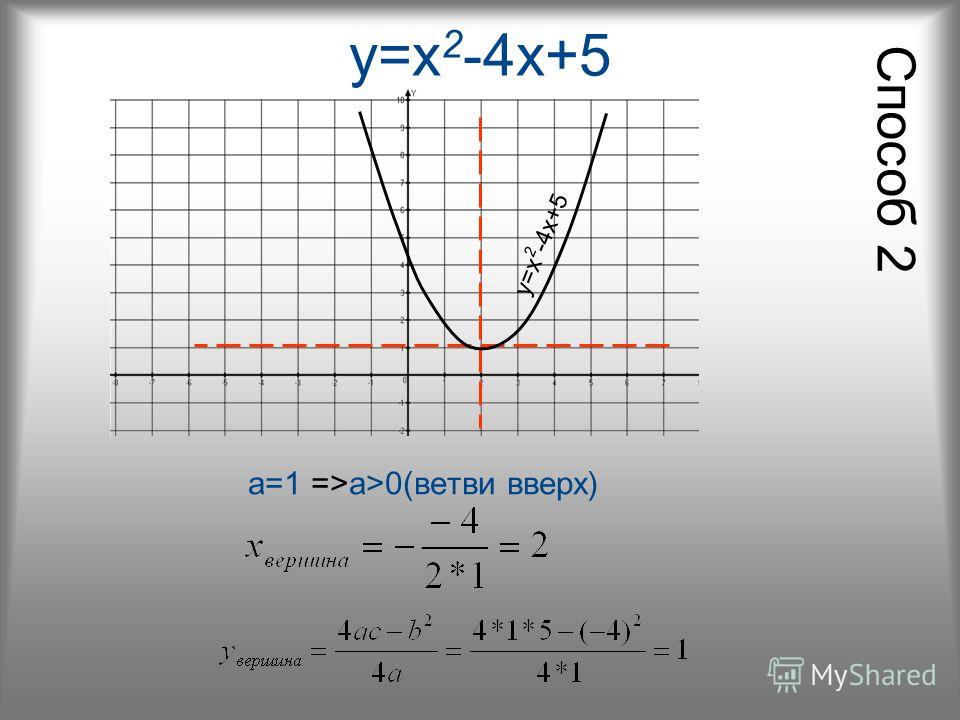
И еще один этап построения графика функции – точка пересечения параболы y=ax2+bx+c с осью OY. Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы y=ax2+bx+c с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c. То есть точка пересечения параболы с осью OY имеет координаты (0;c). Итак, основные моменты построения графика квадратичной функции показаны на рисунке: |
Построение квадратичной функции f(x)
Во-первых, мы должны выбрать область, в которой мы хотим построить f(x) .
Попробуем -10 ≤ x ≤ 10:
# область, в которой мы хотим построить f(x) х = -10:10 # график f(x) plot(x, f(x), type = 'l') # type = 'l' строит линию вместо точек # построить оси x и y аблин (ч = 0) abline(v = 0)
Вывод:
Нахождение вершины
Вершина V квадратного уравнения, в данном случае нижняя точка на графике f(x) , равно: \(V(\frac{-b}{2a}, f(\frac{-b}{2a}))\)
find.vertex = function(a, b, в) { x_vertex = -b/(2 * а) у_вершина = е (х_вершина) с (х_вершина, у_вершина) } V = найти.вершина (а, б, с) # print(V) выводит: -1 -21 # таким образом, вершина является точкой V(-1, -21)
Добавление вершины к графику:
# добавление вершины к графику
точек (х = V[1], y = V[2],
pch = 18, cex = 2) # pch управляет формой точки, а cex управляет ее размером
# добавить метку рядом с точкой
текст (х = V [1], у = V [2],
labels = "Vertex", pos = 3) # pos = 3 размещает текст над точкой 92 - 4 * а * в
если (дискриминант > 0) {
c((-b - sqrt(дискриминант))/(2 * a), (-b + sqrt(дискриминант))/(2 * a))
}
иначе если (дискриминант == 0) {
-б/(2*а)
}
еще {
NaN
}
}
решения = find.roots (a, b, c)
# print(solutions) outputs: -5.582576 3.582576
# таким образом, пересечения по оси x являются точками: (-5. 582576, 0) и (3.582576, 0)
582576, 0) и (3.582576, 0) Добавление пересечений по оси x к графику:
# добавление пересечений по оси x к графику
points(x = решения, y = rep(0, length(solutions)), # координаты x и y точек пересечения x
pch = 18, cex = 2, col = «красный»)
текст (x = решения, y = rep (0, длина (решения)),
labels = rep ("x-intercept", длина (решения)),
pos = 3, col = 'красный') 92 + б * х + с
}
# простой график f(x)
х = -10:10
график (х, е (х), тип = 'л')
# построить оси x и y
аблин (ч = 0)
аблин (v = 0)
# найти вершину
find.vertex = функция (a, b, c) {
x_vertex = -b/(2 * а)
у_вершина = е (х_вершина)
с (х_вершина, у_вершина)
}
V = найти.вершина (а, б, с)
# добавляем вершину на график
точек (х = V[1], y = V[2],
рч = 18, сэкс = 2)
текст (х = V [1], у = V [2],
labels = "Вершина", pos = 3)
# найти точки пересечения x с f(x)
find.


 Организационный
Организационный
 )
) Отвечают и слушают ответы одноклассников, контролируют правильность ответов.
Отвечают и слушают ответы одноклассников, контролируют правильность ответов.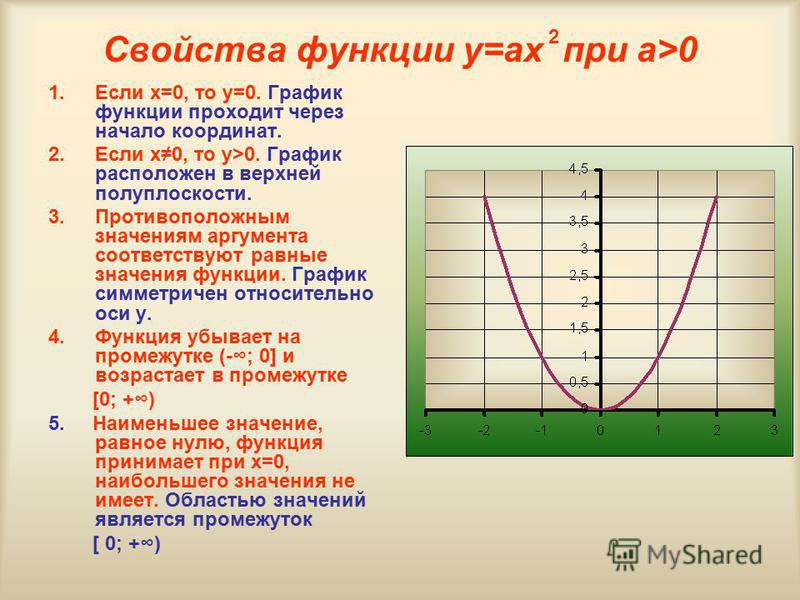 )
)


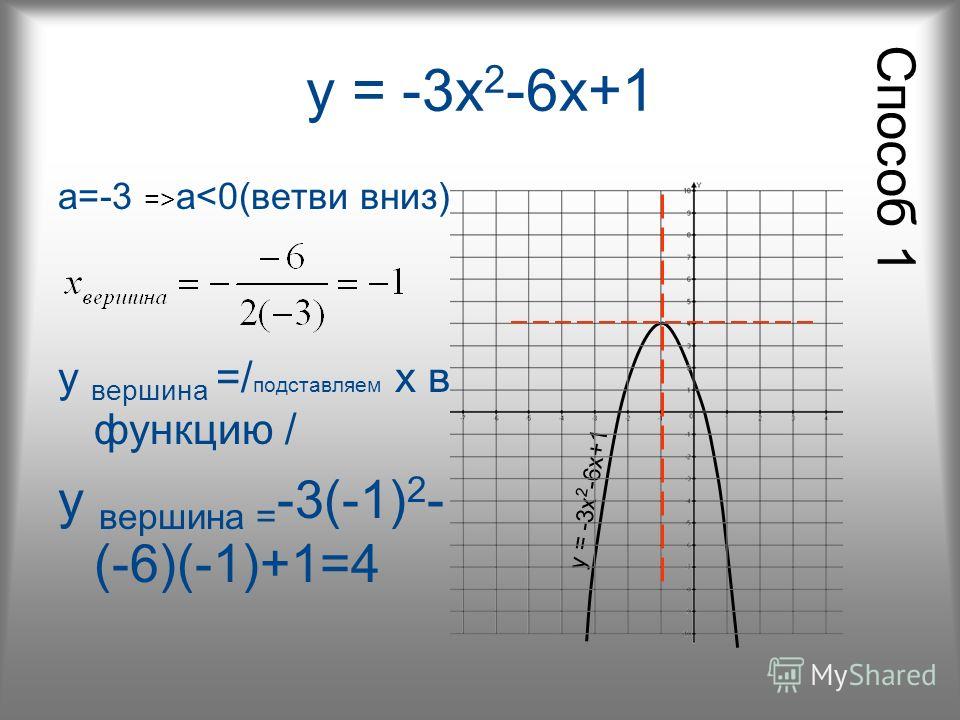

 Домашнее задание
Домашнее задание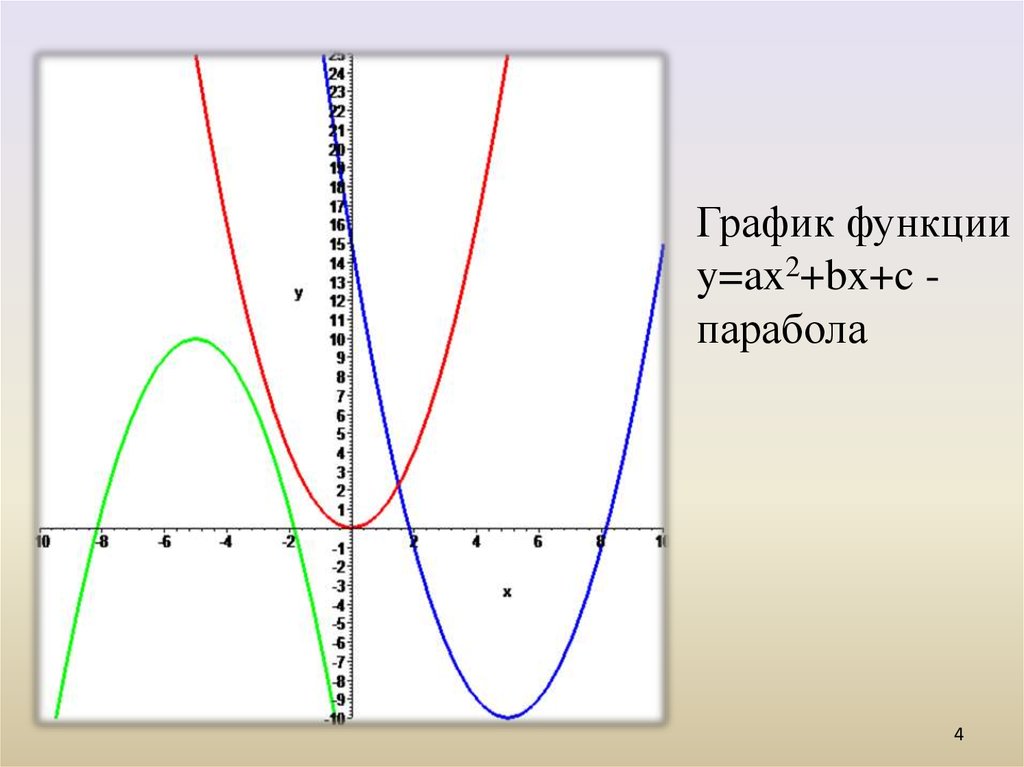
 2.4, № 263, 264, 273.
2.4, № 263, 264, 273.
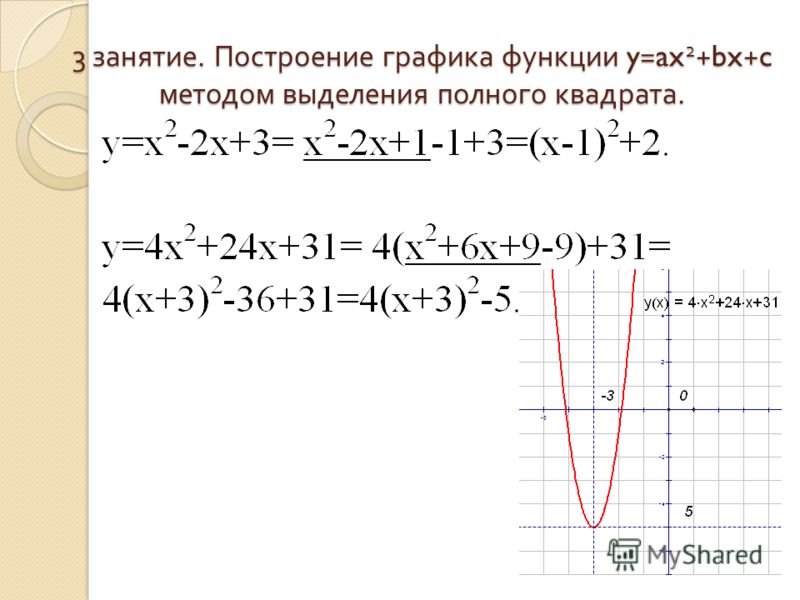 Если D<0 ,то уравнение ax2+bx+c=0 не имеет решений, и, следовательно, парабола y=ax 2+bx+c не имеет точек пересечения с осью ОХ.
Если D<0 ,то уравнение ax2+bx+c=0 не имеет решений, и, следовательно, парабола y=ax 2+bx+c не имеет точек пересечения с осью ОХ.
 vertex = function(a, b, в) {
x_vertex = -b/(2 * а)
у_вершина = е (х_вершина)
с (х_вершина, у_вершина)
}
V = найти.вершина (а, б, с)
# print(V) выводит: -1 -21
# таким образом, вершина является точкой V(-1, -21)
vertex = function(a, b, в) {
x_vertex = -b/(2 * а)
у_вершина = е (х_вершина)
с (х_вершина, у_вершина)
}
V = найти.вершина (а, б, с)
# print(V) выводит: -1 -21
# таким образом, вершина является точкой V(-1, -21) 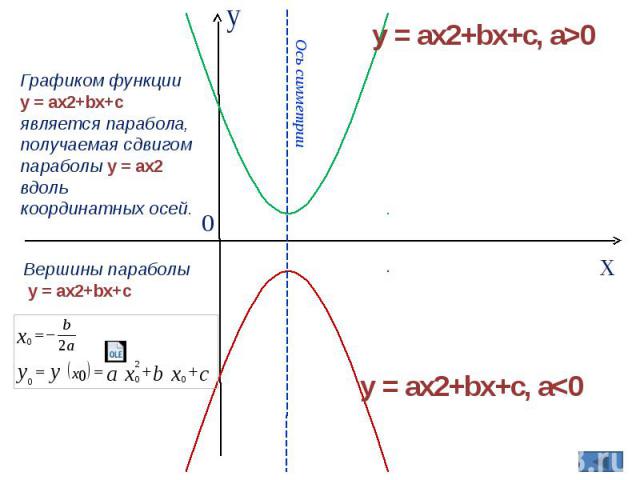 582576, 0) и (3.582576, 0)
582576, 0) и (3.582576, 0)