Как проверить ортогональность векторов: Онлайн калькулятор. Ортогональность векторов

Ортогональные векторы и условие ортогональности: определение, примеры решения задач

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Ортогональные векторы: определение и условие

Определение 1

Ортогональные векторы — это векторы a¯ и b¯, угол между которыми равен 900.

Примечание

Необходимое условие для ортогональности векторов — два вектора a¯ и b¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

a¯ × b¯=0

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a¯={ax×ay} и b¯={bx×by} записывают следующим образом:

a¯×b¯=ax×bx + ay×by=0

Пример 1

Задача 1.  Докажем, что векторы a¯={1;2} и b¯={2;-1} ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=1×2+2×(-1)=2-2=0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Пример 2

Задача 2. Докажем, что векторы a¯={3;-1} и b¯={7;5} ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=3×7+(-1)×5=21-5=16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Пример 3

Задача 3. Найдем значение числа n, при котором векторы a¯={2;4} и b¯={n;1} будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a¯×b¯=2×n+4×1=2n+42n+4=02n=-4n=-2

Ответ: векторы являются ортогональными при значении n=2.

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a¯={1;2;0} и b¯={2;-1;10} условие записывается следующим образом: a¯×b¯=ax×bx+ay×by+az×bz=0.

Пример 4

Задача 4. Докажем, что векторы a¯={1;2;0} и b¯={2;-1;10} являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=1×2+2×(-1)+0×10=2-2=0

Ответ: поскольку произведение векторов  равняется нулю, то они являются ортогональными.

Пример 5

Задача 5. Найдем значение числа n, при котором векторы a¯={2;4;1} и b¯={n;1;-8} будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=2×n+4×1+1×(-8)=2n+4-8=2n-42n-4=02n=4n=2

Ответ: векторы a¯ и b¯ будут ортогональными при значении n=2.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Ортогональность двух векторов: условие, примеры задач

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В данной публикации мы рассмотрим, какие векторы называются ортогональными, какое условие при этом должно выполняться. Также разберем примеры решения задач по этой теме.

• Условие ортогональности векторов
• Примеры задач

Условие ортогональности векторов

Векторы a и b являются ортогональными, если угол между ними прямой (т.е. равен 90°).

Примечание: Скалярное произведение ортогональных векторов равняется нулю. Это и есть существенное условие их ортогональности.

a · b = 0

То есть, если в плоскости a = {a_x; a_y} и b = {b_x; b_y}, то a · b = a_x · b_x + a_y · b_y = 0

Примеры задач

Задание 1

Докажем, что векторы a = {2; 4} и b = {-2; 1} ортогональны.

Решение:
a · b = 2 · (-2) + 4 · 1 = 0

Следовательно, заданные векторы являются ортогональными, так как их скалярное произведение равняется нулю.

Задание 2
При каком значении n векторы a = {3; -9} и b = {6; n} ортогональны.

Решение:
a · b = 3 · 6 + (-9) · n = 0
18 – 9n = 0
n = 2

Таким образом, a и b ортогональны при n, равном двум.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Скалярные произведения и ортогональность

Цели

1. Понять взаимосвязь между скалярным произведением, длиной и расстоянием.
2. Понять взаимосвязь между скалярным произведением и ортогональностью.
3. Словарные слова: скалярное произведение , длина , расстояние , единичный вектор , единичный вектор в направлении x .
4. Основное словарное слово:
   ортогональное .

В этой главе необходимо найти ближайшую точку подпространства к заданной точке, например:

ближайшая точкаx

Ближайшая точка обладает тем свойством, что разница между двумя точками составляет ортогональных или перпендикулярных подпространств. По этой причине нам необходимо разработать понятия ортогональности, длины и расстояния.

Основной конструкцией в этом разделе является скалярное произведение , которое измеряет углы между векторами и вычисляет длину вектора.

Определение

скалярное произведение двух векторов x,y в Rn равно

x·y=GKKIx1x2.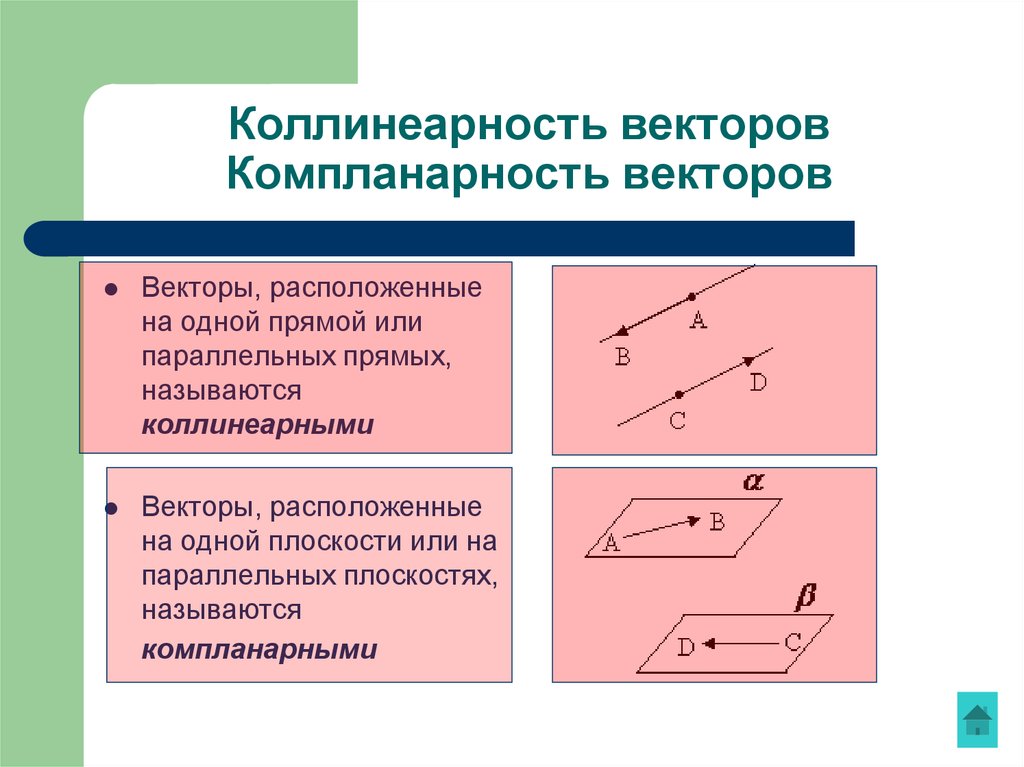 ..xnHLLJ·GKKIy1y2…ynHLLJ=x1y1+x2y2+···+xnyn.

Рассматривая x,y как векторы-столбцы, это то же самое, что и xTy.

Например,

E123F·E456F=A123BE456F=1·4+2·5+3·6=32.

Обратите внимание, что скалярное произведение двух векторов является скаляром .

Вы можете выполнять арифметические действия со скалярными произведениями в основном как обычно, если вы помните, что можете соединить точки только между двумя векторами, и что результат будет скаляром.

Скалярное произведение вектора на самого себя является важным частным случаем:

GKKIx1x2…xnHLLJ·GKKIx1x2…xnHLLJ=x21+x22+···+x2n.

Следовательно, для любого вектора x имеем:

• х·х≥0
• х·х=0⇐⇒х=0.

Это приводит к хорошему определению длины .

Факт

Длина вектора x в Rn есть число

АхА=Вх·х=Nх21+х22+···+х2n.

Легко понять, почему это верно для векторов в R2, по теореме Пифагора.

O34PB32+42=534DDDDO34PDDDD=B32+42=5

Для векторов в R3 можно проверить, что AxA действительно является длиной x, хотя теперь для этого требуется

два применения теоремы Пифагора.

Обратите внимание, что длина вектора равна длине стрелки ; если мы думаем в терминах точек, то длина — это расстояние от начала координат.

Пример

Факт

Если x — вектор, а c — скаляр, то AcxA=|c|·AxA.

Это говорит о том, что масштабирование вектора на c увеличивает его длину на |c|. Например,

ДДДДО68ПДДДД=ДДДД2О34ПДДДД=2ДДДДО34ПДДДД=10.

Теперь, когда у нас есть хорошее представление о длине, мы можем определить расстояние между точками в Rn. Напомним, что разность между двумя точками x,y, естественно, является вектором, а именно вектором y−x, указывающим из x в y.

Определение

Расстояние между двумя точками x,y в Rn равно длине вектора от x до y:

расст(х,у)=Ау-хА.

Пример

Векторы длиной 1 очень часто встречаются в приложениях, поэтому мы даем им имя.

Определение

Единичный вектор представляет собой вектор x длины AxA=Bx·x=1.

Стандартные векторы координат e1,e2,e3,… являются единичными векторами:

Ae1A=DDDDDDE100FDDDDDD=M12+02+02=1.

Для любого отличного от нуля вектора x существует уникальный единичный вектор, указывающий в том же направлении. Получается делением на длину х.

Факт

Пусть x ненулевой вектор в Rn. Единичный вектор в направлении x — это вектор x/AxA.

На самом деле это единичный вектор (учитывая, что AxA — положительное число, поэтому CC1/AxACC=1/AxA):

ДДДДхАхАДДДД=1АхАхА=1.

Пример

В этом разделе мы покажем, как можно использовать скалярное произведение для определения ортогональности , т. е. когда два вектора перпендикулярны друг другу.

Определение

Два вектора x,y в Rn ортогональны или перпендикулярны , если x·y=0.

Обозначение: x⊥y означает x·y=0.

Поскольку 0·x=0 для любого вектора x, нулевой вектор ортогонален каждому вектору в Rn.

Мотивируем приведенное выше определение, используя закон косинусов в R2. На нашем языке закон косинусов утверждает, что если x,y — два ненулевых вектора и если α>0 — угол между ними, то

Ay-xA2=AxA2+AyA2-2AxAAyAcosα.

xyAxAAyAAy−xAα

В частности, α=90◦ тогда и только тогда, когда cos(α)=0, что происходит тогда и только тогда, когда Ay−xA2=AxA2+AyA2. Следовательно,

xandyareperpendicular⇐⇒AxA2+AyA2=Ay−xA2⇐⇒x·x+y·y=(y−x)·(y−x)⇐⇒x·x+y·y=y·y+x·x− 2х·у⇐⇒х·у=0.

Повторить:

х⊥y⇐⇒x·y=0⇐⇒Ay−xA2=AxA2+AyA2.

Пример

Пример

Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)

Определение того, являются ли векторы ортогональными, параллельными или ни тем, ни другим — Krista King Math

Определение векторов, которые являются ортогональными, параллельными или ни теми, ни другими 9\циркуляр??? друг от друга)

???a\cdot b=0???

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

параллельно  если они указывают в одном и том же или противоположном направлении и никогда не пересекаются

после вынесения на множители всех остальных чисел направления будут равны

ни

Так как точку легко взять продукта, неплохо было бы взять за привычку проверять векторы, чтобы увидеть, ортогональны ли они, а затем, если они не ортогональны, проверить, параллельны ли они.

Проверка векторов на предмет того, являются ли они ортогональными, параллельными или ни тем, ни другим

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

Учить больше

Тестирование трех пар векторов для определения того, являются ли они ортогональными, параллельными или ни тем, ни другим

Пример

Скажите, являются ли следующие векторы ортогональными, параллельными или ни тем, ни другим.

???a=\langle2,1\rangle??? и ???b=\langle-1,2\rangle???

???a=2i+3j+5k??? и ???b=i+4j-2k???

???a=\langle1,-2,3\rangle??? и ???b=\langle-2,4,-6\rangle???

Для ???a=\langle2,1\rangle??? и ???b=\langle-1,2\rangle???:

Мы возьмем скалярное произведение наших векторов, чтобы увидеть, ортогональны ли они друг другу.

???a\cdot{b}=(2)(-1)+(1)(2)???

???a\cdot{b}=-2+2???

???a\cdot{b}=0???

Поскольку скалярное произведение равно ???0???, мы можем сказать, что ???a=\langle2,1\rangle??? и ???b=\langle-1,2\rangle??? являются ортогональными. Если мы знаем, что они ортогональны, то по определению они не могут быть параллельны, поэтому мы закончили наше тестирование.

Для ???a=2i+3j+5k??? и ???b=i+4j-2k???:

Сначала приведем векторы в стандартную форму.

???a=2i+3j+5k???

???a=\langle 2,3,5\rangle ???

и

???b=i+4j-2k???

???b=\langle 1,4,-2\rangle ???

Теперь мы возьмем скалярное произведение наших векторов, чтобы увидеть, ортогональны ли они друг другу.

???a\cdot{b}=(2)(1)+(3)(4)+(5)(-2)???

???a\cdot{b}=2+12-10???

???a\cdot{b}=4???

Поскольку скалярное произведение не равно ???0???, мы можем сказать, что ???a=2i+3j+5k??? и ???b=i+4j-2k??? не являются ортогональными.

Поскольку скалярное произведение получить несложно, хорошей идеей будет завести привычку проверять векторы на предмет их ортогональности, а если нет, то на параллельность.

Чтобы сказать, параллельны ли векторы, мы хотим найти общий множитель в числах направления любого вектора и извлечь его, пока оба вектора не станут неприводимыми.

???a=\langle2,3,5\rangle??? уже неприводимо, потому что ???2???, ???3??? и ???5??? не имеют общих множителей. ???b=\langle1,4,-2\rangle??? также неприводимо, потому что ???1???, ???4??? и ???-2??? также не имеют общих множителей.

Следовательно, мы можем сказать, что ???a=2i+3j+5k??? и ???b=i+4j-2k??? не ортогональны и не параллельны.

Для ???a=\langle1,-2,3\rangle??? и ???b=\langle-2,4,-6\rangle???:

Мы возьмем скалярное произведение наших векторов, чтобы увидеть, ортогональны ли они друг другу.

???a\cdot{b}=(1)(-2)+(-2)(4)+(3)(-6)???

???a\cdot{b}=-2-8-18???

???a\cdot{b}=-28???

Поскольку скалярное произведение не равно ???0???, мы можем сказать, что ???a=\langle1,-2,3\rangle??? и ???b=\langle-2,4,-6\rangle??? не являются ортогональными.

Чтобы сказать, параллельны векторы или нет, мы хотим найти общий множитель в числах направления любого вектора и извлечь его, пока оба вектора не станут неприводимыми.

???a=\langle1,-2,3\rangle??? уже неприводимо, потому что ???1???, ???-2??? и ???3??? не имеют общих множителей. С другой стороны, ???b=\langle-2,4,-6\rangle??? имеет общий делитель ???-2??? которые могут быть вынесены из вектора.

???b=\langle-2,4,-6\rangle???

???b=-2\langle1,-2,3\rangle???

Теперь номера направления ???a??? и ???б??? равны, поэтому мы можем сказать, что ???a??? и ???б??? параллельны.