Урок математики по теме: «Решение неравенства», 4-й класс
Тип урока: Изучение нового материала.
Цели: Образовательные:
Сформировать представление о понятии
«решение неравенства», способность
устанавливать, является данное число решением
неравенства или нет.
Развивающие:
- Вывести алгоритм конспектирования учебного текста.
- Развивать различные виды внимания, памяти, речи.
Воспитательные:
- Формировать систему ценностей, направленную на
максимальный личный вклад в коллективную
деятельность в процессе урока.

Оборудование: плакаты, картинки: «заяц», «человек», сборник загадок, учебник математики Л.Г. Петерсон.
Ход урока
I. Самоопределение к деятельности.
На доске написано число, «классная работа».
— Давайте, ребята, вспомним, какие задания вы выполняли в прошлом году на уроках математики? Какие задания казались наиболее интересными? Трудными? (Ответы детей.)
— С помощью каких математических знаков вы могли решить задачи, примеры, составить выражения ? (Ответы детей.)
— Правильно, невозможно представить себе математику без чисел и знаков. А как вы думаете, какие задания вы будете выполнять в 4 классе? (Ответы детей. )
— Действительно, ребята, в этом году вы еще больше узнаете нового, необычного и интересного.
II. Актуализация знаний и фиксация затруднения в деятельности.
Угадайте, ребята, кто пришел к нам сегодня на урок и принес интересные задания?
Много бед таят леса,
Волк, медведь там и лиса!
Наш зверек живет в тревоге,
От беды уносит ноги.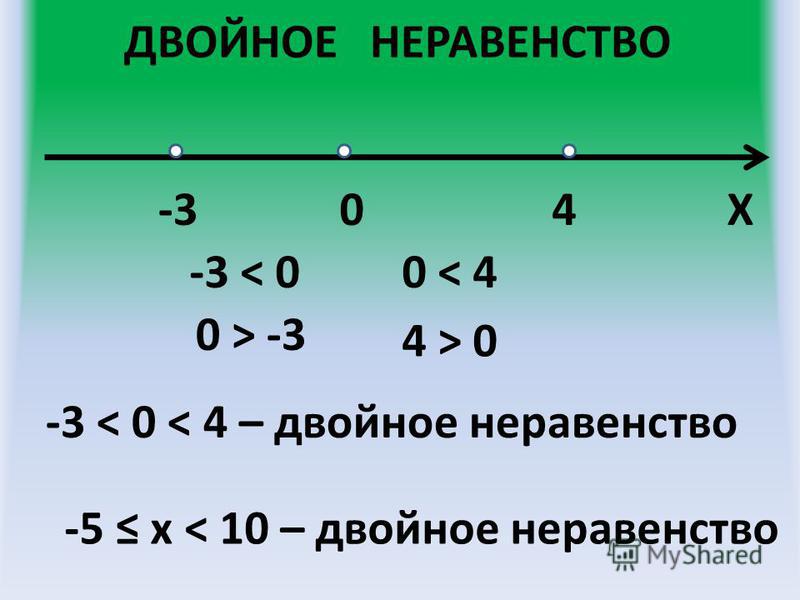
Ну-ка, быстро отгадай-ка,
Как зверек зовется? ( Зайка)
На доске карточки:
140 х 3 |
365 — ( 20 + 65 ) |
( 160 + 40 ) — 70 |
10< 9 |
19 + 9 = 28 |
960 : 3 |
( 30 + 243 ) + 17 |
А – 15 = 17 |
— На какие группы можно разбить данные записи? (Например: буквенные и числовые; выражения, равенства и неравенства.)
Дети расставляют карточки по группам:
Равенства |
Неравенства |
Выражения |
В это время с классом обсуждаются вопросы:
— Какое высказывание называют равенством,
неравенством? (Высказывание, в котором есть
знак «=», знак > или < . )
)
— А выражения, которые являются высказываниями? (О них нельзя сказать, верные они или неверные.)
Затем учащиеся проверяют, как выставлены карточки на доске. Должны появиться следующие 3 столбца:
140 х 3 |
19 + 9 = 28 |
10 < 9 |
960 : 3 |
A -15 = 17 |
y>920 |
| ( 30 + 243 ) + 17 | ||
| 365 – ( 20 + 65 ) | ||
(160 + 40) — 70 |
1.
Дети сигналят ответы: 420, 320, 290, 280, 130. (Приемы вычислений проговариваются, устанавливаются верные варианты.)
2. Запишите в тетрадь полученные числа в порядке возрастания. (130, 280, 290, 320, 420)
Один ученик читает ответы, остальные сравнивают их со своими записями, ошибки исправляются.
— Что интересного вы заметили? (Все числа круглые, в разряде сотен и десятков разные числа.)
3. С доски убираются выражения.
— Как одним словом назвать все записи, которые остались? (Высказывания.)
— На какие группы их можно разбить? (Уравнения и неравенства; высказывания с переменной и без переменной.)
Оставшиеся на доске записи разбиваются на группы: «высказывания» и «высказывания с переменной»
10 < 9 19 + 9 = 28 |
У > 920 а – 15 = 17 |
— Какое из высказываний неверное, а какое верное?
(10 < 9 – неверное, а 19 + 9 = 28– верное. )
)
Записи высказываний 1 столбика убираются с доски.
— Найдите решение уравнения. (а = 32)
— Как проверить, верно ли оно найдено? (Надо подставить число 32 в уравнение, 32 – 15 = 17 – верное равенство.)
— Как еще называют решение уравнения? (Корнем уравнения.)
III. Индивидуальное задание.
— Из составленного ряда чисел выберите и запишите на листках решение неравенства
у < 260.
Варианты детей фиксируются на доске, например: 160, 240, 260.
— Кто же прав? (Мы не знаем.)
— Какое задание выполняли? (Искали решение неравенства у < 260.)
— Почему не можем обосновать свои ответы? (Не знаем, как определить, является число решением или нет.)
— Поставьте перед собой цель. (Научиться определять, является число решением неравенства или нет.)
— Предложите название темы урока («Решение
неравенства». )
)
Тема урока выставляется на доске. Решение неравенства.
IV. Построение проекта выхода из затруднения.
— Каким способом вы предлагаете обосновать, является число решением неравенства или нет? (Надо знать, что такое – «решение неравенства».)
— Предложите свои версии? (Варианты детей.)
— Сравните с текстом учебника.
— Итак, что такое «решение неравенства»?
— Как вы поняли, «решение неравенства» — это действие или число? (Это число.)
— Какие же числа из вашего ряда являются решением неравенства у < 260? (160,240)
— Почему число 260 не является решением? (Неверно, что 260< 260.)
— Итак, какой первый шаг при ответе на данный вопрос? Второй шаг?
Алгоритм поиска решений неравенства с переменной фиксируем в виде блок-схемы:
(Скобки вокруг У обозначают, что число
должно подставляться вместо переменной, а буквы
внизу — что нужно проверить, верно или неверно
полученное числовое неравенство. )
)
Физкультминутка: « Все имеет смысл, пока мы здоровы».
- Крепко зажмурить глаза на 3-5 секунд, а затем открыть их на 3-5 секунд. Продолжительность 6-8 раз. (Укрепляет мышцы век, способствует кровообращению и расслаблению мышц глаз).
- «Написать цифры». Стоя, плечевым суставом, (сначала правым, потом левым) написать поочередно цифры от единицы до 8. Руки опущены.
- Активный массаж мизинца (8-10 секунд) - способствует снятию психического напряжения, нервного переутомления
- Активный массаж большого пальца (8-10 секунд) – повышает функциональную активность головного мозга.
V. Первичное закрепление во внешней речи.
1. № 1, стр 1.
На доске выставлены карточки, напротив которых во время беседы отмечаются соответствующие символы.
Вводная часть — 1
Главная мысль – W
Примеры — µ
Беседа: «Текст, который мы прочитали, как и
любой учебный текст, состоит из нескольких
частей: вводной, которая подготавливает
понимание смысла; главной мысли – смысла
нового; примеров, которые иллюстрируют
главную мысль. Найдите в тексте эти части и
догадайтесь, какими значками они обозначены? Так
устроен любой учебный текст. Почему важно уметь
его понимать?
Найдите в тексте эти части и
догадайтесь, какими значками они обозначены? Так
устроен любой учебный текст. Почему важно уметь
его понимать?
— Для этого мы будем конспектировать текст, т.е. кратко излагать его смысл.
— Какая из главных частей должна войти в конспект? (Главная мысль.) Учитель выставляет на доску карточки.
Отметить части текста |
Выписать главные мысли |
Прочитать текст |
— Расставьте шаги алгоритма конспектирования текста и обсудите в группах.
| Прочитать текст | Отметить части текста | Выписать главные мысли |
— Какие шаги у нас уже сделаны? (Первые два)
Что осталось? (Выписать главную мысль. )
)
— Подчеркните карандашом текст, который надо выписать в конспект. ( Значение переменной, удовлетворяющее неравенству, называют решением неравенства.)
2. №2 , стр 1.
— Прочитайте задание.
— Какие числа вы подчеркнули? (Все числа, которые больше 56. Это 91 и 318.)
— Как можно назвать эти числа? (Решения неравенства.)
— Почему не выбрали письмо 56? (Потому что неверно 56>56.)
3. № 3, стр 1.
Рассмотрите картинку и раскрасьте числа, которые являются решением данного неравенства. ( Дети «цепочкой» комментируют: «Число 75 не является решением, так как неверно, что 75 –75 >4».)
4. № 5, стр 2. — работа в парах.
Соревнование — чья пара быстрее и правильнее выберет нужные числа.
а) 8 х в – 7 > (30,72) б) к : 3 + 9 < 12 (6)
VI. Самостоятельная работа с самопроверкой по
эталону.
№ 4, стр 1.
— Выберите одну любую строчку и подчеркните только то неравенство, решением которого будет число 6.
Затем через готовую запись на доске дети сверяют свой выбор, пользуясь алгоритмом.
(Если задание выполнено правильно, то рядом дети ставят знак «+», если была допущена ошибка, то они выявляют и называют ошибку.)
VII. Повторение.
1. №8, стр 2
На доске таблица. (Один ученик работает над закрытой частью доски.)
— Прочитайте задачу. Заполните таблицу.
— Рассмотрите запись в тетради. Что необычного? ( Записаны вопросы.)
— Для чего нужны вопросы? ( Чтобы определить порядок решения задачи.)
— Как ответить на первый вопрос? (Надо расстояние разделить на время.)
— Надо ли писать пояснение? (Нет, в вопросе все объяснено.)
— Узнайте самостоятельно скорость зайца. Чему она равна? (7км\ч.)
— Ответьте самостоятельно на все следующие
вопросы.
После окончания работы дети сверяют свое решение с записью на доске.
2. № 10, стр 3. – работа в парах.
— Здесь первый пример легче, а второй сложнее. Выберите и решите один пример по желанию. Проверка с доски.
VIII. Итог урока. Рефлексия деятельности.
— Назовите тему урока? (Решение неравенства.)
— Что означает термин «решение неравенства» - действие или число? (Число.)
— Как узнать, является число решением неравенства или нет? (Поставить его вместо буквы и определить, верное неравенство или нет.)
— Посигнальте мне, кому нужна еще помощь? Кто уже разобрался?
— А что еще нового узнали? ( Как составлять конспект, записывать задачи с вопросами.)
— Для чего надо уметь конспектировать текст?
— А записывать задачи с вопросами?
— Как вы думаете, что нужно потренировать дома?
— Д/з: закончить конспект текста и выучить
опорный конспект; потренироваться в решении
неравенств № 6, стр 2 и попробовать записать
решение задачи с помощью вопросов № 9, стр 3. Дополнительно по желанию -№ 12* или № 13*, стр 3.
Дополнительно по желанию -№ 12* или № 13*, стр 3.
Урок математики в 4 классе по теме «Решение неравенств» | План-конспект урока по математике (4 класс) по теме:
Тема: «Решение неравенства».
Основные цели:
Сформировать представление о понятии «решение неравенства», способность устанавливать, является данное число решением неравенства или нет;
1. Мотивация к учебной деятельности:
Учитель открывает на доске запись:
Хорошее начало – залог успеха
– Прочитайте высказывание на доске. Согласны ли вы с ним? (…)
– Докажите, что это высказывания! (…)
– Ребята, а побудительные предложения, такие как «Внимание!», «Стой!», «Докажите!» являются высказываниями? (Нет, так как о таких предложениях нельзя сказать, истинны они или ложны.)
– Что вы можете сказать о высказывании: «В школу вы приходите учиться». (Это высказывание истинное.)
– Докажите, что это высказывание истинное. (…)
– А что вы можете сказать о высказывании: «Вы умеете учиться». (…)
(…)
2. Актуализация знаний и фиксация затруднения в пробном действии.
— Чтобы узнать, что вы не знаете, что надо сначала сделать? (Надо повторить, что мы уже знаем.)
— А где эти знания могут вам помочь? (При открытии новых знаний.)
. На доске открываются расположенные под ними карточки с математическими записями:
170 ∙ 2 585 – (10 + 85) (380 + 90) – 80
4 5 17 + 9 = 26 580 : 2
(384 + 40) +16 х 7 12 – а = 8
— Какие виды математических записей представлены на доске? (Равенства, неравенства и выражения.)
— Вспомните, что вы знаете о равенствах, неравенствах, выражениях. (…)
— Какие из записанных на доске предложений являются высказываниями? Докажите. (Неравенство 4 5 – ложно; равенство 17 + 9 = 26 – истинно.)
(Неравенство 4 5 – ложно; равенство 17 + 9 = 26 – истинно.)
— А математические выражения являются высказываниями? Почему? (Не являются, так как о них нельзя сказать, истинны они или ложны.)
— Передвиньте карточки на доске по группам: выражения, равенства, неравенства.
Трое учащихся работают у доски, остальные – фронтально. На доске должны получиться следующие три столбика:
170 ∙ 2 17 + 9 = 26 4 5
580 : 2 12 – а = 8 х 7
(384 + 40) + 16
(380 + 90) – 80
585 – (10 + 85)
— Что можно сделать с выражениями в первом столбике? (Можно найти значения этих выражений.)Дети находят значения выражений.
— Что вы сейчас повторили? (Способы нахождения значений числовых выражений)
— Я вам предлагаю следующее задание: запишите маркером на обратной стороне своих сигнальных карточек решения неравенства х 7.
— Прежде выполнять задание сравните предложенное задание с предыдущими заданиями, и определите, что в этом задании нового?
— Сформулируйте свою цель и тему урока. (Цель: найти решение неравенства, тема: решение неравенств.)
Тема записывается на доске: «Решение неравенства».
— Выполните задание.
Учащиеся самостоятельно выполняют задание.
— У кого нет ответов?
— Сформулируйте своё затруднение. (Мы не смогли найти решение неравенства.)
— Прикрепите на доску карточки те, у кого есть ответы.
Учитель фиксирует разные позиции, отсутствие единого мнения.
— Что же получилось? (Мнения разделились.)
— Вы можете объяснить, почему получились разные ответы? (…)
— Сформулируйте своё затруднение. (Мы не можем объяснить, почему получились разные ответы.)
— Что же делать? (Надо подумать, почему так получилось.)
3. Выявление места и причины затруднения.
— Какое задание вы выполняли? (Найти решение неравенства х 7. )
)
— Каким правилом вы пользовались при выполнении задания? (…)
-Почему не удалось всем выполнить это задание? (Не знаем, что такое решения неравенства; не знаем способа их нахождения.)
4. Построение проекта выхода из затруднения.
— Поставьте перед собой цель. (Нам надо согласовать, что такое «решение неравенства» и научиться находить их.)
— Что вы сначала должны сделать? (Выяснить, что такое решение неравенств.)
Учитель на доске фиксирует первый пункт плана:
1. Выяснить, что такое решение неравенства.
— А что после этого надо сделать? (Найти способы нахождения решений неравенств.)
Учитель на доске фиксирует второй шаг плана:
2. Найти способ решения неравенств.
5. Построение проекта выхода из затруднения.
Один из учеников читает текст учебника вслух.
— Так что же такое «решение неравенства» – действие или число? (Это число, которое подставляют вместо переменной и получают верное неравенство.)
— Какие числа являются решениями неравенства х 7
— Почему же число 7 не является решением этого неравенства? (7 7 – ложное высказывание. )
)
— Первый шаг плана вы выполнили? Что теперь надо сделать? (…)
— Давайте составим алгоритм поиска решения неравенства. Эту работу я вам предлагаю выполнить в группах
— Я вам предлагаю шаги алгоритма, вам необходимо из предложенных блоков построить алгоритм нахождения решения неравенства, обосновав свой вариант, на работу отводится 2 минуты.
Учащиеся выполняют задание в группах.
—
Учащиеся выполняют задание в группах.
— Запишем алгоритм в виде опорного конспекта на листах бумаги.
— Покажите, что у вас получилось?
Варианты, предложенные группами, обсуждаются и записываются в тетради для опорных конспектов.
Учитель вывешивает карточку с опорным конспектом на доску:
-Что нужно проверить?
-Истинно или ложно получившееся числовое неравенство.
— Вы достигли поставленной цели, что вы узнали? (Да, цель достигнута, мы узнали, что такое решение неравенства, и построили алгоритм нахождения решений неравенств. )
)
— Что надо сделать? (Надо потренироваться в нахождении решений неравенств.)
6. Первичное закрепление во внешней речи.
— Для тренировки я вам предлагаю выполнить № 2, стр. 1.
— Подчеркните числа, удовлетворяющие данному неравенству.
Учащиеся работают в учебниках-тетрадях.
— Какие числа подчеркнули? (91 и 38.)
— Как называются эти числа? (Решениями неравенства.)
— Почему не выбрали число 56? (Потому что высказывание 56 56 – ложно.)
— Что ещё надо сделать, чтобы каждый из вас мог сказать истинным или ложным является высказывание «Мы научились решать неравенства»? (Надо проверить себя.)
7. Самостоятельная работа с самопроверкой по эталону.
— Переделайте ее так, чтобы получилось истинное высказывание. (Мы будем выполнять самостоятельную работу; в самостоятельной работе все задания мне понятны и т. д.).
— Прочитайте задание № 4, стр. 1.
Учащиеся читают задание про себя.
— Что нужно сделать? (Проверить, является ли число 6 решением неравенства. )
)
— Выберите любое неравенство верхней строчки и выполните задание самостоятельно, обведя неравенство в случае, если число 6 является решением неравенства и подчеркните неравенство, если не является решением.
Учащиеся выполняют самостоятельную работу, по окончании которой учитель на доске выставляет эталон для самопроверки.
— Проверяем первый шаг.
— Как вы выполняли шаг?
— У кого этот шаг вызвал затруднение?
— Почему вы допустили ошибку?
— Зафиксируйте результат проверки при помощи знаков «+» или «?».
— Что нам поможет исправить ошибки? (Эталон.)
— Проверяем второй шаг.
— Как вы выполняли второй шаг?
— У кого второй шаг вызвал затруднение?
— Почему вы допустили ошибку?
— Зафиксируйте результат проверки при помощи знаков «+» или «?».
— Исправьте ошибки.
— Проверяем третий шаг.
— Как вы выполняли третий шаг?
— У кого шаг вызвал затруднение?
— Почему вы допустили ошибку?
— Зафиксируйте результат проверки при помощи знаков «+» или «?».
— Исправьте ошибки.
— Поднимите руки, у кого все верно. Вы молодцы!
8. Рефлексия учебной деятельности на уроке.
— Назовите тему урока. (Решение неравенств.)
— Какова была цель урока? (Определить, что такое решение неравенств и найти способ для нахождения способа решения неравенства.)
— Вы достигли поставленной цели? (Да.)
— Как узнать, является ли число решением неравенства? (Поставить его вместо переменной и определить, верно неравенство или нет.)
— У кого остались вопросы на конец урока?
— Кто хорошо разобрался в теме? Молодцы!
— Как вы думаете, с какими заданиями надо поработать дома? (…)
Домашнее задании
№ 6 (в, г), стр. 2; № 9
DSB Ontario North East Math Support
( Приблизительно: 2-60-минутные уроки)
Щелкните здесь: Распечатанный план урока
На компьютере? Нажмите «Файл», затем «Создать копию», чтобы сохранить и внести изменения.
На iPad? Выберите 3 точки в правом верхнем углу. «Поделиться и экспортировать», затем «Сделать копию».
Ожидания:
Алгебра
Большая идея:
На этом уроке ученики в меру своих способностей научатся мыслить критически и творчески, использовать позитивную мотивацию и настойчивость. Они будут применять такие стратегии, как: использование итеративного подхода путем опробования различных методов, включая угадывание и проверку, чтобы способствовать решению проблем. Они будут устанавливать связи, оценивать выбор, размышлять и оценивать стратегии.
Цели обучения
Мы хотим, чтобы учащиеся понимали. ..
..
Что такое неравенство.
Как решить неравенство
Как проверить его правильность.
Как показать выражение на числовой прямой.
Критерии успеха
Я понимаю, что любое отдельное алгебраическое выражение описывает множество ситуаций.
Я понимаю, что такое неравенство.
Я могу проверить переменные, чтобы доказать истинность или ложность неравенства.
Я понимаю, как поставить выражение на числовую прямую.
Я понимаю, как изобразить выражение на числовой прямой.
опыт учителя
В выражениях используются символы-переменные, используемые для представления неизвестных и/или изменяющихся значений.
 Выражение похоже на m + 5, что указывает на то, что 5 добавляется к числу (m), независимо от того, что это за число m. Учащиеся должны научиться распознавать, что «n-10» означает «отнять 10 от значения n» по сравнению с «10-n», что означает «насколько n меньше 10»9.0007
Выражение похоже на m + 5, что указывает на то, что 5 добавляется к числу (m), независимо от того, что это за число m. Учащиеся должны научиться распознавать, что «n-10» означает «отнять 10 от значения n» по сравнению с «10-n», что означает «насколько n меньше 10»9.0007Они должны признать, что любое отдельное алгебраическое выражение описывает множество ситуаций. Например, m + 5 > 10 описывает множество ситуаций и то, как это выразить на числовой прямой.
Графики являются эффективными моделями для описания взаимосвязей между различными переменными и величинами.
Источник: Адаптировано из: Смолл, М. (2013) Делаем математику значимой для канадских школьников, K-8. Nelson Education (стр. 620-621)
Предварительные знания
Понимание переменных
Узнайте, понимают ли ваши ученики переменные, переменные, изменяющие величины, неизвестные величины, пишут выражения с использованием переменных и определяют пропущенные числа в уравнениях сложения и вычитания.

Миссия крюка знаний
Minds On
Источник: https://www.mathsisfun.com/алгебра/инекачество.html
1) Просмотрите символы <, >, =
2) Предоставьте учащимся следующие мысли по заданию: https://docs.google. com/document/d/1vglUaInRFihjoZ-fGQb7osq-KEhafHSjTuVrsYrq6_k/edit?usp=sharing
Дополнительное задание: Введение в неравенства : Беседы о числах: мини-уроки по расширению сложения и вычитания: «Модель денег: эквивалентность, вариация», стр. 63 (нужны канадские монеты и несколько иностранных монет)
Действие!
Источник: https://www.mathsisfun.com/алгебра/inequality.html
По указанию учителя: .
 Математика не всегда говорит о «равно», иногда мы знаем только, что что-то больше или меньше.
Математика не всегда говорит о «равно», иногда мы знаем только, что что-то больше или меньше.б) Посмотрите на их утверждения о неравенстве умов в диагностической деятельности. Они правильные? Использовали ли они символ «меньше»? Что они определили для утверждений о большем, чем неравенство?
c) Обсудите «больше и равно» или «меньше и равно» и как пишутся символы.
Приведите пример: Вы должны быть старше 13 лет, чтобы смотреть некоторые фильмы. Записывается в виде неравенства: ≥ 13
Объединение знаний
Источник: Веб-сайт Math is Fun
3 Следуйте этим пояснениям на указанном выше веб-сайте:0002 Используйте эти примеры и используйте числовую прямую, чтобы показать неравенство.Нажмите на эту ссылку для поддержки и визуальных эффектов: Как график неравенства
Дополнительная поддержка: Неравенства с использованием видео с добавлением и вычитанием
Независимая задача / оценка.
Веб-сайт Math is Fun
Решение неравенств: (перейдите к практике в конце страницы.)
Веб-сайт Kate’s Math Lessons
Графики неравенств (Перейдите к практике в конце страницы)
Создание страниц для практики по Переменные неравенств, сложение и вычитание неравенств, графическое умножение и деление
Неравенства с использованием Desmos
Щелкните здесь , чтобы получить поддержку или узнать, почему Desmos является отличным математическим инструментом/ресурсом.
Приложение Algebra Tiles
Решение неравенств — Математика средней школы
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- Репетиторство ASPIRE
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ISAT
- Обучение SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Мы открыты в субботу и воскресенье!
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы средней школы
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
Справка по математике для старших классов » Алгебра II » Базовая алгебра с одной переменной » Неравенства » Решение неравенств
Найдите:
Возможные ответы:
Правильный ответ:
Объяснение:
К неравенствам можно относиться так же, как и к любым другим уравнениям, за исключением умножения и деления на отрицательные числа. При умножении или делении на отрицательные числа мы просто меняем знак неравенства, чтобы стало , и наоборот.
При умножении или делении на отрицательные числа мы просто меняем знак неравенства, чтобы стало , и наоборот.
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
Объяснение:
К неравенствам можно относиться так же, как и к любым другим уравнениям, за исключением умножения и деления на отрицательные числа. При умножении или делении на отрицательные числа мы просто меняем знак неравенства, чтобы стало , и наоборот. Когда мы решаем биномы, мы должны проявлять особую осторожность, потому что .
Итак, когда мы решаем неравенства с биномами, мы должны создать два сценария: один, где значение в скобках положительное, и другой, где оно отрицательное. Для отрицательного сценария мы должны поменять знак, как обычно делаем для неравенств.
Теперь мы должны создать два сценария:
и
Обратите внимание, что в отрицательном сценарии мы поменяли знак неравенства.
и
и
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
Объяснение:
К неравенствам можно относиться так же, как и к любым другим уравнениям, за исключением умножения и деления на отрицательные числа. При умножении или делении на отрицательные числа мы просто меняем знак неравенства, чтобы стало , и наоборот. Когда мы решаем биномы, мы должны проявлять особую осторожность, потому что .
Итак, когда мы решаем неравенства с биномами, мы должны создать два сценария: один, где значение в скобках положительное, и другой, где оно отрицательное. Для отрицательного сценария мы должны поменять знак, как обычно делаем для неравенств.
Теперь мы должны создать два сценария:
и
Обратите внимание, что в отрицательном сценарии мы поменяли знак неравенства.
и
и
Сообщить об ошибке
Решите неравенство для x:
Возможные ответы:
Правильный ответ:
Объяснение:
Вычесть 4 из обеих сторон:
Разделить обе части на 2:
Сообщить об ошибке
Решить для .
Возможные ответы:
Правильный ответ:
Объяснение:
Добавьте 4 к обеим сторонам.
Разделите обе части на –7. При делении на отрицательное значение мы также должны изменить направление знака неравенства.
Сообщить об ошибке. Объяснение:
Переместите одинаковые члены на одинаковые стороны:
Combine like terms:
Divide both sides by 3:
Report an Error
Solve for :
Possible Answers:
Correct answer:
Объяснение:
К неравенствам можно относиться так же, как и к любым другим уравнениям, за исключением умножения и деления на отрицательные числа. При умножении или делении на отрицательные числа мы просто меняем знак неравенства, чтобы стало , и наоборот.
Сообщить об ошибке
Авторские права Университет Флориды на побережье Мексиканского залива, магистр образования…
Посмотреть репетиторов
Наташа Мохамед
Сертифицированный репетитор
Малабарский христианский колледж, бакалавр наук, математика.


 Выражение похоже на m + 5, что указывает на то, что 5 добавляется к числу (m), независимо от того, что это за число m. Учащиеся должны научиться распознавать, что «n-10» означает «отнять 10 от значения n» по сравнению с «10-n», что означает «насколько n меньше 10»9.0007
Выражение похоже на m + 5, что указывает на то, что 5 добавляется к числу (m), независимо от того, что это за число m. Учащиеся должны научиться распознавать, что «n-10» означает «отнять 10 от значения n» по сравнению с «10-n», что означает «насколько n меньше 10»9.0007
 Математика не всегда говорит о «равно», иногда мы знаем только, что что-то больше или меньше.
Математика не всегда говорит о «равно», иногда мы знаем только, что что-то больше или меньше.