Как решать неравенства с иксом: Линейные неравенства, решение и примеры

Содержание

Линейные неравенства, решение и примеры

Поможем понять и полюбить математику

Начать учиться

133.7K

Тема линейных неравенств непростая, но без нее не получится решать сложные математические задачки. Давайте рассмотрим линейные неравенства и попробуем с ними подружиться.

Основные понятия

Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.

Неравенство — это алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.

Линейные неравенства — это неравенства вида:

ax + b < 0,
ax + b > 0,
ax + b ≥ 0,
ax + b ≤ 0,

где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти все значения переменной, при которой неравенство верное.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Типы неравенств

Строгие — используют только больше (>) или меньше (<):

a < b — это значит, что a меньше, чем b.
a > b — это значит, что a больше, чем b.
a > b и b < a означают одно и тоже, то есть равносильны.

Нестрогие — используют сравнения ≥ (больше или равно) или ≤ (меньше или равно):

a ≤ b — это значит, что a меньше либо равно b.

a ≥ b — это значит, что a больше либо равно b.
знаки ⩽ и ⩾ являются противоположными.

Другие типы:

a ≠ b — означает, что a не равно b.
a ≫ b — означает, что a намного больше, чем b.
a ≪ b — означает, что a намного меньше, чем b.
знаки >> и << противоположны.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Линейные неравенства: свойства и правила

Вспомним свойства числовых неравенств:

Если а > b , то b < а. Также наоборот: а < b, то b > а.

Если а > b и b > c, то а > c. И также если а < b и b < c, то а < c.

Если а > b, то а + c > b+ c (и а – c > b – c).

Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям можно прибавлять или вычитать одну и ту же величину.

Если а > b и c > d, то а + c > b + d.

Если а < b и c < d, то а + c < b + d.

Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять из-за возможных исключений. Например, если из 12 > 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

Если а > b и c < d, то а – c > b – d.

Если а < b и c > d, то а – c < b – d.

Из одного неравенства можно почленно вычесть другое противоположного смысла, оставляя знак того, из которого вычиталось.

Если а > b, m — положительное число, то mа > mb и

Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).

Если же а > b, n — отрицательное число, то nа < nb и

Обе части можно умножить или разделить на одно отрицательное число, при этом знак неравенства поменять на противоположный.

Если а > b и c > d, где а, b, c, d > 0, то аc > bd.

Если а < b и c < d, где а, b, c, d > 0, то аc < bd.

Неравенства одного смысла на множестве положительных чисел можно почленно перемножать.

Следствие данного правила или квадратный пример: если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2. На множестве положительных чисел обе части можно возвести в квадрат.

Если а > b, где а, b > 0, то

Если а < b , то

Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.

Важно знать

Два неравенства можно назвать равносильными, если у них одинаковые решения.

Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.

Свойства выше помогут нам использовать следующие правила.

Правила линейных неравенств

Любой член можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется.

2x − 3 > 6 ⇒ 2x > 6 + 3 ⇒ 2x > 9.

Обе части можно умножить или разделить на одно положительное число. Знак неравенства при этом не меняется.

Умножим обе части на пять 2x > 9 ⇒ 10x > 45.

Обе части можно умножить или разделить на одно отрицательное число. Знак неравенства при этом меняется на противоположный.

Разделим обе части на минус два 2x > 9 ⇒ 2x : (–2) > 9 : (–2) ⇒ x < 4,5.

Решение линейных неравенств

Линейные неравенства с одной переменной x выглядят так:

ax + b < 0,
ax + b > 0,
ax + b ≤ 0,
ax + b ≥ 0,

где a и b — действительные числа.

А на месте x может быть обычное число.

Равносильные преобразования

Для решения ax + b < 0 (≤, >, ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.

Алгоритм решения ax + b < 0 при a ≠ 0

перенесем число b в правую часть с противоположным знаком,
получим равносильное: ax < −b;
произведем деление обеих частей на число не равное нулю.

Когда a положительное, то знак неравенства остается без изменений, если a — отрицательное, знак меняется на противоположный.

Рассмотрим пример: 4x + 16 ≤ 0.

Как решаем: В данном случае a = 4 и b = 16, то есть коэффициент при x не равен нулю. Применим вышеописанный алгоритм.

Перенесем слагаемое 16 в другую часть с измененным знаком: 4x ≤ −16.
Произведем деление обеих частей на 4. Не меняем знак, так как 4 — положительное число: 4x : 4 ≤ −16 : 4 ⇒ x ≤ −4.
Неравенство x ≤ −4 является равносильным. То есть решением является любое действительное число, которое меньше или равно 4.

Ответ: x ≤ −4 или числовой промежуток (−∞, −4].

При решении ax + b < 0, когда а = 0, получается 0 * x + b < 0. На рассмотрение берется b < 0, после выясняется верное оно или нет.

Вернемся к определению решения неравенства. При любом значении x мы получаем числовое неравенство вида b < 0. При подстановке любого t вместо x, получаем 0 * t + b < 0 , где b < 0. Если оно верно, то для решения подойдет любое значение. Когда b < 0 неверно, тогда данное уравнение не имеет решений, так как нет ни одного значения переменной, которое может привести к верному числовому равенству.

Числовое неравенство вида b < 0 (≤, > , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.

Рассмотрим пример: 0 * x + 5 > 0.

Как решаем:

Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.

Ответ: промежуток (− ∞ , + ∞).

Метод интервалов

Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

Метод интервалов заключается в следующем:

вводим функцию y = ax + b;
ищем нули для разбиения области определения на промежутки;
отмечаем полученные корни на координатной прямой;
определяем знаки и отмечаем их на интервалах.

Алгоритм решения ax + b < 0 (≤, >, ≥) при a ≠ 0 с использованием метода интервалов:

найдем нули функции y = ax + b для решения уравнения ax + b = 0.

Если a ≠ 0, тогда решением будет единственный корень — х₀;

начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
определим знаки функции y = ax + b на промежутках.

Для этого найдем значения функции в точках на промежутке;

если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если < или ≤ — над отрицательным промежутком.

Рассмотрим пример: −6x + 12 > 0.

Как решаем:

В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,
−6x = −12,
x = 2.
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
Определим знаки на промежутках.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.
Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6 < 0 . Знак на промежутке является отрицательным.
Штриховку сделаем над положительным промежутком.
По чертежу делаем вывод, что решение имеет вид (−∞, 2) или x < 2.

Ответ: (−∞, 2) или x < 2.

Графический способ

Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

Алгоритм решения y = ax + b графическим способом

во время решения ax + b < 0 определить промежуток, где график изображен ниже оси Ох;
во время решения ax + b ≤ 0 определить промежуток, где график изображается ниже Ох или совпадает с осью;
во время решения ax + b > 0 определить промежуток, где график изображается выше Ох;
во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.

Рассмотрим пример: −5 * x − √3 > 0.

Как решаем

Так как коэффициент при x отрицательный, данная прямая является убывающей.
Координаты точки пересечения с Ох равны (−√3 : 5; 0).
Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.

Ответ: (−∞, −√3 : 5) или x < −√3 : 5.

Линейные неравенства в 8 классе — это маленький кирпич, который будет заложен в целый фундамент знаний. Мы верим, что у все получится!

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

230. 6K

Отрицательная степень

К следующей статье

415.8K

Квадратичная функция. Построение параболы

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс

§ Как решать линейные неравенства

Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин.

Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения.

В отличии от уравнения в неравенстве вместо знака равно «=» используют любой знак сравнения: «>», «

x − 6

Так как в неравенстве «x − 6

Важно!

Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное в первой степени с коэффициентом «1».

При решении линейных неравенств используют правило переноса и правило деления неравенства на число.

Правило переноса в неравенствах

Также как и в уравнениях, в неравенствах можно переносить любой член неравенства из левой части в правую и наоборот.

Запомните!

При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на противоположный.

Вернемся к нашему неравенству и используем правило переноса.

x − 6 x x

Итак, мы получили ответ к неравенству «x

Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить, понятие числовой оси.

Нарисуем числовую ось для неизвестного «x» и отметим на ней число «14».

Запомните!

При нанесении числа на числовую ось соблюдаются следующие правила:

если неравенство строгое, то число отмечается как «пустая» точка. Это означает, что число не входит в область решения;
если неравенство нестрогое, то число отмечается как «заполненная» точка. Это означает, что число входит в область решения.

Заштрихуем на числовой оси по полученному ответу «x

Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство «x − 6

Возьмем, например число «12» из заштрихованной области и подставим его вместо «x» в исходное неравенство «x − 6

12 − 6 6

Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.

Важно!

Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство дают верный результат.

Решением неравенства называют множество чисел из заштрихованной области на числовой оси.

В нашем примере ответ «x

Правило умножения или деления неравенства на число

Рассмотрим другое неравенство.

2x − 16 > 0

Используем правило переноса и перенесём все числа без неизвестного, в правую часть.

2x − 16 > 0
2x > 16

Теперь нам нужно сделать так, чтобы при неизвестном «x» стоял коэффициент «1». Для этого достаточно разделить и левую, и правую часть на число «2».

Запомните!

При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.

Если неравенство умножается (делится) на положительное число, то
знак самого неравенства остаётся прежним.
Если неравенство умножается (делится) на отрицательное число, то
знак самого неравенства меняется на противоположный.

Разделим «2x > 16» на «2». Так как «2» — положительное число, знак неравенства останется прежним.

          2x > 16     | (:2)
2x (:2) > 16 (:2)
x > 8
Ответ: x > 8

Рассмотрим другое неравенство.

9 − 3x ≥ 0

Используем правило переноса.

9 − 3x ≥ 0
−3x ≥ −9

Разделим неравенство на «−3». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.

−3x ≥ −9
−3x ≥ −9 | :(−3)
−3x : (−3) ≤ −9 :(−3)
x ≤ 3
Ответ: x ≤ 3

Примеры решения линейных неравенств

4(x − 1) ≥ 5 + x
4x − 4 ≥ 5 + x
4x − x ≥ 5 + 4
3x ≥ 9 | (:3)
3x (:3) ≥ 9 (:3)
x ≥ 3
Ответ: x ≥ 3
x + 2 x + 2 x − 3x −2x −2x −2x : (−2) > 0 : (−2)
x > 0
Ответ: x > 0

Решение линейных неравенств Как записать ответ неравенства

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:


Отправить

Решение словесных вопросов о неравенстве

(Сначала вы можете прочитать Введение в неравенства и решение неравенств).

Сэм и Алекс играют в одной футбольной команде.

В прошлую субботу Алекс забил на 3 гола больше, чем Сэм, но вместе они забили меньше 9 голов.
Какое возможное количество голов забил Алекс?
Как их решить?
Хитрость заключается в том, чтобы разбить решение на две части:
Превратите английский в алгебру.
Затем используйте алгебру для решения.
Превращение английского языка в алгебру
Превратить английский в алгебру поможет:
Сначала прочитайте все
При необходимости сделайте набросок
Назначить буквы для значений
Найти или вычислить формулы
Мы также должны записать то, что на самом деле просят , чтобы мы знали, куда мы идем и когда мы прибыли!

Лучший способ изучить это на примере, поэтому давайте попробуем наш первый пример:
Сэм и Алекс играют в одной футбольной команде.

В прошлую субботу Алекс забил на 3 гола больше, чем Сэм, но вместе они забили меньше 9 голов.
Какое возможное количество голов забил Алекс?

Назначить буквы:
количество забитых Алексом голов: A
количество забитых Сэмом голов: S
Мы знаем, что Алекс забил на 3 гола больше, чем Сэм, поэтому: A = S + 3
И мы знаем, что вместе они забили меньше 9 голов: S + A < 9
Нас спрашивают сколько голов Алекс мог бы забить: A

Решите:
Начните с: S + A < 9
A = S + 3, поэтому: S + (S + 3) < 9
Упростить: 2S + 3 < 9
Вычесть 3 из обеих сторон: 2S < 9 − 4 9003 Упростите: 2S < 6
Разделите обе стороны на 2: S < 3
Сэм забил менее 3 голов, что означает, что Сэм мог забить 0, 1 или 2 гола.
Алекс забил на 3 гола больше, чем Сэм, поэтому Алекс мог забить 3, 4 или 5 голов .

Проверить:
Если S = 0, то A = 3 и S + A = 3, и 3 < 9 верно
Когда S = 1, тогда A = 4 и S + A = 5, и 5 < 9 верно
Когда S = 2, тогда A = 5 и S + A = 7, и 7 < 9 верно
(Но когда S = 3, то A = 6 и S + A = 9, а 9 < 9 неверно)
Еще много примеров!
Пример: Из 8 щенков девочек больше, чем мальчиков.
Сколько может быть девочек-щенков?
Назначить Буквы:
Количество девушек: г
количество мальчиков: б
Мы знаем, что щенков 8, поэтому: g + b = 8, что можно преобразовать в
b = 8 − g
Мы также знаем, что девочек больше, чем мальчиков, поэтому:
g > b
Нас спрашивают о количестве девочек-щенков: г
Решите:
Начните с: g > b
b = 8 − g , поэтому: g > 8 − g
Добавьте g к обеим сторонам: g + g > 8
Упростите3: 20g3: 20g3: 8
Разделите обе стороны на 2: г > 4
Таким образом, может быть 5, 6, 7 или 8 девочек-щенков.
Может ли быть 8 девочек-щенков? Тогда не было бы мальчиков вообще, и вопрос не ясен на этот счет (иногда такие вопросы).
Проверка
Если g = 8, то правильно b = 0 и g > b (но допустимо ли b = 0?)
Когда g = 7, тогда b = 1 и g > b верно
Когда g = 6, тогда b = 2 и g > b верно
Когда g = 5, тогда b = 3 и g > b верно
(Но если g = 4, то b = 4 и g > b неверно)
Быстрый пример:
Пример: Джо участвует в гонке, где он должен ездить на велосипеде и бежать.
Он проехал 25 км на велосипеде, а затем пробежал 20 км. Его средняя скорость бега составляет половину его средней скорости езды на велосипеде.
Джо завершает гонку менее чем за 2,5 часа, что мы можем сказать о его средней скорости?
Назначить буквы:
Средняя скорость работы: с
Таким образом, средняя скорость езды на велосипеде: 2 с
Формулы:
Скорость = Расстояние Время
Что можно изменить на: Время = Расстояние Скорость
Нас спрашивают его средние скорости: с и 2 с

Гонка делится на две части:
1.
Велоспорт
Дистанция = 259 км
Средняя скорость = 2 с км/ч
Время = Расстояние Средняя скорость = 25 2 с часов
2. Бег
Расстояние = 20 км
Средняя скорость = с км/ч
Время = Расстояние Средняя скорость = 20 с часов
Джо завершает гонку менее чем за 2½ часа
Общее время < 2½
25 2 с + 20 с < 2½
Решите:
Начните с: 25 2s + 20 s < 2½
Умножьте все члены на 2s0033 25 + 40 < 5s
Упростить: 65 < 5s
Разделить обе части на 5: 13 < s
Поменять стороны местами: 900 39 s0 > 343 900 средняя скорость бега больше 13 км/ч, а его средняя скорость на велосипеде превышает 26 км/ч
В этом примере мы используем сразу два неравенства:
Пример: скорость
v м/с мяча, брошенного прямо вверх, равна v = 20 − 10t , где t — время в секундах.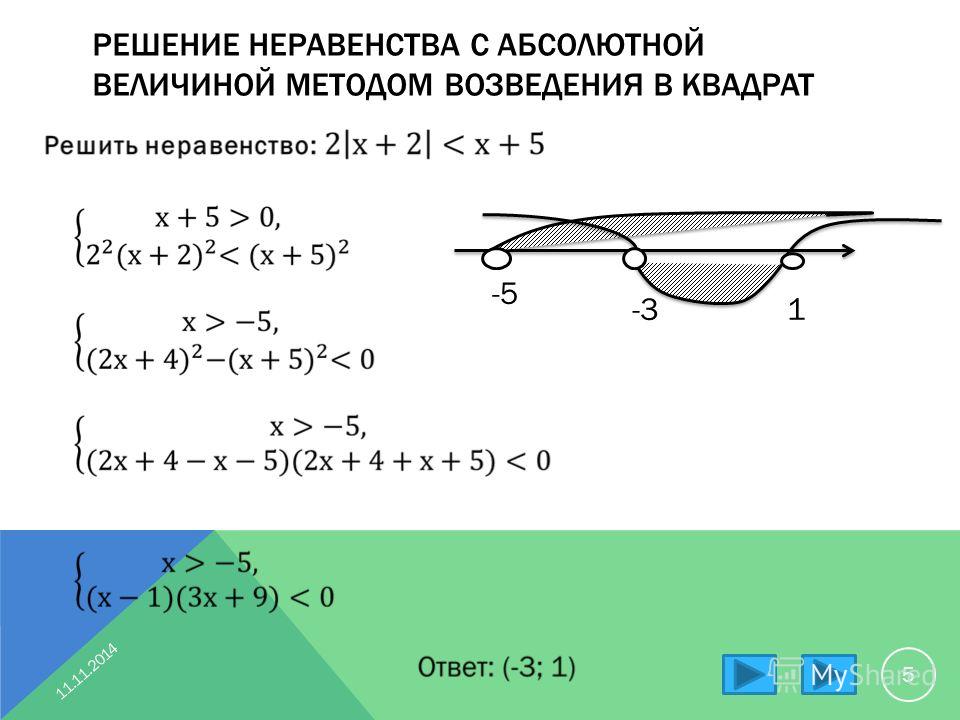
В какие моменты времени скорость будет между 10 м/с и 15 м/с?
Буквы:
скорость в м/с: v
время в секундах: t
Формула:
v = 20 − 10t
Нас спрашивают о времени t , когда v находится между 5 и 15 м/с:
10 < v < 15
10 < 20 − 10t < 15
Решите:
Начните с: 10 < 20 − 10t < 15
Вычтите 20 из каждого:
20 < 15 − 20
Упростить: −10 < −10t < −5
Разделить каждое на 10: −1 < −t < −0,5
Это аккуратнее чтобы сначала показать меньший номер
, так поменяй местами: 0,5 < t < 1
Таким образом, скорость составляет от 10 м/с до 15 м/с между 0,5 и 1 секундой после.
И достаточно сложный пример для завершения:
Пример: прямоугольная комната вмещает как минимум 7 столов, каждый из которых имеет площадь 1 квадратный метр.
Периметр комнаты 16 м.
Какой может быть ширина и длина комнаты?
Сделайте набросок: мы не знаем размеров столов, только их площадь, они могут подойти идеально или нет!
Назначить буквы:
длина комнаты: L
ширина комнаты: Ш
Формула для периметра 2(Ш + Д) , и мы знаем, что это 16 м
2(Ш + Д) = 16
Ш + Д = 8
Д = 8 — Ш
Мы также знаем, что площадь прямоугольника равна произведению ширины на длину: Площадь = Ш × Д
И площадь должна быть больше или равна 7:
Ш × Д ≥ 7
Нас спрашивают о возможных значениях W и L

Решим:
Начнем с: W × L ≥ 7 3 W 0 8e =
× ( 8 — w) ≥ 7
Расширение: 8W — W ² ≥ 7
Принесите все термины в левую сторону: W ² — 8W + 7 ≤ 00034
Это квадратное. . Это можно решить многими способами, здесь мы решим это, заполнив квадрат:
Перенесите числовой член − 7 в правую часть неравенства: W ² − 8W ≤ −7
Заполните квадрат в левой части неравенства и сбалансируйте его, добавив такое же значение к в правая часть неравенства: W ² − 8W + 16 ≤ −7 + 16
Упростим: (W − 4) ² ≤ 9
Извлечем квадратный корень из обеих частей неравенства: −3 ≤ W − 4 ≤ 3
Да, у нас два неравенства, потому что 3 ² = 9 И (−3) ² = 9
Добавьте 4 к обеим частям каждого неравенства: 7 м (включительно) и длина 8−ширина .

Проверить:
Допустим, W = 1, тогда L = 8−1 = 7 и A = 1 x 7 = 7 м ² (подходит ровно для 7 таблиц)
Скажем, W = 0,9 (меньше 1), тогда L = 7,1 и A = 0,9 x 7,1 = 6,39 м ² (7 не подходит)
Скажем, W = 1,1 (чуть выше 1), тогда L = 6,9 и A = 1,1 x 6,9 = 7,59 м ² (7 легко помещаются)
Аналогично для ширины около 7 м

Краткое ознакомление с решением линейных неравенств
Квадратные неравенстваПолиномиальные неравенстваРациональные неравенства
Purplemath
Как решать линейные неравенства?
Решение линейных неравенств очень похоже на решение линейных уравнений в том смысле, что вы по-прежнему хотите изолировать переменную (то есть получить переменную саму по себе), и вы выполняете эту изоляцию путем сложения, вычитания, умножения и деления обеих частей неравенство теми же значениями.
Содержание продолжается ниже
MathHelp.
com
Решение неравенств
Единственное отличие состоит в том, что при работе с неравенствами вы должны переворачивать (т. е. переворачивать) знак неравенства всякий раз, когда вы умножаете или делите обе части неравенства по отрицательному.
Далее приведены несколько простых примеров, которые помогут вам освежить в памяти методы и обозначения.
1) Решить x + 3 < 2
Единственная разница между линейным уравнением x + 3 = 2, и это линейное неравенство заключается в том, что у меня есть знак «меньше» вместо знака «равно». Метод решения точно такой же: вычесть 3 с каждой стороны.
Итак, в записи неравенства решение равно x < −1.
В интервальной записи решение записывается как (−∞, −1)
Графически (то есть на числовой прямой) решение изображается, как показано ниже:
Обратите внимание, что решение для «меньше чем , но не равно» неравенство изображается скобками (или открытой точкой) на конечной точке, что указывает на то, что конечная точка не включена в решение.
2) Решите 2 − x > 0
Единственная разница между линейным уравнением 2 − x = 0 и этим линейным неравенством заключается в том, что вместо знака «равно» используется знак «больше».
Чтобы избежать знака «минус» в переменной, я добавлю x к обеим частям неравенства.
Решение в виде неравенства «2 > x » совершенно верно, но мне удобнее иметь переменную в левой части; часто легче (мне, по крайней мере) представить, что означает решение с переменной слева. Вот почему я изменил неравенство выше, чтобы получить x < 2. Не бойтесь переставлять элементы по своему вкусу.
В интервальных обозначениях решением являются все значения, меньшие (но не включая) 2, что записывается как (−∞, 2).
Графически решение:
3) Решите 4 x + 6 ≥ 3 x − 5
Единственная разница между линейным уравнением «4 x 9023 x + 53 = 3 6 «и это неравенство заключается в том, что вместо знака «равно» стоит знак «меньше или равно». Метод решения точно такой же.
Таким образом, решение в виде неравенства равно x ≤ −11.
Решение в виде интервальной записи (−∞, −11]. Квадратная скобка используется здесь вместо круглой скобки, которая использовалась в предыдущих примерах, потому что это неравенство «или равно», означающее, что конечная точка (в данном случае -11) включается в решение.
Графически решение выглядит следующим образом:
4) Решите 2 x > 4
Метод решения здесь состоит в том, чтобы разделить обе части на положительное число два.
Таким образом, решение в виде неравенства равно x > 2
Решение в виде интервала (2, +∞).
Графически решение выглядит следующим образом:
Поскольку я разделил обе части на положительное значение, я не перевернул символ неравенства.
5) Решить −2 > 4
Если бы меня попросили решить уравнение −2 = 4, я бы решил, разделив обе части на минус 2. Я решу это неравенство таким же образом. Однако, поскольку я буду делить обе части неравенства на минус, я должен не забыть перевернуть символ неравенства.
Таким образом, решение в виде неравенства равно x < −2.
Решение с интервальной записью (−∞, −2).
Графически решение выглядит следующим образом:
Приведенное выше правило (5) часто кажется учащимся неразумным при первом знакомстве с ним. Но подумайте о неравенствах, используя числа вместо переменных. Вы знаете, что число четыре больше числа два:
4 > 2
Умножая обе части этого неравенства на −1, мы получаем −4 < −2, что, как показывает числовая прямая, верно:
Если бы мы не перевернули неравенство, то получили бы «−4 > −2», что явно *не* верно.
URL: https://www.purplemath.com/modules/ineqsolv.htm
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении линейных неравенств. Попробуйте введенное упражнение или введите свое собственное упражнение.
No related posts.