Как решать обратные матрицы: Обратная матрица онлайн

alexxlab / / Разное

§6. Обратная матрица.

Для квадратной матрицы важную роль играет понятие обратной матрицы.

Определение 1. Матрицей, обратной матрице А (обозначается ), называется матрица, удовлетворяющая условию: .

Теорема 1. Обратная матрица (если она существует) − единственна.

{Пусть у матрицы А есть 2 обратных: В и С. Рассмотрим произведение ВАС:

ВАС = (ВА)С = ЕС = С. С другой стороны ВАС = В(АС) = ВЕ = В. Отсюда В = С}

Для вычисления обратной матрицы необходимо ввести еще несколько понятий.

Легко заметить, что минор (n – 1) − го порядка у квадратной матрицы Аn можно определять, не задавая строки и столбцы, а, указав один элемент , вычеркнуть i−ю строку и j−ый столбец, на пересечении которых он находится. Поэтому минор Мп−

1 матрицы Ап обычно обозначают .

Определение 2. Алгебраическим дополнением элемента называется величина .

Из определения детерминанта матрицы An сразу следует, что определитель матрицы равен сумме произведений элементов любой строки (столбца) на алгебраические дополнения этой строки (столбца): ………………………………………….(*)

С другой стороны, …………….(**)

Т.е. сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (столбца) равна нулю. {Фактически, мы получаем определитель с двумя одинаковыми строками (столбцами)}

Определение 3. Транспонированная матрица из алгебраических дополнений называется присоединенной матрицей:.

Теорема 2.

{При умножении k −ой строки А на k − ый столбец получается det(A) (*), при умножении на любой другой столбец получается ноль (**) }

Следствие.

Пример. Найти обратную матрицу для . {

.(проверка)}

Замечания. 1. Полезно запомнить, что обратная матрица второго порядка получается из исходной следующим образом: элементы главной диагонали меняются местами, у элементов второй диагонали изменяется знак. Полученная матрица делится на определитель.

2. Обратная матрица может быть получена с помощью элементарных преобразований. Для этого составляется матрица и левая часть элементарными преобразованиями приводится к единичной. При этом матрица Е преобразуется в обратную {б/д}. Последний пример:

;.

Свойства обратной матрицы.

1. { (св.7,8 §3) }

2.

3. {Из определения следует, что А и − взаимно обратные матрицы.}

В заключение докажем критерий существования обратной матрицы:

Теорема 3. Обратная матрица существует тогда и только тогда, когда А − невырожденная матрица, т.е.

{1. Пусть существует. Т.к. она равна присоединенной матрице, деленной на определитель, то последний не равен нулю. 2. Пусть По Сл.Т.2 обратную матрицу можно вычислить.}

Использование обратных матриц позволяет решать простые матричные уравнения относительно квадратных матриц. Рассмотрим пример одной из таких задач. Решить уравнение AXB + C = D, где − неизвестная матрица.

Матрица Х равна: Пользуясь замечанием 1 предыдущего параграфа, имеем:

Замечание. Так как умножение матриц не коммутативно, необходимо внимательно смотреть за тем, с какой стороны следует умножать правую часть на обратные матрицы.

ПРЕЗЕНТАЦИЯ по высшей математике на тему: «ОБРАТНАЯ МАТРИЦА»

ПРЕЗЕНТАЦИЯ на тему: «Обратная матрица»

Демьянова Светлана Васильевна

преподаватель математики

высшей квалификационной категории

ГОУ СПО «Днестровский техникум энергетики

и компьютерных технологий»

Введение. Понятие матрицы

Система линейных уравнений имеет вид

Таблица, составленная из коэффициентов при неизвестных,

называется матрицей . Для данной системы основная матрица:

Матрица размера ( mxn)

Любая прямоугольная таблица чисел, состоящая

из m строк и n столбцов, называется матрицей размера ( m х n) .

Числа, образующие матрицу, называются элементами матрицы.

Например, система из трех уравнений с тремя неизвестными

и ее основная матрица

Квадратная матрица размера (3х3) или

матрица 3-го порядка

В этой же системе можно выписать в виде матрицы столбец

свободных членов

Матрица — столбец размера (3х1)

, размер матрицы (1х4)

Можно записать матрицу-строку

В квадратных матрицах можно выделить главную и побочную диагонали

побочная

главная

Для квадратных матриц можно вычислить определитель.

Определитель квадратной матрицы есть некоторое число, которое вычисляется из элементов матрицы по определенному правилу, которое будет сформулировано после введения понятий миноров и алгебраических дополнений элементов определителя.

Минором элемента определителя называется определитель,

полученный после вычеркивания из исходного строки и столбца,

на пересечении которых стоит этот элемент.

Алгебраическое дополнение элемента – это минор этого элемента, взятый со знаком (+), если сумма номеров строки и столбца,

на которых находится элемент – четная,

и со знаком (-), если эта сумма – нечетная.

Вычисление определителей

1. Определитель 1-го порядка равен самому элементу

Например:

2. Определитель 2-го порядка находится по правилу

Определитель 2-го порядка равен разности произведений

элементов главной и побочной диагонали.

Например:

Определитель 3-го порядка находится путем разложения

определителя по элементам строки или столбца.

При этом используется

Основное правило вычисления определителя :

Определитель равен сумме произведений элементов

какой-либо строки или столбца

на соответствующие им алгебраические дополнения

Например, разложение определителя по элементам 1-ой строки

будет иметь вид

Пример вычисления определителя путем разложения

по элементам первой строки:

Наиболее выгодным является разложение определителя по элементам

того ряда, в котором все элементы, кроме одного, равны нулю

Например, данный определитель наиболее выгодно

разложить по элементам 2-й строки

Если строк или столбцов с нулями нет, то их можно получить, используя элементарные преобразования, не меняющие величины определителя.

Согласно свойству определителей: Величина определителя

не изменится, если к элементам какого-либо ряда прибавить

соответствующие элементы другого ряда, предварительно

умноженные на число.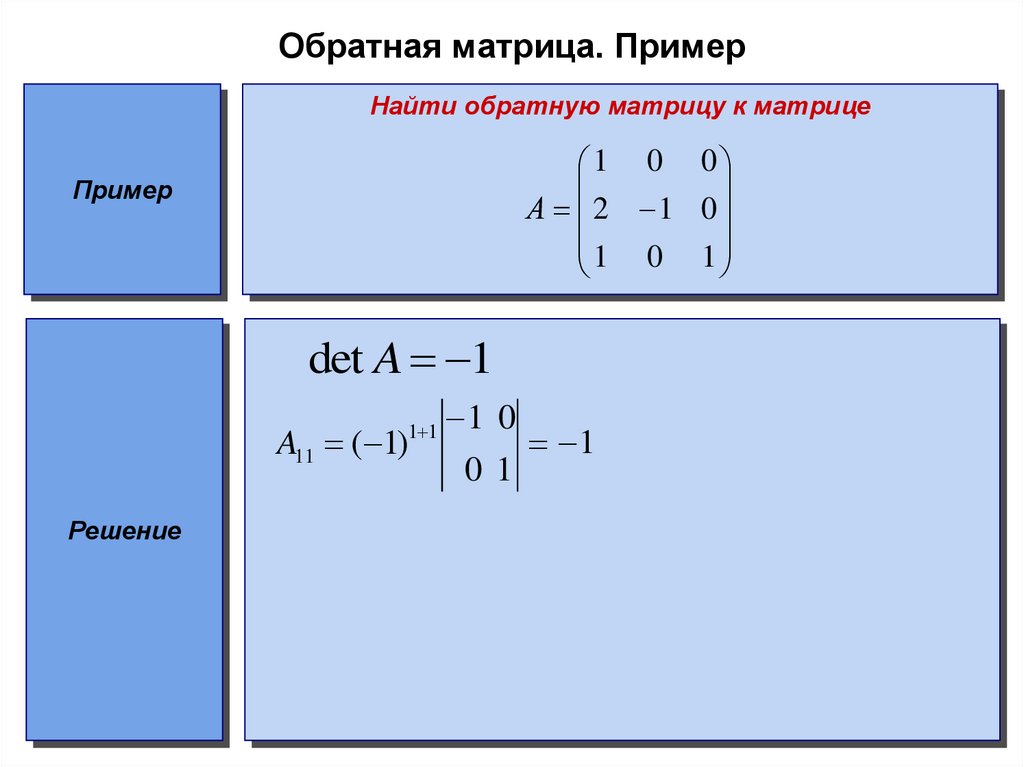

Свойства определителей

1. Постоянный множитель из элементов какого либо ряда

можно выносить за знак определителя

2. Определитель равен нулю, если все элементы какого-либо

ряда равны нулю

3. Определитель равен нулю, если есть два ряда,

соответствующие элементы которых равны или пропорциональны

Решение систем методом Крамера

С вычислением определителей связан один из методов решения

систем линейных уравнений – метод Крамера.

Рассмотрим его на примере.

Для решения системы необходимо

вычислить 4 определителя 3-го порядка.

1. Вычисляем главный определитель из коэффициентов

при неизвестных

2. Вычисляем побочные определители для каждого неизвестного,

для этого поочередно в главном определители заменяем столбцы ,

соответствующие одному из неизвестных, столбцом свободных

членов

Метод Крамера

а) Находим определитель для первого неизвестного, заменяя

в главном определителе первый столбец на столбец свободных членов

б) Находим определитель для второго неизвестного, заменяя в главном определителе второй столбец на столбец свободных членов

в) Находим определитель для третьего неизвестного, заменяя в главном

определителе третий столбец на столбец свободных членов

Метод Крамера

Для нахождения значений неизвестных используем формулы Крамера

Значения неизвестных

находятся делением побочных

определителей

на главный определитель

Это означает, что методом Крамера

можно решать только такие системы,

у которых главный определитель

отличен от нуля

Полученное решение запишем в виде матрицы-столбца

Легко проверить подстановкой в каждое уравнение

Системы, что полученное решение верно.

Обратная матрица. Матричные уравнения

Обратной матрицей для квадратной матрицы А называется матрица произведение которой на исходную матрицу равно единичной матрице

Единичная матрица

Обратная матрица существует только для квадратных

невырожденных матриц, т.е. таких матриц, определитель

которых отличен от нуля

Служит для проверки правильности

нахождения обратной матрицы

Равенство

Матричные уравнения

Матричные уравнения – это уравнения, в которых участвуют

как известные матрицы, так и неизвестная матрица, которую

и нужно найти. Существуют два основных типа матричных уравнений.

2 тип (правое умножение)

1 тип (левое умножение)

В виде матричного уравнения может быть

записана система линейных уравнений, решение которой

существует, если определитель основной

матрицы отличен от нуля.

Если в системе количество уравнений и неизвестных разное,

то нельзя говорить об определителе основной матрицы и решать

систему матричным методом нельзя.

Для решения таких систем применяется метод Гаусса

Схема нахождения обратной матрицы

  • 1) Находится определитель матрицы.

Если он отличен от нуля , то обратная матрица существует.

  • 2) Составляется союзная матрица , элементами которой являются алгебраические дополнения элементов исходной матрицы.
  • 3) Полученную союзную матрицу транспонируем, т.е. меняем ролями строки и столбцы матрицы. Получаем матрицу .
  • 4) Матрицу делим на определитель матрицы и получаем обратную матрицу. (При делении матрицы на число все ее элементы нужно разделить на это число)

Рассмотрим примеры.

1. Найти матрицу, обратную данной

1)

2)

4)

3)

Нахождение обратной матрицы

2. Найти матрицу, обратную данной

1) Находим определитель матрицы

Т.о. обратная матрица существует.

2) Составляем союзную матрицу

3) Полученную матрицу транспонируем

4) Обратная матрица

Решение систем методом Гаусса

Метод Гаусса – метод последовательного исключения неизвестных.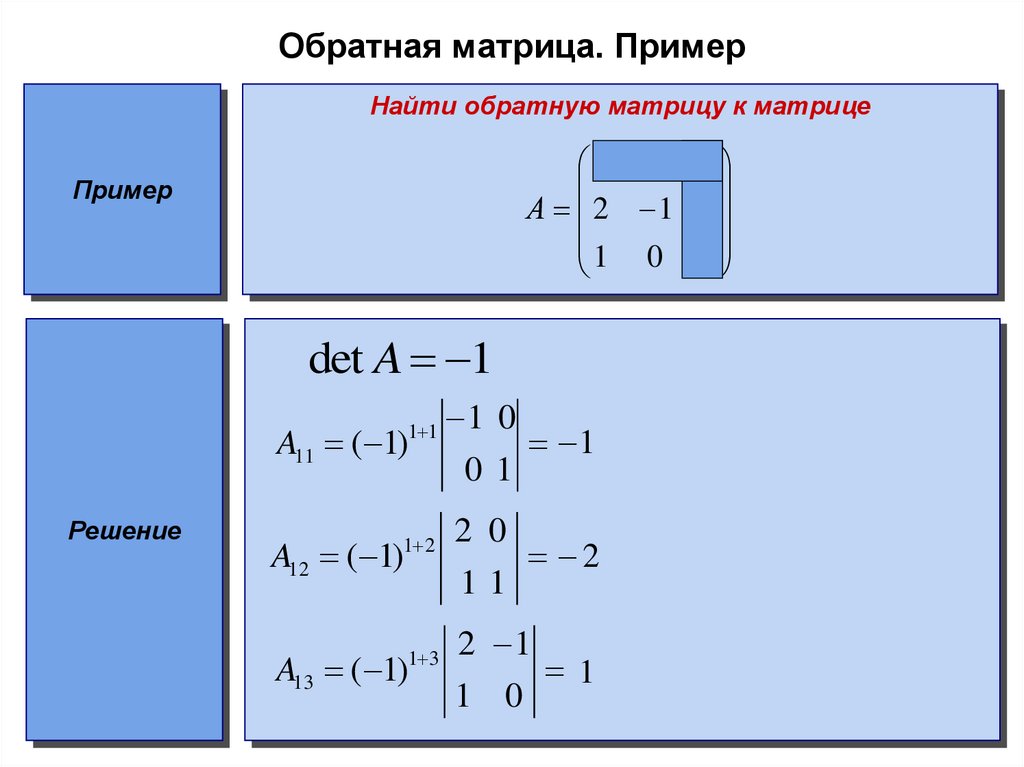

При решении системы методом Гаусса все действия проводятся над

строками расширенной матрицы.

Понятие ранга матрицы.

Понятие ранга помогает при анализе системы уравнений.

Определение. Рангом матрицы называется максимальное число

линейно независимых строк этой матрицы.

и запишем ее основную матрицу и

расширенную матрицу

Рассмотрим систему уравнений

Определение 1. Система линейных уравнений называется

совместной, если она имеет решение. Это возможно только в том

случае, когда ранг основной матрицы равен рангу расширенной .

Определение 2. Система называется несовместной, если она

не имеет решений.

Определение 3. Система называется определенной, если она имеет

единственное решение. Это возможно, если ранг системы равен

количеству неизвестных:

Определение 4. Система называется неопределенной, если она имеет

бесчисленное множество решений. Это возможно в том случае,

когда ранг системы меньше количества неизвестных:

Таким образом, при решении системы необходимо установить

ее совместность, а затем определить единственное или множество

решений она будет иметь.

Рассмотрим на примере системы

  • Рассмотрим на примере системы
  • Рассмотрим на примере системы
  • Рассмотрим на примере системы

Расширенная матрица – это матрица коэффициентов

при неизвестных с добавлением столбца свободных членов.

Видно, что 3-я и 4-я строки получаются умножением первой на

числа (-2) и 3, значит соответствующие уравнения системы

являются лишними. И система будет иметь множество решений.

Решаем ее методом Гаусса.

Схема решения системы методом Гаусса.

  • Выписываем расширенную матрицу системы и приводим ее

к ступенчатому или треугольному виду также, как это делалось при

вычислении определителей (процедура получения нулей).

2. В процессе всех этих действий могут проявиться линейно зависимые

строки (т.е. строки, соответствующие элементы которых одинаковые или

пропорциональные, нулевые строки и т.п.), которые можно вычеркнуть

Т.о. осталось 2

линейно независимых

строки и ранг матрицы

равен 2

Например:

3. В полученной матрице нужно выбрать базисный минор .

Базисный минор – это отличный от нуля минор, порядок которого

равен рангу матрицы. Соответственно определяются базисные

и свободные неизвестные.

В нашем примере базисный минор можно составить из элементов

1-го и 3-го столбцов

, тогда так как минор, составленный

из элементов 1-го и 2-го столбцов, равен нулю

и

Для данной ситуации базисными будут неизвестные

4. Записываем эквивалентную систему, при этом базисные

неизвестные остаются в левой части уравнений, а свободные

переносятся в правую.

5. В итоге решается эта система и находится общее решение,

в котором базисные неизвестные выражаются через свободные.

Этим свободным неизвестным даются произвольные числовые

значения, по ним вычисляются базисные и получается каждый раз

новое частное решение. Таких решений можно составить

бесчисленное множество.

-частное решение

(при

— общее решение

)

Замечание. Если в матрице системы не вычеркивается ни одна строка, то есть все строки линейно независимы, то ранг будет равен числу неизвестных и решение получится единственным.

Система линейных однородных уравнений имеет вид и решается также,

как и неоднородная

{-1}$, если существует, путем вычисления расширенной матрицы $[A|I]$, где $I$ — единичная матрица $3\times 3$.
(a) $A=\begin{bmatrix}
1 & 3 & -2 \\
2 &3 &0 \\
0 & 1 & -1
\end{bmatrix}$
(b) $ A=\begin{bmatrix}
1 & 0 & 2 \\
-1 &-3 &2 \\
3 & 6 & -2
\end{bmatrix}$.
  • Пусть A будет матрицей
    \[\begin{bmatrix}
    1 & -1 & 0 \\
    0 &1 &-1 \\
    0 & 0 & 1
    \end{bmatrix}.\] Является ли матрица $A$ обратимой? Если нет, то объясните, почему оно необратимо. Если да, то найти обратное.
    ( Университет штата Огайо )
  • Найдите обратную матрицу
    \[A=\begin{bmatrix}
    1 & 1 & 2 \\
    0 &0 &1 \\
    1 & 0 & 1
    \end{bmatrix}\] если он существует. Если вы считаете, что обратной матрицы $A$ не существует, то объясните причину.
    ( Университет штата Огайо ) 9{-1}$.
    ( Государственный университет Огайо , задача выпускного экзамена по линейной алгебре )
  • Пусть $A, B, C$ — следующие матрицы $3\times 3$.
    \[A=\begin{bmatrix}
    1 & 2 & 3 \\
    4 &5 &6 \\
    7 & 8 & 9
    \end{bmatrix}, B=\begin{bmatrix}
    1 & 0 & 1 \\
    0 &3 &0 \\
    1 & 0 & 5
    \end{bmatrix}, C=\begin{bmatrix}
    -1 & 0\ & 1 \\
    0 &5 &6 \\
    3 & 0 & 1
    \end{bmatrix}. \] Затем вычислите и упростите следующее выражение. 9{2017}\mathbf{х}.\] ( Университет штата Огайо )
  • (a) Пусть $A$ — матрица $6\x 6$, и предположим, что $A$ можно записать в виде $A=BC$, где $B$ — матрица $6\times 5$, а $C$ представляет собой матрицу $5\times 6$. Докажите, что матрица $A$ необратима.
    (b) Пусть $A$ — матрица $2\times 2$, и предположим, что $A$ можно записать в виде $A=BC$, где $B$ — матрица $2\times 3$, а $C $ — матрица $3\times 2$. Может ли матрица $A$ быть обратимой?
    • 92=Q$, (4) $PQ=O$, (5) $QP=O$, где $O$ — нулевая матрица $2\times 2$. Затем выполните следующие задачи.
    (a) Докажите, что $(P+Q)A=A$.
    (b) Предположим, что $a$ — положительное действительное число, и пусть $A=\begin{bmatrix}
    a & 0\\
    1& a+1
    \end{bmatrix}$. Затем найти все матрицы $P, Q$, удовлетворяющие условиям (1)-(5).
    (c) Пусть $n$ — целое число, большее $1$. Для любого целого числа $k$, $2\leq k \leq n$ определим матрицу $A_k=\begin{bmatrix} 9{-1}=A$.
  • Рассмотрим систему линейных уравнений
    \begin{align*}
    x_1&= 2, \\
    -2x_1 + x_2 &= 3, \\
    5x_1-4x_2 +x_3 &= 2
    \end{align*}
    ( а) Найдите матрицу коэффициентов и обратную ей матрицу.
    (b) Используя обратную матрицу, решите систему линейных уравнений.
    ( Университет штата Огайо )
  • Рассмотрим следующую систему линейных уравнений
    \begin{align*}
    2x+3y+z&=-1\\ 9{-1}$. Если вы считаете, что матрица $A$ необратима, то объясните почему.
    (b)  Являются ли векторы
    \[ \mathbf{A}_1=\begin{bmatrix}
    1 \\
    2 \\
    1
    \end{bmatrix}, \mathbf{A}_2=\begin {bmatrix}
    2 \\
    5 \\
    1
    \end{bmatrix},
    \text{ и } \mathbf{A}_3=\begin{bmatrix}
    1 \\
    4 \\
    0
    \ конец{bmatrix}\] линейно независимы?
    (c)  Запишите вектор $\mathbf{b}=\begin{bmatrix}
    1 \\
    1 \\
    1 92)=5$ и $\tr(A)=3$. Найдите $\det(A)$.