Выяснить является ли функция четной нечетной: Чётные и нечётные функции — урок. Алгебра, 9 класс.

как выяснить, является ли функция чётной, нечётной или ни чётной, ни нечётной? Алгебра. 9 класс. Алимов Ш. А. Параграф 14. Упражнение №173.

как выяснить, является ли функция чётной, нечётной или ни чётной, ни нечётной? Алгебра. 9 класс. Алимов Ш. А. Параграф 14. Упражнение №173. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

 Привет всем! Скоро самостоялка, помогите подготовиться;)

1) у = х^-4;
2) у = х^-3;
3) у = x⁴ + x²;
4) у = x³ + x⁵;
5) у = x² — х + 1;

ответы

1) у = х^-4 — четная;                      2) у = х^-3   — нечетная;
3) у = х⁴ + х² — четная;               4) у = х³ + х⁵ — нечетная;
5)  у = х^-2  — х + 1   —  ни чётная, ни нечётная;
6) у =    —   ни четная, ни нечетная.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

10 класс

11 класс

Химия

похожие вопросы 5

Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство

Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)

ГДЗАлгебраАлимов Ш.А.Школа9 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)

ГДЗ11 классКолмогоров А.Н.Алгебра

Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!

ГИА9 класс

Это правда, что будут сокращать иностранные языки в школах?

 Хочется узнать, когда собираются сократить иностранные языки в школе? Какой в итоге оставят? (Подробнее…)

ШколаНовостиИностранные языки

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Выяснить является функция четной или нечетной. Четность функции

Выяснить является функция четной или нечетной. Четность функции

Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией. Для обозначения используют запись y=f(x). У каждой функции существует ряд основных свойств, таких как монотонность, четность, периодичность и другие. 3 симметрична относительно начала координат.

Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.

Определение 1.

Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).

Определение 2.

Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).

Доказать, что у = х 4 — четная функция.

Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.

Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.

Доказать, что у = х 3 ~ нечетная функция.

Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т. е. функция является нечетной.

Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.

Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.

Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).

Итак, функция может быть четной, нечетной, а также ни той ни другой. {2}} \neq 1 для любого x \in [-1;1] .

Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .

Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .

Возрастающая и убывающая функция

О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .

Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})

Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0 ).

а) Если при x > 0 четная функция возрастает, то убывает она при x

б) Когда при x > 0 четная функция убывает, то возрастает она при x

в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x

г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x

Экстремумы функции

Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.

Точкой максимума функции

y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)

Необходимое условие

Согласно теореме Ферма: f»(x)=0 тогда, когда у функции f(x) , что дифференцируема в точке x_{0} , появится экстремум в этой точке.

Достаточное условие

1. Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
2. x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .

Наибольшее и наименьшее значение функции на промежутке

Шаги вычислений:

1. Ищется производная f»(x) ;
2. Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
3. Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .

Исследование функции.

1) D(y) – Область опрделения: множество всех тех значений переменной х. при которых алгебраические выражения f(x) и g(x) имеют смысл.

Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл.

2) Свойства функции: четность/нечетность, периодичность:

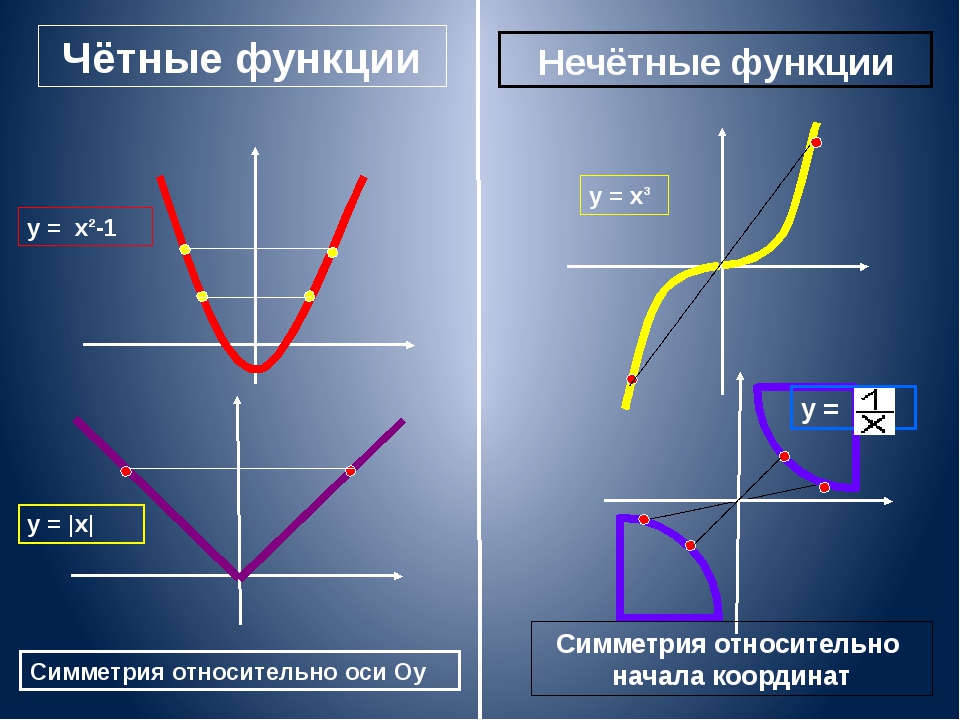
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента.

Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (симметричная относительно центра координат).

Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (симметричная относительно оси ординат).

Ни чётная ни нечётная функция (функция общего вида) — функция, не обладающая симметрией. В эту категорию относят функции, не подпадающие под предыдущие 2 категории.

Функции, не принадлежащие ни одной из категорий выше, называются ни чётными ни нечётными (или функциями общего вида).

Нечётные функции

Нечётная степень где — произвольное целое число.

Чётные функции

Чётная степень где — произвольное целое число.

Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода функции) на всей области определения.

3) Нули (корни) функции — точки, где она обращается в ноль.

Нахождение точки пересечения графика с осью Oy . Для этого нужно вычислить значение f (0). Найти также точки пересечения графика с осью Ox , для чего найти корни уравнения f (x ) = 0 (или убедиться в отсутствии корней).

Точки, в которых график пересекает ось , называют нулями функции . Чтобы найти нули функции нужно решить уравнение , то есть найти те значения «икс» , при которых функция обращается в ноль.

4) Промежутки постоянства знаков, знаки в них.

Промежутки, где функция f(x) сохраняет знак.

Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.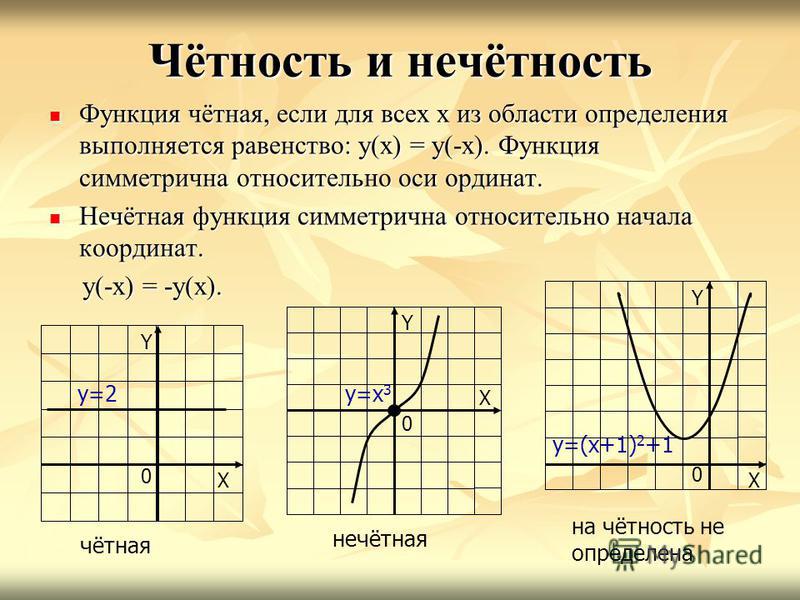

ВЫШЕ оси абсцисс.

НИЖЕ оси .

5) Непрерывность (точки разрыва, характер разрыва, ассимптоты).

Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

Устранимые точки разрыва

Если предел функции существует , но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:

,

то точка называется точкой устранимого разрыва функции (в комплексном анализе -устранимая особая точка).

Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности , что и обосновывает название точки, как точки устранимого разрыва.

Точки разрыва первого и второго рода

Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов :

если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода . Точки устранимого разрыва являются точками разрыва первого рода;

если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода .

Аси́мпто́та — прямая , обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви вбесконечность.

Вертикальная

Вертикальная асимптота — прямая предела .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

Горизонтальная

Горизонтальная асимптота — прямая вида при условии существования предела

.

Наклонная

Наклонная асимптота — прямая вида при условии существования пределов

Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.

Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует.

если в п. 2.), то , и предел находится по формуле горизонтальной асимптоты, .

6) Нахождение промежутков монотонности. Найти интервалы монотонности функции f (x )(то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f (x ). Для этого находят производную f (x ) и решают неравенство f (x )0. На промежутках, где это неравенство выполнено, функция f (x )возрастает. Там, где выполнено обратное неравенство f (x )0, функция f (x )убывает.

Нахождение локального экстремума. Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием — локальные минимумы.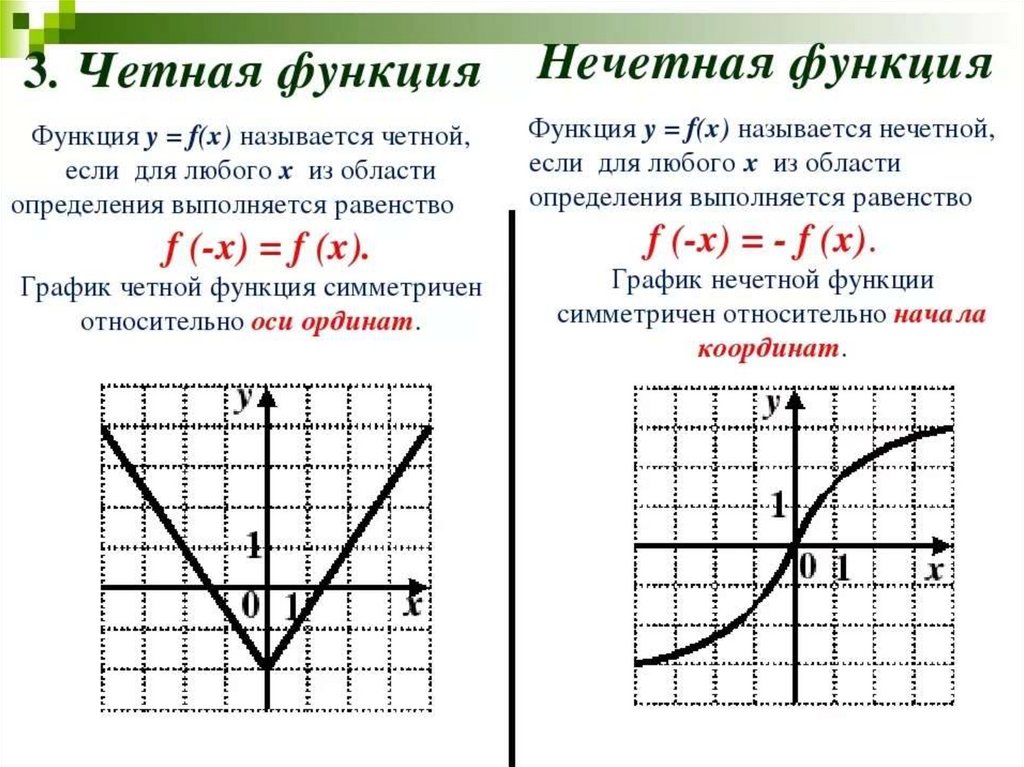 Вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.

Нахождение наибольшего и наименьшего значений функции y = f(x) на отрезке (продолжение)

1. Найти производную функции: f (x ). 2. Найти точки, в которых производная равна нулю: f (x )=0x 1, x 2 ,… 3. Определить принадлежность точек х 1 , х 2 , … отрезку [a ; b ]: пусть x 1a ;b , а x 2a ;b .

Преобразование графиков.

Словесное описание функции.

Графический способ.

Графический способ задания функции является наиболее наглядным и часто применяется в технике. В математическом анализе графический способ задания функций используется в качестве иллюстрации.

Графиком функции f называют множество всех точек (x;y) координатной плоскости, где y=f(x), а x «пробегает» всю область определения данной функции.

Подмножество координатной плоскости является графиком какой-либо функции, если оно имеет не более одной общей точки с любой прямой, параллельной оси Оу.

Пример. Является ли графиками функций фигуры, изображенные ниже?

Преимуществом графического задания является его наглядность. Сразу видно, как ведёт себя функция, где возрастает, где убывает. По графику сразу можно узнать некоторые важные характеристики функции.

Вообще, аналитический и графический способы задания функции идут рука об руку. Работа с формулой помогает построить график. А график частенько подсказывает решения, которые в формуле и не заметишь.

Почти любой ученик знает три способа задания функции, которые мы только что рассмотрели.

Попытаемся ответить на вопрос: «А существуют ли другие способы задания функции?»

Такой способ есть.

Функцию можно вполне однозначно задать словами.

Например, функцию у=2х можно задать следующим словесным описанием: каждому действительному значению аргумента х ставится в соответствие его удвоенное значение. Правило установлено, функция задана.

Более того, словесно можно задать функцию, которую формулой задать крайне затруднительно, а то и невозможно.

Например: каждому значению натурального аргумента х ставится в соответствие сумма цифр, из которых состоит значение х. Например, если х=3, то у=3. Если х=257, то у=2+5+7=14. И так далее. Формулой это записать проблематично. А вот табличку легко составить.

Способ словесного описания — достаточно редко используемый способ. Но иногда встречается.

Если есть закон однозначного соответствия между х и у — значит, есть функция. Какой закон, в какой форме он выражен — формулой, табличкой, графиком, словами – сути дела не меняет.

Рассмотрим функции, области определения которых симметричны относительно начала координат, т. е. для любого х из области определения число (-х ) также принадлежит области определения. Среди таких функций выделяют четные и нечетные .

Определение. Функция f называется четной , если для любого х из ее области определения

Пример. Рассмотрим функцию

Она является четной. Проверим это.

Для любого х выполнены равенства

Таким образом, у нас выполняются оба условия, значит функция четная. Ниже представлен график этой функции.

Определение. Функция f называется нечетной , если для любого х из ее области определения

Пример. Рассмотрим функцию

Она является нечетной. Проверим это.

Область определения вся числовая ось, а значит, она симметрична относительно точки (0;0).

Для любого х выполнены равенства

Таким образом, у нас выполняются оба условия, значит функция нечетная. Ниже представлен график этой функции.

Графики, изображенные на первом и третьем рисунках симметричны относительно оси ординат, а графики, изображенные на втором и четвертом рисункам симметричны относительно начала координат.

Какие из функций, графики которых изображены на рисунках являются четными, а какие нечетными?

2} = h(x)$. Так даже.

3) если $g(x) = x$, то $g(-x) = -x = -g(x)$ так нечетно.

4) если $k(x) = \frac{1}{x}$, то $k(-x) = \frac{1}{(-x)} = -\frac{1}{x} = -к(х) $ так странно.

$\endgroup$

2

$\begingroup$

$F$ является $\mathbf{четным}$, если $F(x) = F(-x)$ для всех $x$.

$F$ является $\mathbf{нечетным}$, если $F(-x) = — F(x) $ для всех $x$

$\mathbf{Домашнее задание}$: Существуют ли функции, одновременно четные и странный?. [Подсказка: ровно один.]

$\endgroup$

6

$\begingroup$

Нечетная функция графически симметрична относительно начала координат, а четная функция симметрична относительно оси Y, так что вы можете видеть это таким образом. ..

$\endgroup$

$\begingroup$

Я нашел объяснение, которое было действительно ясным, и оно, похоже, дополняло ответ, который дал Махидевран.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Как найти четные и нечетные функции?

В математике существуют различные типы функций. Мы можем определить, является ли функция нечетной или четной, алгебраически и графически. В этом пошаговом руководстве вы узнаете больше о четных и нечетных функциях и о том, как их решать.

В математике мы изучаем различные типы функций. Мы можем определить, является ли функция четной или нечетной, алгебраически и графически.

Четная функция

Для действительнозначной функции \(f(x)\), когда выходное значение \(f(-x)\) совпадает с \(f(x)\), для всех значений \(x\) в области определения \(f\) функция является четной функцией. Четная функция должна иметь следующее уравнение:

\(\color{blue}{f(-x) = f(x)}\)

Для всех значений \(x\) в \(D\: (f)\), где \(D \: (f)\) является областью определения \(f\).

 Другими словами, мы можем сказать, что уравнение \(f(-x)\: – f(x) = 0\) выполняется для четной функции для всех \(x\).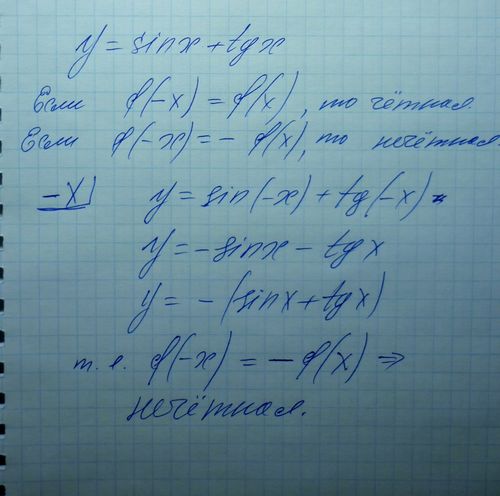

Нечетная функция

Для действительнозначной функции \(f(x)\), когда выходное значение \(f(-x)\) совпадает с отрицательным значением \(f(x) \), для всех значений \(x\) в области определения \(f\) функция является нечетной. Нечетная функция должна содержать следующее уравнение:

\(\color{blue}{f(-x) = -f(x)}\)

Для всех значений \(x\) в \(D\:(f)\), где \( D\:(f)\) — область определения функции \(f\).

Другими словами, мы можем сказать, что уравнение \(f(-x) + f(x) = 0\) верно для нечетной функции, для всех \(x\).

И четные, и нечетные функции

Действительнозначная функция \(f(x)\) называется одновременно четной и нечетной, если:

\(\color{blue}{f(-x) = f(x)}\) и \(\color{blue}{f(-x) = -f(x)}\)

Для всех значений \(x\) в области определения функции \(f (Икс)\). Существует только одна функция, одновременно четная и нечетная, и это нулевая функция \(f(x) = 0\) для всех \(x\).

Ни четная, ни нечетная функция

Действительнозначная функция \(f(x)\) не является ни четной, ни нечетной, если она не удовлетворяет условию \(\color{blue}{f(-x) = f( x)}\) и \(\color{blue}{f(-x) = -f(x)}\) хотя бы для одного значения \(x\) в области определения функции \(f(x )\).

Свойства четных и нечетных функций

• Сумма двух нечетных функций нечетна, а сумма двух четных функций четна.
• Разница между двумя нечетными функциями является нечетной, а разница между двумя четными функциями — четной.
• Сумма нечетной и четной функций не является ни четной, ни нечетной, если только одна из них не является нулевой функцией.
• Произведение двух нечетных функций также является четной функцией, а произведение двух четных функций является четным.
• Произведение четной и нечетной функции нечетно.
• Частное двух нечетных функций является четной функцией, а частное двух четных функций четным.
• Частное четной и нечетной функции нечетно.
• Композиция двух нечетных функций нечетна, а композиция двух четных функций четна.
• Композиция четной и нечетной функций четна.

График четных и нечетных функций

График четной функции симметричен относительно оси \(y\).