Как обозначается параллелограмм: Параллелограмм — урок. Геометрия, 8 класс.

Параллелограмм: основание, высота и площадь

• Высота
• Площадь

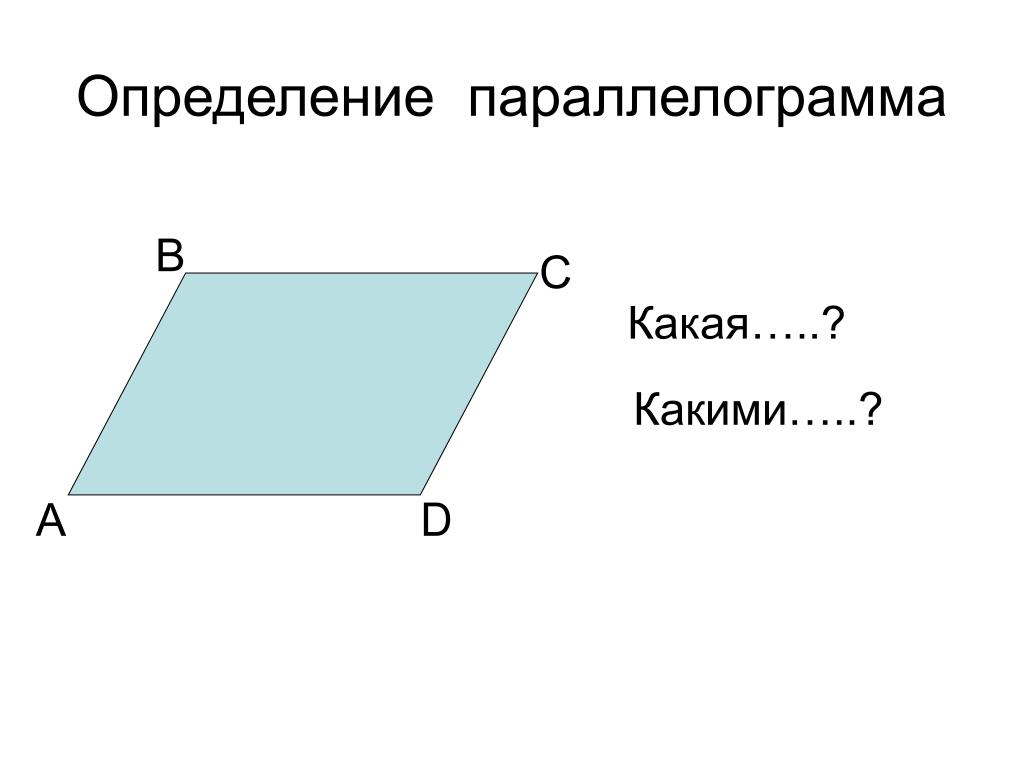
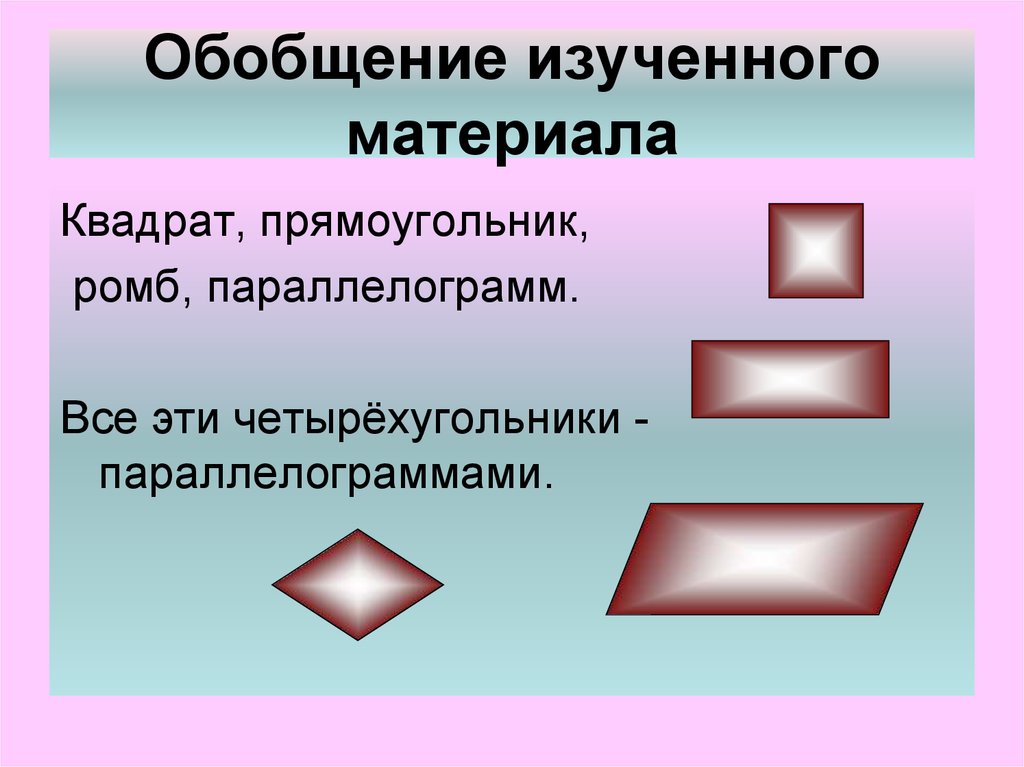
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Если у параллелограмма все углы прямые, то такой параллелограмм называется прямоугольником, а прямоугольник, у которого все стороны равны, называется квадратом.

Все параллелограммы обладают следующими свойствами:

• противоположные стороны равны:

  AB = CD    и    BC = DA;

• противолежащие углы равны:

  ∠ABC = ∠CDA    и    ∠DAB = ∠BCD;

• сумма углов, прилежащих к одной стороне, равна  180°:

  ∠ABC + ∠BCD = 180°,

  ∠BCD + ∠CDA = 180°,

  ∠CDA + ∠DAB = 180°,

  ∠DAB + ∠ABC = 180°;

• в точке пересечения диагонали делятся пополам:
  AO = OC    и    BO = OD;

• каждая диагональ делит параллелограмм на два равных треугольника:

  ΔABC = ΔCDA    и    ΔABD = ΔBCD;

• точка пересечения диагоналей — это центр симметрии параллелограмма:

  Точка  O  — это центр симметрии.

Высота

Нижняя сторона параллелограмма называется его основанием, а перпендикуляр, опущенный на основание из любой точки противоположной стороны, — высотой.

AD  — это основание параллелограмма,  h  — высота.

Высота выражает расстояние между противоположными сторонами, поэтому определение высоты можно сформулировать ещё так: высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны на противоположную ей сторону.

Площадь

Для измерения площади параллелограмма можно представить его в виде прямоугольника. Рассмотрим параллелограмм  ABCD:

Построенные высоты  BE  и  CF  образуют прямоугольник  EBCF  и два треугольника:  ΔABE  и  ΔDCF.  Параллелограмм  ABCD  состоит из четырёхугольника  EBCD  и треугольника  ABE,  прямоугольник  EBCF  состоит из того же четырёхугольника и треугольника  DCF.   Треугольники  ABE  и  DCF  равны (по четвёртому признаку равенства прямоугольных треугольников), значит и площади прямоугольника с параллелограммом равны, так как они составлены из равных частей.

Итак, параллелограмм можно представить в виде прямоугольника, имеющего такое же основание и высоту. А так как для нахождения площади прямоугольника перемножаются длины основания и высоты, значит и для нахождения площади параллелограмма нужно поступить также:

площадь  ABCD = AD · BE.

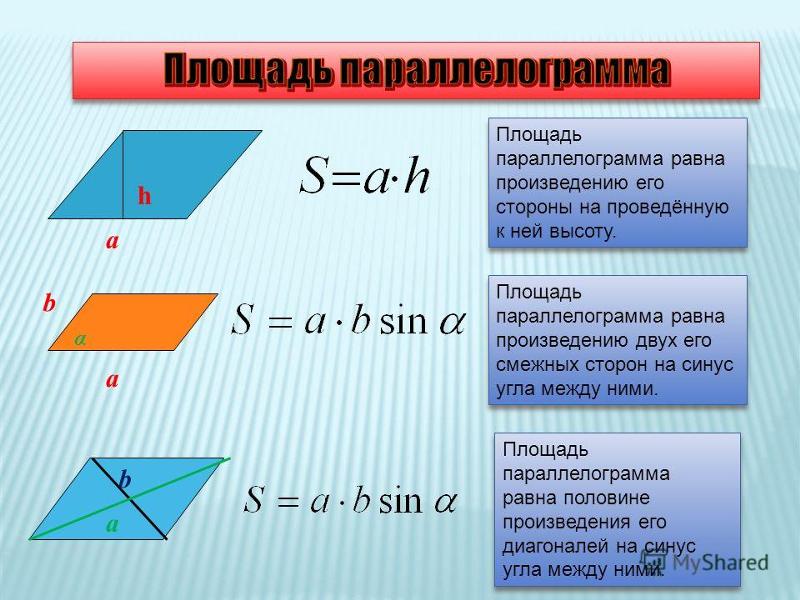
Из данного примера можно сделать вывод, что площадь параллелограмма равна произведению его основания на высоту.

Общая формула площади параллелограмма:

S = ah,

где  S  — это площадь параллелограмма,  a  — основание,  h  — высота.

Что такое Прямоугольный Параллелепипед? Примеры, Свойства, Диагональ

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.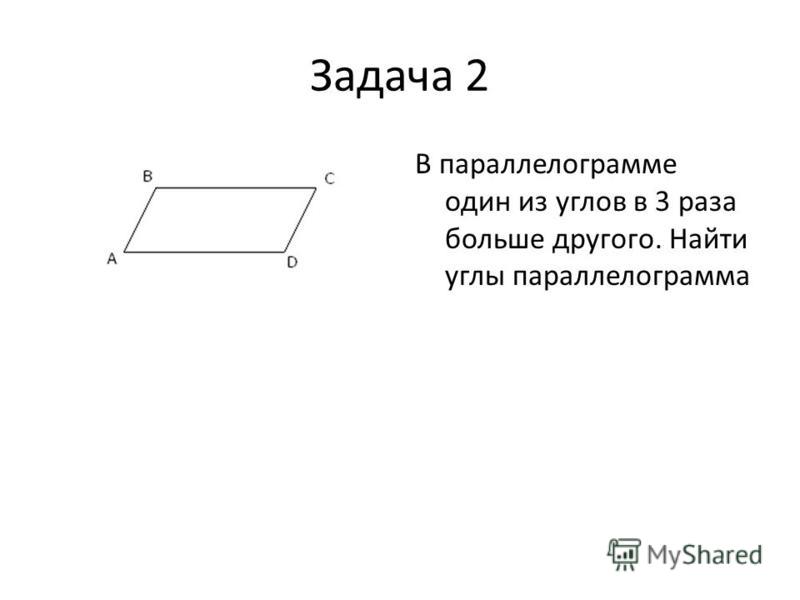

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA

1, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

• основание;
• грани;
• ребра;
• диагонали;
• диагонали граней;
• высота.

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

 

1. Противолежащие грани параллелепипеда равны и параллельны друг другу.


2. Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.


3. Параллелепипед симметричен относительно середины его диагонали.


4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.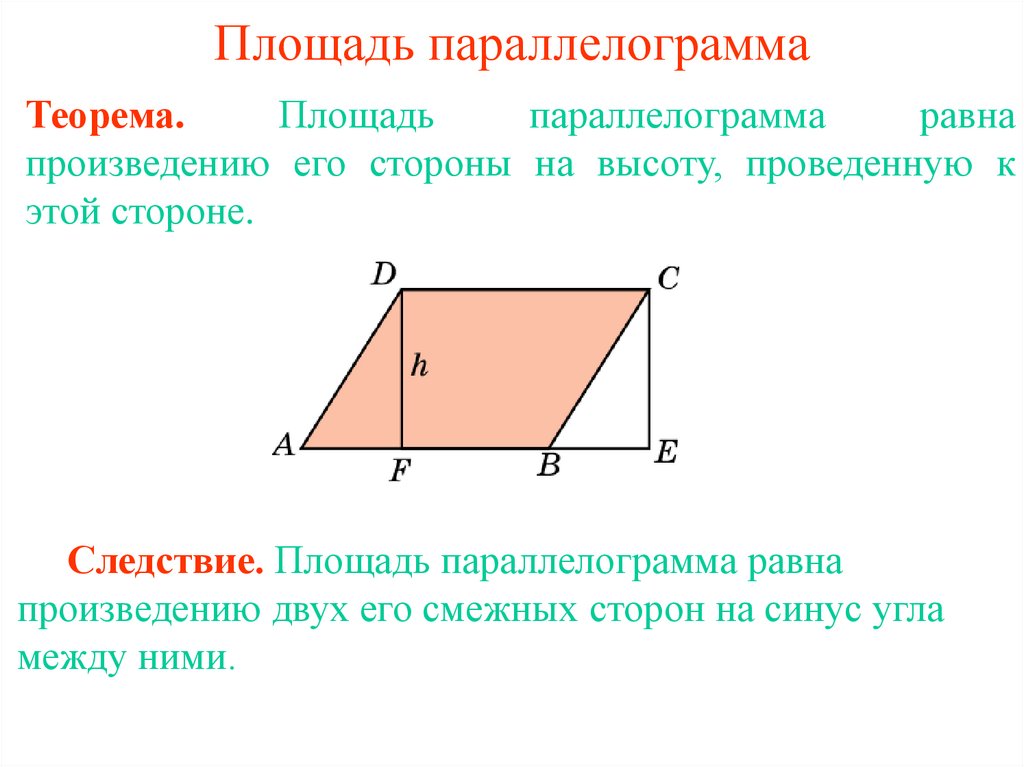

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

На рисунке: ребро АА1 перпендикулярно основанию ABCD. АА1 перпендикулярна прямым АB и АD, которые лежат в плоскости основания

Свойства прямого параллелепипеда:

 

1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.


2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.


3. Высота прямого параллелепипеда равна длине бокового ребра.


4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.


5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

• Площадь боковой поверхности прямого параллелепипеда
  Sб = Ро*h
  Ро — периметр основания
  h — высота
• Площадь полной поверхности прямого параллелепипеда
  Sп = Sб+2Sо
  Sо — площадь основания
• Объем прямого параллелепипеда
  
  V = Sо*h

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.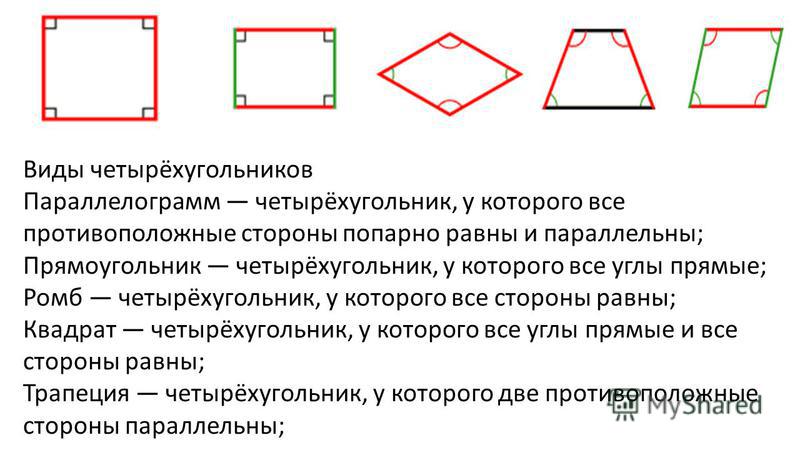

На рисунке: основание прямоугольного параллелепипеда ABCD; боковое ребро АА1 перпендикулярно АВСD; угол BAD = 90°

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

 

1. Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.


2. Противолежащие грани параллелепипеда попарно параллельны и равны.


3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.


4. Диагонали прямоугольного параллелепипеда равны.


5. В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.


6. Любая грань прямоугольного параллелепипеда может быть принята за основание.


7. Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.


8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

• Объем прямоугольного параллелепипеда
  V = a · b · h
  a — длина, b — ширина, h — высота
• Площадь боковой поверхности
  Sбок = Pосн·c=2(a+b)·c
  Pосн — периметр основания, с — боковое ребро
• Площадь поверхности
  Sп.п = 2(ab+bc+ac)

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.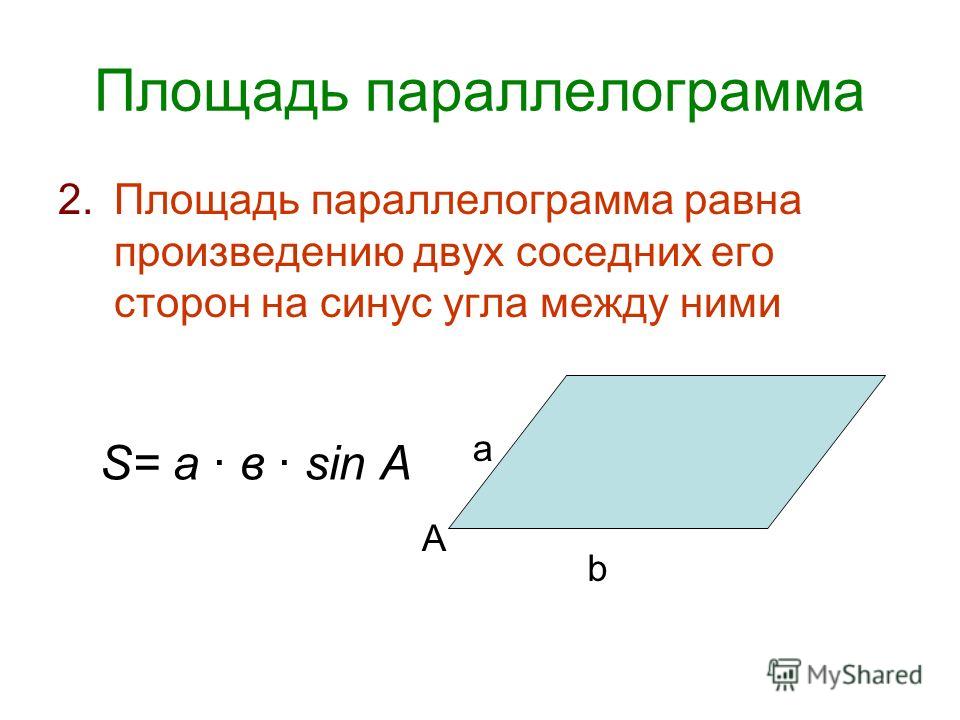

Если есть теорема, нужно ее доказать. (с) Пифагор

Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Применяем формулу:

d² = a² + b² + c²

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

d₁² = a² + b²

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

 

1. В кубе 6 граней, каждая грань куба — квадрат.


2. Противолежащие грани параллельны друг другу.


3. Все углы куба, образованные двумя гранями, равны 90°.


4. У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.


5. Диагонали куба равны.


6. Диагональ куба в √3 раз больше его ребра.


7. Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

• Объем куба через длину ребра a
  V = a3
• Площадь поверхности куба
  S = 6a2
• Периметр куба
  P = 12a

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.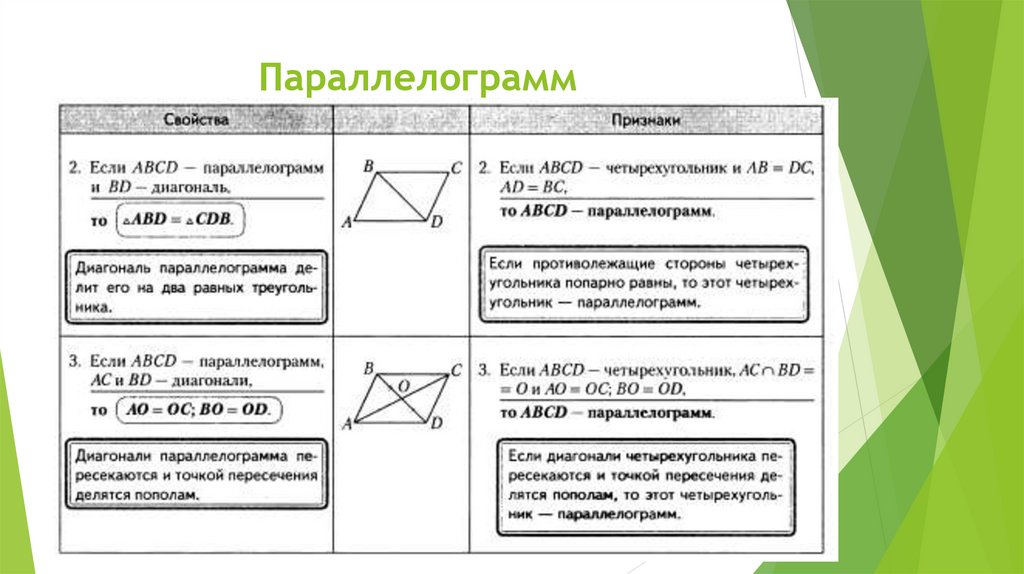

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

D₁B = √26
BB₁ = 3
A₁D₁ = 4

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD₁² = DD₁² + BD²
BD² = BD₁² – DD₁²
BD² = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD² = AD² + AB²
AB² = BD² — AD² = (√17)2 — 4² = 1
A₁B₁ = AB = 1.

Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD² = AB²+AD²
BD² = 4² + 6² = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁² = 52 + 25 = 77
BD₁ = √77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AC₁= 15
C₁D₁ = 3
B₁C₁= 12

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

• прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
• параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
• основание прямоугольного параллелепипеда — прямоугольник;
• три измерения прямоугольного параллелепипеда: длина, ширина, высота;
• диагональ параллелепипеда равна сумме квадратов его измерений.

фактов о параллелограммах | Наука

••• AndreaAstes/iStock/Getty Images

Обновлено 25 апреля 2017 г.

Автор: Kristine Tucker

Параллелограмм — это двумерный четырехугольник — фигура, имеющая четыре стороны, которые пересекаются в четырех точках, также известная как как вершины. Две противоположные стороны параллелограмма всегда параллельны и конгруэнтны — или равны по длине. Прямоугольники, квадраты и ромбы — все это примеры параллелограммов.

Противоположные стороны

Обе пары противоположных сторон параллелограмма всегда параллельны, и обе пары противоположных сторон параллелограмма всегда конгруэнтны. Вы можете найти расстояние вокруг параллелограмма, также известное как периметр, измерив и сложив длины четырех сторон вместе. Поскольку противоположные стороны параллелограмма параллельны, они никогда не пересекаются .

Диагональные линии

Диагонали параллелограмма — линии, идущие от одного угла к противоположному, — делят друг друга пополам. Другими словами, каждая диагональ делит противоположную диагональ на две равные части . Как бы вы ни изменяли форму параллелограмма, например, делая стороны короче или длиннее, увеличивая и уменьшая высоту, диагонали всегда будут пересекаться пополам.

Площадь параллелограмма

Вычислите площадь параллелограмма путем умножения основания на высоту , также известную как высота. В качестве основания можно использовать любую сторону параллелограмма. Высота — это перпендикулярное расстояние от основания до противоположной стороны. В некоторых случаях может потребоваться расширить противоположную сторону параллелограмма, чтобы иметь возможность найти и измерить перпендикулярное расстояние.

Внутренние углы

Противолежащие внутренние углы параллелограмма всегда равны . Например, если один внутренний угол равен 36 градусам, то и противоположный внутренний угол также будет равен 36 градусам.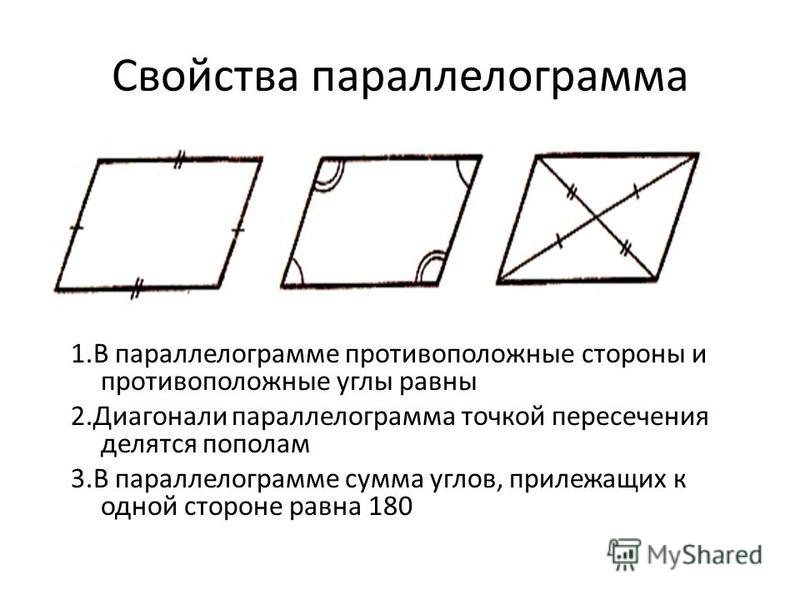 Последовательные внутренние углы в параллелограмме — углы, расположенные рядом — являются дополнительными. Это означает, что когда вы складываете два внутренних последовательных угла вместе, сумма всегда равна 180 градусам. Когда вы складываете все четыре внутренних угла вместе, сумма всегда равна 360 градусам.

Середины четырехугольников

Когда вы определяете середины — середину отрезка или середину — на каждой стороне четырехугольника и соединяете эти точки последовательными прямыми линиями, результатом всегда является параллелограмм .

Определенные геометрические фигуры

Прямоугольники и квадраты являются примерами параллелограммов с углами 90 градусов, также известными как прямые углы. Ромбы и квадраты являются примерами параллелограммов со сторонами одинаковой длины.

Связанные статьи

Ссылки

• Математика Открытый справочник: Параллелограмм
• Университет Кентукки; Параллелограммы — MA 341 — Темы лекции по геометрии 05; Дэвид Ройстер
• Государственный университет Сономы; Math 150 — Теоремы о параллелограммах; Стив Уилсон

Об авторе

Кристин Такер, как разработчик учебных программ и педагогов, с удовольствием читала (и оценивала!) множество заданий по английскому языку. Ее опыт работы в качестве вице-президента консалтинговой фирмы по энергетике дал ей возможность изучить бизнес-письмо и HR. Такер имеет степень бакалавра и имеет право преподавать в Огайо.

Авторы фотографий

AndreaAstes/iStock/Getty Images

Что хорошего в параллелограмме?

Опубликовано 05.02.2001

Вы помните, как учили названия странных фигур в начальной школе, а затем в геометрии? Были равнобедренные треугольники, параллелограммы и додекаэдры. Какая польза от всех этих причудливых знаний в «реальной жизни»? Что ж, оказывается, по крайней мере одна из этих форм очень важна для тех из нас, кто раскладывает измерительные установки или выбирает инструменты для точных измерений.

Джордж Шютц

Директор прецизионных измерительных приборов, Махр Инк.

Доля

Читать дальше

• Открыть собственный механический цех? Вот совет о том, как начать с малого
• Как пассивировать детали из нержавеющей стали
• Обработка Вопросы? Спросите эксперта

Вы помните, как учили названия странных фигур в начальной школе, а затем в геометрии? Были равнобедренные треугольники, параллелограммы и додекаэдры. Какая польза от всех этих причудливых знаний в «реальной жизни»?

Оказывается, по крайней мере одна из этих форм очень важна для тех из нас, кто раскладывает измерительные установки или выбирает инструменты для точных измерений. Это параллелограмм, и он может сделать высокоточные измерения очень воспроизводимыми и сэкономить много денег за счет минимизации износа дорогих датчиков. Но прежде чем мы перейдем к преимуществам, мы должны немного поговорить о задействованных принципах.

Параллелограмм имеет четыре прямые стороны. Каждая из двух пар противоположных сторон имеет одинаковую длину и параллельна. Уникальные свойства параллелограмма широко применяются в промышленности для точной передачи механического движения из одного места в другое. Возможно, наиболее известным применением является пантограф, четырехстороннее устройство, используемое граверами для воспроизведения контура изображения в определяемом пользователем масштабе.

В датчиках и измерительных установках простые устройства, называемые «тростниковыми пружинами», имитируют поведение параллелограмма для передачи движения от одного компонента к другому. Один тип язычковой пружины состоит из двух параллельных блоков, соединенных двумя или более стальными полосами одинакового размера и жесткости, образуя изгибную связь язычкового типа. Один из блоков крепится к неподвижной поверхности. Когда к свободному блоку прикладывается усилие, соединительные планки изгибаются, что приводит к смещению подвижного блока.

Некоторые наблюдатели заметят, что когда происходит это движение, соединительные полосы слегка изгибаются и что, технически говоря, параллелограмм нарушен. Тем не менее, я уверен, что вы не были бы таким придиркой. Важно то, что неподвижный и подвижный блоки все еще параллельны и что подвижный блок не деформируется при контакте. Таким образом, к степени переданного движения ничего не прибавляется и не убавляется. Для высокоточной передачи движения с диапазоном в несколько тысячных язычковые пружины могут быть изготовлены методом электроэрозионной обработки из цельного куска стали.

Итак, теперь, когда мы прошли через все это, в чем же дело? Если вас не волнует повреждение сенсора или постоянная повторяемость, вы можете использовать простую подставку и сенсор и позволять захлопывать под ним одну деталь за другой. Или вы можете передать движение внутри датчика таким образом, чтобы защитить датчик и обеспечить воспроизводимость. Для этих целей можно использовать язычковые пружины:

   A.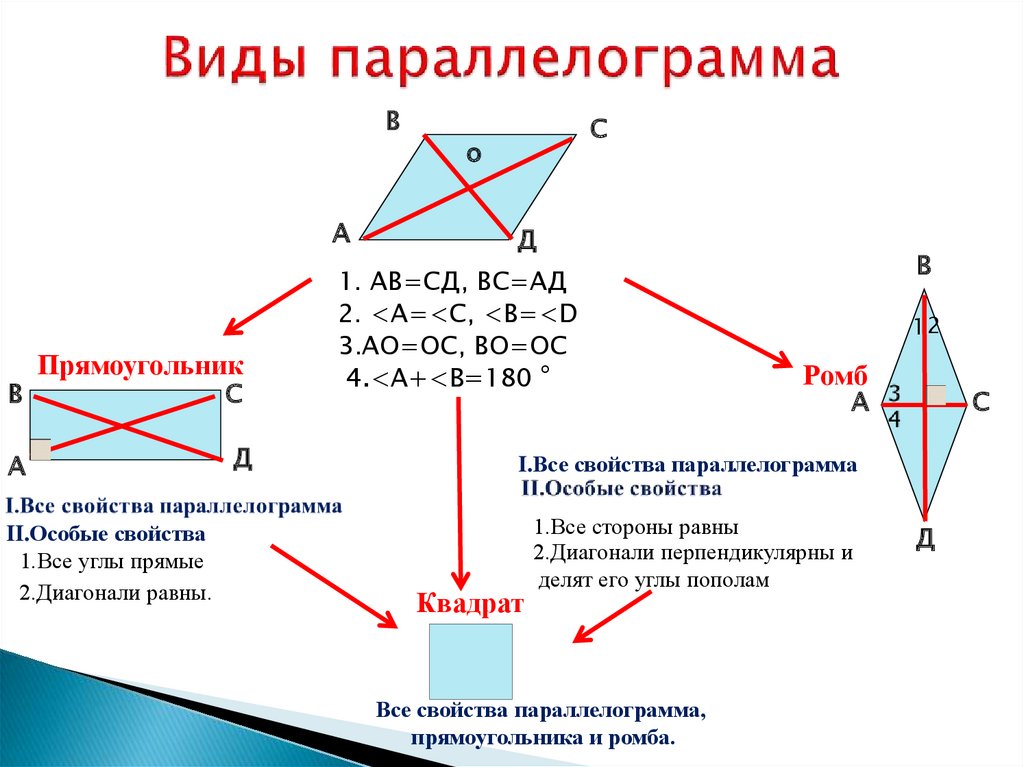 В ситуации измерения, когда может потребоваться защита индикатора измерения, язычок будет воспринимать всю боковую нагрузку, а не передавать ее на датчик. Таким образом, сам геркон берет на себя всю нагрузку, а не дорогой датчик.

   B. Герконовые пружины также можно использовать для калибровки в ситуациях, когда точка контакта и датчик должны находиться в разных местах. Опять же, язычок поглощает боковую нагрузку, поскольку он позволяет размещать контакт в местах, где датчик может не поместиться, в данном случае в ограниченном внутреннем диаметре.

   C. Наконец, язычковая пружина может быть превращена в микроточный датчик. Пластинчатая пружина защищает ценный датчик, а ее движение без трения приводит к воспроизводимым микродюймовым измерениям.

Есть ли другие способы сделать то же самое? Безусловно. Сразу приходят на ум прецизионные подшипники и направляющие. Однако язычковая пружина дешевле, и между ее компонентами нет подвижного контакта. Это последнее качество практически бросает вызов законам физики, сопротивляясь натиску грязи и жира.