Сложение десятичных дробей: правила и примеры
- Сложение путём перевода в обыкновенные дроби
- Сложение десятичных дробей столбиком
- Сложение десятичной дроби с натуральным числом
- Сложение десятичной дроби с обыкновенной дробью
Сложение десятичных дробей можно выполнить двумя способами:
- Представить десятичные дроби в виде обыкновенных дробей и выполнить их сложение.
- Выполнить сложение десятичных дробей столбиком.
Сложение путём перевода в обыкновенные дроби
При сложении десятичных дробей путём их перевода в обыкновенные дроби следует руководствоваться следующим правилом:
- Нужно сравнить количество десятичных знаков у десятичных дробей.
- Если количество десятичных знаков одинаково, то переводим десятичные дроби в обыкновенные и складываем их.
- Если количество десятичных знаков различно, то сначала нужно уравнять их количество, приписав справа к десятичной дроби с меньшим количеством знаков необходимое число нулей.
Пример 1. Выполнить сложение чисел 3,1 и 4,7.
Решение. Так как количество десятичных знаков одинаково, то просто переводим десятичные дроби в обыкновенные и складываем. Десятичной дроби 3,1 соответствует обыкновенная дробь , а десятичной дроби 4,7 — обыкновенная дробь , значит:
Пример 2. Сложить числа 3,45 и 7,368.
Решение. Так как количество десятичных знаков различно, то сначала уравняем их количество, приписав справа к дроби 3,45 цифру 0. Десятичной дроби 3,450 соответствует обыкновенная дробь , а десятичной дроби 7,368 — обыкновенная дробь , значит:
Сложение десятичных дробей столбиком
Десятичные дроби можно складывать столбиком.
При сложении десятичных дробей столбиком следует руководствоваться следующим правилом:
- Записать десятичные дроби в столбик так, чтобы цифры одинаковых разрядов стояли друг под другом. Запятые десятичных дробей так же должны стоять друг под другом.
- Если количество десятичных знаков у дробей различно, для удобства можно уравнять их число, приписав справа к десятичной дроби с меньшим количеством десятичных знаков необходимое число нулей.
- Не обращая внимание на запятые, выполнить сложение так, как выполняется сложение столбиком натуральных чисел.
- В полученной сумме поставить запятую так, чтобы она стояла под запятыми слагаемых.
Пример 1. Сложить числа 3,1 и 4,7.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел, не обращая внимание на запятые:
Пример 2. Сложить 3,45 и 7,368.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел. Для удобства, можно уравнять количество десятичных знаков в складываемых дробях:
Сложение десятичной дроби с натуральным числом
Правило сложения десятичных дробей с натуральными числами:
Чтобы сложить десятичную дробь и натуральное число, нужно данное натуральное число прибавить к целой части десятичной дроби, а дробную часть оставить без изменений.
Пример. Вычислить сумму 14,3 и 29.
Решение. Для удобства сложения, любое натуральное число можно представить в виде десятичной дроби. Для этого нужно поставить запятую после разряда единиц и приписать после запятой нужное количество нулей. Сложение выполняется по правилу сложения десятичных дробей столбиком:
Сложение десятичной дроби с обыкновенной дробью
Правило сложения десятичных дробей с обыкновенной дробью:
Сложение десятичной дроби с обыкновенной дробью сводится к сложению обыкновенных дробей. Для этого десятичная дробь переводится в обыкновенную дробь.
Пример. Выполнить сложение десятичной дроби 0,28 и обыкновенной дроби .
Решение. Переводим десятичную дробь 0,28 в обыкновенную: . И далее выполняем уже сложение обыкновенных дробей и :
Чтение и запись десятичных дробей
Часто бывает, что показать значение лучше в дробном выражении. К примеру, одну десятую часть дециметра можно представить так: \[\frac{1}{10} \text{дм}\].
Выражение обозначает, что дециметр разделили на 10 равных частей, и одна из этих частей была взята. В данном случае эта часть будет равна 1 сантиметру.
Если нужно показать в дробном виде 6 см и 3 мм в сантиметрах, представим выражение в виде десятичной дроби. Один миллиметр – это десятая часть сантиметра, соответственно 3 мм это три десятых, записываются так: \[\frac{3}{10} \mathrm{см}\].
Выражение обозначает, что один сантиметр был разделен на 10 равных частей и взяли три из них. В результате получается: \[6 \frac{3}{10}см\].
Дробь можно прочитать как шесть целых три десятых сантиметра. Если знаменатель дроби представлен числами 10, 100, 1000 эту дробь можно записать без знаменателя в виде целой и дробной части без знаменателя. Целая и дробная часть между собой разделяются запятой, получается 6,3 см. Каждое число, записанное в таком виде, считается десятичной дробью.
Что такое десятичная дробь
Десятичные дроби представляют собой целые числовые выражения, в знаменатель которых десять в какой-либо степени.
Для чего нужны десятичные дроби
- удобнее сравнивать;
- сокращение вычислений;
- удобная запись в одну строчку.
Чтобы записать десятичную дробь выполняют следующие действия:
- Отдельно написать числитель.
- Передвинуть десятичную точку на количество нулей знаменателя.
- После того, как десятичная точка сдвинулась, зачеркните нули, которые остались в конце записи.
Если на втором шаге недостаточно цифр для завершения действия, на недостающих позициях проставляются нули. Примеры десятичной записи.
\[\frac{73}{10} ; \frac{9}{100} ; \frac{10029}{1000} ; \frac{10500}{1000}\]
В знаменателе первой дроби стоит 10, значит, числитель первой дроби 73 сдвинем на один знак. Получается 7,3.
Знаменатель второй дроби 100, а числитель 9. Сдвигаем десятичный знак на два знака и получаем 0,09.
Знаменатель третьей дроби 1000, а числитель 10029. Сдвигаем десятичную точку на три знака и получаем 10,029.
В последней дроби числитель 10500, перемещаем точку на три знака 10,500.
Образовавшиеся в конце записи нули убираем, и получаем ответ 10,5.
Два последних примера показывают, как правильно поступать с нулями. Если нули получились справа в конце – их следует зачеркнуть, а если в середине, как в третьем примере, то их оставляем. Это цифры внутри числа.
Конечные десятичные дроби
Определение
Конечные десятичные дроби – это вид десятичной дроби, в которых содержится конечное число знаков после запятой. Например: 0,367; 3,7. Каждую из этих дробей можно записать как смешанном числом либо обыкновенной дроби.
Приведем пример, конечную десятичную дробь 5,63 легко представить как \[5 \frac{63}{100}\], десятичную дробь 0,2 можно привести к виду \[\frac{2}{10}\].
Обратные процесс записи обыкновенной дроби в десятичном виде выполняется не в каждом случае. Например, дробь \[\frac{5}{13}\] заменить, на аналогичную дробь со знаменателем 100, 10 нельзя.
Класс периодических и непериодических дробей
Если в десятичной дроби после запятой стоит бесконечное количество цифр, такие дроби называют бесконечными.
Такие дроби целиком записать невозможно, следовательно, при записи указывается лишь часть из них, далее записывается многоточие. Это обозначает бесконечную последовательность знаков после запятой. Примеры класса бесконечных десятичных дробей: 0,143346732…; 3,1415989032…; 2,6666666666…
После запятой могут стоять периодичные повторения одного знака или группы знаков.
Определение
Периодические дроби – это бесконечные десятичные дроби, в которых после запятой стоят повторяющиеся группы цифр или повторяется одна цифра.
Например, для десятичной дроби 3,444444… периодом будет 4, для 76,134134134134… периодом будет группа чисел 134.
Чтобы записать представить запись десятичной периодичной бесконечной дроби в сокращенном виде, достаточно указать период одни раз в скобках. Так для 3,444444… запись выглядит так 3,(4), дробь 76,134134134134… можно представить в виде 76,(134). Смысл остается тем же самым. Такую запись используют, чтобы избежать ошибок.
В скобки заключают максимально короткую последовательность цифр, которые расположены ближе всего к запятой.
Каждую конечную дробь можно выразить как периодическую. В таком случае, добавляют бесконечное множество нулей в правой части выражения. Например, конечная дробь 45,32 в периодическом виде записывается как 45,32(0). Таким образом, добавление нулей в правую часть десятичной дроби дает равную ей дробь.
Бесконечные десятичные периодические дроби являются рациональными числами. Любую десятичную можно записать в виде обыкновенной и наоборот.
Дроби, у которых нет бесконечной последовательности после запятой, называют непериодическими. Внешне они бывают похожими на периодические, с записями наподобие 9,03003000300003… нужно быть внимательно, знаки после запятой одинаковые, но не повторяются. Такие дроби являются иррациональными и в обыкновенные дроби их не переводят.
Арифметические действия с десятичными дробями
Теоритические и практические уроки предполагают следующие действия с десятичными дробями, их можно: складывать, вычитать, умножать делить, сравнивать между собой.
Правила действий с десятичными дробями
- Сделать одинаковым число знаков после запятой.
- Выполнить запись в столбик друг под другом, запятая должна быть под запятой.
- Выполнить сложение (вычитание).
Действия с десятичными дробями: сложение
Действия удобнее выполнять в столбик. Целые и дробные части складывают по отдельности. Например, выполним сложение дробей 3,2 и 5,3. Для этого запишем две дроби в столбик, при этом целые части следует записать под целыми, а дробные под дробными (запятая под запятой).
\[\begin{array}{r} + \begin{array}{r} 3,2\\ 5,3\\ \end{array} \\ \hline \begin{array}{r} 8,5 \end{array} \end{array}\]
В первую очередь складываем дробные части и записываем пятерку под чертой. Далее складываем целые части, пишем восьмерку в целой части ответа. Дробную часть от целой отделяем запятой. Получаем ответ 8,5.
Пример правильной записи:
\[\begin{array}{r} + \begin{array}{r} 10,234\\ 0,12\;\,\\ \end{array} \\ \end{array}\]
Пример неправильной записи:
\[\begin{array}{r} + \begin{array}{r} 10,234\\ 0,12\\ \end{array} \\ \end{array}\]
Место расположения цифр в десятичной дроби влияет на значение в десятичной дроби.
Разряды различаются по старшинству, если рассматривать цифры слева на право, то будем двигаться от старших разрядов к младшим.
В качестве примера возьмем десятичную дробь 0,345
Позиция тройки находится в разряде десятых.
Позиция четверки – в разряде сотых.
Пятерки – тысячных.
Расположение тройки в разряде десятых сообщает о том, что в рассматриваемой дроби 0,345 содержится три десятых \[\frac{3}{10}\]; четыре сотых \[\frac{4}{100}\]; пять десятитысячных \[\frac{5}{1000}\]. При сложении дробей получим изначальную.
\[\frac{100 / 3}{10}+\frac{10 / 4}{100}+\frac{1 / 5}{1000}=\frac{3 * 100}{10 * 100}+\frac{4 * 10}{100 * 10}+\frac{5 * 1}{1000 * 1}=\frac{300}{1000}+\frac{40}{1000}+\frac{5}{1000}=\frac{345}{1000}=0,345\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Сложение десятичных дробей
Правила сложения десятичных дробей те же, аналогичные сложению обычных чисел.
Сложение выполняется согласно разрядам: десятки с десятками, сотые с сотыми. Соблюдение правила «запятая под запятой» обеспечит этот порядок. Сложение начинают с крайнего правого ряда и двигаются влево к предыдущему.
Математические действия с десятичными дробями:
- для сложения периодических десятичных дробей следует их заменить обыкновенными;
- бесконечные непериодические дроби складывают, предварительно округлив до некоторого разряда, чем меньше разряд, тем выше точность;
- для сложения десятичной дроби и натурального числа, натуральное число складывают с целой частью десятичной дроби, а дробную оставляют неизменной.
Вычитание десятичных дробей
Для выполнения вычитания соблюдаются правила, идентичные сложению: запятая под запятой и одинаковое количество цифр после запятой.
Пример
Найти значение разности 2,5 — 2,2
Записываем выражение, соблюдая правило запятой и вычисляем дробную часть 5-2=3. Далее выполняем действие с
целой частью 2-2=0.
Получаем следующую запись:
\[\begin{array}{r}-\begin{array}{r}2,5\\2,2\\\end{array} \\\hline\begin{array}{r}0,3\end{array}\end{array}\]
Ответ: 2,5-2,2=0,3
Действия с десятичными дробями: примеры
>Пример 1
Вычислить 7,353-3,1
Для решения выражения, нужно сделать равным количество цифр в дробях. Для этого следует добавить два нуля в
дроби 3,1. Записываем выражение в столбик:
\[\begin{array}{r}-\begin{array}{r}7,353\\3,100\\\end{array}
\\\hline\begin{array}{r}4,253\end{array}\end{array}\]
Ответ: 4,253
При выполнении вычитания десятичных дробей, в отдельных случаях придется занимать единицу, как и в обычных числах.
Умножение десятичных дробей производится аналогично натуральным числам. Метод вычисление столбиком тоже подходит. Выполняя действие, на запятые можно не обращать внимание. Вычислив ответ, нужно отделить дробную часть от целой. Для этого в обеих дробях подчитайте количество цифр после запятой. В ответе подсчитываем столько же цифр и ставим запятую.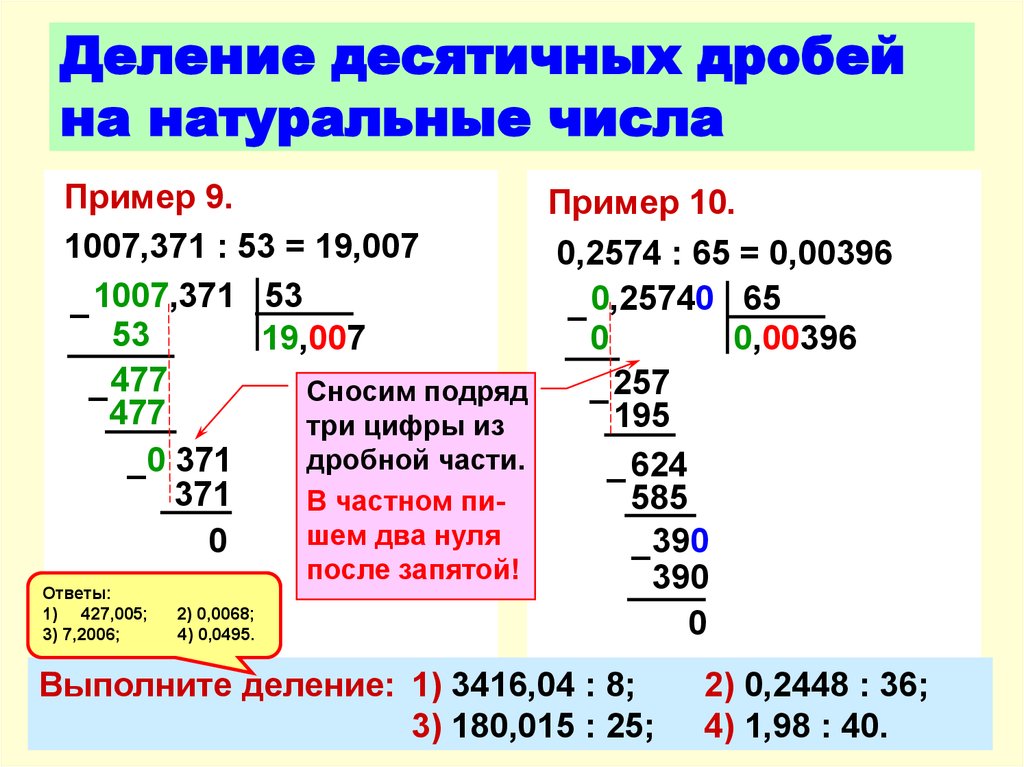
Пример 2
Вычислить 2,5х1,5
Перемножаем дроби, не обращая внимания на запятые.
\[\begin{array}{r}*\begin{array}{r}25\\15\\\end{array}
\\\hline+\begin{array}{r}125\\25\\\hline\begin{array}{r}375\end{array}\end{array}\end{array}\]
\[\begin{array}{r}*\begin{array}{r}2,5\\1,5\\\end{array} \\\hline\begin{array}{r}3,75\end{array}\end{array}\]
Запятая сдвигается на два знака, с учетом того, что в первой дроби один знак и во второй один знак.
Ответ: 3,75
Деление десятичной дроби на натуральное число производят по правилам деления в столбик. при выполнении действия на запятую не обращают внимания. В полученном частном запятая проставляется, когда заканчивается целая часть делимого. В случае, когда целая часть делимого меньше делителя, тогда в частном будет 0 целых.
Сравнение десятичных дробей
При сравнении двух дробей, большей будет та, у которой больше целая часть.
7,99>6,399
Если целые части дробей одинаковы, большей будет та, у которой больше десятых.
Если равны десятые, то больше сотые и т.д.
85,7>85,679
Десятичная дробь— определение, преобразование, примеры
Дробь, знаменатель которой представляет собой степень числа 10, называется десятичной дробью . Некоторые примеры десятичных дробей: 1/10, 4/10, 35/100 и т. д. Давайте узнаем об этом больше в этой статье.
| 1. | Что такое десятичная дробь? |
| 2. | Типы десятичных дробей |
| 3. | Преобразование десятичной дроби |
| 4. | Часто задаваемые вопросы о десятичной дроби |
Что такое десятичная дробь?
Десятичная дробь определяется как дробь, знаменатель которой представляет собой степень числа 10, например, 10, 100, 1000, 10000 и т. д. Дробь – это отношение части к целому. Итак, в десятичной дроби целое всегда делится на части, равные степени 10, например 10, 100, 1000 и так далее.
Теперь давайте разберемся с операциями над десятичными дробями.
Сложение десятичных дробей
К настоящему времени вам должно быть ясно, что десятичные дроби имеют 10, 100, 1000 и т. д. в качестве знаменателя. Чтобы сложить две или более десятичные дроби, есть два способа, которые приведены ниже:
- Путем преобразования десятичных дробей в десятичные и последующего сложения.
- Преобразовав данные десятичные дроби в подобные дроби, а затем сложив.
Следуя первому методу, мы сначала преобразуем десятичные дроби в десятичные, а затем складываем эти значения. Например, добавим 2/10 + 34/100. 2/10 можно записать как 0,2, а 34/100 можно записать как 0,34. Теперь 0,2 + 0,34 = 0,54. Следовательно, 2/10 + 34/100 = 0,54, что можно записать как 54/100. Складываем те же числа вторым способом. Чтобы преобразовать данные дроби (2/10 и 34/100) в подобные дроби, находим НОК знаменателей. Наименьшее общее кратное 10 и 100 равно 100. Итак, умножьте числитель и знаменатель 2/10 на 10.
⇒ 2/10 = (2 × 10)/(10 × 10)
⇒ 2/10 = 20/100
Теперь 20/100 + 34/100 = 54/100. Следовательно, 2/10 + 34/100 = 54/100.
Вычитание десятичных дробей
Вычитание десятичных дробей выполняется так же, как и сложение. Например, 44/100 — 1/10 можно решить как 0,44 — 0,1, что равно 0,34 или 34/100. Другой способ вычесть 1/10 из 44/100 — найти НОК знаменателей и преобразовать их в одинаковые дроби. НОК 100 и 10 равно 100.
Итак, умножьте числитель и знаменатель 1/10 на 10.
⇒ 1/10 = (1 × 10)/(10 × 10)
⇒ 1/10 = 10/100
Теперь 44/100 — 10/100 = 34/100. Следовательно, 44/100 — 1/10 = 34/100.
Умножение десятичных дробей
Умножение десятичных дробей осуществляется путем раздельного умножения числителей и знаменателей. Чтобы умножить степени 10, мы просто добавляем количество нулей. Например, 7/10 × 3/100 = (7 × 3)/(10 × 100) = 21/1000. Чтобы узнать больше об умножении дробей, нажмите на предоставленную ссылку.
Деление десятичных дробей
Чтобы разделить две десятичные дроби, выполните следующие действия:
- Шаг 1: Найдите обратную величину второй дроби.
- Шаг 2: Умножьте первую дробь на обратную величину второй дроби. Это будет требуемый ответ.
Это то же самое, что и обычное деление дробей. Например, 25/10 ÷ 5/100 = 25/10 × 100/5. Отсюда следует, что 5 × 10 = 50. Следовательно, 25/10 ÷ 5/100 = 50.
Типы десятичных дробей
Десятичные знаки можно разделить на следующие типы в зависимости от их десятичных разрядов:
- Завершающие десятичные знаки
- Непрерывные повторяющиеся десятичные дроби
- Непрерывные неповторяющиеся десятичные дроби
Когда дело доходит до десятичных дробей, мы знаем, что каждая десятичная дробь может быть записана как десятичная, где количество десятичных знаков конечно и равно количеству нулей в степени 10, записанных в знаменателе. Итак, десятичные дроби относятся к разряду конечных десятичных дробей.
Преобразование десятичных дробей
В этом разделе мы узнаем, как преобразовать дробь или десятичную дробь в десятичную дробь . Если знаменатель дроби можно записать в виде разложения на простые множители либо 2, либо 5, либо того и другого, это означает, что его можно преобразовать в десятичную дробь. Например, в дроби 3/4 знаменатель равен 4.
4 можно разложить на множители как 2 × 2. Таким образом, эту дробь можно преобразовать в десятичную дробь. Поскольку 10 не кратно 4, мы рассмотрим следующую степень 10, которая равна 100. 100 — это 25-е число, кратное 4. Итак, нам нужно умножить числитель и знаменатель 3/4 на 25, чтобы преобразовать его. в десятичную дробь. Отсюда следует, что 3/4 = (3 × 25)/(4 × 25) = 75/100. Возьмем еще один пример.
Можем ли мы преобразовать 5/12 в десятичную дробь? Ответ — нет. Это потому, что знаменатель 12 нельзя разложить на множители на произведение ни 2, ни 5, ни того и другого.
Но не волнуйтесь, мы все еще можем преобразовать его в десятичную дробь, используя другой метод. Разделите 5 на 12. Вы получите примерно 0,42. Теперь преобразуйте эту десятичную дробь в десятичную дробь. 0,42 это то же самое, что 42/100. Давайте узнаем, как преобразовать десятичную дробь в десятичную дробь, выполнив несколько простых шагов.
- Шаг 1: Подсчитайте количество знаков после запятой в заданном десятичном числе.
- Шаг 2: Удалите точку из числа и разделите его на степень 10, в которой количество нулей будет таким же, как количество знаков после запятой, подсчитанное на предыдущем шаге.
Преобразуем 0,42 в дробь. 0,42 имеет два десятичных знака. Это означает, что мы должны разделить его на 100, что является вторым показателем степени 10 (10 2 ). Следовательно, 0,42 = 42/100.
Посмотрите на таблицу десятичных дробей , приведенную ниже, чтобы научиться преобразовывать некоторые дроби и десятичные дроби в десятичные дроби.
| Дробь | Десятичная дробь | Десятичный |
|---|---|---|
| 1/2 | 5/10 | 0,5 |
| 3/2 | 15/10 | 1,5 |
| 3/4 | 75/100 | 0,75 |
| 1/8 | 125/1000 | 0,125 |
| 7/8 | 875/1000 | 0,875 |
| 3/5 | 6/10 | 0,6 |
| 1/4 | 25/100 | 0,25 |
| 1/50 | 2/100 | 0,02 |
| 2/5 | 4/10 | 0,4 |
► Похожие темы
Ознакомьтесь с интересными статьями о десятичных дробях в математике.
- Неправильные дроби
- Эквивалентные дроби
- Правильная дробь
- Доля единицы измерения
Примеры десятичных дробей
Пример 1: Сюзан хочет преобразовать 1/8 в десятичную дробь. Можете ли вы помочь ей сделать преобразование?
Решение: Дана дробь 1/8. Если мы умножим числитель и знаменатель 1/8 на 125, то получим 1000 в знаменателе. Итак, 1/8 = (1 × 125)/(8 × 125) = 125/1000. Следовательно, 1/8 = 125/1000.
Пример 2: Добавьте следующие десятичные дроби: 35/10 + 12/100.
Решение: Чтобы сложить десятичные дроби, давайте сначала найдем НОК знаменателей. НОК 10 и 100 равно 100. Итак, умножьте числитель и знаменатель 35/10 на 10.
⇒ 35/10 = (35 × 10)/(10 × 10)
⇒ 35/10 = 350/ 100
Теперь 350/100 + 12/100 = (350 + 12)/100 = 362/100. Следовательно, 35/10 + 12/100 = 362/100.
Пример 3: Выберите десятичные дроби из предложенных вариантов: 3/4, 5/30, 1/11, 121/100, 5/70, 545/1000.
Решение: Десятичные дроби — это те, у которых в знаменателе степень 10. Среди приведенных вариантов 121/100 и 545/1000 являются десятичными дробями, так как знаменатели являются степенями числа 10.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Забронировать бесплатный пробный урок
Практические вопросы по десятичной дроби
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о десятичных дробях
Что такое десятичная дробь?
В математике десятичная дробь определяется как дробь, знаменатель которой является степенью числа 10. Таким образом, в знаменателе не должно быть никаких других чисел, кроме 1, за которой следуют нули. Некоторые примеры десятичных дробей: 1/10, 3/100, 54/10 и т.
д.
Что такое десятичная дробь и как ее учить?
Десятичные дроби — это дроби, которые можно записать в виде десятичной дроби с использованием десятичной точки. Они имеют степень 10 в знаменателе. Преподавание десятичных дробей следует начинать после того, как учащиеся освоятся с понятиями дробей и десятичных знаков. Возьмите любую прямоугольную или круглую модель, разделенную на 10 или 100 равных частей, и объясните десятичные дроби как число частей, взятое из общего числа частей (которое в этом типе является степенью числа 10). Возьмите в качестве примера десятичные дроби и покажите их преобразование в десятичные дроби.
Какова десятичная дробь преобразования 18,5?
Данное число равно 18,5. Десятичная дробь 18,5 равна 185/10, так как она имеет 1 десятичный знак, который можно удалить, чтобы записать 10 в знаменателе.
Как 1/2 выражается десятичной дробью?
1/2 в виде десятичной дроби можно выразить как 5/10.
Какая десятичная дробь равна 40 мл литра?
В 1 литре 1000 миллилитров.
Десятичная дробь 40 мл литра равна 40/1000, что можно еще уменьшить до 4/100.
Как превратить десятичную дробь в десятичную дробь?
Чтобы превратить десятичную дробь в десятичную дробь, подсчитайте количество знаков после запятой и разделите данное число на степень 10, которая равна количеству знаков после запятой. Например, 0,4 можно записать как 4/10, 0,75 можно записать как 75/100.
3 простых шага — Mashup Math
Готовы ли вы узнать, как преобразовать десятичную дробь в дробь ?
(и если вы хотите узнать, как преобразовать дробь в десятичную, нажмите здесь)
Прежде чем вы изучите простой способ выполнения обоих этих преобразований (с калькулятором и без него), давайте удостоверимся, что вы понять, что такое десятичные дроби и дроби:
Ключевой вывод из этих определений состоит в том, что десятичные дроби и дроби представляют собой разные способы представления одного и того же — нецелое число.
Вы можете преобразовать десятичную дробь в дробь, выполнив следующие три простых шага.
В этом случае в качестве примера вы будете использовать десятичное число 0,25 (см. рисунок ниже).
Шаг первый: Перепишите десятичное число больше единицы (в виде дроби, где десятичное число — числитель, а знаменатель — единица).
Шаг второй: Умножьте числитель и знаменатель на 10 в степени количества цифр после запятой. Если после запятой стоит одно значение, умножьте на 10, если два, то умножьте на 100, если три, то умножьте на 1000 и т. д.
В случае преобразования 0,25 в дробь после запятой идут две цифры. Поскольку 10 во 2-й степени равно 100, мы должны умножить и числитель, и знаменатель на 100 на втором шаге.
Шаг третий: Выразите дробь в простейшей (или сокращенной) форме.
Если вам нужна дополнительная помощь в упрощении дробей, посмотрите этот бесплатный видеоурок.
Выполнив эти три шага в приведенном выше примере преобразования десятичной дроби в дробь, вы можете сделать вывод, что десятичное число 0,25 при преобразовании в дробь равно 1/4.
Вот еще один пример преобразования десятичной дроби в дробную:
Обратите внимание, что ответом на этот пример является смешанное число (целое число и дробь вместе взятые).
Если вам нужен быстрый и простой способ преобразования десятичных чисел в дроби, вы можете воспользоваться многочисленными бесплатными онлайн-калькуляторами преобразования десятичных чисел в дроби.
Этот бесплатный калькулятор десятичных дробей от www.calculatorsoup.com не только выполняет преобразование, но также показывает расчеты (используя трехэтапный метод, показанный выше), что является удобным инструментом, поскольку он не только поможет вам найти правильный ответ, но также понять процесс.
Чтобы использовать калькулятор преобразования десятичных дробей в дроби, просто введите десятичное значение и нажмите «Рассчитать».
В зависимости от введенного значения калькулятор преобразует десятичную дробь в дробь или смешанное число.
Существует также повторяющийся калькулятор десятичной дроби (для выполнения этой функции следуйте инструкциям на веб-странице).
Вы хотите узнать больше о работе с десятичными знаками и понять разрядность? Щелкните здесь для получения дополнительных бесплатных ресурсов
Вам нужно больше практики, чтобы научиться преобразовывать десятичную дробь в дробь? Следующий рабочий лист десятичной дроби и ключ к ответу дадут вам множество возможностей применить трехэтапный процесс для преобразования десятичной дроби в дробь.
Щелкните здесь, чтобы загрузить бесплатную таблицу преобразования десятичных дробей с ответами.
И если вы ищете более подробный урок о том, как преобразовать десятичную дробь в дробную, посмотрите этот бесплатный видео-урок десятичной дроби :
Поделитесь своими идеями, вопросами и комментариями ниже!
(Никогда не пропустите блог Mashup Math — щелкните здесь, чтобы получать наш еженедельный информационный бюллетень!)
Автор: Энтони Персико.