Нормальное распределение системы случайных величин: Нормальное распределение непрерывной случайной величины

Нормальное распределение системы случайных величин

3.1. Двумерное нормальное распределение

В теории вероятностей и её приложениях большую роль играет двумерное нормальное распределение. Плотность двумерной нормальной случайной величины (X,Y) имеет вид

(52)

Здесь — математические ожидания величинX и Y; — средние квадратичные отклонения величинX и Y; r – коэффициент корреляции величин X и Y.

Предположим, что случайные величины X и Y не коррелированы, то есть r=0. Тогда имеем:

(53)

Получили, что плотность распределения системы двух случайных величин (X,Y) равна произведению плотностей распределения компонент X и Y, а это значит, что X и Y – независимые случайные величины.

Таким образом, доказана следующая теорема: из некоррелированности нормально распределенных случайных величин следует их независимость. Поскольку из независимости любых случайных величин следует их некоррелированность, то можно сделать вывод, что термины «некоррелированные» и «независимые» величины для случая нормального распределения эквивалентны.

Приведём формулы для вероятности попадания нормально распределённой двумерной случайной величины в различные области на плоскости.

Пусть случайный вектор (X,Y), компоненты которого независимы, распределён по нормальному закону (53). Тогда вероятность попадания случайной точки (X,Y) в прямоугольник R, стороны которого параллельны координатным осям, равна

y R d c х a b

(54)

где — функция Лапласа.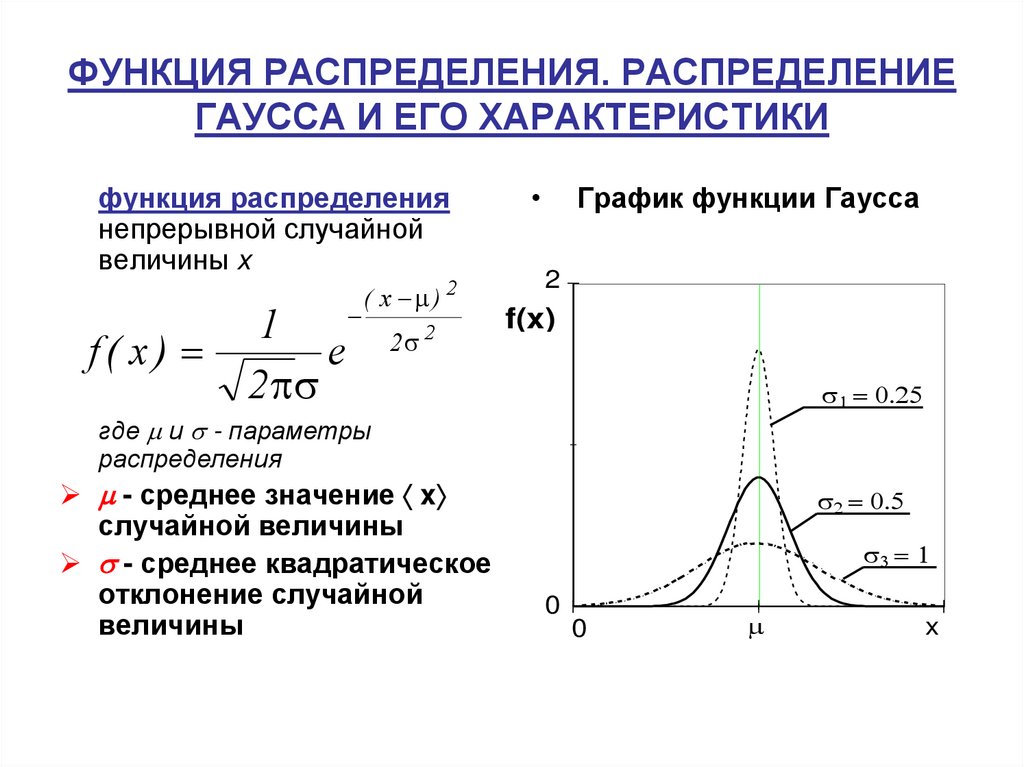 Эта функция табулирована.

Пусть плотность распределения нормального закона системы случайных величин (X,Y) задана в виде (52). Ясно, что данная плотность сохраняет постоянное значение на эллипсах:

(55)

где С – постоянная; на этом основании такие эллипсы носят название эллипсов равных вероятностей. Можно показать, что вероятность попадания точки (X,Y) внутрь эллипса равной вероятности равна

(56)

Пример 10. Случайные величины X и Y независимы и нормально распределены с Найти вероятность того, что случайная точка (X,Y) попадет в кольцо

Решение: Так как случайные величины X и Y независимы, то они не коррелированы и, следовательно, r = 0. Подставляя в (С), получаем

,

то есть эллипс равной вероятности выродился в круг равной вероятности. Тогда

Ответ: 0,1242.

3.2. Общий случай n-мерного нормального распределения

Плотность нормального распределения системы n случайных величин имеет вид:

, (57)

где — определитель матрицы С — обратной к ковариационной матрице;- математическое ожидание случайной величины Х_i — i-той компоненты n-мерного нормального случайного вектора.

Из общего выражения вытекают все формы нормального закона для любого числа измерений и для любых видов зависимости между случайными величинами. В частности, при

n = 2 ковариационная матрица имеет вид:

(58)

её определитель ; матрица С, обратная к ковариационной матрице,имеет вид

. (59)

Подставляя и элементы матрицы С в общую формулу (57), получаем формулу для нормального распределения на плоскости (52).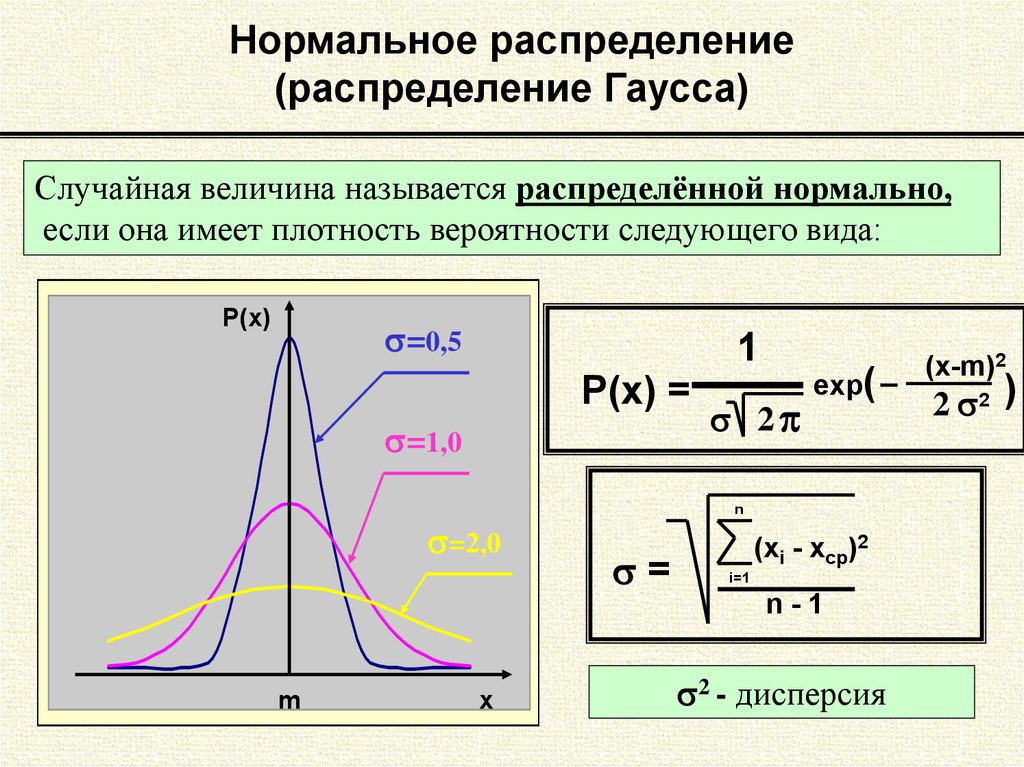

Если случайные величины независимы, то плотность распределения системыравна

. (60)

При n = 2 эта формула принимает вид (53).

Непрерывные случайные величины. Системы случайных величин. Функция двух случайных аргументов. Формула свертки. Устойчивость нормального распределения

§ 15. Непрерывные случайные величины.

o  Говорят, что случайная величина Х имеет плотность вероятности или плотность распределения вероятностей , если существует функция p(x) такая, что функция распределения  

(1).

Пример. Нужно определить массу стержня длины l, если плотность массы равна p(x).

                  

o  Случайная величина называется непрерывной, если она имеет плотность распределения.

Пусть р(х)—непрерывная функция. Тогда  Где , α—бесконечно малая величина при Δх→0.

Т.к. , при Δх→0. Таким образом, .

  .

Свойства плотности распределения.

Свойство 1.  .

Свойство 2.  Плотность распределения—неотрицательная функция: .

Поскольку F(x)—неубывающая функция, то F’(x)≥0. Следовательно —неотрицательная функция.

Геометрически это свойство означает, что график плотности распределения расположен либо над осью ох, либо на этой оси. График плотности распределения называют кривой распределения.

Свойство 3.  Несобственный интеграл от плотности распределения в пределах от -∞ до +∞ равен единице:

.

В формуле (1) подставим х=+∞, . Поскольку , то .

Свойство 4.  Вероятность того, что непрерывная случайная величина Х примет значение из множества В, равна интегралу по множеству В от плотности распределения.

.

Пример. Задана плотность вероятности случайной величины Х.

.

Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).

Искомая вероятность .

o  Говорят, что случайная величина Х равномерно распределена на отрезке [a, b], если она непрерывна и имеет плотность вероятности:

Найдем функцию распределения равномерно распределенной случайной величины X.

а) x<a

;

б) a≤x≤b

.

в) x>b

.

         

  Примером равномерно распределенной случайной величины может служить Х-координата точки, наудачу брошенной на [a, b].

o  Говорят, что случайная величина Х имеет показательное (экопоненциальное) распределение с параметром λ>0, если она непрерывна и имеет плотность распределения

; обозначают Х~M(λ).

Найдем функцию распределения показательно распределенной случайной величины Х.

а) x≤0

.

б) x>0

.

Таким образом

  Мы определили показательный закон с помощью плотности распределения. Ясно, что его можно определить, используя функцию распределения.

Пример. Непрерывная случайная величина Х распределена по показательному закону . Найти вероятность того, что в результате испытания Х попадет в интервал (0,3; 1).

1.  .

2.  .

o  Говорят, что случайная величинf Х имеет нормальное распределение с параметрами a, G², если она непрерывна и имеет плотность .

Обозначение Х~N(a, G²), те Х имеет нормальное распределение с параметрами a, G².

График плотности нормально распределенной случайной величины имеет вид:

o  Если случайная величина Х~N(0,1), то говорят, что случайная величина Х имеет стандартное нормальное распределение. В этом случае плотность обозначается . Через N(x) обозначим , где Х₀~N(0,1).

.

.

 

o  Любая функция (правило, характеристика), позволяющая вычислить вероятность того, что случайная величина Х принадлежит В—числовому множеству на прямой, т.е. P(XB), называется законом распределения

случайной величины Х.

1.  F(x)—функция распределения является законом распределения любой случайной величины. .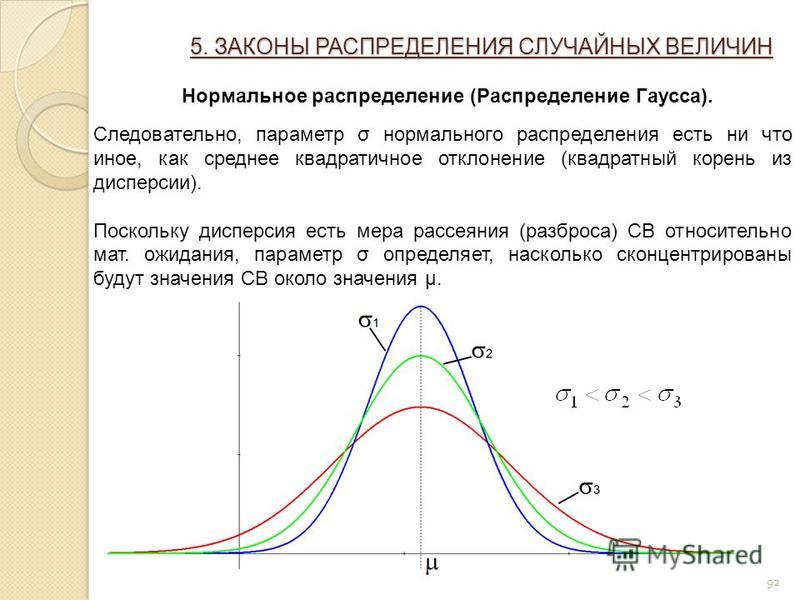

2.  Ряд распределения дискретной случайной величины также является законом  распределения дискретной случайной величины.

3.  Плотность распределения непрерывной случайной величины p(x) является законом распределения непрерывной случайной величины.

.

o  Математическим ожиданием или средним значением непрерывной случайной величины Х с плотностью p(x) называется число  при условии, что этот интеграл сходится абсолютно.

Пример 1. Пусть Х имеет равномерное распределение на [a, b].

   .

Пример 2. Пусть случайная величина Х~N(a, G²).

Поскольку . (интеграл от плотности φ(t)).

          Таким образом, , т.е. смысл параметра а—математическое ожидание случайной величины Х.

  Пример 3.

Найти математическое ожидание случайной величины Х, имеющей показательное распределение с параметром λ>0, т.е. X~M(λ)

    

o  Дисперсией непрерывной случайной величины Х называется число . Если случайная величина имеет плотность p(x), .

Математическоеожидание и дисперсия непрерывных случайных величин обладают теми же свойствами, что и для дискретных случайных величин.

Пример 4. Найти дисперсию случайной величины Х, распределенной равномерно на [a, b]:. Нашли, что .

Нормальные случайные величины » Биостатистика » Колледж общественного здравоохранения и медицинских профессий » Университет Флориды

• Наблюдения за нормальными распределениями
• Правило стандартного отклонения для нормальных случайных величин

CO-6:  Применять основные понятия вероятности, случайных вариаций и широко используемых статистических распределений вероятностей.

LO 6.2:

 Применить правило стандартного отклонения к частному случаю распределений, имеющих «нормальную» форму.

Видео:  Нормальные случайные величины (2:08)

В разделе «Исследовательский анализ данных» этого курса мы столкнулись с наборами данных, таких как продолжительность беременностей человека , распределение которых естественным образом следует симметричной унимодальной колоколообразной форме, выпуклые в середине и сужающиеся к концам.

Многие переменные, такие как продолжительность беременности, размер обуви, длина стопы и другие физические характеристики человека, обладают следующими свойствами: взять значение на такое же расстояние выше его среднего значения; форма колокола указывает на то, что значения, близкие к среднему, более вероятны, и становится все менее вероятным получение значений, далеких от среднего в любом направлении.

Конкретная форма, демонстрируемая этими переменными, изучалась с начала девятнадцатого века, когда их впервые назвали «нормальными», чтобы предположить, что они изображают общий, естественный паттерн.

Наблюдения за нормальными распределениями

Существует множество нормальных распределений. Несмотря на то, что все они имеют форму колокола, они различаются по центру и распространению.

Более конкретно, форма распределения определяется его означает  (mu, µ), а разброс определяется его стандартным отклонением (сигма, σ).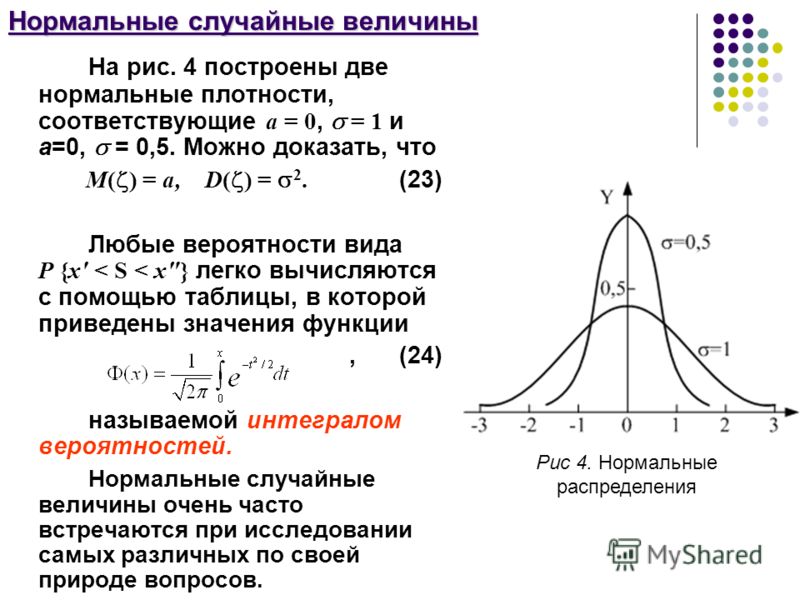

Глядя на этот график, мы можем сделать следующие наблюдения:

• Черная и красная нормальные кривые имеют средние значения или центры в μ = mu = 10. Однако красная кривая более растянута и, следовательно, имеет большую стандартное отклонение. Когда вы смотрите на эти две нормальные кривые, обратите внимание, что по мере того, как красный график сжимается, разброс становится больше, что позволяет площади под кривой оставаться неизменной.
• Черная и зеленая нормальные кривые имеют одинаковое стандартное отклонение или разброс (диапазон черной кривой составляет 6,5–13,5, а диапазон зеленой кривой — 10,5–17,5).

Еще более важным, чем тот факт, что многие переменные следуют нормальной кривой, является роль, которую нормальная кривая играет в теории выборки, как мы увидим в следующем разделе нашего модуля, посвященного вероятности.

Понимание нормального распределения является важным шагом в направлении нашей общей цели, которая состоит в том, чтобы связать средние или пропорции выборки со средними или пропорциями генеральной совокупности. Цель этого раздела — лучше понять нормальные случайные величины и их распределения.

Правило стандартного отклонения для нормальных случайных величин

Мы начали понимать нормальное распределение в разделе «Исследовательский анализ данных» (EDA), когда ввели правило стандартного отклонения (или правило 68-95-99,7 ) как значения в наборе выборочных данных нормальной формы ведут себя по отношению к их выборочному среднему (x-bar) и выборочному стандартному отклонению (s).

Это то же правило, которое определяет распределение нормальной случайной величины ведет себя относительно своего среднего значения (mu, μ) и стандартного отклонения (сигма, σ). Теперь мы используем вероятностный язык и нотацию для описания поведения случайной величины.

Например, в разделе EDA мы бы сказали: «68% беременностей в нашем наборе данных находятся в пределах 1 стандартного отклонения (s) от их среднего значения (x-столбец)». Аналогичным утверждением теперь было бы: «Если X, продолжительность случайно выбранной беременности, является нормальной со средним значением (mu, μ) и стандартным отклонением (сигма, σ), то

В общем, если X является нормальной случайной величиной, тогда вероятность равна

• 68%, что X находится в пределах 1 стандартного отклонения (сигма, σ) от среднего (mu, μ)
• 95% X находится в пределах 2 стандартных отклонений (сигма, σ) от среднего (mu, μ)
• 99,7 %, что X находится в пределах 3 стандартных отклонений (сигма, σ) от среднего значения (mu, μ).

Используя обозначение вероятности, мы можем написать

Комментарий

• Обратите внимание, что информацию из правила можно интерпретировать с точки зрения хвостов нормальной кривой:
  • Поскольку 0,68 — это вероятность оказаться в пределах 1 стандартного отклонения от среднего значения, (1 — 0,68)/2 = 0,16 — это вероятность того, что значение будет ниже среднего более чем на 1 стандартное отклонение (или выше среднего более чем на 1 стандартное отклонение). )
  • Аналогично, (1 – 0,95) / 2 = 0,025 – это вероятность того, что значение будет более чем на 2 стандартных отклонения ниже (или выше) среднего значения.
  • И (1 – 0,997) / 2 = 0,0015 – это вероятность того, что значение будет более чем на 3 стандартных отклонения ниже (или выше) среднего значения.
• Три рисунка ниже иллюстрируют это.

ПРИМЕР: Длина стопы

Предположим, что длина стопы случайно выбранного взрослого мужчины является нормальной случайной величиной со средним значением μ = mu = 11 и стандартным отклонением σ = сигма = 1,5. Тогда правило стандартного отклонения позволяет начертить распределение вероятностей X следующим образом:

(a)  Какова вероятность того, что случайно выбранный взрослый мужчина будет иметь длину стопы от 8 до 14 дюймов?

0,95 или 95%.

(b)  Взрослый мужчина почти гарантированно (вероятность 0,997) будет иметь длину стопы между какими двумя значениями?

6,5 и 15,5 дюймов.

(c)  Вероятность того, что длина стопы взрослого мужчины будет больше, чем на сколько дюймов, составляет всего 2,5%?

14. (см. изображение ниже)

Теперь вы должны попробовать несколько. (Используйте рисунок непосредственно перед часть (а)  , чтобы помочь вам.)

Учитесь, делая: Использование правила стандартного отклонения

Комментарий

• Обратите внимание, что есть два типа задач, которые мы можем решить: такие, как (a)
0 , 9 (г) и (д) , в которых задан конкретный интервал значений нормальной случайной величины, и нас просят найти вероятность, и такие, как (б) , (в) и (f) , в котором задается вероятность, и нас просят определить, какими будут нормальные значения случайной величины.

Я понял?:  Используя правило стандартного отклонения

Учитесь на практике: Нормальные случайные величины

Вернемся к нашему примеру длины стопы:

длина стопы мужчины должна быть больше 13 дюймов?

Поскольку 13 дюймов не отличаются точно на 1, 2 или 3 стандартных отклонения от среднего значения, мы могли бы дать только очень грубую оценку вероятности в этой точке.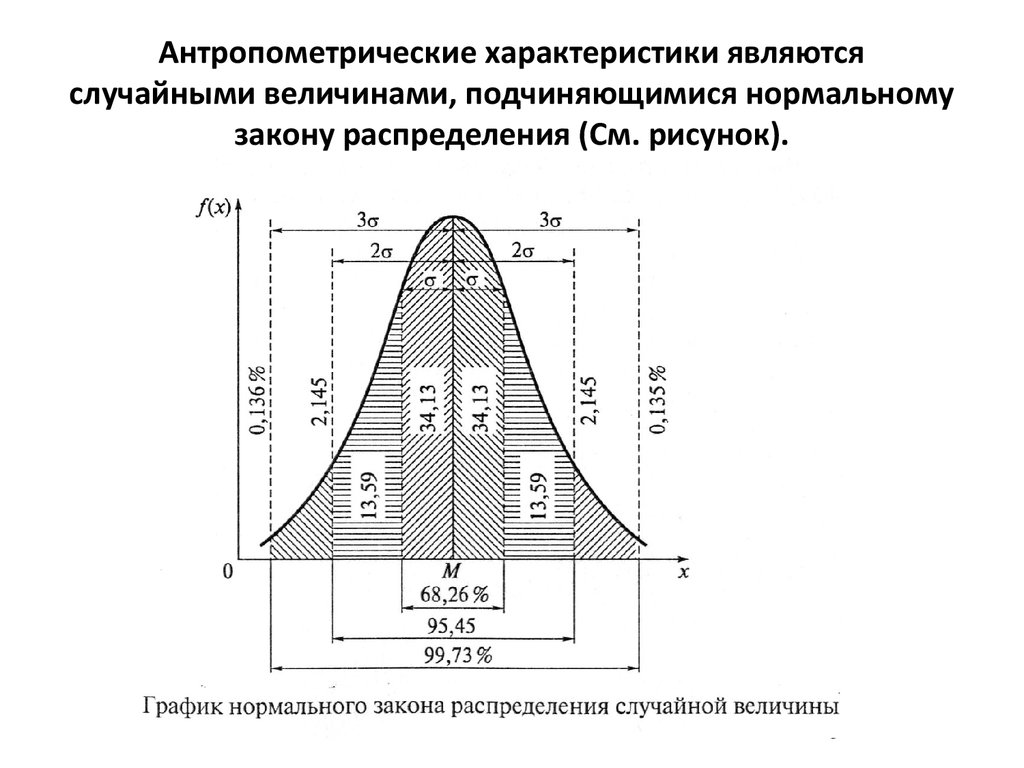

Ясно, что правило стандартного отклонения описывает только верхушку айсберга, и хотя оно хорошо служит введением в нормальную кривую и дает нам хорошее представление о том, какие значения можно считать вероятными, а какие маловероятными, оно очень ограничено в вероятностные вопросы, на которые он может помочь нам ответить.

Вот еще одно знакомое нормальное распределение:

ПРИМЕР: Результаты SAT

Предположим, нас интересует вероятность того, что случайно выбранный студент наберет 633 или более баллов по математической части своего SAT (это представлено по красной области). Опять же, 633 не падает ровно на 1, 2 или 3 стандартных отклонения выше среднего.

Обратите внимание, однако, что результат SAT 633 и длина стопы 13 составляют примерно 1/3 пути между 1 и 2 стандартными отклонениями. Продолжая читать, вы поймете, что это позиционирование относительно среднего является ключом к нахождению вероятностей.

Нормальное распределение | Примеры, формулы и использование

Опубликован в 23 октября 2020 г. к Прита Бхандари. Отредактировано 25 ноября 2022 г.

При нормальном распределении данные распределяются симметрично без перекоса. При нанесении на график данные имеют форму колокола, при этом большинство значений группируются вокруг центральной области и сужаются по мере удаления от центра.

Нормальные распределения также называют распределениями Гаусса или кривыми нормального распределения из-за их формы.

Содержание

1. Почему нормальное распределение имеет значение?
2. Каковы свойства нормального распределения?
3. Эмпирическое правило
4. Центральная предельная теорема
5. Формула нормальной кривой
6. Что такое стандартное нормальное распределение?
7. Часто задаваемые вопросы о нормальном распределении

Почему нормальное распределение имеет значение?

Все виды переменных в естественных и социальных науках нормально или приблизительно нормально распределены. Рост, вес при рождении, умение читать, удовлетворенность работой или результаты SAT — вот лишь несколько примеров таких переменных.

Поскольку нормально распределенные переменные очень распространены, многие статистические тесты предназначены для нормально распределенных совокупностей.

Понимание свойств нормального распределения означает, что вы можете использовать статистику логического вывода для сравнения различных групп и делать оценки совокупности с использованием выборок.

Каковы свойства нормального распределения?

Нормальные распределения имеют ключевые характеристики, которые легко заметить на графиках:

• Среднее значение, медиана и мода совпадают.
• Распределение симметрично относительно среднего — половина значений ниже среднего и половина выше среднего.
• Распределение можно описать двумя значениями: средним значением и стандартным отклонением.

Среднее значение — это параметр местоположения, а стандартное отклонение — параметр масштаба.

Среднее значение определяет центр пика кривой. Увеличение среднего значения сдвигает кривую вправо, а уменьшение — влево.

Стандартное отклонение растягивает или сжимает кривую. Небольшое стандартное отклонение приводит к узкой кривой, а большое стандартное отклонение приводит к широкой кривой.

Эмпирическое правило

Эмпирическое правило , или правило 68-95-99,7, говорит вам, где находится большинство ваших значений в нормальном распределении:

• Около 68% значений находятся в пределах 1 стандартного отклонения от среднего.
• Около 95% значений находятся в пределах 2 стандартных отклонений от среднего значения.
• Около 99,7% значений находятся в пределах 3 стандартных отклонений от среднего значения.

Пример: Использование эмпирического правила в нормальном распределенииВы собираете баллы SAT от учащихся на новом курсе подготовки к экзаменам. Данные подчиняются нормальному распределению со средним значением ( M ) 1150 и стандартным отклонением ( SD ) 150.

Следуя эмпирическому правилу:

• Около 68% баллов находятся в диапазоне от 1000 до 1300, что на 1 стандартное отклонение выше и ниже среднего.
• Около 95% баллов находятся в диапазоне от 850 до 1450, что на 2 стандартных отклонения выше и ниже среднего.
• Около 99,7% баллов находятся в диапазоне от 700 до 1600, что на 3 стандартных отклонения выше и ниже среднего.

Эмпирическое правило — это быстрый способ получить обзор ваших данных и проверить любые выбросы или экстремальные значения, которые не соответствуют этому шаблону.

Если данные из небольших выборок не соответствуют этой схеме, то другие распределения, такие как t-распределение, могут быть более подходящими. Как только вы определите распределение вашей переменной, вы можете применить соответствующие статистические тесты.

Центральная предельная теорема

Центральная предельная теорема является основой того, как нормальные распределения работают в статистике.

В исследованиях, чтобы получить хорошее представление о среднем значении популяции, в идеале вы должны собирать данные из нескольких случайных выборок в популяции. Распределение выборки среднего значения является распределением средних значений этих различных выборок.

Центральная предельная теорема показывает следующее:

• Закон больших чисел: по мере увеличения размера выборки (или количества выборок) среднее значение выборки будет приближаться к среднему значению генеральной совокупности.
• При наличии нескольких больших выборок выборочное распределение среднего имеет нормальное распределение, даже если ваша исходная переменная не имеет нормального распределения.

Параметрические статистические тесты обычно предполагают, что выборки поступают из нормально распределенных совокупностей, но центральная предельная теорема означает, что это допущение не обязательно выполнять при наличии достаточно большой выборки.

Вы можете использовать параметрические тесты для больших выборок из совокупностей с любым типом распределения, если выполняются другие важные предположения. Размер выборки 30 и более обычно считается большим.

Для небольших выборок предположение о нормальности важно, поскольку выборочное распределение среднего значения неизвестно. Чтобы получить точные результаты, вы должны быть уверены, что популяция распределена нормально, прежде чем вы сможете использовать параметрические тесты с небольшими выборками.

Формула нормальной кривой

Когда у вас есть среднее значение и стандартное отклонение нормального распределения, вы можете подогнать к вашим данным нормальную кривую, используя функцию плотности вероятности .

В функции плотности вероятности площадь под кривой говорит о вероятности. Нормальное распределение представляет собой распределение вероятностей , поэтому общая площадь под кривой всегда равна 1 или 100%.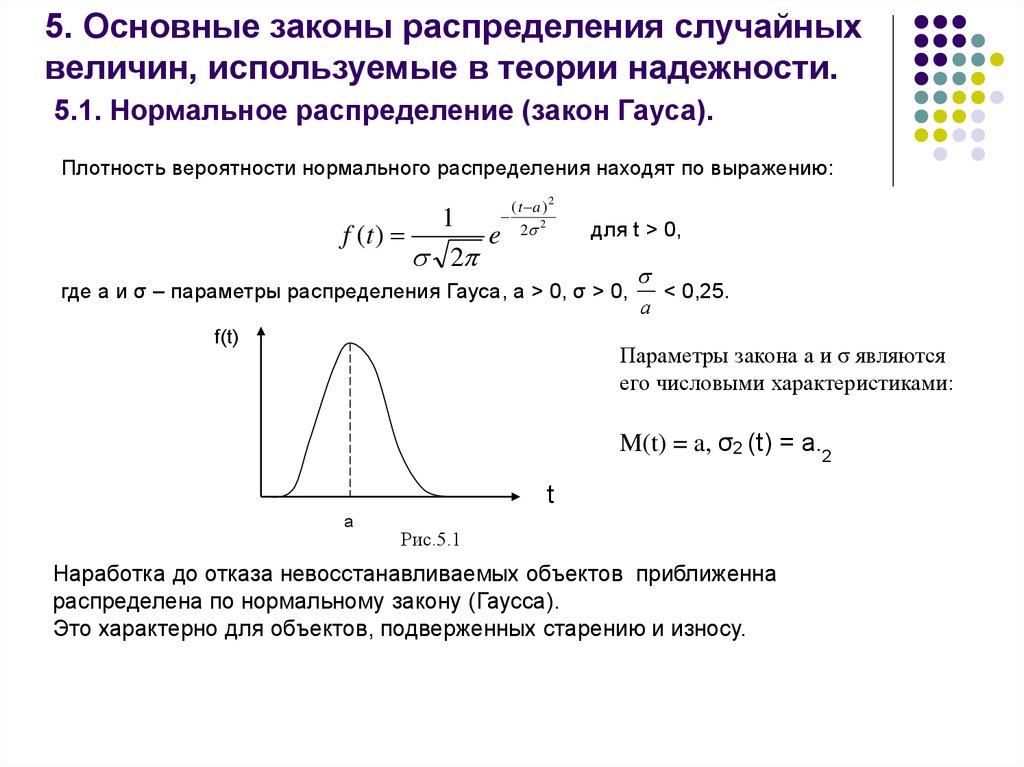

Формула для нормальной функции плотности вероятности выглядит довольно сложной. Но чтобы использовать его, вам нужно знать только среднее значение генеральной совокупности и стандартное отклонение.

Для любого значения x вы можете подставить среднее значение и стандартное отклонение в формулу, чтобы найти плотность вероятности переменной, принимающей это значение х .

Формула плотности нормальной вероятности	Пояснение
	f ( x ) = вероятность x = значение переменной мк = среднее значение σ = стандартное отклонение σ 2 = дисперсия

Пример: использование функции плотности вероятностиВы хотите узнать вероятность того, что баллы SAT в вашей выборке превысят 1380.

На вашем графике функции плотности вероятности вероятность — это заштрихованная область под кривой, расположенной справа от того места, где ваш результат SAT равен 1380.

Вы можете найти значение вероятности этой оценки, используя стандартное нормальное распределение.

Что такое стандартное нормальное распределение?

Стандартное нормальное распределение , также называемое z -распределением , представляет собой специальное нормальное распределение, где среднее значение равно 0, а стандартное отклонение равно 1.

Каждое нормальное распределение представляет собой версию стандартного нормального распределения, которая была растянута или сжата и перемещена по горизонтали вправо или влево.

В то время как отдельные наблюдения из нормального распределения обозначаются как x , они обозначаются как z в распределении z . Любое нормальное распределение можно преобразовать в стандартное нормальное распределение, превратив отдельные значения в z -баллов.

Z -оценки показывают, на сколько стандартных отклонений от среднего лежит каждое значение.

 

Вам нужно знать только среднее значение и стандартное отклонение вашего распределения, чтобы найти z -оценку значения.

Z — формула счета	Пояснение
	x = индивидуальное значение мк = среднее значение σ = стандартное отклонение

Мы конвертируем нормальное распределение в стандартное нормальное распределение по нескольким причинам:

• Чтобы найти вероятность наблюдений в распределении выше или ниже заданного значения.
• Чтобы найти вероятность того, что среднее значение выборки значительно отличается от известного среднего значения генеральной совокупности.
• Для сравнения оценок по разным распределениям с разными средними значениями и стандартными отклонениями.

Нахождение вероятности с помощью

з -распределение

Каждая z -оценка связана с вероятностью, или p -значением, которая сообщает вам вероятность появления значений ниже этой z -оценки. Если вы преобразуете отдельное значение в z -значение, вы можете затем найти вероятность того, что все значения до этого значения встречаются в нормальном распределении.

Пример: Нахождение вероятности с использованием распределения z 0266 z — счет.

Среднее значение нашего распределения равно 1150, а стандартное отклонение равно 150. z -оценка показывает, на сколько стандартных отклонений от 1380 от среднего значения.

Формула	Расчет

Для z -значения 1,53 значение p равно 0,937. Это вероятность того, что баллы SAT будут равны 1380 или меньше (93,7%), и это область под кривой слева от заштрихованной области.

Чтобы найти заштрихованную площадь, нужно от 1 отнять 0,937, то есть общую площадь под кривой.

Вероятность x > 1380 = 1 – 0,937 = 0,063

Это означает, что, вероятно, только 6,3% баллов SAT в вашей выборке превышают 1380.

Часто задаваемые вопросы о нормальном распределении

Что такое нормальное распределение?

При нормальном распределении данные распределяются симметрично без перекоса. Большинство значений группируются вокруг центральной области, при этом значения сужаются по мере удаления от центра.

Меры центральной тенденции (среднее, мода и медиана) в нормальном распределении точно такие же.

Что такое эмпирическое правило?

Эмпирическое правило, или правило 68-95-99,7, говорит вам, где большинство значений находится в нормальном распределении:

• Около 68% значений находятся в пределах 1 стандартного отклонения от среднего.
• Около 95% значений находятся в пределах 2 стандартных отклонений от среднего значения.
• Около 99,7% значений находятся в пределах 3 стандартных отклонений от среднего значения.

Эмпирическое правило — это быстрый способ получить обзор ваших данных и проверить любые выбросы или экстремальные значения, которые не соответствуют этому шаблону.

Что такое t-распределение?

t -распределение — это способ описания набора наблюдений, где большинство наблюдений падают близко к среднему, а остальные наблюдения составляют хвосты с обеих сторон. Это тип нормального распределения, используемый для небольших выборок, когда дисперсия данных неизвестна.

Распределение t образует колоколообразную кривую при нанесении на график.

No related posts.