Тест на проверку сообразительности и логики «Тренировка для мозга» — справитесь с непростыми заданиями?. Dropi
/ Автор: Мария
Проявите логическое мышление и внимательность, потренировав свой мозг — для этого достаточно провести сравнительно немного времени в поисках ответов к заданиям-головоломкам. Ваше потраченное время окупится пользой для интеллекта — более живым и острым умом, который не боится логических квестов!
Тесты IQ #логика
Вопрос 1 из 15
Каким числом нужно заменить вопросительный знак?
9
10
11
12
Вопрос 2 из 15
Угадайте слово, которое обозначает то же, что и определения за скобками: ЧУВСТВО МЕРЫ (.
 1c» data-question-id=»q!*0()8$xc4v» data-test-id=»3111″ data-post-id=»7676″ data-answer-count=»674″> 5
1c» data-question-id=»q!*0()8$xc4v» data-test-id=»3111″ data-post-id=»7676″ data-answer-count=»674″> 56
Вопрос 7 из 15
Каков результат уравнения: 77 + (88 х 2) =
223
243
253
257
Вопрос 8 из 15
Каков результат уравнения: (33 х 20) + (52 х 2) =
667
764
746
674
Вопрос 9 из 15
Какой буквой следует заменить знак вопроса: Г, Ё, ?, С, Ъ
К
Л
М
Н
Вопрос 10 из 15
Укажите лишнюю фигуру:
1
2
3
4
5
Вопрос 11 из 15
Найдите фигуру, которая отличается от остальных.

1
2
3
4
5
6
Вопрос 12 из 15
Какая фигура следующая?
А
Б
В
Г
Д
Вопрос 13 из 15
Укажите слово, образующее новые слова со следующими начальными буквами:
ЗОВ
ВОЛ
КОЛ
АУЛ
РОД
Вопрос 14 из 15
Какой фигуры не хватает?
1
2
3
4
5
6
Вопрос 15 из 15
Укажите подходящее число:
55
56
58
Комментарии
3-8Видео-урок: Законы экспоненты
Стенограмма видео
В этом видео мы научимся
применять законы показателей для умножения и деления степеней, а также как вычислить
мощность возведена в степень. Мы подведем итоги и пойдем
через некоторые вопросы, в том числе вопрос, который выглядит так. Используя законы экспонент, мы будем
посмотрите, как такие вопросы можно сделать намного более управляемыми. Начнем с того, что вспомним основы
показателей или степеней.
Мы подведем итоги и пойдем
через некоторые вопросы, в том числе вопрос, который выглядит так. Используя законы экспонент, мы будем
посмотрите, как такие вопросы можно сделать намного более управляемыми. Начнем с того, что вспомним основы
показателей или степеней.
Небольшой номер здесь часто
называется индексом или показателем степени. Три в четвертой степени или
три в степени четыре означает, что у нас есть четыре тройки, все умноженные
все вместе. Мы могли бы рассчитать стоимость
это несколькими способами. Мы могли бы начать с умножения трех
умножить на три, что равно девяти. Умножение девяти еще на три
даст нам 27. А затем умножив 27 на
последние три дали бы нам 81. В качестве альтернативы мы могли бы получить
трижды три, что равно девяти, и умножается на второй лот в три раза
три, что снова девять. И девять умножить на девять равно
81. Итак, давайте посмотрим, что
происходит, когда мы умножаем два значения с показателями степени.
И девять умножить на девять равно
81. Итак, давайте посмотрим, что
происходит, когда мы умножаем два значения с показателями степени.
Заполните пропуск: Минус два до умножение на минус два в седьмой степени в пятой степени равно минус два в сила чего.
В этом вопросе нас просят
найдите индекс или степень, в которую будут возведены отрицательные два в ответе. Мы можем начать с размышлений о том, что
как будет выглядеть значение минус два в седьмой степени. Это означало бы, что у нас будет
минус два семь раз. И все это было бы
умноженные вместе. Точно так же минус два в
пятая степень означает, что у нас есть пять отрицательных двоек, умноженных вместе. И наша отрицательная двойка до седьмого
мощность умножается на наши отрицательные два в пятой степени. Итак, это означает, что наши семь отрицательных
двойки умножаются на наши пять отрицательных двоек.
Итак, сколько отрицательных двоек у нас получил в общей сложности сейчас? Ну, теперь у нас есть 12, что означает что мы могли бы записать это как отрицательное число два, возведенное в степень 12. Итак, наше отсутствующее значение показателя степени равно 12. Мы могли бы также ответить на этот вопрос используя правило экспоненты, что 𝑥 в степени 𝑎 умножается на 𝑥 в степени 𝑏 равно 𝑥 в степени 𝑎 плюс 𝑏. Значение 𝑥 в оригинале вопрос будет отрицательным два; наши два показателя степени 𝑎 и 𝑏 равны семи и пяти. Таким образом, наше значение показателя степени в конце равно равно 𝑎 плюс 𝑏, что будет семь плюс пять, что дает нам 12, подтверждая наше оригинальный ответ.
В этом вопросе мы впервые увидели
экспоненциальное правило, согласно которому 𝑥 в степени 𝑎, умноженное на 𝑥 в степени 𝑏, равно
равно 𝑥 в степени 𝑎 плюс 𝑏.
В следующем вопросе у нас будет посмотрите на деление значений с показателями.
Три в 74-й степени три в 75-й степени больше, меньше или равно трем?
Давайте начнем этот вопрос с
думая о том, что будет три в 74-й степени и три в 75-й степени
на самом деле задействовать. Мы можем вспомнить, что, например,
три в четвертой степени означает, что мы пишем три четыре раза и умножаем
все вместе. Итак, три в 74-й степени означает
что будет 74 жребия по три, умноженных вместе.
Мы можем отменить первый тройки и вторые две тройки и так далее, пока мы не отменили 74 тройки на числитель и знаменатель, оставив нам только три на знаменатель. Мы знаем, что это будет эквивалентно одной трети. Итак, три в 74-й степени три в 75-й степени равно одной трети. Есть еще один способ, которым мы могли бы хотя бы это вычислил. Частное правило показателей говорит нам, что 𝑥 в степени 𝑎 над 𝑥 в степени 𝑏 равно 𝑥 в степени из 𝑎 минус 𝑏.
Здесь значение 𝑥 будет
три, и наши два показателя степени 𝑎 и 𝑏 будут равны 74 и 75. Таким образом, наш ответ здесь будет три
в степени 74 минус 75. И это эквивалентно трем в
сила негатива. Три в степени минус один
является обратной величиной трех, и это то же самое, что одна треть. Наш вопрос спрашивает, если это
больше, меньше или равно трем. Одна треть меньше трех. И таков наш ответ.
Таким образом, наш ответ здесь будет три
в степени 74 минус 75. И это эквивалентно трем в
сила негатива. Три в степени минус один
является обратной величиной трех, и это то же самое, что одна треть. Наш вопрос спрашивает, если это
больше, меньше или равно трем. Одна треть меньше трех. И таков наш ответ.
Мы можем сделать паузу на секунду и добавить
этот второй частный закон к нашим законам показателей. 𝑥 в степени 𝑎 над 𝑥 в
мощность 𝑏 равна 𝑥 степени 𝑎 минус 𝑏. Мы, конечно, можем видеть
эквивалентный вопрос, написанный вместо знака деления, 𝑥 в степени 𝑎
разделить на 𝑥 в степени 𝑏. Значение этого по-прежнему будет
такой же. До сих пор мы видели, что происходит
когда мы умножаем значения с показателями и делим значения с показателями. Но что происходит, когда мы берем
сила власти? Узнаем в следующем
вопрос.
Найдите значение минус три в третья степень, умноженная на три в квадрате в третьей степени.
В этом вопросе мы видим, что наши значения здесь — это значения, которые имеют показатели степени или степени. Стоит отметить, что формулировка «найти значение» означает, что мы не ищем ответ, который имеет экспонента. Например, если мы обнаружили, что это было три в третьей степени, то вместо этого нам нужно было бы дать ответ как 27. Мы можем вспомнить, что отрицательная тройка в третьей степени означает, что у нас есть три множества отрицательных трех, умноженных все вместе. Когда мы смотрим на три в квадрате в третьей степени, мы можем вспомнить, что три в квадрате означает трижды три. И поэтому пишу это третьему власть означает, что у нас есть три раза три три раза.
Все становится довольно
сложно сказать. Итак, давайте сравним это с правилом
что у нас есть для нахождения силы власти.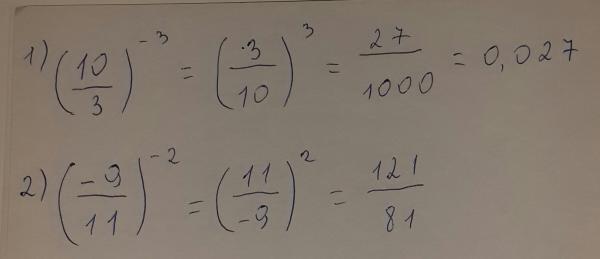 В этом случае 𝑥 в степени 𝑎
в степени 𝑏 равно 𝑥 в степени 𝑎𝑏. Если мы посмотрим на три в квадрате на
третья степень, наше значение три здесь является нашим 𝑥-значением. Таким образом, наш ответ будет три на
степень два умножить на три, три в степени шесть. И мы действительно написали шесть лотов
три, и мы умножили вместе. Итак, давайте вычислим нашу ценность, когда мы
есть минус три в третьей степени, умноженные на три в квадрате в третьей степени
степени или три в степени шесть.
В этом случае 𝑥 в степени 𝑎
в степени 𝑏 равно 𝑥 в степени 𝑎𝑏. Если мы посмотрим на три в квадрате на
третья степень, наше значение три здесь является нашим 𝑥-значением. Таким образом, наш ответ будет три на
степень два умножить на три, три в степени шесть. И мы действительно написали шесть лотов
три, и мы умножили вместе. Итак, давайте вычислим нашу ценность, когда мы
есть минус три в третьей степени, умноженные на три в квадрате в третьей степени
степени или три в степени шесть.
Начнем с отрицательной тройки
умножить на минус три. Мы знаем, что два отрицательных значения
умножение даст нам положительное значение, поэтому мы начнем с девяти. Затем умножаем на следующее
отрицательное три и девять раз отрицательное три равно отрицательному 27. Продолжая умножать на три, мы
отрицательное 27 умножить на три, что равно отрицательному 81. Мы можем продолжать умножать на
три, опуская наши тройки, пока мы не получим окончательный ответ.
Мы можем продолжать умножать на
три, опуская наши тройки, пока мы не получим окончательный ответ.
Стоит отметить, что есть, конечно, ряд способов, которыми мы могли бы умножиться. Мы знаем, что отрицательное три раза минус три раза минус три минус 27 и трижды трижды три равно 27. Итак, умножив минус 27 на 27 дало бы нам отрицательные 729, и умножение этого числа на 27 также дало бы нам значение минуса 19683. И это будет наш окончательный ответ для значения отрицательного числа три в третьей степени, умноженное на три в квадрате в третьей степени мощность.
Давайте сделаем паузу на минуту, чтобы обновить
наши заметки. Мы увидели, что можем взять власть
степени, такой как 𝑥 в степени 𝑎 в степени 𝑏, путем умножения
степени, чтобы дать нам 𝑥 в степени 𝑎𝑏. До сих пор в этом видео мы
глядя на целые числа, возведенные в степень. Теперь давайте посмотрим на некоторые
дроби, возведенные в степень.
Теперь давайте посмотрим на некоторые
дроби, возведенные в степень.
Что из следующего равно минус полтора в третьей степени умножить на минус полтора в квадрате? Вариант (А) семь и 19старше 32 лет, вариант (B) минус семь и 19 больше 32, вариант (C) 32 больше 243, вариант (D) отрицательный 3125 вместо 1024 или вариант (E) отрицательный 243.
В этом вопросе нас просят умножьте эти два значения на показатели степени. Когда мы работаем с дробями и писать их с показателями, всегда полезно убедиться, что дроби записываются в виде толстых или неправильных дробей, а не в виде смешанных количество. В обоих этих случаях имеем минус полтора. И поэтому мы можем записать это как минус три больше двух в третьей степени умножить минус три больше двух в квадрате.
Полезно запомнить товар
Закон показателей, когда мы умножаем значение 𝑥 в степень 𝑎 на 𝑥 в
сила 𝑏. Затем мы добавляем показатели, чтобы дать
возьмем значение 𝑥 в степени 𝑎 плюс 𝑏. В этом случае наше 𝑥-значение будет
минус три на два, и наш показатель степени можно рассчитать, добавив наши индексы
три и два, что дает нам пять. Итак, у нас есть минус три на два
в степени пять. То, что мы сделали, упростилось
наш расчет, чтобы дать значение с показателем степени. Однако, если мы посмотрим на ответ
варианты, то, что мы ищем здесь, это фактически найти значение отрицательных трех
больше двух в пятой степени.
Затем мы добавляем показатели, чтобы дать
возьмем значение 𝑥 в степени 𝑎 плюс 𝑏. В этом случае наше 𝑥-значение будет
минус три на два, и наш показатель степени можно рассчитать, добавив наши индексы
три и два, что дает нам пять. Итак, у нас есть минус три на два
в степени пять. То, что мы сделали, упростилось
наш расчет, чтобы дать значение с показателем степени. Однако, если мы посмотрим на ответ
варианты, то, что мы ищем здесь, это фактически найти значение отрицательных трех
больше двух в пятой степени.
Разбираемся в том, что на самом деле
означает иметь минус три больше двух в пятой степени, это означает, что у нас есть пять
много отрицательных трех на два, все умноженные вместе. Вкратце, когда мы
работая с дробью, такой как минус три на два, есть несколько способов
что мы можем записать это, во-первых, со знаком минус перед дробью или
с минусом три в числителе или с минусом внизу, чтобы сделать
минус два. Хотя окончательная форма
математически правильно, мы склонны либо иметь отрицательный знак в числителе, либо
вне фракции.
Хотя окончательная форма
математически правильно, мы склонны либо иметь отрицательный знак в числителе, либо
вне фракции.
Возвращаясь к проблеме, мы можно представить это как гигантскую дробь с пятью лотами, умноженными на три отрицательных числа. в числителе и пяти лотах по два, умноженных на знаменатель. Таким образом, вычисляя значение, отрицательное три раза отрицательное три равно девяти. Еще один минус трижды другая отрицательная тройка равна девяти. Девять раз девять равно 81. И 81 раз минус три дает минус 243 в числителе. В знаменателе мы знаем, что два раза два равно четырем, четыре раза четыре равно 16, а умножение еще на два дает нам 32 в знаменателе.
Теперь нам нужно написать наш неправильный
дробь отрицательного числа 243 на 32 в виде смешанного числа. Когда мы выполняем длинное деление
243 разделить на 32, мы получим значение семь с остатком 19. Значение семь представляет собой
целая часть нашего ответа. Остаток образует числитель
нашей фракции. А так как мы поделили на 32, то
это будет наш знаменатель. Мы не должны забывать, что мы были
деление минус 243 на 32. Таким образом, наше значение будет минус семь
и 19старше 32. Мы видим, что это ответ
дано в варианте (Б).
Значение семь представляет собой
целая часть нашего ответа. Остаток образует числитель
нашей фракции. А так как мы поделили на 32, то
это будет наш знаменатель. Мы не должны забывать, что мы были
деление минус 243 на 32. Таким образом, наше значение будет минус семь
и 19старше 32. Мы видим, что это ответ
дано в варианте (Б).
Теперь рассмотрим один последний вопрос, связанный с показателями.
Вычислить минус три и a в пятой степени в седьмой степени умножить на минус полтора в шестой степени минус 16 больше пяти в шестой степени, умноженное на минус три больше двух в четвертой степени власть, давая ваш ответ в его простейшей форме.
Хотя этот вопрос может выглядеть
довольно сложно, мы собираемся начать с того, что запишем смешанные числа как неправильные
дроби, а затем посмотреть, какие законы экспоненты мы могли бы применить. Начнем со смешанного числа
минус три и одна пятая. Целая часть числа три
составленный из трех пяти пятых плюс одна пятая оставшаяся часть, даст нам шестнадцать
пятые. Мы имели дело не только с тремя
и пятый; это было минус три и пятая. Таким образом, у нас будет минус 16 на пять.
в седьмой степени.
Начнем со смешанного числа
минус три и одна пятая. Целая часть числа три
составленный из трех пяти пятых плюс одна пятая оставшаяся часть, даст нам шестнадцать
пятые. Мы имели дело не только с тремя
и пятый; это было минус три и пятая. Таким образом, у нас будет минус 16 на пять.
в седьмой степени.
Далее минус полтора эквивалентно отрицательным трем на два, и это в шестой степени. Мы можем сохранить знаменатель, как это так как наши дроби здесь неуместны и не смешаны. На данный момент, мы могли бы надеяться начинают замечать что-то в том, что мы написали. Мы видим, что у нас отрицательный 16 больше пяти в числителе и знаменателе. А еще у нас есть отрицательная тройка больше двух в числителе и знаменателе. На этом этапе мы можем начать подумайте, можем ли мы сократить верхнюю и нижнюю часть этой дроби.
Рассмотрим первую часть
эта дробь. Мы можем использовать показатель степени
закон 𝑥 в степени 𝑎 над 𝑥 в степени 𝑏 равно 𝑥 в степени 𝑎
минус 𝑏, потому что у нас одно и то же значение, которое возведено в степень. Это наша ценность 𝑥. В нашем ответе будет наш 𝑥. Это минус 16 против пяти рейзов
к власти. Чтобы вычислить эту мощность, мы имеем
семь отнять шесть, что дает нам один. Отрицательное 16 больше пяти в степени
из одного такое же, как отрицательное 16 на пять.
Мы можем использовать показатель степени
закон 𝑥 в степени 𝑎 над 𝑥 в степени 𝑏 равно 𝑥 в степени 𝑎
минус 𝑏, потому что у нас одно и то же значение, которое возведено в степень. Это наша ценность 𝑥. В нашем ответе будет наш 𝑥. Это минус 16 против пяти рейзов
к власти. Чтобы вычислить эту мощность, мы имеем
семь отнять шесть, что дает нам один. Отрицательное 16 больше пяти в степени
из одного такое же, как отрицательное 16 на пять.
Теперь упростим вторую часть
этой фракции. Используя то же правило показателей для
упростить отрицательную тройку над двумя в шестой степени отрицательную тройку над двумя до
четвертая степень дает нам минус три в квадрате два, помня, что
квадрат получается из шести вычесть четыре. Итак, теперь у нас есть упрощенный
расчет, минус 16 на пять раз минус три на два в квадрате. Если мы посмотрим на отрицательную тройку
два в квадрате, это эквивалентно отрицательным трем в квадрате числителя и двум
в квадрате знаменателя. Это потому, что мы можем применить
экспоненциальный закон 𝑥 над 𝑦 в степени 𝑎 равен 𝑥 в степени 𝑎 над 𝑦 в
сила 𝑎.
Это потому, что мы можем применить
экспоненциальный закон 𝑥 над 𝑦 в степени 𝑎 равен 𝑥 в степени 𝑎 над 𝑦 в
сила 𝑎.
Итак, давайте упростим то, что мы можем в наш расчет. Минус три в квадрате это девять и два в квадрате четыре. Мы можем умножать дроби на умножая числители и знаменатели, но перед этим заметим, что мы можем упростить это. Четыре является общим фактором обоих минус 16 и четыре. Таким образом, мы вычисляем отрицательное значение четыре раза девять, что составляет отрицательное число 36. И пять раз один дает нам 5. Итак, наш окончательный ответ отрицательный 36 более пяти. Также было бы справедливо дайте наш ответ как минус семь и одна пятая.
Теперь мы можем обобщить то, что мы
узнал в этом видео. Мы видели, что существует ряд
законы, которые мы можем использовать при работе с показателями.
