Производная косинуса синуса тангенса котангенса: тангенса, синуса, косинуса и других

Производная тангенса, синуса, косинуса, котангенса, арксинуса, арккосинуса и арктангенса

Из курса геометрии и математики школьники привыкли, что понятие производной доносится до них через площадь фигуры, дифференциалы, пределы функций, а также лимиты. Попробуем посмотреть на понятие производной под другим углом, и определить, как можно увязать производную и тригонометрические функции.

Содержание

• 1 Понятие производной
• 2 Производная и тригонометрические функции
• 3 Формулы производных для тригонометрических функций

Понятие производной

Итак, рассмотрим некую произвольную кривую, которая описывается абстрактной функцией y = f(x).

Представим что график — это карта туристического маршрута. Приращение ∆x (дельта икс) на рисунке — это определенный промежуток пути, а ∆y – это изменение высоты тропы над уровнем моря.
Тогда получается, что отношение ∆x/∆y будет характеризовать сложно маршрута на каждом отрезке пути. Узнав это значение можно с уверенностью сказать крутой ли подъем/спуск, понадобится ли альпинистское снаряжение и нужна ли туристам определенная физическая подготовка. Но показатель этот будет справедлив только для одного маленького промежутка ∆x.

Если организатор похода возьмет значения для начальной и конечной точек тропы, то есть ∆x – будет равен длине маршрута, то не сможет получить объективные данные о степени сложности путешествия.  Следовательно, необходимо построить еще один график, который будет характеризовать скорость и «качество» изменений пути, другими словами определять отношение ∆x/∆y для каждого «метра» маршрута.

Этот график и будет являться наглядной производной для конкретной тропы и объективно опишет ее изменения на каждом интересующем интервале. Убедиться в этом очень просто, значение  ∆x/∆y – есть не что иное, как дифференциал, взятый для конкретного значения x и y. Применим же дифференцирование не определенным координатам, а к функции в целом:

Производная и тригонометрические функции

Тригонометрические функции неразрывно связаны с производной.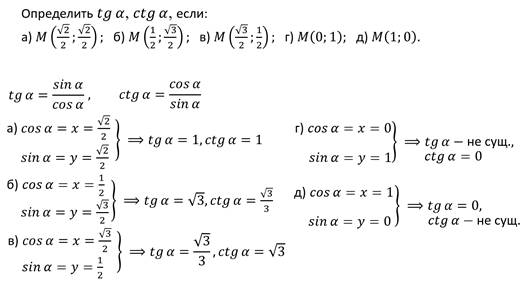 Понять это можно из следующего чертежа. На рисунке координатной оси изображена функция  Y = f (x) – синяя кривая.

K (x0; f (x0)) – произвольная точка, x0 + ∆x – приращение по оси OX, а f (x0 + ∆x) – приращение по оси OY в некой точке L.

Проведем прямую через точки K и L и построим прямоугольный треугольник KLN. Если мысленно перемещать отрезок LN по графику Y = f (x), то точки L и N будут стремиться к значениям K (x0; f (x0)). Назовем эту точку условным началом графика — лимитом, если же функция бесконечна, хотя бы на одном из промежутков  – это стремление также будет бесконечным, а его предельное значение близким к 0.

Характер данного стремления можно описать касательной к выбранной точке y = kx + b или графиком производной первоначальной функции dy – зеленая прямая.

Но где же здесь тригонометрия?! Все очень просто рассмотрим прямоугольный треугольник KLN. Значение дифференциала для конкретной точки K есть тангенс угла α или ∠K:

Таким образом можно описать геометрический смымсл производной и ее взаимосвязь с тригонометрическими функциями.

Формулы производных для тригонометрических функций

Преобразования синуса, косинуса, тангенса и котангенса при определении производной необходимо заучить наизусть.

Последние две формулы не являются ошибкой, дело в том, что существует разница между определением производной простого аргумента и  функции в том же качестве.

Рассмотрим сравнительную таблицу с формулами производных от синису, косинуса, тангенса и котангенса:

Также выведены формулы для производных арксинуса, арккосинуса, арктангенса и арккотангенса, хотя они применяются крайне редко:

Стоит отметить, что приведенных формул явно недостаточно для успешного решения типовых заданий ЕГЭ, что будет продемонстрированно при решении конкретного примера поиска производной тригонометрического выражения.

Задание: Необходимо найти производную функции и найти ее значение для π/4:

Решение:  Чтобы найти y’ необходимо вспомнить основные формулы преобразования исходной функции в производную, а именно:

Теперь следует приступить к поэтопному преобразованию исходной функции y, сначала применим формулу (1):

Согласно формуле (2) преобразуем числитель выражения:

Избавимся от производным числа 1 по правилу (3) и заменим sin x его производной (4):

Осталось посчитать значение производной для π/4:

Поделиться с друзьями:

Производные тригонометрических функций – методическая разработка для учителей, Козлов Леонтий Михайлович

Цель:	вывести формулы производных основных тригонометрических функций; научится применять полученные формулы при решении задач.
Ключевые идеи:	для нахождения производных тригонометрических функций используются формулы
Результаты обучения:	учащиеся умеют решать различные примеры на нахождение производной, используя формулы производных тригонометрических функций.
Оборудование урока:	интерактивная доска, слайдовая презентация, таблички с названиями групп, видео «Веселая физминутка», тесты, стикеры.
Форма работы:	групповая, индивидуальная.

 

Ход урока

Этап	Содержание	Деятельность учителя	Деятельность учеников	Оценивание
1. Организационный момент	Разделить учащихся на структурированные группы, учащиеся получают карточки с названием группы. Начать со слов Н.А. Назарбаева: «Развитие Казахстана в ХХІ веке будет напрямую связано с повышением уровня образования. — Наша задача – поднять Казахстан на уровень международного стандарта, и наша молодежь, подрастая, будут важной элитой, которая будет вести Казахстан в большой глобальный мир. «Только высокообразованная нация может быть конкурентоспособной», – отметил Президент РК Н.А. Назарбаев. Раздать оценочные листы. Объяснить принцип работы с ними.     (3 мин)	Приветствует обучающихся, отмечает отсутствующих. Обеспечивает позитивный настрой урока. Следит за дисциплиной. Оглашает девиз урока. Раздает оценочные листы, объясняет правила заполнения.	Делятся на группы, психологически настраиваются на урок.	Оценочные листы
Проверка домашнего задания. Актуализация опорных знаний	Группы получают названия по теме урока «Синус», «Косинус», «Тангенс», «Котангенс». На доске представлено задание. Каждая группа получают задания на повторение: 1 группа «Синус», – «Таблица производных», 2 группа «Косинус» – «Правила вычисления производных», 3 группа «Тангенс» – «Алгоритм нахождения производной функции». Таким образом, ответить на вопрос, что мы будем изучать.        (5 мин)	Объясняет работу. Слушает ответы групп. Диагностирует уровень опорных знаний	Вспоминают формулы. Отвечают на вопрос на карточке.	1 балл за выполненное задание, оценивают другие группы.
Работа в группах	Группы получают индивидуальные задания (Приложение 1)   Карточка №1 Используя возможности общеобразовательного ресурса BilimLand, выведите формулу для нахождения производной функции y = sin x. Перейдите по ссылке: https://bilimland.kz/ru/courses/math-ru/nachala-analiza/proizvodnaya-i-ee-primeneniya/proizvodnaya/lesson/proizvodnye-trigonometricheskix-funkczij Карточка №1 Используя возможности общеобразовательного ресурса BilimLand, выведите формулу для нахождения производной функции y = cos x. Перейдите по ссылке: https://bilimland.kz/ru/courses/math-ru/nachala-analiza/proizvodnaya-i-ee-primeneniya/proizvodnaya/lesson/proizvodnye-trigonometricheskix-funkczij   Карточка №1 Используя возможности общеобразовательного ресурса BilimLand, выведите формулу для нахождения производной функции y = tg x. Перейдите по ссылке: https://bilimland.kz/ru/courses/math-ru/nachala-analiza/proizvodnaya-i-ee-primeneniya/proizvodnaya/lesson/proizvodnye-trigonometricheskix-funkczij   Карточка №1 Используя возможности общеобразовательного ресурса BilimLand, выведите формулу для нахождения производной функции y = ctg x. Перейдите по ссылке: https://bilimland.kz/ru/courses/math-ru/nachala-analiza/proizvodnaya-i-ee-primeneniya/proizvodnaya/lesson/proizvodnye-trigonometricheskix-funkczij   Время для работы в группе – 5 мин. Защита у доски каждой группе – по 3 мин.	Дает задание. Выводит задания на интерактивной доске. Наблюдает за их выполнением за работой в группе, за осуществление коллаборативной среды. Наблюдает за работой сильных учащихся и слабых учащихся.	Решают задания, работая в группе, сильные учащиеся объясняют более слабым ход решения заданий. Затем из группы представители показывают вывод формул на доске.	1 балл учащиеся, работающие у доски, оценивают другие группы
«Веселая физминутка»	Выполнить танцевальные движения под музыку. (2 мин)	Предоставляет видеоматериал для выполнения физминутки	Выполняют танцевальные движения под музыку.
Первичное закрепление	Используя возможности общеобразовательного ресурса BilimLand, выполняем задание №5-6. Перейдите по ссылке: https://bilimland.kz/ru/courses/math-ru/nachala-analiza/proizvodnaya-i-ee-primeneniya/proizvodnaya/lesson/proizvodnye-trigonometricheskix-funkczij (7-8 минут)	Объясняет принцип работы. Следит за выполнением, за дисциплиной в классе.	Решают примеры на скорость. Вспоминают все опорные формулы, применяемые ранее. Учатся работать быстро и качественно	Используя страницу сайта https://bilimland. kz/ru/courses/math-ru/nachala-analiza/proizvodnaya-i-ee-primeneniya/proizvodnaya/lesson/proizvodnye-trigonometricheskix-funkczij результаты, ученики оценивают свою работу, подсчитывают количество допущенных ошибок
Домашнее задание	Используя возможности общеобразовательного ресурса BilimLand, выполняем задание №7-8. Перейдите по ссылке: https://bilimland.kz/ru/courses/math-ru/nachala-analiza/proizvodnaya-i-ee-primeneniya/proizvodnaya/lesson/proizvodnye-trigonometricheskix-funkczij	Поясняет домашнее задание.	Записывают домашнее задание.
Подведение итогов урока. Оценивание. Рефлексия	1) Подсчитать общее количество баллов в оценочных листах. Выставить оценку по следующим критериям: От 2 балла и выше и 1 ошибка – оценка «5» 1 балл и выше и 2-3 ошибки – «4» более 4 ошибок – «2» (2 мин)   3) Оценить работу в классе на изображении Дерева достижений, поместить стикеры на ветви дерева, если урок понравился, особых затруднений не вызвал, если урок не понравился, тема осталась непонятной. (3 мин)	Выставляет итоговые оценки урока учащимся. Анализирует результаты рефлексии. Выявляет учащихся, которым тема осталась непонятна. Назначает им при необходимости консультантов из числа более сильных учащихся. Проводит рефлексию «Дерево успеха»	Подсчитывают баллы, выставляют оценку. Выбирают наиболее активных учеников. Рефлексируют.	Самооценивание Критериальное оценивание. Формативное оценивание.

 

 

Исчисление I. Производные триггерных функций

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3.5: Производные триггерных функций

В этом разделе мы начнем рассмотрение производных функций, отличных от многочленов или корней многочленов. Мы начнем этот процесс с рассмотрения производных шести триггерных функций. Две производные будут получены. Остальные четыре оставлены вам и будут следовать аналогичным доказательствам для двух, приведенных здесь.

Прежде чем мы на самом деле перейдем к производным тригонометрических функций, нам нужно указать пару пределов, которые будут проявляться при выводе двух производных.

Факт

\[\ mathop {\ lim} \ limits _ {\ theta \ to 0} \ frac {{\ sin \ theta}} {\ theta} = 1 \ hspace {0,75 дюйма} \ mathop {\ lim} \ limits _ {\ theta \to 0} \frac{{\cos\theta — 1}}{\theta} = 0\]

См. раздел «Доказательство пределов срабатывания» в главе «Дополнительно», чтобы увидеть доказательство этих двух пределов.

Прежде чем продолжить, небольшое примечание. Студенты часто спрашивают, почему мы всегда используем радианы на уроках исчисления. Вот почему! Доказательство формулы, включающей синус, требует, чтобы углы были в радианах. Если углы выражены в градусах, предел, включающий синус, не равен 1, поэтому формулы, которые мы выведем ниже, также изменятся. В приведенных ниже формулах будет использоваться дополнительная константа, которая будет мешать нашей работе, поэтому мы используем радианы, чтобы этого избежать. Итак, не забывайте всегда использовать радианы в классе исчисления!

Прежде чем мы начнем различать триггерные функции, давайте быстро поработаем над набором предельных задач, которые теперь позволяет нам решить этот факт.

Пример 1 Оцените каждый из следующих пределов.

1. \(\displaystyle \mathop {\lim }\limits _{\theta \to 0} \frac{{\sin \theta}}{{6\theta}}\)
2. \(\displaystyle \mathop {\lim}\limits_{x \to 0} \frac{{\sin\left({6x} \right)}}{x}\)
3. \(\displaystyle \mathop {\lim }\limits_{x \to 0} \frac{x}{{\sin\left({7x} \right)}}\)
4. \(\displaystyle \mathop {\lim}\limits_{t \to 0} \frac{{\sin\left({3t}\right)}}{{\sin\left({8t}\right)} }\)
5. \(\displaystyle \mathop {\lim}\limits_{x \to 4} \frac{{\sin\left({x — 4} \right)}}{{x — 4}}\)
6. \(\displaystyle \mathop {\lim}\limits_{z \to 0} \frac{{\cos\left({2z} \right) — 1}}{z}\)

Показать все решения Скрыть все решения

a \(\displaystyle \mathop {\lim }\limits_{\theta \to 0} \frac{{\sin \theta}}{{6\theta}}\) Показать решение

Этот предел на самом деле невелик. На самом деле, это только сравнение со следующим примером, чтобы вы могли увидеть разницу в том, как они работают. В этом случае, поскольку в знаменателе всего 6, мы просто вынесем это из множителя, а затем воспользуемся этим фактом.

\[\ mathop {\ lim } \ limits _ {\ theta \ to 0} \ frac {{\ sin \ theta}} {{6 \ theta}} = \ frac {1} {6} \ mathop {\ lim } \ пределы _ {\ theta \ to 0} \ frac {{\ sin \ theta}} {\ theta } = \ frac {1} {6} \ left ( 1 \ right) = \ frac {1} {6} \]

b \(\displaystyle \mathop {\lim }\limits_{x \to 0} \frac{{\sin \left({6x} \right)}}{x}\) Показать решение

Теперь, в этом случае мы не можем вынести 6 из синуса, поэтому мы застряли с ним, и нам нужно найти способ справиться с этим. Чтобы решить эту задачу, нам нужно заметить, что на самом деле аргумент синуса совпадает со знаменателем (, т.е. оба \(\тета\)). Поэтому нам нужно, чтобы аргумент синуса и знаменатель были одинаковыми. Мы можем сделать это, умножив числитель и знаменатель на 6 следующим образом.

\[\ mathop {\ lim } \ limit_ {x \ to 0} \ frac {{\ sin \ left ( {6x} \ right)}} {x} = \ mathop {\ lim } \ limit_ {x \ to 0 } \frac{{6\sin \left( {6x} \right)}}{{6x}} = 6\mathop {\lim }\limits_{x \to 0} \frac{{\sin \left({ 6x} ​​\справа)}}{{6x}}\]

Обратите внимание, что мы учли 6 в числителе за пределом. На этом этапе, хотя это может показаться не так, мы можем использовать приведенный выше факт, чтобы закончить ограничение.

Чтобы увидеть, что мы можем использовать факт на этом пределе, давайте сделаем изменение переменных . Изменение переменных — это просто переименование частей проблемы, чтобы что-то выглядело более похожим на то, с чем мы знаем, как справляться. Их не всегда можно сделать, но иногда, как в этом случае, они могут упростить задачу. Замена переменных здесь состоит в том, чтобы позволить \(\theta = 6x\) и затем заметить, что как \(x \to 0\) мы также имеем \(\theta \to 6\left(0 \right) = 0\) . При замене переменных в пределе нам нужно заменить все \(x\) на \(\theta\), в том числе и в пределе.

Выполнение замены переменных на этом пределе дает,

\[\ begin{align*}\mathop {\lim}\limits_{x \to 0} \frac{{\sin\left({6x}\right)}}}{x} & = 6\mathop {\lim }\limits_{x \to 0} \frac{{\sin\left({6x} \right)}}{{6x}}\hspace{0.5in}{\rm{let}}\theta = 6x\\ & = 6 \ mathop {\ lim} \ limits _ {\ theta \ to 0} \ frac {{\ sin \ left (\ theta \ right)}} {\ theta} \\ & = 6 \ left ( 1 \ right) \\ & = 6\hspace{0,25 дюйма}\end{выравнивание*}\]

Вот и все. Обратите внимание, что здесь нам действительно не нужно было менять переменные. Все, что нам действительно нужно заметить, это то, что аргумент синуса совпадает со знаменателем, и тогда мы можем использовать этот факт. Замена переменных в этом случае нужна только для того, чтобы стало ясно, что факт действительно работает.

c \(\displaystyle \mathop {\lim }\limits_{x \to 0} \frac{x}{{\sin\left({7x} \right)}}\) Показать решение

В этом случае у нас возникла небольшая проблема, заключающаяся в том, что функция, предел которой мы здесь берем, перевернута по сравнению с фактической. Это не проблема, как кажется, если мы заметим, что

\[\ frac{x}{{\sin\left({7x}\right)}} = \frac{1}{{\,\,\,\frac{{\sin\left({7x}\right) )}}{Икс}\,\,\,}}\]

, а затем все, что нам нужно сделать, это вспомнить хорошее свойство пределов, которое позволяет нам делать

\[\ begin{align*}\mathop {\lim}\limits_{x \to 0} \frac{x}{{\sin\left({7x}\right)}} & = \mathop {\lim} \limits_{x \to 0} \frac{1}{{\,\,\,\frac{{\sin\left({7x} \right)}}{x}\,\,\,}}\ \ & = \frac{{\mathop {\lim}\limits_{x \to 0} 1}}{{\,\,\,\mathop {\lim}\limits_{x \to 0} \frac{{ \sin \left( {7x} \right)}}{x}\,\,\,}}\\ & = \frac{1}{{\,\,\,\mathop {\lim }\limits_{ x \to 0} \frac{{\sin\left({7x} \right)}}{x}\,\,\,}}\end{align*}\]

Немного переписав, мы можем увидеть, что на самом деле нам нужно установить ограничение, подобное тому, которое мы сделали в предыдущей части. Итак, давайте сделаем предел здесь, и на этот раз мы не будем возиться с заменой переменной, чтобы помочь нам. Все, что нам нужно сделать, это умножить числитель и знаменатель дроби в знаменателе на 7, чтобы настроить все, чтобы использовать этот факт. Вот работа для этого предела.

\[\begin{align*}\mathop {\lim}\limits_{x \to 0} \frac{x}{{\sin\left({7x}\right)}} & = \frac{1}{ {\,\,\,\mathop {\lim }\limits_{x \to 0} \frac{{7\sin\left({7x} \right)}}{{7x}}\,\,\, }} \\ & = \ frac {1} {{\, \, \, 7 \ mathop {\ lim} \ limit_ {x \ to 0} \ frac {{\ sin \ left ({7x} \ right)} }{{7x}}\,\,\,}}\\ & = \frac{1}{{\left( 7 \right)\left( 1 \right)}}\\ & = \frac{1} {7}\конец{выравнивание*}\]

d \(\displaystyle \mathop {\lim}\limits_{t \to 0} \frac{{\sin\left({3t}\right)}}{{\sin\left({8t}\right)} }\) Показать решение

Этот предел на самом деле совсем не похож на предел, однако его можно рассматривать как комбинацию двух предыдущих частей, немного переписав. Во-первых, мы разделим дробь следующим образом:

. \[\ mathop {\lim }\limits_{t \to 0} \frac{{\sin\left({3t}\right)}}{{\sin\left({8t}\right)}} = \ mathop {\ lim } \ limit_ {t \ to 0} \ frac {{\ sin \ left ({3t} \ right)}} {1} \ frac {1} {\ sin \ left ({8t} \ right) )}}\]

Теперь факт требует \(t\) в знаменателе первого и в числителе второго. Это достаточно легко сделать, если мы умножим все это на \({\textstyle{t \over t}}\) (что в конце концов равно единице и поэтому не изменит проблему), а затем сделаем небольшую перестановку как следует,

\[\ begin{align*}\mathop {\lim}\limits_{t \to 0} \frac{{\sin\left({3t}\right)}}{{\sin\left({8t}\ справа)}} & = \ mathop {\ lim } \ limit_ {t \ to 0} \ frac {{\ sin \ left ( {3t} \ right)}} {1} \ frac {1} {{\ sin \ влево ({8t} \right)}} \ frac {t} {t} \\ & = \ mathop {\ lim } \ limit_ {t \ to 0} \ frac {{\ sin \ left ({3t} \ right) )}}}{t}\frac{t}{{\sin\left({8t}\right)}}\\ & = \left({\mathop {\lim}\limits_{t\to 0}\frac {{\ sin \ left ({3t} \ right)}} {t}} \ right) \ left ( {\ mathop {\ lim} \ limit_ {t \ to 0} \ frac {t} {{\ sin \ влево( {8t} \вправо)}}} \вправо)\конец{выравнивание*}\]

На данный момент мы видим, что это действительно два предела, которые мы видели раньше. Вот работа для каждого из них, и обратите внимание на второй предел, что мы собираемся работать с ним немного иначе, чем в предыдущей части. На этот раз мы заметим, что на самом деле не имеет значения, находится ли синус в числителе или знаменателе, пока аргумент синуса такой же, как и в числителе, предел по-прежнему равен единице.

Вот работа для этого лимита.

\[\ begin{align*}\mathop {\lim}\limits_{t \to 0} \frac{{\sin\left({3t}\right)}}{{\sin\left({8t}\ справа)}} & = \ слева ( {\ mathop {\ lim} \ limit_ {t \ to 0} \ frac {{3 \ sin \ left ({3t} \ right)}} {{3t}}} \ right )\left( {\mathop {\lim}\limits_{t \to 0} \frac{{8t}}{{8\sin\left({8t} \right)}}} \right)\\ & = \left( {3\mathop {\lim }\limits_{t \to 0} \frac{{\sin \left({3t} \right)}}{{3t}}} \right)\left( {\ frac {1} {8} \ mathop {\ lim} \ limit_ {t \ to 0} \ frac {{8t}} {{\ sin \ left ({8t} \ right)}}} \ right) \\ & = \left( 3 \right)\left( {\frac{1}{8}} \right)\\ & = \frac{3}{8}\end{align*}\]

e \(\displaystyle \mathop {\lim }\limits_{x \to 4} \frac{{\sin\left({x — 4} \right)}}{{x — 4}}\) Показать решение

Этот предел выглядит почти так же, как и в факте, в том смысле, что аргумент синуса такой же, как и в знаменателе. Однако обратите внимание, что в пределе \(x\) становится равным 4, а не 0, как того требует факт. Однако, заменив переменные, мы видим, что этот предел на самом деле установлен для использования вышеуказанного факта независимо от него.

Итак, пусть \(\theta = x — 4\) и затем обратите внимание, что в качестве \(x \to 4\) мы имеем \(\theta \to 0\). Следовательно, после изменения переменной предел становится

. \[\ mathop {\lim}\limits_{x \to 4} \frac{{\sin\left({x — 4} \right)}}{{x — 4}} = \mathop {\lim}\ пределы _ {\ тета \ до 0} \ гидроразрыва {{\ грех \ тета}} {\ тета} = 1 \]

f \(\displaystyle \mathop {\lim }\limits_{z \to 0} \frac{{\cos \left({2z} \right) — 1}}{z}\) Показать решение

Во всех предыдущих частях этого примера использовалась синусоидальная часть факта. Однако мы могли бы просто использовать часть косинуса, поэтому вот краткий пример использования части косинуса, чтобы проиллюстрировать это. Мы не будем вдаваться в подробности, так как это действительно работает так же, как и синусоидальная часть.

\[\ begin{align*}\mathop {\lim}\limits_{z \to 0} \frac{{\cos\left({2z}\right) — 1}}{z} & = \mathop {\ lim }\limits_{z \to 0} \frac{{2\left( {\cos \left({2z} \right) — 1} \right)}}{{2z}}\\ & = 2\mathop {\lim}\limits_{z \to 0} \frac{{\cos\left({2z}\right) — 1}}{{2z}}\\ & = 2\left(0\right)\\ & 0\конец{выравнивание*}\]

Все, что требуется для использования факта, это то, что аргумент косинуса совпадает со знаменателем.

Хорошо, теперь, когда мы разобрались с этим набором предельных примеров, давайте вернемся к главному пункту этого раздела — различению триггерных функций.

Начнем с нахождения производной функции синуса. Для этого нам потребуется использовать определение производной. Прошло некоторое время с тех пор, как мы должны были использовать это, но иногда мы просто ничего не можем с этим поделать. Вот определение производной для синуса.

\[\ frac{d}{{dx}}\left( {\sin\left(x\right)}\right) = \mathop {\lim}\limits_{h \to 0} \frac{{\sin \left( {x + h} \right) — \sin \left( x \right)}}{h}\]

Поскольку мы не можем просто подставить \(h = 0\) для оценки предела, нам нужно будет использовать следующую тригонометрическую формулу для первого синуса в числителе.

\[\sin \left( {x + h} \right) = \sin \left( x \right)\cos \left( h \right) + \cos \left( x \right)\sin \left( h \Правильно)\]

Это дает нам

\[\ begin{align*}\frac{d}{{dx}}\left( {\sin\left(x\right)} \right) & = \mathop {\lim }\limits_{h \to 0 } \ frac {{\ грех \ влево ( х \ вправо) \ соз \ влево ( ч \ вправо) + \ соз \ влево ( х \ вправо) \ грех \ влево ( ч \ вправо) — \ грех \ влево ( х \ справа)}} {ч} \\ & знак равно \ mathop {\ lim} \ limit_ {h \ to 0} \ frac {{\ sin \ left (x \ right) \ left ({\ cos \ left (h \ right) ) — 1} \right) + \cos \left( x \right)\sin \left( h \right)}}{h}\\ & = \mathop {\lim }\limits_{h \to 0} \ грех \ влево ( х \ вправо) \ гидроразрыва {{\ соз \ влево ( ч \ вправо) — 1}} {ч} + \ mathop {\ lim } \ limits_ {ч \ до 0} \ соз \ влево ( х \ справа) \ frac {{\ sin \ left (h \ right)}} {h} \ end {align *} \]

Как вы можете видеть, используя тригонометрическую формулу, мы можем объединить первый и третий члены, а затем вывести из них синус. Затем мы можем разбить дробь на две части, с каждой из которых можно работать отдельно.

Теперь оба предела здесь являются пределами, когда \(h\) приближается к нулю. В первом пределе мы имеем \(\sin\left(x\right)\), а во втором пределе имеем \(\cos\left(x\right)\). Оба они являются функциями только \(x\), и по мере того, как \(h\) приближается к нулю, это не влияет на значение \(x\). Следовательно, что касается пределов, эти две функции являются константами и могут быть вынесены за пределы соответствующих пределов. Это дает

\[\ frac{d}{{dx}}\left({\sin\left(x\right)} \right) = \sin\left(x\right)\mathop {\lim }\limits_{h \ до 0} \ frac {{\ cos \ left (h \ right) — 1}} {h} + \ cos \ left ( x \ right) \ mathop {\ lim } \ limits_ {h \ to 0} \ frac { {\ грех \ влево (ч \ вправо)}} {ч} \]

На данный момент все, что нам нужно сделать, это использовать ограничения в приведенном выше факте, чтобы закончить эту задачу.

\[\ frac{d}{{dx}}\left( {\sin\left(x\right)} \right) = \sin\left(x\right)\left(0\right) + \cos\ влево( x \вправо)\влево( 1 \вправо) = \cos \влево( x \вправо)\]

Дифференцирование косинуса выполняется аналогичным образом. Для этого потребуется другая формула триггера, но в остальном это почти идентичное доказательство. Детали будут оставлены вам. Когда закончите с доказательством, которое вы должны получить,

\[\ frac {d}{{dx}}\left( {\cos\left(x\right)} \right) = — \sin\left(x\right)\]

Если убрать эти две карты, остальные четыре получить довольно просто. Все остальные четыре триггерные функции могут быть определены в терминах синуса и косинуса, и эти определения вместе с соответствующими правилами производных могут использоваться для получения их производных.

Давайте посмотрим на тангенс. Тангенс определяется как

\[\ загар \ влево ( х \ вправо) = \ гидроразрыв {{\ грех \ влево ( х \ вправо)}} {{\ соз \ влево ( х \ вправо)}}} \]

Теперь, когда у нас есть производные синуса и косинуса, все, что нам нужно сделать, это применить к ним правило частных. 2} \ left ( x \ right) \\ \ displaystyle \ frac {d }{{dx}}\left( {\sec\left(x\right)} \right) = \sec\left(x\right)\tan\left(x\right) & \hspace{0.5in}\ displaystyle \frac{d}{{dx}}\left( {\csc \left( x \right)} \right) = — \csc \left( x \right)\cot \left( x \right)\end {множество}\] 92}\загар \влево(ш\вправо)\)

\(y = 5\sin\left(x\right)\cos\left(x\right) + 4\csc \left(x\right)\)

\(\displaystyle P\left(t\right) = \frac{{\sin\left(t\right)}}{{3 — 2\cos\left(t\right)}}\)

Показать все решения Скрыть все решения

a \(g\left( x \right) = 3\sec \left( x \right) — 10\cot \left( x \right)\) Показать решение

На самом деле в этой проблеме нет ничего сложного. Мы просто продифференцируем каждый термин, используя приведенные выше формулы. 92}\tan \left( w \right)\) Показать решение

В этой части нам нужно будет использовать правило произведения во втором члене, и обратите внимание, что здесь нам действительно понадобится правило произведения. 2}\) и \(\tan \left( w \right)\). Это дает 92}\влево( ш \вправо)\]

Итак, как бы вы ни подошли к этой задаче, вы получите одну и ту же производную.

c \(y = 5\sin \left( x \right)\cos \left( x \right) + 4\csc \left( x \right)\) Показать решение

Как и в предыдущей части, нам нужно использовать правило произведения для первого члена. Мы также будем думать о 5 как о части первой функции в продукте, чтобы убедиться, что мы правильно с ней работаем. В качестве альтернативы вы можете использовать набор скобок, чтобы убедиться, что 5 обрабатывается правильно. Любой способ будет работать, но мы будем думать о 5 как о части первого члена произведения. Вот производная этой функции. 92}\left( x \right) — 4\csc \left( x \right)\cot \left( x \right)\end{align*}\]

d \(\displaystyle P\left( t \right) = \frac{{\sin \left( t \right)}}{{3 — 2\cos \left( t \right)}}\) Показать решение

В этой части нам нужно будет использовать правило частных, чтобы найти производную. 2}}} \ end {align *}\] 92}}}\end{выравнивание*}\]

В качестве последней проблемы давайте не будем забывать, что у нас все еще есть наши стандартные интерпретации производных.

Пример 3. Предположим, что сумма денег на банковском счете определяется выражением \[P\left( t \right) = 500 + 100\cos \left( t \right) — 150\sin \left( t \right)\]

где \(t\) в годах. В течение первых 10 лет, в течение которых счет открыт, когда увеличивается сумма денег на счете?

Показать решение

Чтобы определить, когда количество денег увеличивается, нам нужно определить, когда скорость изменения положительна. Поскольку мы знаем, что скорость изменения определяется производной, это первое, что нам нужно найти.

\[P’\left( t \right) = — 100\sin \left( t \right) — 150\cos \left( t \right)\]

Теперь нам нужно определить, где в первые 10 лет это будет положительным. Это эквивалентно вопросу, где в интервале \(\left[ {0,10} \right]\) положительная производная. Напомним, что и синус, и косинус являются непрерывными функциями, поэтому производная также является непрерывной функцией. Затем теорема о промежуточном значении говорит нам, что производная может изменить знак только в том случае, если она сначала проходит через нуль.

Итак, нам нужно решить следующее уравнение.

\[\begin{align*} — 100\sin \left( t \right) — 150\cos \left( t \right) & = 0\\ 100\sin \left( t \right) & = — 150\ cos \left( t \right)\\ \frac{{\sin \left( t \right)}}{{\cos \left( t \right)}} & = — 1.5\\ \tan \left( t \right) & = — 1.5\end{align*}\]

Решение этого уравнения:

\[\begin{array}{ll}t = 2,1588 + 2\pi n,&\hspace{0,25in}n = 0, \pm 1, \pm 2, \ldots \\ t = 5,3004 + 2\pi n , & \hspace{0.25in}n = 0, \pm 1, \pm 2, \ldots \end{массив}\]

Если вы не помните, как решать тригонометрические уравнения, вернитесь назад и просмотрите разделы, посвященные решению триггерных уравнений в главе «Обзор».

Нас интересуют только те решения, которые попадают в диапазон \(\left[ {0,10} \right]\). Подставляя значения \(n\) в приведенные выше решения, мы видим, что нам нужны следующие значения:

\[\begin{align*} & t = 2,1588\hspace{0,5 дюйма} t = 2,1588 + 2\pi = 8,4420\\ & t = 5,3004\end{align*}\]

Итак, как и при решении полиномиальных неравенств, все, что нам нужно сделать, это начертить числовую прямую и добавить в нее точки. Эти точки будут делить числовую прямую на участки, в которых производная всегда должна быть одного знака. Все, что нам нужно сделать, это выбрать контрольную точку в каждой области, чтобы определить знак производной в этой области.

Вот числовая строка со всей информацией на ней.

Итак, похоже, что сумма денег на банковском счете будет увеличиваться в следующие промежутки времени.

\[2,1588 < t < 5,3004 \ hspace {0,5 дюйма} 8,4420 < t < 10 \]

Обратите внимание, что мы ничего не можем сказать о том, что происходит после \(t = 10\), так как мы не выполнили никакой работы для \(t\) после этой точки.

В этом разделе мы увидели, как различать триггерные функции. Мы также видели в последнем примере, что наши интерпретации производной по-прежнему действительны, поэтому мы не можем их забыть.

Кроме того, важно, чтобы мы могли решать тригонометрические уравнения, поскольку это то, что время от времени будет возникать в этом курсе. Также важно, что мы можем использовать типы числовых линий, которые мы использовали в последнем примере, чтобы определить, где функция положительна, а где функция отрицательна. Это то, что мы будем время от времени делать как в этой главе, так и в следующей.

3.5: Производные тригонометрических функций

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2494

• Гилберт Странг и Эдвин «Джед» Герман
• ОпенСтакс

Цели обучения

• Найти производные функции синуса и косинуса.
• Найдите производные стандартных тригонометрических функций.
• Вычислите высшие производные синуса и косинуса.

Одним из важнейших видов движения в физике является простое гармоническое движение, которое связано с такими системами, как объект с массой, колеблющейся на пружине. Простое гармоническое движение может быть описано с помощью функции синуса или косинуса. В этом разделе мы расширим наши знания о формулах производных, включив в них производные этих и других тригонометрических функций. Мы начнем с производных функций синуса и косинуса, а затем используем их для получения формул для производных оставшихся четырех тригонометрических функций. Способность вычислять производные функций синуса и косинуса позволит нам найти скорость и ускорение простого гармонического движения.

Производные функции синуса и косинуса

Мы начнем исследование производной функции синуса, используя формулу, чтобы сделать обоснованное предположение о ее производной. Напомним, что для функции \(f(x),\)

\[f′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}. \nonumber \]

Следовательно, для значений \(h\), очень близких к \(0\),

\[f′(x)≈\dfrac{f(x+h)−f(x)} {час}. \nonumber \]

Мы видим, что, используя \(h=0,01\),

\[\dfrac{d}{dx}(\sin x)≈\dfrac{\sin (x+0,01)−\sin х}{0,01} \номер \]

Установив

\[D(x)=\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber \]

и используя графическую утилиту, мы можем получить график приближение к производной \(\sin x\) (рисунок \(\PageIndex{1}\)).

Рисунок \(\PageIndex{1}\): График функции \(D(x)\) очень похож на косинусоидальную кривую.

При осмотре график \(D(x)\) кажется очень близким к графику функции косинуса. Действительно, мы покажем, что

\[\dfrac{d}{dx}(\sin x)=\cos x. \номер\]

Если бы мы проделали те же шаги для аппроксимации производной функции косинуса, мы бы обнаружили, что

\[\dfrac{d}{dx}(\cos x)=-\sin x. \nonumber \]

Производные от \(\sin x\) и \(\cos x\)

Производной функции синуса является косинус, а производной функции косинуса является отрицательный синус.

\[\dfrac{d}{dx}(\sin x)=\cos x \nonumber \]

\[\dfrac{d}{dx}(\cos x)=-\sin x \nonumber \ ]

Доказательство

Поскольку доказательства для \(\dfrac{d}{dx}(\sin x)=\cos x\) и \(\dfrac{d}{dx}(\cos x)=-\sin x\) используют аналогичные методы, мы приводим только доказательство для \(\dfrac{d}{dx}(\sin x)=\cos x\). Прежде чем начать, вспомните два важных тригонометрических предела:

\(\displaystyle \lim_{h→0}\dfrac{\sin h}{h}=1\) и \(\displaystyle \lim_{h→0}\dfrac {\ cos ч-1} {ч} = 0 \).

Графики \(y=\dfrac{\sin h}{h}\) и \(y=\dfrac{\cos h−1}{h}\) показаны на рисунке \(\PageIndex{2 }\).

Рисунок \(\PageIndex{2}\): На этих графиках показаны два важных предела, необходимых для установления формул производных для функций синуса и косинуса.

Напомним также следующее тригонометрическое тождество для синуса суммы двух углов:

\[\sin (x+h)=\sin x\cos h+\cos x\sin h. \nonumber \]

Теперь, когда мы собрали все необходимые уравнения и тождества, приступим к доказательству.

\[\begin{align*} \dfrac{d}{dx}(\sin x) &=\lim_{h→0}\dfrac{\sin(x+h)−\sin x}{h} & & \text{Применить определение производной.}\\[4pt]
&=\lim_{h→0}\dfrac{\sin x\cos h+\cos x\sin h−\sin x}{h } & & \text{Используйте тождество триггера для синуса суммы двух углов.}\\[4pt]
&=\lim_{h→0}\left(\dfrac{\sin x\cos h−\sin x}{h}+\dfrac{\cos x\sin h}{h}\right) & & \ text{Перегруппировать.}\\[4pt]
&=\lim_{h→0}\left(\sin x\left(\dfrac{\cos h−1}{h}\right)+(\cos x) \left(\dfrac{\sin h}{h}\right)\right) & & \text{Умножить}\sin x\text{и}\cos x \\[4pt]
&=(\sin x )\lim_{h→0}\left(\dfrac{\cos h−1}{h}\right)+(\cos x)\lim_{h→0}\left(\dfrac{\sinh}{ h}\right) & & \text{Коэффициент }\sin x\text{ и }\cos x \text{ вне пределов.} \\[4pt]
&=(\sin x)(0)+(\ cos x)(1) & & \text{Применить формулы ограничения триггеров.}\\[4pt]
&=\cos x & & \text{Упростить.} \end{align*} \nonumber \]

□

На рисунке \(\PageIndex{3}\) показано соотношение между графиком \(f( x)=\sin x\) и его производная \(f′(x)=\cos x\). Обратите внимание, что в точках, где \(f(x)=\sin x\) имеет горизонтальную касательную, ее производная \(f′(x)=\cos x\) принимает нулевое значение. Мы также видим, что где f\((x)=\sin x\) возрастает, \(f′(x)=\cos x>0\) и где \(f(x)=\sin x\) убывает, \(f′(x)=\cos x<0.\)

Рисунок \(\PageIndex{3}\): где \(f(x)\) имеет максимум или минимум, \(f’ (x)=0\), то есть \(f'(x)=0\), где \(f(x)\) имеет горизонтальную касательную. Эти точки отмечены точками на графиках 92x}\)

Пример \(\PageIndex{3}\): приложение к скорости

Частица движется вдоль координатной оси таким образом, что ее положение в момент времени \(t\) определяется выражением \(s(t)= 2\sin t−t\) при \(0≤t≤2π.\) В какие моменты времени частица покоится?

Решение

Чтобы определить, когда частица находится в состоянии покоя, установите \(s′(t)=v(t)=0.\) Начните с нахождения \(s′(t).\) Мы получим

\[s′(t)=2 \cos t−1, \nonumber \]

поэтому мы должны решить

\[2 \cos t−1=0\text{ для }0≤t≤2π. \nonumber \]

Решениями этого уравнения являются \(t=\dfrac{π}{3}\) и \(t=\dfrac{5π}{3}\). Таким образом, частица покоится в моменты времени \(t=\dfrac{π}{3}\) и \(t=\dfrac{5π}{3}\).

Упражнение \(\PageIndex{3}\)

Частица движется вдоль координатной оси. Его положение в момент времени \(t\) определяется как \(s(t)=\sqrt{3}t+2\cos t\) для \(0≤t≤2π.\) В какие моменты времени частица находится в отдыхать?

Подсказка

Используйте предыдущий пример в качестве руководства.

Ответить

\(t=\dfrac{π}{3},\quad t=\dfrac{2π}{3}\)

Производные других тригонометрических функций

Поскольку оставшиеся четыре тригонометрические функции могут быть выражены в виде частных, содержащих синус, косинус или и то, и другое, мы можем использовать правило частных, чтобы найти формулы для их производных.

Пример \(\PageIndex{4}\): производная касательной функции 92x\\[4pt]

\dfrac{d}{dx}(\sec x)&=\sec x \tan x\\[4pt]
\dfrac{d}{dx}(\csc x)&=- \csc х \кот х. \end{align} \nonumber \]

Пример \(\PageIndex{5}\): нахождение уравнения касательной

Найдите уравнение касательной к графику \(f(x)=\ кроватка x \) в точке \(x=\frac{π}{4}\).

Решение

Чтобы найти уравнение касательной, нам нужна точка и наклон в этой точке. Чтобы найти точку, вычислите

\(f\left(\frac{π}{4}\right)=\cot\frac{π}{4}=1\). 92 \ влево (\ гидроразрыва {π} {4} \ вправо) = −2 \).

Используя уравнение точки-наклона линии, мы получаем

\(y−1=−2\left(x−\frac{π}{4}\right)\)

или эквивалентно,

\ (y=−2x+1+\frac{π}{2}\).

Пример \(\PageIndex{6}\): нахождение производной тригонометрических функций

Найдите производную \(f(x)=\csc x+x\tan x .\)

Решение

Чтобы найти эту производную, мы должны использовать как правило сумм, так и правило произведения. По правилу сумм находим 92 х\)

Упражнение \(\PageIndex{6}\)

Найдите наклон линии, касательной к графику \(f(x)=\tan x \) в точке \(x=\dfrac{π}{6} \).

Подсказка

Вычислите производную в точке \(x=\dfrac{π}{6}\).

Ответить

\(\dfrac{4}{3}\)

Производные высшего порядка

Производные высшего порядка от \(\sin x\) и \(\cos x\) повторяются. Следуя шаблону, мы можем найти любую производную более высокого порядка от \(\sin x\) и \(\cos x.\) 9{4⋅14+3}}(\sin x)\)

Ответить

\(-\cos х\)

Пример \(\PageIndex{9}\): приложение к ускорению

Частица движется вдоль координатной оси таким образом, что ее положение в момент времени \(t\) определяется выражением \(s(t)= 2−\sint\). Найдите \(v(π/4)\) и \(a(π/4)\). Сравните эти значения и решите, ускоряется или замедляется частица.

Раствор

Сначала найдите \(v(t)=s′(t)\)

\[v(t)=s′(t)=−\cos t . \nonumber \]

Таким образом,

\(v\left(\frac{π}{4}\right)=-\dfrac{1}{\sqrt{2}}=-\dfrac{\sqrt{2 }}{2}\).

Затем найдите \(a(t)=v′(t)\). Таким образом, \(a(t)=v′(t)=\sin t\), и мы имеем

\(a\left(\frac{π}{4}\right)=\dfrac{1}{\ sqrt{2}}=\dfrac{\sqrt{2}}{2}\).

Так как \(v\left(\frac{π}{4}\right)=-\dfrac{\sqrt{2}}{2}<0\) и \(a\left(\frac{π} {4}\right)=\dfrac{\sqrt{2}}{2}>0\), мы видим, что скорость и ускорение действуют в противоположных направлениях; то есть объект ускоряется в направлении, противоположном направлению, в котором он движется. Следовательно, частица замедляется.

Упражнение \(\PageIndex{9}\)

Блок, прикрепленный к пружине, движется вертикально. Его положение в момент времени t определяется выражением \(s(t)=2\sin t\). Найдите \(v\left(\frac{5π}{6}\right)\) и \(a\left(\frac{5π}{6}\right)\). Сравните эти значения и решите, ускоряется блок или замедляется.

Подсказка

Используйте пример \(\PageIndex{9}\) в качестве руководства.

Ответить

\(v\left(\frac{5π}{6}\right)=-\sqrt{3}<0\) и \(a\left(\frac{5π}{6}\right)=-1 <0\). Блок ускоряется.

Ключевые понятия

• Мы можем найти производные от \(\sin x\) и \(\cos x\), используя определение производной и предельные формулы, найденные ранее. Результат

\(\dfrac{d}{dx}\big(\sin x\big)=\cos x\quad\text{and}\quad\dfrac{d}{dx}\big(\cos x\big )=−\sin x\).

• С помощью этих двух формул мы можем определить производные всех шести основных тригонометрических функций. 92x\)
  • Производная секущей функции

  \(\dfrac{d}{dx}(\sec x)=\sec x\tan x \)

  • Производная функции косеканса

  \(\dfrac{d}{dx}(\csc x)=-\csc x\cot x \)

  ---

  Эта страница под названием 3.5: Производные тригонометрических функций распространяется в соответствии с лицензией CC BY-NC-SA 4. 0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Германом (OpenStax) через исходный контент, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

  1. Наверх
  • Была ли эта статья полезной?

  1. Тип изделия

     Раздел или страница

     Автор

     ОпенСтакс

     Лицензия

     CC BY-NC-SA

     Версия лицензии

     4,0

     Программа OER или Publisher

     ОпенСтакс

     Показать страницу Содержание

     нет

  2. Теги

     1. автор @ Эдвин «Джед» Герман
     2. автор@Гилберт Странг
     3. Производная функции косеканса
     4. Производная функции косинуса
     5. Производная функции котангенса
     6. Производная секущей функции
     7. Производная синусоидальной функции
     8. Производная функции тангенса
     9. https://math.

        No related posts.