Высота цилиндра 15 см а радиус его основания равен 4 см: Высота цилиндра 15 см, а радиус его основания равен 4 см. Найдите периметр прямоугольника АВСД,…

КОМБИНАЦИИ ГЕОМЕТРИЧЕСКИХ ТЕЛ — Мегаобучалка

ТЕЛА ВРАЩЕНИЯ

Цилиндр.

I уровень

1.1. Найдите диагональ осевого сечения цилиндра, высота которого равна 8 см, а радиус основания – 3 см.

1.2. Осевое сечение цилиндра – квадрат, площадь которого 64 см². Найдите площадь основания цилиндра.

1.3. Площадь осевого сечения цилиндра равна S. Найдите площадь его боковой поверхности.

1.4. Высота цилиндра равна 12 см, диагональ осевого сечения – 13 см. Найдите площадь боковой поверхности цилиндра.

1.5. Диагональ осевого сечения цилиндра равна см и составляет угол 45º с плоскостью основания. Найдите площадь боковой поверхности цилиндра.

1.6. Цилиндр образован вращением прямоугольника вокруг меньшей из сторон. Найдите площадь полной поверхности цилиндра, если диагональ прямоугольника равна 6 см и наклонена к большей стороне под углом 30º.

1.7. Определите давление кирпичной цилиндрической колонны на фундамент, если высота колонны равна 2 м, диаметр основания равен 0,75 м. Вес одного кубического метра кирпича необходимо принять равным 1,8 т.

1.8. Развертка боковой поверхности цилиндра – квадрат со стороной 18 см. Найдите объем цилиндра.

1.9. Как изменится объем цилиндра, если радиус основания увеличить в три раза, а высоту уменьшить в четыре раза?

1.10. Два различных цилиндра имеют равные площади боковых поверхностей. Найдите отношение радиусов оснований, если их высоты относятся как 3 : 1.

II уровень

2.1. Цилиндр, радиус основания которого равен 13 см, а высота – 10 см, пересечен плоскостью так, что в сечении получился квадрат. Определите, на каком расстоянии от оси цилиндра проведено сечение.

2.2. Через образующую цилиндра проведены две взаимно перпендикулярные плоскости. Площадь каждого из полученных сечений равна 71 дм². Найдите площадь осевого сечения цилиндра.

2.3. Радиус основания цилиндра в три раза меньше его высоты. Найдите угол между диагоналями осевого сечения цилиндра.

2.4. Цилиндрическая дымовая труба диаметром 60 см имеет высоту 20 м. Определите, сколько квадратных метров листового железа потребуется на ее изготовление, если на заклепки уходит 10 % всего необходимого количества железа.

2.5. Развертка боковой поверхности цилиндра – квадрат. Найдите объем цилиндра, если радиус его основания на 3 см меньше высоты.

2.6. Площадь основания цилиндра равновелика площади развертки его боковой поверхности. Найдите тангенс угла наклона диагонали осевого сечения к плоскости основания цилиндра.

2.7. Прямоугольник со сторонами m и b является разверткой боковых поверхностей двух различных цилиндров. Найдите отношение объемов этих цилиндров.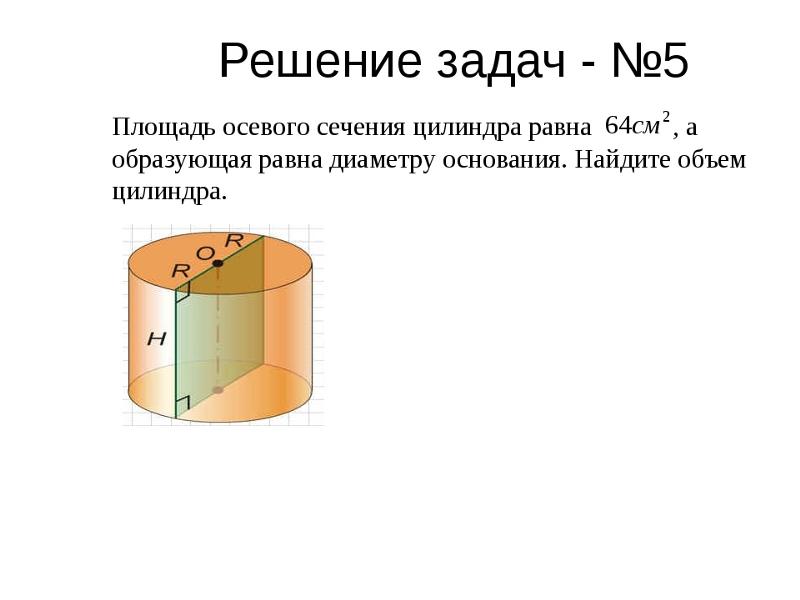

2.8. Кусок льда, имеющий форму прямоугольного параллелепипеда, размером 0,6 м ´ 0,4 м ´ 0,5 м, помещен в цилиндрический сосуд диаметра 0,9 м. Определите, какова будет высота слоя воды после того, как лед растает. Удельный вес льда необходимо считать равным 0,92 г/см³.

III уровень

3.1. Точка окружности верхнего основания цилиндра соединена с точкой окружности нижнего основания. Угол между радиусами, проведенными в эти точки, равен a. Найдите угол между осью цилиндра и отрезком, соединяющим данные точки, если высота цилиндра равна его диаметру.

3.2. К цилиндру проведена касательная прямая под углом a к плоскости основания. Определите расстояние от центра нижнего основания до прямой, если расстояние от центра до точки касания равно d, а радиус основания равен R.

3.3. Высота цилиндра равна радиусу его основания и имеет длину а. Через ось цилиндра проведена вторая цилиндрическая поверхность, которая делит окружность основания на две дуги, длины которых относятся как 2 : 1. Найдите объем большей части цилиндра, на которые цилиндрическая поверхность делит цилиндр.

3.4. Два равных цилиндра, высоты которых больше их диаметров, расположены так, что их оси пересекаются под прямым углом и точка пересечения осей равноудалена от оснований цилиндров. Найдите объем общей части этих цилиндров, если радиус каждого из них равен 1 см.

 

Конус. Усеченный конус

I уровень

1.1. Площадь основания конуса равна 16p см², образующая – 5 см. Найдите высоту конуса.

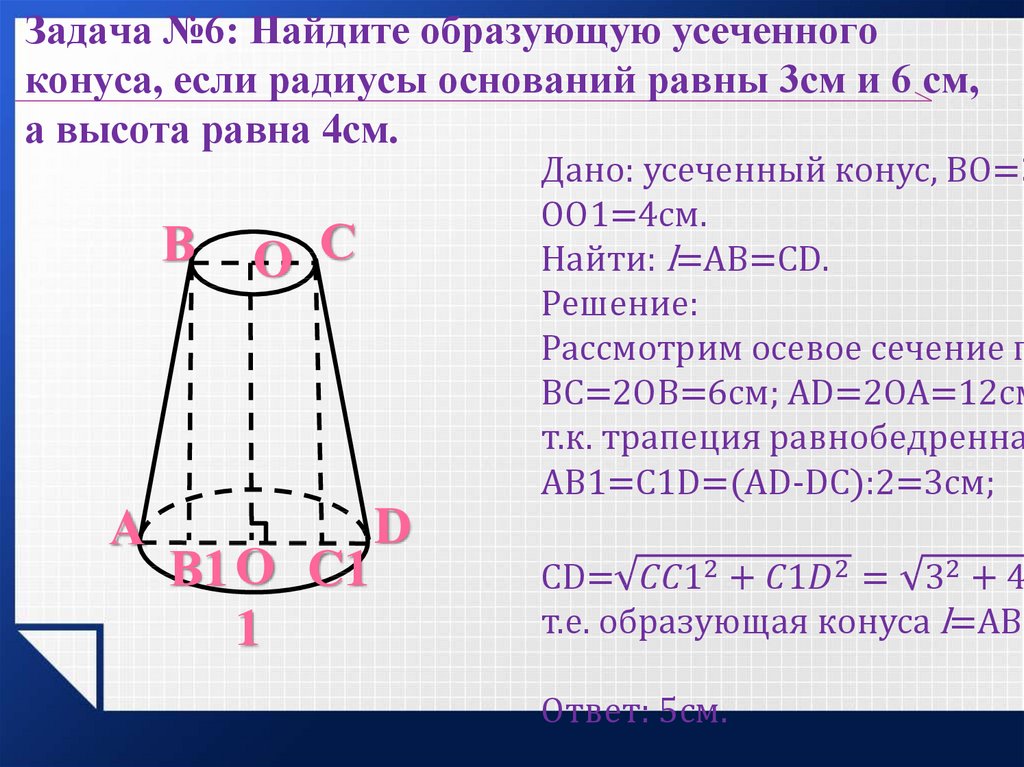
1.2. Высота усеченного конуса 8 см, радиус нижнего основания на 6 см больше радиуса верхнего основания. Найдите длину образующей усеченного конуса.

1.3. Крыша флигеля имеет коническую форму. Диаметр башни равен 12 м, высота крыши – 8 м. Найдите площадь поверхности крыши.

1.4. Определите, как изменится площадь боковой поверхности конуса, если радиус основания уменьшить в два раза, а образующую увеличить в три раза.

1.5. Щебень укладывается в кучу, имеющую форму конуса с углом откоса 30°. Определите, какой высоты должна быть куча, чтобы ее объем был равен 25 120 м³. (Число p принять равным 3,14).

1.6. Найдите объем конуса, высота которого 3 см, а осевое сечение – равносторонний треугольник.

1.7. В усеченном конусе через середину высоты, длина которой 5 см, проведено сечение, параллельное основаниям конуса. Найдите его площадь, если площадь осевого сечения усеченного конуса равна 30 см².

1.8. Высота усеченного конуса равна 6 см, радиусы оснований – 10 см и 2 см. Найдите площадь полной поверхности конуса.

1.9. Определите, сколько квадратных дециметров материала потребуется на изготовление ведра, если его размеры таковы: диаметр дна 20 см, высота 24 см, диаметр верхней части в два раза больше диаметра дна.

1.10. В усеченном конусе проведено осевое сечение, средняя линия которого равна 11 см.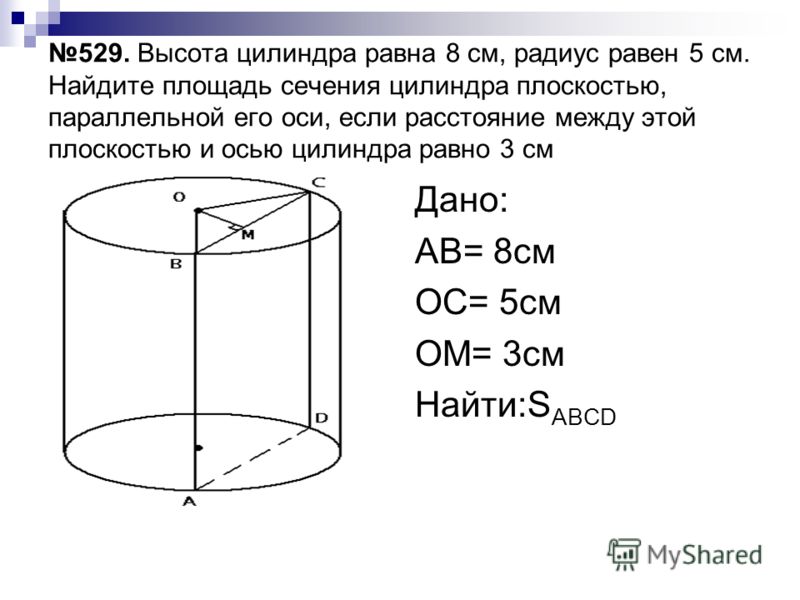 Высота усеченного конуса равна 8 см, а радиус одного из оснований больше другого на 3 см. Найдите объем усеченного конуса.

II уровень

2.1. Найдите высоту конуса, если площадь осевого сечения равна 13 см², а площадь основания – 14 см².

2.2. В конусе, радиус основания которого 5 см, проведено сечение, параллельное основанию на расстоянии 4 см от него. Площадь сечения равна 4p см². Найдите образующие конуса и усеченного конуса.

2.3. Угол развертки боковой поверхности конуса равен 120°. Образующая конуса равна 15 см. Найдите площадь полной поверхности конуса.

2.4. Образующая конуса равна 25 см, а середина его высоты отстоит от образующей на 6 см. Найдите площадь боковой поверхности конуса.

2.5. Площадь основания в два раза меньше площади боковой поверхности конуса. Найдите угол при вершине осевого сечения конуса.

2. 6. Для изготовления указки конической формы был взят брусок квадратного сечения размером 20 мм ´ 20 мм и длиной 500 мм. У полученной указки диаметр основания 18 мм и длина 500 мм. Найдите, какой процент материала пошел в отходы.

2.7. Найдите радиусы оснований усеченного конуса, если высота равна 12 см, образующая – 13 см, а диагональ осевого сечения – 20 см.

2.8. Длины окружностей оснований усеченного конуса равны 96p см и 66p см, а его высота – 20 см. Найдите площадь полной поверхности усеченного конуса.

2.9. Найдите площадь боковой поверхности усеченного конуса, если его образующая равна 17 см, а площадь сечения, проходящего через середину высоты параллельно основаниям, равна 196p см².

2.10. Объем усеченного конуса равен 2580p дм³, его высота равна 15 дм и составляет высоты полного конуса. Найдите радиусы оснований усеченного конуса.

III уровень

3.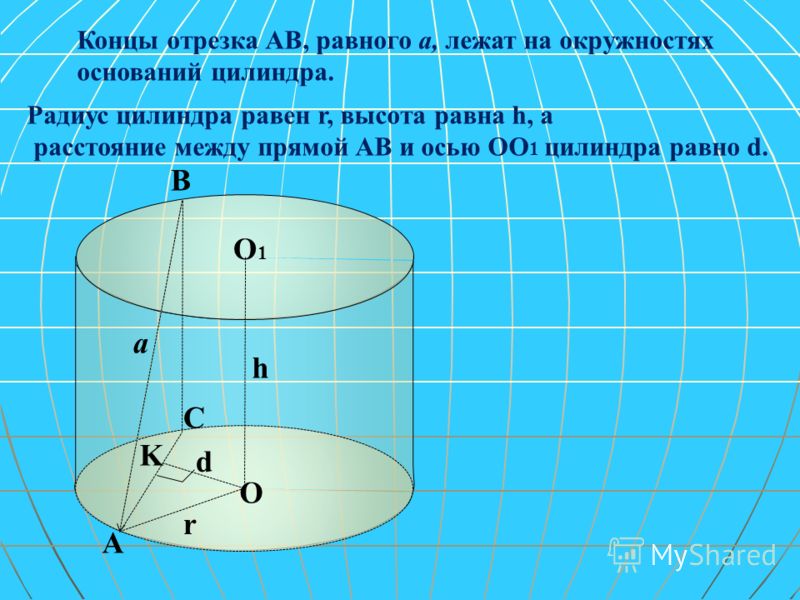 1. Радиус основания конуса равен R, образующая наклонена к плоскости основания под углом a. В конусе через вершину под углом j к его высоте проведена плоскость. Найдите площадь полученного сечения.

3.2.Площади оснований усеченного конуса равны 81p см² и 225p см², образующая относится к высоте как 5 : 4. Найдите площадь осевого сечения.

3.3.Диагонали осевого сечения усеченного конуса взаимно перпендикулярны. Площадь осевого сечения равна 324 см². Найдите площади оснований конуса, зная, что радиус одного основания на 2 см больше другого.

3.4. Дана трапеция ABCD, у которой AD = 15 см, BC = 9 см, AB = CD = 5 см. Трапеция вращается вокруг оси, проходящей через вершину A и перпендикулярно AD. Найдите площадь поверхности полученного тела вращения.

3.5. Прямая отсекает от сторон прямоугольного треугольника, угол между которыми 60°, отрезки, длины которых составляют четвертую часть длины гипотенузы, считая от вершины этого угла. Найдите отношение площади треугольника к площади поверхности тела, полученного при вращении этого треугольника вокруг прямой.

3.6. Конус лежит на плоскости и катится по ней, вращаясь вокруг своей неподвижной вершины. Высота конуса равна h, образующая – b. Найдите площадь поверхности, описываемой высотой конуса.

3.7. Два конуса имеют общее основание. В общем осевом сечении образующая одного из конусов перпендикулярна противолежащей образующей другого. Объем одного из них вдвое меньше объема другого. Найдите угол между образующей большего конуса и плоскостью оснований конусов.

3.8. Треугольник АВС, у которого АВ = 13 см, ВС = 20 см, АС = 21 см, вращается вокруг оси, проходящей через вершину А перпендикулярно АС. Найдите объем полученного тела вращения.

3.9. Параллелограмм вращается вокруг оси, проходящей через вершину острого угла перпендикулярно большей диагонали. Найдите объем тела вращения, если стороны параллелограмма и его большая диагональ равны соответственно 15 см, 37 см и 44 см.

3.10. Образующая усеченного конуса, равная l, наклонена к плоскости основания под углом a. Отношение площадей оснований конуса равно 4. Найдите объем усеченного конуса.

 

Шар.

.I уровень

1.1. В шаре на расстоянии 9 см от центра проведено сечение, площадь которого равна 144p см². Найдите радиус шара.

1.2. Два равных шара радиусом R = 17 см, взаимно пересекаясь, образуют двояковыпуклую линзу. Найдите ее диаметр, если расстояние между центрами шаров равно R.

1.3. Найдите высоту шарового сегмента, если радиус его основания равен 15 см, а радиус шара – 25 см.

1.4. Шар, радиус которого 15 см, пересечен плоскостью на расстоянии 9 см от центра. Найдите площадь сферической части шарового сегмента.

1.5. Найдите площадь сферы, диаметр которой равен диагонали куба с ребром, равным 2 см.

1.6. Определите, во сколько раз объем Земли больше объема Луны. (Диаметр Земли следует принять за 13 тыс. км, диаметр Луны – 3,5 тыс. км.)

1.7. Объем стенок полого шара равен 876p см³, а толщина стенок – 3 см. Найдите радиусы наружной и внутренней поверхностей шара.

1.8. Найдите объем шарового сектора, если радиус шара равен 10 см, а радиус основания соответствующего шарового сегмента – 6 см.

1.9. Объем одного шара в 8 раз больше объема другого шара. Определите, во сколько раз площадь поверхности первого шара больше площади поверхности второго.

II уровень

2.1. Стороны треугольника, равные 5 см, 5 см и 6 см, касаются шара, радиус которого 2,5 см. Найдите расстояние от центра шара до плоскости треугольника.

2.2. На поверхности шара даны три точки. Расстояния между ними равны по 7 см. Радиус шара равен 7 см. Найдите расстояние от центра шара до плоскости, проходящей через данные три точки.

2.3. Радиусы оснований шарового слоя равны 63 см и 39 см, его высота – 36 см. Найдите радиус шара.

2.4. Дан шар радиуса 12 см. Через одну точку его поверхности проведены две плоскости: первая поверхность касается шара, вторая – под углом 60° к радиусу, проведенному в точку касания. Найдите площадь сечения.

2.5. Определите, какую площадь имеет часть поверхности шара, которая видна наблюдателю, находящемуся на расстоянии 10 м от него, если радиус воздушного шара равен 15 м.

2.6. Шар пересечен двумя плоскостями, проходящими через одну точку поверхности шара и образующими угол 60°. Радиус шара равен 4 см. Найдите площади поверхностей отсекаемых сегментов, если окружности их оснований имеют равные радиусы.

 

2. 7. Шар касается граней двугранного угла в 120°. Расстояние от центра шара до ребра угла равно 10 см. Найдите площадь поверхности шара.

2.8. Из шара вырезали шаровой слой, толщина которого равна 9 см, площади оснований – 400p см² и 49p см². Найдите объемы оставшихся шаровых сегментов.

2.9. Диаметр шара разделен на четыре равные части и через точки деления проведены секущие плоскости, перпендикулярные диаметру. Найдите объемы полученных частей шара, если его радиус равен R.

2.10. В шаре радиуса R просверлено цилиндрическое отверстие. Ось цилиндра проходит через центр шара, диаметр отверстия равен радиусу шара. Найдите объем оставшейся части шара.

III уровень

3.1. Плоскости двух сечений шара взаимно перпендикулярны. Одна из этих плоскостей проходит через центр шара, другая – удалена от него на 12. Общая хорда сечений равна 18.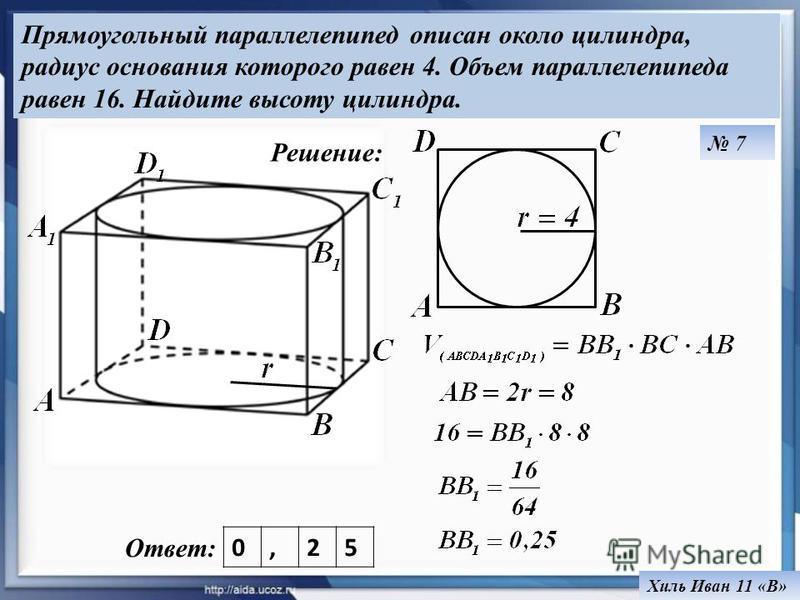 Найдите сумму площадей этих сечений.

3.2. Радиус шара равен 15 м. Вне шара дана точка А на расстоянии 10 м от его поверхности. Найдите радиус такой окружности на поверхности шара, все точки которой отстоят от точки А на 20 м.

3.3. Из точки, взятой на поверхности шара, проведены три равные хорды, угол между каждой парой которых равен a. Найдите длину хорды, если радиус шара равен R.

3.4. Два шара внутренне касаются в точке А, АВ – диаметр большего из шаров, ВС – касательная к меньшему из них. Найдите радиусы шаров, если ВС = 20 см, а разность площадей поверхностей шаров равна 700p см².

3.5. Вычислите объем шара, радиус которого равняется ребру октаэдра, имеющего поверхность площадью

3.6. Круговой сектор с углом 60° и радиусом R вращается около одного из боковых радиусов. Найдите объем полученного тела вращения.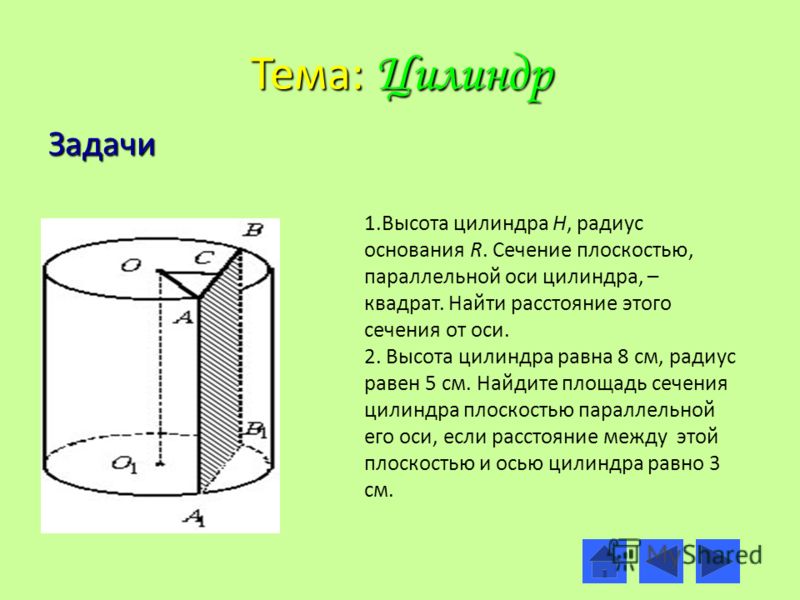

 

КОМБИНАЦИИ ГЕОМЕТРИЧЕСКИХ ТЕЛ.

Найти объем цилиндра онлайн

Пример решили: 18677 раз Сегодня решили: 0 раз

Введите радиус цилиндра и высоту

Радиус r Высота h

Вычисление объема прямого кругового цилиндра

Скачать решение в PDF

Порекомендуйте наш сервис друзьям

Вконтакте

Facebook

Twitter

Одноклассники

Google+

Данный сервис поможет вам найти объём цилиндра онлайн.

Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями. Цилиндрическая поверхность – поверхность, производимая движением прямой линии AB (образующей), сохраняющей одно и то же направление и пересекающей данную линию (направляющую).

Объём прямого кругового цилиндра равна произведению квадрата радиуса на высоту и на π:

$$V = \pi \cdot r^2 \cdot h$$

Примеры решений

1. Найдите объем цилиндра, если его радиус равен 5 см , а высота 4 см. 3 $$

Попробуйте другие сервисы

• Найти объем параллелепипеда

• Найти объем куба

• Найти объем шара

• Найти объем усеченного конуса

• Найти объем усеченной пирамиды

Калькулятор высоты цилиндра

Этот калькулятор высоты цилиндра быстро находит высоту прямого кругового цилиндра десятью различными способами . Интересно, как найти высоту цилиндра? Просто выберите два известных параметра, введите указанные значения и вычислите высоту.

Продолжайте читать, если хотите узнать, какова возможная высота цилиндра. В большинстве случаев вы можете оценить его, зная только две из следующих величин:

• Радиус ;
• Том ;
• Самая длинная диагональ ;
• Площадь основания ;
• Площадь боковой поверхности ; или
• Общая площадь поверхности .

Наш калькулятор высоты цилиндра представляет собой удобный инструмент, предназначенный для правильного кругового цилиндра . Этот тип цилиндра состоит из двух конгруэнтных окружностей (называемых основаниями ). Они лежат точно одна над другой, и поэтому мы называем это 9.0003 правый цилиндр. С другой стороны, если одно из оснований сдвинуто, то цилиндр косой . Термин круговой более очевиден — основания имеют форму кругов. Вы должны помнить, что слово цилиндр может соответствовать разным формам (обобщенный цилиндр), но обычно мы имеем в виду правильный круговой цилиндр.

Калькулятор отвечает на вопрос как найти высоту цилиндра . Если вы хотите оценить другие параметры, ознакомьтесь с нашим расчетом правильного цилиндра! 92 — \frac{2}{\pi}A_\mathrm{b}}h=d2−π2​Ab​

​

10. Даны боковая площадь и общая площадь :

h=Al2π(A−Al)\quad h = \frac{A_\mathrm{l}}{\sqrt{2 \pi (A — A_\mathrm{l})}}h=2π(A−Al ​)

​Al​​

Вас интересуют расчеты прямоугольного цилиндра? Вам обязательно нужно проверить калькулятор объема цилиндра и калькулятор площади поверхности цилиндра!

Как найти высоту цилиндра

Калькулятор высоты цилиндра очень удобен для решения самых разных задач.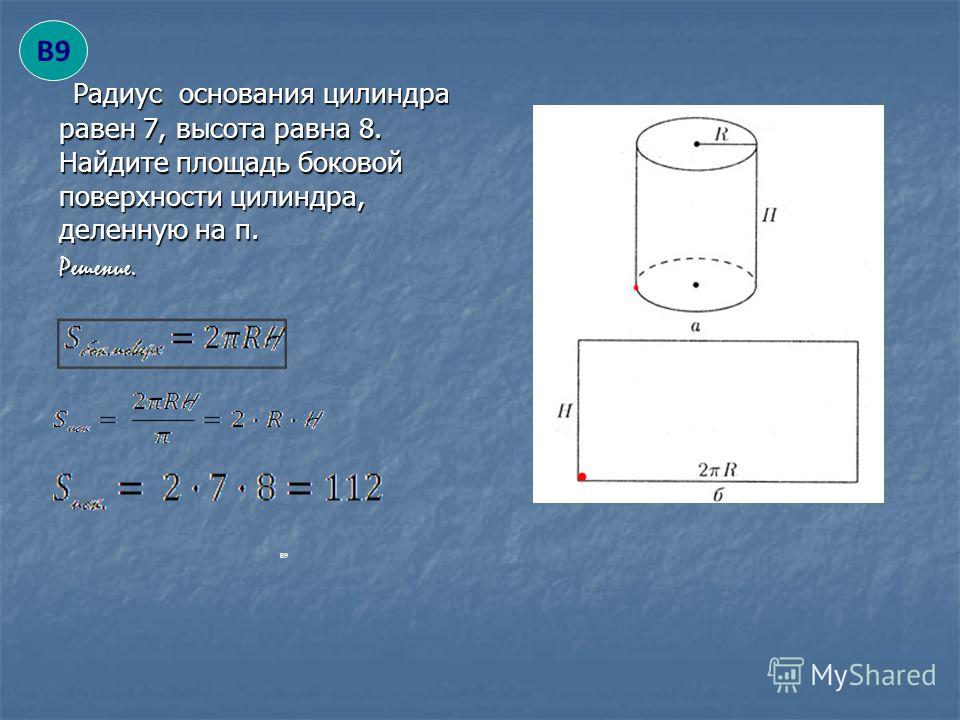 Иногда вы знаете объем и площадь основания цилиндра, но не знаете его высоту. В другой раз у вас будут указаны только площади поверхности. Если вы когда-либо сталкивались с такой проблемой, используйте этот калькулятор, чтобы оценить высоту в три простых шага:

1. Определите , какие параметры цилиндра вы знаете. Их нужно иметь как минимум два.
2. Введите значения выбранных переменных.
3. Считать результат вычислений.

Помните, что с помощью калькулятора высоты цилиндра вы можете выбрать единицы измерения любого параметра. Обязательно ознакомьтесь с конвертером длины и инструментами преобразования объема. Они могут быть очень полезны во многих вычислениях.

Часто задаваемые вопросы

Как найти высоту цилиндра по площади его поверхности?

Чтобы найти высоту цилиндра по его общей площади поверхности и радиусу, выполните следующие действия:

1. Умножьте квадрат радиуса на 2π и вычтите

   значение из общей площади поверхности .

2. Разделите результат шага 1 на значение 2π × радиус .

3. Поздравляем! Вы вычислили высоту цилиндра.

Как рассчитать высоту цилиндра по объему и радиусу?

Чтобы рассчитать высоту цилиндра по его объему и радиусу, следуйте приведенным инструкциям:

1. Возьмите квадрат радиуса и умножьте это на π .

2. Разделить объем цилиндра на результат шага 1 .

3. Вы получите высоту цилиндра.

Какова высота цилиндра радиусом 5 см и объемом 900 см³?

11,46 см . Формула для расчета высоты цилиндра с учетом его объема и радиуса: высота = объем / (π × радиус²) .

Подставляя значения в формулу получаем, высота = 900 см³ / (π × 5 см × 5 см) = 11,46 см

Чему равна высота цилиндра, имеющего радиус 8 см и боковую поверхность площадь 1005,5 см²?

20 см . Для нахождения высоты цилиндра воспользуемся формулой высота = площадь боковой поверхности / (2π × радиус) .

Следовательно, высота цилиндра будет высоты = 1005,5 см² / (2π × 8 см) = 20 см .

Математическая задача: Поверхность — вопрос № 49121, алгебра, квадратное уравнение

Поверхность цилиндра 1570 см ² ; его высота 15 см. Найдите объем и радиус основания.

Правильный ответ:

V = 4712,389 см ³
r = 10 см

Пошаговое объяснение:

S=1570 см2 h=15 см S=2∗pi∗r(r+h) 1570=2⋅ 3,1415926⋅ r(r+15) −6,283185r2−94,248r+1570 =0 6,283185r2+94,248r−1570=0  a=6,283185;b=94,248;c=-1570 D=b2-4ac=94,2482−4⋅6,283185⋅(-1570)=48341,045457937 D>0  r1,2​=2a −b±D

​​=12.56637−94.25±48341.05

​​ r1,2​=−7.50000024±17.496378952553 r1​=9. 996378713821 r2​=−24.996379191286   Factored form of the equation:  6.283185(r−9.996378713821)(r +24,996379191286)=0  r=[r1​]=[9,9964]=10 см V=π⋅ r2⋅ h=3,1416⋅ 102⋅ 15=4712,389см3

Наш калькулятор квадратных уравнений вычисляет это.

Нашли ошибку или неточность? Не стесняйтесь

написать нам

. Благодарю вас!

Советы для связанных онлайн-калькуляторов

Вам нужна помощь в вычислении корней квадратного уравнения?
Совет: конвертер единиц объема поможет вам преобразовать единицы объема.

Для решения этой математической задачи вам необходимо знать следующие знания:

• Алгебра
• Квадратичное уравнение
• Экспрессия переменной из Формулы
• Сплошная геометрия
• Цилиндер
• Площадь поверхности

UNITS

. задача:

• средняя школа

• Поверхность цилиндра, объем
  Площадь основания и площадь оболочки относятся как 3:5. Его высота на 5 см меньше радиуса основания. Вычислите площадь поверхности и объем.
• Ролик
  Корпус цилиндра имеет ту же площадь, что и одно из его оснований. Высота цилиндра 15 дм. Чему равен радиус основания цилиндра?
• Цилиндр 60463
  Найдите поверхность и объем цилиндра, высота которого равна 10 дм, а радиус окружности основания равен 20 см.
• Цилиндр 2
  Найдите объем и площадь поперечного сечения цилиндра высотой 12 дюймов и радиусом основания 4 дюйма.
• Цилиндрический контейнер
  Цилиндрический контейнер с открытым верхом имеет объем V = 3140 см³. Найдите такие размеры цилиндра (радиус основания r, высота v), чтобы для изготовления сосуда потребовалось наименьшее количество материала.
• Площадь поверхности цилиндра
  Объем цилиндра, высота которого равна радиусу основания, составляет 678,5 дм³. Вычислите площадь его поверхности.
• Рассчитать 20893
  Объем цилиндра 193 см³, а радиус его основания 6,4 см. Вычислите высоту и поверхность цилиндра с точностью до 1 знака после запятой.
• Рассчитать 24011
  Имеется цилиндр с радиусом основания 3 см и высотой 12 см. Рассчитать а) поверхность цилиндра б) объем цилиндра
• Вычислить 24941
  Вычислить поверхность и объем цилиндра с радиусом основания 5 см и высотой 8 см.
• Цилиндр — основы
  Цилиндр с радиусом основания r = 54 см и высотой h = 35 см. Рассчитайте: а) Площадь основания
• Цилиндр S,V
  Каковы объем и площадь поверхности цилиндра, диаметр основания которого 3,15 см, а высота 25 см?
• Поверхность и объем
  Рассчитайте поверхность и объем цилиндра, высота которого равна 8 дм, а радиус основания равен 2 дм.
• Пропитанный соком 17173
  
  1. Найдите размеры 5-литровой цилиндрической емкости, если высота емкости равна радиусу основания. 2. В цилиндрическом стакане с внутренним диаметром 8 см находится 3 дл сока. Вычислите площадь пропитанного соком портвейна
• Цилиндрическое тело
  Найдите площадь поверхности цилиндрического тела, радиус которого 7,7 см, а высота 12 см.

  No related posts.