Пределы, пределы функций
Задача с касательнойДана функция f(x) и точка P(x0, y0) на графике этой функции. Найдите уравнение прямой, касательной к графику функции в точке P
Задача с площадью
Дана функция f, найдите площадь между графиком f и отрезеом [a,b] на x-axis
Прямая называется касательной к окружности, если она касается окружности только в одной точке.
Но это определение не является удовлетворительным для другого вида кривых, таких как
Прямая, являющаяся касательной, касается кривой более чем один раз.
Прямую, которая занимает эту позицию, мы рассматриваем как касательную в точке P.
Площади некоторых плоских фигур могут быть вычислены путем разделения их на конечное число прямоугольников или треугольников, а затем сложением площадей этих фигур.

Для многих площадей нужен более общий подход.
Аппроксимируем площадь этого области, вписывая прямоугольники одинаковой ширины под кривую и складывая площади этих прямоугольников.
Наша аппроксимация будет приближаться к точной площади под кривой как «предельное значение».
Давайте возьмем
f(x) = sin(x)/x
Где x — в радианах.
Предел справа
limx → 0+ sin(x)/x «Пределы функции f(x) когда x стремится к 0 справа»
Предел слева
limx → 0+ sin(x)/x
«Пределы функции f(x) когда x стремится к 0 слева.»
Переключив калькулятор в режим «радианы», мы получим
|
|
Когда x стремится к 0 слева или справа, f(x) стремится 1.
В таблице приведено несколько примеров пределов функций.

| ЗАПИСЬ | КАК ЧИТАТЬ ЗАПИСЬ |
| limx→ x0+ = L1 | Предел f(x) когда x стремится x0 справа, равен L1 |
| limx→ x0- = L2 | Предел f(x) когда x стремится x0 слева, равен L2 |
| limx→ x0 = L | Предел f(x) когда x стремится x0 равен L |
Числовые ловушки
f(x) = sin(φ/x)
limx → 0 sin(φ/x) = limx → 0+ sin(φ/x) = limx → 0- sin(φ/x)
Таблица 2.
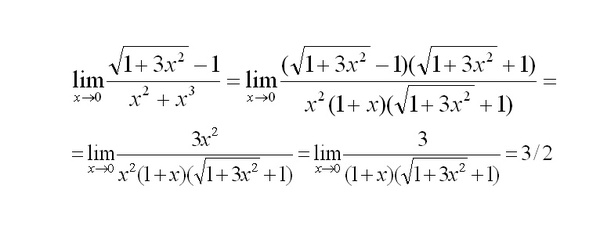 4.4
4.4 | x | f(x) | x | f(x) |
| 1 | 0 | -1 | 0 |
| 0.1 | 0 | -0.1 | 0 |
| 0.01 | 0 | -0.01 | 0 |
| 0.001 | 0 | -0.001 | 0 |
| 0.0001 | 0 | -0.0001 | 0 |
Существование пределов
limx→ x0- f(x) = limx→ x0+ f(x) = limx→ x0 f(x) = +∞
x стремится к x0 слева
limx→ x0- f(x) = limx→ x0+ f(x) = limx→ x0 f(x) = -∞
x стремится к x0 справа
Пример
limx→ x0- f(x) = -∞ limx→ x0+ f(x) = +∞
Предел функции не существует в X0
Пример
Here
limx→ —∞ f(x) = -1 limx → +∞ f(x) = 4
So, limit of function does not exist.

Example
Здесь
as x → -∞, f(x) → +∞
as x → +∞, f(x) → -2
Поэтому, предела функции не существует.
Пример
Здесь
as x → -∞, f(x) → -∞
as x → +∞, f(x) → oscillates
Поэтому, предела функции не существует.
исчисление — Каков предел |x| когда х приближается к 0?
Задавать вопрос
спросил
Изменено 4 года, 10 месяцев назад
Просмотрено 19 тысяч раз
$\begingroup$ 9+} \frac{|x|}{x} = 1$$
Почему делится на x, откуда это взялось? И, кроме того, почему оно приближается к 1, когда существуют другие числа, существующие между 1 и 0, к которым x может приблизиться.
- исчисление
- пределы
$\endgroup$
$\begingroup$
Чтобы ограничение существовало, вам нужны боковые ограничения для поездок на работу. В этом случае: 9-} -x, \space x<0\end{cases} = \begin{cases} 0, \space x \geq 0 \\ 0, \space x <0 \end{cases}$$
что означает, что боковые пределы равны и таким образом: $\lim_{x \to 0} |x| = 0$.
Что касается части $\frac{|x|}{x}$, если вы делите что-то на количество, вам также нужно будет умножить это на это число. Вот почему вы получаете $1$ за неправильный ответ.
$\endgroup$
3$\begingroup$
У вас есть $\lim_{x\to0}|x|=0$, потому что для каждого $\varepsilon>0$, если взять $\delta=\varepsilon$, то $$|x|<\delta\ подразумевает|x|<\varepsilon\iff\bigl||x|-0\bigr|<\varepsilon. $$
$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Расчет— Нахождение предела при приближении $x$ к $0$
спросил
Изменено 5 лет, 3 месяца назад
Просмотрено 3к раз
$\begingroup$
Сегодня на уроке математического анализа мне показали вышеупомянутую задачу.
Однако я не понимаю, какова точная связь между этими двумя пределами. Моя ТА прошла через это довольно быстро. Кто-нибудь может объяснить, что он хотел сказать?
- исчисление
- пределы
$\endgroup$
3 92+1})$ и $f'(0)=0$
Таким образом, предел равен $0$
$\endgroup$
2
$\begingroup$
Это следует рассматривать как комментарий, который слишком длинный, чтобы поместиться в поле комментария.
Техника, указанная в вашем вопросе, заключается в наблюдении за тем, что предел имеет форму $$\lim_{x\to a} \frac{f(x) — f(a)} {x-a} $$ для подходящего $f$ и $a$, и тогда вы можете просто оценить это как $f'(a) $.

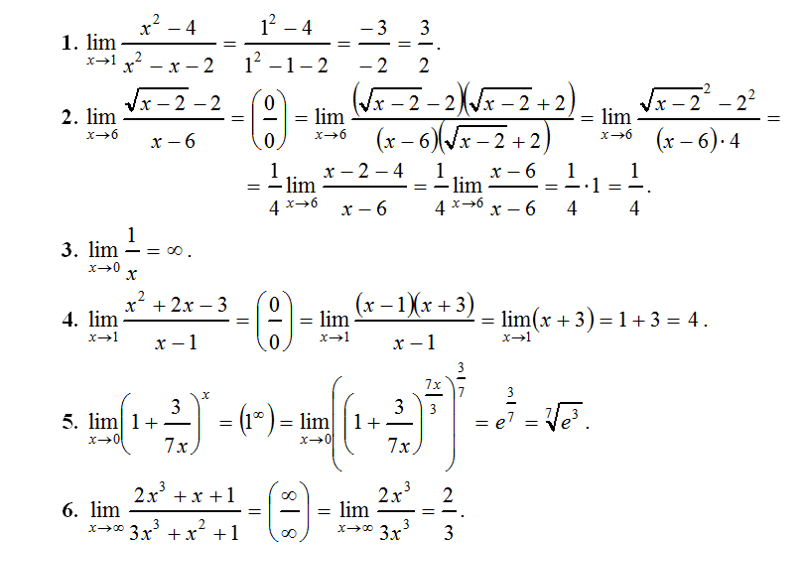 89670
89670