ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I.  ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ§ 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11. 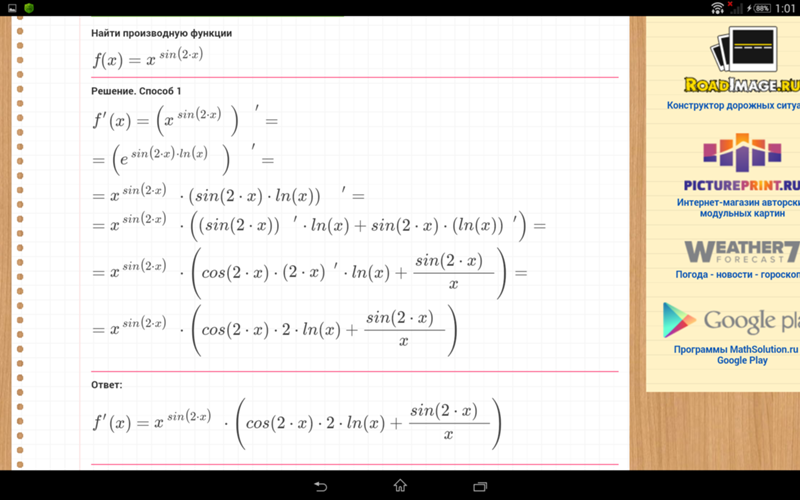 n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 23.  x, sin x, cos xУпражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2.  Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратов§ 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  Формула Чебышева§ 10. Интегралы, зависящие от параметра. Гамма-функция Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII |
4. Производная неявной функции
Определение
2. Если
функция у = f(x), определенная на некотором
интервале (а; b), такова, что уравнение
F(x; y) = 0 при подстановке в него у = f(x)
обращается в тождество относительно
х, то функция y = f(x) называется неявно
заданной уравнением F(x; y) = 0.
Чтобы найти производную неявной функции у по аргументу х, заданной уравнением F(x; y)=0, необходимо продифференцировать левую и правую части этого уравнения, считая у функцией от х . Из полученного линейного уравнения находим искомую производную.
Пример 3. Вычислить производную неявной функции.
x2 + x2y + y2x + y2 + 3 = 0.
Решение
2x + 2xy + x2 2y= 0
Вычислить производные неявных функций
75. x3 + y3 3xy = 0 76. x2 + y2 = 4
77.
x4
6x
79.
x sin y + y sin x = 0 80. ex +
ey
2xy
1 = 0
81. 82. x2 sin y + y2 cos x = 0
83. 84. еу/х ex/y = 1
85. xy + yx = 0 86. + y2 ln x = 4
5. Производные высших порядков
Определение 3. Производная называется производной первого порядка.
Производная от называется производной второго порядка или второй производной от функции f(x) и обозначается,,
или .
Производная от называется производной третьего порядка или третьей производной от функции f(x) и обозначается,,
или и т.д.
Производная n-го порядка есть производная от производной (n-1)-го порядка, т.е. .
Пример
4.
Найти
производную второго порядка от функции
у=.
Решение
Найти производные второго порядка от функций:
87. у = tg x 88. y = ctg x
89. y = sin2x 90. y = cos2x
91. y = 92. y = ln (2x3)
93. y = x sin x 94. y =
95. y = 2x 96. y = e1/x
97. y = x2 ln x 98. y = ax x3
99. 100. y = ln
6. Правило Лопиталя Устранение неопределенностей вида ,
Правило
Лопиталя.
Если
функции f(x) и g(x) дифференцируемы в
некоторой окрестности точки x0 за исключением, быть может самой точки
x0,
причем, в этой окрестности
и, если== 0 или==
, то
,
если последний предел существует.
Иными словами, для неопределенностей вида илипредел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).
Здесь x0 может быть числом, +, либо.
Пример 5. Вычислить предел .
Решение. Имеем неопределенность вида . Для ее устранения воспользуемся правилом Лопиталя
Пример 6. Вычислить предел .
Решение. Имеем неопределенность вида . Применяя трижды правило Лопиталя, получим
.
Вычислить пределы
101.
102.
103. 104.
105. 106.
107. 108.
109. 110.
111. 112.
113. 114., a >1
115. 116.
117. 118.
119. 120.
121. 122.
7. Неопределенности вида 0 , 00, 1, 0 и их устранение
Неопределенность вида 0 сводится путем алгебраических преобразований к неопределенностям вида , а затем раскрываются с помощью правила Лопиталя.
Неопределенности вида 00, 1, 0 с помощью тождества
f(x)g(x) eg(x) lnf(x)сводятся к неопределенности вида 0 .
Пример 7. Вычислить предел
Решение. Имеем неопределенность вида 0.
Но x ln |x| =
получена неопределенность вида
.
Применяя правило Лопиталя, получим=.
Пример 8. Вычислить предел
Решение. Имеем неопределенность вида 00. Но xx = ex ln x и получаем в показателе степени неопределенность вида 0 , которая рассмотрена в предыдущем примере. Следовательно
.
Пример 9. Вычислить .
Решение. Имеем неопределенность вида 1. Но (1 + x)1/x = e1/xln(1+x)
и в показателе степени получена неопределенность вида . Устраним ее, используя правило Лопиталя.
.
Пример 10. Вычислить .
Решение. Имеем неопределенность вида 0.
Но и в показателе степени получена неопределенность видаПрименяя правило Лопиталя, находим
Следовательно
.
Вычислить пределы
123. 124.
125. 126.
127. 128.
129. 130.
131. 132.
133. 134.
135. 136.
137. 138.
139. 140.
141. 142.
{b}} \right)=b\log \left( a \right)$Где $a,b$ может быть любой константой или переменной
Получаем,
$\log \left( y \right)=x\ log \left( 5 \right)$…..$\left( 2 \right)$
Дифференцируя уравнение (2) по $x$ с помощью неявного дифференцирования получаем,
$\begin{align}
& \log \left( y \right)=x\log \left( 5 \right) \\
& \Стрелка вправо \dfrac{1}{y}\times \dfrac{dy}{dx}=\log \left( 5 \ right)\times \dfrac{d\left( x \right)}{dx} \\
& \Стрелка вправо \dfrac{1}{y}\times y=\log \left( 5 \right)\times 1 \ \ 9{x}}{{\log }_{e}}5$.
Экспоненциальное правило для производной: теория и приложения
Когда дело доходит до расчета производной, существует эмпирическое правило, которое звучит примерно так: либо функция является базовой , и в этом случае мы можем обратиться к таблица производных , или функция составная , и в этом случае мы можем дифференцировать ее рекурсивно — разбив ее на производные ее составляющих через ряд производных правил .
{r-1}$ для всех $x \in \mathbb{R}$ . В случае, когда $r$ меньше $1$ (и 9{r-1}$ для всех $x \ne 0$.
Правило сумм
Если функция $f+g$ корректно определена на интервале $I$, причем $f$ и $g$ , обе дифференцируемы на $I$, то $\displaystyle (f+ g)’ = f’ + g’$ на $I$.
Правило разности
Если функция $f-g$ корректно определена на интервале $I$, причем $f$ и $g$ дифференцируемы на $I$, то $\displaystyle (f-g)’ = f’ – g’$ на $I$.
Правило произведения
Если функция $fg$ корректно определена на интервале $I$, где $f$ и $g$ равны 9{-1}(x)]} \qquad (x \in I) \end{align*}
(подробности см. в руководстве по теореме об обратной функции )
По большей части эти правила более чем достаточно для обработки подавляющего большинства функций, с которыми можно столкнуться. Однако, когда мы смотрим на наш репертуар функций , мы видим, что чего-то еще не хватает, а именно:
А как насчет функций, построенных с помощью возведения в степень ?
Здесь, подсказка необычное чувство безотлагательности, мы продолжаем играть с идеей производной степени , впоследствии закончив тем, что разработали правило именно для этой цели.
g (A+B)$, где:
- $A$ получается путем взятия производной степени , умноженной на логарифм основания .
- $B$ получается путем взятия производной от по основанию , умноженной на отношение с показателем степени наверху.
На самом деле, немного потренировавшись, можно освоить Экспонентное правило так же хорошо, как мы делаем это с Частным правилом — и это не говоря уже о том, какой новый мир он открывает для наших фанатики ментального исчисления !
Традиционно, чтобы вычислить производную степенной функции , нужно было бы либо прибегнуть к логарифмическому дифференцированию , либо стандартизации base-e перед дифференцированием. С появлением правила экспоненты оба эти подхода в основном устарели — не потому, что они неуместны сами по себе, а потому, что они уже применялись во время вывода правила экспоненты.
x$ и его производной здесь: 9{\, \ln x}$, из которого видно, что:
- $\ln x$ определяется только тогда, когда $x>0$.
- $\cos x>0$ только тогда, когда $\displaystyle -\frac{\pi}{2} < x < \frac{\pi}{2} \pmod{2\pi}$.
Таким образом, если мы обозначим через $I$ множество, удовлетворяющее обоим ограничениям. То есть
\begin{align*}I \stackrel{df}{=} \left\{ x \in \mathbb{R_+} \mathrel{\Big|} -\frac{\pi}{2} < x < \frac{\pi}{2} \,\, (\mathrm{mod \ } 2\pi ) \right\} \end{align*}
9{\, \ln x}}$ и его производная. Довольно круто. Верно? Да. Это было немного перебором символов, но, надеюсь, это иллюстрирует, почему правило экспоненты может быть ценным активом в нашем арсенале производных правил . В то время как для простой степенной функции этот подход может показаться излишним , для неоднократно возводимых в степень степенных функций с одной вложенной внутри другой, становится очевидным, что правило экспоненты является абсолютно правильным.
В дополнение к автоматизации процесса дифференцирования степенных функций, правило экспоненты — особенно когда сочетает с другими традиционными производными правилами — действительно может творить чудеса с точки зрения использования функций, которые ранее были слишком пугающими / утомительные для решения — например, те, которые нам трудно найти в типичном учебнике по математическому анализу. 🙂
В любом случае, давайте пока на этом закончим. Для полноты картины вот interactive table summarizing what we have discovered thus far:
- Standard Derivative Rules
- Exponent Rule (Theory)
- Exponent Rule (Examples)
| Constant Rule |
| Power Rule |
| Правило суммы |
| Правило разности |
| 6 9 Правило произведения6 9{\, \ln x} )} \right]’ = $ вы знаете |
Короче говоря, несмотря на то, что правило экспоненты относительно неизвестно, оно может быть мощным инструментом дифференцирования в нашем распоряжении.