Доказательство несчетности Кантора и рациональные числа. : Чулан (М)
| Sneg0vik |
| ||
21/10/10 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Sneg0vik |
| ||
21/10/10 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Sneg0vik |
| ||
21/10/10 |
| ||
| |||
| Dan B-Yallay |
| |||
11/12/05 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 6 ] |
Модераторы: Модераторы Математики, Супермодераторы
Является ли квадратный корень из 3 рациональным числом?
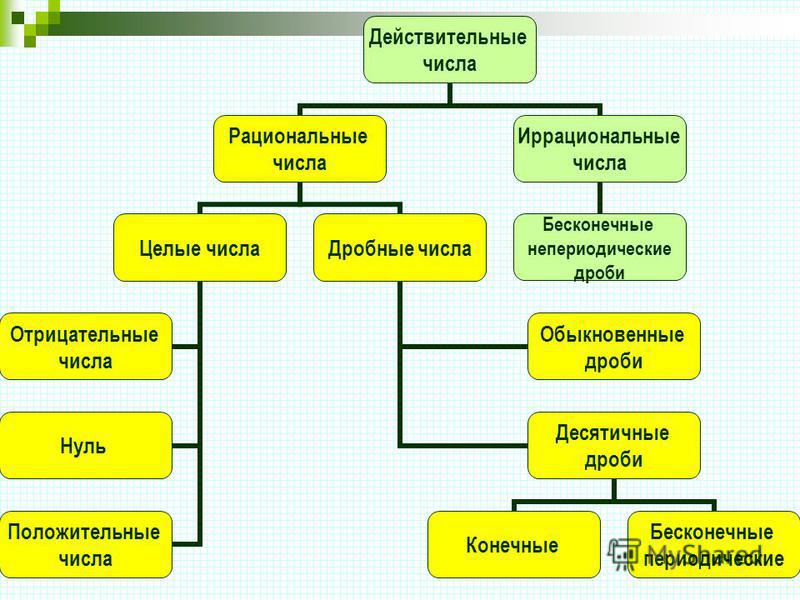
Действительные числа, которые не могут быть представлены простой дробью, называются иррациональными числами. Его нельзя представить в виде отношения типа p/q, где p и q — целые числа, q≠0. Это несоответствие рациональных чисел. Иррациональные числа обычно записываются как R \ Q, где знак обратной косой черты означает «установить минус». Его также можно записать как R-Q, что представляет собой разницу между набором действительных и рациональных чисел.
Его нельзя представить в виде отношения типа p/q, где p и q — целые числа, q≠0. Это несоответствие рациональных чисел. Иррациональные числа обычно записываются как R \ Q, где знак обратной косой черты означает «установить минус». Его также можно записать как R-Q, что представляет собой разницу между набором действительных и рациональных чисел.
Вычисления, основанные на этих цифрах, немного сложнее. К иррациональным числам относятся √5, √11, √21 и так далее. Если такие числа используются в арифметических операциях, сначала должны быть оценены значения под корнем.
Что такое рациональные числа? Рациональные числа имеют вид p/q, где p и q — целые числа, а q ≠ 0. Из-за лежащей в основе структуры чисел, формы p/q, большинству людей трудно отличить дроби от рациональных чисел. Когда рациональное число делится, вывод находится в десятичной форме, которая может быть как оканчивающейся, так и повторяющейся. 3, 4, 5 и т. д. — некоторые примеры рациональных чисел, поскольку они могут быть выражены дробью как 3/1, 4/1 и 5/1.
Иррациональные числа — это любые числа, не являющиеся рациональными числами. Иррациональные числа могут быть представлены десятичными знаками, но не дробями, что означает, что они не могут быть представлены как отношение двух целых чисел. После запятой иррациональные числа имеют бесконечное количество неповторяющихся цифр.
Вещественное число, которое не может быть представлено как отношение целых чисел, называется иррациональным числом. Например, √2 — иррациональное число.
Десятичное расширение иррационального числа не заканчивается и не повторяется. Определение иррационального — это число, которое не имеет отношения или для которого нельзя установить отношение, то есть число, которое не может быть представлено никаким другим способом, кроме как с использованием корней. Иными словами, иррациональные числа нельзя представить в виде отношения двух целых чисел.
Примеры иррациональных чисел
√2, √5, √7 и т. д. — некоторые примеры иррациональных чисел, поскольку они не могут быть выражены в форме p/q. Число Эйлера, золотое сечение, π и т. д. также являются примерами иррациональных чисел. 1/0, 2/0, 3/0 и т. д. иррациональны, потому что дают нам неограниченные значения.
Является ли √3 рациональным числом?Решение:
Похожие вопросыИррациональные числа — это действительные числа, которые нельзя записать в виде p/q, где p и q — целые числа, а q≠0. Например, √2 и √5 и так далее иррациональны. Рациональное число — это любое число, которое можно записать в виде p/q, где p и q — целые числа, а q≠0.
Рациональное число — это своего рода действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √3 не может быть выражено в виде p/q.
Альтернативно, 3 — простое число или рациональное число, но √3 — не рациональное число.
Здесь заданное число √3 равно 1,73205080756, что дает результат бесконечного и неповторяющегося десятичного числа и продолжает расширяться, и не может быть выражено дробью .., поэтому √3 является иррациональным числом.
Вопрос 1: Является ли √7 рациональным или иррациональным числом?
Ответ:
Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √7 не может быть выражено в виде p/q. Альтернативно, 7 является простым числом. Это означает, что число 7 не имеет пары и не делится на 2. Следовательно, √7 — иррациональное число.
Вопрос 2: Определите, является ли 5.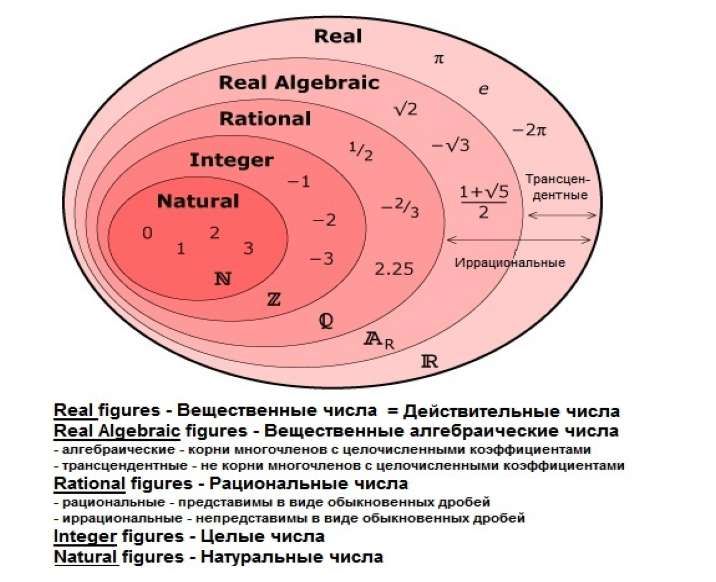 152152…. является рациональным числом.
152152…. является рациональным числом.
Ответ:
Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь заданное число 5.152152…. имеет повторяющиеся цифры. Следовательно, 5,152152…. является рациональным числом.
Вопрос 3: Является ли √11 рациональным или иррациональным числом?
Ответ:
Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √11 не может быть выражено в виде p/q. Альтернативно, 11 — простое число. Это означает, что число 11 не имеет пары и не делится на 2. Следовательно, √11 — иррациональное число.
Вопрос 4: Определите, является ли 8,2333 рациональным или иррациональным числом.
Ответ:
Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь заданное число 8,2333…. имеет завершающие цифры и повторяется после запятой. Следовательно, 8,2333 — рациональное число.
Является ли ноль рациональным числом?
18 августа 2021 г.
Является ли ноль рациональным числом?
Если в настоящее время вы изучаете целые числа на уроке математики, возможно, вы обнаружите, что следующей темой вашего учителя станут рациональные числа. Они могут спросить класс: «Является ли ноль рациональным числом?» Хотя вы знаете определение рационального числа, этот вопрос может поставить вас в тупик.
Знание основных свойств целых и рациональных чисел может показаться разовым уроком в вашей математической карьере, но способность полностью понять цель и правила рациональных чисел может напрямую помочь вам с другими сложными математическими понятиями. Вместо того, чтобы просто думать о старом учении о том, что урок математики будет относиться только к вашему конкретному уроку, викторинам и тестам, правильное понимание рациональных чисел может помочь вам научиться решать многошаговые задачи в будущем.
Вместо того, чтобы просто думать о старом учении о том, что урок математики будет относиться только к вашему конкретному уроку, викторинам и тестам, правильное понимание рациональных чисел может помочь вам научиться решать многошаговые задачи в будущем.
Кроме того, изучение рациональных чисел и освоение целых чисел поможет вам понять, как все эти математические понятия соотносятся друг с другом по мере вашего обучения. Изучение связи между рациональными числами облегчает понимание математики в целом.
Используя навыки критического мышления, чтобы найти ответы на такие вопросы, как «является ли ноль рациональным числом?», вы сможете упростить сложные уравнения и найти решение.
Во-первых, что такое рациональное число?
Прежде чем вы сможете определить, является ли ноль рациональным числом, нам нужно освежить ваше определение рациональных чисел. Рациональное число — это любое число, которое может быть представлено как a над b , где b не равно нулю. Вот так:
Вот так:
Таким образом, практически любую дробь, с которой вы работали в прошлом, можно определить как рациональное число. Единственным условием является то, что «нижнее» число в дроби — также известное как знаменатель — не может быть равно нулю. Следовательно, все целые числа рациональны, поскольку любое рациональное целое число можно представить в виде дроби с 1 в ячейке знаменателя.
Но как отличить рациональные числа от иррациональных? Иррациональные числа не могут следовать правилу, согласно которому их можно представить как a над b , где b не равно нулю.
В этом случае вы можете встретить иррациональные числа следующего вида:
При просмотре дроби иногда числитель может быть равен нулю. Это означает, что a может равняться нулю, но b не равно нулю. Для новичков простое появление нуля в уравнении иногда может сбить с толку их мыслительный процесс. Однако имейте в виду, что рациональное число с нулем в числителе можно легко упростить следующим образом:
Однако имейте в виду, что рациональное число с нулем в числителе можно легко упростить следующим образом:
Поскольку наибольший общий знаменатель между 0 и 12 равен 0, вы можете упростить дробь рационального числа с нулем в числителе. путем деления обоих целых чисел на ноль. Если вы видите дробь с нулем в числителе, ответ будет ВСЕГДА равно нулю.
Примеры рациональных чисел
Некоторые примеры рациональных чисел включают ¼, ⅔, 0/1, 8/6 и т. д. Как видите, одно из включенных сюда чисел было на 0 больше другого числа — это считается рациональным числом, поскольку знаменатель может быть либо положительным, либо отрицательным числом и не равен нулю.
Операции над рациональными числами
То, что число является дробью или содержит ноль внутри дроби, не означает, что арифметические операции невозможны. Арифметические операции — это основные процессы функций, которые вы можете использовать с целыми числами, включая сложение, вычитание, умножение и деление.
- Сложением можно сложить два дробных рациональных числа, сделав знаменатель одинаковым.
- При вычитании сделать знаменатель одинаковым числом перед вычитанием одного рационального числа из другого.
- В случае умножения двух рациональных чисел убедитесь, что вы умножаете и числитель, и знаменатель рациональных чисел.
- Когда дело доходит до деления дроби, вы должны вычислить обратное значение рационального числа. В этом процессе поменяйте местами числитель и знаменатель.
- Например, 2/4 сменится на 4/2. Вы можете перепроверить свою работу, перемножив два значения вместе, чтобы увидеть, равны ли они 1, с уравнением (2/4)x(4/2)=1.
Что такое иррациональные числа?
Существуют явные различия между рациональными и иррациональными числами. Теперь, когда вы знаете, что рациональные числа — это любые целые числа, которые могут быть выражены как a/b, где b не равно нулю, вы можете сузить все целые числа, не соответствующие этой формуле, до иррациональных чисел.
Рациональные числа — это либо положительные числа, либо отрицательные числа, либо эквивалентные нулю. Однако иррациональные числа не могут быть записаны в виде a/b, а должны быть записаны в виде десятичной дроби.
Одним из самых распространенных иррациональных чисел является Пи (), которое имеет бесконечные цифры после запятой. Если вы когда-то изучали геометрию, то знаете, что Пи — это отношение длины окружности к ее диаметру — число, которое получается приблизительно равным 3,14. Однако это решение является всего лишь приближением, но недостаточно точным, чтобы его можно было записать в виде дроби или классифицировать как рациональное число. Поскольку десятичные цифры числа Пи почти бесконечны, вы не может использовать простую дробь, которая представляет Пи.
Кроме того, число Эйлера () — еще одно иррациональное число, которое нельзя упростить или записать в виде дроби. Это число является основанием натуральных логарифмов и важным понятием, используемым в экспоненциальной функции. Число Эйлера обычно записывается как 2,718, но содержит более 1 триллиона десятичных знаков, что делает невозможным его составление в дробной форме.
Число Эйлера обычно записывается как 2,718, но содержит более 1 триллиона десятичных знаков, что делает невозможным его составление в дробной форме.
Другим распространенным иррациональным числом является Золотое сечение (), отношение, называемое «божественной пропорцией». Это уникальное соотношение является обычным числом, которое встречается в различных аспектах нашей жизни и культуры, а не только в математике. Появляясь в картинах, произведениях искусства, скульптурах и зданиях, золотое сечение известно своей эстетической привлекательностью. Это число обычно приблизительно равно 1,618, но не может быть выражено в форме простой дроби.
Итак, является ли ноль рациональным числом?
Теперь, когда вы знаете разницу между рациональными и иррациональными числами, вы все еще можете спросить себя: является ли ноль рациональным числом? Вы знаете, что ноль не может быть знаменателем рационального числа, так как это классифицирует рациональную функцию как неопределенную. Однако ноль может быть числителем дроби, что квалифицирует ноль как допустимое рациональное число.
Однако ноль может быть числителем дроби, что квалифицирует ноль как допустимое рациональное число.
Поскольку ноль является целым числом, его можно записать как A в формуле A/B (например: 0/1, 0/3, 0/6 и т. д.). Запись нуля в качестве числителя над положительным или отрицательным знаменателем подтверждает, что ноль можно считать рациональным числом (например: 0/2, 0/-2 и т. д.).
Имейте в виду, что 0 нельзя использовать в качестве знаменателя в уравнении с рациональными числами. Если бы это было так, любое число, деленное на 0, давало бы бесконечность — как мы узнали ранее, иррациональные числа нельзя записать в виде дроби с целыми числами как в числителе, так и в знаменателе. Любое целое число, деленное на 0, является иррациональным числом.
Почему важно знать, является ли ноль рациональным числом?
Если у вас проблемы с математикой, и вы, наконец, разгадали код к дебатам о рациональных и иррациональных числах, вы, возможно, все еще задаетесь вопросом, как это поможет вам понять сложные математические понятия.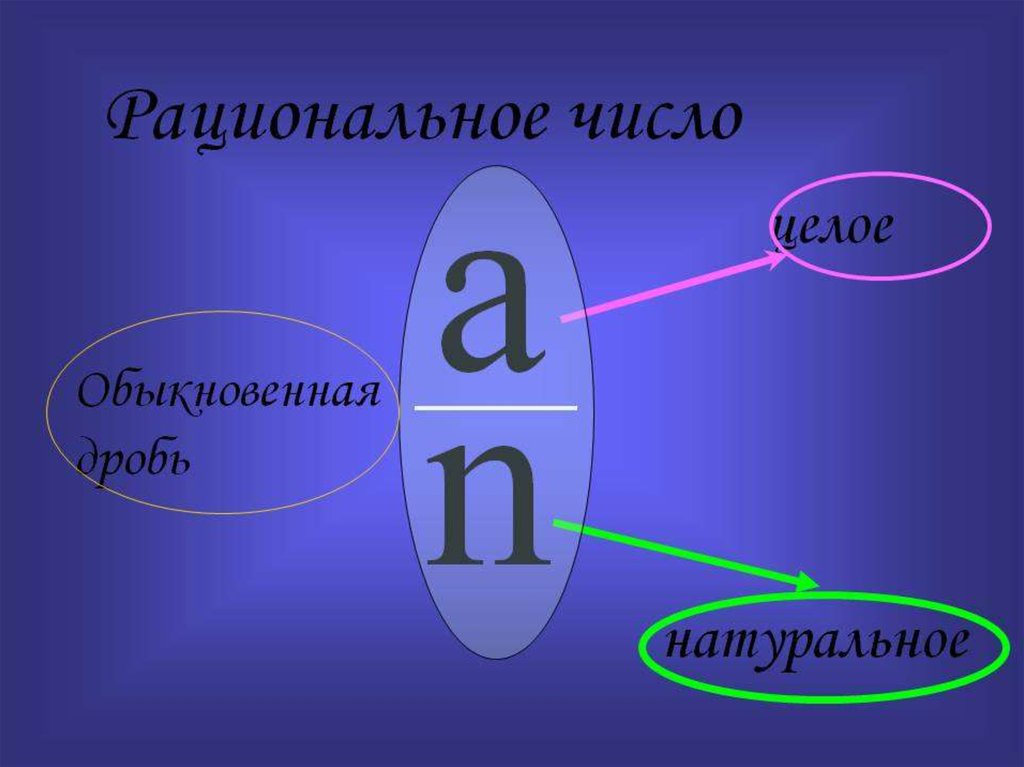




 И что нам это даст? Что существует хотя бы одно вещественное число, не являющееся рациональным?… — так мы это и без того знаем.
И что нам это даст? Что существует хотя бы одно вещественное число, не являющееся рациональным?… — так мы это и без того знаем. Мы предположили, что рациональные числа пронумерованы. И построили дробь, не относящуюся к рациональным. Следовательно, она и не периодична.
Мы предположили, что рациональные числа пронумерованы. И построили дробь, не относящуюся к рациональным. Следовательно, она и не периодична.

 Тогда оно рационально и значит, пронумеровано в нашем списке….
Тогда оно рационально и значит, пронумеровано в нашем списке…. Альтернативно, 3 — простое число или рациональное число, но √3 — не рациональное число.
Альтернативно, 3 — простое число или рациональное число, но √3 — не рациональное число.