Рациональные уравнения и системы — Математика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Формулы сокращенного умножения
- Квадратное уравнение и квадратный трехчлен
- Основные свойства степеней
- Основные свойства математических корней
- Некоторые дополнительные сведения из алгебры
- Решение рациональных уравнений
- Решение систем рациональных уравнений
Формулы сокращенного умножения
К оглавлению…
При выполнении различных алгебраических преобразований часто удобно пользоваться формулами сокращенного умножения. Зачастую эти формулы применяются не столько для того чтобы сократить процесс умножения, а наоборот скорее для того, чтобы по результату понять, что его можно представить как произведение некоторых множителей. Таким образом, данные формулы нужно уметь применять не только слева направо, но и справа налево. Перечислим основные формулы сокращенного умножения. Квадрат суммы:
Перечислим основные формулы сокращенного умножения. Квадрат суммы:
Квадрат разности:
Предыдущие две формулы также иногда записывают в несколько другом виде, который даёт нам какое-то выражение для суммы квадратов:
Также нужно понимать, что будет получаться если в скобках в квадрате знаки будут расставлены «нестандартным» способом:
Теперь идём далее. Формула сокращенного умножения разность квадратов:
Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
Квадратное уравнение и квадратный трехчлен
К оглавлению…
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения согласно теореме Виета может быть вычислено по формуле:
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Игрек вершины параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:
Основные свойства степеней
К оглавлению. ..
..
У математических степеней есть несколько важных свойств, перечислим их. При умножении степеней с одинаковыми основаниями показатели степеней складываются:
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель степени делителя:
При возведении степени в степень показатели степеней перемножаются:
Если перемножаются числа с одинаковой степенью, но разным основанием, то можно сначала перемножить числа, а затем произведение возвести в эту степень. Обратная процедура также возможна, если имеется произведение в степени, то можно каждое из умножаемых возвести в эту степень по отдельности а результаты перемножить:
Также, если делятся числа с одинаковой степенью, но разным основанием, то можно сначала поделить числа, а затем частное возвести в эту степень (обратная процедура также возможна):
Несколько простых свойств степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:
Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:
Основные свойства математических корней
К оглавлению…
Математический корень можно представить в виде обычной степени, а затем пользоваться всеми свойствами степеней приведёнными выше. Для представления математического корня в виде степени используют следующую формулу:
Тем не менее можно отдельно выписать ряд свойств математических корней, которые основываются на свойствах степеней описанных выше:
Для арифметических корней выполняется следующее свойство (которое одновременно можно считать определением корня):
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при неотрицательном a. Для корня нечетной степени выполняется также следующее равенство (из под корня нечетной степени можно выносить знак «минус»):
Так как значение корня четной степени может быть только неотрицательным, то для таких корней имеется следующее важное свойство:
Некоторые дополнительные сведения из алгебры
К оглавлению. ..
..
Если x0 – корень многочлена n-ой степени Pn(x), то выполняется следующее равенство (здесь Qn-1(x) – некоторый многочлен (n – 1)-ой степени):
Процедура в рамках которой квадратный трехчлен представляется как скобка в квадрате и еще некоторое слагаемое называется выделением полного квадрата. И хотя операцию выделения полного квадрата проще выполнять каждый раз «с ноля» в конкретных цифрах, тем не менее имеется и общая формула, с помощью которой можно записывать сразу результат выделения полного квадрата:
Существует операция, обратная операции сложения дробей с одинаковыми знаменателями, и которая называется почленным делением. Она заключается в том, чтобы наоборот каждое слагаемое из суммы в числителе некоторой дроби, записать отдельно над знаменателем этой дроби. Для операции почленного деления также можно записать общую формулу:
Существует также формула для разложения суммы квадратов на множители:
Решение рациональных уравнений
К оглавлению. ..
..
Решить уравнение – значит найти все его корни. Основной метод решения – путем алгебраических преобразований или замены переменных свести уравнение к равносильному, которое решается просто (например, к квадратному). Если свести уравнение к равносильному не получается, то могут возникать побочные корни. Сомневаетесь – проверяйте корни подстановкой.
Для многих уравнений важно понятие области допустимых значений для корней, далее – ОДЗ. На данном этапе (в рациональных уравнениях, т.е. тех, которые не содержат арифметических корней, тригонометрических функций, логарифмов и т.д.), основное условие которому должны отвечать корни уравнения, это чтобы при их подстановке в изначальный вид уравнения знаменатели дробей не обращались в ноль, т.к. на ноль делить нельзя. Таким образом, ОДЗ включает все возможные значения кроме тех которые обращают в ноль знаменатели дробей.
При решении уравнений (а в дальнейшем и неравенств) нельзя сокращать множители с переменной в левой и правой части уравнения (неравенства), в этом случае Вы потеряете корни. Нужно переносить все выражения налево от знака равно и выносить «сокращающийся» множитель за скобки, в дальнейшем нужно учесть корни, которые он дает.
Нужно переносить все выражения налево от знака равно и выносить «сокращающийся» множитель за скобки, в дальнейшем нужно учесть корни, которые он дает.
Для того чтобы произведение двух или более скобок было равно нулю, достаточно чтобы любая из них по отдельности была равна нулю, а остальные существовали. Поэтому в таких случаях нужно по очереди приравнивать все скобки к нулю. В итоговый ответ нужно записать корни всех этих «веток» решения (если конечно эти корни входят в ОДЗ).
Иногда некоторые из дробей в рациональном уравнении можно сократить. Это нужно обязательно попытаться сделать и не упустить ни одной такой возможности. Но при сокращении дроби Вы можете потерять ОДЗ, поэтому дроби нужно сокращать только после записи ОДЗ, или же в конце решения полученные корни подставлять в первоначальное уравнение для проверки существования знаменателей.
Итак, для решения рационального уравнения необходимо:
- Разложить все знаменатели всех дробей на множители.

- Перенести все слагаемые влево, чтобы справа получился ноль.
- Записать ОДЗ.
- Сократить дроби, если это возможно.
- Привести к общему знаменателю.
- Приравнять числитель к нулю и решать полученное уравнение.
- Не забыть проверить корни на соответствие ОДЗ.
Одним из самых распространённых методов решения уравнений является метод замены переменных. Зачастую замена переменных выбирается индивидуально для каждого конкретного примера. При этом важно помнить о двух основных критериях введения замены в уравнения. Итак после введения замены в некоторое уравнение это уравнение должно:
- во-первых, стать проще;
- во-вторых, больше не содержать первоначальной переменной.
Кроме того, важно не забывать выполнять обратную замену, т.е. после нахождения значений для новой переменной (для замены), записывать вместо замены то, чему она равна через первоначальную переменную, приравнивать это выражение к найденным значениям для замены и опять решать уравнения.
Отдельно остановимся на алгоритме решения очень распространённых однородных уравнений. Однородные уравнения имеют вид:
Здесь А, В и С – числа, не равные нулю, а f(x) и g(x) – некоторые функции с переменной х. Однородные уравнения решают так: разделим все уравнение на g2(x) и получим:
Производим замену переменных:
И решаем квадратное уравнение:
Получив корни этого уравнения не забываем выполнить обратную замену, а также проверить корни на соответствие ОДЗ.
Также при решении некоторых рациональных уравнений хорошо бы помнить про следующие полезные преобразования:
Решение систем рациональных уравнений
К оглавлению…
Решить систему уравнений – значит найти не просто решение, а комплекты решений, то есть такие значения всех переменных которые, будучи одновременно подставленными в систему, обращают каждое ее уравнение в тождество.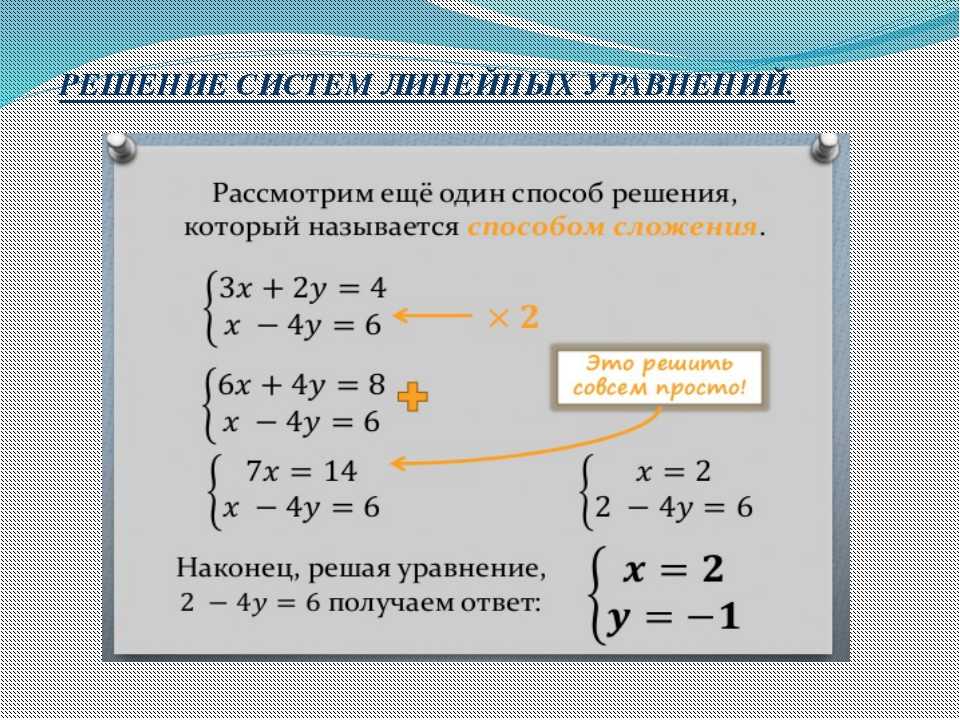
- Метод подстановки. Метод состоит в том, чтобы выразив одну из переменных из одного из уравнений, подставить это выражение вместо данной неизвестной в остальные уравнения, уменьшив таким образом количество неизвестных в оставшихся уравнениях. Данная процедура повторяется пока не останется одно уравнение с одной переменной, которое затем и решается. Остальные неизвестные последовательно находятся по уже известным значениям найденных переменных.
- Метод расщепления системы. Этот метод состоит в том, чтобы разложить одно из уравнений системы на множители. При этом необходимо чтобы справа в этом уравнении был ноль. Тогда приравнивая по очереди каждый множитель этого уравнения к нолю и дописывая остальные уравнения первоначальной системы, получим несколько систем, но каждая из них будет проще первоначальной.
- Метод сложения и вычитания.
 Данный метод состоит в том, чтобы складывая либо вычитая два уравнения системы (их предварительно можно и часто нужно умножать на некоторый коэффициент) получить новое уравнение, и заменить им одно из уравнений первоначальной системы. Очевидно, что такая процедура имеет смысл, только если новое уравнение будет получаться значительно проще ранее имевшихся.
Данный метод состоит в том, чтобы складывая либо вычитая два уравнения системы (их предварительно можно и часто нужно умножать на некоторый коэффициент) получить новое уравнение, и заменить им одно из уравнений первоначальной системы. Очевидно, что такая процедура имеет смысл, только если новое уравнение будет получаться значительно проще ранее имевшихся. - Метод деления и умножения. Данный метод состоит в том, чтобы разделив либо умножив соответственно левые и правые части двух уравнений системы получить новое уравнение, и заменить им одно из уравнений первоначальной системы. Очевидно, что такая процедура опять таки имеет смысл, только если новое уравнение будет получаться значительно проще ранее имевшихся.
Существуют и другие методы решения систем рациональных уравнений. В числе которых — замена переменных. Зачастую замена переменных подбирается индивидуально под каждый конкретный пример. Но есть два случая, где всегда нужно вводить совершенно определённую замену. Первый из этих случаев, это случай когда оба уравнения системы с двумя неизвестными являются однородными многочленами приравненными к некоторому числу. В этом случае нужно использовать замену:
Первый из этих случаев, это случай когда оба уравнения системы с двумя неизвестными являются однородными многочленами приравненными к некоторому числу. В этом случае нужно использовать замену:
После применения этой замены, к слову, нужно будет для продолжения решения таких систем использовать метод деления. Второй случай, это симметричные системы с двумя переменными, т.е. такие системы, которые не изменяются при замене x на y, а y на x. В таких системах необходимо применять следующую двойную замену переменных:
При этом, для того чтобы ввести такую замену в симметричную систему, первоначальные уравнения скорее всего придется сильно преобразовывать. Про ОДЗ и обязательность выполнения обратной замены в обоих этих методах, конечно нельзя забывать.
Последние новости туризма на сегодня 2022
Отдых и Туризм — Новости туризма 2022
Февраль 12, 2022 8 комментариев
С чем у любого туриста ассоциируется Хорватия? В первую очередь — отличная экология, чистейшее лазурного цвета Адриатическое море и невероятно живописные берега. ..
..
Февраль 1, 2022
Февраль 1, 2022
Февраль 2, 2022
Правильное питание
Ноябрь 19, 2021 5 комментариев
Хотя общая идея заключается в том, что замороженные фрукты не несут никакой пользы для здоровья, многочисленные доказательства противоречат…
Ноябрь 19, 2021 17 комментариев
Ноябрь 19, 2021 10 комментариев
Ноябрь 19, 2021 20 комментариев
Общество
Ноябрь 19, 2021 7 комментариев
Найти идеальный подарок на Новый год для близких и друзей — непростая задача. Если нет уверенности в правильности своего решения, то может…
Если нет уверенности в правильности своего решения, то может…
Ноябрь 19, 2021 20 комментариев
Ноябрь 19, 2021 4 комментария
Ноябрь 19, 2021 5 комментариев
Cпорт отдых туризм
Ноябрь 20, 2021 16 комментариев
Занять всю семью непросто.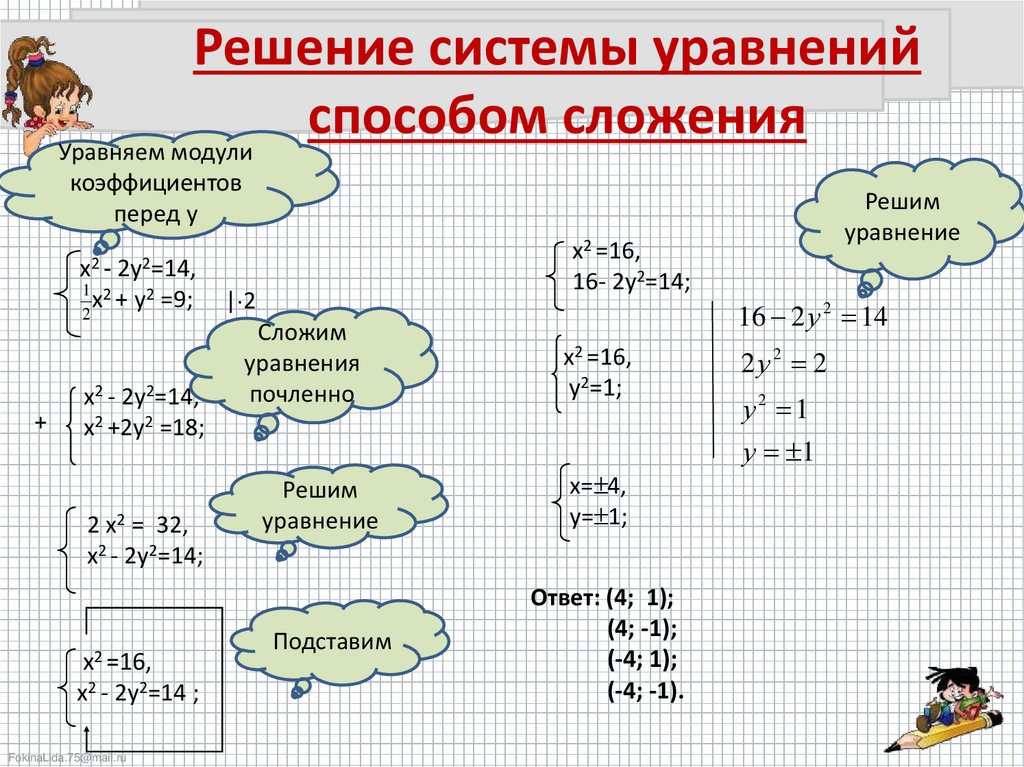 И что ж, нужно время, чтобы постоянно придумывать новые…
И что ж, нужно время, чтобы постоянно придумывать новые…
Бизнес
Ноябрь 20, 2021 2 комментария
Во французском языке существительное menu имеет два совершенно разных…
Спорт
Ноябрь 21, 2021 8 комментариев
Если вы все-таки решились на покупку первого сноуборда, при выборе однозначно не стоит…
Решение квадратных систем — квадратичные функции и уравнения
Система квадратных уравнений состоит только из .
{у=х2-6х+3у=-х2+2х-5
Графики квадратичных систем с двумя уравнениями могут иметь 0, 1, 2 или бесконечно много . Следовательно, число решений квадратичной системы также равно 0, 1, 2 или бесконечно много.
Квадратичные системы могут быть решены графически или алгебраически. Так как уравнения в квадратичной системе не являются линейными, эти системы .
Подобно решению и решению , решение квадратных систем можно выполнить, построив оба уравнения в виде графика. Решение(я) можно найти, указав координаты точки .
Квадратичные системы можно решать с помощью замены так же, как . Одно уравнение подставляется в другое, в результате получается либо квадратное, либо линейное уравнение. Решение полученного уравнения дает значения x для решения всей системы. Наконец, они подставляются в одно из исходных уравнений, чтобы найти соответствующие значения y.
Решите систему с помощью подстановки.
{y=x2−4x+2y=-x2+2x−2
Показать решение expand_more
Мы можем решить систему, подставив одно уравнение в другое.
х2-4х+2=-х2+2х-2
Теперь у нас есть . Его решения дадут нам значения x для решений системы. Перестроим уравнение так, чтобы оно стало равным 0.
x2-4x+2=-x2+2x-2
2×2-4x+2=2x-2
2×2-6x+2=-2
2×2-6x+4=0
Отсюда мы можем решить уравнение, используя .
2х2−6х+4=0
х=2⋅2-(-6)±(-6)2−4⋅2⋅4
х=2⋅26±(-6)2 −4⋅2⋅4
х=46±36−32
х=46±4
х=46±2
х=46+2 x=46−2
x=8/4x=4/4
x1=2×2=1
Значения x для решений равны x=2 и x=1. Теперь мы подставляем их в одно из исходных уравнений, чтобы найти соответствующие значения y. Мы будем использовать первое уравнение, но неважно какое.
Теперь мы подставляем их в одно из исходных уравнений, чтобы найти соответствующие значения y. Мы будем использовать первое уравнение, но неважно какое.
y=22−4⋅2+2=-2y=12−4⋅1+2=-1
Таким образом, решения квадратичной системы
(2,-2) и (1,-1).
Квадратичная система может также состоять из квадратичных неравенств, таких как
{y Решением системы квадратных неравенств является, подобно , вся область в координатной плоскости. Систему квадратных неравенств можно решить графически, подобно системе . В частности, отдельные неравенства изображены на графике, а пересечение заштрихованных областей является решением системы. Например, {y≥0,5×2−4x+6y≤-x2+8x−12 можно решить таким образом. Чтобы найти решения для системы, начните с . Здесь y≥0,5×2−4x+6 имеет граничную кривую y=0,5×2−4x+6, а область, соответствующая множеству решений, лежит внутри . Далее нарисуйте другое неравенство. Здесь y≤-x2+8x−12 имеет границу y=-x2+8x−12. Область, соответствующая множеству решений, также лежит внутри параболы. Решения системы являются решениями обоих индивидуальных неравенств. Это означает, что они лежат в перекрывающихся заштрихованных областях. Вот, это фиолетовая область. Поскольку кривые в целом не являются частью , обрежьте их так, чтобы они ограничивали только фиолетовую область. Теперь показано множество решений системы. спросил Изменено
3 года, 2 месяца назад Просмотрено
386 раз
9k$$ или $$\mathbf{0} = \mathbf{a} + \mathbf{b} \cdot \mathbf{x} + \mathbf{c} \cdot \mathbf{x} \cdot \ mathbf{x}$$ и если да, то какие? $\endgroup$ 6 $\begingroup$ Как показал ответ Роберта Исраэля на аналогичный вопрос, частные случаи этой схемы задач не обязательно должны иметь решения, которые просто выражаются (в отличие от линейного случая, где решение всегда выражается в виде конечных выражений с заданными коэффициентами, в квадратичном и более высоких степеней, для решения могут потребоваться корни многочленов высоких степеней, для которых не требуется никакого выражения в исходных коэффициентах).
линейная алгебра — Решение систем квадратных уравнений



 Данный метод состоит в том, чтобы складывая либо вычитая два уравнения системы (их предварительно можно и часто нужно умножать на некоторый коэффициент) получить новое уравнение, и заменить им одно из уравнений первоначальной системы. Очевидно, что такая процедура имеет смысл, только если новое уравнение будет получаться значительно проще ранее имевшихся.
Данный метод состоит в том, чтобы складывая либо вычитая два уравнения системы (их предварительно можно и часто нужно умножать на некоторый коэффициент) получить новое уравнение, и заменить им одно из уравнений первоначальной системы. Очевидно, что такая процедура имеет смысл, только если новое уравнение будет получаться значительно проще ранее имевшихся.