Как решать уравнения корень уравнения: Ошибка 403 — доступ запрещён

Уравнение и его корни: определение, правила, примеры

Основные понятия уравнения

Определение

Уравнением называют равенство, в котором одна из переменных неизвестна, и её нужно найти. Значение этой неизвестной должно быть таким, чтобы равенство было верным.

К примеру: 3+4=7 это числовое равенство, при вычислении которого с левой стороны получается 7=7.

Уравнением же будет называться следующее равенство: 3+х=7, поскольку есть неизвестная переменная х, её значение можно найти.

Из этого уравнения следует, что переменная х=4, только при таком его значении равенство 3+х=7, будет верным.

Неизвестные переменные принято писать в виде маленьких латинских букв, можно любыми, но чаще используют x,y,z.

Получается, чтобы равенство сделать уравнением необходимо, чтобы в нем была буква, значение которой неизвестно.

Как мы понимаем существует множество примеров уравнений с разными арифметическими действиями.

Пример: х + 5 = 1= 9; z — 2 = 7; 9 * y = 18, 6 :  f = 2

Помимо этого существуют уравнения со скобками. К таким уравнениям относится 8 : (х — 4) = 2 * (8 — х), неизвестных может быть несколько, они могут быть, как слева уравнения, так и справа или в обеих частях.

Помимо таких простых уравнений они могут быть с корнями, логарифмами, степенями и тд. 

Уравнение может содержать несколько переменными, тогда их принято называть, соответственно уравнениями с двумя, тремя и более переменными.

Пример:

3 * а = 15 : х — уравнение с двумя переменными:

8 — а = 5 * х — z — уравнение с тремя переменными.

Корень уравнения

Мы часто слышим фразу на уроках математики, «найдите корень уравнения», давайте разберёмся, что же это значит.

Пример:

В примере 3+х=7, можно представить вместо буквы число, и уравнение тогда станет равенством, оно может быть либо верным, либо неверным, если поставить х=3, то первичное равенство примет вид 3+3 = 7 и станет неверным, а если х= 4 то равенство 3+4=7 будет верным, а значит х = 4 будет называться корнем или по другому решением уравнения 3+х=7.

Определение.

Отсюда можно выделить следующее определение: корень уравнения — это такое значение неизвестной переменной, при котором числовое равенство будет верным.

Стоит отметить, что корней может быть несколько или не быть вовсе.

Рассмотрим подробнее пример который не будет иметь корней. Таким примером станет 0 * х = 7, сколько бы чисел мы сюда не подставляли равенство не будет верным, так как умножая на ноль будет ноль, а не 7.

Но существуют и уравнения с множественным числом корней, к примеру, х — 3 = 6, в таком уравнении только один корень 9, а в уравнении квадратного вида х2 = 16, два корня 4 и -4,  можно привести пример и с тремя корнями х * (х — 1) * (х — 2) = 0,  в данном случае три решения ноль, два и один.

Для того чтобы верно записать результат уравнения мы пишем так:

• Если корня нет, пишем уравнение корней не имеет;
• Если есть и их несколько, они либо прописываются через запятые, либо в фигурных скобках, например, так: {-2, 3, 5};
• Еще одним вариантом написания корней, считается запись в виде простого равенства, к примеру неизвестная х а корни 3,5 тогда результат прописывается так: х=3, х=5.  
• или прибавляя индекс снизух1 =3 , х2 = 5. данным способом указывается номер корня;
• Если решений уравнения бесконечное множество, то запись будет либо в виде числового промежутка от и до, или общепринятыми обозначениями. множество натуральных чисел N, целых –  Z, действительных — R.

Стоит отметить, что если уравнение имеет два и более корней, то чаще употребляется понятие решение уравнения.  Рассмотрим определение уравнения с несколькими переменными.

Решение уравнения с двумя и более переменными, означает, что эти несколько значений превращают уравнение в верное равенство.

Примеры:

Представим, что мы имеем следующее уравнение х + а = 5, такое уравнение имеет две переменные. Если мы поставим вместо них числа 3 и 6 то равенство не будет верным, соответственно и данные числа не являются решением для данного примера.  А если взять числа 2 и 3 то равенство превратится в верное, а числа 2 и 3 будут решением уравнения. Представленные уравнения с несколькими переменными, тоже могут или не иметь корня вообще или наоборот иметь множество решений.

Правила нахождения корней

Таких правил существует несколько рассмотрим их ниже.

Пример 1 

Допустим мы имеем уравнение 4 + х = 10, чтобы найти корень уравнения или значение  х в данном случае необходимо  найти неизвестное слагаемое, для этого есть следующее правило или формула. Для нахождения неизвестного слагаемого, нужно из суммы вычесть известное значение.

Решение:

х = 10 — 4

х = 6

Чтобы проверить является ли 6 решением, мы ставим его на место неизвестной переменной х в исходное уравнение, получаем следующее равенство 4 + 6 = 10, такое равенство является верным, что означает число корня уравнения, равно 6.

Пример 2

Возьмём уравнение вида х — 5 = 3, в данном примере х это неизвестное уменьшаемое, для того чтобы его найти необходимо следовать следующему правилу:

Для нахождения уменьшаемого необходимо сложить разность и вычитаемое.

Решение:

х = 3 + 5

х = 8

Проверяем правильность нахождения корня уравнения, подставляем, вместо переменной неизвестной, найденное число 8, получаем равенство 8 — 5 = 3, так как оно верное, то и корень уравнения найден правильно.

Пример 3

Берём уравнение, в котором неизвестное х будет вычитаемое к примеру: 8 — х = 4. для того чтобы найти х необходимо воспользоваться правилом:

Для нахождения вычитаемого, нужно из уменьшаемого вычесть разность.

Решение:

х = 8 — 4

х = 4

Проверяем правильность нахождения корня уравнения, для этого полученное значение ставим вместо неизвестного вычитаемого в исходный пример, и получаем следующее равенство 8 — 4 = 4, равенство верно, значит и корень найден правильно.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Пример 4

Возьмём уравнение вида х * 3 = 9, в данном уравнении неизвестна переменная х, является множимым. Для того, чтобы найти корень такого уравнения необходимо использовать следующее правило.

Для нахождения неизвестного множимого, нужно произведение разделить на множитель.

Решение:

х = 9 : 3

х = 3

Для проверки подставим найденное значение х в исходное уравнение, получим равенство 3 * 3 =9, так как равенство является верным, то и решение уравнения верное.

Такое же правило действует и для множителя, чтобы его найти необходимо произведение разделить на множимое.

Пример 5

Возьмём уравнение следующего вида: х : 2 = 10 , в данном уравнении х- это неизвестное делимое, 2 — делитель, а 10 — частное. Для нахождения неизвестного значения х, воспользуемся правилом:

Чтобы найти делимое, необходимо частное умножить на делитель.

Решение:

х = 10 * 2

х = 20

Проверим, вместо неизвестного х, поставим его значение 20, получим следующее равенство 20: 2 = 10. Равенство верное, значит и решение было верным.

Пример 6

Теперь рассмотрим пример с делителем.

Возьмём уравнение 22: х = 11, где х неизвестный делитель. Для того чтобы его найти существует правило:

При нахождении неизвестного делителя нужно делимое разделить на частное.

Решение:

х = 22 : 11

х = 2

Проверяем, 2 ставим на место неизвестного х в исходное уравнение, получаем равенство 22 : 2 = 11. Так как равенство верно, то мы нашли верный корень уравнения.

Пример применения правил в более сложном уравнении: 2х — 5 =5

Решение:

2х = 5 + 5

2х = 10

х = 10 : 2

х = 5

Проверяем, для этого полученное значение х = 5, ставим в исходное уравнение, получаем равенство 2 * 5 — 5 = 5, так как равенство верно, корень найден правильно.

Квадратные уравнения

Существует также уравнения квадратного вида, например: 2х² = 32, для того, чтобы найти неизвестное или корень квадратного уравнения, в таком уравнении необходимо:

Решение:

х² = 32 : 2

х² = 16

х = √16

х = 4

Проверим, для этого полученное значение подставим в исходное уравнение, и получим равенство 24² = 32. так как равенство верное, то и решение уравнения верно.

Как мы видим нахождение корня уравнения не такой сложный процесс, главное запомнить правила. Стоит отметить, что помимо решения различного вида задач, уравнения применяются в других различных науках. Применение уравнений можно найти в экономике, в физике, химии, биологии и других. При их помощи можно вычислить и описать процессы, происходящие вокруг нас.

Калькулятор квадратных корней

2 класс. Математика. Понятие «уравнение». Корень уравнения. Решение уравнений — Понятие «уравнение». Корень уравнения. Решение уравнений

Комментарии преподавателя

§1. Что такое уравнение?

Вам уже знакомы такие математические понятия, как «выражение», «равенство», «неравенство».

«Уравнение» — это еще одно математическое понятие, с ним мы и познакомимся в этом уроке.

Давайте попробуем решить следующую задачу:

Фрекен Бок испекла 5 пирожков и положила их на тарелку.   Когда она отошла от стола, Карлсон подлетел и взял несколько пирожков.   На тарелке осталось только 2 пирожка.   Сколько пирожков взял Карлсон?

На основании условий задачи мы можем сделать такую запись: Всего Фрекен Бок испекла 5 пирожков. Запишем число 5. Карлсон взял пирожки, следовательно, количество пирожков уменьшилось, поэтому поставим знак  « – ». Сколько Карлсон взял пирожков, неизвестно, поэтому вместо числа оставим пустую клетку. Всего на тарелке осталось 2 пирожка. Запишем = 2.

Теперь давайте вместо пустой клетки – неизвестного числа, вставим букву, например, а. Получится следующая запись: 5 – а = 2

Такие равенства, в которых есть неизвестные числа, обозначенные буквой, называютуравнениями.

§2. Корень уравнение и метод подбора при решении уравнения

В уравнениях могут присутствовать любые математические знаки,  как «–», так  «+», например:  5 – а = 2, 5 + а = 9

В уравнениях неизвестное число принято обозначать малыми буквами латинского алфавита: a, b, c и т.д. Часто используют буквы x, y, z.

Например:

6 + у = 13

z – 8 = 3

х + 5 = 9

Вернемся к задаче про пирожки.

Полученное нами уравнение выглядит таким образом: 5 – а = 2.

Давайте попытаемся определить, какое число спряталось за буквой а?

Для этого будем подставлять вместо а разные числа до тех пор, пока не найдем число, подстановка которого сделает это равенство верным.

Подставим вместо а число 1.

Получим 5 – 1 = 2.

Но это неверное равенство, так как 5 – 1 = 4, а не 2.

Значит, а не может быть равным 1.

Подставим вместо а число 2.

Получим 5 – 2 = 2.

Это тоже неверное равенство, т.к. 5 – 2 = 3, а не 2.

Следовательно, а не может быть равным 2.

Подставим вместо а число 3.

Получим 5 – 3 = 2.

Мы получили верное равенство.

Значит, в уравнении 5 – а = 2 за  буквой а спряталось число 3.

Число, которое превращает уравнение в верное равенство, называется корнем уравнения.

Следовательно, в нашем случае число 3 является корнем уравнения 5 – а = 2.

Способ, с помощью которого мы нашли корень уравнения, называется методом подбора.

Итак, подведем итоги урока:

Уравнение – это равенство, в котором есть неизвестное число, обозначенное латинской буквой.

Число, которое превращает уравнение в верное равенство, называется корнем уравнения.

 

ИСТОЧНИКИ

https://vimeo.com/112468248

http://znaika.ru/catalog/2-klass/matematika/Ponyatie-%C2%ABuravnenie%C2%BB.-Koren-uravneniya.-Reshenie-uravneniy

http://www.youtube.com/watch?v=Hbm7kWk5J34

http://www.youtube.com/watch?v=uzAgNOT5D0E

Файлы

Нет дополнительных материалов для этого занятия.

Решение радикальных уравнений | Начальная алгебра

 

Цели обучения

• Решение радикальных уравнений
  • Извлечение квадратных корней в уравнениях и решение для переменной
  • Идентифицировать посторонние решения радикальных уравнений
• Квадратные корни и заполнение квадрата для решения радикальных уравнений
  • Использование квадратных корней для решения квадратных уравнений
  • Заполните квадрат, чтобы решить квадратное уравнение
• Использование квадратичной формулы для решения квадратных уравнений
  • Напишите квадратное уравнение в стандартной форме и определите значения a , b и c в квадратном уравнении стандартной формы.
  • Используйте квадратную формулу, чтобы найти все действительные решения.
  • Решение прикладных задач, требующих использования квадратичной формулы.

Основная стратегия решения радикальных уравнений состоит в том, чтобы сначала выделить радикальный член, а затем возвести обе части уравнения в степень, чтобы удалить радикал. (Причина использования степеней станет ясна через мгновение.) Это тот же тип стратегии, который вы использовали для решения других нерадикальных уравнений — перестройте выражение, чтобы изолировать переменную, которую вы хотите знать, а затем решите полученное уравнение. . 9{2}}=x[/латекс]. (Это свойство позволяет вам «удалить» радикалы из ваших уравнений.)

Давайте начнем с радикального уравнения, которое вы можете решить за несколько шагов: [латекс] \sqrt{x}-3=5[/латекс].

Чтобы проверить свое решение, вы можете заменить x на 64 дюйма в исходном уравнении. [латекс] \sqrt{64}-3=5[/латекс]? Да, квадратный корень из 64 равен 8, а [латекс]8−3=5[/латекс].

Обратите внимание, как вы объединили одинаковые члены, а затем возвели в квадрат обе

сторон уравнения в этой задаче. Это стандартный метод удаления радикала из уравнения. Важно выделить радикал с одной стороны уравнения и максимально упростить до в квадрате. Чем меньше членов перед возведением в квадрат, тем меньше дополнительных членов будет сгенерировано в процессе возведения в квадрат.

В приведенном выше примере под радикалом находилась только переменная x . Иногда вам нужно будет решить уравнение, которое содержит несколько членов под корнем. Выполните те же действия, чтобы решить их, но обратите внимание на критическую точку — возведите в квадрат обе сторон уравнения, а не отдельные членов . Посмотрите, как решаются следующие две задачи. 9{2}[/латекс].

После удаления радикала найдите неизвестное.

Проверить все ответы.

Идентификация посторонних решений

Соблюдение правил важно, но не менее важно обращать внимание на математику перед вами, особенно при решении радикальных уравнений. Взгляните на следующую проблему, которая демонстрирует потенциальную ловушку, связанную с согласованием обеих сторон для устранения радикала.

Посмотрите на это — ответ [латекс]а=9[/латекс] не дает истинного утверждения при подстановке обратно в исходное уравнение. Что случилось?

Проверьте исходную проблему: [латекс]\sqrt{a-5}=-2[/латекс]. Обратите внимание, что радикал установлен равным [латекс]-2[/латекс], и помните, что главный квадратный корень числа может быть только положительным . Это означает, что никакое значение для и не приведет к подкоренному выражению, положительный квадратный корень которого равен [латекс]-2[/латекс]! Вы могли сразу это заметить и сделать вывод, что для и решений нет.

Посмотрите на следующую проблему. Обратите внимание, что исходная задача имеет вид [латекс] x+4=\sqrt{x+10}[/латекс], но после возведения обеих сторон в квадрат она становится [латекс] {{x}^{2}}+8x+16. {2}[/латекс].

В следующем видео мы покажем больше примеров решения простых квадратных уравнений с использованием квадратных корней.

Иногда возводится в квадрат больше, чем просто x :

В этом видеопримере вы увидите больше примеров решения квадратных уравнений с использованием квадратных корней.

Завершение квадрата для решения квадратного уравнения

Конечно, квадратные уравнения часто не приходят в формате приведенных выше примеров. У большинства из них будет 9{2}[/латекс]. Разложим совершенный квадратный трехчлен на квадратный двучлен.

Вы можете использовать процедуру из следующего примера, чтобы помочь вам решить уравнения, в которых вы идентифицируете совершенные квадратные трехчлены, даже если уравнение не установлено равным 0.

Один из способов решения квадратных уравнений состоит в том, чтобы завершить квадрат . Если у вас нет идеально квадратного трехчлена, вы можете создать , добавив постоянный член, который является идеальным квадратом, к обеим частям уравнения. Давайте посмотрим, как найти этот постоянный член. 9{2}+bx[/латекс].

В этом примере площадь всего прямоугольника определяется как [латекс]x\влево(х+b\вправо)[/латекс].

Теперь давайте превратим этот прямоугольник в квадрат. Сначала разделите красный прямоугольник площадью b x

на два равных прямоугольника площадью [латекс] \frac{b}{2}x[/латекс]. Затем поверните и переместите один из них. Вы не изменили размер красной области — в сумме он по-прежнему составляет [latex]bx[/latex].

9{2}}[/latex] всегда положителен, так как это квадрат числа. Когда вы завершаете квадрат, вы всегда добавляете положительное значение.

В следующем видео мы покажем больше примеров того, как найти постоянный член, который сделает трехчлен идеальным квадратом.

Заполнение квадрата можно использовать для решения квадратного уравнения, которое нельзя решить с помощью факторизации.

Давайте начнем с того, что произойдет, если вы закончите квадрат в уравнении. Обратите внимание, что в приведенном ниже примере заполнение квадрата приведет к добавлению числа к 9.0026 обе

стороны уравнения — вы должны сделать это, чтобы обе стороны были равны!

Вы видите, что построение квадрата в уравнении очень похоже на завершение квадрата в выражении? Основное отличие состоит в том, что вы должны добавить новое число (в данном случае [латекс]+9[/латекс]) к обеим частям уравнения, чтобы сохранить равенство.

Теперь давайте рассмотрим пример, в котором вы используете заполнение квадрата, чтобы решить уравнение и найти значение переменной. 9{2}+16x+64=0[/латекс]. Можете ли вы факторизовать это уравнение, используя группировку? (Подумайте о двух числах, произведение которых равно 64, а сумма равна 16). {2}+bx+c=0[/латекс] и затем решите 9{2}+bx+c=0[/latex] называется стандартной формой квадратного уравнения. Прежде чем решать квадратное уравнение с помощью квадратной формулы,

важно убедиться, что уравнение имеет именно такую ​​форму. Если вы этого не сделаете, вы можете использовать неправильные значения для a , b или c , и тогда формула даст неверные решения.

Решение квадратного уравнения с помощью квадратной формулы

Квадратная формула будет работать с любым квадратным уравнением , кроме 9{2}+bx+c=0[/латекс]. Чтобы использовать его, выполните следующие действия.

• Сначала приведите уравнение в стандартной форме.
• Определите коэффициенты a , b , и c . Будьте внимательны при включении отрицательных знаков, если вычитаются члены bx или c .
• Подставить значения коэффициентов в квадратичную формулу.
• Максимально упростить.
• Используйте [latex]\pm[/latex] перед радикалом, чтобы разделить решение на два значения: одно, в котором добавляется квадратный корень, и другое, в котором он вычитается 9{2}+4\влево(-5\вправо)=5\,\,\,\,\,\\25-20=5\,\,\,\,\,\\5=5\,\ ,\,\,\,\end{массив}[/латекс]

Вы получаете два верных утверждения, поэтому вы знаете, что оба решения работают: [латекс]x=1[/латекс] или [латекс]-5[/латекс]. Вы успешно решили уравнение, используя квадратную формулу!

Сила Квадратной Формулы в том, что с ее помощью можно решить любое квадратное уравнение , даже такое, в котором невозможно найти комбинации чисел.

В следующем видео мы показываем пример использования формулы квадратного уравнения для решения уравнения с двумя действительными решениями. 9{2}-2\влево(4\вправо)=6\влево(4\вправо)-16\\16-8=24-16\,\,\,\,\,\,\\8=8\ ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{массив}[/ латекс]

В следующем видео мы показываем пример использования квадратной формулы для решения квадратного уравнения, которое имеет одно повторяющееся решение.

В этом видео примере мы показываем, что решения квадратных уравнений могут иметь рациональные ответы.

Применение квадратичной формулы

Квадратные уравнения широко используются в науке, бизнесе и технике. Квадратные уравнения обычно используются в ситуациях, когда две вещи перемножаются, и обе они зависят от одной и той же переменной. Например, при работе с площадью, если оба измерения записываются в терминах одной и той же переменной, вы используете квадратное уравнение. Поскольку количество проданного продукта часто зависит от цены, иногда вы используете квадратное уравнение, чтобы представить доход как произведение цены и проданного количества. Квадратные уравнения также используются, когда задействована сила тяжести, например, траектория движения мяча или форма тросов подвесного моста.

Очень распространенное и простое для понимания приложение — это высота мяча, брошенного на землю со здания. Поскольку гравитация будет увеличивать скорость мяча при падении, можно использовать квадратное уравнение для оценки его высоты в любое время до того, как он упадет на землю. Примечание. Уравнение не совсем точное, поскольку трение о воздух немного замедляет мяч. Для наших целей это достаточно близко.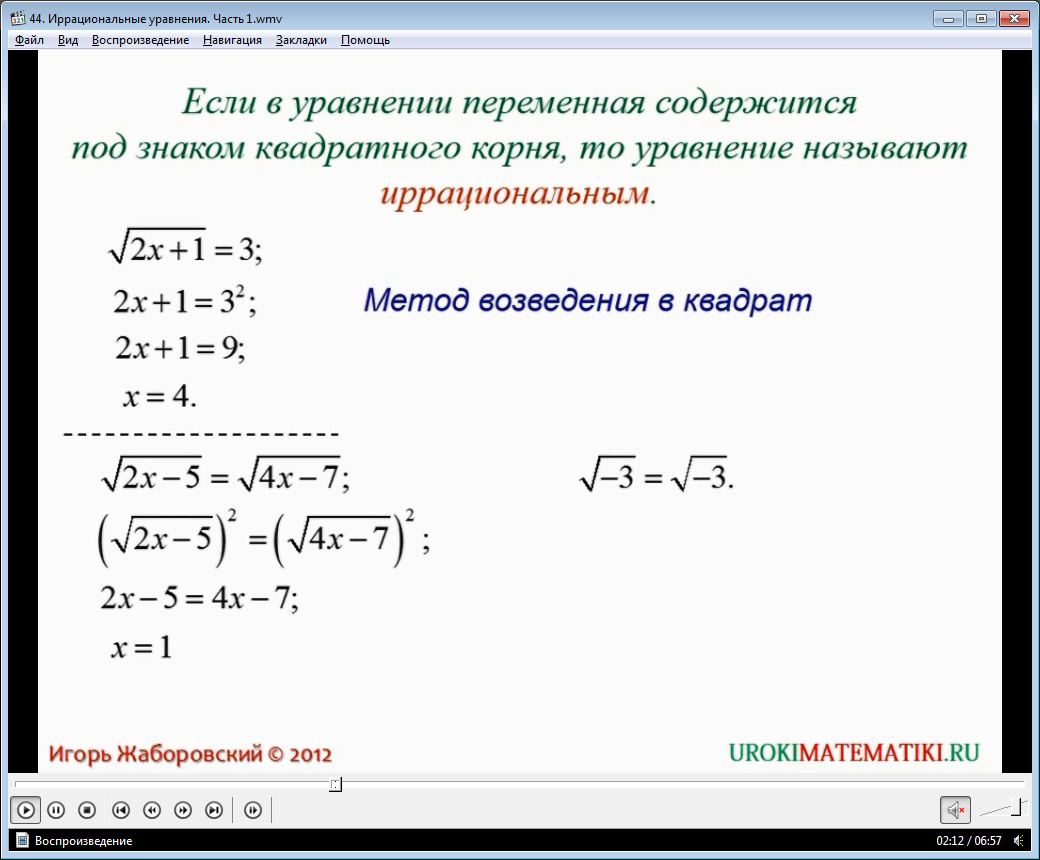

Приведенная ниже задача с площадями не выглядит так, как будто она включает квадратную формулу любого типа, и кажется, что эту задачу вы уже много раз решали простым умножением. Но для того, чтобы решить ее, вам нужно будет использовать квадратное уравнение.

В этом последнем видеоролике мы покажем, как использовать квадратичную формулу для решения задачи, связанной с рамкой изображения.

Резюме

Обычный метод решения радикальных уравнений состоит в том, чтобы возвести обе части уравнения в любую степень, чтобы убрать знак радикала из уравнения. Но будьте осторожны — когда обе части уравнения возводятся в степень и даже , существует вероятность того, что будут введены посторонние решения. При решении радикального уравнения важно всегда проверять свой ответ, подставляя значение обратно в исходное уравнение.

{2}}-4ac}}{2a}[/latex] находится путем заполнения квадрата квадратного уравнения [латекс] [/латекс]. 92=9$$

Извлеките квадратный корень из обеих частей уравнения и не забудьте использовать как положительные, так и отрицательные корни. Мы можем сделать это благодаря правилу, которое гласит, что если два выражения равны, то равны и их квадратные корни.

$$x=\pm3$$

Разделить уравнение на $$2$$ возможных случаев (с отрицательным корнем и с плюсовым корнем):

$$x=-3$$

$$ x=3$$

Следовательно, уравнение имеет $$2$$ решений:

$$x_1 =-3, ~x_2=3$$ 92}}\times\sqrt{2}$$

Уменьшить индекс радикала и показателя степени с $$2$$:

$$t=\pm{2}\sqrt{2}$$

Разделить уравнение на $$2$$ возможных случаев (с отрицательным корнем и с плюсовым корнем):

$$t=-2\sqrt{2}$$

$$t=2\sqrt{2} $$

Следовательно, уравнение имеет $$2$$ решений:

$$t_1 =-2\sqrt{2}, ~t_2=2\sqrt{2} $$

Это было не так уж и плохо, правда? Теперь, когда мы рассмотрели подробный пример, давайте рассмотрим весь процесс в целом, чтобы вы могли научиться использовать его с любая проблема:

Резюме исследования

1. При необходимости перепишите наше квадратное уравнение, переместив переменную в левую часть и константы в правую часть уравнения.

   No related posts.