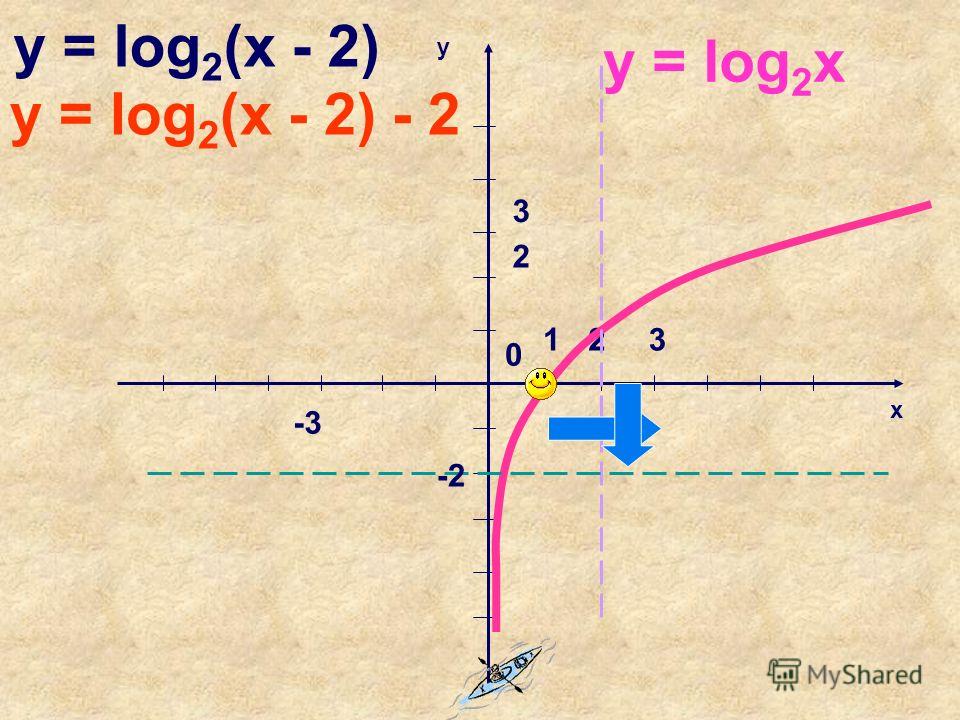Y log2 3 x: y = log2(x — 3); — Элементарная математика_Сканави — Сканави_ Сборник задач по математике _1.001_13.450 — Головоломки

Найти область значения функции: y=log2(6-3x) — Учеба и наука

Ответы

28. 12.21

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

В кубе ABCDA1B1C1D1 на ребре DD1 выбрана точка Е так, что DE : ED1 = 1 : 3.

2+2(a-1)x+1=0 имеет решение? Ответы а) 1/2, б)0, в)-1/3, г)12

Пользуйтесь нашим приложением

VvedvmathZO2 — Стр 4

Варианты заданий контрольной работы

4.1Пример выполнения заданий контрольной работы

1.Задать с помощью перечисления элементов множества A, B,

A[B, A\B, AnB, åñëè A = fa 2 Nj a 5g , B = f 3; 0; 1; 4; 7; 8g.

Решение. Сначала найдем элементы множества A. Определим решения неравенства a 5, которые принадлежат множеству натуральных чисел. Получим, что A = f1; 2; 3; 4; 5g. По определению, объединением двух множеств A и B является множество, состоящее из элементов, которые принадлежат хотя бы одному из множеств A, B, т.е. A [ B = f 3; 0; 1; 2; 3; 4; 5; 7; 8g. Пересе- чением множеств A и B называется множество, состоящее из элементов, входящих и в A, и в B, поэтому A \ B = f1; 4g. Разность множеств A и B определяется как множество, состоящее из элементов множества A, которые не принадлежат множеству

B, следовательно, AnB = f2; 3; 5g.

2.Решить уравнение z2 2z + 2 = 0.

Решение. Для уравнения z2 2z + 2 = 0, получаем, что

D = ( 2)2 4 1 2 = 4 8 = 4 = i2 22 = (2i)2;

	p		2
z1;2 =	2	(2i)2	=	2 2i	= 1			i; z1 = 1			i, z2 = 1 + i.
2
3. Найти область определения функции y = log2 (3x + 2).
Решение.		Чтобы найти				область			определения функции

y= log2 (3x + 2) надо решить неравенство 3x + 2 > 0. Получаем,

÷òî D(f) = 23; +1 .

x3

4. Дана функция y = x2 4. Требуется: 1) найти область определения функции;

31

2)исследовать функцию на ч¼тность, неч¼тность;

3)исследовать функцию на периодичность, если функция периодическая, указать е¼ наименьший период;

4)найти нули функции.

Решение.

1) Формула y =	x3			имеет смысл, когда x2 4 6= 0. Найдем
	x2		4
			2		4 = 0, получим корни: x = 2
сначала решение уравнения x

и x = 2. Для нахождения области определения функции, ис-

ключим данные точки из множества действительных чисел и получим, что D(f) = (1; 2) [ ( 2; 2) [ (2; +1).

2) Заметим, что множество D(f) = (1; 2) [ ( 2; 2) [ (2; +1)

симметрично относительно

нуля. Далее, для лю-

áîãî x

справедлива

следующая цепочка равенств:

f(

x) =

( x)3

=

x3

=

f(x). Т. к. область опре-

( x)2 4

x2 4

деления данной функции симметрична относительно нуля и f( x) = f(x), то она является неч¼тной.

x3

3) Поскольку функция y = x2 4 не является тригонометриче- ской, то и периодической она не будет.

x3

4) Для того, чтобы найти нули функции y = x2 4, íàäî ðå-

x3

шить уравнение x2 4 = 0. Получим единственное решение: x = 0.

x

p

5. Даны функции

,

2

. Записать функ-

f(x) = px2 1

g(x) = x + 1

öèþ y(x) = f(g(x)).

p

u

Решение. Пусть

2

,

+ 1

f(u) = p

. Тогда

u = g(x) =

x

2

1

p

p

u

f(g(x)) =

x2 + 1

=

x2 + 1

.

q

x

(p

x2 + 1)2 1

32

6. Для функции f(x) = log3(x 2) найти обратную f 1(x).

Решение. Функция y = f(x) = log3(x 2) монотонно возрастает на всей числовой оси. Выразим x из равенства y = log3(x 2) и получим, что x = 3y + 2. Отсюда f 1(x) = 3x + 2.

33

4.2Варианты заданий контрольной работы

Вариант 1

1. Задать с помощью перечисления элементов множества A, B, A [ B, A \ B, BnA, если A = f 4; 0; 3; 6; 9g,

B = fb 2 Zj 4 < b < 3g.

2.Решить уравнение z2 4z + 5 = 0.

3.Найти область определения функции y = log3 (7 x).

			x2
4.	Дана функция y =			. Требуется:
			x 1
	1)	найти область определения функции;
	2)	исследовать функцию на ч¼тность, неч¼тность;
	3)	исследовать функцию на периодичность, если функция пери-
		одическая, указать е¼ наименьший период;
	4)	найти нули функции.
	Даны функции f(x) = sin(2x + 1), g(x) = p					. Записать
5.					3x + 1
	функцию y(x) = g(f(x)).
6.	Для функции f(x) = 23x + 4 найти обратную f 1(x).

Вариант 2

1.Задать с помощью перечисления элементов множества A, B,

A [ B, A \ B, AnB, åñëè A = f3; 5; 7; 10g, B = fb 2 Nj b < 8g.

2.Решить уравнение z2 6z + 10 = 0.

3.Найти область определения функции y = log4 (1 2x).

	4. Дана функция y =	x2 4	. Требуется:
		x

34

1)найти область определения функции;

2)исследовать функцию на ч¼тность, неч¼тность;

3)исследовать функцию на периодичность, если функция периодическая, указать е¼ наименьший период;

4)найти нули функции.

5.Даны функции f(x) = ln1x, g(x) = e x + 4. Записать функцию y(x) = f(g(x)).

6.	Для функции f(x) = p					найти обратную f 1(x).
			3x		7
			Вариант 3
1.	Задать	с помощью	перечисления				элементов множества
	A, B,	A [ B, A \ B,	BnA, åñëè				A = fa 2 Zj 4 < a 1g,

B = f2; 0; 2; 4g.

2.Решить уравнение z2 + 8z + 17 = 0.

3.Найти область определения функции y = log21 (4x 1).

x2 + 3

4. Дана функция y = x2 1. Требуется:

1) найти область определения функции;

2) исследовать функцию на ч¼тность, неч¼тность;

3) исследовать функцию на периодичность, если функция периодическая, указать е¼ наименьший период;

4) найти нули функции.

5. Даны функции f(x) = 1 x2, g(x) = lg3(2x 1). Записать функцию y(x) = g(f(x)).

6. Для функции f(x) =	5	найти обратную f 1(x).
	4x 3

35

Вариант 4

1.Задать с помощью перечисления элементов множества A, B,

A [ B, A \ B, AnB, åñëè A = fa 2 Zj jaj < 5g, B = f 3; 2; 5; 20g.

2.Решить уравнение z2 + 10z + 26 = 0.

3.Найти область определения функции y = log6 (4x 3).

2x 1

4. Дана функция y = x + 1 . Требуется:

1) найти область определения функции;

2) исследовать функцию на ч¼тность, неч¼тность;

3) исследовать функцию на периодичность, если функция периодическая, указать е¼ наименьший период;

4) найти нули функции.

	1				, g(x) = 7x 1. Записать функ-
5.	Даны функции f(x) =	p
			3x + 2
	öèþ y(x) = f(g(x)).
6.	Для функции f(x) = 5×3 + 4 найти обратную f 1(x).

Вариант 5

1.Задать с помощью перечисления элементов множества A, B,

A [ B, A \ B, BnA, åñëè A = f 3; 0; 2g, B = fb 2 Zj 2 < b < 6g.

2.Решить уравнение z2 + 2z + 2 = 0.

3.Найти область определения функции y = log12 (6x 8).

x4

4. Дана функция y = x3 + 8. Требуется: 1) найти область определения функции;

2) исследовать функцию на ч¼тность, неч¼тность;

36

3)исследовать функцию на периодичность, если функция периодическая, указать е¼ наименьший период;

4)найти нули функции.

5. Даны функции f(x) = tg x, g(x) = ex2 . Записать функцию y(x) = g(f(x)).

6. Для функции f(x) = 2arctg x + 1 найти обратную f 1(x).

Вариант 6

1.Задать с помощью перечисления элементов множества A, B,

A [ B, A \ B, AnB, åñëè A = f 1; 1; 3; 7g, B = fb 2 Nj 5 b < 9g.

2.Решить уравнение z2 + 8z + 25 = 0.

3.Найти область определения функции y = log3 (5x + 12).

4.	Дана функция y =			2×3		. Требуется:
				x2 2
	1)	найти область определения функции;
	2)	исследовать функцию на ч¼тность, неч¼тность;
	3)	исследовать функцию на периодичность, если функция пери-
		одическая, указать е¼ наименьший период;
	4)	найти нули функции.
5.	Даны функции f(x) = log2(2x 7), g(x) = x 1. Записать функ-
	öèþ y(x) = f(g(x)).
6.	Для функции f(x) = 1 + arcsin 2x найти обратную f 1(x).
					Вариант 7
1.	Задать		с помощью		перечисления		элементов множества
	A,	B,	A [ B, A \ B,			BnA, åñëè	A = fa 2 Zj 4 a < 10g,

B = f 2; 1; 4; 8g.

37

2.Решить уравнение z2 + 4z + 5 = 0.

3.Найти область определения функции y = log3 (5x 9).

x2 4

4. Дана функция y = x3 + 1. Требуется:

1) найти область определения функции;

2) исследовать функцию на ч¼тность, неч¼тность;

3) исследовать функцию на периодичность, если функция периодическая, указать е¼ наименьший период;

4) найти нули функции.

p

5. Даны функции f(x) = ln x, g(x) = arctg x. Записать функцию

y(x) = g(f(x)).

p

6. Для функции f(x) = 5x + 7 1 найти обратную f 1(x).

Вариант 8

1.Задать с помощью перечисления элементов множества A, B,

A [ B, A \ B, AnB, åñëè A = f 3; 2; 1; 15g, B = fb 2 Nj b 5g.

2.Решить уравнение z2 8z + 17 = 0.

3.Найти область определения функции y = log7 (5 16x).

x3

4. Дана функция y = x2 1. Требуется:

1) найти область определения функции;

2) исследовать функцию на ч¼тность, неч¼тность;

3) исследовать функцию на периодичность, если функция периодическая, указать е¼ наименьший период;

4) найти нули функции.

p

5. Даны функции f(x) = 3 1 x3, g(x) = x3 + 1. Записать функ-

öèþ y(x) = f(g(x)).

38

6.	Для функции f(x) = arccos(x + 2) + 1 найти обратную f 1(x).
			Вариант 9
1.	Задать	с помощью	перечисления	элементов множества
	A, B,	A [ B, A \ B,	BnA, åñëè	A = fa 2 Zj 3 < a 2g,

B = f 7; 5; 3g.

2.Решить уравнение z2 10z + 26 = 0.

3.Найти область определения функции y = log4 (12 7x).

x4

4. Дана функция y = x3 27. Требуется:

1) найти область определения функции;

2) исследовать функцию на ч¼тность, неч¼тность;

3) исследовать функцию на периодичность, если функция периодическая, указать е¼ наименьший период;

4) найти нули функции.

5. Даны функции f(x) = x1 , g(x) = cos(3x 2). Записать функцию y(x) = g(f(x)).

6. Для функции f(x) = lg(x 4) + 2 найти обратную f 1(x).

Вариант 10

1.Задать с помощью перечисления элементов множества A, B,

A [ B, A \ B, AnB, åñëè A = fa 2 Nj a < 5g, B = f 1; 2; 9; 12g.

2.Решить уравнение z2 + 2z + 5 = 0.

3.Найти область определения функции y = log7 (8 6x).

4x

4. Дана функция y = x 3. Требуется:

39

1)найти область определения функции;

2)исследовать функцию на ч¼тность, неч¼тность;

3)исследовать функцию на периодичность, если функция периодическая, указать е¼ наименьший период;

4)найти нули функции.

x

5. Даны функции f(x) = 2x 1, g(x) = x + 1. Записать функцию y(x) = f(g(x)).

6. Для функции f(x) = 2log5(x + 4) найти обратную f 1(x).

	Вариант 11
1. Задать	с помощью перечисления элементов множества
A, B,	A [ B, A \ B, BnA, åñëè A = f 18; 11; 0; 9g,

B = fb 2 Zj 15 b < 11g.

2.Решить уравнение z2 + 6z + 10 = 0.

3.Найти область определения функции y = log5 (3x 1).

7×2

4. Дана функция y = x + 4. Требуется:

1) найти область определения функции;

2) исследовать функцию на ч¼тность, неч¼тность;

3) исследовать функцию на периодичность, если функция периодическая, указать е¼ наименьший период;

4) найти нули функции.

p

5. Даны функции f(x) = 3x + 5, g(x) = 102x+1. Записать функ- öèþ y(x) = g(f(x)).

6. Для функции f(x) = 3x 1 2 найти обратную f 1(x).

40

3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт.