Формулы cos sin tg: формулы cos, sin, tg, ctg

формулы cos, sin, tg, ctg

Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных тригонометрических формул можно находить и решать практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь все тригонометрические формулы, а не их вывод, которому будут посвящены отдельные статьи.

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую (посредством преобразования).

Тригонометрические тождества

sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg) и их свойств.

Основные формулы приведения в тригонометрии

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов, то есть, преобразовывать их.

Формулы приведения

sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα

Формулы приведения являются следствием периодичности тригонометрических функций.

Все формулы сложения в тригонометрии

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.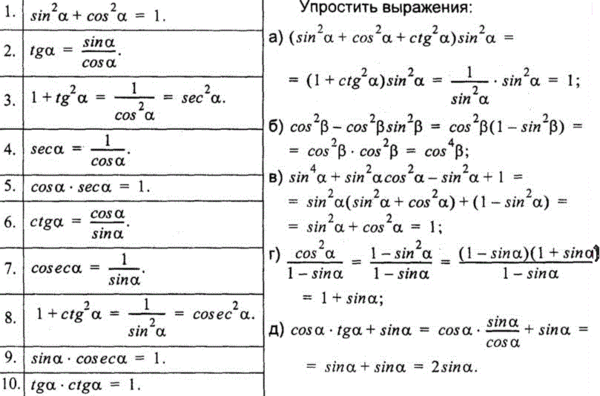

Тригонометрические формулы сложения

sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ

На основе формул сложения выводятся тригонометрические формулы кратного угла. 

Формулы кратного угла: двойного, тройного и т.д.

Формулы двойного и тройного угла

sin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы понижения степени

Формулы понижения степени

sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8

Часто при расчетах действовать с громоздкими степенями неудобно.  Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

для четных n решение 

sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)

для нечетных n

sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно для применения при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2

Произведение тригонометрических функций

Если формулы суммы и разности функций позволяют перейти к их произведению или умножению, то формулы произведения (здесь нужно умножать) тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.

Формулы произведения тригонометрических функций

sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))

Универсальная тригонометрическая подстановка

Все основные тригонометрические функции — тангенс, котангенс, синус, косинус — могут быть выражены через тангенс половинного угла. 

Универсальная тригонометрическая подстановка

sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

формулы cos, sin, tg, ctg

Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных тригонометрических формул можно находить и решать практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь все тригонометрические формулы, а не их вывод, которому будут посвящены отдельные статьи.

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую (посредством преобразования).

Тригонометрические тождества

sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg) и их свойств.

Основные формулы приведения в тригонометрии

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов, то есть, преобразовывать их.

Формулы приведения

sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα

Формулы приведения являются следствием периодичности тригонометрических функций.

Все формулы сложения в тригонометрии

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

Тригонометрические формулы сложения

sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ

На основе формул сложения выводятся тригонометрические формулы кратного угла.  

Формулы кратного угла: двойного, тройного и т.д.

Формулы двойного и тройного угла

sin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы понижения степени

Формулы понижения степени

sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8

Часто при расчетах действовать с громоздкими степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

для четных n решение 

sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)

для нечетных n

sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно для применения при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2

Произведение тригонометрических функций

Если формулы суммы и разности функций позволяют перейти к их произведению или умножению, то формулы произведения (здесь нужно умножать) тригонометрических функций осуществляют обратный переход — от произведения к сумме.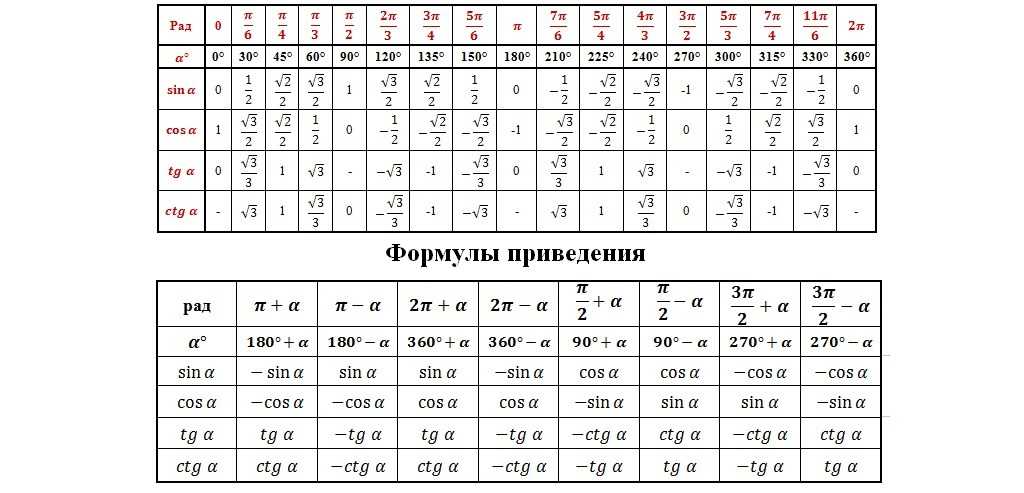 Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.

Формулы произведения тригонометрических функций

sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))

Универсальная тригонометрическая подстановка

Все основные тригонометрические функции — тангенс, котангенс, синус, косинус — могут быть выражены через тангенс половинного угла. 

Универсальная тригонометрическая подстановка

sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Сводка тригонометрических формул

Сводка тригонометрических формул

Эти формулы связывают длины и площади определенных кругов или треугольников.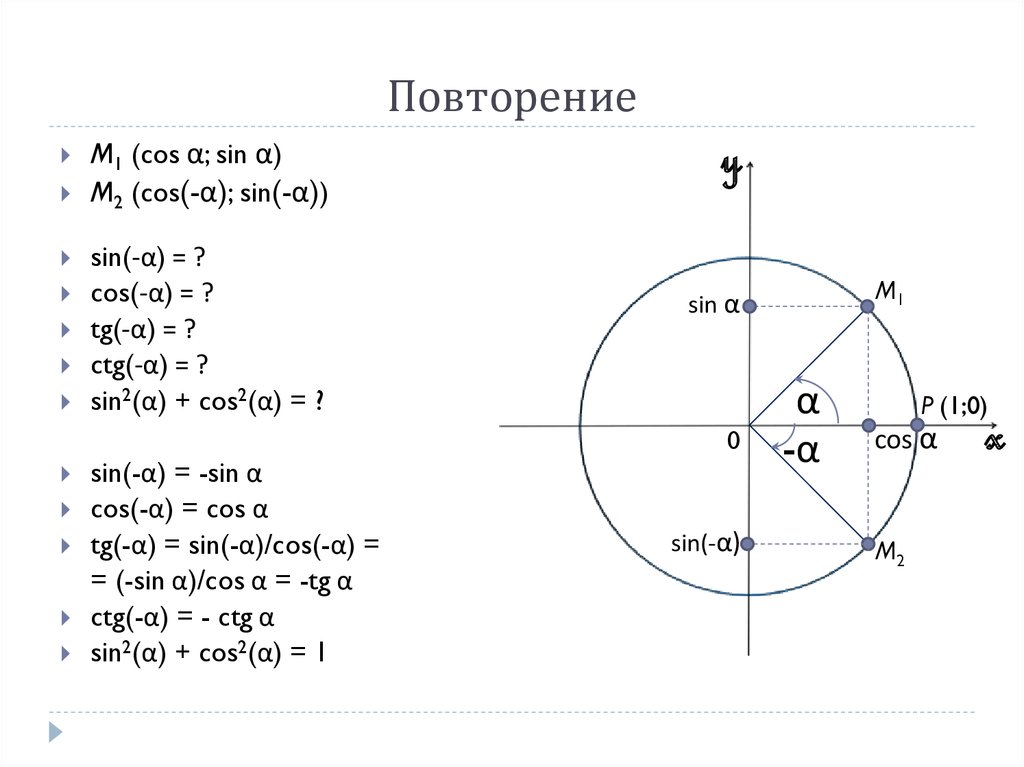 На следующей странице вы найдете личности. Тождества не относятся к конкретным геометрическим фигурам, но справедливы для всех углов.

Формулы для дуг и секторов окружностей

Вы можете легко найти длину дуги и площадь сектора для угла θ в круге радиусом r .

Длина дуги. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах. Чтобы перевести градусы в радианы, умножьте количество градусов на π /180.
Площадь сектора. Площадь сектора равна половине квадрата радиуса, умноженного на угол, где, опять же, угол измеряется в радианах.

Формулы для прямоугольных треугольников

Наиболее важными формулами тригонометрии являются формулы прямоугольного треугольника. Если θ — один из острых углов в треугольнике, то синус теты — это отношение противолежащего катета к гипотенузе, косинус — отношение прилежащего катета к гипотенузе, а тангенс — это отношение противоположная сторона соседней стороне.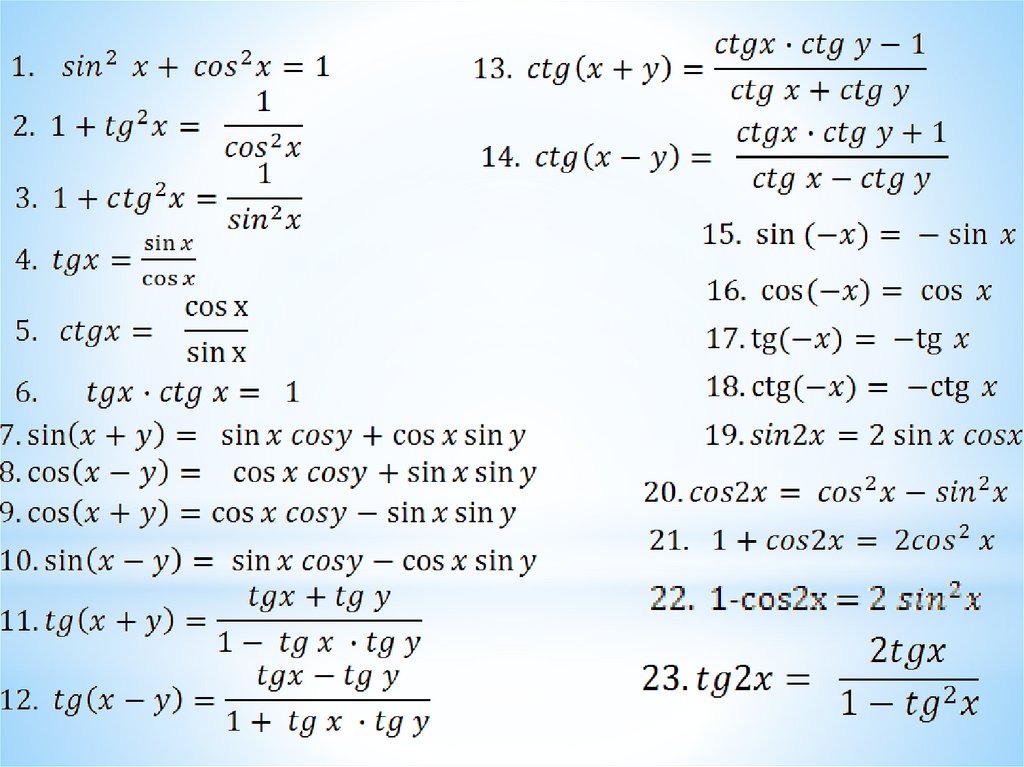

Эти три формулы вместе известны мнемоникой SohCahToa. Кроме того, есть очень важная формула Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон.

Зная, что два острых угла дополняют друг друга, то есть дают в сумме 90°, можно решить любой прямоугольный треугольник:

• Если известны две из трех сторон, то можно найти третью сторону и оба острых угла.
• Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.

Формулы для косоугольных треугольников

Эти формулы работают для любого треугольника, острого, тупоугольного или прямоугольного. Мы будем использовать стандартные обозначения, в которых три вершины треугольника обозначены прописными буквами A , B и C , а три противоположные им стороны соответственно обозначены строчными буквами a , б и в .

Есть две важные формулы для косых треугольников. Они называются законом косинусов и законом синусов.

Закон косинусов обобщает формулу Пифагора на все треугольники. Он говорит, что c ² , квадрат одной стороны треугольника, равен a ²  +  b ² , сумма квадратов двух других сторон минус 2. ab  cos&nbsp C , удвоенное произведение их на косинус противоположного угла. Когда угол C правильный, он становится формулой Пифагора.

Закон синусов гласит, что отношение синуса одного угла к противоположной стороне одинаково для всех трех углов.

С помощью этих двух формул вы можете решить любой треугольник:

• Если вам известны два угла и сторона, вы можете найти третий угол и две другие стороны.
• Если известны две стороны и угол между ними, можно найти третью сторону и оба других угла.
• Если вы знаете две стороны и угол, противолежащий одной из них, то существует два варианта угла, противоположного другому (один острый и один тупой), и для обоих вариантов вы можете определить оставшийся угол и оставшуюся сторону.

Формулы площади треугольников

Существует три различных полезных формулы площади треугольника, и какую из них использовать, зависит от имеющейся у вас информации.

Половина основания, умноженная на высоту. Это обычный способ использования, так как он самый простой, и у вас обычно есть эта информация. Выберите любую сторону для вызова базы b . Тогда, если h — это расстояние от противоположной вершины до b , то площадь равна половине bh .
Формула Герона. Это полезно, когда вы знаете три стороны a , b и c треугольника, и все, что вы хотите знать, это площадь. Пусть s составляют половину их суммы, называемой полупериметром . Тогда площадь является квадратным корнем произведения s , s  —  a , s  — b и s  — c 90 008 .
Формула «бок-угол-бок». Используйте это, когда вы знаете две стороны, a и b , и прилежащий угол, C . Площадь равна половине произведения двух сторон на синус прилежащего угла.

Sin, Cos, Tan — тригонометрия

Все ресурсы по тригонометрии

6 диагностических тестов 155 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Тригонометрия Помощь » Тригонометрические операции » Sin, Cos, Tan

Найдите значение тригонометрической функции в виде дроби для треугольника .

Что такое косинус?

Возможные ответы:

Правильный ответ:

Объяснение:

Косинус угла — это значение прилежащего катета к гипотенузе.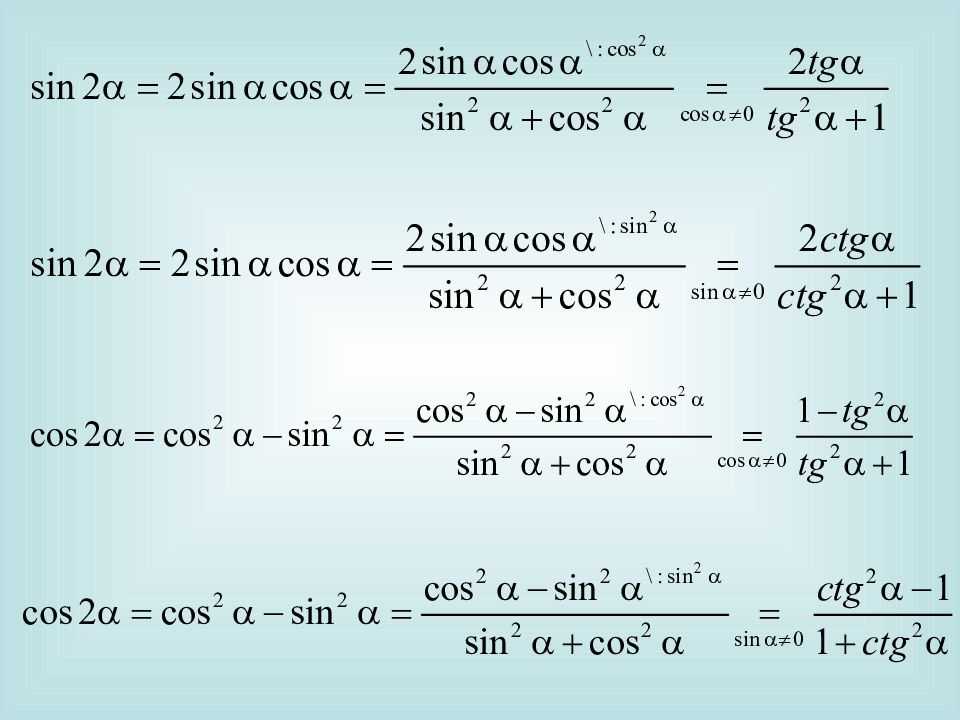

Следовательно:

Сообщить об ошибке

Каково значение ?

Возможные ответы:

Правильный ответ:

Объяснение:

Решите каждое условие отдельно.

Добавьте оба термина.

Сообщить об ошибке

Определите значение .

Возможные ответы:

Правильный ответ:

Объяснение:

Переписать в терминах синусов и косинусов.

Упростите сложную дробь.

Сообщить об ошибке

Найдите значение .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти значение , решите каждое условие отдельно.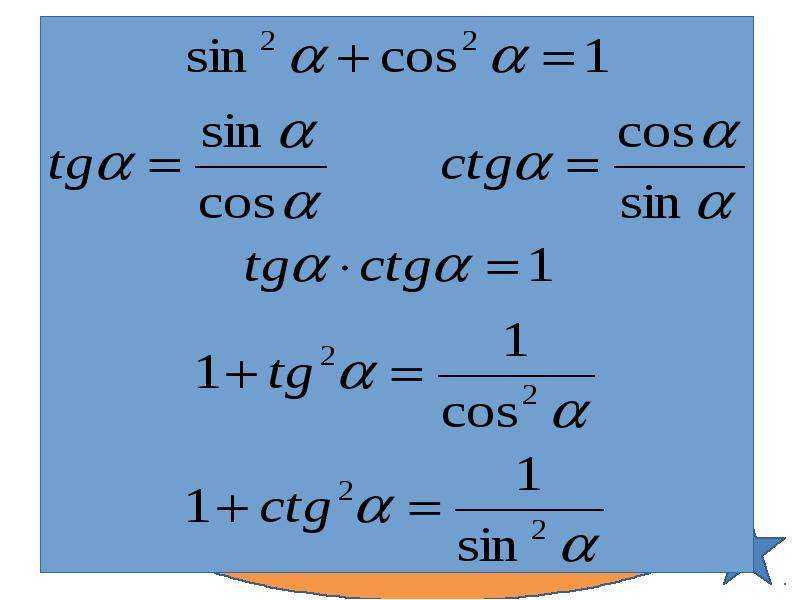

Суммируйте два члена.

Сообщить об ошибке

Выберите соотношение, которое даст Tan B.

Возможные ответы:

Ни один из других ответов.

Правильный ответ:

Пояснение:

Нам нужен Tan B. Длины каких сторон соответствуют этому соотношению?

  

Сообщить об ошибке

Рассчитать .

Возможные ответы:

Правильный ответ:

Объяснение:

Функция тангенса имеет период  единиц. То есть

для всех.

Так как , мы можем переписать исходное выражение  следующим образом:

                                               

               

Следовательно, 

Сообщить об ошибке

Рассчитать .

Возможные ответы:

Правильный ответ:

Объяснение:

Во-первых, преобразуйте данную меру угла из радианов в градусы:

Далее, вспомним, что лежит в четвертом квадранте единичной окружности, где косинус положительный. Кроме того, опорный угол равен

Следовательно, все, что требуется, — это признать из этих наблюдений, что

,

что есть .

Следовательно,

Сообщить об ошибке

Что получится, если максимально упростить следующее выражение?

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку это нечетная функция, мы можем переписать второй член в выражении.

.

Теперь мы используем формулу двойного угла, чтобы расширить первый член.

.

Поскольку они обратны, .

Сообщить об ошибке

Округлить до сотых.

Найдите на калькуляторе:

 

Возможные ответы:

Ни один из вышеперечисленных 03

Объяснение:

Прежде чем подключать функцию к калькулятору, убедитесь, что режим калькулятора установлен на градусы,

Подключить , что равно .

Сообщить об ошибке

Округлить до сотых.

Найдите на калькуляторе:

Возможные ответы:

Ничего из вышеперечисленного

Правильный ответ: 900 03

Объяснение:

Перед подключением функции к калькулятору убедитесь, что режим калькулятора установлен на радианы,

подключите

 

, что равно  .

No related posts.