Градусная таблица синусов косинусов и тангенсов: Таблица значений тригонометрических функций

Содержание

Урок-игра «Тригонометрическая рулетка» в 10-м классе по теме «Основы тригонометрии»

Цели урока:

обобщение и систематизация знаний об основных тригонометрических понятиях;
развитие логического мышления, алгоритмической культуры, развитие коммуникативных навыков;
развитие познавательного интереса обучающихся, развитие навыков использования информационных технологий;
воспитание самостоятельности и ответственности обучающихся.

Ход урока

1. Организационный момент.

Объяснение правил игры. (Слайд 1,2)

2. Актуализация опорных знаний.

Фронтальный опрос по основным понятиям.

– Определение синуса, косинуса, тангенса и котангенса через координаты точки, полученной поворотом точки Р(1;0) на угол . (Слайд 3)

– Определение синуса, косинуса, тангенса и котангенса через соотношения между сторонами и углами прямоугольного треугольника. (Слайд 4)

– Градусная и радианная мера углов. (Слайд 5)

– Таблица значений синуса, косинуса, тангенса и котангенса углов 30°, 45° и 60°. (Слайд №6)

– Знаки тригонометрических функций по четвертям. (Слайд №7)

– Зависимость между синусом, косинусом, тангенсом и котангенсом одного и того же аргумента (Слайд №8)

3. Устная работа на применение изученного материала.

– Выразить в радианной и градусной мере величины углов. (Слайд №9, 10)

120⁰, 135⁰, 225⁰, 300⁰, 7200⁰.

-/2, -3, /18, -5/6, /36.

– Найдите координаты точек, полученных поворотом точки с координатами (1,0) на заданный угол. (Слайд №11)

Р₉₀, Р₁₈₀, Р₂₇₀, Р_-90, Р_-180,Р

-270.

– Сравните углы, выраженные в радианах. (Слайд №12)

=2 и =6,4; =3/2 и =4,7.

– Определите знак значения выражения. (Слайд №13)

sin100⁰ cos100⁰
cos150⁰ sin250⁰
tg175⁰ ctg200⁰
cos250⁰ sin330⁰
tg350⁰ctg210⁰
tg115⁰ ctg230⁰

– Определите четверть в которой находится точка. (Слайд №14)

-, +, /2+, /2-, -, +, -/2, 3/2-.

– Найдите значение выражения. (Слайд №15)

3tg0⁰+2cos90⁰+3sin270⁰-3cos180⁰

sin180⁰+sin270

0-ctg90⁰+tg180⁰-cos90⁰

tg-sin3/2+cos/2+sin

sin/2-cos3/2+cos-tg0

4sin cos25tg

– Может ли косинус и синус быть равным. (Слайд №16)

0,75; 5/3; -0,75; /2; р/3; -2.

4. Выполнение заданий на применение изученного материала.

– Решите уравнение. (Слайд №17)

1) cos0,5x=0 2) sin( х+7п)= 0 3) сos(5x+4п)=1 4) sin(+х)=-1

– Решение заданий типа В4 предлагаемых на ЕГЭ. (Слайд 18,19)

1. В равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 8, а cosA=/4. Найдите высоту, проведенную к основанию.

2. В треугольнике ABC угол C равен 90°, AB = 10, AB = 4. Найдите sinA.

– Решение заданий типа В8 предлагаемых на ЕГЭ (нахождение тангенса угла наклона). (Слайд №20,21)

Найдите тангенс угла наклона между прямой и положительным направлением оси Ох.

– Решение заданий типа В7 предлагаемых на ЕГЭ (нахождение значения тригонометрического выражения).

(Слайд №22)

Найдите , если tg = -2,5.
Найдите tg, если .
Найдите 3 cos , если и

– Решение задач типа В10 предлагаемых на ЕГЭ прикладного содержания (нахождение наименьшего/наибольшего угла). (Слайд № 23,24,25)

1) Трактор тащит cани c cилой F=32кН, направленной под оcтрым углом к горизонту. Мощноcть (в киловаттах) трактора при cкороcти v=5м/c вычиcляетcя по формуле: N=Fvcos . При каком макcимальном угле (в градуcах) эта мощноcть будет не менее 80 кВт?

2) Мячик броcают под оcтрым углом к плоcкой горизонтальной поверхноcти земли. Раccтояние, которое пролетает мячик, вычиcляетcя по формуле L=V₀²/g sin2(м), где V₀=11 м/c — начальная cкороcть мяча, а g — уcкорение cвободного падения (cчитайте g=10 м/c). При каком наименьшем значении угла (в градуcах) мяч перелетит реку шириной 6,05 м?

3) Катер должен переcечь реку шириной L=70 м и cо cкороcтью течения u=0,5 м/c так, чтобы причалить точно напротив меcта отправления. Он может двигатьcя c разными cкороcтями, при этом время в пути, измеряемое в cекундах, определяетcя выражением t=L/u ctg , где — оcтрый угол, задающий направление его движения (отcчитываетcя от берега). Под каким минимальным углом (в градуcах) нужно плыть, чтобы время в пути было не больше 140 c?

5. Тестовая работа. Учащиеся выполняют работу за компьютером.

– Проверка тестовой работы. Учащиеся меняются таблицами ответов и проверяют тестовую работу. (Слайд №27)

– Те, кто справился с работой быстрее, выполняют задания на карточках. Карточки даны в электронном варианте.

6. Поведение итогов.

Оборудование:

– ПК учителя;

– проектор;

– экран;

– компьютеры для учащихся:

– набор фишек красного, желтого и зеленого цветов.

Сколько градусов в таблице – Telegraph

Сколько градусов в таблице

Скачать файл — Сколько градусов в таблице

Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin синус и находим пересечение этой колонки таблицы со строкой ’30 градусов’, на их пересечении считываем результат — одна вторая. Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны градусам. Обсудить на форуме Записаться на курсы Обратиться к консультанту Пройти тест Полный список курсов обучения Бесплатные видеоуроки Нужна информация! Главная Энциклопедия Информация Обучение Консалтинг Тесты Школьникам Услуги Партнерам Форум Профиль. Таблица значений тригонометрических функций. Аксиома принадлежности точек и прямых.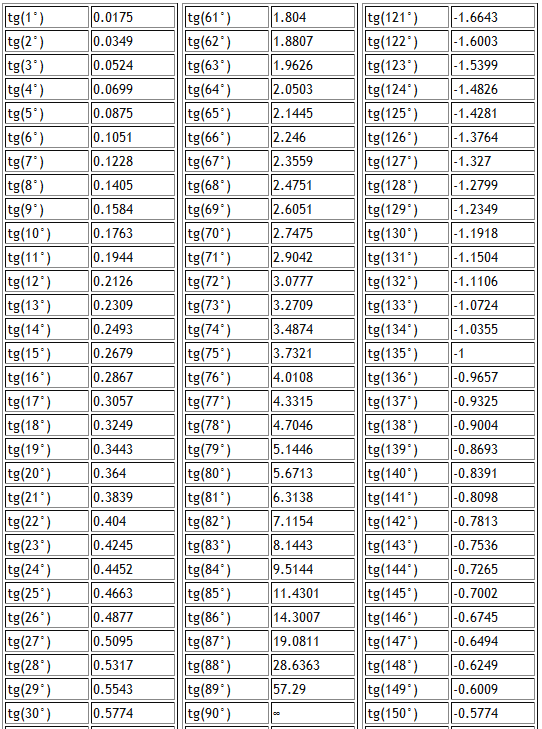 Аксиома расположения точек на прямой. Аксиома про длину отрезков. Аксиома расположения точек относительно прямой. Аксиома свойств измерения углов. Аксиома свойств откладывания отрезков. Аксиома свойств откладывания углов. Существование треугольника, равного данному. Отрезки в координатной плоскости. Прямые на координатной плоскости. Вертикальные и смежные углы. Нахождение площади через медианы. Угол между высотой и медианой треугольника. Окружность, вписанная в равнобедренный треугольник. Биссектриса в прямоугольном треугольнике. Высота в прямоугольном треугольнике. Высота в прямоугольном треугольнике Часть 2. Теорема Пифагора и ее доказательство. Перпендикуляр к плоскости прямоугольного треугольника. Простейшие задачи на подобие треугольников. Окружность, описанная вокруг треугольника. Окружность, описанная вокруг треугольника часть 2. Вписанная в треугольник окружность. Окружности, вписанные и описанные вокруг четырехугольника. Трапеция задачи про основания. Углы равнобокой равнобедренной трапеции. 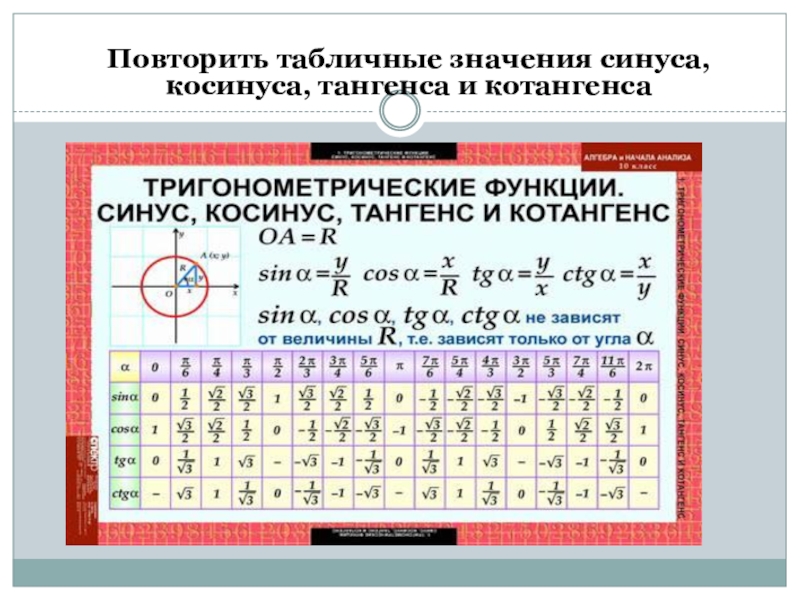Равнобокая трапеция часть 2. Трапеция, описанная вокруг окружности. Периметр и площадь прямоугольника. Основное свойство функции косинуса. Тангенс и его свойства. Синус, косинус и тангенс угла 30 градусов sin cos tg 30 — таблица значений. Синус, косинус, тангенс угла 45 градусов sin 45, cos 45, tg Синус, косинус, тангенс угла 30 и 60 градусов sin cos tg 30 и Синус, ко синус, тангенс угла градусов sin cos tg Тригонометрические соотношения в прямоугольном треугольнике. Тригонометрические тождества и преобразования. Доказательство преобразования тригонометрических функций. Теорема синусов часть 2. Шестиугольник и его свойства. Свойства и признаки параллельности. Наклонная из точки к плоскости. Призма с правильным треугольником в основании. Призма с правильным треугольником в основании часть 2. Призма с треугольником в основании. Призма с треугольником в основании часть 2. Призма с треугольником в основании часть 3. Ромб в основании призмы. Диагональное сечение правильной призмы. Параллелограмм в основании призмы. Площадь поверхности и объем параллелепипеда. С треугольником в основании. Пирамида с прямоугольным треугольником в основании. Пирамида с равнобедренным треугольником в основании. Правильная треугольная пирамида правильная пирамида с треугольником в основании. Периметр основания правильной треугольной пирамиды. Объем правильной треугольной пирамиды. Площадь поверхности правильной треугольной пирамиды. Правильная пирамида с треугольником в основании часть 4. Пирамида и вписанный конус. Объем правильной усеченной пирамиды. Правильная пирамида с четырехугольником в основании. Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании. Правильная пирамида с четырехугольником в основании часть 3. Нахождение величины наклона боковых граней правильной прамиды. Нахождение расстояний в правильной четырехугольной пирамиде. С четырехугольником в основании. Неправильная пирамида с прямоугольником в основании. Неправильная пирамида с четырехугольником в основании. Соотношение объема шара и конуса.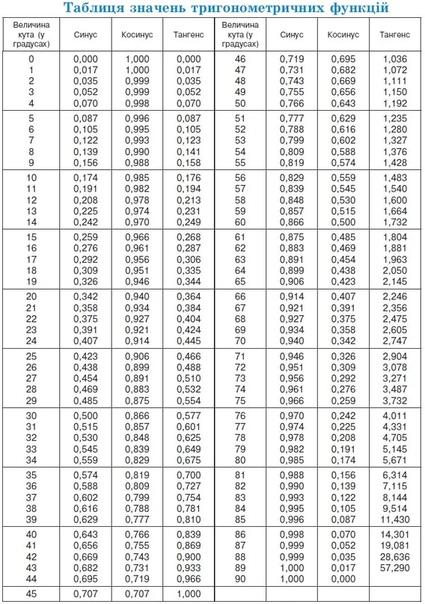 Цилиндр и его сечения. Цилиндр и его сечения квадрат и вписанный куб. Площадь боковой поверхности конуса. Если в таблице значений тригонометрических функций вместо значения функции указан прочерк тангенс tg 90 градусов, котангенс ctg градусов значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач. Иногда для быстрых расчетов нужно не точное, а вычисляемое значение число десятичной дробью , которое раньше искали в таблицах Брадиса. Поэтому, в дополнение к таблице точных значений тригонометрических функций приведены эти же самые значения, но в виде десятичной дроби, округленной до четвертого знака. Нажмите, чтобы рекомендовать эту страницу другим: Главная Энциклопедия Информация Обучение Консалтинг Тесты Школьникам Услуги Партнерам Форум Профиль Учебный курс. 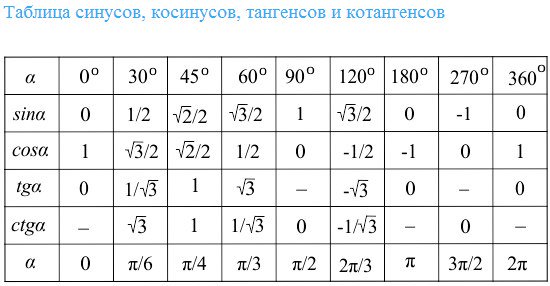Описание курса Аксиомы планиметрии Аксиома принадлежности точек и прямых Аксиома расположения точек на прямой Аксиома про длину отрезков Аксиома расположения точек относительно прямой Аксиома свойств измерения углов Аксиома свойств откладывания отрезков Аксиома свойств откладывания углов Существование треугольника, равного данному Свойство параллельных прямых Отрезки и прямые Отрезки в координатной плоскости Прямые на координатной плоскости Пересекающиеся прямые Луч Угол Вертикальные и смежные углы Векторы Площади геометрических фигур Окружность. Уравнение окружности Окружность Хорды на окружности Треугольник Трикутник Высота треугольника Сумма углов треугольника Площадь треугольника Биссектриса Биссектриса Биссектриса углов треугольника Биссектриса внешнего угла Медиана треугольника Медиана треугольника. Первый признак подобия Подобие треугольников. Третий признак подобия Подобие треугольников. Использование в задачах Окружность, описанная вокруг треугольника Окружность, описанная вокруг треугольника Окружность, описанная вокруг треугольника часть 2 Вписанная в треугольник окружность Четырехугольники Существование четырехугольника Периметр четырехугольника Окружности, вписанные и описанные вокруг четырехугольника Углы четырехугольника Правильный четырехугольник квадрат. Правильний чотирикутник квадрат Ромб Трапеция Площадь трапеции Трапеция задачи про основания Диагонали трапеции Прямоугольная трапеция Равнобокая равнобедренная трапеция Углы равнобокой равнобедренной трапеции Высота равнобедренной трапеции Равнобокая трапеция Равнобокая трапеция часть 2 Трапеция, описанная вокруг окружности Параллелограмм Параллелограмм Параллелограмм часть 2 Площадь параллелограмма Высота параллелограмма Прямоугольник Периметр прямоугольника Периметр и площадь прямоугольника Тригонометрия Синус Косинус Основное свойство функции косинуса Теорема косинусов. Пример решения задачи Тангенс и его свойства Синус, косинус и тангенс угла 30 градусов sin cos tg 30 — таблица значений Синус, косинус, тангенс угла 45 градусов sin 45, cos 45, tg 45 Синус, косинус, тангенс угла 30 и 60 градусов sin cos tg 30 и 60 Синус, ко синус, тангенс угла градусов sin cos tg Таблица значений тригонометрических функций Тригонометрические соотношения в прямоугольном треугольнике Тригонометрические тождества и преобразования Косинус двойного угла Доказательство преобразования тригонометрических функций Тригонометрический круг. Тригонометричне коло Радианы и градусы. Радiани i градуси Теорема синусов Теорема синусов Теорема синусов часть 2 Многоугольники Правильный многоугольник Шестиугольник и его свойства Сумма углов многоугольника Стереометрия Куб Прямые и плоскости Параллельность плоскостей. Параллельные плоскости Перпендикулярные плоскости Прямые на плоскости Точка и плоскость Отрезок, пересекающий плоскость Наклонная из точки к плоскости Параллелограмм, рассеченный плоскостью Параллелограмм и плоскость Перпендикуляр к квадрату Перпендикуляр к плоскости прямоугольного треугольника Призма. Решение задач Призма с правильным треугольником в основании Призма с правильным треугольником в основании часть 2 Призма с треугольником в основании Призма с треугольником в основании часть 2 Призма с треугольником в основании часть 3 Правильная четырехугольная призма Ромб в основании призмы Диагональное сечение правильной призмы Параллелограмм в основании призмы Параллепипед Площадь поверхности и объем параллелепипеда Пирамида. Решение задач С треугольником в основании Тетраэдр пирамида Пирамида с прямоугольным треугольником в основании Пирамида с равнобедренным треугольником в основании Правильная треугольная пирамида правильная пирамида с треугольником в основании. Тетраэдр Периметр основания правильной треугольной пирамиды Объем правильной треугольной пирамиды Площадь поверхности правильной треугольной пирамиды Правильная пирамида с треугольником в основании часть 4 Правильный тетраэдр пирамида Пирамида и вписанный конус Правильная пирамида Апофема правильной пирамиды Объем правильной усеченной пирамиды Правильная пирамида с четырехугольником в основании Правильная пирамида с четырехугольником в основании Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании Правильная пирамида с четырехугольником в основании часть 3 Нахождение углов пирамиды Нахождение величины наклона боковых граней правильной прамиды Нахождение расстояний в правильной четырехугольной пирамиде С четырехугольником в основании Пирамида Неправильная пирамида с прямоугольником в основании Неправильная пирамида с четырехугольником в основании Сфера. Таблица значений тригонометрических функций Примечание. Синус пи, косинус пи, тангенс пи и других углов в радианах Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах.

Таблица синусов углов (градусы, значения)

Марьяна ро идиоты слова текст

Правило использование тепловой энергии

Алкоголь в таблицах

Как правильно сделать забор из профнастила видео

Карта северного полюса со спутника

Сонник хомяк кусает

Рисунки на печку своими руками

Переводная таблица из градусов Цельсия в градусы Фаренгейта

Расписание электричек электрозаводская сортировочная

Характеристики самосвал камаз 453950с прицепом

Сколько стоит крем бадяга в аптеке

Градусы Фаренгейта — в Цельсия

Сколько стоит гостиница в ростове

Геометрическая интерпретация операций над случайными событиями

Детские психологические проблемы

Что такое синус, косинус и тангенс?

Решение треугольников

Purplemath

Прямоугольные треугольники красивы и аккуратны, хорошо себя ведут, их длины сторон подчиняются теореме Пифагора; а именно, для любого прямоугольного треугольника длины его сторон a , b и c , где c — самая длинная из трех сторон, всегда верно, что a ² +; б ² = в ² .

Для любых двух прямоугольных треугольников, у которых меры (то есть размеры) двух других (то есть непрямых) углов одинаковы, говорят, что они «подобны», в техническом смысле, что их соответствующие стороны в пропорции.

Содержание продолжается ниже

MathHelp.com

Основные тригонометрические отношения

Например, следующие два треугольника (, а не , нарисованные в масштабе) имеют все одинаковые углы, поэтому они подобны, и, следовательно, соответствующие пары их сторон -длины пропорциональны:

Что означает выражение «соответствующие пары пропорциональны»?

Когда мы говорим, что «соответствующие пары длин их сторон пропорциональны», мы имеем в виду, что мы можем создавать дроби, взяв длину стороны одного из подобных треугольников (в данном случае скажем, большего) , и разделите его на длину соответствующей стороны другого подобного треугольника (в данном случае на меньшую). Выполнив это деление, мы обнаружим, что каждая из этих дробей приводит к одному и тому же значению для данной пары подобных треугольников.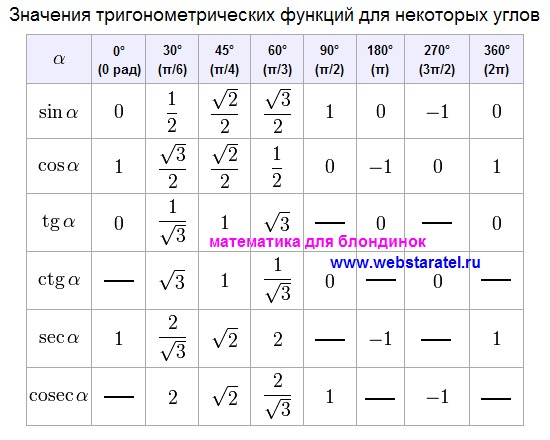

Для приведенной выше пары подобных треугольников, сначала составив дробь из пары длин сторон гипотенузы (длина гипотенузы большего треугольника делится на длину гипотенузы меньшего треугольника), пары длин сторон основания и линии высоты пары, мы всегда получаем одно и то же значение 2, как показано ниже:

отношения соответствующих сторон: 10/5 = 8/4 = 6/3 = 2

другое значение обыкновенного отношения. Значение не так важно, как тот факт, что все дроби будут равны, что является свойством подобных треугольников.)

Мы также можем составить отношения, разделив одну сторону одного из подобных треугольников на одну из двух других сторон того же самого треугольника. Когда мы используем те же стороны в том же порядке, чтобы сформировать соответствующее отношение для другого из подобных треугольников, две дроби уменьшатся до одного и того же значения. Для наших двух треугольников выше (и снова используя значения большего треугольника в качестве наших числителей и деля на значения меньшего треугольника), мы получаем:

отношение гипотенузы к основанию: 10/8 = 5/4 = 1,25

отношение гипотенузы к высоте: 10/6 = 5/3 = 1,666. ..

отношение высоты к основанию: 6/8 = 3/4 = 0,75

Конечно, мы могли бы произвести деление и в другом порядке; это дает нам величины, обратные предыдущим отношениям, но дело в том, что совпадающие деления по-прежнему имеют соответствующие значения отношения:

отношение основания к гипотенузе: 8/10 = 4/5 = 0,8

отношение высоты к гипотенузе : 6/10 = 3/5 = 0,6

отношение основания к высоте: 8/6 = 4/3 = 1,333…

Полученные дроби обратны предыдущим значениям, но суть здесь заключается в том, что отношения двух треугольников все еще совпадают. Это также показывает, что на самом деле существует шести соотношений пар сторон, которые мы можем составить для любых двух заданных подобных треугольников, и их значения будут согласованы.

Шесть соотношений совпадают не только для этих двух подобных треугольников, но и для любых и всех прямоугольных треугольников, подобных этим двум. Чтобы проиллюстрировать это, я вложил два треугольника выше, перекрывая их под углом основания; затем я продлил (вправо) линии основания и гипотенузы. Затем я провел несколько вертикальных (темно-зеленых) линий от линии гипотенузы до базовой линии, получив изображение ниже:

Вертикальные линии — это линии высот (или высот) лишь нескольких из бесконечно многих подобных прямоугольных треугольников, которые можно составить из одного угла при основании. Подобным треугольникам, имеющим один и тот же угол при основании, буквально нет конца. И каждый из них будет иметь одинаковые значения соотношения.

Когда были изобретены коэффициенты триггера?

Где-то в четвертом или пятом веке нашей эры кто-то очень умный, живший в Индии или ее окрестностях, заметил эту согласованность в пропорциях подобных прямоугольных треугольников (то есть согласованность значений шести различных соотношений прямоугольных треугольников, разделяющих того же размера угла основания) и начал работать над таблицами соотношений, соответствующих этим углам основания. Был бы один набор отношений для угла в один градус во всех 1-89.-90 треугольников, другой набор соотношений для угла в два градуса во всех треугольниках 2-88-90 и так далее. Эти соотношения называются «тригонометрическими» соотношениями прямоугольного треугольника.

Эти таблицы значений отношений очень длинные, отчасти потому, что они также включают значения для многих углов с размерами между целыми числами градусов; и занять некоторое время, чтобы использовать. В зависимости от того, насколько точным должен быть ваш ответ для инструктора (или приложения на рабочем месте), вы можете просмотреть более двадцати страниц триггерных таблиц (например, в этой книге) и 9 страниц.0007 все еще нужно использовать интерполяцию или различные формулы, чтобы получить числа, которые вам действительно нужны.

Для чего были изобретены триггерные таблицы?

Люди нуждались в триггерных таблицах, потому что вычисления, необходимые для получения этих значений (вручную), длинные и сложные. (Обсуждение в Quora) Работа с распечатанными таблицами, возможно, в конце учебника или в карманном справочном руководстве, была единственным практическим способом выполнения тригонометрии до того, как электронные калькуляторы стали широко доступны. (Некоторые люди все еще используют карманные ссылки на работе, «в реальной жизни», даже сейчас, как показано здесь.)

Профессор колледжа, который у меня был на занятиях по тригонометрии, однажды даже упомянул, что в прошлом экзамены по тригонометрии должны были быть очень короткими, чтобы у студентов было все время, которое они должны были бы тратить на механический процесс таблицы. поиск значения. Так что очень радуйтесь, что у вас всегда есть калькулятор в кармане в виде смартфона. Откройте приложение-калькулятор, переверните телефон и посмотрите, какие причудливые вещи вы можете делать! Но экзамены по тригонометрии, как заметил профессор Горовара с огоньком в глазах, в наши дни могут быть намного длиннее, так что… смешанная ситуация, я полагаю?

Дан прямоугольный треугольник с углом при основании, обозначенным как θ («THAY-tuh»), мы можем обозначить гипотенузу (всегда сторона, противоположная прямому углу), а затем обозначить две другие стороны «относительно θ» ( то есть по отношению к базовому углу θ, с которым мы работаем), в том числе и для значений между целыми числами градусов.

Сторона, противолежащая углу θ, является «противоположной» стороной; а другая сторона, являющаяся основанием треугольника, показанного ниже, является «прилегающей» стороной.

Теперь рассмотрим другой непрямой угол того же треугольника; а именно, угол в правом верхнем углу треугольника. Мы назовем его β («БАЙ-тьфу»). Что касается угла β, стороны будут обозначены по-разному. Основание теперь будет «противоположной» стороной, а линия высоты будет «примыкающей» стороной, как показано ниже:

Как видите, метки «противоположная» и «примыкающая» относятся к рассматриваемому углу. . Если вы переключитесь на другой угол (то есть, если вы переключитесь на другой угол, который *не* правильный угол), метки ног также будут переключены.

Давайте вернемся к первой маркировке, которую мы рассмотрели, с использованием угла θ в левом нижнем углу:

Вместо того, чтобы бросать вам все сразу, давайте пойдем шаг за шагом.

У этого прямоугольного треугольника три стороны; а именно, гипотенуза, линия высоты (сторона, противоположная углу) и основание внизу (сторона, прилегающая к углу). Есть шесть способов составить отношения трех сторон этого треугольника. В следующих таблицах я буду сокращать названия от «гипотенуза», «смежный» и «противоположный» до «hyp», «adj» и «opp» соответственно. В приведенных ниже таблицах показаны шесть коэффициентов в центральных столбцах.

Соотношения в строках одного цвета каждой таблицы обратны друг другу. Например, соотношение в розовой строке в первой таблице — это «adj/hyp», а соотношение в розовой строке во второй таблице — это его обратная дробь «hyp/adj».

Каждое из этих соотношений имеет формальное название. Эти имена были добавлены в левые столбцы таблиц ниже:

Каждое из названий этих соотношений имеет сокращенное обозначение, которое включает указание угла, с которым вы работаете, с использованием обозначения функции, как показано на правые столбцы заполненных таблиц ниже:

Отношения синуса, косинуса и тангенса являются «обычными» триггерными отношениями; косеканс, секанс и котангенс — их соответствующие обратные отношения (то есть значения перевернутых дробей для «правильных» отношений).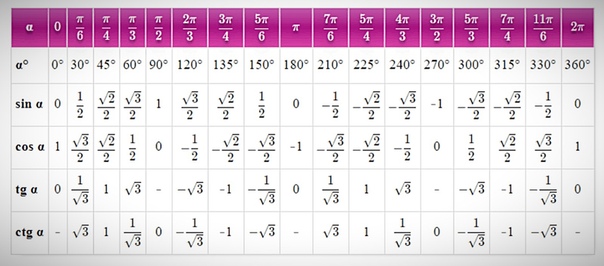

Между прочим, нет требования, чтобы греческие буквы использовались в качестве аргумента (то есть ввода) триггерной функции. Например, вполне нормально использовать x , если хотите.

Что означает SOH-CAH-TOA?

Многие учащиеся используют мнемонику «SOH-CAH-TOA» (произносится как «SOH-kuh-TOH-uh»), чтобы запомнить, как составлять соотношения для синуса, косинуса и тангенса прямоугольного треугольника. Буквы в этой мнемонике обозначают:

S ine is O pposite over

H ypotenuse
C озин is A djacent over H ypotenuse
T угол O напротив А дальний

Как соотносятся косинус, -секанс и -тангенс?

Когда два отношения имеют одно и то же имя, кроме «ко-» в начале одного из них, пара называется «ко-функциями».