Как решать задачи с помощью кругов эйлера: Решение задач с помощью кругов Эйлера

Содержание

Решение задач с помощью кругов Эйлера

17,128
просмотров

Презентации / Математика / Решение задач с помощью кругов Эйлера

Скачать презентацию Понравилось | 30

Текст этой презентации

Слайд 1

Для тех , кому интересно
«Решение задач с помощью кругов Эйлера»
5-6 класс

Слайд 2

Изображение множеств в виде кругов подходит для того, чтобы облегчить рассуждения при решении задач

Слайд 3

Задача:
Все мои друзья занимаются каким-нибудь видом спорта. 17 из них увлекаются футболом, а 14 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Угадайте, сколько у меня друзей?

Слайд 4

1.Изобразим два множества , так как два вида спорта. В одном будем фиксировать друзей, которые увлекаются футболом, а в другом — баскетболом
2.Поскольку некоторые из друзей увлекаются и тем и другим видом спорта, то круги нарисуем так, чтобы у них была общая часть (пересечение)

Слайд 5

2
15
12
17 из них увлекаются футболом, а 14 — баскетболом. И только двое увлекаются и тем и другим видом спорта.
Расставить числа , согласно условию задачи: 1)В общей части ставим цифру 2(двое увлекаются и тем и другим видом спорта)
2)В оставшейся части «футболистов» круга ставим цифру 15 (17 − 2 = 15). В свободной части «баскетболистов» круга ставим цифру12 (14 − 2 = 12).
футболом
баскетболом
3)Всего друзей 15+2+12=29 Ответ:29 друзей

Слайд 6

Задача: В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

Слайд 7

1.Изобразим три множества , так как три увлечения. В одном будем фиксировать ребят из драмкружка, во втором ребят , которые поют. В третьем будем фиксировать ребят, которые увлекаются спортом.
2.Поскольку некоторые из ребят увлекаются всем , то круги нарисуем так, чтобы у них было пересечение.

Слайд 8

драмкружок
хор
спорт

Слайд 9

драмкружок
хор
спорт
3 спортсмена посещают и драмкружок и хор , поэтому заполняем эту общую часть.
3
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

Слайд 10

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает занятие ребят в драмкружке и хоре.

Слайд 11

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в драмкружке 10 ребят из хора . А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 7 (10-3=7)

Слайд 12

Слайд 13

Слайд 14

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в драмкружке 8 спортсменов . А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 5 (8-3=5)

Слайд 15

3
5
драмкружок
хор
спорт
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

Слайд 16

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько спортсменов поют в хоре .

Слайд 17

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию в хоре 6 спортсменов . А так как в предыдущих рассуждениях поставлено число 3 ,то в оставшейся части ставим число 3 (6-3=3)

Слайд 18

Слайд 19

драмкружок
хор
спорт
3
7
5
3

Слайд 20

Слайд 21

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию 27 занимаются в драмкружке . А так как в предыдущих рассуждениях поставлены числа 3,5,7 ,то в оставшейся части ставим число 12 (27-(3+5+7)=12)

Слайд 22

драмкружок
хор
спорт
3
7
5
12
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?

Слайд 23

Слайд 24

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
По условию 32 поют в хоре . А так как в предыдущих рассуждениях поставлены числа 3,3,7 ,то в оставшейся части ставим число 19 (32-(3+3+7)=19)
3
7
3
19

Слайд 25

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
драмкружок
хор
спорт
Окрашенная часть показывает сколько ребят занимаются спортом.

Слайд 26

В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке?
По условию 22 человека увлекаются спортом. А так как в предыдущих рассуждениях поставлены числа 3,5,3 ,то в оставшейся части ставим число 11 (22-(3+5+3)=11)
драмкружок
хор
спорт

Слайд 27

Слайд 28

драмкружок
хор
спорт
3
7
5
3
19
11
12

Слайд 29

Всего занимаются 12+19+11+7+3+3+5=60 человек. Не поют, не увлекаются спортом, не занимаются в драмкружке 70-60=10 человек
Ответ: 10 человек

Слайд 30

Задача:
Из 220 студентов 163 играют в шахматы,175-в футбол,22 человека не играют в эти игры . Сколько студентов одновременно играют в шахматы и в футбол?
шахматы
футбол
х
163-х
175-х
220-22=198(чел)-играют в игры
163-х+х+175-х=198 338-х=198 х=140 140 студентов одновременно играют в шахматы и в футбол

Слайд 31

Реши :
9 моих друзей любят бананы, 8 – апельсины, а 7 – сливы, 5 – бананы и апельсины, 3 – бананы и сливы, 4 – апельсины и сливы, 2 бананы, апельсины и сливы. Сколько у меня друзей?

Слайд 32

Проверь решение:
бананы
апельсины
сливы
3
2
3
1
2
1
2
3+3+2+1+2+2+1=14 друзей
Ответ:14 друзей

Слайд 33

Домашнее задание:
1.Каждый из членов команды играет либо в футбол , либо в хоккей , либо в футбол и в хоккей . Сколько человек в команде ,если известно , что 18 человек играют в обе игры,22 человека играют в футбол,21 в хоккей?
2.В некоторой школе есть класс увлеченных ребят.Семь учеников из этого класса увлекаются математикой,шесть-физикой,пять-астрономией. Четверо из учеников увлекаются математикой и физикой,трое-математикой и астрономией,двое-физикой и астрономией,а один –и математикой,и физикой,и астрономией.Сколько учеников в классе?

Слайд 34

Проверь:
футбол
хоккей
1)
18
22-18=4
21-18=3
4+18+3=25(чел.)
Ответ:25 человек

Слайд 35

2)
математика
физика
астрономия
1
2
1
1
1
1
3
Ответ:10 человек
1+1+1+1+1+2+3=10(чел)

Слайд 36

Спасибо за внимание

Развитие детей. Как решать логические задачи с помощью кругов Эйлера?

Как легче всего объяснить что-либо человеку? Наглядно! Как весело и просто описать для ребенка условие задачи? Оживив задачу в виде картинки или схемы с рисунками! Давайте разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.

Круги Эйлера — это геометрическая схема. С ее помощью можно изобразить отношения между подмножествами (понятиями), для наглядного представления. Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения.

Леонард Эйлер был гениальным математиком, который умел применять математические приемы на практике. Он успешно использовал для решения различных задач идею изображения понятий и классов предметов в виде кругов. Впервые Эйлер их применил в письмах к немецкой принцессе. Он писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». И действительно, с помощью этих диаграмм можно легко и наглядно решить задачи, для решения которых обычным способом понадобилось бы составление системы из нескольких уравнений, например, с тремя неизвестными.

Способ изображения понятий в виде кругов позволяет развивать воображение и логическое мышление не только детям, но и взрослым (конечно, для взрослых подойдут более сложные логические задачи). Начиная с 4−5 лет детям доступно решение простейших задач с кругами Эйлера, сначала с разъяснениями взрослых, а потом и самостоятельно. Овладение методом решения задач с помощью кругов Эйлера формирует у ребенка способность анализировать, сопоставлять, обобщать и группировать свои знания для более широкого применения.

Вот несколько задач для маленьких детей на логическое мышление:

Определить круги, которые подходят к описанию предмета. При этом желательно обратить внимание на те качества, которыми предмет обладает постоянно и которыми временно. Например, стеклянный стакан с соком всегда остается стеклянным, но сок в нем есть не всегда. Или существует какое-то обширное определение, которое включает в себя разные понятия, подобную классификацию тоже можно изобразить с помощью кругов Эйлера. Например, виолончель — это музыкальный инструмент, но не каждый музыкальный инструмент окажется виолончелью.

Определение круга, который не подходит к описанию предмета.

Например, баранка — она круглая и вкусная, а определение зеленая к ней не подходит. Можно также придумать, какой предмет подойдет для пересечения другой пары кругов. Пример — круглая и зеленая может быть пуговица.

Определить предмет, который подходит под описание всех кругов. Для каждого круга выбирается какое-либо качество (например — сладкое, оранжевое, круглое). Ребенок должен назвать предмет, который одновременно соответствует всем этим описаниям (в данном примере подойдет апельсин), также можно спросить ребенка, какие предметы могут соответствовать двум описаниям из трех, то есть будут находиться на пересечении каждой пары кругов (например, сладкое и оранжевое — карамелька, оранжевое и круглое — мяч, круглое и сладкое — арбуз).

Для детей постарше можно предлагать варианты задач с вычислениями — от достаточно простых до совсем сложных. Причем самостоятельное придумывание этих задач для детей обеспечит родителям очень хорошую разминку для ума. Приведем два простых примера с диаграммами.

1. Из 27 пятиклассников все изучают иностранные языки — английский и немецкий. 12 изучают немецкий язык, а 19 — английский. Необходимо определить, сколько пятиклассников заняты изучением двух иностранных языков; сколько не изучают немецкий; сколько не изучают английский; сколько изучают только немецкий и только английский?

При этом первый вопрос задачи намекает в целом на путь к решению этой задачи, сообщая, что некоторые школьники изучают оба языка, и в этом случае использование схемы также упрощает понимание задачи детьми.

2. В одном доме в 45 квартирах есть домашние животные. При этом в 22 квартирах хозяева держат только кошек, а еще в 7 квартирах есть и кошка, и собака. Нужно узнать, в скольких квартирах находятся собаки, в скольких кошки, а в скольких нет кошки, но есть собака.

Задача, по сути, такая же, однако изменены исходные данные, сектор пересечения кругов известен, но нужно узнать информацию о каждом полном круге. Собаки находятся в числе квартир, оставшемся после вычитания из количества всех квартир с животными количества квартир только с кошками. Круг с общим числом кошек состоит из известных данных секторов «только кошек» и «кошек и собак», поэтому общее число кошек находится объединением сумм этих секторов. Последнее неизвестное находится соответственно. Определенно, значительно проще объяснить решение этой задачи с помощью кругов Эйлера.

Задачи, связанные с множествами, могут быть гораздо более сложными, причем чем более запутанными будут условия задачи, тем более очевидна рациональность применения диаграмм для ее решения. Конечно, иногда встречаются задачи, которые проще решить с помощью арифметических действий, поэтому, прежде чем приступить к решению, желательно проанализировать условия задачи.

Круги Эйлера имеют прикладное значение не только в решении школьных задач, ими также пользуются для усвоения и структуризации изучаемых материалов, конспектирования и добавления наглядности в некоторых обучающих курсах. Кстати, некоторые предлагают использовать круги Эйлера для того, чтобы сделать выбор в каком-нибудь вопросе, например, определиться с профессией.

Так что обязательно научите ребенка рисовать такие кружочки, это, несомненно, обернется пользой в развитии логического мышления, поможет решать задачи интересно и с пониманием происходящего.

Вся информация взята из открытых источников.
Если вы считаете, что ваши авторские права нарушены, пожалуйста, напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.

Мы убедимся в этом и сразу снимем публикацию.

MATH0043 §2: Вариационное исчисление

Многие задачи связаны с поиском функции, которая максимизирует или минимизирует интегральное выражение.
Одним из примеров является нахождение кривой, дающей кратчайшее расстояние между двумя точками — прямая линия, конечно, в декартовой геометрии (но можете ли вы это доказать?), но менее очевидная, если две точки лежат на искривленной поверхности (задача нахождения геодезические .)
Математические методы, разработанные для решения этого типа задач, известны под общим названием 9b~F(x,y,y’)~{\rm d}x. \] Типичная задача вариационного исчисления заключается в нахождении конкретной функции $y(x)$ для максимизации или минимизации интеграла $ I(y)$ при граничных условиях $y(a)=A$ и $y(b)=B$.

Интеграл $I(y)$ является примером

функционала , который (в более общем виде) представляет собой отображение набора допустимых функций в действительные числа.

Мы говорим, что $I(y)$ имеет экстремум , когда $I(y)$ принимает максимальное или минимальное значение. 92[a,b]\) такой, что $y(a)=A, y(b)=B$, то $Y(x)$ удовлетворяет обыкновенному дифференциальному уравнению второго порядка \[\label{ele } \frac{{\rm d}}{{\rm d} x}\left( \frac{\partial F}{\partial y’} \right)- \ гидроразрыв {\ частичный F{\partial y} = 0.\]

Equation ([ele]) — это уравнение Эйлера-Лагранжа , а иногда просто уравнение Эйлера .

Вам может быть интересно, что означает $\frac{\partial F}{\partial y’}$: как мы можем дифференцировать относительно производной? Думайте об этом так: $F$ дается вам как функция трех переменных, скажем, $F(u,v,w)$, и когда мы оцениваем функционал $I$, мы подставляем $Икс, y(x), y'(x)$ для $u,v,w$, а затем проинтегрировать.

Производная $\frac{\partial F}{\partial y’}$ есть просто частная производная от $F$ по второй переменной $v$. Другими словами, чтобы найти $\frac{\partial F}{\partial y’}$, просто представьте, что $y’$ является переменной .

Точно так же существует важное различие между $\frac{{\rm d} F}{{\rm d} x}$ и $\frac{\partial F}{\partial x}$. Первый является производной от $F$ по $x$, принимая во внимание тот факт, что $y= y(x)$ и $y’= y'(x)$ равны функции $x$ тоже. Последняя является частной производной от $F$ по первой переменной, поэтому она находится путем дифференцирования $F$ по $x$ и предположения, что $y$ и $y’ $ являются просто переменными и не зависят от $x$. Надеюсь, следующий пример прояснит это: 92 + xyy\prime\prime + 2y\prime\prime y\prime + {y\prime}\end{aligned}\] и уравнение Эйлера – Лагранжа имеет вид \[y+xy’+2{y’} ‘ = xy’+1 \qedhere\]

$Y$, удовлетворяющее уравнению Эйлера–Лагранжа, является необходимым, но недостаточным условием того, что $I(Y)$ является экстремумом. 2[a,b]\) удовлетворяет $\eta(a)=\eta(b)=0$, так что $Y_\epsilon(a)=A$ и $Y_\epsilon(b )=B$, т. е. $Y_\epsilon$ по-прежнему удовлетворяет граничным условиям. Неформально $Y_\epsilon$ — это функция, которая удовлетворяет нашим граничным условиям и «близка» к $Y$, когда $\epsilon$ мало. 9b_a \frac{{\rm d}F}{{\rm d} \epsilon}(x,Y_\epsilon, Y_\epsilon’)~{\rm d}x\] Теперь мы используем цепное правило с несколькими переменными, чтобы дифференцировать $F$ по $\epsilon$. Для общей функции трех переменных $F(u(\epsilon), v(\epsilon),w(\epsilon))$, три аргумента которого зависят от $\epsilon$, цепное правило говорит нам, что \[\frac{{\rm d} F}{{\rm d} \ эпсилон} = \ гидроразрыва {\ парциальное F} {\ парциальное u} \ frac {{\ rm d} u} {{\ rm d} \ epsilon} + \ frac {\ partial F} {\ partial v} \ frac {{\ rm d} v} {{\ rm d} \ epsilon} + \ frac {\ partial F} {\ partial w}\frac{{\rm d} w}{{\rm d} \epsilon}.\] В нашем случае первый аргумент $x$ не зависит от $\epsilon$, поэтому $\ frac{{\rm d} x}{{\rm d} \epsilon}= 0$, а поскольку $Y_\epsilon = Y+\epsilon \eta$ имеем $\frac{{\rm d} Y_\epsilon}{{\rm d} \epsilon} = \eta$ и $\frac{{\rm d} Y_\epsilon’}{{\rm d} \epsilon} = \eta’$.

b_a \, \left( \frac{\partial F}{\partial y} — \frac{{\rm d}}{{\rm d} Икс} \ гидроразрыв {\ частичный F}{\partial y’}\right) \eta(x)~ {\rm d}x = 0.\] Приведенное выше уравнение верно для 92 ~{\rm d}x, ~~~~~~y(0)=0,~y(1)=2,~~~~\left[ \mbox{Ответ:} ~~ y(x)=2 \frac{\sin{x}}{\sinh{1}} \right]. \qedздесь\]

Рассматривая $y+g$, где $y$ — решение из упражнения 1, а $g(x)$ — вариант в $y(x)$, удовлетворяющий $g (0)=g(1)=0$, а затем, рассматривая $I(y+g)$, явно показать, что $y(x)$ минимизирует $I(y)$ в упражнении 1 выше. (Подсказка: используйте интегрирование по частям и уравнение Эйлера – Лагранжа, которому удовлетворяет $y(x)$, чтобы упростить выражение для $I(y+g)$). 9b ~y(x)\eta(x)~{\rm d}x =0.\] Тогда $y(x)=0$ для всех $a \le x \le b$.

Вот набросок доказательства. Предположим от противного, что для некоторого $a < \alpha < b$ имеем $y(\alpha)>0$ (случай, когда $\alpha=a$ или $\alpha = б$ можно сделать аналогично, но не будем усложнять). 2[a,b]\) — трудно дать формальное доказательство без использования формального определения непрерывности и дифференцируемости, но, надеюсь, следующий график показывает, что происходит: 91 y(x)\eta(x)\;{\rm d}x= 0\). Но $y(x)\eta(x)$ непрерывен, равен нулю вне $(\alpha_0, \alpha_1)$ и строго положителен для всех $x \in (\alpha_0, \alpha_1)$ . Строго положительная непрерывная функция на таком интервале имеет строго положительный интеграл, так что это противоречие. Точно так же мы можем показать, что $y(x)$ никогда не принимает значений $<0$, поэтому оно равно нулю везде на $[a,b]$.

Классическим примером вариационного исчисления является нахождение брахистохроны , определяемой как плавная кривая, соединяющая две точки A и B (не одна под другой), по которой частица будет скользить из A в B под действием силы тяжести с максимально возможной скоростью. время. 9{-1}{\left(\sqrt{\frac{x}{\alpha}}\right)}-\sqrt{x}\sqrt{\alpha-x}.\]

Эта кривая называется циклоидой .

Константа $\alpha$ определяется неявно оставшимся граничным условием $y(h)=a$. Уравнение циклоиды часто задается в следующей параметрической форме (которую можно получить из подстановки в интеграле) \[\begin{aligned} х (\ тета) & = & \ гидроразрыва {\ альфа} {2} (1- \ соз {2 \ тета}) \\ y(\theta) & = & \frac{\alpha}{2}(2\theta-\sin{2\theta}) \end{aligned}\] и может быть построена по геометрическому месту начальной точки контакт, когда круг радиуса $\альфа/2$ прокатывается (угол $2\тета$) по прямой линии. 92[a,b]\) такая, что $y(a)=A,y(b)=B$, то $Y(x)$ удовлетворяет условию \[\label{belt} F — y’ \frac {\ парциальное F} {\ парциальное у’} = С\] для некоторой константы $С$.

([пояс]) называется тождеством Бельтрами или уравнением Бельтрами.

Рассмотрим \[\label{dif} \frac{{\rm d}}{{\rm d} x}\left( F — y’\frac{\partial F}{\partial y’} \верно) = \frac{{\rm d} F}{{\rm d} x}-{y’}’ \frac{\partial F}{\partial y’} -y’ \frac{{\rm d}} {{\ гм д} х} \left( \frac{\partial F}{\partial y’} \right). {\ простое \ простое} \ гидроразрыва {\ парциальное F} {\ парциальное у ‘} — у ‘ \ гидроразрыва {{\ rm d}} {{\ rm d} х} \ гидроразрыва {\ парциальное F{\ парциальное у’} = y’ \left( \frac{\partial F}{\partial y} — \frac{{\rm d}}{{\rm d} x}\frac{\partial F}{\partial y’} \right)\] Поскольку $Y$ является экстремалью, оно является решением уравнения Эйлера–Лагранжа и, следовательно, равно нулю для $y=Y$. Если что-то имеет нулевую производную, это константа, поэтому $Y$ является решением \[F — y’ \frac{\partial F}{\partial y’}= C\] для некоторой константы \(C\ ). 92 ~{\rm d}x, ~~~~~~y(0)=0,~y(1)=2,\] Ответ: \[y=f(x)=2 \frac{\sinh{ x}}{\sinh{1}}\] (снова).

До сих пор мы имели дело с граничными условиями вида $y(a)=A,y(b)=B$ или $y(a)=A, y'(b)=B$. Для некоторых задач естественные граничные условия выражаются с помощью интеграла. Стандартный пример: Задача Дидоны ³ : если у вас есть кусок веревки фиксированной длины, какую форму вы должны придать ей, чтобы охватить как можно большую площадь? Здесь мы пытаемся выбрать функцию $y$ для максимизации интеграла $I(y)$, дающего площадь, заключенную в $y$, но ограничение фиксированной длины также выражается в терминах интеграла, включающего $у$. Такая задача, в которой мы ищем экстремаль некоторой функции с «обычными» граничными условиями, а также с интегральным ограничением, называется 9b~F(x,y,y’)+ \lambda G(x,y,y’) \;{\rm d}x\] для некоторой константы $\lambda$.

Вам нужно знать о множителях Лагранжа, чтобы понять это доказательство: см. раздаточный материал на moodle (константа $\lambda$ окажется множителем Лагранжа).

Предположим, что $I(Y)$ является максимальным или минимальным значением $J(y)=L$, и рассмотрим двухпараметрическое семейство функций, заданное \[Y(x) + \epsilon \eta (x) + \delta \zeta(x)\], где $\epsilon$ и $\delta$ — константы, а $\eta(x)$ и $\zeta(x)$ — дважды дифференцируемые функции такие, что $\eta(a)=\zeta(a)=\eta(b)=\zeta(b)=0$, причем $\zeta$ выбраны так, что $Y+\epsilon \eta + \delta \zeta$ подчиняется интегральному ограничению. 9bG(x,Y+\эпсилон\эта+ \delta \zeta,Y’+\epsilon \eta’ +\delta \zeta’) \, {\rm d}x.\] Поскольку $I$ имеет максимум или минимум в точке $Y(x)\ ) при условии \(J=L$, в точке $(\epsilon,\delta)$=$(0,0)$ наша функция $I[\epsilon, \delta]$ принимает экстремальное значение, зависящее от $J[\epsilon, \delta]=L$. b \eta \left( \frac{\partial}{\partial y}\left( F+\lambda G \right) — \ frac {{\ rm d}} {{\ rm d} x} \ left ( \ frac {\ partial {\ partial y’} \ left ( F + \ lambda G \ right) \right) \right) \,{\rm d}x ~~~~\mbox{(интегрирование по частям)} \\ & & \\ & = & 0~~~~~{\mbox{когда $\epsilon=\delta=0$, независимо от того, что такое $\eta$.}} \end{aligned}\] Так как это верно для любого $\ eta$, по FLCV (лемма [flcv]) получаем \[(F_y + \lambda G_y) ( x,Y,Y’) + \frac{{\rm d}}{{\rm d} x} (F_{у’} + \лямбда G_{у’}) (x,Y,Y’) = 0\], что говорит о том, что $Y$ является решением уравнения Эйлера–Лагранжа для $K$, что и требовалось. 92+\фракция{5}{2}. \справа]\]

(задача проектирования загона для овец): забор длиной $l$ должен быть прикреплен к прямой стене в точках A и B (расстояние $a$ друг от друга, где \(a

Существует множество вводных учебников по вариационному исчислению, но большинство из них содержат гораздо больше математических деталей, чем требуется для MATH0043. Если вы хотите узнать больше о теории, Гельфанд и Фомин Вариационное исчисление доступно в библиотеке. Менее техническим источником является глава 9 Боаса Математические методы в физических науках . В Интернете есть много коротких вводных статей по вариационному исчислению, например.

https://courses.maths.ox.ac.uk/node/view_material/37762
http://www-users.math.umn.edu/olver/ln_/cv.pdf
https://personalpages.manchester.ac.uk/staff/david.harris/MT30021/30021CalcVarLec.pdf

, хотя все они описаны гораздо подробнее, чем нам нужно в MATH0043. Наконец, а также раздаточный материал Moodle вы можете найти

полезно для освежения знаний о множителях Лагранжа.

Функция $\epsilon \eta(x)$ известна как вариация в $Y$.↩
Не путайте это с «экстремумом». Терминология стандартная, т.е. Гельфанд и Фомин стр.15, но может сбить с толку.↩
См. Blå sjö — Изопериметрическая задача для истории.↩

кругов, Базельская проблема и кажущаяся яркость звезд

В День числа числа числа числа 2016 я написал в этом посте о замечательном факте, открытом Эйлером, что вероятность того, что два случайно выбранных целых числа не имеют общих простых множителей, равна . Доказательство использует известное тождество, часто называемое «проблемой Базеля», которое также принадлежит Эйлеру. В сообщении 2016 года я представил оригинальное решение Эйлера для Базельской проблемы с использованием разложения в ряд Тейлора для .

В честь Дня Пи 2018 я хотел бы объяснить простое и интуитивно понятное решение Базельской проблемы, предложенное Йоханом Вестлундом. (Статья Вестлунда находится здесь; см. также это видео на YouTube, где я впервые услышал об этом подходе — спасибо Фрэнсису Су за то, что он поделился им на Facebook!) Подход Вестлунда мотивирован физическими соображениями (закон обратных квадратов, который управляет яркость источника света) и использует только базовую евклидову геометрию и тригонометрию.

План доказательства

Краткий план аргументации Вестлунда выглядит следующим образом:

Шаг 1: С помощью некоторых простых алгебраических манипуляций достаточно доказать эквивалентную формулу . Это, в свою очередь, следует (устанавливая ) из следующего более общего факта:

Теорема: Для каждого действительного числа, которое не является целым числом, мы имеем

Шаг 2: Пусть четно, и думать о (что, без ограничения общности, мы можем предположить, удовлетворяет) как точка на прямой с действительными числами. Расположите на числовой прямой звезды одинаковой яркости, по одной звезде в каждой целой (т. е. «решетчатой») точке полуоткрытого интервала. Тогда, по закону обратных квадратов, мы можем интерпретировать частичную сумму как полную видимую яркость в -звездной системе.

Шаг 3: Мы можем аппроксимировать (с любой желаемой точностью) точки решетки равноотстоящими точками по периметру окружности очень большого радиуса, которая касается прямой с действительными числами в точке . Поэтому мы можем заменить нашу систему звезд на прямой системой звезд, лежащих на некоторой дуге с центром внутри большого круга (подобно синим точкам на рис. 1).

Рисунок 1

Шаг 4: Предположим, мы размещаем звезды одинаковой яркости на одинаковом расстоянии друг от друга по всему периметру окружности и измеряем общую видимую яркость в некоторой точке окружности, имеющей расстояние (измеряемое по окружности) от ближайшей звезды (см. рис. 2).

Рисунок 2

Тогда закон обратных квадратов подразумевает, что для «большая часть» (в точном количественном смысле) этой яркости исходит от звезд, ближайших к .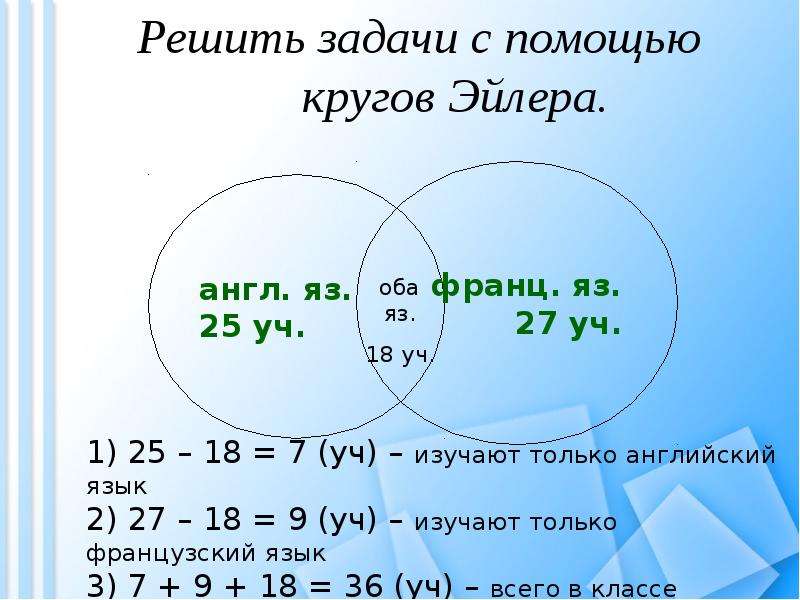

Шаг 5: Итерируя это наблюдение, обозначим общую видимую яркость ближайших звезд к моменту, когда мы размещаем равноотстоящие звезды по периметру окружности, причем ближайшая звезда находится на расстоянии дуги от (снова см. Рисунок 1) . Затем .

Шаг 6. С помощью элегантного геометрического рассуждения, связанного с «обратной теоремой Пифагора» (см. рис. 3), получается, что для каждого имеем . Другими словами, мы можем заменить систему равноотстоящих звезд вдоль окружности , касательной к реальной линии в точке , системой равноотстоящих звезд вдоль окружности , также касательной к реальной линии в такой таким образом, что общая видимая яркость при остается неизменной.

Рисунок 3

Отсюда по индукции следует, что для всех натуральных чисел . Объединив это с предыдущим шагом, мы получаем .

Шаг 7: В частности, если сама является большой степенью двойки, то примерно для всех . Когда также большой, примерно (где как раньше). Следует, что .

Шаг 8: По элементарной тригонометрии имеем , что доказывает теорему.

Немного евклидовой геометрии

Важнейшей и самой инновационной частью аргумента является факт из шага 6, что . Легче всего это объяснить для , хотя доказательство в общем случае по существу такое же. Итак, давайте посмотрим, как Вестлунд доказывает это.

Аргумент основан на «обратной теореме Пифагора», которая является утверждением, что в условиях рисунка 4 (где ACB — прямой угол) мы имеем .

Рисунок 4

Это элементарное упражнение, чтобы вывести это из обычной теоремы Пифагора.

Имея единственную звезду (обозначенную красной точкой R на рисунке 5) на окружности радиуса 1, касательной к реальной линии в точке , мы можем заменить ее двумя равноотстоящими звездами (синие точки и ) на окружности радиуса 2, также касательной к реальной линии в , таким образом, что видимая яркость красной звезды в равна сумме видимых яркостей двух голубых звезд в .

Рисунок 5

Построение и из происходит следующим образом. Пусть будет центром меньшего круга, и пусть будет центром большего круга. Тогда и две точки, где линия пересекает больший круг.

Так как это диаметр меньшего круга, это прямой угол. Формула, выражающая равенство между видимой яркостью в красной и синей звездных системах, будет немедленно следовать из обратной теоремы Пифагора, как только мы покажем, что расстояние по дуге (против часовой стрелки) от до равно расстоянию по дуге (против часовой стрелки) от до .

Чтобы убедиться в этом, сначала обратите внимание, что произведение дугового расстояния от до равно величине (в радианах) центрального угла . И умноженное на расстояние по дуге от до, равно 2 (длина окружности большего круга), умноженное на меру центрального угла . Так что достаточно показать это. Это следует из того, что , которая пересекает ту же дугу малого круга, что и центральный угол .

Аналогичным образом, заменив каждую красную звезду двумя синими звездочками, как на рисунке 3 выше, следует, что для всех .

Базовый случай (Шаг 8)

В базовом случае количество равно где окружность окружности 1 (и, следовательно, радиус ), точки, на которых находятся на расстоянии, измеренном по окружности , и обозначает евклидово (хордальное) расстояние между и . Это элементарное упражнение по тригонометрии, чтобы показать это (см. рис. 6). Рис. 60009

Остальные технические подробности

Теперь покажем, что когда большое, приблизительно равно .

Рассмотрим звездную систему по окружности окружности (и радиусом ). Суммарная яркость при по определению равна . Теперь удалите звезды, наиболее удаленные от , и посчитайте суммарную яркость оставшихся звезд. Поскольку каждая из вычеркнутых звезд имеет расстояние не менее , отсюда следует, что .

Аналогичным образом, если мы начнем с -звездной системы на круге радиуса и удалим все звезды, кроме ближайших к , и обозначим через общую яркость оставшихся звезд, мы получим

С другой стороны, геометрически ясно (поскольку радиусы окружностей стремятся к бесконечности), что

Согласно неравенству треугольника, разница между и ограничена

Принимая за произвольно большую степень числа 2 и применяя предложение 1, теперь получаем теорему 1 (в частном случае , но из этого легко следует общий случай).

Заключительные замечания

Приведенные выше оценки можно использовать для доказательства апостериорных того, что для все положительных целых чисел , а не только степени двойки. Это напоминает индуктивное доказательство Коши неравенства между средним арифметическим и средним геометрическим, которое сначала устанавливает результат для степени 2.
Чтобы перейти от теоремы 1 к теореме Эйлера, равной , можно поступить следующим образом. Во-первых, установка в теореме 1 дает . Умножение обеих частей этого равенства на дает Но и, следовательно, желаемое.
В качестве альтернативы, как указал мне Кит Конрад, из теоремы 1 можно сделать следующий вывод. Вычитание из обеих частей формулы в теореме 1 дает ряд Тейлора в правой части, равный Сеттингу, и, таким образом, . И дифференцируя обе части дважды, а затем устанавливая, мы получаем и, таким образом, аналогичным образом получаем явную формулу для всех положительных целых чисел.
No related posts.