Тригонометрические формулы. Таблица углов. Формулы приведения
Факт 1.
\(\bullet\) Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:
Факт 2.
\(\bullet\) Знаки синуса, косинуса:
Так как \(\mathrm{tg}\,\alpha=\dfrac{\sin\alpha}{\cos\alpha}\) и \(\mathrm{ctg}\,\alpha=\dfrac{\cos\alpha}{\sin\alpha}\), то тангенс и котангенс положительны в \(I\) и \(III\) четвертях и отрицательны во \(II\) и \(IV\) четвертях.
Факт 3.
Формулы приведения.
\(\bullet\) Случай 1. Если угол можно представить в виде \(n\cdot \pi\pm \alpha\), где \(n\in\mathbb{N}\), то \[\sin(n\cdot \pi\pm
\alpha)=\bigodot \sin\alpha\] где на месте \(\bigodot\) стоит знак синуса угла \(n\cdot \pi\pm \alpha\). \[\cos(n\cdot \pi\pm
\alpha)=\bigodot \cos\alpha\] где на месте \(\bigodot\) стоит знак косинуса угла \(n\cdot \pi\pm \alpha\).
Знак угла можно найти, определив, в какой четверти он находится.
Знак определяется таким же образом, как и в случае \(1\).
Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию).
Алгоритм применения формул приведения для тангенса и котангенса полностью аналогичен.
Пример 1. Найти \(\cos \dfrac{13\pi}{3}\).
Преобразуем угол: \(\dfrac{13\pi}{3}=\dfrac{12\pi+\pi}{3}=4\pi+\dfrac{\pi}3\), следовательно, \(\cos \dfrac{13\pi}{3}=\cos \left(4\pi+\dfrac{\pi}3\right)=\cos\dfrac{\pi}3=\dfrac12\)
Пример 2. Найти \(\sin \dfrac{17\pi}{6}\).
Найти \(\sin \dfrac{17\pi}{6}\).
Преобразуем угол: \(\dfrac{17\pi}{6}=\dfrac{18\pi-\pi}{6}=3\pi-\dfrac{\pi}6\), следовательно, \(\sin \dfrac{17\pi}{6}=\sin \left(3\pi-\dfrac{\pi}6\right)=\sin\dfrac{\pi}6=\dfrac12\)
Пример 3. Найти \(\mathrm{tg}\,\dfrac{15\pi}4\).
Преобразуем угол: \(\dfrac{15\pi}4=\dfrac{16\pi-\pi}4=4\pi-\dfrac{\pi}4\), следовательно, \(\mathrm{tg}\,\dfrac{15\pi}4=\mathrm{tg}\left(4\pi-\dfrac{\pi}4\right)= -\mathrm{tg}\,\dfrac{\pi}4=-1\)
Пример 4. Найти \(\mathrm{ctg}\,\dfrac{19\pi}3\).
Преобразуем угол: \(\dfrac{19\pi}3=\dfrac{18\pi+\pi}3=6\pi+\dfrac{\pi}3\), следовательно, \(\mathrm{ctg}\,\dfrac{19\pi}3=\mathrm{ctg}\left(6\pi+\dfrac{\pi}3\right)= \mathrm{ctg}\,\dfrac{\pi}3=\dfrac{\sqrt3}3\)
Значения синуса, косинуса, тангенса и котангенса углов.
Класс 9 Дата Предмет алгебра Подпись проверяющего — Урок № 56
Тема урока: Глава 3. Значения синуса, косинуса, тангенса и котангенса углов.
Значения синуса, косинуса, тангенса и котангенса углов.
Цели урока:
Оценка: определяют результаты своей работы на уроке Синтез: используют значения тригонометрических функций в решении задач Анализ: изучают значения тригонометрических функций, работают с таблицей Применение: демонстрируют применение значения синуса, косинуса, тангенса и котангенса произвольного угла Понимание: обсуждают значения синуса, косинуса, тангенса и котангенса произвольного угла Знание: рассказывают значения синуса, косинуса, тангенса и котангенса произвольного угла |
Учебно-воспитательные задачи: Образовательная: |
Познакомиться со значениями синуса, косинуса, тангенса и котангенса произвольного угла, обеспечить усвоение новых знаний по данной теме, сформировать навыки применения знаний по данной теме |
Развивающая: развитие способности выражать мысли, познавательных способностей, формирование алгоритмического мышления, расширение кругозора |
Воспитательная: способствовать выявлению, раскрытию способностей учащихся, возбуждать интерес к предмету, побуждать учащихся к применению полученных знаний |
Результаты обучения: Учащиеся знают значения синуса, косинуса, тангенса и котангенса произвольного угла |
Учащиеся умеют: применять значения тригонометрических функций в решении задач, ясно выражать мысли, участвовать в дискуссии, умеют слушать и слышать |
Тип урока: сообщение новых знаний
Форма проведения урока: беседа
Методы обучения:
По источнику получения знаний: словесные, наглядные, практические.
По способу организации познавательной деятельности: объяснительно-иллюстративные, репродуктивные.
Методы воспитания: Организация деятельности, формирование мировоззрения, стимулирование деятельности, осуществление контроля, взаимоконтроля, самоконтроля.
Формы обучения: коллективные, индивидуальные, групповые
Основные понятия темы:
Задание на дом: №368, 372
Оборудование, ресурсы, наглядные пособия: учебник, раздаточный материал
Учитель: Шуринова Е.К.
Ход урока
Этапы урока | Содержание этапа |
Оргмомент. Задачи: обеспечить нормальную внешнюю обстановку на уроке, психологически подготовить детей к общению | Приветствие Проверка подготовленности к уроку Организация внимания школьников Ознакомление с планом проведения урока |
Проверка домашнего задания. Задачи: установить правильность, полноту и осознанность выполнения всеми учащимися домашнего задания, выявить пробелы в знаниях, устранить в ходе проверки обнаруженные пробелы | Выявление степени усвоения заданного учебного материала Ликвидация обнаруженных недостатков. Проверка выполнения домашнего задания у доски |
Вызов. Задачи: обеспечить включение школьников в совместную деятельность по определению целей учебного занятия. | Сообщение темы урока Формулируют цели: сформировать навыки применения знаний по данной теме |
Актуализация знаний и умений Задачи: психологическая подготовка ученика: сосредоточение внимания, осознание значимости предстоящей деятельности, возбуждение интереса к уроку; учащиеся воспроизводят известные им знания, осознают их, обобщают факты, связывают старые знания с новыми условиями, с новыми данными и т. | У доски игра «крестики-нолики» sin 30° cos 45° tg 0° тg 90° sin 60° cos 0° сos 60° tg 180° sin 0° tg π/3 sin π/4 tg π/6 sin π/2 cos π/6 tg π/4 cos π/2 cos π sin π Переведите:60°, 120°, 270°, в радианную меру. Переведите:90°, 135°, 360°, в радианную меру. Переведите: π/2, π/4, 3π/4, в градусную меру. Переведите: π, π/6, 5 π/6, в градусную меру. |
Осмысление Изучение нового материала. Задачи: обеспечить восприятие, осмысление и первичное запоминание изучаемого материала, осознание своих способов проработки учебной информации | Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов Тригонометрические определения синуса, косинуса, тангенса и котангенсапозволяют указать значения тригонометрических функций для углов 0 и 90градусов: В курсе геометрии из прямоугольных треугольников с углами 30, 60 и 90 градусов, а также 45, 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов: Занесем указанные значения тригонометрических функций для углов 0, 30, 45, 60 и90 градусов (0, π/6, π/4, π/3, π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса. Используя формулы приведения, только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120, 135, 150, 180, 210, 225, 240, 270, 300,315, 330 и 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид. Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса, таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число. Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть |
Закрепления новых знаний и умений. Задачи: обеспечить повышение уровня осмысления учащимися изученного материала, глубины его усвоения | tg π/4*cos π/6+2sin45° 4cos60°-3sinπ/2+1/2tg45° 6sin π/2-1,5tg180°-√3cos π/6 √2cos π/4+√3tg30°+1,5cosπ |
Проверка новых знаний Задачи: установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления | Работа с учебником №369-372 Уровень В № 375,376 |
Коррекция знаний. Задачи: скорректировать выявленные проблемы | Организация деятельности учащихся по коррекции выявленных недостатков Индивидуальное задание. Повторное разъяснение учителя. |
Подведение итогов. Рефлексия. Задачи: инициировать рефлексию учащихся по поводу своего эмоционального состояния, дать оценку работе отдельных учащихся и всего класса | Мобилизация учащихся на рефлексию В занятии для меня было: Самым полезным_________________________________________________ Самым приятным __________________________________________________ самым интересным ______________________________________________ .Выставление оценок. |
Рефлексия учителя о проведенном уроке:
Интерполяция синусов и косинусов
В предыдущем посте показано, как можно использовать линейную интерполяцию для заполнения пробелов в таблице логарифмов. Вы можете сделать то же самое для таблицы синусов и косинусов, но есть способ получше. Как и прежде, мы предполагаем, что вы работаете вручную, используя только карандаш, бумагу и справочник таблиц.
Вы можете сделать то же самое для таблицы синусов и косинусов, но есть способ получше. Как и прежде, мы предполагаем, что вы работаете вручную, используя только карандаш, бумагу и справочник таблиц.
Линейная интерполяция
Предположим, вы хотите найти синус 12,3456° и у вас есть таблица синусов для углов с шагом 0,1°. В Таблице 4.10 A&S мы находим
sin 12,3° = 0,21303 03862 74977
sin 12,4° = 0,21473 53271 67063
Если бы мы использовали линейную интерполяцию, мы бы оценили
sin 12,5° 12,6 дюйма + 0,3456°3 = sin 12,5° 3456°3. 4° – sin 12,3° ) = 0,21380 78393 21768
с точностью до шести знаков после запятой.
Лучший подход
Другим подходом может быть использование тождества
sin(θ + φ) = sin θ cos φ + cos θ sin φ
вместо линейной интерполяции, установив θ = 12,3° и φ = 0,0456°. Мы можем найти синус и косинус θ в нашей таблице, но как нам найти синус и косинус φ?
Косинус вычислить легко: установите его равным 1. Для небольшого угла x (в радианах) косинус x приблизительно равен 1 с погрешностью менее x ²/2. В радианах
Для небольшого угла x (в радианах) косинус x приблизительно равен 1 с погрешностью менее x ²/2. В радианах
φ = 0,0456 π/180 = 0,00079 58701 38909
, поэтому ошибка усечения при аппроксимации cos φ с 1 составляет около 3×10 -7 .
Вычислить синус φ несложно, но для этого нужно преобразовать φ в радианы. Вы, вероятно, могли бы найти коэффициент преобразования в своем справочнике, например. в Таблице 1.1 A&S.
0,0456° = 0,0456 × 0,01745 32925 19943
Когда φ выражено в радианах, sin φ = φ с погрешностью менее φ³/6 (см. здесь).
Соединяя части вместе, мы получаем
sin(θ + φ) = sin 12,3° × 1 + cos 12,3° × φ
, что, используя приведенные выше числа, дает нам 0,2138078524
76, что примерно на 6×10 -8 .
Больше точности
Если мы хотим еще больше точности, нам нужно найти самое слабое звено в наших расчетах. Ошибка аппроксимации sin φ как φ порядка φ³, а ошибка аппроксимации cos φ как 1 порядка φ², поэтому последний является самым большим источником ошибки.
Если мы аппроксимируем cos φ как 1 – φ²/2, ошибка будет порядка φ 4 , а самым слабым звеном будет синусоидальная аппроксимация с ошибкой порядка φ³, которая все еще довольно мала. Общая ошибка при вычислении sin 12,3456° будет меньше 10 -10 , если мы используем это приближение более высокого порядка для косинуса φ.
Сравните и сопоставьте
Вернемся к аппроксимации косинуса малого угла на 1 и сравним два приведенных выше подхода аппроксимации.
Линейная интерполяция:
sin 12,3456° = sin 12,3° + 0,456(sin 12,4° – sin 12,3°)
Формула сложения:
sin 12,3456° = sin 12,3° + 0,01801 (π2/s 0,01801) )
Вторые члены в двух подходах равны
0,0456(sin 12,4° – sin 12,3°)/0,1
и
0,0456 (π/180) (cos 12,3°).
Эти два числа похожи, потому что
(sin 12,4° – sin 12,3°)/0,1 ≈ (π/180) (cos 12,3°).
Член слева представляет собой разностный коэффициент для синуса при 12,3° с шагом ч = 0,1, а член справа представляет собой производную синуса при 12,3°.
Подожди, а производная от синуса не просто косинус? Это когда вы работаете в радианах , поэтому в исчислении почти всегда используются радианы, но когда вы работаете в градусах, производная синуса равна π/180, умноженной на косинус.
Это показывает, что если вы аппроксимируете косинусы малых углов как 1, формула суммы сводится к одночленной аппроксимации Тейлора.
Таблица интегралов синуса и косинуса для аргументов от 10 до 100
Эта система будет проходить техническое обслуживание 27 апреля с 8:00 до 12:00 по центральному поясному времени.
Один из 8 отчетов в ряд: На этом сайте доступна серия статей по прикладной математике (Вашингтон, округ Колумбия).
Показаны 1-4 из 204 страницы в этом отчете.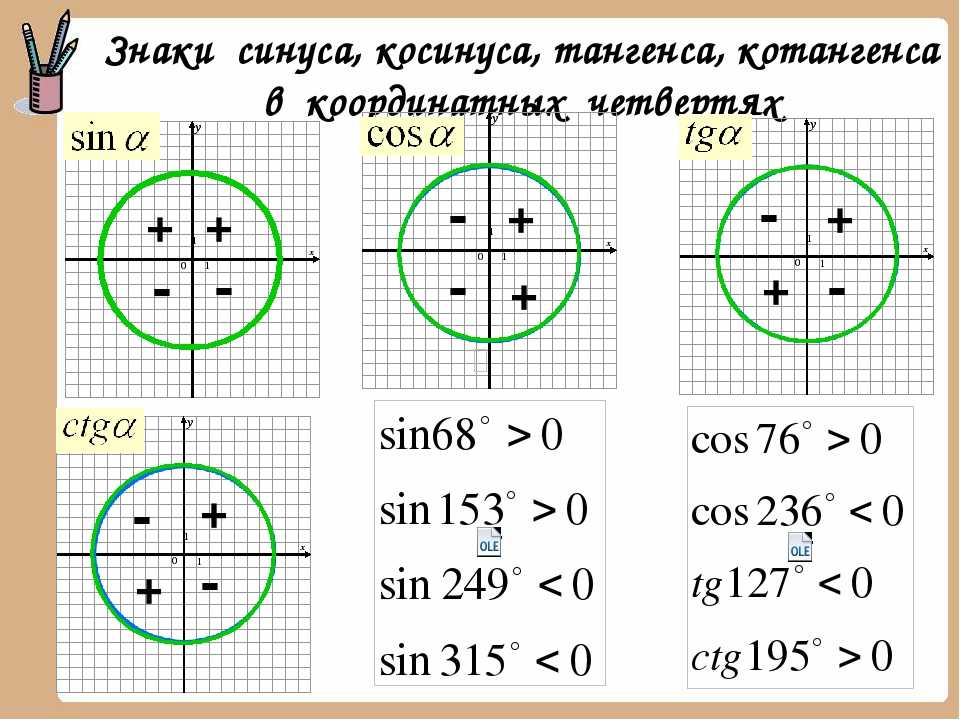
PDF-версия также доступна для скачивания.
Описание
Отчет, содержащий таблицы и интегралы синуса и косинуса для различных волн.
Физическое описание
xv, 187 стр. : диаг. ; 27 см.
Информация о создании
Соединенные Штаты. Национальное бюро стандартов. Вычислительная лаборатория. 1954.
Контекст
Этот отчет входит в состав сборника под названием:
Архив технических отчетов и библиотека изображений
и
предоставлено отделом государственных документов библиотек ЕНТ
к
Электронная библиотека ЕНТ,
цифровой репозиторий, размещенный на
Библиотеки ЕНТ.
Поиск
Открытый доступ
ВОЗ
Люди и организации, связанные либо с созданием этого отчета, либо с его содержанием.
Автор
- Соединенные Штаты.
 Национальное бюро стандартов. Вычислительная лаборатория.
Национальное бюро стандартов. Вычислительная лаборатория.
Издатель
- Соединенные Штаты. Государственная типография. Место публикации: Вашингтон, округ Колумбия
Аудитории
Мы определили это отчет как первоисточник в наших коллекциях.
Предоставлено
Библиотеки ЕНТ Отдел государственных документов
Являясь одновременно федеральной и государственной депозитарной библиотекой, отдел государственных документов библиотек ЕНТ хранит миллионы единиц хранения в различных форматах. Департамент является членом Программы партнерства по контенту FDLP и Аффилированного архива Национального архива.
О | Просмотрите этого партнера
Свяжитесь с нами
Исправления и проблемы Вопросы
Что
Описательная информация, помогающая идентифицировать этот отчет.
Перейдите по ссылкам ниже, чтобы найти похожие элементы в электронной библиотеке.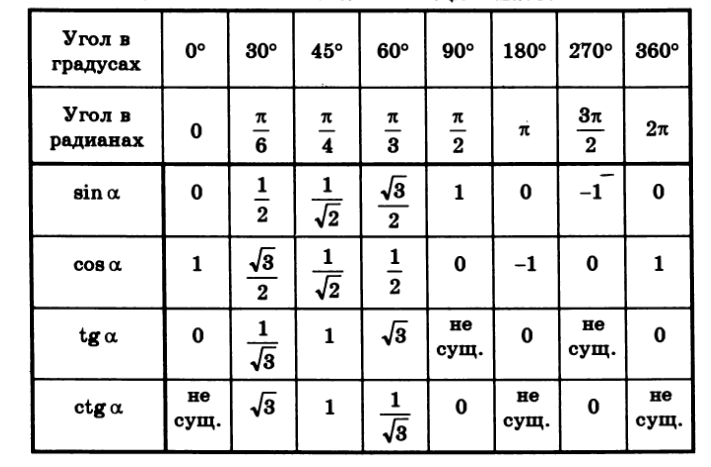
Титулы
- Основное название: Таблица синусоидальных и косинусных интегралов для аргументов от 10 до 100
- Добавлен заголовок: Соединенные Штаты.
 Национальное бюро стандартов. Серия «Прикладная математика», 32
Национальное бюро стандартов. Серия «Прикладная математика», 32 - Название серии: Отчеты Национального бюро стандартов
- Добавлен заголовок: Серия «Прикладная математика», бюллетень 32
Описание
Отчет, содержащий таблицы и интегралы синуса и косинуса для различных волн.
Физическое описание
xv, 187 стр. : диаг. ; 27 см.
Предметы
Тематические рубрики Библиотеки Конгресса
- Тригонометрические функции.
- Тригонометрия — Таблицы.
Язык
- Английский
Тип вещи
- Отчет
Идентификатор
Уникальные идентификационные номера для этого отчета в электронной библиотеке или других системах.
- ОСЛК : 852744
- Архивный ресурсный ключ : ковчег:/67531/metadc40300
Коллекции
Этот отчет является частью следующего сборника связанных материалов.
Архив технических отчетов и библиотека изображений
Эта подборка материалов из Архива технических отчетов и библиотеки изображений (TRAIL) включает труднодоступные отчеты, опубликованные различными государственными учреждениями. Технические публикации содержат отчеты, изображения и технические описания исследований, выполненных для правительственных учреждений США. Темы варьируются от добычи полезных ископаемых, опреснения и радиации до более широких исследований в области физики, биологии и химии. Некоторые отчеты включают карты, раскладки, чертежи и другие материалы большого размера.
О | Просмотрите эту коллекцию
Какие обязанности у меня есть при использовании этого отчета?
Цифровые файлы
- 204 файлы изображений доступны в нескольких размерах
- 1
файл
(.
 pdf)
pdf) - API метаданных: описательные и загружаемые метаданные, доступные в других форматах
Когда
Даты и периоды времени, связанные с этим отчетом.
Дата создания
- 1954 г.

Добавлено в цифровую библиотеку ЕНТ
- 2 сентября 2011 г., 22:21
Описание Последнее обновление
- 3 апреля 2019 г.
 , 12:58
, 12:58
Статистика использования
Когда последний раз использовался этот отчет?
Вчера: 0
Последние 30 дней: 643
Всего использовано: 27 135
Дополнительная статистика
Взаимодействие с этим отчетом
Вот несколько советов, что делать дальше.
Поиск внутри
Поиск
Начать чтение
PDF-версия также доступна для скачивания.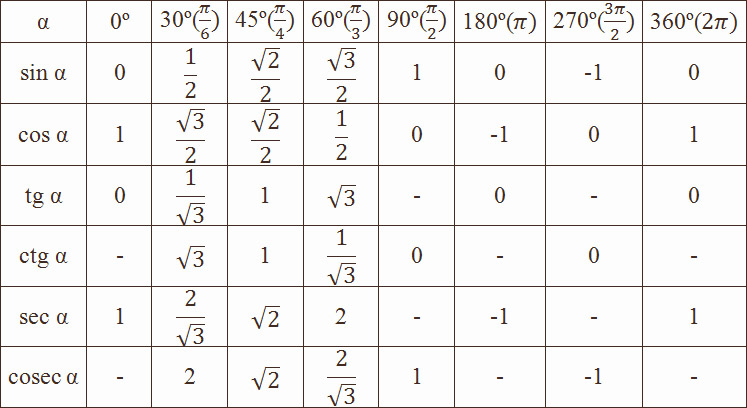
- Все форматы
Цитаты, права, повторное использование
- Ссылаясь на этот отчет
- Обязанности использования
- Лицензирование и разрешения
- Связывание и встраивание
- Копии и репродукции
Международная структура взаимодействия изображений
Мы поддерживаем IIIF Презентация API
Распечатать/поделиться
Полезные ссылки в машиночитаемом формате.
Архивный ресурсный ключ (ARK)
- ERC Запись: /арк:/67531/metadc40300/?
- Заявление о стойкости: /ark:/67531/metadc40300/??
Международная структура совместимости изображений (IIIF)
- IIIF Манифест: /арк:/67531/metadc40300/манифест/
Форматы метаданных
- UNTL Формат:
/ark:/67531/metadc40300/metadata.
 untl.xml
untl.xml - DC РДФ: /ark:/67531/metadc40300/metadata.dc.rdf
- DC XML: /ark:/67531/metadc40300/metadata.dc.xml
- OAI_DC : /oai/?verb=GetRecord&metadataPrefix=oai_dc&identifier=info:ark/67531/metadc40300
- МЕТС :
/ark:/67531/metadc40300/metadata.
 mets.xml
mets.xml - Документ OpenSearch: /ark:/67531/metadc40300/opensearch.xml
Изображений
- Миниатюра: /ark:/67531/metadc40300/миниатюра/
- Маленькое изображение: /ковчег:/67531/metadc40300/маленький/
URL-адреса
- В текст:
/ark:/67531/metadc40300/urls.


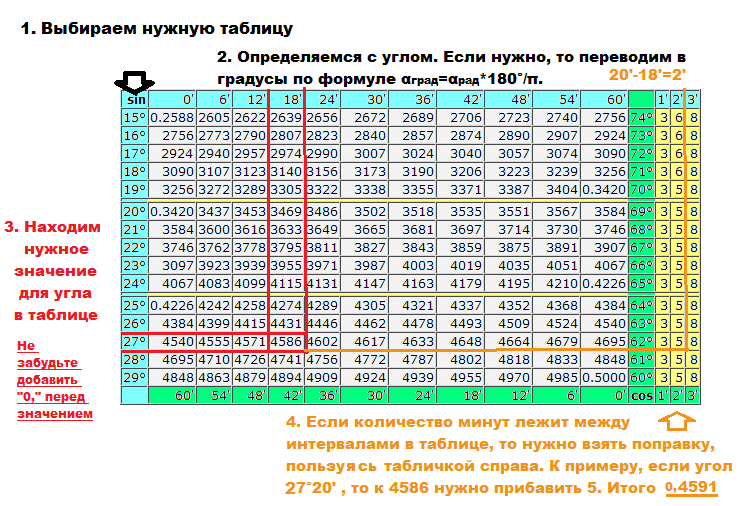
 д.
д. 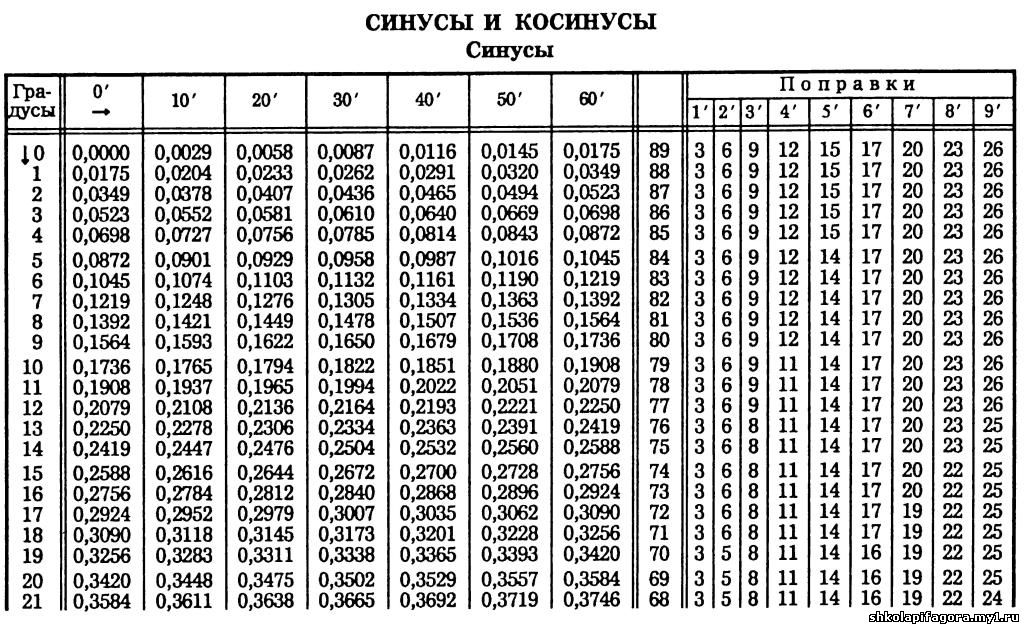
 Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.
Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.
 Национальное бюро стандартов. Вычислительная лаборатория.
Национальное бюро стандартов. Вычислительная лаборатория. Национальное бюро стандартов. Серия «Прикладная математика», 32
Национальное бюро стандартов. Серия «Прикладная математика», 32 pdf)
pdf)
 , 12:58
, 12:58 untl.xml
untl.xml mets.xml
mets.xml