Что называется хордой окружности в математике и геометрии: определение, основные свойства
Главная » Наука
Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.
Оглавление:
- Как построить геометрическую хорду
- Свойства
- Взаимосвязь с радиусом и диаметром
- Хорда и радиус
- Отношения со вписанными углами
- Взаимодействия с дугой
Содержание
Как построить геометрическую хорду
Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.
Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.
Это интересно: в геометрии луч это что такое, основное понятие.
Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.
Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.
Свойства
Существует ряд закономерностей, связывающих между собой хорды и центр круга:
- Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
- Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.

- Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
- Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
- Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
- Отрезок с наименьшей длиной представляет собой точку.
- Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.
Это интересно: разность векторов, определение разности.
Взаимосвязь с радиусом и диаметром
Вышеуказанные математические понятия связаны между собой следующими закономерностями:
- Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.

- С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
- Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
- Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
- Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
- Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.
Хорда и радиус
Между этими понятиями существуют следующие связи:
- Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
- Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.

- Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
- Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
- Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
- Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.
Отношения со вписанными углами
Углы, вписанные в окружность, подчиняются следующим правилам:
- Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
- Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
- Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.

- Вписанный угол, который опирается на диаметр круга, является прямым.
- Равные между собой по размеру отрезки стягивают равные центральные углы.
- Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
- Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.
Взаимодействия с дугой
Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:
- Две равные между собой хорды стягивают равные дуги.
- Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
- Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает.
 И чем больше дуга, тем меньше ограничивающая её хорда.
И чем больше дуга, тем меньше ограничивающая её хорда.
Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.
Раздел долгосрочного планирования: 7.4 Школа: Дата: ФИО учителя: Тургульдинов М.Ж. Класс: 7 Участвовали: Не участвовали: | ||||||||||||||||||||||||
Тема: Окружность, круг их элементы и части. | ||||||||||||||||||||||||
Цель обучения, достигаемые на этом уроке: | 7.1.1.28 знать определение окружности и круга, их элементов (центр, радиус, диаметр, хорда) | |||||||||||||||||||||||
Цель урока: | Знать определение окружности и круга, их элементов (центр, диаметр, радиус, дуга, хорда) Знать определение ГМТ Решать задачи по теме 7.1.1.31 знать определение геометрического места точек; | |||||||||||||||||||||||
Критерии оценивания: |
| |||||||||||||||||||||||
Языковые задачи: | используют в речи ключевые термины и понятия: окружность, круг, точка плоскости, внутрення и внешняя область, центр, радиус, диаметр, хорда, дуга, циркуль. умеет работать с математическими понятиями при решении задач | |||||||||||||||||||||||
Воспитание ценностей: | Единство истории, культуры и языка: Казахстанский патриотизм и гражданская ответственность ,уважение, солидарность, прозрачность | |||||||||||||||||||||||
Межпредметная связь: | История Казахстана, естествознание | |||||||||||||||||||||||
Предыдущие знания: | Знают определение окружности, круга, радиуса, диаметра, | |||||||||||||||||||||||
Ход урока | ||||||||||||||||||||||||
Запланирован- ные этапы урока | Виды упражнений запланированных на урок | Ресурсы | ||||||||||||||||||||||
Начало урока | Учитель. Вокруг нас огромное множество предметов, связанных с геометрическими фигурами. Сегодня мы систематизируем известные нам сведения об одной из самых распространенных геометрических фигур. Философы древности уделяли ей огромное внимание. Аристотель, например, говорил, что небесная материя, из которой состоят планеты и звезды, как самая совершенная, должна двигаться по этой совершенной линии. А в Древней Греции она считалась «венцом совершенства», потому что в каждой своей точке она устроена одинаково, что позволяет ей двигаться «по самой себе» И для того, чтобы вам было легче догадаться, о чем мы сегодня будем говорить, давайте встанем в «Круг пожеланий». В руках у вас будет клубок, передавая который соседу слева, и оставляя ниточку в руках, вы должны будете произнести ему пожелание. (по окончании тренинга учащиеся получают окружность из нитки клубка)
— Посмотрите на нитку в ваших руках. — Окружность. — А какая еще геометрическая фигура созвучна с окружностью? — Круг — Значит какая тема нашего урока? — окружность и круг ФО «Словесная похвала» Молодцы, вы сами сформулировали тему нашего урока «Окружность, круг и их элементы». Давайте вместе сформулируем цели нашего урока (записать основные на доску) ХОРОШО Данная тема знакома вам из курса математики 5 класса. Подумайте и Оцените уровень своих знаний по данной теме на ФО «Шкале знаний» (0-5) | Клубок ниток Подписанные стикеры | ||||||||||||||||||||||
Индивидуальная работа на актуализацию знаний обучающихся Соедините линиями соответствующие высказывания:
Дескрипторы: — знает определения: окружности, радиуса, диаметра, хорды, дуги; — сопоставляет математические требования и определения А теперь поработайте в парах, сравните и проанализируйте ваши ответы Метод «Думай – В паре – Делись» Что заметили, какие сделали выводы? Сравните ответы вашего партнера с правильными и оцените смайликом
ФО «Смайлик» -Теперь, ребята, посмотрите на эти фигуры на слайде и скажите в чем отличие фигуры от А от фигуры от В. А В В -Попробуйте самостоятельно определить, какая фигура называется кругом Круг – фигура, состоящая из всех точек плоскости, удаленных от данной точки на расстояние, не превосходящее данное — Какие элементы круга вам известны? Дайте определение ФО «Словесная похвала» -Используя материал учебника и «Таблицу ответов», запишите в тетрадь те определения, которые вы увидели впервые, вызвали у вас затруднения или в которых вы допустили ошибки -Зачитайте друг другу, обсудите, что узнали Метод «Глоссарий» | Тестовые задания Слайд с правильными ответами Карточки со смайликами Слайд | |||||||||||||||||||||||
Середина урока | Первичное усвоение знаний. Задача на построение (индивидуальная работа) Начертите окружность с центром в точке О и радиусом 3,5см. Дескрипторы: — строит окружность заданного радиуса с помощью циркуля — выделяет красным карандашом диаметр — выделяет зеленым карандашом радиус — вычисляет диаметр Взаимопроверка ФО «Сигнальная карточка» Работа в парах с картинками Юрта –древнейшее и в то же время современное жилище кочевников( рис 54.6.а) Юрты бывают разные по размерам. Найдите радиусы, образованные от шанырака (купол юрты, рис 54.6.б) и кереге (круглая вертикальная стена, рис 54.6.в), если диаметр шанырака 2 метра, а диаметр кереге – 10 метров Проверка в парах сменного состава Физминутка «Молекулы» (Деление на группы по 3 атома) Метод Джигсо. (Разноуровневые задания) Прием «Право выбора» Каждый учащийся выбирает задание и решает самостоятельно, затем объединяются в экспертные группы по заданиям, обсуждают решение и записывают его в тетрадь, затем возвращаются в свои первичные группы и объясняют решение своей задачи одноклассникам
Оценивание «Светофор» Зеленый – решение задачи мне понятно Желтый – решение задачи понятно не совсем Красный – решение задачи мне не понятно, необходима помощь | Учебник № 226 http://expert.mektep.kz/ru/shop/25836-7_klass/29804-matematika_chast_2/1 Карточки с заданиями, сигнальные карточки | ||||||||||||||||||||||
Конец урока | Графический диктант «Верные и неверные утверждения» 1. 2. Диаметр – это отрезок, соединяющий две любые точки окружности и проходящий через её центр. 3. Все радиусы одной окружности имеют разную длину. 4. Радиус окружности – это отрезок, соединяющий две точки окружности. Самопроверка и указать свою оценку на «Шкале знаний» Рефлексия: Вернуться к написанным в начале урока целям, определить какие были достигнуты, а над какими еще необходимо потрудиться Итог урока «Ладошка» | Утверждения на слайде и слайд с ключом . | ||||||||||||||||||||||
Домашняя работа. Все: Выучить определения Большинство: Придумать задачи к определениям Некоторые: Подготовить сообщение «Окружности в окружающем нас мире» | ||||||||||||||||||||||||
Дифференциация | Оценивание | Охрана здоровья и соблюдение техники безопасности | ||||||||||||||||||||||
Подбор заданий от простого к сложному, разноуровневые задания в группе Дифференцированное домашнее задание | Словесная похвала Шкала знаний Смайлики Сигнальная карточка Самооценивание Взаимооценивание Светофор Ладошка | Соблюдение правил техники безопасности Соблюдение здоровьесберегающего режима школьников через проведение физминутки | ||||||||||||||||||||||
Хорда круга | Что такое хорда окружности
Содержание
Этот пост также доступен в: हिन्दी (хинди)
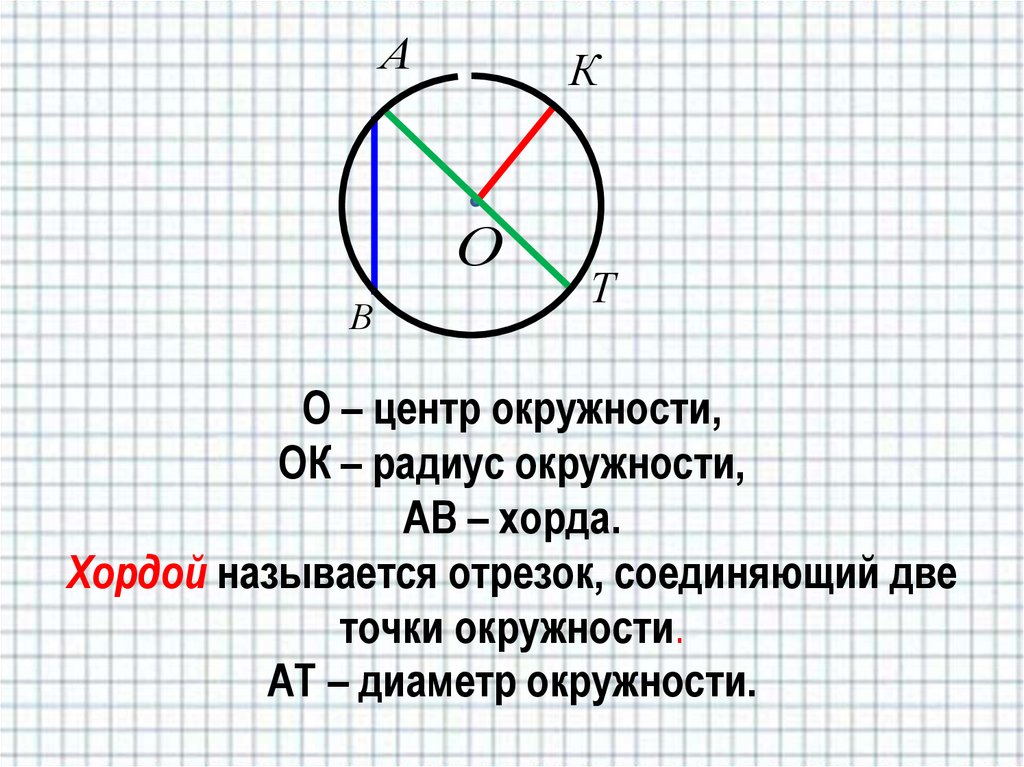
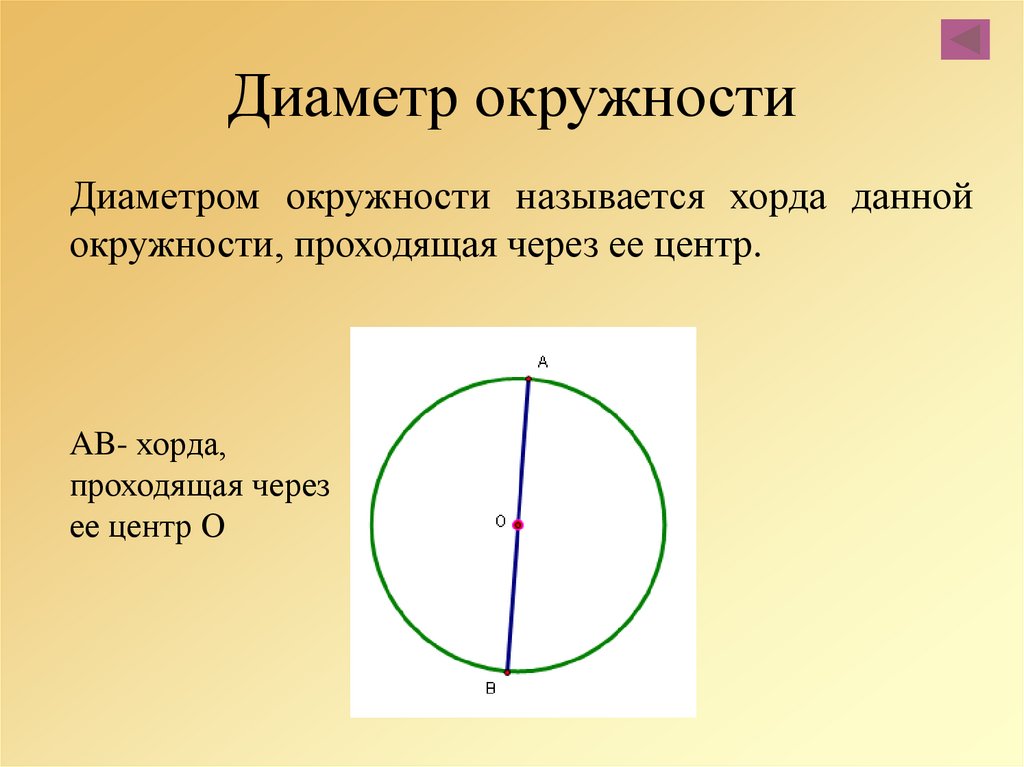
Отрезок, соединяющий две точки окружности, называется хордой окружности. Хорда окружности, проходящая через центр окружности, называется диаметром окружности и является наибольшей хордой окружности.
Хорда окружности, проходящая через центр окружности, называется диаметром окружности и является наибольшей хордой окружности.
Давайте разберемся, что такое хорда окружности и ее свойства на примерах.
Что такое хорда окружности?
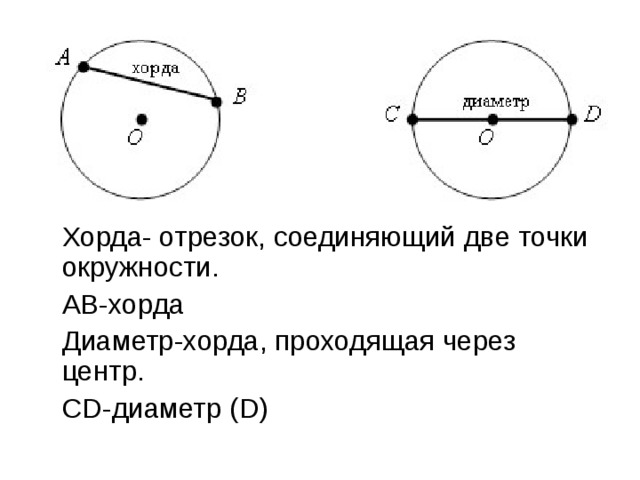
Отрезок, соединяющий две точки окружности, называется хордой окружности. Другими словами, любой отрезок, концы которого лежат на окружности, является хордой окружности.
На приведенном выше рисунке $\text{AB}$ и $\text{DE}$ являются хордами, так как концы отрезков лежат на окружности окружности. Хорда $\text{DE}$ также является диаметром окружности.
Отрезок $\text{OC}$ не является хордой, так как только один конец лежит на окружности.
Примечание: Хорда, проходящая через центр окружности, называется диаметром окружности.
СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:
Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.
Свойства хорды окружности
Ниже приведены важные свойства хорды окружности.
- Перпендикуляр к хорде, проведенный из центра окружности, делит хорду пополам.
- Хорды окружности, равноудаленные от центра окружности, равны.
- Когда хорда окружности рисуется, она делит окружность на две области, называемые сегментами окружности: большой сегмент и меньший сегмент.
- Хорда, продолженная бесконечно в обе стороны, становится секущей окружности.
Формула длины хорды
Существуют две основные формулы для определения длины хорды окружности. Первый — с помощью теоремы Пифагора, а второй — с помощью тригонометрии. 92}$
Используя тригонометрию: Длина хорды с использованием перпендикулярного расстояния от центра = $2 \times r \times \sin \frac{\theta}{2}$.
Рассмотрим окружность с центром $\text{O}$, хордой $\text{AB}$ и радиусом $\text{OA}$. Расстояние хорды $\text{AB}$ от центра равно $\text{OC}$. Далее, пусть вертикаль $\angle \text{AOB} = \theta$.
Далее, пусть вертикаль $\angle \text{AOB} = \theta$.
Следовательно, в прямоугольном $\треугольнике \text{OAC}$ $\sin \frac{\theta}{2} = \frac{\text{AC}}{r}$
$=> \text{AB} = 2 \times r \times \sin \frac{\theta}{2}$
Теоремы хорды окружности
Есть несколько теорем, основанных на хорде окружности.
Теорема 1: Равные хорды окружности опираются на равные углы в центре.
Рассмотрим окружность с центром $\text{O}$ и двумя равными хордами $\text{AB}$ и $\text{CD}$, и мы хотим доказать, что $\angle \text{AOB} = \angle \ текст {COD} $.
В треугольниках $\text{AOB}$ и $\text{COD}$,
$\text{OA} = \text{OC}$ (радиусы окружности)
$\text{OB} = \text{OD}$ (Радиусы окружности)
$\text{AB} = \text{CD}$ (Дано)
Следовательно, $\triangle \text{AOB} \cong \triangle \text{COD}$ (правило SSS)
Это дает $\angle \text{AOB} = \angle \text{COD}$ (соответствующие стороны конгруэнтных треугольников)
youtube.com/embed/T29j3c1AAA8?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Величайшие математические открытияТеорема 2: Перпендикуляр к хорде, проведенный из центра круга, делит хорду пополам.
Рассмотрим приведенный выше рисунок, где $\text{O}$ — центр окружности, а $\text{AB}$ — хорда. 9{\circ}$
По правилу RHS, $\triangle \text{OAP} \cong \triangle \text{OBP}$
Следовательно, $\text{AP} = \text{PB}$ (соответствующие стороны конгруэнтных треугольников)
Таким образом, перпендикуляр к хорде, проведенный из центра окружности, делит хорду пополам.
Практические задачи
- Две равные хорды AB и CD окружности при построении пересекаются в точке P. Докажите, что PB = PD.
- Две окружности радиусами 5 см и 3 см пересекаются в двух точках, а расстояние между их центрами равно 4 см. Найдите длину общей хорды.
 2}$.
2}$.Является ли диаметр хордой окружности?
Да, диаметр тоже считается хордой окружности. Диаметр — это самая длинная хорда в окружности, которая делит окружность на две равные части.
Заключение
Отрезок, соединяющий две точки окружности, называется хордой окружности. Среди всех хорд окружности та, которая проходит через центр окружности, является самой длинной хордой и называется также диаметром окружности.
Рекомендуемое чтение
- Что такое круг — части, свойства и примеры
- Как построить перпендикулярную линию (с шагами и примерами)
- Как построить параллельные линии (с шагами и примерами)
- Как построить сегмент линии (с шагами и примерами)
- Что такое коллинеарные точки в геометрии — определение, свойства и примеры
- Что такое поперечная линия в геометрии – определение, свойства и примеры
- Что такое параллельные линии в геометрии — определение, свойства и примеры
- Что такое параллельные линии в геометрии — определение, условия и примеры
- Что такое полупрямая в геометрии — определение, свойства и примеры
- Что такое перпендикулярная линия в геометрии – определение, свойства и примеры
- Разница между аксиомой, постулатом и теоремой
- Линии в геометрии (определение, типы и примеры)
- Что такое 2D-фигуры — имена, определения и свойства
- 3D-фигуры — определение, свойства и типы
Вам также может понравиться
Гармоническая прогрессия – значение, формулы и примеры
Содержание Что такое гармоническая прогрессия? Примеры гармонической прогрессииГармоническая прогрессия
Читать далее
Геометрическая прогрессия – значение, формулы и примеры
Содержание Что такое геометрическая прогрессия? Примеры геометрической прогрессии 9-й член0003
Читать далее
Арифметическая прогрессия – значение, формулы и примеры
Содержание Что такое арифметическая прогрессия? Примеры арифметической прогрессии Член
Читать далее
хорд круга: определение, формула, примеры
- Автор Прия_Сингх
- Последнее изменение 30-01-2023
Хорды круга: Хорда окружности определяется как отрезок, соединяющий любые две точки на окружности окружности.
 Следует отметить, что диаметр — это самая длинная хорда окружности, проходящая через центр окружности. В этой статье мы узнаем о различных компонентах круга, уделяя особое внимание аккордам, их свойствам и некоторым другим вещам, связанным с аккордами.
Следует отметить, что диаметр — это самая длинная хорда окружности, проходящая через центр окружности. В этой статье мы узнаем о различных компонентах круга, уделяя особое внимание аккордам, их свойствам и некоторым другим вещам, связанным с аккордами.Здесь, в Embibe, вы можете получить бесплатный пересмотренный пробный тест CBSE MCQ 2022 по всем темам. Тест MCQ, предлагаемый Embibe, курируется на основе пересмотренных учебников CBSE, бумажных шаблонов и учебного плана на 2022 год. В этой серии пробных тестов представлен широкий выбор соответствующих вопросов и их решений. Учащиеся совета CBSE могут пройти эти бесплатные пробные тесты, чтобы попрактиковаться и найти области, в которых им нужно улучшить свои навыки перед экзаменами совета.
Окружность — это совокупность всех точек плоскости, расстояние до которых от фиксированной точки всегда одинаково. Неподвижная точка известна как центр окружности.
Различные компоненты кругаЦентр: Центром круга называется точка внутри круга, от которой расстояния до точек на окружности равны.

Радиус: Радиус окружности — это отрезок, соединяющий центр и любую точку окружности.
Диаметр: Диаметр круга — это отрезок, начинающийся из любой точки на окружности круга, проходящий через центр и заканчивающийся в точке на окружности на противоположной стороне круга. Длина диаметра в два раза больше длины радиуса окружности. Формула диаметра окружности: диаметр окружности \(d = 2\,r,\), где \(r\) — радиус окружности.
Окружность: Граница круга называется окружностью круга.
Полукруг : Полукруг — это половина круга. Диаметр делит окружность на две полуокружности.
Хорда окружностиХорда окружности обсуждается ниже:
Хорда окружности ОпределениеХорда — это прямая линия, соединяющая две точки на окружности.
Разница между хордой и диаметром
Диаметр окружности считается самой длинной хордой, поскольку она соединяет две точки на окружности окружности.
Хорда: Хорда — это отрезок, соединяющий любые две точки окружности.
Диаметр: Хорда окружности, проходящая через центр окружности, называется диаметром окружности.
Все диаметры окружности являются хордами, но не все хорды являются диаметрами окружности.
Длины хорд окружности могут различаться, но длина диаметра окружности фиксирована для конкретной окружности.
Сегмент кругаХорда круга делит круговую область круга на две части. Каждая из частей известна как сегмент круга.
Если хорда — это диаметр, то она делит круговую область на две равные части. Однако, если хорда не является диаметром, она делит область на две неравные части. Большая область содержит центр круга. Эта область называется Большим Сегментом, а меньшая область называется Малым Сегментом круга.
Дуга кругаЛюбая часть окружности называется дугой окружности.
Свойства хорды Если длина дуги окружности больше полуокружности, она называется большой дугой, а если длина дуги окружности меньше полуокружности, она называется малой дугой. Сумма длин большой дуги и малой дуги всегда дает длину окружности.
Если длина дуги окружности больше полуокружности, она называется большой дугой, а если длина дуги окружности меньше полуокружности, она называется малой дугой. Сумма длин большой дуги и малой дуги всегда дает длину окружности.1. Если радиус окружности перпендикулярен хорде, то он делит хорду пополам.
2. При увеличении расстояния от центра окружности до хорды длина хорды уменьшается и наоборот.
3. Диаметр — это самая длинная хорда окружности, так как перпендикулярное расстояние от центра окружности до хорды равно нулю.
4. Треугольник, образованный хордой и двумя радиусами от концов хорды к центру окружности, является равнобедренным треугольником.5. Две хорды равны по длине, если они равноудалены от центра окружности. Пример: хорда \(PQ = RS,\), если \(TU\) равно \(UV.\)
Теоремы о хорде окружностиТеорема 1: Равные хорды окружности образуют равные углы в центре.
Решенный пример s o n Хорды окружности {\rm{o} }}.\) 92}} ,\) где \(p\) — расстояние по перпендикуляру от центра окружности до хорды.
{\rm{o} }}.\) 92}} ,\) где \(p\) — расстояние по перпендикуляру от центра окружности до хорды.
2. Длина хорды с использованием тригонометрии с углом справа)\)Q.1. Определите длину хорды окружности с радиусом \(7\,{\rm{см}}.\) Кроме того, перпендикулярное расстояние от хорды до окружности равно \(4\,{\rm{см}} .\) Используйте формулу длины хорды. 92}} \right)} \)
\( = 2 \times \sqrt {\left( {49 – 16} \right)} \)
\( = 2 \times 5,744\)
\( = 11,48\)
Следовательно, длина хорды будет приблизительно равна \(11,48\,{\rm{см}}\).Q.2. Радиус окружности равен \(14\,{\rm{см}},\), а расстояние по перпендикуляру от хорды до центра равно \(8\,{\rm{см}}{\rm{.} }\) Определите длину хорды.
Ответ: Заданный радиус, \(r = 14\,{\rm{см}}\)
Перпендикулярное расстояние \(p = 8\,{\rm{см}}\) 92}} \right)} \)
\( = 2\sqrt {\left( {198 – 64} \right)} \)
\( = 2\sqrt {\left({132} \right)} \ )
\( = 2 \times 11,5\)
\( = 23\)
Следовательно, длина хорды приблизительно равна \(23\,{\rm{см}}\).
Q.3. Расстояние по перпендикуляру от центра окружности до хорды равно \(8\,{\rm{m}}.\) Вычислите длину хорды, если диаметр окружности равен \(34\,{\rm{m}}. \)
Ответ: Расстояние равно \(p = 8\,{\rm{m}}.\)
Диаметр равен \(D = 34\,{\rm{m}}.\) Таким образом, радиус равен \(r = \frac{D}{2} = \frac{{34}}{2} = 17\,{\rm{m}}.\) 92}} \right)} \)
\( = 2\sqrt {\left( {289 – 64} \right)} \)
\( = 2\sqrt {\left( {225} \right)} \ )
\( = 2 \times 15\)
\( = 30\)
Таким образом, длина хорды равна \(30\,{\rm{m}}{\rm{.}}\)Q.4. Длина хорды окружности равна \(40\) дюймов. Предположим, что перпендикулярное расстояние от центра до хорды составляет \(15\) дюймов. Каков радиус хорды?
Ответ: Длина хорды \(40\) дюймов.
Расстояние равно \(p = 15\) дюймам 92}} = 625\)
\(r = – 25\) или \(25\)
Длина никогда не может быть отрицательным числом, поэтому она равна \(25.\)
Следовательно, радиус окружности равен \ (25\) дюймов.

 И чем больше дуга, тем меньше ограничивающая её хорда.
И чем больше дуга, тем меньше ограничивающая её хорда.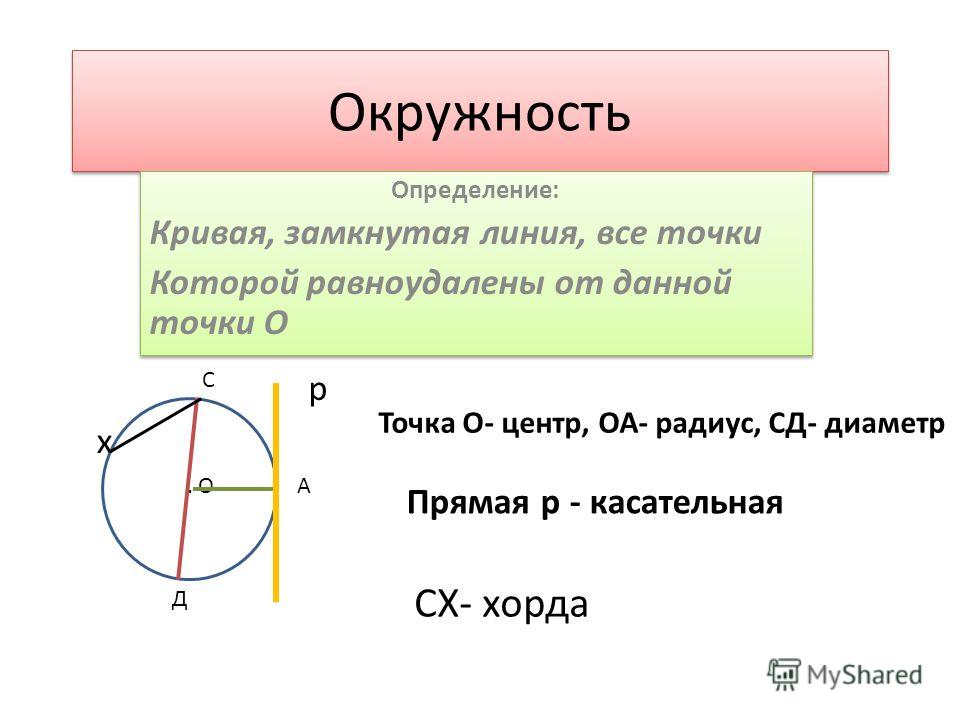

 Добрый день. Я рада приветствовать вас на нашем уроке.
Добрый день. Я рада приветствовать вас на нашем уроке. Какую геометрическую фигуру мы получили?
Какую геометрическую фигуру мы получили? Окружность – это ….
Окружность – это ….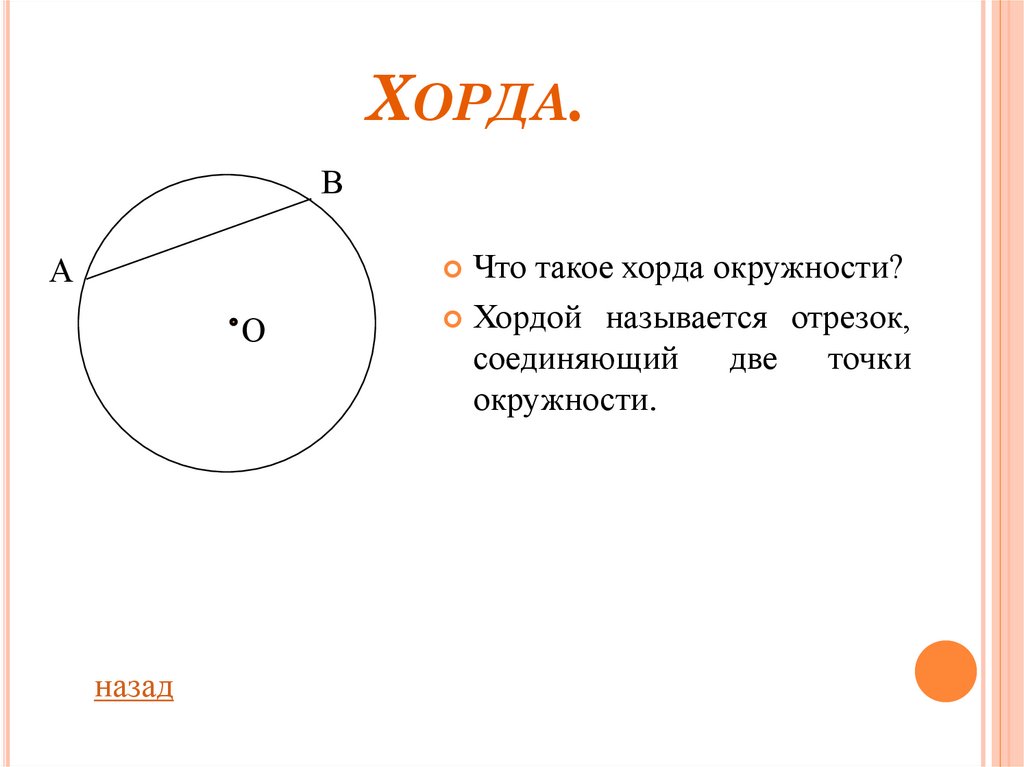
 Проведите диаметр красным карандашом и радиус зеленым карандашом. Чему равен диаметр?
Проведите диаметр красным карандашом и радиус зеленым карандашом. Чему равен диаметр?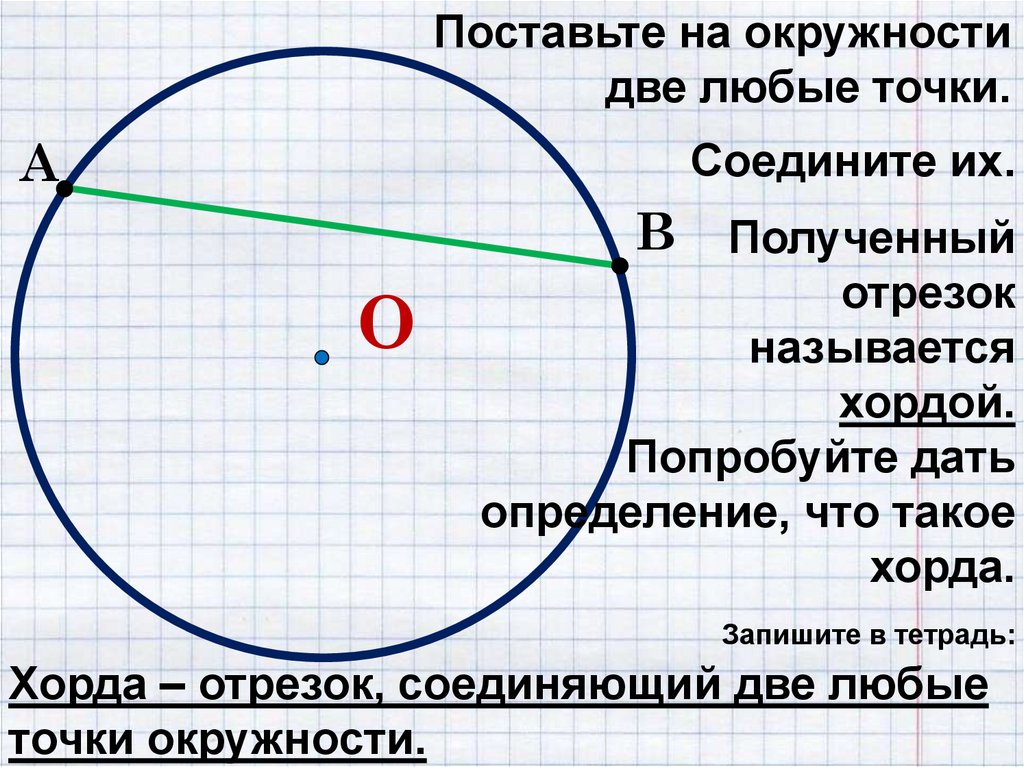 Дано: окружность,
Дано: окружность, Окружность – это фигура, состоящая из всех точек плоскости, находящихся от данной точки на одинаковом расстоянии.
Окружность – это фигура, состоящая из всех точек плоскости, находящихся от данной точки на одинаковом расстоянии. 2}$.
2}$.