Как решить с уравнение параметром: Уравнения с параметром | LAMPA

Решение уравнения или неравенства с параметром обычно предполагает несколько случаев, и ни один из них нельзя потерять. Для того, чтобы решить задачу с параметром, необходимо для начала преобразовать заданное выражение к более простому виду, если это, конечно, возможно. При этом необходимо понимать, какие преобразования являются равносильными, а какие нет. В противном случае могут появиться посторонние корни, которые будет нужно проверить (это не всегда просто, поэтому рекомендую стараться использовать равносильные преобразования).

Рекомендации к выполнению задания 18 ЕГЭ:

1. Надо избавиться от логарифмов, модулей, показательных степеней и т.д.
2. Еще раз внимательно прочитать задание. Понять, что от вас требуется.
3. Попытаться проанализировать получившееся после преобразований выражение на наличие каких-либо специальных свойств функции (периодичность, возрастание/убывание, четность/нечетность и т. 2-3*x+1=0\), при \(a=0\) выражение принимает вид \(-3*x+1=0\), т.е. превращается в линейную функцию, а способы решения квадратного и линейного уравнений различны.

Электронный научный журнал // Информационно-коммуникационные технологии в педагогическом образовании

Научный руководитель: Алдакишкина Валентина Владимировна

Изучение многих физических и геометрических закономерностей нередко приводит к решению задач с параметрами.

В настоящее время на выпускных экзаменах школьники часто встречаются с уравнениями, неравенствами и системами с параметрами, которые часто бывают весьма сложными и требующими нестандартного подхода к решению. Решение задач с параметрами вызывает большие трудности, так как их изучение не является отдельной составляющей школьного курса математики, и рассматривается только на немногочисленных факультативных занятиях, а их решение требует не только знания свойств функций и уравнений, умения выполнять алгебраические преобразования, но также высокой логической культуры и хорошей техники исследования.

Трудности при изучении данного вида уравнений связаны со следующими их особенностями: обилие формул и методов, используемых при решении уравнений данного вида; возможность решения одного и того же уравнения, содержащего параметр, различными методами.

Уравнение вида

Параметром называется независимая переменная, значение которой в задаче считается заданным, фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.

Выделяют несколько типов задач с параметрами.

1. Задачи, которые необходимо решить для всех значений параметра или для значений параметра из заданного промежутка.

Например. Решите уравнение в зависимости от параметра a.

1. Задачи, где требуется найти количество решений в зависимости от значения параметра.

Например. Определить количество решений уравнения .

1. Задачи, где необходимо найти значения параметра, при которых задача имеет заданное количество решений.

Например. Дано уравнение . Определить значения параметра a, при которых оно имеет единственное решение.

1. Задачи, в которых необходимо найти значения параметра, при которых множество решений удовлетворяет заданным условиям.

Например. При каком значении параметра a решением уравнения является множество .

К основным методам решения задач с параметрами относятся:

• метод «ветвления»;

• использование свойств функций в задачах с параметрами;

• графический метод.

Метод «ветвления»

Поскольку уравнение с параметром это целый класс уравнений, то решать надо сразу весь этот класс, что влечет за собой необходимость разбора различных случаев в зависимости от определенных значений параметра.

Именно этот факт и позволяет нам решать уравнения с параметром таким методом («ветвления»).

Пример 1. Решить уравнение

В зависимости от значений параметра m.

Решение. .

.

ОДЗ:

Достаточно рассмотреть три случая, т. к. число m стоит под знаком модуля, следовательно, может принимать как положительные, так и отрицательные значения, и отдельно следует рассмотреть случай, когда m=0.

1. m=0.

Уравнение будет выполняться при любых значениях

1. .

.

Замена: , .

Проверим, являются ли данные корни корнями исходного уравнения.

.

— посторонние корни.

Выполняя аналогичные действия для , заключаем, что — корни исходного уравнения.

1. Аналогично пункту 2 рассматриваем случай и заключаем, что — корни исходного уравнения.

Ответ: при ; при ; при

Свойства функций в задачах с параметром

Для успешного решения уравнений с параметрами нужно не только владеть основными приемами их решения, но и знать и уметь применять некоторые преобразования, основанные на свойствах функций. Сформулируем некоторые из них в виде теорем.

Теорема 1. Если функция f(x) возрастает (убывает) на промежутке I и функция g(x) возрастает (убывает) на промежутке I, то функция h(x)=f(x)+g(x)+C также возрастает (убывает) на промежутке I (C – произвольная постоянная).

Теорема 2. Если функция f(x) неотрицательна и возрастает на промежутке I, функция g(x) неотрицательна и возрастает на промежутке I, , то функция также возрастает на промежутке I.

Аналогичное свойство имеет место и для убывающих функций, а также для .

Теорема 3. Если функция f(t) монотонна на промежутке I, то уравнение f(g(x))=f(h(x)) равносильно на промежутке I уравнению g(x)=h(x).

Теорема 4. Если функция f(x) монотонна на промежутке I, то уравнение f(x)=C имеет на промежутке I не более одного корня.

Теорема 5. Если функция f(x) возрастает на промежутке I, а функция g(x) убывает на промежутке I, то уравнение f(x

Теорема 6. Если функция f(x) возрастает на промежутке I, то уравнение f(f(x))=x равносильно на промежутке I уравнению f(x)=x.

Теорема 7. Если для функций f(x) и g(x) , то

Пример 2. Найдите все значения параметра a, при которых уравнение имеет ровно один корень.

Решение.

Рассмотрим функцию .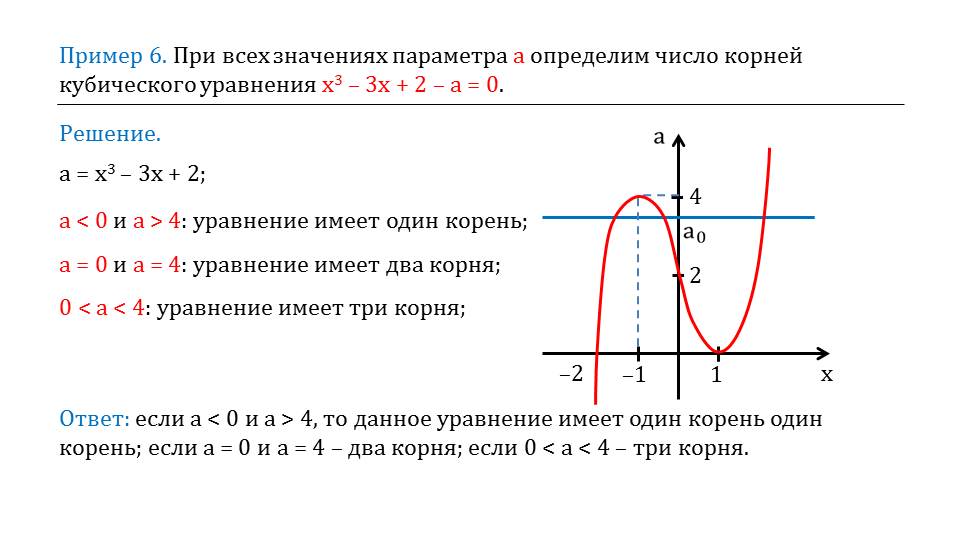 По теореме 1 она является возрастающей на множестве всех действительных чисел.

Тогда исходное уравнение можно записать в виде .

По теореме 3 оно равносильно уравнению .

Т. к. по условию задачи нужно найти те значения параметра, при которых уравнение имеет ровно один корень, а это возможно, когда дискриминант полученного равносильными преобразованиями квадратного уравнения равен нулю, то .

Ответ: при уравнение имеет ровно один корень.

Графические методы

Координатная плоскость (x;y)

Задачи, содержащие параметр, требуют к себе своеобразный подход, здесь необходимо грамотное и тщательное исследование. Для применения графических методов требуется умение выполнять дополнительное построение различных графиков, вести графические исследования, соответствующие данным значениям параметра.

Пример 3.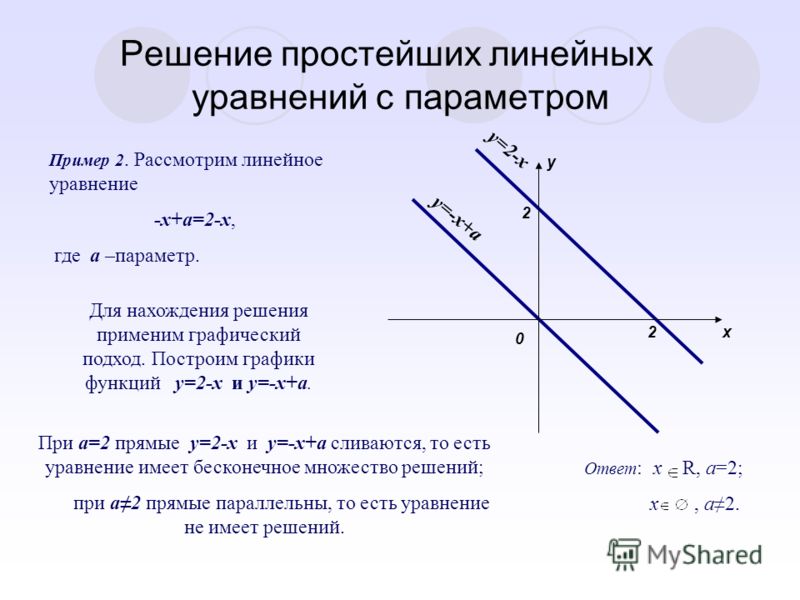 Для каждого значения параметра определить число решений уравнения .

Решение. Построим график функции .

Пусть , тогда

— окружность с центром в точке (1;0) и радиусом 1.

Пусть , тогда

— окружность с центром в точке (-1;0) и радиусом 1.

Рассмотрим функцию . Это прямая параллельна оси Оx. Построим следующие случаи этой прямой: .

Из полученного графика хорошо видно, что при уравнение решений не имеет, при уравнение имеет два решения, при – три решения, при — четыре решения.

Ответ: при уравнение решений не имеет, при уравнение имеет два решения, при – три решения, при — четыре решения.

Координатная плоскость (x;a)

Рассмотрим метод, упрощающий работу по решению уравнений с параметром. Метод состоит в следующем:

• из уравнения с переменной x и параметра a выразим параметр как функцию от x: ;

• в координатной плоскости xOa строим график функции ;

• Рассмотрим прямые и выделим те промежутки оси Oa, на которых эти прямые удовлетворяют следующим условиям: a) не пересекает график функции ,

б) пересекает график функции в одной точке,

в) в двух точках,

г) в трех точках и так далее.

• Если поставлена задача найти значения x, то выражаем x через a для каждого из найденных промежутков значения a в отдельности.

Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах. Таким образом, возникает координатная плоскость . Казалось бы, такая незначительная деталь, как отказ от традиционного обозначения координатной плоскости буквами x и y определяет один из эффективнейших методов решения задач с параметрами.

Описанный метод очень нагляден. Кроме того, в нем находят применение почти все основные понятия курса алгебры и начал анализа. Задействуется весь набор знаний, связанных с исследованием функции: применение производной к определению точек экстремума, нахождение предела функции, асимптот и т. д.

Пример 4. При каких значениях параметра уравнение имеет два корня?

Решение. Переходим к равносильной системе

Найдем координаты вершины параболы: (0,5; -0,25).Построим график функции.

Из графика видно, что при уравнение имеет 2 корня.

Ответ: при уравнение имеет два корня.

Трансцендентное уравнение – уравнение, содержащее трансцендентные функции (иррациональные, логарифмические, показательные, тригонометрические и обратные тригонометрические) от неизвестного (переменного), например уравнения: .

Решить уравнение с параметром означает:

1. Найти все системы значений параметров, при которых данное уравнение имеет решение.

2. Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.

Трансцендентные уравнения с параметрами включают в себя ряд различных трансцендентных функций, именно поэтому решения этих уравнений в большей степени зависят от свойств функций. Рассмотрим каждый вид трансцендентных уравнений с параметрами и попробуем заметить эти особенности при решении задач.

Уравнение называется иррациональным с одним неизвестным x, если одна или обе его части содержат выражения, иррациональные относительно x.

При решении иррациональных уравнений с параметрами следует помнить, что уравнение вида равносильно системе

Неравенство следует из уравнения .

Пример 5. Решить уравнение в зависимости от значений параметра a.

Решение. Преобразуем данное уравнение к виду

Возведем в квадрат обе части уравнения, получим:

Получили квадратное уравнение относительно x. Оно, как известно, имеет решение при , значит для дальнейшего решения необходимо найти дискриминант квадратного уравнения.

1)

.

Подставим полученное значение параметра a в уравнение (2) и найдем значение x.

,

,

,

.

Итак, при .

2)

.

При .

3)Исходя из того, что при уравнение не имеет решений, определим значения параметра a, при которых данное условие выполняется.

.

При уравнение решений не имеет.

Теперь необходимо выполнить проверку.

При подстановке в уравнение (2), имеем: . Получили неверное равенство, так как корень есть число положительное. Значит не является корнем исходного уравнения.

Подставим в уравнение (2), имеем:

,

.

Получили, что правая часть – число отрицательно, следовательно не является решением исходного уравнения.

Подставим в уравнение (2), имеем:

,

. (3) Если , то можем возвести обе части уравнения (3) в квадрат.

.

.

.

Имеем истинное равенство при условии, что . Это условие выполняется при , а может быть корнем уравнения (1) при , следовательно, — корень уравнения (1) при .

Ответ: при ; при уравнение решений не имеет.

Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением. Простейшим логарифмическим уравнением является уравнение вида , где .

При решении логарифмических уравнений удобно использовать следующие утверждения:

Утверждение 1. Если , уравнение при любом действительном b имеет единственное решение .

Утверждение 2. Уравнение равносильно одной из систем:

Утверждение 3. Уравнение равносильно одной из систем:

Пример 6. Найдите все значения параметра а, при которых уравнение

loga + loga=1 не имеет решения.

Решение.

ОДЗ:

Воспользовавшись основным свойством логарифма, запишем: 1=logaa. Преобразуя наше уравнение, получим равносильное уравнение:

=а,

Проделав равносильные преобразования, и заметив, что знаменатель дробей 1+ всегда положителен, получим уравнение:

(3+2)(4+)=а(1+)2,

(6-а)х+(17-2а)+12-а=0.

Замена: =y, y0.

(6-а)y2+(17-2а)y+12-а=0. (1)

D=(17-2а2)-4(6-а)(12-а)=4а+1.

Так как а>0, то D>0 и квадратное уравнение (1) имеет 2 корня. Учитывая условие y0, имеем y1<0 и y2<0, то есть y1y2>0, y1+y2<0.

y1y2=, y1+y2=.

Значит,

С учетом условия а>0 и а≠1, имеем а(0;1)(1;6)(12;+∞).

Рассмотрим отдельно случай а=6. Тогда квадратное уравнение становится линейным 5y+6=0, то есть y=-6/5, что не удовлетворяет условию y0.

Ответ: при а(0;1)(1;6)(12;+∞) уравнение не имеет решений.[4, № 58]

Показательные уравнения с параметрами

Уравнение, содержащее переменную в показателе степени, называется показательным.

Большинство показательных уравнений с параметрами сводятся к показательным уравнениям вида

где .

Область допустимых значений такого уравнения находится как пересечение областей допустимых значений функций и . Для решения уравнения (1) следует рассмотреть следующие случаи:

1. при a=b=1 решением уравнения (1) является его ОДЗ;

2. при решением уравнения (1) служит решение уравнения на ОДЗ;

3. при решением уравнения (1) служит решение уравнения на ОДЗ;

4. при уравнение (1) равносильно уравнению на ОДЗ;

5. при уравнение (1) тождественно уравнению

(2)

на ОДЗ.

Тождественное преобразование (2) называют логарифмированием. Такое преобразование может привести к потере корней.

Следует отметить, что, исходя из определения показательной функции, случай, когда основание a отрицательно, рассматривать не следует.

Пример 7. Найдите все значения параметра a, при которых уравнение

имеет ровно три корня.

Решение.

Данное уравнение можно записать в виде ,где функция на основании теоремы 2 является возрастающей.

В самом деле, так как , то , следовательно, . Таким образом, исходное уравнение равносильно (по теореме 3) следующему .

Дальнейшее решение проведем графическим способом. Для этого определим, при каких значениях параметра a графики функций

и имеют ровно три общих точки на координатной плоскости yOx.

По графику видим, что требованию задачи отвечает случай . Решая полученное уравнение, находим или .

Ответ: при уравнение имеет ровно три решения.

Тригонометрические уравнения с параметрами

Тригонометрическое уравнение — уравнение, содержащее тригонометрические функции неизвестного аргумента. Формулы решений простейших тригонометрических уравнений:

.

.

.

При решении тригонометрических уравнений удобно использовать следующие принципы:

1. При решении простейшего тригонометрического уравнения удобно понизить его степень за счет изменения его аргумента.

2. В случае необходимости проверки удобно подставлять в уравнение не значение найденного аргумента, а значения используемых в решении тригонометрических функций.

Пример 8. Найдите все значения параметра a, при которых число 2 является корнем уравнения

Решение.

Поставим в уравнение Получим уравнение относительно параметра a:

Ответ: при корнем уравнения является .

Помимо тригонометрических уравнений среди задач с параметрами встречаются и задачи с параметрами, содержащие обратные тригонометрические функции.

Напомним определения обратных тригонометрических функций:

1. — это функция, определенная на отрезке [-1;1], обратная функции

. Таким образом,

Для любого x из отрезка [-1;1] имеем:

1. — это функция, определенная на отрезке [-1;1], обратная функции

. Таким образом,

Для любого x из отрезка [-1;1] имеем:

1. — это функция, определенная на интервале , обратная функции

. Таким образом,

Для любого x имеем:

1. — это функция, определенная на интервале , обратная функции

. Таким образом,

Для любого x имеем:

Функции называются обратными тригонометрическими функциями или аркфункциями.

Отметим некоторые важные тождества:

Пример 9. Найдите все значения параметра a, при каждом из которых уравнение

имеет ровно три решения.

Решение.

Перепишем исходное уравнение в виде

.

Поскольку равенство равносильно тому, что и , исходное уравнение равносильно тригонометрическому уравнению

Решим уравнение (1).

Если , то

При совокупность, а значит и уравнение (1), имеет бесконечно много корней вида: , которые удовлетворяют условию (2). Т. е. не удовлетворяет требованию задачи.

При уравнение (1) имеет бесконечно много корней вида: .

Для них условие (2) превращается в неравенство

Параметр a включается в ответ тогда и только тогда, когда это неравенство имеет ровно три целочисленных решения. Используя геометрическую интерпретацию модуля разности двух чисел, видно, что это равносильно неравенству

Учитывая условие , получаем

Если решением уравнения (1) являются все действительные числа, условие же (2) принимает вид: , так что множество решений исходного уравнение – это интервал . Поскольку это множество бесконечно, значение не входит в ответ.

Ответ: при уравнение имеет ровно три решения.

Исходя из всех рассмотренных задач, можно сделать вывод, что решать трансцендентные уравнения с параметрами первого и четвертого типов лучше всего методом «ветвления», т. к. требуется найти все значения переменной при каждом возможном значении параметра (или при значениях параметра из заданного промежутка) или же при которых множество решений удовлетворяет заданным условиям. Однако такой метод не всегда надежен, поскольку ход решения достаточно длителен и сложен, поэтому изначально целесообразно определить, возможно ли применить к заданному уравнению функциональный подход, который значительно упрощает решение.

А вот решать трансцендентные уравнения с параметрами второго и третьего типов значительно проще, используя графический метод, поскольку в условии всего лишь требуется определить либо количество решений в зависимости от значения параметра, либо, наоборот, значения параметра, при которых задача имеет заданное количество решений. Из построенных графиков наглядно видно, когда выполняются заданные условия.

Однако не всегда возможно применение того или иного метода, иногда встречаются и такие задачи, для решения которых нужно применить не один, а несколько методов решения.

Задачи с параметрами представляют собой весьма широкое поле для полноценной математической деятельности. Решение такого рода задач открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применимых в исследованиях и на любом другом математическом материале.

Спецификой задач с параметрами является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа.

Уравнения с параметрами. — Математика

Файл к уроку

Решение уравнений с параметрами.

Не так давно 8 класс познакомился с квадратными уравнениями и алгоритмами их решения. Сегодня мы рассмотрим еще один вид уравнений, который часто встречается на олимпиадах и турнирах, и включен в ЕГЭ по профильной математике – это уравнения с параметром. Что такое параметр? Обычно это число, в зависимости от значения которого уравнение, будь оно линейным или квадратным, может иметь корни, а может их не иметь.

Задачи с параметрами считаются сложными ,однако если разобраться досконально, из каких шагов состоит путь к решению уравнения, то параметр уже не кажется такой злобной величиной.

Линейные уравнения с параметрами.

Уравнение вида

где a, b из R, x — переменная, называется уравнением первой степени (линейным уравнением).

Уравнение равносильно уравнению

ax = – b

откуда следует следующее утверждение.

1. Если a ≠ 0, то уравнение имеет единственное решение x = – ^b/_a;

2. Если a = 0, b ≠ 0, то множество решений уравнения пусто;

3. Если a = 0, b = 0, то любое действительное число является решением уравнения.

Решить уравнение с параметром – значит указать решение при всех значениях параметра, то есть фактически решить бесконечное множество уравнений, объединив их в одно по неким схожим зависимостям от параметра.

Пример 1. Решить уравнение: a²x – 1 = x + a.

Пример 2. Решить уравнение с параметром |6 – x| = a.

Решение.

Легко видеть, что здесь a ≥ 0.

По правилу модуля 6 – x = ±a, выразим х:

x = 6 ± a.

Ответ: х = 6 ± a, где a ≥ 0.

Пример 3. Решить уравнение x/a + 1 = а + х относительно переменной х.

Решение.

Если а = 0, то преобразуем уравнение к виду а + х = а² + ах или (а – 1)х = —а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.

Если а ≠ 1, то последнее уравнение примет вид х = —а.

Данное решение можно проиллюстрировать на координатной прямой (рис. 1)

Ответ: нет решений при а = 0; х – любое число при а = 1; х = —а при а ≠ 0 и а ≠ 1.

Пример 4. При каких значениях параметра b уравнение не имеет корней:

Графический метод

Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.

Пример 5. Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?

Решение. Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2).

На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.

Ответ: корней у уравнения не будет, если а a 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0 a

Пример 6. При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?

Решение.

Изобразим графики функций  y = 2|x| + |x – 1| и y = a. Для  y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:

      {-3x + 1, при x

y = {x + 1, при  0 ≤ x ≤ 1,

      {3x – 1, при x 1.

На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.

Ответ: а = 1.

Пример 7. При каких значениях параметра а неравенство имеет решением все действительные числа:

Системы линейных уравнений с параметрами.

– Система имеет единственное решение.

– Система имеет бесконечное множество решений.

– Система не имеет решений.

Пример 8. Для всех значений параметра а решить систему уравнений

Квадратичные уравнения с параметрами.

Решение уравнений второй степени сводится к исследованию поведения квадратного трехчлена, исследованию знака дискриминанта при различных значениях параметра. Часто при решении нам может помочь теорема Виета, когда вопрос стоит о корнях разных знаков, о корнях одного знака.

Квадратное уравнение может не иметь решений (Da=0 или D=0), два решения (D0) или бесконечное множество решений (когда при каком-то значении параметра получаем 0=0).

Пример 9. Решить уравнение в зависимости от параметра а:

Пример 10. При каких значениях корни уравнения положительны?

Пример 11. Найти значения параметра а, при которых среди корней уравнения имеется ровно один отрицательный:

Пример 12. Найти все значения параметра а, при которых уравнение имеет два различных отрицательных корня:

Пример 13. При каких значениях m корни уравнения 4x² – (3m + 1) x – m – 2 = 0 лежат в промежутке между –1 и 2?

Пример 14: Найти все значения параметра а, при которых меньший корень уравнения x² + (a + 1) x + 3 = 0 лежал в интервале (–1; 3)

Решение уравнений с параметром онлайн подробно

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. В математике существуют задачи, в которых необходимо произвести поиск решений линейных и квадратных уравнений в общем виде или произвести поиск количества корней, которое имеет уравнение в зависимости от значения параметра. Все эти задачи с параметрами.

Так же читайте нашу статью «Решить уравнение пропорцией онлайн»

Рассмотрим следующие уравнения в качестве наглядного примера:

\[у = kx,\] где \[x, y\] — переменные, \[k \]- параметр;

\[у = kx + b,\] где \[x, y\] — переменные, \[k, b\] — параметр;

\[аx^2 + bх + с = 0,\] где \[x\] — переменная, \[а, b, с\] — параметр.

Решить уравнение с параметром значит, как правило, решить бесконечное множество уравнений.

Однако, придерживаясь определенного алгоритма, можно легко решить такие уравнения:

1. Определить «контрольные» значения параметра.

2. Решить исходное уравнение относительно [\x\] при значениях параметра, определенных в первом пункте.

3. Решить исходное уравнение относительно [\x\] при значениях параметра, отличающихся от выбранных в первом пункте.

Допустим, дано такое уравнение:

\[\mid 6 — x \mid = a.\]

Проанализировав исходные данные, видно, что a \[\ge 0.\]

По правилу модуля \[6 — x = \pm a, \] выразим \[x:\]

\[x = 6 \pm a. \]

Ответ: \[x = 6 \pm a,\] где \[a \ge 0.\]

Где можно решить уравнение с параметром онлайн?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Квадратные уравнения с параметром | О математике понятно

Задачи с параметрами. Простейшие задачи на квадратный трёхчлен.

        Сегодня мы рассмотрим задачи на квадратный трёхчлен, про который, в зависимости от параметра, надо будет что-то выяснить. Это «что-то» может быть самым разнообразным, насколько только хватит фантазии у составителей задачи. Это самый простой тип задач с параметрами. И, если на ЕГЭ вам попалась такая — считайте, что вам повезло!

        Но, прежде чем приступать к разбору самих задач, ответьте сами себе на такие простые вопросы:

        — Что такое квадратное уравнение, как оно выглядит и как решается?

        — Что такое дискриминант и куда его пристроить?

        — Что такое теорема Виета и где её можно применить?

        Если вы верно отвечаете на эти простые вопросы, то 50% успеха в решении параметрических задач на квадратный трёхчлен вам обеспечены! А остальные 50% — это обычная алгебра и арифметика: раскрытие скобок, приведение подобных, решение уравнений, неравенств и систем и т.д.

        Итак, приступим!

        Для начала рассмотрим совсем безобидную задачку. Для разминки. 🙂

        Пример 1

        Приступаем к решению. Во-первых, чтобы в будущем не накосячить в коэффициентах, всегда полезно выписать их отдельно. Прямо в столбик. Вот так:      

        a = 1

        b = -(a-1)

        c = a-2

        Да-да! Часть коэффициентов в уравнении (а именно — b и с) зависит от параметра. В этом как раз и состоит вся фишка таких задач. А теперь снова въедливо перечитываем условие. Ключевой зацепкой в формулировке задания являются слова «единственный корень». И когда же квадратное уравнение имеет единственный корень? Подключаем наши теоретические знания о квадратных уравнениях. Только в одном единственном случае — когда его дискриминант равен нулю.

        Так и пишем:

        D = 0

        Осталось составить выражение для дискриминанта и приравнять его к нулю. Поехали!

        Теперь надо приравнять наш дискриминант к нулю:

       Можно, конечно, решать это квадратное уравнение через дискриминант, а можно немного схитрить. На что у нас похожа левая часть, если как следует присмотреться? Она у нас похожа на квадрат разности (a-3)²!

        Респект внимательным! Верно! Если заменить наше выражение слева на (a-3)², то уравнение будет решаться в уме!

        (a — 3)² = 0

        a — 3 = 0

        a = 3

        Вот и всё. Это значит, что единственный корень наше квадратное уравнение с параметром будет иметь только в одном единственном случае — когда значение параметра «а» равно тройке.)

        Ответ: 3

        Это был разминочный пример. Чтобы общую идею уловить.) Теперь будет задачка посерьёзнее.

        Пример 2

        Вот такая задачка. Начинаем распутывать.  Первым делом выпишем наше квадратное уравнение:

        0,5x² — 2x + 3a + 1,5 = 0

        Самым логичным шагом, было бы умножить обе части на 2. Тогда у нас исчезнут дробные коэффициенты и само уравнение станет посимпатичнее. Умножаем:

        Выписываем в столбик наши коэффициенты a, b, c:

          a = 1

          b = -4

          c = 6a+3

         Видно, что коэффициенты a и b у нас постоянны, а вот свободный член с зависит от параметра «а»! Который может быть каким угодно — положительным, отрицательным, целым, дробным, иррациональным — всяким!

         А теперь, чтобы продвинуться дальше, вновь подключаем наши теоретические познания в области квадратных уравнений и начинаем рассуждать. Примерно так:

         «Для того чтобы сумма кубов корней была меньше 28, эти самые корни, во-первых, должны существовать. Сами по себе. В принципе. А корни у квадратного уравнения существуют, тогда и только тогда, когда его дискриминант неотрицательный. Кроме того, в задании говорится о двух различных корнях. Эта фраза означает, что наш дискриминант обязан быть не просто неотрицательным, а строго положительным!»

         Если вы рассуждаете таким образом, то вы движетесь правильным курсом! Верно.) Составляем условие положительности для дискриминанта:

          D = (-4)² — 4·1·(6a+3) = 16-24a-12 = 4-24a

          4-24a > 0

          -24a > -4

          a < 1/6

        Полученное условие говорит нам о том, что два различных корня у нашего уравнения будет не при любых значениях параметра «а», а только при тех, которые меньше одной шестой! Это глобальное требование, которое должно выполняться железно. Неважно, меньше 28 наша сумма кубов корней или больше. Значения параметра «а», большие или равные 1/6, нас заведомо не устроят. Гуд.) Соломки подстелили. Движемся дальше.

        Теперь приступаем к загадочной сумме кубов корней. По условию она у нас должна быть меньше 28. Так и пишем:

        Значит, для того чтобы ответить на вопрос задачи, нам надо совместно рассмотреть два условия:

        А дальше начинаем отдельно работать с этой самой суммой кубов. Есть два способа такой работы: первый способ для трудолюбивых и второй способ — для внимательных.

        Способ для трудолюбивых заключается в непосредственном нахождении корней уравнения через параметр. Прямо по общей формуле корней. Вот так:

        Теперь составляем нужную нам сумму кубов найденных корней и требуем, чтобы она была меньше 28: 

        А дальше — обычная алгебра: раскрываем сумму кубов по формуле сокращённого умножения, приводим подобные, сокращаем и т.д. Если бы корни нашего уравнения получились покрасивее, без радикалов, то такой «лобовой» способ был бы неплох. Но проблема в том, что наши корни выглядят немного страшновато. И подставлять их в сумму кубов как-то неохота, да. Поэтому, для того чтобы избежать этой громоздкой процедуры, я предлагаю второй способ — для внимательных.

        Для этого раскрываем сумму кубов корней по соответствующей формуле сокращенного умножения. Прямо в общем виде:

        А дальше проделываем вот такой красивый фокус: во вторых скобках выражаем сумму квадратов корней через сумму корней и их произведение. Вот так:

        Итого:

        Казалось бы, и что из этого? Сейчас интересно будет! Давайте, посмотрим ещё разок на наше уравнение. Как можно внимательнее:

        Чему здесь равен коэффициент при x²? Правильно, единичке! А как такое уравнение называется? Правильно, приведённое! А, раз приведённое, то, стало быть, для него справедлива теорема Виета:

        Вот и ещё одна теорема нам пригодилась! Теперь, прямо по теореме Виета, подставляем сумму и произведение корней в наше требование для суммы кубов:

         Осталось раскрыть скобки и решить простенькое линейное неравенство:

          4·(16-18a-9) < 28

          64–72a+36 < 28

          -72a < 28-64+36

          -72a < 0

          a > 0

          Вспоминаем, что ещё у нас есть глобальное требование a < 1/6. Значит, наше полученное множество a > 0 необходимо пересечь с условием a < 1/6. Рисуем картинку, пересекаем, и записываем окончательный ответ.

          Ответ:

          Да. Вот такой маленький интервальчик. От нуля до одной шестой… Видите, насколько знание теоремы Виета, порой, облегчает жизнь!

          Вот вам небольшой практический совет: если в задании говорится о таких конструкциях, как сумма, произведение, сумма квадратов, сумма кубов корней, то пробуем применить теорему Виета. В 99% случаев решение значительно упрощается.

          Это были довольно простые примеры. Чтобы суть уловить. Теперь будут примеры посолиднее.

          Например, такая задачка из реального варианта ЕГЭ:

          Пример 3

          Что, внушает? Ничего не боимся и действуем по нашему излюбленному принципу: «Не знаешь, что нужно, делай что можно!»

          Опять аккуратно выписываем все коэффициенты нашего квадратного уравнения:

          a = 1

          b = -6

          c = a²-4a

          А теперь вчитываемся в условие задачи и находим слова «модуль разности корней уравнения». Модуль разности нас пока не волнует, а вот слова «корней уравнения» примем во внимание. Раз говорится о корнях (неважно, двух одинаковых или двух различных), то наш дискриминант обязан быть неотрицательным! Так и пишем:

          D ≥ 0

          Что ж, аккуратно расписываем наш дискриминант через параметр а:

          D = (-6)² — 4·1·(12 + a²-4a) = 36 — 48 — 4а² + 16а = -4а²+16а-12.

          А теперь решаем квадратное неравенство. По стандартной схеме, через соответствующее квадратное уравнение и схематичный рисунок параболы:

          Значит, для того чтобы у нашего уравнения в принципе имелись хоть какие-то корни, параметр а должен находиться в отрезке [-1; 3]. Это железное требование. Хорошо. Запомним.)

          А теперь приступаем к этому самому модулю разности корней уравнения. От нас хотят, чтобы вот такая штука

         принимала бы наибольшее значение. Для этого, ничего не поделать, но теперь нам всё-таки придётся находить сами корни и составлять их разность: x₁ — x₂. Теорема Виета здесь в этот раз бессильна.

          Что ж, считаем корни по общей формуле:

          Дальше составляем модуль разности этих самых корней:

          Теперь вспоминаем, что корень квадратный — величина заведомо неотрицательная. Стало быть, без ущерба для здоровья, модуль можно смело опустить. Итого наш модуль разности корней выглядит так:

         И эта функция f(a) должна принимать наибольшее значение. А для поиска наибольшего значения у нас есть такой мощный инструмент, как производная! Вперёд и с песнями!)

         Дифференцируем нашу функцию и приравниваем производную к нулю:

         Получили единственную критическую точку a = 2. Но это ещё не ответ, так как нам ещё надо проверить, что найденная точка и в самом деле является точкой максимума! Для этого исследуем знаки нашей производной слева и справа от двойки. Это легко делается простой подстановкой (например, а = 1,5 и а = 2,5).

          Слева от двойки производная положительна, а справа от двойки — отрицательна. Это значит, что наша точка a = 2 и вправду является точкой максимума. Заштрихованная зона на картинке означает, что нашу функцию  мы рассматриваем только на отрезке [1; 3]. Вне этого отрезка нашей функции f(a) попросту не существует. Потому, что в заштрихованной области наш дискриминант отрицательный, и разговоры о каких-либо корнях (и о функции тоже) бессмысленны. Это понятно, думаю.

          Всё. Вот теперь наша задача полностью решена.

          Ответ: 2.

          Здесь было применение производной. А бывают и такие задачи, где приходится решать уравнения либо неравенства с так ненавистными многими учениками модулями и сравнивать некрасивые иррациональные числа с корнями. Главное — не бояться! Разберём похожую злую задачку (тоже из ЕГЭ, кстати).

          Пример 4

          Итак, приступаем. Первым делом замечаем, что параметр а ни в коем случае не может быть равен нулю. Почему? А вы подставьте в исходное уравнение вместо а нолик. Что получится?

          Получили линейное уравнение, имеющее единственный корень x=2. А это уже совсем не наш случай. От нас хотят, чтобы уравнение имело два различных корня, а для этого нам необходимо, чтобы оно, как минимум, было хотя бы квадратным.)

          Итак, а ≠ 0.

          При всех остальных значениях параметра наше уравнение будет вполне себе квадратным. И, следовательно, чтобы оно имело два различных корня, необходимо (и достаточно), чтобы его дискриминант был положительным. То есть, первое наше требование будет D > 0.

          А далее по накатанной колее. Считаем дискриминант:

          D = 4(a-1)² — 4a(a-4) = 4a²-8a+4-4a²+16a = 4+8a

          Вот так. Значит, наше уравнение имеет два различных корня тогда и только тогда, когда параметр a > -1/2. При прочих «а» у уравнения будет либо один корень, либо вообще ни одного. Берём на заметку это условие и движемся дальше.

          Далее в задаче идёт речь о расстоянии между корнями. Расстояние между корнями, в математическом смысле, означает вот такую величину:

         Зачем здесь нужен модуль? А затем, что любое расстояние (что в природе, что в математике) — величина неотрицательная. Причём здесь совершенно неважно, какой именно корень будет стоять в этой разности первым, а какой вторым: модуль — функция чётная и сжигает минус. Точно так же, как и квадрат.

          Значит, ответом на вопрос задачи является решение вот такой системы:

          Теперь, ясен перец, нам надо найти сами корни. Здесь тоже всё очевидно и прозрачно. Аккуратно подставляем все коэффициенты в нашу общую формулу корней и считаем:

          Отлично. Корни получены. Теперь начинаем формировать наше расстояние:

         Наше расстояние между корнями должно быть больше трёх, поэтому теперь нам надо решить вот такое неравенство:

         Неравенство — не подарок: модуль, корень… Но и мы всё-таки уже решаем серьёзную задачу №18 из ЕГЭ! Делаем всё что можно, чтобы максимально упростить внешний вид неравенства. Мне здесь больше всего не нравится дробь. Поэтому первым делом я избавлюсь от знаменателя, умножив обе части неравенства на |a|. Это можно сделать, поскольку мы, во-первых, в самом начале решения примера договорились, что а ≠ 0, а во-вторых, сам модуль — величина неотрицательная.

          Итак, смело умножаем обе части неравенства на положительное число |a|. Знак неравенства сохраняется:

         Вот так. Теперь в нашем распоряжении имеется иррациональное неравенство с модулем. Ясное дело, для того чтобы решить его, надо избавляться от модуля. Поэтому придётся разбивать решение на два случая — когда параметр а, стоящий под модулем, положителен и когда отрицателен. Другого пути избавиться от модуля у нас, к сожалению, нет.

          Итак!

          Случай 1 (a>0, |a|=a)

          В этом случае наш модуль раскрывается с плюсом, и неравенство (уже без модуля!) принимает следующий вид:

          Неравенство имеет структуру: «корень больше функции». Такие иррациональные неравенства решаются по следующей стандартной схеме:

          Отдельно рассматривается случай а), когда обе части неравенства возводятся в квадрат и правая часть неотрицательна и отдельно — случай б), когда правая часть всё-таки отрицательна, но зато сам корень при этом извлекается.) И решения этих двух систем объединяются.

          Тогда, в соответствии с этой схемой, наше неравенство распишется вот так:

         А теперь можно существенно упростить себе дальнейшую работу. Для этого вспомним, что в случае 1 мы рассматриваем только a>0. С учётом этого требования, вторую систему можно вообще вычеркнуть из рассмотрения, поскольку, второе неравенство в ней (3a<0) эквивалентно неравенству a<0, а условия a>0 и a<0 — это два взаимно исключающих требования.

          Упрощаем нашу совокупность с учётом главного условия a>0:

         Вот так. А теперь решаем самое обычное квадратное неравенство:

         Нас интересует промежуток между корнями. Стало быть,

         Отлично. Теперь этот промежуток пересекаем со вторым условием системы a>0:

         Есть. Таким образом, первым кусочком ответа к нашему неравенству (а пока не ко всей задаче!) будет вот такой интервал:

         Всё. Случай 1 разложен по полочкам. Переходим к случаю 2.

          Случай 2 (a<0, |a|=-a)

         В этом случае наш модуль раскрывается с минусом, и неравенство принимает следующий вид:

         Опять имеем структуру: «корень больше функции». Применяем нашу стандартную схему с двумя системами (см. выше):

         С учётом общего требования a<0, мы снова, как и в предыдущем случае, проводим максимальные упрощения: вычёркиваем вторую систему в силу противоречивости двух требований -3а < 0 и нашего общего условия a<0 для всего случая 2.

          А дальше снова решаем обычное квадратное неравенство:

          И опять сокращаем себе работу. Ибо оно у нас уже решено в процессе разбора случая 1! Решение этого неравенства выглядело вот так:

          Осталось лишь пересечь этот интервал с нашим новым условием a<0.

          Пересекаем:

          Вот и второй кусочек ответа готов:

          Кстати сказать, как я узнал, что ноль лежит именно между нашими иррациональными корнями? Легко! Очевидно, что правый корень заведомо положителен. А что касается левого корня, то я просто в уме сравнил иррациональное число

         с нулём. Вот так:

          А теперь объединяем оба найденных интервала. Ибо мы решаем совокупность (а не систему):

         Готово дело. Эти два интервала — это пока ещё только решение неравенства

         Кто забыл, данное неравенство отвечает у нас за расстояние между корнями нашего уравнения. Которое должно больше 3. Но! Это ещё не ответ!

         Ещё у нас есть условие положительного дискриминанта! Неравенство a>-1/2, помните? Это значит, что данное множество нам ещё надо пересечь с условием a>-1/2. Иными словами, теперь мы должны пересечь два множества:

         Но есть одна проблемка. Мы не знаем, как именно расположено на прямой число -1/2 относительно левого (отрицательного) корня. Для этого нам придётся сравнить между собой два числа:

         Поэтому сейчас берём черновик и начинаем сравнивать наши числа. Примерно так:

          Это значит, что дробь -1/2 на числовой прямой находится левее нашего левого корня. И картинка к окончательному ответу задачи будет какая-то вот такая:

          Всё, задача полностью решена и можно записывать окончательный ответ.

          Ответ:

         Ну как? Уловили суть? Тогда решаем самостоятельно.)

         1. Найдите все значения параметра b, при которых уравнение

         ax² + 3x +5 = 0 

         имеет единственный корень.

         2. Найдите все значения параметра а, при каждом из которых больший корень уравнения

         x² — (14a-9)x + 49a² — 63a + 20 = 0

         меньше 9.

         3. Найдите все значения параметра а, при каждом из которых сумма квадратов корней уравнения

         x² — 4ax + 5a = 0

         равна 6.

         4. Найдите все значения параметра а, при каждом из которых уравнение

         x² + 2(a-2)x + a + 3 = 0

         имеет два различных корня, расстояние между которыми больше 3.

          Ответы (в беспорядке):

параметрических уравнений | Алгебра и тригонометрия

Цели обучения

В этом разделе вы:

• Параметризация кривой.
• Удалите параметр.
• Найдите прямоугольное уравнение для параметрической кривой.
• Найдите параметрические уравнения для кривых, заданных прямоугольными уравнениями.

Рассмотрим путь, по которому следует Луна, вращаясь вокруг планеты, которая одновременно вращается вокруг Солнца, как показано на (Рисунок).В любой момент Луна находится в определенном месте относительно планеты. Но как нам написать и решить уравнение для положения Луны, когда расстояние от планеты, скорость орбиты Луны вокруг планеты и скорость вращения вокруг Солнца — все это неизвестны? Мы можем решать только одну переменную за раз.

Рисунок 1.

В этом разделе мы рассмотрим системы уравнений, задаваемые [latex] \, x \ left (t \ right) \, [/ latex] и [latex] \, y \ left (t \ right) \, [/ латекс], где [латекс] t [/ латекс] — независимая переменная времени.Мы можем использовать эти параметрические уравнения в ряде приложений, когда мы ищем не только конкретное положение, но и направление движения. Когда мы отслеживаем последовательные значения [latex] \, t, \, [/ latex], ориентация кривой становится ясной. Это одно из основных преимуществ использования параметрических уравнений: мы можем отслеживать движение объекта по траектории в зависимости от времени. Мы начинаем этот раздел с рассмотрения основных компонентов параметрических уравнений и того, что означает параметризация кривой.Затем мы узнаем, как исключить параметр, преобразовать уравнения кривой, определенной параметрически, в прямоугольные уравнения и найти параметрические уравнения для кривых, определяемых прямоугольными уравнениями.

Параметризация кривой

Когда объект движется по кривой — или криволинейной траектории — в заданном направлении и за заданный промежуток времени, положение объекта в плоскости задается координатой x- и координатой y-. Однако, как [latex] \, x \, [/ latex], так и [latex] \, y \, [/ latex]
изменяются со временем и, следовательно, являются функциями времени.По этой причине мы добавляем еще одну переменную, параметр, от которого оба [latex] \, x \, [/ latex] и [latex] \, y \, [/ latex] являются зависимыми функциями. В примере в открывателе раздела параметром является время, [latex] \, t. \, [/ Latex] [latex] \, x \, [/ latex] положение луны в момент времени, [latex] \ , t, \, [/ latex] представлен как функция [latex] \, x \ left (t \ right), \, [/ latex] и положение [latex] \, y \, [/ latex] луна в момент времени, [латекс] \, t, \, [/ latex] представлена ​​как функция [latex] \, y \ left (t \ right). \, [/ latex] Вместе, [latex] \, x \ left (t \ right) \, [/ latex] и [latex] \, y \ left (t \ right) \, [/ latex] называются параметрическими уравнениями и генерируют упорядоченную пару [latex] \, \ влево (х \ влево (т \ вправо), \, у \ влево (т \ вправо) \ вправо).\, [/ latex] Параметрические уравнения в первую очередь описывают движение и направление.

Когда мы параметризуем кривую, мы переводим одно уравнение с двумя переменными, такими как [latex] \, x \, [/ latex] и [latex] \, y, [/ latex], в эквивалентную пару уравнений в три переменные, [латекс] \, x, y, \, [/ latex] и [latex] \, t. \, [/ latex] Одна из причин, по которой мы параметризуем кривую, заключается в том, что параметрические уравнения дают больше информации: в частности , направление движения объекта во времени.

При графическом отображении параметрических уравнений мы можем наблюдать индивидуальное поведение [latex] \, x \, [/ latex] и [latex] \, y.{2}}. \, [/ Latex] Если построить график [latex] \, {y} _ {1} \, [/ latex] и [latex] \, {y} _ {2} \, [/ latex ] вместе, график не пройдет проверку вертикальной линии, как показано на (Рисунок). Таким образом, уравнение графика круга не является функцией.

Рисунок 2.

Однако, если бы мы построили график для каждого уравнения отдельно, каждое из них прошло бы тест вертикальной линии и, следовательно, представляло бы функцию. В некоторых случаях концепция разделения уравнения для круга на две функции аналогична концепции создания параметрических уравнений, поскольку мы используем две функции для получения нефункции.Это станет яснее по мере нашего продвижения вперед.

Параметрические уравнения

Предположим, [latex] \, t \, [/ latex] — это число на интервале, [latex] \, I. \, [/ Latex] Множество упорядоченных пар, [latex] \, \ left (x \ left (t \ right), \, \, y \ left (t \ right) \ right), \, [/ latex] где [latex] \, x = f \ left (t \ right) \, [/ latex ] и [латекс] \, y = g \ left (t \ right), [/ latex] образует плоскую кривую на основе параметра [latex] \, t. \, [/ latex] Уравнения [latex] \, x = f \ left (t \ right) \, [/ latex] и [latex] \, y = g \ left (t \ right) \, [/ latex] являются параметрическими уравнениями.{2} -1. [/ Латекс]

Попробуйте

Создайте таблицу значений и постройте параметрические уравнения: [латекс] \, x \ left (t \ right) = t-3, \, \, y \ left (t \ right) = 2t + 4; \, \ , \, — 1 \ le t \ le 2. [/ Латекс]

Объект движется с постоянной скоростью по прямому пути [латекс] \, \ left (-5, \, 3 \ right) \, [/ latex] к [latex] \, \ left (3, \, — 1 \ right) \, [/ latex] в одной плоскости за четыре секунды. Координаты измеряются в метрах. Найдите параметрические уравнения для положения объекта.

Параметрические уравнения представляют собой простые линейные выражения, но нам нужно рассматривать эту проблему поэтапно.Значение x объекта начинается с [latex] \, — 5 \, [/ latex] метров и достигает 3 метров. Это означает, что расстояние x изменилось на 8 метров за 4 секунды, что соответствует скорости [latex] \, \ frac {\ text {8 m}} {4 \ text {s}}, [/ latex] или [latex] \, 2 \, \ text {m} / \ text {s}. \, [/ latex] Мы можем записать координату x как линейную функцию относительно времени как [latex] \, x \ left (t \ right) = 2t-5. \, [/ latex] В шаблоне линейной функции [latex] \, y = mx + b, 2t = mx \, [/ latex] и [latex] \, — 5 = Б. [/ латекс]

Точно так же значение y объекта начинается с 3 и переходит в [latex] \, — 1, \, [/ latex], что представляет собой изменение расстояния y на −4 метра за 4 секунды, который представляет собой коэффициент [латекс] \, \ frac {-4 \ text {m}} {4 \ text {s}}, [/ latex] или [латекс] \, — 1 \ text {m} / \ text {s}.\, [/ latex] Мы также можем записать координату y как линейную функцию [latex] \, y \ left (t \ right) = — t + 3. \, [/ latex] Вместе это параметрические уравнения для положения объекта, где [латекс] \, x \, [/ latex]
и [latex] \, y \, [/ latex]
выражаются в метрах, а [latex] \, t \, [/ latex]
представляет время:

[латекс] \ begin {array} {l} x \ left (t \ right) = 2t-5 \ hfill \\ y \ left (t \ right) = — t + 3 \ hfill \ end {array} [/ латекс]

Используя эти уравнения, мы можем построить таблицу значений для [latex] \, t, x, \, [/ latex] и [latex] \, y [/ latex] (см. (Рисунок)).В этом примере мы ограничили значения [latex] \, t \, [/ latex] неотрицательными числами. Как правило, можно использовать любое значение [latex] \, t \, [/ latex].

Из этой таблицы мы можем создать три графика, как показано на (Рисунок).

Рис. 5. (a) График зависимости [латекса] \, x \, [/ latex] от [latex] \, t, \, [/ latex], представляющий горизонтальное положение во времени. (b) График зависимости [латекса] y [/ латекса] от [латекса] \, t, \, [/ latex], представляющий вертикальное положение во времени. (c) График [латекс] \, y \, [/ latex] по сравнению с [latex] \, x, \, [/ latex], представляющий положение объекта в плоскости в момент времени [latex] \, t . [/ латекс]

Анализ

Опять же, мы видим, что на (Рисунок) (c), когда параметр представляет время, мы можем указать движение объекта по пути с помощью стрелок.

Удаление параметра

Во многих случаях у нас может быть пара параметрических уравнений, но оказывается, что проще нарисовать кривую, если уравнение включает только две переменные, такие как [latex] \, x \, [/ latex] и [latex] \ , y. \, [/ latex] Удаление параметра — это метод, который может упростить построение графиков некоторых кривых. Однако, если нас интересует отображение уравнения по времени, тогда также необходимо указать ориентацию кривой. Существуют различные методы исключения параметра [латекс] \, t \, [/ latex] из набора параметрических уравнений; не каждый метод работает для всех типов уравнений.Здесь мы рассмотрим методы для наиболее распространенных типов уравнений.

Исключение параметра из полиномиальных, экспоненциальных и логарифмических уравнений

Для полиномиальных, экспоненциальных или логарифмических уравнений, выраженных в виде двух параметрических уравнений, мы выбираем уравнение, которым легче всего манипулировать, и решаем для [латекс] \, t. \, [/ Латекс] Мы подставляем полученное выражение для [латекс] \ , t \, [/ latex]
во второе уравнение. Это дает одно уравнение в [latex] \, x \, [/ latex] и [latex] \, y.{2} +1 \, [/ latex] и [latex] \, y \ left (t \ right) = 2 + t, \, [/ latex] исключают параметр и записывают параметрические уравнения как декартово уравнение.

Мы начнем с уравнения для [latex] \, y \, [/ latex], потому что линейное уравнение для [latex] \, t решить проще. [/ Latex]

[латекс] \ begin {массив} {l} \, \, \, \, \, \, \, \, \, \, y = 2 + t \ hfill \\ y-2 = t \ hfill \ end {array} [/ latex]

Затем замените [латекс] \, y-2 \, [/ latex] на [латекс] \, t \, [/ latex] в [латекс] \, x \ left (t \ right).{2} -4г + 5. [/ Латекс]

Анализ

Это уравнение параболы, в которой в прямоугольных терминах [латекс] \, x \, [/ latex] зависит от [latex] \, y. \, [/ Latex] От вершины кривой в [latex ] \, \ left (1,2 \ right), \, [/ latex] график выметает вправо. См. (Рисунок). В этом разделе мы рассматриваем системы уравнений, задаваемые функциями [latex] \, x \ left (t \ right) \, [/ latex] и [latex] \, y \ left (t \ right), \, [ / latex], где [latex] \, t \, [/ latex] — независимая переменная времени. Обратите внимание, как [latex] \, x \, [/ latex] и [latex] \, y \, [/ latex] являются функциями времени; так что в целом [латекс] \, y \, [/ latex] не является функцией [latex] \, x.{t} \ hfill \\ y = 3 \ left (\ frac {1} {x} \ right) \ hfill \\ y = \ frac {3} {x} \ hfill \ end {array} [/ latex]

Декартова форма [latex] \, y = \ frac {3} {x}. {2} \, [/ латекс] в [латекс] \, x> 2.{2} \ hfill \\ y \ left (t \ right) = \ mathrm {ln} \, t \, \, \, \, \, \, \, \, t> 0 \ hfill \ end {array} \ end {array} [/ latex]

[латекс] y = \ mathrm {ln} \ sqrt {x} [/ латекс]

Исключение параметра из тригонометрических уравнений

Исключение параметра из тригонометрических уравнений является простой заменой. Мы можем использовать несколько знакомых тригонометрических тождеств и теорему Пифагора.

Сначала мы используем идентификаторы:

[латекс] \ begin {array} {l} x \ left (t \ right) = a \ mathrm {cos} \, t \\ y \ left (t \ right) = b \ mathrm {sin} \, t \ end {array} [/ latex]

Решая для [latex] \, \ mathrm {cos} \, t \, [/ latex] и [latex] \, \ mathrm {sin} \, t, \, [/ latex], получаем

[латекс] \ begin {массив} {l} \ frac {x} {a} = \ mathrm {cos} \, t \\ \ frac {y} {b} = \ mathrm {sin} \, t \ end {array} [/ latex]

Затем используйте теорему Пифагора:

[латекс] {\ mathrm {cos}} ^ {2} t + {\ mathrm {sin}} ^ {2} t = 1 [/ latex]

Замена дает

[латекс] {\ mathrm {cos}} ^ {2} t + {\ mathrm {sin}} ^ {2} t = {\ left (\ frac {x} {a} \ right)} ^ {2} + {\ left (\ frac {y} {b} \ right)} ^ {2} = 1 [/ латекс]

Исключение параметра из пары тригонометрических параметрических уравнений

Удалите параметр из данной пары тригонометрических уравнений, где [latex] \, 0 \ le t \ le 2 \ pi \, [/ latex], и нарисуйте график.

[латекс] \ begin {array} {l} x \ left (t \ right) = 4 \ mathrm {cos} \, t \\ y \ left (t \ right) = 3 \ mathrm {sin} \, t \ end {array} [/ latex]

Решая для [latex] \, \ mathrm {cos} \, t \, [/ latex] и [latex] \, \ mathrm {sin} \, t, [/ latex], получаем

[латекс] \ begin {array} {l} \, x = 4 \ mathrm {cos} \, t \ hfill \\ \ frac {x} {4} = \ mathrm {cos} \, t \ hfill \\ \, y = 3 \ mathrm {sin} \, t \ hfill \\ \ frac {y} {3} = \ mathrm {sin} \, t \ hfill \ end {array} [/ latex]

Затем используйте тождество Пифагора и сделайте замены.{2}} {9} = 1 \, [/ latex] в виде эллипса с центром в [latex] \, \ left (0,0 \ right). \, [/ Latex] Обратите внимание, что когда [latex] \, t = 0 \, [/ latex] координаты: [latex] \, \ left (4,0 \ right), \, [/ latex], а когда [latex] \, t = \ frac {\ pi} {2} \, [/ latex] координаты [latex] \, \ left (0,3 \ right). \, [/ latex] Показывает ориентацию кривой с возрастающими значениями [latex] \, t. [/ латекс]

Попробуйте

Удалите параметр из данной пары параметрических уравнений и запишите как декартово уравнение: [latex] \, x \ left (t \ right) = 2 \ mathrm {cos} \, t \, [/ latex] и [latex ] \, у \ влево (т \ вправо) = 3 \ mathrm {sin} \, т.{2}} {9} = 1 [/ латекс]

Нахождение декартовых уравнений по параметрически определенным кривым

Когда нам дается набор параметрических уравнений и нам нужно найти эквивалентное декартово уравнение, мы, по сути, «исключаем параметр». Однако есть различные методы, которые мы можем использовать, чтобы переписать набор параметрических уравнений в декартово уравнение. Самый простой способ — установить одно уравнение, равное параметру, например [латекс] \, x \ left (t \ right) = t. \, [/ Latex] В этом случае [latex] \, y \ left ( t \ right) \, [/ latex] может быть любым выражением.{2} -3. [/ Латекс]

Нахождение декартова уравнения альтернативными методами

Используйте два разных метода, чтобы найти декартово уравнение, эквивалентное заданному набору параметрических уравнений.

[латекс] \ begin {массив} {l} \\ \ begin {array} {l} x \ left (t \ right) = 3t-2 \ hfill \\ y \ left (t \ right) = t + 1 \ hfill \ end {array} \ end {array} [/ latex]

Метод 1 . Сначала давайте решим уравнение [latex] \, x \, [/ latex] для [latex] \, t. \, [/ Latex]. Затем мы можем подставить результат в уравнение [latex] y [/ latex].

[латекс] \ begin {array} {l} \ text {} x = 3t-2 \ hfill \\ \ text {} x + 2 = 3t \ hfill \\ \ frac {x + 2} {3} = t \ hfill \ end {array} [/ latex]

Теперь подставьте выражение для [latex] \, t \, [/ latex] в уравнение [latex] \, y \, [/ latex].

[латекс] \ begin {array} {l} y = t + 1 \ hfill \\ y = \ left (\ frac {x + 2} {3} \ right) +1 \ hfill \\ y = \ frac { x} {3} + \ frac {2} {3} +1 \ hfill \\ y = \ frac {1} {3} x + \ frac {5} {3} \ hfill \ end {array} [/ latex]

Метод 2 . Решите уравнение [latex] \, y \, [/ latex] для [latex] \, t \, [/ latex] и замените это выражение в уравнение [latex] \, x \, [/ latex].

[латекс] \ begin {массив} {l} \ text {} y = t + 1 \ hfill \\ y-1 = t \ hfill \ end {array} [/ latex]

Сделайте замену и решите [латекс] \, y. [/ Latex]

[латекс] \ begin {array} {l} \ text {} x = 3 \ left (y-1 \ right) -2 \ hfill \\ \ text {} x = 3y-3-2 \ hfill \\ \ текст {} x = 3y-5 \ hfill \\ \, x + 5 = 3y \ hfill \\ \ frac {x + 5} {3} = y \ hfill \\ \ text {} y = \ frac {1} {3} x + \ frac {5} {3} \ hfill \ end {array} [/ latex]

Попробуйте

Запишите данные параметрические уравнения как декартово уравнение: [latex] \, x \ left (t \ right) = {t} ^ {3} \, [/ latex] and [latex] \, y \ left (t \ справа) = {t} ^ {6}.[/ латекс]

Нахождение параметрических уравнений для кривых, определяемых прямоугольными уравнениями

Хотя мы только что показали, что существует только один способ интерпретировать набор параметрических уравнений как прямоугольное уравнение, существует несколько способов интерпретировать прямоугольное уравнение как набор параметрических уравнений. Любая стратегия, которую мы можем использовать для поиска параметрических уравнений, действительна, если она обеспечивает эквивалентность. Другими словами, если мы выберем выражение для представления [latex] \, x, \, [/ latex], а затем подставим его в уравнение [latex] \, y \, [/ latex], и получится тот же график в той же области, что и прямоугольное уравнение, то система параметрических уравнений справедлива.{2} +1 \ hfill \ end {array} [/ latex]

См. (Рисунок).

Рисунок 6.

Ключевые концепции

• Параметризация кривой включает преобразование прямоугольного уравнения с двумя переменными, [latex] \, x \, [/ latex] и [latex] \, y, \, [/ latex] в два уравнения с тремя переменными, x , y и t . Часто больше информации получают из набора параметрических уравнений. См. (Рисунок), (Рисунок) и (Рисунок).
• Иногда уравнения проще изобразить, если они записаны в прямоугольной форме.В результате исключения [latex] \, t, \, [/ latex] получается уравнение в [latex] \, x \, [/ latex] и [latex] \, y \, [/ latex].
• Чтобы исключить [латекс] \, t, \, [/ latex], решите одно из уравнений для [latex] \, t, \, [/ latex] и подставьте выражение во второе уравнение. См. (Рисунок), (Рисунок), (Рисунок) и (Рисунок).
• Нахождение прямоугольного уравнения для параметрической кривой в основном то же самое, что и удаление параметра. Решите относительно [латекс] \, t \, [/ latex] в одном из уравнений и подставьте выражение во второе уравнение.См. (Рисунок).
• Существует бесконечное количество способов выбрать набор параметрических уравнений для кривой, определенной как прямоугольное уравнение.
• Найдите такое выражение для [latex] \, x \, [/ latex], что область определения системы параметрических уравнений остается такой же, как и в исходном прямоугольном уравнении. См. (Рисунок).

Упражнения по разделам

Устный

Что такое система параметрических уравнений?

Пара функций, зависящих от внешнего фактора.Две функции записываются с использованием одного и того же параметра. Например, [латекс] \, x = f \ left (t \ right) \, [/ latex] и [latex] \, y = f \ left (t \ right). [/ Latex]

Некоторые примеры третьего параметра: время, длина, скорость и масштаб. Объясните, когда время используется в качестве параметра.

Объясните, как исключить параметр из набора параметрических уравнений.

Выберите одно уравнение, которое нужно решить для [латекс] \, t, \, [/ latex], замените его в другое уравнение и упростите.

В чем преимущество записи системы параметрических уравнений в виде декартова уравнения?

В чем преимущество использования параметрических уравнений?

Некоторые уравнения нельзя записать в виде функций, например круга. Однако, записанные в виде двух параметрических уравнений, по отдельности уравнения являются функциями.

Почему существует множество наборов параметрических уравнений для представления декартовых функций?

Алгебраические

Для следующих упражнений удалите параметр [latex] \, t \, [/ latex], чтобы переписать параметрическое уравнение как декартово уравнение.{3} -2 [/ латекс]

Для следующих упражнений перепишите параметрическое уравнение как декартово уравнение, построив таблицу [latex] x \ text {-} y [/ latex].

[латекс] \ {\ begin {array} {l} x (t) = 2t-1 \\ y (t) = t + 4 \ end {array} [/ latex]

[латекс] \ {\ begin {array} {l} x (t) = 4-t \\ y (t) = 3t + 2 \ end {array} [/ latex]

[латекс] \ {\ begin {array} {l} x (t) = 2t-1 \\ y (t) = 5t \ end {array} [/ latex]

[латекс] \ {\ begin {array} {l} x (t) = 4t-1 \\ y (t) = 4t + 2 \ end {array} [/ latex]

Для следующих упражнений параметризуйте (напишите параметрические уравнения для) каждое декартово уравнение, задав [latex] x \ left (t \ right) = t [/ latex] или задав [latex] \, y \ left (t \ right ) = t.{2} +3 [/ латекс]

[латекс] y \ left (x \ right) = 2 \ mathrm {sin} \, x + 1 [/ latex]

[латекс] \ {\ begin {array} {l} x (t) = t \ hfill \\ y (t) = 2 \ mathrm {sin} t + 1 \ hfill \ end {array} [/ latex]

[латекс] x \ left (y \ right) = 3 \ mathrm {log} \ left (y \ right) + y [/ latex]

[латекс] x \ влево (y \ вправо) = \ sqrt {y} + 2y [/ латекс]

[латекс] \ {\ begin {array} {l} x (t) = \ sqrt {t} + 2t \ hfill \\ y (t) = t \ hfill \ end {array} [/ latex]

Для следующих упражнений параметризуйте (напишите параметрические уравнения для) каждое декартово уравнение, используя [latex] x \ left (t \ right) = a \ mathrm {cos} \, t [/ latex] и [latex] \, y. \ слева (т \ справа) = Ь \ mathrm {грех} \, т.{2} = 10 [/ латекс]

[латекс] \ {\ begin {array} {l} x (t) = \ sqrt {10} \ mathrm {cos} t \ hfill \\ y (t) = \ sqrt {10} \ mathrm {sin} t \ hfill \ end {array}; \, [/ latex]
Круг

Параметризуйте строку от [latex] \, \ left (3,0 \ right) \, [/ latex] до [latex] \, \ left (-2, -5 \ right) \, [/ latex] так, чтобы линия находится в [latex] \, \ left (3,0 \ right) \, [/ latex] в [latex] \, t = 0, \, [/ latex] и в [latex] \, \ left ( -2, -5 \ right) \, [/ latex] at [latex] \, t = 1. [/ Latex]

Параметризуйте строку от [latex] \, \ left (-1,0 \ right) \, [/ latex] до [latex] \, \ left (3, -2 \ right) \, [/ latex] так, чтобы линия находится в [latex] \, \ left (-1,0 \ right) \, [/ latex] в [latex] \, t = 0, \, [/ latex] и в [latex] \, \ left (3, -2 \ справа) \, [/ латекс] в [латекс] \, t = 1.[/ латекс]

[латекс] \ {\ begin {array} {l} x (t) = — 1 + 4t \ hfill \\ y (t) = — 2t \ hfill \ end {array} [/ latex]

Параметризуйте строку от [latex] \, \ left (-1,5 \ right) \, [/ latex] до [latex] \, \ left (2,3 \ right) [/ latex] так, чтобы линия была в [латекс] \, \ влево (-1,5 \ вправо) \, [/ латекс] в [латекс] \, t = 0, \, [/ латекс] и в [латекс] \, \ влево (2, 3 \ right) \, [/ latex] at [latex] \, t = 1. [/ Latex]

Параметрируйте строку от [latex] \, \ left (4,1 \ right) \, [/ latex] до [latex] \, \ left (6, -2 \ right) \, [/ latex] так, чтобы линия находится в [latex] \, \ left (4,1 \ right) \, [/ latex] в [latex] \, t = 0, \, [/ latex] и в [latex] \, \ left (6 , -2 \ справа) \, [/ латекс] в [латекс] \, t = 1. {2} \ hfill \\ {y} _ {1} (t) = 2t-1 \ hfill \ end {array} \ text {and} \ {\ begin {array} {l} {x} _ {2} (t) = — t + 6 \ hfill \\ {y} _ {2} (t ) = t + 1 \ hfill \ end {array} [/ latex]

да, при [латексе] t = 2 [/ латексе]

В следующих упражнениях воспользуйтесь графическим калькулятором, чтобы заполнить таблицу значений для каждого набора параметрических уравнений.{2} -1 \ hfill \ end {array} [/ latex]

[латекс] \ {\ begin {array} {l} {x} _ {1} (t) = {t} ^ {4} \ hfill \\ {y} _ {1} (t) = {t} ^ {3} +4 \ hfill \ end {array} [/ latex]

параметр

переменная, часто представляющая время, от которого зависят [latex] \, x \, [/ latex] и [latex] \, y \, [/ latex].

Решение уравнений с параметрами

Творческое образование
Vol.5 No 11 (2014), статья ID: 47178,6 страницы DOI: 10.4236 / ce.2014.511110

Решение уравнений с параметрами

Бат-Шева Иланы ¹ , Дина Хасидов ²

¹ Колледж Бейт-Берл, Кфар-Саба, Израиль

² Колледж Западной Галилеи, Акко, Израиль

Электронная почта: bat77i @ gmail.com, [email protected]

Авторские права © 2014 авторов и Scientific Research Publishing Inc.

Эта работа находится под лицензией Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Поступило 23.04.2014 г .; пересмотрена 16 мая 2014 г .; принята к печати 6 июня 2014 г.

РЕФЕРАТ

В этом исследовании изучается, как старшеклассники и учителя решают уравнения, которые представлены различными способами.Некоторые презентации нестандартны, например, необходимо выразить «а» (обычно воспринимаемое как параметр) через «х» (обычно воспринимаемое как переменная). Мы исследуем, как испытуемые решают эти уравнения, а также исследуем различия между учениками и учениками-учителями. Наши результаты показывают, что уравнения, содержащие параметры, труднее решить, чем уравнения без параметров. Трудности связаны с буквами, которые следует выражать, и с расположением уравнения.Результаты этого исследования могут расширить знания учителей о уравнениях с параметрами и о конкретных трудностях, с которыми студенты сталкиваются в процессе решения.

Ключевые слова: Уравнения, Параметры, Ученики старших классов, Студенты-учителя, Математическое образование, Математические знания, Познание и математика

1. Теоретическая основа

«Проблемы с параметрами проверяют знания решателя в математике и выявляют его. слабые места »(Седивы, 1976).Седивый также утверждает, что ученики сталкиваются с большими трудностями с уравнениями с параметрами, чем с уравнениями с числовыми коэффициентами. Алгебраические уравнения, содержащие параметры, представляют собой более широкие классы уравнений и более общие формы количественных соотношений по сравнению с уравнениями без параметров.

Дэвис и Хенкин (1978) писали о важности квадратных уравнений в целом и с параметрическими коэффициентами в частности. Они описывают, как они интерпретируют понимание квадратных уравнений.Они предоставляют длинный список навыков, а также математические знания, необходимые для понимания и решения квадратных уравнений. Дэвис и Хенкин утверждают, что понимание и решение уравнений с параметрами улучшает понимание учащимися уравнений в целом.

Скемп (1987) утверждает, что правила обучения без причины позволяют ученику функционировать только в узких рамках и иметь дело только со стандартными задачами. Однако такой подход ограничивает понимание учащимися, и они не смогут справиться с более сложными задачами.Понимание позволяет ученику решать нестандартные задачи, которые нельзя решить механическим применением формул. Fischbein и Muzicant (2002) указывают, что ученики обучались в основном процедурным образом, и поэтому они часто не могут различать концептуальные и процедурные знания. Многим ученикам трудно распознать, что буква представляет собой число, и они не знают, как работать с символическими значениями (Kieran, 1992, 2014).

Широко признано, что учителям важно осознавать, как их ученики воспринимают математические темы, в частности, конкретные причины совершения ошибок (Almog & Ilany, 2012).

На начальных курсах студенты привыкают к тому, что x (а позже y и z) являются переменными, а буквы, такие как a, b, c, являются константами или параметрами. Однако на более продвинутых курсах они сталкиваются с вопросами, в которых буквы используются по-другому, и это очень сбивает их с толку. Например, задачи интеграции, где x фиксировано, а y — переменная. Или объемные вопросы, где a, b, c используются в качестве переменных.

Ученики решают в школе бесчисленные упражнения с уравнениями, в которых буква x представляет собой переменную, которая должна быть выражена буквами a, b, c и т. Д. В этом исследовании испытуемым предлагалось множество уравнений с нестандартным представлением. , как уже упоминалось выше.

2. Цель

Цели исследования — изучить и выявить трудности старшеклассников и старших школьных учителей при решении уравнений с параметрами. Кроме того, выяснить, есть ли существенные различия между учениками и учениками-учителями в решении таких уравнений. Какие процедуры используются и какие трудности возникают при решении уравнений с параметрами.

3. Вопросы для исследования

1) Как испытуемые решают уравнения с параметрами, в которых они должны выражать различные буквы через другие буквы и параметры? В частности, когда уравнения не построены стандартным образом.

2) Есть ли различия между учениками и студентами-учителями в том, как они решают такие уравнения. И если да, то в чем отличия.

Примеры уравнений, исследованных в статье (нумерация вопросов соответствует нумерации вопросов в анкете):

• Вопрос 16: Найдите x (в терминах a) в (довольно стандартном уравнении с переменной x и параметром a).

• Вопрос 1. Найдите c (через x) в (менее стандартно, поскольку требуется выражать c через x).

• Вопрос 9: Найдите b (в терминах x) в (менее стандартно, так как требуется переставить уравнение «должным образом», а затем выразить b через x).

• Вопрос 21: Следующее уравнение линейно по x, хотя может ошибочно показаться квадратным уравнением в терминах a :.

Мы называем знания, необходимые для решения простых уравнений, процедурными. Уравнения с нестандартными представлениями требуют более гибкого подхода.

4.Метод

Исследуемая выборка состояла из 115 учителей математики на третьем и четвертом году обучения и 133 учеников двенадцатых классов с высшим уровнем математики (5 курсов математики) в четырех средних школах.

Инструменты. Для исследования был разработан вопросник, который был разослан обеим группам. Часть анкеты состоит из шести вопросов, которые включают уравнения с параметрами. В этом исследовании сообщается о результатах двух вопросов уравнений первой степени (вопросы (5) и (21)) и трех вопросов уравнений второй степени (вопросы 16, 1 и 9).Вопросы перечислены в Таблице 1 и Таблице 3

Процедура: Чтобы понять процесс решения предметов, были опрошены пять учеников и шесть студентов-учителей. Вопросы для интервью были разработаны после заполнения и анализа анкеты. Цель заключалась в том, чтобы прояснить и продвинуть результаты анкеты. Кроме того, были проведены открытые наблюдения, чтобы внимательно изучить ответы испытуемых.

Таблица 1. Вопросы 5 и 21, анализ результатов (уравнения первой степени с параметрами).

Примечание: (P = ученики, S.T. = ученики-учителя). ^* Испытуемые правильно выразили x, но некоторые из них не смогли указать допустимый домен, а затем упростить выражение. См. Подробности в таблице 2.

Анализ данных: количественный анализ проводился с помощью описательной статистики (таблицы, в которых указан процент успеха), c ² тестов и t-тестов. Качественный анализ проводился путем наблюдений и интервью, как упоминалось выше.Затем результаты были проанализированы в соответствии с новыми критериями.

5. Результаты

Результаты уравнений первой степени5 и 21 представлены в Таблице 1

Таблица 1 показывает, что большой процент старшеклассников (22%) не ответили на вопрос 21. Очень небольшой процент испытуемых. кто правильно выразил x через a, также указал правильную область решения. Некоторые испытуемые справлялись только со стандартными вопросами, которые требовали прямого подхода.В целом, только 36% учеников и 73% студентов-учителей ответили на вопрос 21 полностью.

В вопросе 5 испытуемых попросили выразить буквенное значение x. m — буква, которая обычно воспринимается как параметр (Ilany, 1997, 1998). В этом вопросе есть уравнение первой степени, для которого процесс решения должен быть простым, но только 67% учеников дали правильный ответ и 29% ошиблись. Мы утверждаем, что ошибки происходят из-за путаницы, связанной с нестандартным использованием параметров и переменных (примеры приведены ниже).Для студентов-преподавателей ситуация была лучше, 88% решили правильно и 10% допустили ошибки, связанные с нестандартной презентацией.

В вопросе 21 уравнение имеет первую степень по x, и x нужно было выразить через a. Такое представление уравнения было связано с различными ошибками в процессе решения испытуемых, поскольку x обычно воспринимается как переменная (Ilany, 1997). Стоит отметить, что уравнение 21 на самом деле линейно по x, поскольку x является переменной первой степени.Однако из-за ² в уравнении некоторые студенты были сбиты с толку и восприняли уравнение как квадратное.

Чтобы решить указанное выше уравнение, необходимо раскрыть скобки, собрать похожие выражения и переставить уравнение. Существует ограничение на a (a ≠ −1), и для решения уравнения требуется несколько алгебраических операций. Многочисленные ошибки были допущены испытуемыми, которые пытались решить этот вопрос, особенно учениками. Только 36% учеников правильно ответили на x.То есть они обнаружили, что:

Однако большинство студентов, которые правильно выразили x, не смогли указать допустимую область и упростить полученное уравнение (см. Таблицу 2).

У студентов-преподавателей ситуация была лучше: 73% из них правильно ответили на вопрос 21. Анализ ошибок показал, что 41% учеников по сравнению с 14% студентов-учителей допустили ошибки, связанные с «нестандартными» буквами (см. Таблицу 1).

Мы решили изучить три уравнения второй степени в этом исследовании.В каждом уравнении требуется выразить одну букву другой. Ошибки были разделены на два типа: ошибки в вычислениях и ошибки, возникающие из-за путаницы, связанной с незнакомым использованием букв: игнорирование букв, поиск неправильной буквы и круговое выражение букв. (Примеры будут приведены в Таблице 3: вопросы 16, 1 и 9).

Согласно Таблице 3, высокий процент учеников (16%) не ответили на вопрос 9. Наблюдалась значительная разница между учениками-учителями и учениками старших классов по всем трем вопросам.Три уравнения имеют аналогичную структуру (Таблица 3). Разница между ними состоит в том, что в вопросе 16 (5x ² + 8ax + 4a ² = 0) необходимо найти x, буква воспринимается как переменная согласно Илани (1997, 1998), а в другом уравнения

Таблица 2. Вопрос 21 — Субъекты, которые правильно выразили x (некоторые из них не завершили процесс).

Примечание: (P = ученики, S.T. = ученики-учителя).

Таблица 3.Вопросы 16, 1 и 9, анализ результатов.

Примечание: (P = ученики, S.T. = ученики-учителя).

буквы, которые должны быть найдены: b или c. Эти буквы обычно воспринимаются как параметры, поэтому вызывали путаницу.

Результаты показывают, что больше студентов ответили на вопрос 16 правильно по сравнению с вопросами 1 и 9 (см. Таблицу 3), которые касаются вопроса исследования 1. (То есть решатели имеют тенденцию путаться, когда требуется выразить a, b, c или m (обычно функционируют как параметры) в терминах x (который обычно обозначает переменную).

Было обнаружено существенное различие между учениками-учителями и учениками в двух отношениях. Начнем с того, что студенты-преподаватели набрали больше баллов по всем вопросам. Кроме того, меньшая часть студентов-учителей, похоже, была сбита с толку из-за изменения и перестановки переменных (70% учеников правильно ответили на вопрос 16 по сравнению с 28% на вопрос 9; соответствующие цифры для студентов-учителей составляют 88% против 43%. ).

В таблице 3 представлены три вопроса схожей структуры.Первый вопрос (16) довольно стандартный (выражение x через другие параметры).

Во втором вопросе (1) у нас нестандартное использование букв (выражение x через c).

Третий вопрос также связан с нестандартным использованием переменных, поскольку b должно быть выражено через x. Более того, вам нужно переставить уравнение, чтобы его решить.

Сравнение результатов вопросов 9 и 1 подчеркивает важность построения уравнения.В вопросе 9 уравнение () похоже на уравнение в вопросе 1 (), но не упорядочено в обычном порядке, то есть сначала записываются более высокие показатели. Здесь мы получили самые низкие результаты (только 28% учеников и 43% студентов-учителей правильно решили уравнение). Причины этих результатов объясняются сложностью составления уравнения и нахождения нестандартной буквы b через x.

Вопрос 1 также обсуждался в интервью. Интервьюер подчеркнул, что b или c необходимо выражать через x.Несмотря на это, большинство респондентов выразили x через b или c. Один собеседник, допустивший эту ошибку, сказал: «Даже если вы не хотите x, вам нужно b, я автоматически нахожу x, потому что это квадратное уравнение». Она попыталась выразить b, сказав: «Я не могу найти b, я знаю, что есть два решения, потому что D> 0, но я не могу его найти, я думаю, что это невозможно». В конце интервью мы вернулись к вопросу. На этот раз мы переписали уравнение как:, и респондент без труда выразил b через x.Другими словами, студентке было трудно даже начать процесс решения, когда она сталкивалась с нестандартным расположением и буквами, хотя у нее не было технических трудностей, решая такие уравнения после того, как они были правильно переставлены. Тот же ученик-учитель сумел перестроить и успешно решить «неаккуратное» уравнение, в котором x нужно было выразить через b, то есть стандартное использование букв. После интервью она сказала: «Отныне я буду просить своих учеников выражать разные буквы, не обязательно в обычном порядке».

Интересно отметить, что изменение уравнения в вопросе 9 — это один из способов его решения. Другой способ — поменять местами буквы, то есть поменять местами x и b, найти x, а затем снова поменять местами буквы. Ни один из испытуемых не применил этот метод.

Примеры ошибок, вызванных использованием нестандартных букв в приведенных выше вопросах:

На вопрос 1 правильный ответ :. В этом случае некоторым участникам было трудно принять «незавершенное решение», даже несмотря на то, что это выражение нельзя упростить дальше, за исключением того, что область должна быть указана.

Следовательно, некоторые испытуемые, решившие вопрос правильно, не удовлетворились своим ответом и перечеркнули его. Однако мы действительно сочли скрещенные решения правильными.

Связанная ошибка заключалась в выражении x вместо c (2% студентов-учителей).

«Вы не можете найти c, поскольку это параметр» (5% студентов-преподавателей).

«c — параметр, поэтому может быть любым числом».

Интересная ошибка в вопросе 16 заключалась в том, что при получении правильных ответов в них отсутствовала буква «а».То есть ученик написал:

Аналогичная ошибка смешивала «x» и «a»:

Примеры ошибок в вопросе 9: поиск x вместо b (11% учеников, 5% ученики учителей).

Выражение b через b. (6% учеников, 10% студентов-учителей):

Аналогичным образом, в вопросе 21 4% старшеклассников выразили x через x, например:

Примеры ошибок, допущенных при попытке для решения:

«Невозможно выразить x самостоятельно.

«Не знаю» (32% студентов, 5% студентов преподавателей).

Превратите x в x ² (6% студентов, 2% студентов-преподавателей).

Выражается a вместо x (3% студентов).

Примеры ошибок, которые произошли при попытке решить вопрос 5: Найдите m в:

Найдено x (3% студентов).

«Невозможно» (10% студентов, 7% студентов-преподавателей).

Превратил уравнение в квадратное уравнение для m (3% студентов).

6. Обсуждение

Результаты этого исследования показывают, что для уравнений с параметрами большой процент студентов-учителей и еще большая доля учеников ошиблись из-за путаницы, связанной с нестандартным использованием букв (например, необходимо выразить a через x). Столкнувшись с уравнениями, в которых параметры и переменные не были расположены стандартным образом, испытуемым было еще труднее решить эти уравнения.

В общем, уравнения, содержащие параметры, труднее решить, чем уравнения без параметров.Испытуемые склонны решать уравнения механически, и поэтому они совершают множество ошибок, когда сталкиваются с нестандартными вопросами, требующими более глубокого понимания.

Ключевыми факторами, которые часто создают проблемы для студентов, являются тип буквы, которую нужно выразить, порядок решаемого уравнения, мощность переменной, мощность параметра и тип требуемых алгебраических методов. .

Значение для обучения решению уравнений с параметрами Результаты этого исследования, в частности большое количество ошибок, поднимают вопросы относительно эффективности преподавания этой темы.Следовательно, чтобы улучшить понимание учащимися уравнений с параметрами, рекомендуется улучшить понимание учащимися использования букв в таких уравнениях. Например, внимательно прочитав то, что требуется в вопросе, приняв более гибкий подход в отношении того, какие буквы могут быть выражены в терминах других букв, убедившись, что выражение упрощено должным образом, и зная о различия и сходства между уравнениями с параметрами или без них.

Мы рекомендуем включать в школьную программу математики больше уравнений с различными параметрами и переменными, а также уравнения, которые представлены не в обычном порядке. Это побудит учащихся глубже задуматься над темой и получить более глубокое понимание.

Ссылки

1. Almog, N., & Ilany, B.-S. (2012). Абсолютное неравенство ценностей: решения и заблуждения старшеклассников. Образовательные исследования по математике, 81 , 347-364.http://dx.doi.org/10.1007/s10649-012-9404-z
2. Дэвис Р. Б. и Хенкин Л. (1978). Неадекватно проверенные аспекты изучения математики — тестирование, преподавание и обучение . Отчет о конференции по исследованиям в области тестирования, Национальный институт образования, 49-63.
3. Fischbein, E., & Muzicant, B. (2002). Ричард Скемп и его концепция реляционного и инструментального понимания: открытые предложения и открытые фразы. В Д. Толл и М. Томас (ред.), Интеллект, обучение и понимание в математике: дань уважения Ричарду Скемпу (стр.49-77). Flaxton, QLD: Post Pressed Publishers.
4. Илани Б. (1998). Неуловимый параметр. В 23-е ежегодное собрание Международной группы психологии математического образования (том 4, стр. 265). Стелленбос: Стелленбосский университет.
5. Илани Б. (1997). Концепции переменных и параметров для учителей и учеников старших классов . Докторская диссертация, Тель-Авив: Тель-Авивский университет. (на иврите)
6. Киран, К. (1992).Изучение и преподавание школьной алгебры. В Д. А. Гроуза (ред.), Справочник по исследованиям в области преподавания и обучения математике (стр. 390-419).
7. Киран, К. (2014). Преподавание и изучение алгебры. Энциклопедия математического образования (стр. 27-32). Springer: Ссылка на Springer.
8. Седивий Дж. (1976). Примечание о роли параметров в обучении математике. Образовательные исследования по математике, 7 , 121-126. http://dx.doi.org/10.1007/BF00144365
9. Скемп Р.(1987). Психология изучения математики . Хиллсдейл, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс.

Решатель уравнений и систем — MATLAB решает

(PDF) Решение уравнений с параметрами

Б.-С. Илани, Д. Хасидов

Скемп (1987) утверждает, что правила обучения без причины позволяют ученику функционировать только в узких рамках

и иметь дело только со стандартными задачами.Однако такой подход ограничивает понимание учащимися, и они не смогут справиться с более сложными задачами. Понимание позволяет ученику решать

нестандартных задач, которые не могут быть решены механическим применением формул. Fischbein и Muzicant

(2002) указывают на то, что ученики обучались в основном процедурным образом и, следовательно, они часто не различают

концептуальных и процедурных знаний. Многие ученики затрудняются распознать, что буква представляет собой число

, и не знают, как работать с символическими значениями (Kieran, 1992, 2014).

Широко признано, что учителям важно осознавать, как их ученики воспринимают математические темы

, в частности, конкретные причины совершения ошибок (Almog & Ilany, 2012).

На начальных курсах студенты привыкают к тому, что x (а позже y и z) являются переменными, а буквы, такие как a, b, c

, являются константами или параметрами. Однако на более продвинутых курсах они сталкиваются с вопросами, в которых буквы

используются по-другому, и они находят это очень запутанным.Например, задачи интеграции, где x фиксировано, а y равно

переменной. Или объемные вопросы, где a, b, c используются в качестве переменных.

Ученики решают в школе бесчисленные упражнения с уравнениями, в которых буква x представляет собой переменную, которая должна быть выражена

буквами a, b, c и т. Д. В этом исследовании испытуемым предлагалось множество уравнений с

нестандартная подача, о чем говорилось выше.

2. Цель

Цели исследования — изучить и выявить трудности старшеклассников и старшеклассников

учителей при решении уравнений с параметрами.Кроме того, выяснить, есть ли существенные различия между

учениками и студентами-учителями в отношении решения таких уравнений. Какие процедуры используются и какие трудности возникают при решении уравнений с параметрами.

3. Вопросы для исследования

1) Как испытуемые решают уравнения с параметрами, в которых они должны выражать различные буквы через

других букв и параметров? В частности, когда уравнения не построены стандартным образом.

2) Есть ли различия между учениками и студентами-учителями в том, как они решают такие уравнения.

И если да, то в чем отличия.

Примеры уравнений, исследованных в статье (нумерация вопросов соответствует нумерации вопросов

анкеты):

• Вопрос 16: Найдите x (через a) в

(довольно стандартное уравнение с переменной x и

параметр a).

• Вопрос 1. Найдите c (в терминах x) в

(менее стандартно, поскольку требуется выразить c в терминах

x).

• Вопрос 9: Найдите b (в терминах x) в

(менее стандартно, поскольку требуется переставить уравнение

«правильно», а затем выразить b через x).

• Вопрос 21: Следующее уравнение линейно по x, хотя может ошибочно показаться квадратичным уравнением

в терминах a:

()

2

11 2a xx ax− + = −−

.

Мы называем знания, необходимые для решения простых уравнений, процедурными.Уравнение

с нестандартными презентациями требует более гибкого подхода.

4. Метод

Исследуемая выборка состояла из 115 учителей математики на третьем и четвертом году обучения и

133 учеников двенадцатых классов с высшим уровнем математики (5 единиц математического направления) в четырех средних школах.

Инструменты. Для исследования был разработан вопросник, который был разослан обеим группам. Часть анкеты

состоит из шести вопросов, которые включают уравнения с параметрами.Это исследование сообщает о результатах

двух вопросов уравнений первой степени (вопросы (5) и (21)) и трех вопросов уравнений второй степени

(вопросы 16, 1 и 9). Вопросы перечислены в Таблице 1 и Таблице 3.

Процедура: Чтобы понять процесс решения предметов, были просмотрены пять учеников и шесть студентов-учителей. Вопросы для интервью были разработаны после заполнения и анализа анкеты. Целью

было прояснить и продвинуть результаты анкеты.Кроме того, были проведены открытые наблюдения в

, чтобы внимательно изучить ответы испытуемых.

Метод изменения параметров

Эта страница посвящена дифференциальным уравнениям второго порядка этого типа:

d ² y dx ² + P (x) dy dx + Q (x) y = f (x)

где P (x), Q (x) и f (x) — функции от x.

Более простой случай, когда f (x) = 0:

d ² y dx ² + P (x) dy dx + Q (x) y = 0

является «однородным» и объясняется во введении в дифференциальные уравнения второго порядка.Пожалуйста, сначала изучите этот метод, чтобы помочь вам понять эту страницу.

Два метода

Существует два основных метода решения уравнений, например

d ² y dx ² + P (x) dy dx + Q (x) y = f (x)

Undetermined Coefficients, который работает только тогда, когда f (x) является полиномом, экспонентой, синусом, косинусом или их линейной комбинацией.

Варианты параметров (которые мы узнаем здесь), который работает с широким спектром функций, но немного беспорядок в использовании.

Изменение параметров

Для простоты рассмотрим только корпус:

d ² y dx ² + p dy dx + qy = f (x)

Полное решение такого уравнения можно найти сочетая два типа решения:

1. Общее решение однородное уравнение d ² y dx ² + p dy dx + qy = 0
2. Частные решения неоднородное уравнение d ² y dx ² + p dy dx + qy = f (x)

Обратите внимание, что f (x) может быть одной функцией или суммой двух или более функции.

Как только мы нашли общее решение и все частные решений, то окончательное полное решение находится путем добавления всех решения вместе.

Этот метод основан на интеграции.

Проблема с этим методом заключается в том, что, хотя он может дать решение, в некоторых случаях решение необходимо оставить в виде интеграла.

Начните с общего решения

При введении в дифференциальные уравнения второго порядка мы узнаем, как найти общее решение.

В основном мы берем уравнение

d ² y dx ² + p dy dx + qy = 0

и свести его к «характеристическому уравнению»:

р ² + пр + д = 0

Квадратное уравнение, которое имеет три возможных типа решения в зависимости от дискриминанта p ² — 4q . Когда p ² — 4q равно

положительный получаем два действительных корня, и решение равно

y = Ae ^{r ₁ x} + Be ^{r ₂ x}

ноль получаем один действительный корень, а решение —

y = Ae ^rx + Bxe ^rx

отрицательный получаем два комплексных корня r ₁ = v + wi и r ₂ = v — wi , и решение равно

y = e ^vx (Ccos (wx) + iDsin (wx))

Фундаментальные решения уравнения

Во всех трех случаях «y» состоит из двух частей:

• y = Ae ^{r ₁ x} + Be ^{r ₂ x} состоит из y ₁ = Ae ^{r ₁ x} и y ^{_{10 = r 2 x}}
• y = Ae ^rx + Bxe ^rx состоит из y ₁ = Ae ^rx и y ₂ = Bxe ^rx
• y = e ^vx (Ccos (wx) + iDsin (wx)) состоит из y ₁ = e ^vx Ccos (wx) и y ₂ = e ^vx iDsin (шх)

y ₁ и y ₂ известны как фундаментальные решения уравнения

И y ₁ и y ₂ называются линейно независимый , потому что ни одна из функций не является постоянным кратным Другие.

Вронскианец

Когда y ₁ и y ₂ являются двумя фундаментальными решениями однородного уравнения

d ² y dx ² + p dy dx + qy = 0

, то вронскиан W (y ₁ , y ₂ ) является определяющим матрицы

Так

W (y ₁ , y ₂ ) = y ₁ y ₂ ‘ — y ₂ y ₁ ‘

Вронскиан назван в честь польского математика и философ Юзеф Хене-Вронский (1776–1853).

Поскольку y ₁ и y ₂ линейно независимы, значение вронскиана не может равняться нулю.

Особое решение

Используя вронскиан, мы можем теперь найти частное решение дифференциального уравнения

d ² y dx ² + p dy dx + qy = f (x)

по формуле:

y _p (x) = −y ₁ (x) ∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx + y ₂ (x) ∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx

Пример 1: Решить

1.Найдите общее решение для d ² y dx ² — 3 dy dx + 2y = 0

Характеристическое уравнение: r ² — 3r + 2 = 0

Фактор: (r — 1) (r — 2) = 0

r = 1 или 2

Итак, общее решение дифференциального уравнения y = Ae ^x + Be ^2x

Итак, в этом случае фундаментальные решения и их производные:

y ₁ (x) = e ^x

y _{1 916 10 ‘(x) = e ^x}

y ₂ (x) = e ^2x

y _{2 916 10 ‘(x) = 2e ^2x}

2.Найдите вронскианца:

W (y ₁ , y ₂ ) = y ₁ y ₂ ‘ — y ₂ y ₁ ‘= 2e ^3x — e ^3x = e ^3x

3. Найдите конкретное решение по формуле:

y _p (x) = −y ₁ (x) ∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx + y ₂ (x) ∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx

4.Сначала решаем интегралы:

∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx

= ∫e ^2x dx

= 1 2e ^2x

Итак:

−y ₁ (x) ∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx = — (e ^x ) ( 1 2e ^2x ) = — 1 2e ^3x

А также:

∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx

= ∫e ^x dx

= e ^x

Итак:

y ₂ (x) ∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx = (e ^2x ) (e ^x ) = e ^3x

Наконец:

y _p (x) = −y ₁ (x) ∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx + y ₂ (x) ∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx

= — 1 2e ^3x + e ^3x

= 1 2e ^3x

и полное решение дифференциального уравнения d ² y dx ² — 3 dy dx + 2y = e ^3x is

y = Ae ^x + Be ^2x + 1 2e ^3x

Что выглядит следующим образом (примеры значений A и B):

Пример 2: Решить

Характеристическое уравнение: r ² — 1 = 0

Фактор: (r — 1) (r + 1) = 0

r = 1 или −1

Итак, общее решение дифференциального уравнения: y = Ae ^x + Be ^−x

Итак, в этом случае фундаментальные решения и их производные:

y ₁ (x) = e ^x

y _{1 916 10 ‘(x) = e ^x}

y ₂ (x) = e ^−x

y ₂ ‘(x) = −e ^−x

2.Найдите вронскианца:

W (y ₁ , y ₂ ) = y ₁ y ₂ ‘ — y ₂ y ₁ ‘= −e ^x e ^−x — e ^x e ^−x = −2

3. Найдите конкретное решение по формуле:

y _p (x) = −y ₁ (x) ∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx + y ₂ (x) ∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx

4.Решите интегралы:

∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx

= — 1 2 ∫ (2x ² −x − 3) e ^−x dx

= — 1 2 [- (2x ² −x − 3) e ^−x + ∫ (4x − 1) e ^−x dx]

= — 1 2 [- (2x ² −x − 3) e ^−x — (4x — 1) e ^−x + ∫4e ^−x dx ]

= — 1 2 [- (2x ² −x − 3) e ^−x — (4x — 1) e ^−x — 4e ^−x ]

= e ^−x 2 [2x ² — x — 3 + 4x −1 + 4]

= e ^−x 2 [2x ² + 3x]

Итак:

−y ₁ (x) ∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx = (−e ^x ) [ e ^−x 2 ( 2x ² + 3x)] = — 1 2 (2x ² + 3x)

А этот:

∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx

= — 1 2 ∫ (2x ² −x − 3) e ^x dx

= — 1 2 [(2x ² −x − 3) e ^x — ∫ (4x − 1) e ^x dx]

= — 1 2 [(2x ² −x − 3) e ^x — (4x — 1) e ^x + ∫4e ^x dx ]

= — 1 2 [(2x ² −x − 3) e ^x — (4x — 1) e ^x + 4e ^x ]

= −e ^x 2 [2x ² — x — 3 — 4x + 1 + 4]

= −e ^x 2 [2x ² — 5x + 2]

Итак:

y ₂ (x) ∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx = (e ^−x ) [ −e ^x 2 ( 2x ² — 5x + 2)] = — 1 2 ( 2x ² — 5x + 2)

Наконец:

y _p (x) = −y ₁ (x) ∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx + y ₂ (x) ∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx

= — 1 2 (2x ² + 3x) — 1 2 (2x ² — 5x + 2)

= — 1 2 (4x ² — 2x + 2)

= −2x ² + x — 1

и полное решение дифференциального уравнения d ² y dx ² — y = 2x ² — x — 3 равно

y = Ae ^x + Be ^−x — 2x ² + x — 1

(Это тот же ответ, который мы получили в Примере 1 на странице Метод неопределенных коэффициентов.)

Пример 3: Решить

Характеристическое уравнение: r ² — 6r + 9 = 0

Фактор: (r — 3) (r — 3) = 0

г = 3

Итак, общее решение дифференциального уравнения: y = Ae ^3x + Bxe ^3x

Итак, в этом случае фундаментальные решения и их производные:

y ₁ (x) = e ^3x

y _{1 916 10 ‘(x) = 3e ^3x}

y ₂ (x) = xe ^3x

y _{2 916 10 ‘(x) = (3x + 1) e ^3x}

2.Найдите вронскианца:

W (y ₁ , y ₂ ) = y ₁ y ₂ ‘ — y ₂ y ₁ ‘= (3x + 1) e ^3x e ^3x — 3xe ^3x e ^3x = e ^6x

3. Найдите конкретное решение по формуле:

y _p (x) = −y ₁ (x) ∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx + y ₂ (x) ∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx

4.Решите интегралы:

∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx

= ∫e ^−3x dx

= — 1 3e ^−3x

Итак:

−y ₁ (x) ∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx = — (e ^3x ) (- 1 3e ^−3x ) = 1 3

А этот:

∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx

= ∫e ^−3x x ⁻¹ dx

Это не может быть интегрировано, поэтому это пример, когда ответ оставить как интеграл.

Итак:

y ₂ (x) ∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx = (xe ^3x ) (∫e ^−3x x ⁻¹ dx ) = xe ^3x ∫e ^−3x x ⁻¹ dx

Наконец:

y _p (x) = −y ₁ (x) ∫ y ₂ (x) f (x) W (y ₁ , y ₂ ) dx + y ₂ (x) ∫ y ₁ (x) f (x) W (y ₁ , y ₂ ) dx

= 1 3 + xe ^3x ∫e ^−3x x ⁻¹ dx

Итак, полное решение дифференциального уравнения d ² y dx ² -6 dy dx + 9y = 1 x равно

y = Ae ^3x + Bxe ^3x + 1 3 + xe ^3x ∫e ^−3x x ⁻¹ dx

Пример 4 (более сложный пример): Решить