РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ — Студопедия
Задача 1. В течение 300 дней фиксировалась цена акции ООО «Мир окон». Затем была проведена случайная выборка объёмом n=20, и получены следующие результаты: 35,9; 35,3; 42,7; 45,3; 25,6; 35,3; 33,4; 27,0; 35,9; 38,8; 33,7; 38,6; 40,8; 35,5; 44,1; 37,4; 34,2; 30,8; 38,4; 31,3.
Требуется получить вариационный ряд и построить гистограмму относительных частот; найти основные выборочные характеристики: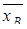 
, 
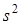, s, 
, 
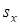; с надежностью 
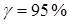указать доверительный интервал для оценки генеральной средней
Решение. Запишем исходные данные в виде ранжированного ряда, то есть, располагая их в порядке возрастания: 25,6; 27,0; 30,8; 31,3; 33,4; 33,7: 34,2; 35,3; 35,3; 35,5; 35,9; 35,9; 37,4; 38,4; 38,6; 38,8; 40,8; 42,7; 44,1; 45,3.
Максимальное значение признака составляет 45,3 ц, а минимальное –
25,6 ц. Разница между ними составляет 19,7 ц. Этот интервал надо разбить на определенное количество частей. При малом объеме выборки (20–40 вариант) намечают 4–7 интервалов. Возьмем длину интервала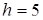 
. Получаем пять интервалов: первый 25 – 30, второй 30 – 35, третий 35 – 40, четвертый 40 – 45, пятый 45 – 50. С помощью ранжированного ряда определим частоту попадания вариант выборки в каждый интервал. В первый интервал 25 – 30 попадают два значения: 25,6 и 27,0; поэтому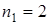 
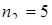. Аналогично, 
, 
, 
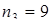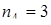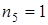.Теперь найдем относительные частоты попадания вариант выборки в каждый интервал:
; 
; 
;
; 
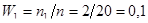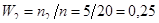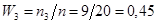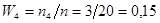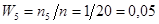
Для проверки вычисляем сумму относительных частот:
.
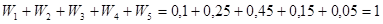Тот факт, что в сумме получена единица, подтверждает правильность вычислений.
Вычислим плотности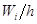 
относительных частот вариант. Получаем
;
;
;
;
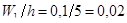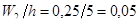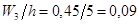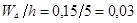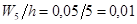
Полученные результаты сведем в таблицу 5.
Таблица 5.
| Интервал значений | 25–30 | 30–35 | 35–40 | 40–45 | 45–50 |
| Частоты вариант | 2 | 5 | 9 | 3 | 1 |
| Относительные частоты | 0,10 | 0,25 | 0,45 | 0,15 | 0,05 |
| Плотность относительных частот | 0,02 | 0,05 | 0,09 | 0,03 | 0,01 |
Строим гистограмму относительных частот – ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются интервалы, а высотами соответствующие значения плотности относительных частот.
Рис.12. Гистограмма относительных частот.
Так как объем выборки небольшой ( 
) и почти все наблюдаемые значения различны, то для вычисления выборочных характеристик составим вспомогательную таблицу (таблица 6).
Основные выборочные характеристики вычисляются по формулам: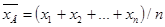 
– выборочная средняя; 
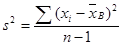– «исправленная» дисперсия; 
– «исправленное» среднее квадратическое отклонение;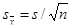 
– коэффициент вариации. Таблица 6
| № | Результат обследования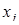 
| 
| 
|
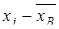
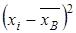
| 1 | 35,9 | – 0,1 | 0,01 |
| 2 | 35,3 | – 0,7 | 0,49 |
| 3 | 42,7 | 6,7 | 44,89 |
| 4 | 45,3 | 9,3 | 86,49 |
| 5 | 25,6 | –10,4 | 108,16 |
| 6 | 35,3 | – 0,7 | 0,49 |
| 7 | 33,4 | – 2,6 | 6,76 |
| 8 | 27,0 | – 9,0 | 81,00 |
| 9 | 35,9 | – 0,1 | 0,01 |
| 10 | 38,8 | 2,8 | 7,84 |
| 11 | 33,7 | – 2,3 | 5,29 |
| 12 | 38,6 | 2,6 | 6,76 |
| 13 | 40,8 | 4,8 | 23,04 |
| 14 | 35,5 | – 0,5 | 0,25 |
| 15 | 44,1 | 8,1 | 65,61 |
| 16 | 37,4 | 1,4 | 1,96 |
| 17 | 34,2 | – 1,8 | 3,24 |
| 18 | 30,8 | – 5,2 | 27,04 |
| 19 | 38,4 | 2,4 | 5,76 |
| 20 | 31,3 | – 4,7 | 22,09 |
| Σ | 720,0 | 0 | 497,20 |
Подставляя полученные значения в формулы, получаем
;
;
;
.
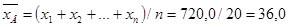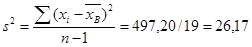
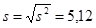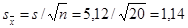Доверительный интервал для оценки генеральной средней имеет вид:
.
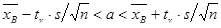Вычисляем теперь точность оценки 
:
;
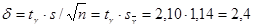где значение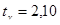 
находим по таблице приложения 3.
Таким образом, с надежностью 95% можно утверждать, что средняя цена акции за 300 дней заключена в пределах от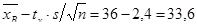 
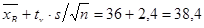ц. (возможный максимум).Задача 2. Для определения средней урожайности сахарной свеклы в колхозе на площади 
га была определена ее урожайность на 100 га. Результаты выборочного обследования представлены следующим распределением:
| Урожайность, ц/га | 23–25 | 25–27 | 27–29 | 29–31 | 31–33 | 33–35 | 35–37 |
| Площадь, га | 3 | 10 | 6 | 16 | 15 | 30 | 20 |
Требуется найти:
1) величину, которую следует принять за среднюю урожайность на всем массиве;
2) величину, которую следует принять за среднее квадратическое отклонение урожайности на всем массиве;
3) доверительный интервал, в котором с вероятностью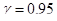 
заключена средняя урожайность на всем массиве.
Решение. В качестве приближенного значения средней урожайности на всем массиве принимаем среднюю арифметическую данного распределения, то есть выборочную среднюю. За значения признака нужно принять середины интервалов. Получим:
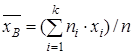= (24∙3+26∙10+28∙6+30 ∙16+32 ∙15+34∙30+36∙ 20)/100 =
= 3200/100 = 32.
Для оценки дисперсии генеральной совокупности вычисляем исправленное среднее квадратическое отклонение:
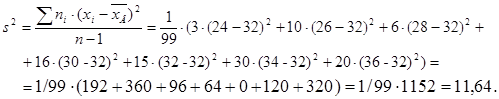
Отсюда можно найти среднее квадратическое отклонение урожайности на всем массиве
= 
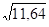= 3,4.
Найдем среднее квадратическое отклонение выборочной средней по формуле
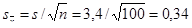ц.
Итак, оценка средней урожайности сахарной свеклы на всем массиве равна 32 ц со средней квадратической ошибкой 0,34 ц. Оценка среднего квадратического отклонения урожайности на всем массиве равна 3,4 ц.
Для вычисления доверительного интервала воспользуемся двойным неравенством:
.
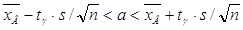Так как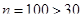 
, то значение 
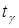найдем из условия 
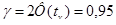. По таблице приложения 2 находим значение 
и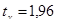 
, следовательно, получаем:
.
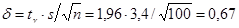Концы доверительного интервала:
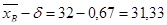и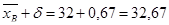 
.
Таким образом, с вероятностью 0,95 средняя урожайность сахарной свеклы на всем массиве заключена в границах от 31,33 ц до 32,67 ц.
Учебно-методический материал (7 класс) по теме: Задачи по статистике. Тема: «Вычисление и сопоставление среднего арифметического и медианы числовых наборов»
КУРСОВАЯ РАБОТА
КУРСЫ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ МА-3
Задачи по статистике
Тема: «Вычисление и сопоставление среднего арифметического и медианы числовых наборов»
Выполнила Яркова О.В.,
учитель математики
городского лицея № 1535
г. Москва, 2008 г.
Задача о возрасте детей
При проведении социологического опроса о количестве и возрасте детей в семьях в 20 квартирах одного дома были получены следующие данные о возрасте детей (в годах): 2, 16, 4, 5, 4, 7, 12, 10, 8, 7, 2, 4, 12, 6, 4, 8, 12, 5, 2, 4, 12, 5, 4, 8, 5, 6, 4, 4, 5, 4, 6, 5, 5, 10, 6, 8, 5, 6, 10, 6.
Заполните таблицу:
Возраст (лет) | Количество детей данного возраста |
2 | |
4 | |
5 | |
6 | |
7 | |
8 | |
10 | |
11 | |
12 | |
16 |
Вычислите:
- Средний возраст детей (среднее арифметическое) с помощью калькулятора.
- Медиану возрастов.
- % детей, чей возраст меньше среднего и чей возраст больше среднего.
- % детей, чей возраст меньше, чем медиана.
Какие выводы могли бы вы сделать на основе каждой из средних оценок?
Решение:
- В таблице указаны возрасты 40 детей.
- Среднее арифметическое приблизительно равно 6.5 лет.
- Медиана равна 5.5 лет.
- Младше среднего 65 % детей, старше, соответственно, 35 %.
- Младше 5.5 лет 50 %, что следует из определения медианы.
Возможные выводы:
Большая часть детей дошкольного возраста. Только примерно третья часть — школьники. А половина всех детей имеют возраст 5 лет и младше.
Возраст (лет) | Количество детей данного возраста |
2 | 3 |
4 | 9 |
5 | 8 |
6 | 6 |
7 | 2 |
8 | 3 |
10 | 3 |
11 | 1 |
12 | 4 |
16 | 1 |
Задача о демографии
Известно, что каждый день численность населения России уменьшается в среднем на 2500 человек.
Для того, чтобы страна могла развиваться, улучшать жизнь своих граждан, необходимо, чтобы её население увеличивалось. То есть, было бы хорошо, когда (если так можно выразиться) количество детей было больше количества их родителей.
Ребята! Мы, конечно же, вынуждены рассматривать «идеальные» ситуации, когда в каждой семье по 2 родителя. Известно, что в жизни все немного иначе. Но в среднем по нашей стране, насчитывающей примерно 147 млн. граждан, в подавляющее большинство семей — полные, т.е. с двумя родителями.
Итак, продолжим. Если в каждой семье будет по 1-2 ребенка, то количество граждан будет неуклонно уменьшаться, что приведёт к отрицательным последствиям (об этом вы узнаете из курса обществознания в старших классах).
И только если в большинстве семей будет по 3 и больше детей, то страна сможет выйти из трудной ситуации или даже избежать её.
Приведем пример применения оценок среднего арифметического и медианы для оценки количества детей в российских семьях. По опросу учеников одной школы было выяснено, что:
Количество детей в семьях | Число семей |
1 | 68 |
2 | 103 |
3 | 26 |
4 | 2 |
5 | 1 |
Итого: детей 365 | 200 |
Вычислите среднее количество детей в семье (среднее арифметическое) и медиану. При вычислении среднего арифметического пользуйтесь калькулятором. Для того чтобы вычислить медиану, воспользуйтесь тем, что количество семей 200, значит, значение медианы равно среднему арифметическому 100 и 101 чисел во втором столбце таблицы.
Решение:
Количество детей в семьях | Число семей |
1 | 68 |
2 | 103 |
3 | 26 |
4 | 2 |
5 | 1 |
Итого: детей 365 | 200 |
Среднее арифметическое | 1.875 |
Медиана | 2 |
В этом примере медиана, равная 2, показывает, что половина семей имеет одного или двух детей, а вторая половина- трех и более. Казалось бы, все обстоит не так уж плохо, и в среднем количество детей в семьях равно количеству их родителей или даже больше. Но среднее арифметическое «говорит», что, к сожалению, в «средней», типичной семье, количество детей менее двух.
Оценка физической подготовки спортсменов
Физическая подготовка команды 9 спортсменов была проверена при поступлении в спортивную школу, а затем после трех месяцев тренировки. Оценку физической подготовки проводила одна и та же бригада тренеров, по одной и той же системе баллов. Итоги проверки оказались следующими:
№№ спортсмена | |||||||||
Баллы перед поступлением | 76 | 71 | 57 | 49 | 70 | 69 | 26 | 65 | 69 |
Баллы после обучения | 81 | 85 | 52 | 52 | 70 | 63 | 33 | 83 | 62 |
Прокомментируйте изменение оценок каждого спортсмена: у кого они повысились, у кого понизились?
Вычислите среднее арифметическое и медианы оценок спортивной команды при поступлении и после тренировок. На основе этих средних значений сделайте вывод: улучшилась ли спортивная подготовка команды? Объясните свои выводы, опираясь на изменение среднего арифметического и медианы оценок команд.
Решение.
Упорядоченные ряды оценок: 26 49 57 65 69 69 70 71 76
33 52 52 62 63 70 81 83 85
Среднее арифметическое | Медиана | |
До поступления | 61.3 | 69 |
После тренировок | 64.4 | 63 |
Возможные выводы: если в соревнованиях учитывается общий результат всей команды, то физическая подготовка улучшилась, т.к. повысился «средний балл» — среднее арифметическое. Если же будет личное первенство, то однозначный вывод сделать невозможно, т.к. медиана оценок уменьшилась.
Победитель «Недели моды»
На «Неделе моды» были представлены коллекции «Зима-Лето» пяти модельеров: Федора Волкова, Романа Лисичкина, Веры Чешуйкиной, Дины Флагмининой, Мольче и Дивано. Для выбора лучшей коллекции жюри из 8 судей оценивало каждую из пяти коллекций по 100- балльной шкале. В результате были получены такие результаты:
Федор Волков | Роман Лисичкин | Вера Чешуйкина | Дина Флагминина | Мольче и Дивано | |
1 судья | 100 | 23 | 98 | 13 | 87 |
2 судья | 51 | 88 | 32 | 67 | 14 |
3 судья | 34 | 94 | 47 | 33 | 32 |
4 судья | 90 | 29 | 62 | 55 | 68 |
5 судья | 90 | 66 | 89 | 77 | 65 |
6 судья | 12 | 19 | 99 | 98 | 34 |
7 судья | 77 | 99 | 48 | 99 | 99 |
8 судья | 34 | 67 | 16 | 44 | 89 |
Определите победителя «Недели моды», вычислив среднюю оценку коллекции каждого модельера (среднее арифметическое всех 8 оценок его коллекции) и медиану его оценок.
Решение:
Упорядоченные ряды оценок:
Федор Волков: 12, 34, 34, 51, 77, 90, 90, 100
Роман Лисичкин: 19, 23, 29, 66, 67, 88, 94,99
Вера Чешуйкина: 16, 32, 47, 48, 62, 89, 98, 99
Дина Флагминина: 13, 33, 44, 55, 67, 77, 98, 99
Мольче и Дивано: 14, 32, 34, 65, 68, 87, 89, 99
Федор Волков | Роман Лисичкин | Вера Чешуйкина | Дина Флагминина | Мольче и Дивано | |
1 судья | 100 | 23 | 98 | 13 | 87 |
2 судья | 51 | 88 | 32 | 67 | 14 |
3 судья | 34 | 94 | 47 | 33 | 32 |
4 судья | 90 | 29 | 62 | 55 | 68 |
5 судья | 90 | 66 | 89 | 77 | 65 |
6 судья | 12 | 19 | 99 | 98 | 34 |
7 судья | 77 | 99 | 48 | 99 | 99 |
8 судья | 34 | 67 | 16 | 44 | 89 |
Среднее арифметическое | 61 | 61 | 61 | 61 | 61 |
Медиана | 64 | 66.5 | 55 | 61 | 66.5 |
Возможные выводы: победили коллекции Вера Чешуйкина и Мольче и Дивано. Или их коллекции должны быть оценены заново, возможно, другой командой судей.
Сравнение успеваемости двух классов.
По итогам учебы 1 четверти в лицее сравнили успеваемость двух 7-х классов по математике. Для этого классные руководители предметам записали в таблицу четвертные оценки по математике и решили сравнить их.
№ ученика по списку | Четвертная оценка | № ученика по списку | Четвертная оценка | № ученика по списку | Четвертная оценка | № ученика по списку | Четвертная оценка |
4 | 16. | 4 | 4 | 16. | 3 | ||
4 | 17. | 4 | 4 | 17. | 4 | ||
3 | 18. | 3 | 4 | 18. | 3 | ||
3 | 19. | 4 | 4 | 19. | 4 | ||
4 | 20. | 3 | 5 | 20. | 3 | ||
3 | 21. | 5 | 4 | 21. | 5 | ||
5 | 22. | 4 | 3 | 22. | 5 | ||
5 | 23. | 4 | 4 | 23. | 3 | ||
4 | 24. | 3 | 3 | 24. | 5 | ||
5 | 25. | 4 | 4 | 25. | 5 | ||
4 | 26. | 3 | 3 | 26. | 3 | ||
3 | 27. | 5 | 3 | 27. | 3 | ||
4 | 4 | 28. | 5 | ||||
4 | 4 | ||||||
4 | 4 |
Вычислите среднее арифметическое оценок каждого класса и медиану оценок. При вычислении пользуйтесь калькулятором.
Решение:
7 «а» класс | Ср. арифм. | 3.9 | 7 «б» класс | Ср. арифм. | 3.8 |
медиана | 4 | медиана | 4 |
В этом примере и медианы, и средние арифметические оценок настолько близки, что можно сделать вывод о примерно одинаковой успешности классов в изучении математики.
Выбор сценария праздничного концерта
Ученики 7 «А» класса вызвались подготовить сценарий новогоднего праздничного концерта. Но ребята оказались людьми творческими, и подготовили целых 4 сценария, вместо одного!
Для окончательного выбора ученики 7 «Б» и 7 «В» классов прочли все сценарии и, на классных часах, разбившись на группы, их баллами от 1 до 4: чем интереснее им казался сценарий, тем больше баллов он заслуживал.
Поскольку ребята уже начали изучать курс «Теории вероятности и статистики», то они решили для каждого набора оценок вычислить и медиану, а затем сравнить среднее арифметическое с медианой.
Получились таблицы оценок:
Команда | 1 сценарий | 2 сценарий | 3 сценарий | 4 сценарий |
№ 1 из 7 «а» | 2 | 1 | 4 | 3 |
№ 2 из 7 «а» | 2 | 1 | 3 | 4 |
№ 3 из 7 «а» | 1 | 3 | 1 | 2 |
№ 4 из 7 «а» | 1 | 2 | 3 | 4 |
№ 1 из 7 «б» | 2 | 1 | 4 | 3 |
№ 2 из 7 «б» | 1 | 3 | 4 | 2 |
№ 3 из 7 «б» | 1 | 2 | 3 | 4 |
№ 4 из 7 «б» | 4 | 3 | 1 | 2 |
Определите сценарий-победитель, пользуясь значением среднего арифметического оценок и пользуясь значением медианы каждого набора оценок.
Решение:
Выбор сценариев | ||||
Среднее арифметическое оценок команд | 1.75 | 2 | 3 | 3.25 |
Итоговое место сценария по среднему арифметическому | 4 | 3 | 2 | 1 |
Медианы оценок команд | 1.5 | 2 | 3 | 3 |
Итоговое место сценария по медианам | 4 | 3 | 1 или 2 | 1 или 2 |
Возможные выводы: Итак, если по средним арифметическим баллам, безусловно, побеждает 4-й сценарий, то равные медианы оценок третьего и четвертого сценария подсказывают, что неплохо было бы ещё раз внимательнее рассмотреть и оценить заново сценарии под номерами 3 и 4.
Задачи по статистике
Задача — Ряды распределения и статистические таблицы.
Теория по решению задачи.
Статистический ряд распределения – упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.
Дискретный вариационный ряд – характеризует распределение единиц совокупности по дискретному (прерывному) признаку.
Интервальный вариационный ряд – характеризует распределение единиц совокупности по интервальному (непрерывному) признаку.
Для изображения дискретных вариационных рядов распределения используется «полигон распределения». Для графического изображения интервального вариационного ряда применяются «гистограмма» и «кумулята».
Задача 1.
На экзамене по истории студенты получили оценки:
3 4 4 4 3 4
3 4 3 5 4 4
5 5 2 3 2 3
3 4 4 5 3 3
5 4 5 4 4 4
Построить дискретный вариационный ряд распределения студентов по баллам и изобразить его графически.
Ход решения задачи:
Определяем элементы ряда распределения: варианты, частоты, частоты.
Оценка, баллы | Кол-во студентов с такой оценкой, человек | В процентах к итогу |
2 | 2 | 6,7 |
3 | 9 | 30 |
4 | 13 | 43,3 |
5 | 6 | 20 |
Итого | 30 | 100 |
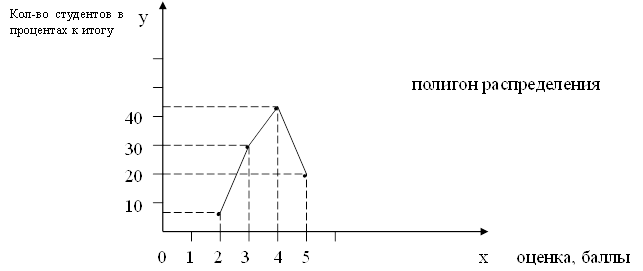
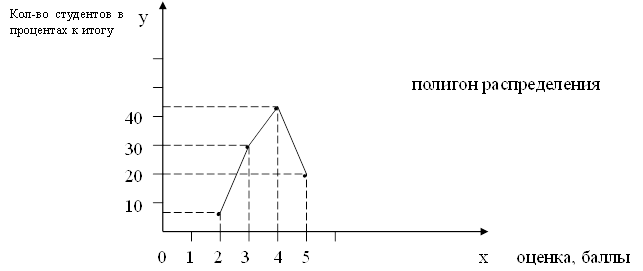
Теперь графически изобразим дискретный ряд распределения в виде помпона распределения.
Можно сделать вывод о том, что преобладающее большинство студентов получило «4» (43,3 %).
Задача 2.
Во время выборочной проверки было установлено, что продолжительность одной покупки в кондитерском отделе магазина была такой: (секунды).
77 70 82 81 81
82 75 80 71 80
81 89 75 67 78
73 76 78 73 76
82 69 61 66 84
72 74 82 82 76
Построить интервальный вариационный ряд распределения покупок по продолжительности, создав 4 группы с одинаковыми интервалами. Обозначить элементы ряда. Изобразить его графически, сделать вывод.
Ход решения задачи по статистике:
Определяем элементы ряда распределения: варианты, частоты, частости, накопленные частоты.
Но прежде рассчитаем границы 4 заданных групп с одинаковыми интервалами:
Величину
интервала определим по формуле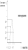 
.
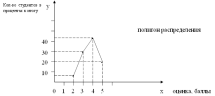В
нашем случае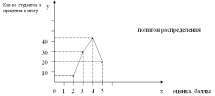 
Границы групп соответственно равны:
I 61+7=68 (61-68)
II 68+7=75 (68-75)
III 75+7=82 (75-82)
IV 82+7=89 (82-89)
Группы покупок по продолжительности, сек. | Число покупок | В процентах к итогу | Накопленные частоты |
61-68 | 3 | 10 | 3 |
68-75 | 9 | 30 | 12 |
75-82 | 16 | 53,3 | 28 |
82-89 | 2 | 6,7 | 30 |
Итого | 30 | 100 |
|
Теперь графически отобразим наш интервальный вариационный ряд в виде гистограммы и кумуляты.
По таблице и графика можно сделать вывод о том, что преобладающее большинство покупок (16 или 53.3%) находится во временном интервале 75-82, сек.
Статистика задача — Абсолютные и относительные величины.
Теория по решению статистической задачи.
Абсолютные величины – показатели, которые выражают размеры общественных явлений и процессов числом единиц совокупности.
Относительные величины – показатели, выражающие количественные соотношения численностей или величин признаков изучаемых явлений.
Виды относительных величин:
1) Относительная величина выполнения плана:
2) Относительная величина планового задания:
3) Относительная величина динамики:
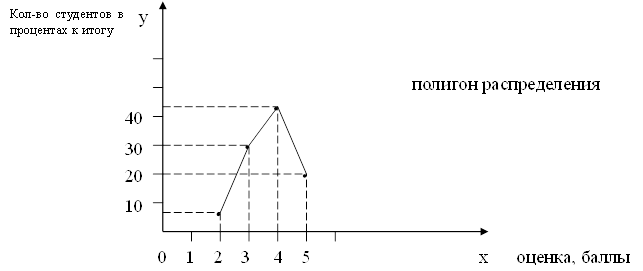
4) Относительная величина структуры:
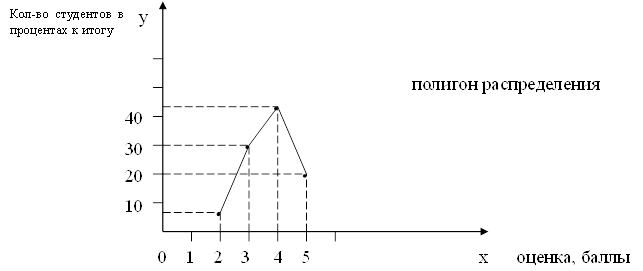
5) Относительная величина сравнения отражает соотношение двух объемов или уровней в пространстве: соотношение производства автомобилей в Украине и России, соотношение уровней оплаты труда в разных хозяйствах, соотношение уровней производительности на разных предприятиях отрасли и т. д.
6) Относительная величина координации получается посредством деления друг на друга разноименных исходных показателей, она дает типичную характеристику соотношения одно-порядковых по значимости исходных показателей, во-первых, непосредственно связанных между собой, во-вторых, обладающих некоторой общностью.
7) Относительная величина интенсивности:
Типовая задача № 1
Два консервных завода выработали по 100 тыс. шт. банок виноградного сока. На первом заводе емкость каждой банки составляет 500 см3, а на втором – 200 см3. Можно ли сказать, что оба завода работали одинаково?
Ход решения задачи по статистике:
Для того, чтобы ответить на этот вопрос необходимо установить коэффициенты перевода фактического объема банок в условные банки и затем умножить количество выпущенных банок на эти коэффициенты. Представим расчет в таблице № 1.
Таблица № 1
Заводы | Количество выпущенных банок, тыс. шт. | Объем банки см3 | Коэффициенты перевода | Количество выпущенных условных банок, тыс. шт. |
№ 1 | 100 | 500 |
| 100*1,414=141,4 |
№ 2 | 100 | 200 |
| 100*0,566=56,6 |
Таким образом, завод № 1 по сравнению с заводом № 2 выпустил виноградного сока на 84,8 тыс. Банок больше (141,4-56,6).
Статистика — Типовая задача № 2
Имеются следующие данные розничного товарооборота:
Таблица № 2
Универмаги | Розничный товарооборот (млн. грн.) | ||
Фактически за базисный год | Отчетный год | ||
По плану | Фактически | ||
«Крым» | 105 | 110 | 98 |
«Центральный» | 137 | 148 | 150 |
Определить:
1. Относительную величину выполнения плана.
2. Относительную величину планового задания.
3. Относительную величину динамики.
Ход решения задачи:
1. Определяем относительную величину выполнения плана по двум универмагам:
2. Определим относительную величину планового задания:
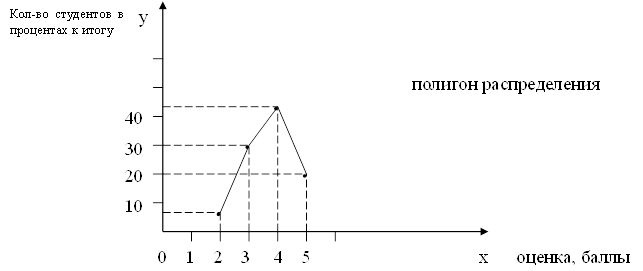
3. Определяем относительную величину динамики:
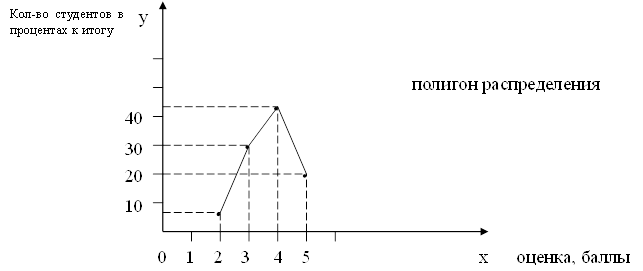
Статистическая задача — Средние и структурные средние величины.
Теория по решению статистической задачи:
Средние величины – это показатели. Выражающие типичные черты и дают обобщающую количественную характеристику уровня признака по совокупности однородных явлений.
1. Средняя арифметическая:
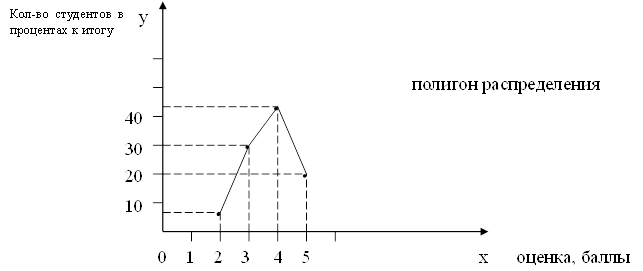
2. Средняя гармоническая:
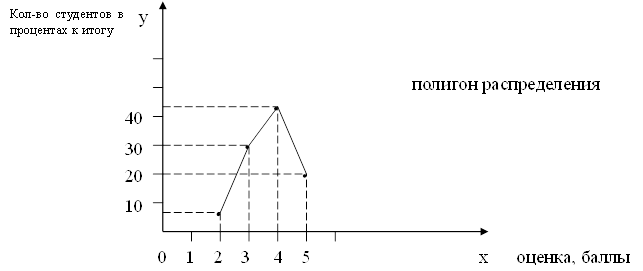
3. Средняя квадратическая:
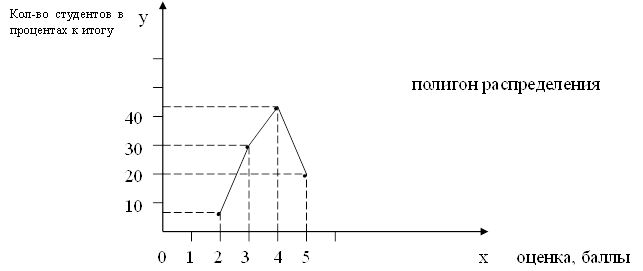
4. Средняя хронологическая:
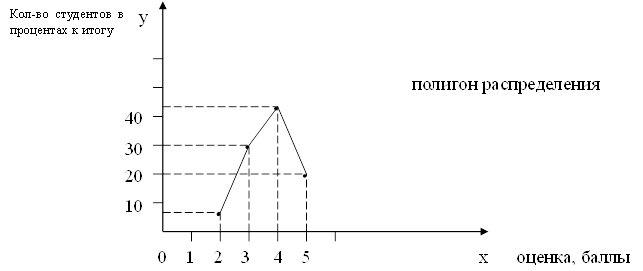
5. Средняя геометрическая:
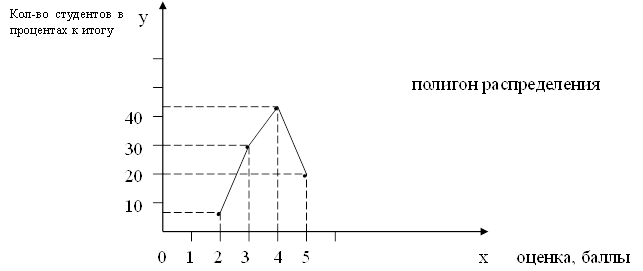
К1, К2, К3 и Кn – коэффициенты динамики по отношению к предыдущему периоду.
6. мода интервальных рядов распределения вычисляется по следующей формуле:
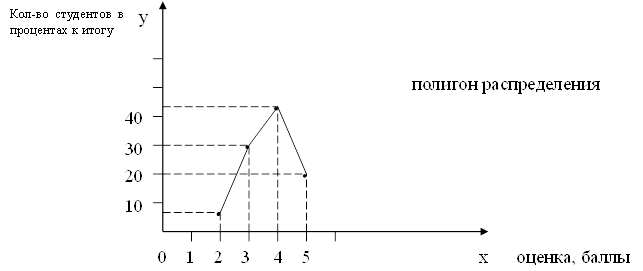
х0 – минимальная граница модального интервала;
i – величина интервала;
f2 – частота модального интервала;
f1 – частота интервала, предшествующего модальному;
f3 – частота интервала, следующего за модальным.
Мода для дискретных рядов распределения – это наиболее часто встречающаяся величина признака в данной совокупности.
7. Медиана для интервальных рядов распределения вычисляется по формуле:
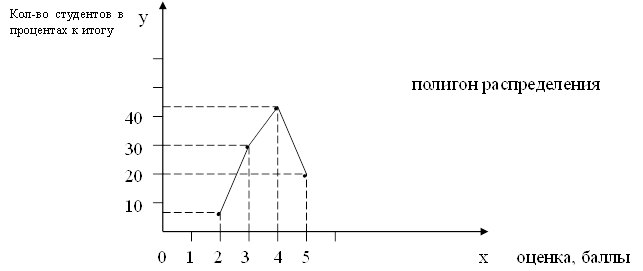
x0 – нижняя граница медианного интервала;
i – величина медианного интервала;
∑f – сумма частот ряда;
SМЕ-1 – сумма накопленных частот, предшествующих медианному интервалу;
fМЕ – частота медианного интервала.
Чтобы определить медиану в дискретном вариационном ряду. Необходимо сумму частот разделить пополам и к полученному результату добавить ½.
Типовая задача № 1
Имеются следующие данные о заработной плате рабочих:
Таблица № 1
Месячная заработная плата (грн.) (х) | Число рабочих (f) | х*f |
х1=120 | 27 | 3240 |
х2=145 | 33 | 4785 |
х4=200 | 48 | 9600 |
х5=208 | 51 | 10608 |
х6=250 | 16 | 4000 |
х7=337 | 28 | 9436 |
Итого | 203 | 41669 |
Определите среднюю заработную плату одного рабочего.
Ход решения:
Среднюю заработную плату определим по формуле средней арифметической взвешенной:
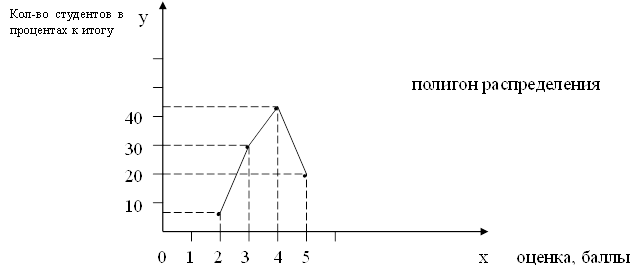
Т. о. средняя заработная плата рабочего составила 205,27 грн.
Типовая задача (статистика) № 2
Имеются, следующие данные выпуска литья в литейном цехе завода за пятилетний период:
Таблица № 2
Годы | 1-й | 2-й | 3-й | 4-й | 5-й |
Выпуск литья, тонн | 528,34 | 336,98 | 439,24 | 297,55 | 672,17 |
В % к предыдущему году | — | 63,8 | 130,3 | 67,7 | 225,9 |
Требуется определить средний темп выпуска литья.
Ход решения задачи:
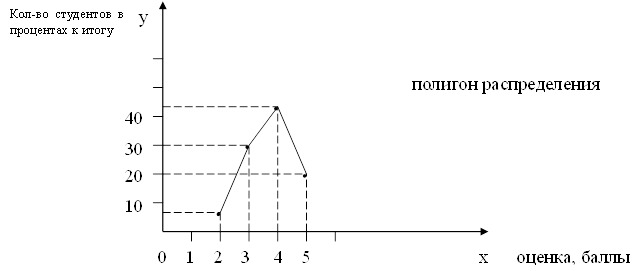
Для определения среднего темпа выпуска литья используем формулу средней геометрической:
Типовая задача № 3
Имеются следующие данные:
Таблица № 3
Група рабочих по размеру заработной платы (в грн.) | Число рабочих | SМЕ |
150-200 | 28 | 28 |
200-250 | 54 | 82 |
250-300 | 30 | 112 |
300-350 | 47 | 159 |
350-400 | 63 | 222 |
400-450 | 18 | 240 |
450-500 | 22 | 262 |
Итого | 262 | — |
Определить моду и медиану.
Ход решения задачи:
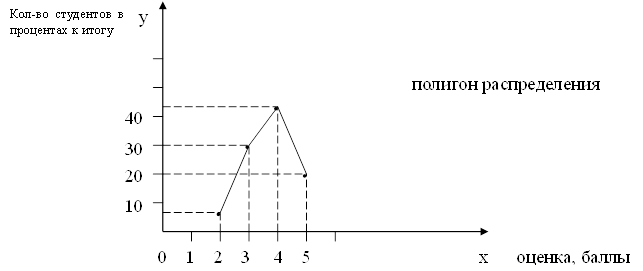
1. Определяем моду:
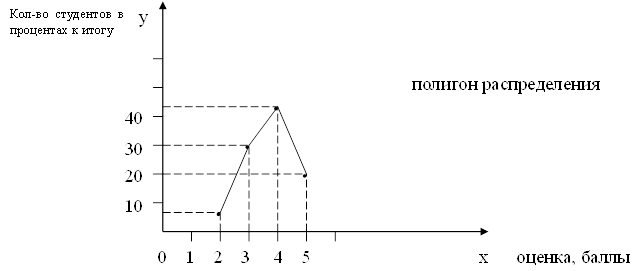
2. Определяем медиану:
Социально-экономическая статистика. Практикум
ТЕМА 1. Статистика населения.
1.1. Методические указания и решение типовых задач.
Общество, его социальная и экономическая базы не являются чем-то застывшим. Процесс взаимодействия различных компонентов общественного развития есть взаимосвязь процессов, а не комплекс неизменных форм.
Поэтому необходимо говорить о взаимосвязи процессов экономического и демографического воспроизводства, а не о каких-то статистических формах,
например, соотношении численности населения и объема продукции на какую-то дату.
Воспроизводство населения – это непрерывный процесс взаимозаменяемости различного рода социально-экономических и демографических структур, составляющих основу населения. В исследовании проблем воспроизводства населения остановимся на их демографо-
экономическом аспекте.
В задачи статистики населения входит изучение его численности,
состава, естественного и миграционного движения. Население в демографии – это совокупность людей, самовоспроизводящаяся в процессе смены поколений.
При определении численности населения статистика использует ряд показателей. В зависимости от характера проживания на данной территории различают наличное и постоянное население. Выделяется и третья категория – юридическое (приписное) население, которая в современных переписях не используется. К наличному населению относятся лица, которые живут в данном населенном пункте на момент учета, независимо от места их постоянного жительства. К постоянному населению относятся лица, которые постоянно живут в данном населенном пункте, включая временно отсутствующих.
Категории постоянного и наличного населения связаны с категориями временно отсутствующих и временно живущих по данному адресу. К числу временно отсутствующих относятся лица, выехавшие из места постоянного жительства на срок не более 6 месяцев. К числу временно живущих по адресу относятся лица, которые живут в данном населенном пункте временно не более 6 месяцев и имеют постоянное место жительства в другом месте.
ПРОБЛЕМЫ ПО СТАТИСТИКЕ И ВЕРОЯТНОСТЬ С РЕШЕНИЯМИ Виджая К. Малхотра
В разделе «Статистика и вероятность» были рассмотрены в основном следующие пять тем:1. Базовая статистика
2. Вероятность
3. Вероятностные распределения случайных величин
4. Корреляционный и регрессионный анализ
5. Статистический вывод
Этот материал дает вам проблемы по вышеупомянутым темам. Вопросы объективного типа с четырьмя альтернативными ответами и одним
В основном в разделе «Статистика и вероятность» были рассмотрены следующие пять тем:1.Базовая статистика
2. Вероятность
3. Вероятностные распределения случайных величин
4. Корреляционный и регрессионный анализ
5. Статистический вывод
Этот материал дает вам проблемы по вышеупомянутым темам. Вопросы объективного типа с четырьмя альтернативными ответами, и нужно выбрать один правильный. Они предназначены для подготовки различных конкурсных экзаменов, которые могут проводиться как в режиме онлайн, так и в режиме бумаги и карандаша. Вопросы можно прочитать на его / ее kindle / ipad / планшете / iphone / компьютере и т. Д.и решите, как обычно, с помощью бумаги и карандаша, используя авторизованный калькулятор, и запишите ответы после того, как решите то же самое. Если для экзамена разрешено использование книги предписанных формул, то она также может быть использована. Ответ также был дан вместе с его подробным решением в электронной книге для каждого практического вопроса. Даже если ответ правильный, нужно обязательно увидеть решение, предоставленное для подтверждения различных концепций и лучшего понимания теории.Решения представляют собой дальнейшее обучение на материале, который необходимо знать для различных экзаменов. Вопросы были классифицированы по тематике, и программа каждой темы была принята в соответствии с некоторыми известными конкурсными экзаменами. Некоторые конкурсные экзамены носят субъективный характер. Материал также можно использовать после игнорирования четырех альтернативных вариантов ответа на различные вопросы. Учебные решения действительно дают вам руководство по каждой теме статистики и вероятности. Решения действительно дают формулы, используемые для решения проблем.
15 лучших книг для изучения Вероятность и статистика
Теория вероятностей — это математическое исследование неопределенности. Он играет центральную роль в машинном обучении, поскольку разработка алгоритмов обучения часто основывается на вероятностном допущении данных. Теперь вы ищете хорошие книги в разделе Вероятность чтения? Вот наш список.
1. Курс теории вероятностей от Кай Лай Чанга
В этой книге предполагается, что вы обладаете определенной степенью математической зрелости, но при этом даются очень подробные доказательства основных концепций строгой вероятности.
2. Введение в теорию вероятностей и ее приложения Уильяма Феллера
Это двухтомная книга, и первый том, вероятно, заинтересует новичка, поскольку он охватывает дискретную вероятность. В книге вероятность рассматривается как отдельная теория.
3. Набор алгоритмов на Java, третье издание, части 1-5: основы, структуры данных, сортировка, поиск и графические алгоритмы Роберта Седжвика
Отличный ресурс (студенты, инженеры и даже предприниматели), если вы ищете код, который можно взять и реализовать прямо на работе.
4. Интеллектуальный анализ данных: практические инструменты и методы машинного обучения, автор — Ян Х. Виттен.
Если вы хотите изучить машинное обучение, вам просто необходимо иметь его. Книга прекрасно написана и идеально подходит для инженера / студента, который не хочет вдаваться в подробности подхода с машинным обучением, но хочет получить его практические знания.
5. Обнаружение статистики с помощью R Энди Филд
Это хорошая книга, если вы плохо знакомы со статистикой и вероятностью и одновременно начинаете изучать язык программирования.Книга поддерживает R и написана в непринужденной юмористической манере, поэтому ее легко читать.
6. Пятьдесят проблемных проблем в вероятности с решениями Фредерика Мостеллера
Эта книга представляет собой отличный сборник, в котором решается довольно много загадок. Что мне нравится в этих головоломках, так это то, что они все решаемы и не требуют слишком сложных математических знаний для решения.
7. Первый курс теории вероятностей Шелдона Росс
Это введение представляет математическую теорию вероятностей для читателей в области инженерии и естественных наук, обладающих знаниями элементарного исчисления.Представлены новые примеры и упражнения повсюду. Предлагает новый раздел, который представляет элегантный способ вычисления моментов случайных величин, определяемых как количество происходящих событий.
8. Введение в алгоритмы Томаса Х. Кормена
Книга подробно описывает широкий спектр алгоритмов, но при этом делает их разработку и анализ доступными для всех уровней читателей. Каждая глава относительно автономна и может использоваться как единица изучения.
9. Введение в вероятность, Димитри П.Bertsekas
Если вы хотите изучать вероятность вне физического класса, эта книга — отличный выбор. Это не требует предварительных знаний в других областях, но в книге мало проработанных примеров.
10. Введение в теорию вероятностей Пола Г. Хоэля
Эта книга — отличный выбор для всех, кто интересуется изучением элементарной теории вероятностей (т.е. вероятности, основанной на исчислении, а не теоретической вероятности измерения). Книга предполагает, что читатели не знакомы с этой темой.
11. Вероятность и статистика Морриса Х. ДеГрута
Это выдающаяся книга для тех, кто хорошо разбирается в математике. Он охватывает все, что можно было бы изучить на годичном курсе статистики и более, включая множество разделов по байесовским методам.
12. Теория вероятностей: Краткий курс (Дуврские книги по математике) Ю.А. Розанов
Эта книга не для всех, так как требует небольшой математической сложности. Но он окажется наиболее полезным для очень большой аудитории.Для серьезных начинающих студентов, изучающих математику и естественные науки, это самый быстрый способ выучить предмет.
13. Теория вероятностей: логика науки Э. Джейнс
Эта книга выходит за рамки традиционной математики теории вероятностей и рассматривает этот предмет в более широком контексте. В нем обсуждаются новые результаты, а также приложения теории вероятностей к множеству проблем.
14. Учебное пособие по вероятности: интуитивно понятный курс для инженеров и ученых (и всех остальных!) Кэрол Эш
Это руководство для практикующих инженеров, ученых и студентов. В этой книге предлагаются практические отработанные примеры. по непрерывной и дискретной вероятности для курсов по решению проблем.Он наполнен удобными диаграммами, примерами и решениями, которые очень помогают в понимании множества вероятностных проблем.
15. Понимание вероятности: правила случайности в повседневной жизни Хенк Теймс
Это отличная книга. Вторая половина книги может потребовать некоторых знаний в области математического анализа. Кажется, это подходящее сочетание для тех, кто хочет учиться, но не хочет пугаться «лемм».