III Таблица дифференциалов
Так как дифференциал dyлишь множителемdxотличается от производной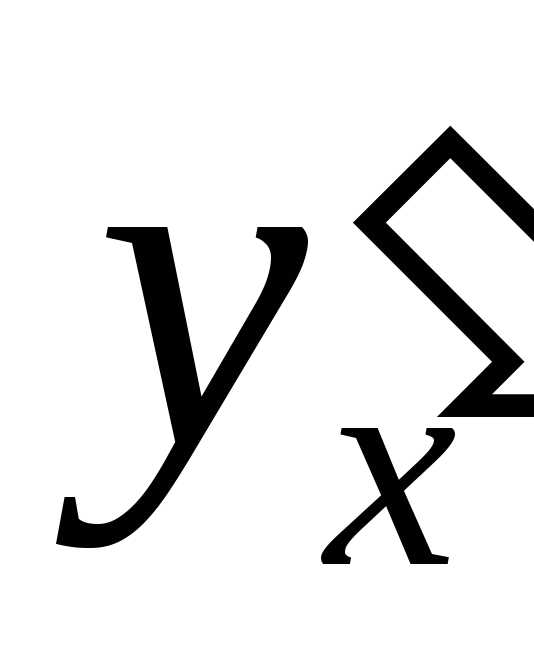 ,
то по таблице производных легко составить
таблицу дифференциалов.
,
то по таблице производных легко составить
таблицу дифференциалов.
1.
,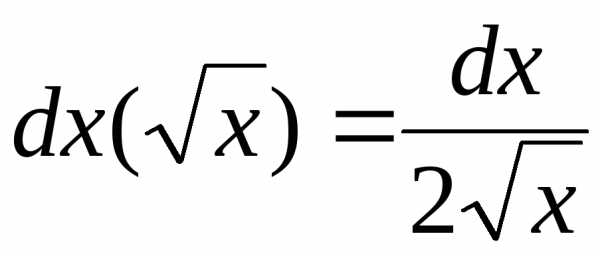 ,
,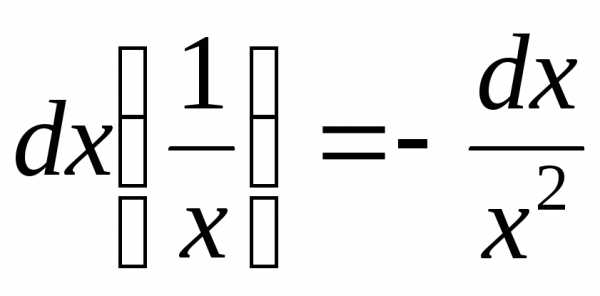 .
.
2. ,.
3. 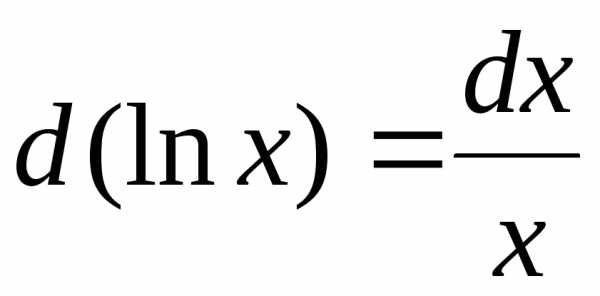 ,
,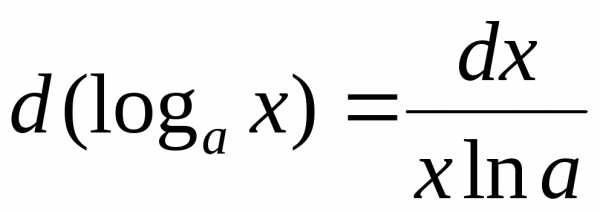 .
.
4. . 5..
6. 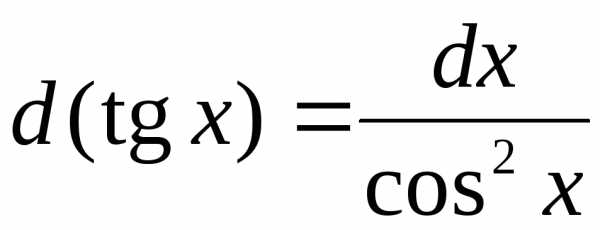 . 7..
. 7..
8. . 9..
10. . 11..
Также легко получить формулы для дифференциалов суммы, разности, произведения и частного функций:
а)
б)
в) 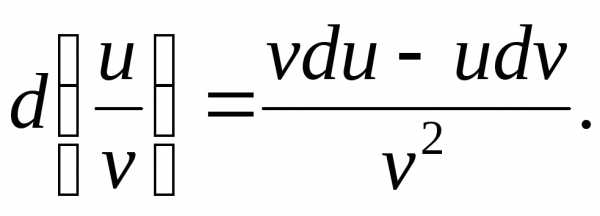
Отметим, что в таблице дифференциалов переменная xможет быть как независимой, так и некоторой функцией. В таблице же производных (§6)x– это только независимая переменная.
Замечание.Формула для дифференциала
функции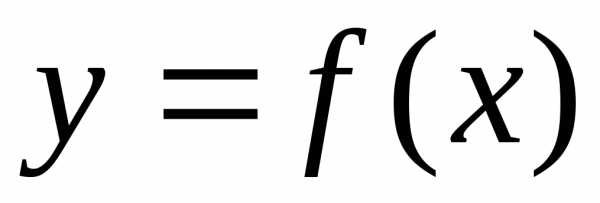 ,
а именно:
,
а именно:
,
позволяет написать формулу, выражающую производную функции через дифференциалы dxиdy:
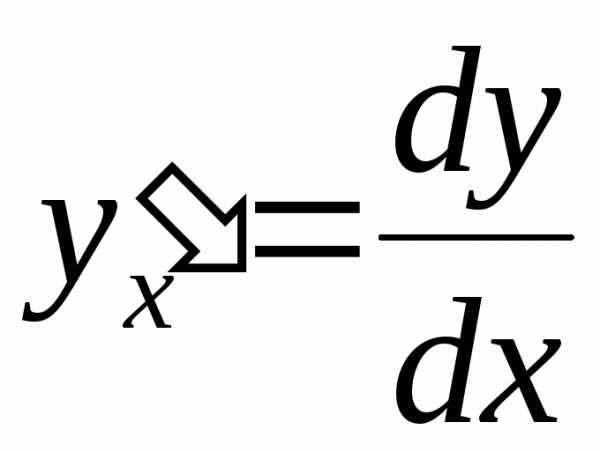 .
.
При этом такая формула сохраняет силу, по какой бы независимой переменной ни были вычислены dxиdy. Эта формула позволяет легко запоминать (но не доказывать!) некоторые правила дифференцирования:
для сложной функции
;
для обратной функции
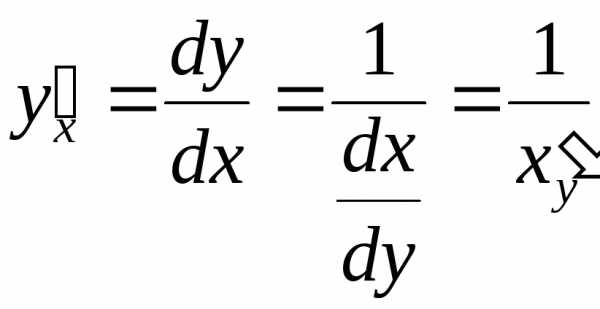
для функции, заданной параметрически
.
§8. Производные высших порядков
I Определение и обозначения
Если функция  дифференцируема на некотором промежутке,
то её производная
дифференцируема на некотором промежутке,
то её производная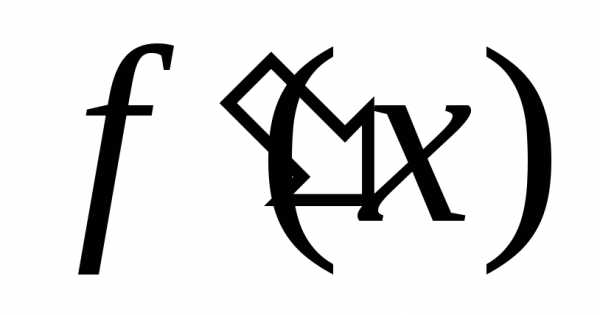 сама является функцией, определенной
на этом промежутке. Следовательно, по
отношению к ней можно ставить вопрос о
существовании и нахождении производной.
Если она существует, то её называют
второй производной (или производной
2гопорядка), и обозначают одним
из символов
сама является функцией, определенной
на этом промежутке. Следовательно, по
отношению к ней можно ставить вопрос о
существовании и нахождении производной.
Если она существует, то её называют
второй производной (или производной
2гопорядка), и обозначают одним
из символов
.
Аналогично, если существует производная
от второй производной, то её называют
третьей производной и обозначают,
например,  .
.
Вообще, производной n-го порядка называют производную от производной (n–1)-го порядка и обозначают. Итак, по определению
.
II Производные некоторых функций
1. y=sinx, y=cosx
Первые производные этих функций и формулы приведенияпозволяют методом математической индукции получить выражения для производныхn-го порядка:
.
2. y=x
Если 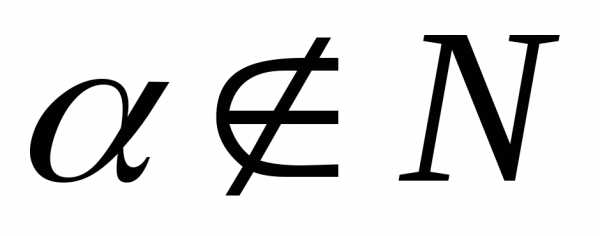 ,
то, последовательно дифференцируя,
получим,,
и вообще:
,
то, последовательно дифференцируя,
получим,,
и вообще:
.
Если же показатель степени натуральный, то:
3. y=ax
, в частности,,.
4. y=lnx
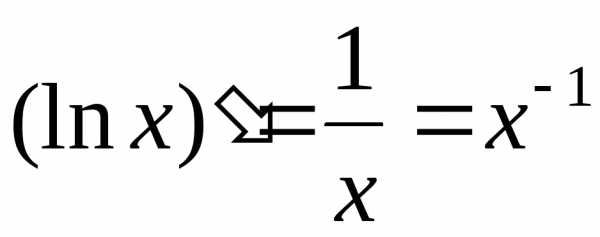
.
III Некоторые правила
Очевидно, что и. Для производной
n-го порядка от произведения функций имеется т.н. формула Лейбница. Приведем ее без доказательства:
,
где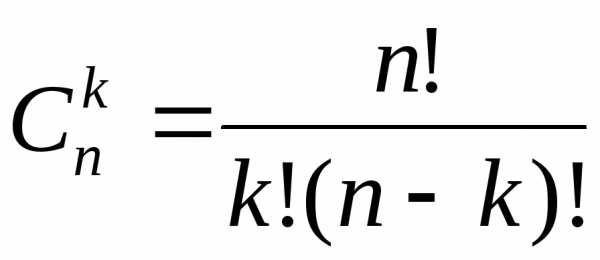 .
.
Заметим, что под производной нулевого порядка принято понимать саму
функцию: 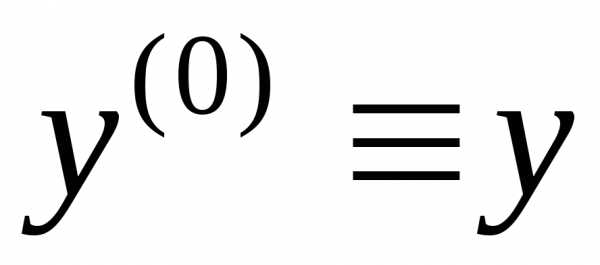 .
.
IV Функция, заданная параметрически
Пусть функция задана параметрическими уравнениями
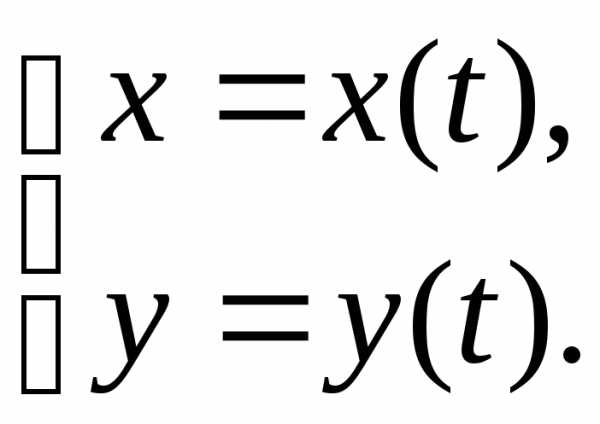
Её первая производная – это также функция, заданная параметрически:
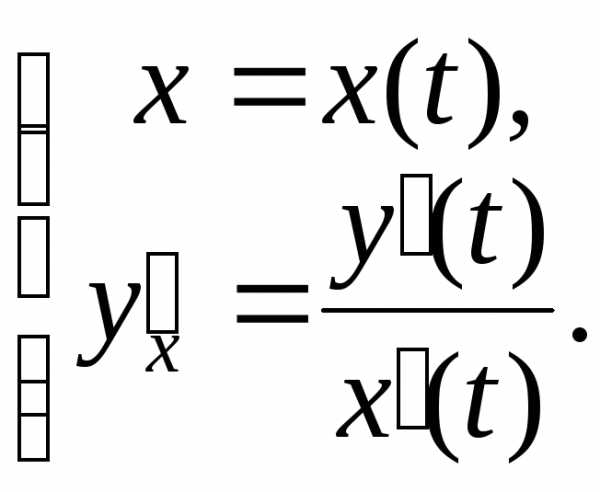
Тогда
Пример.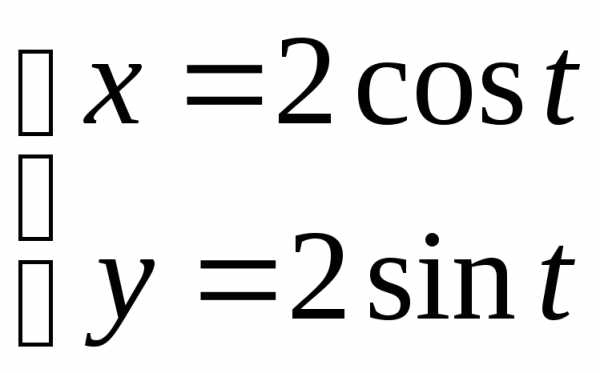 первая производная имеет вид
первая производная имеет вид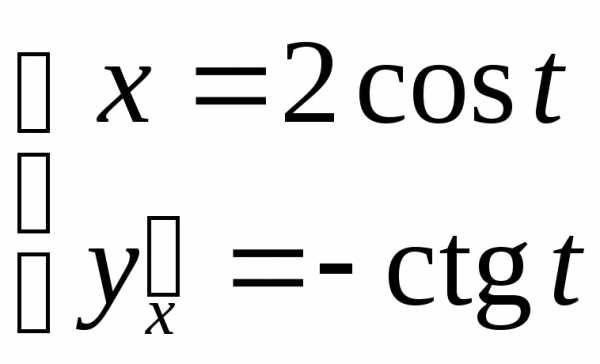 Тогдаи вторая производная такова:
Тогдаи вторая производная такова: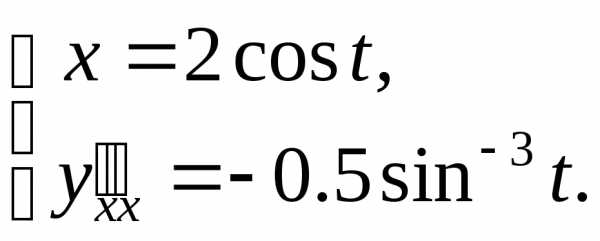
V Функция, заданная неявно
Повторное дифференцирование такой функции покажем на примере:
Тогда по определению:
.
Остается подставить в последнее выражение
значение 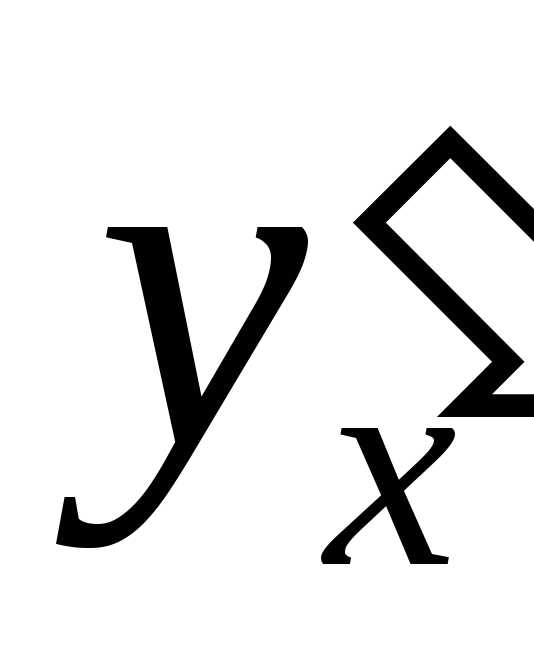 :
:
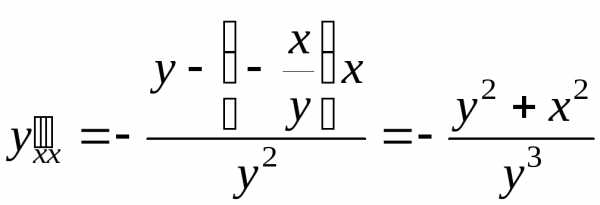 .
.
Полученное выражение можно упростить, используя само уравнение:
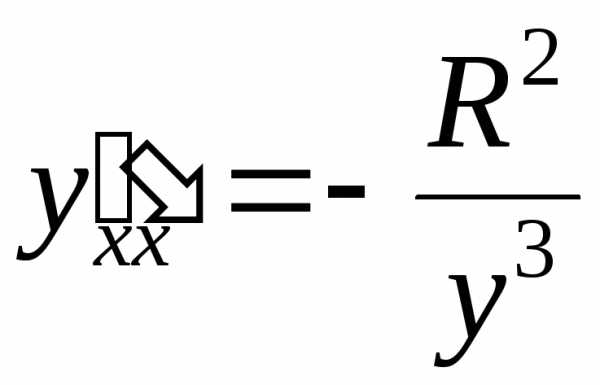 .
.
Тема ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Лекция 10
§1. Необходимое условие экстремума
Рассмотрим функцию
,
определенную на промежутке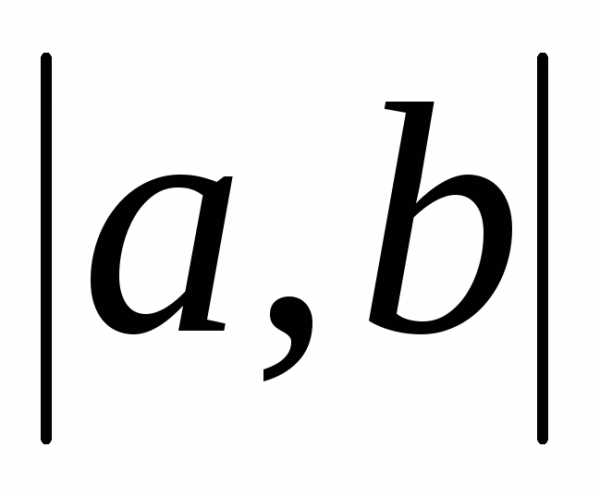 ,
и пусть точка
,
и пусть точка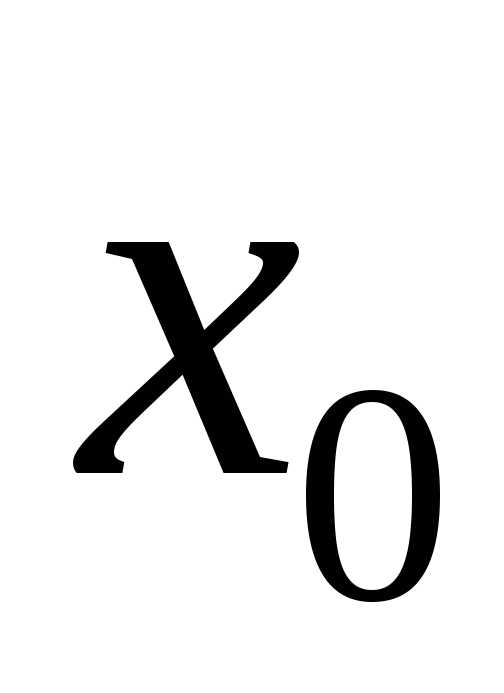 –внутренняяточка промежутка:
–внутренняяточка промежутка: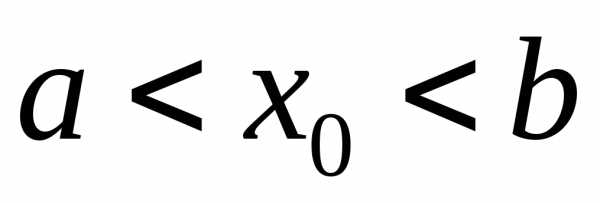 .
.
Определение 1.Точка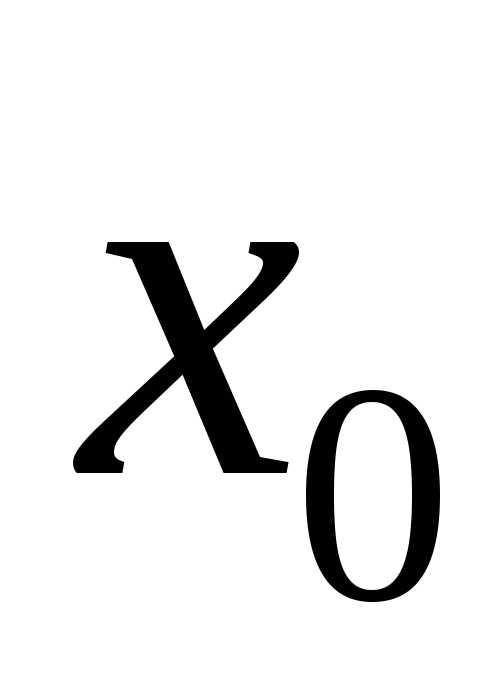 называется точкой (локального) максимума
функции,
если существует окрестность этой точки,
в которой (при
называется точкой (локального) максимума
функции,
если существует окрестность этой точки,
в которой (при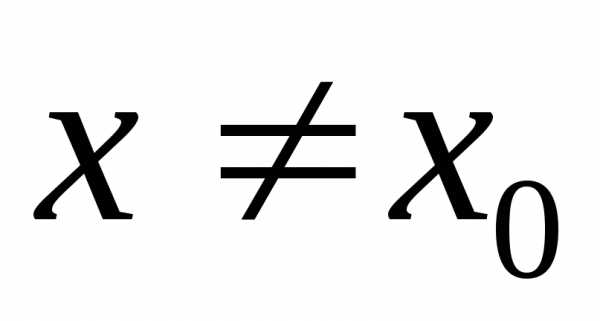 )
выполняется неравенство.
Другими словами для малых приращений
аргумента
)
выполняется неравенство.
Другими словами для малых приращений
аргумента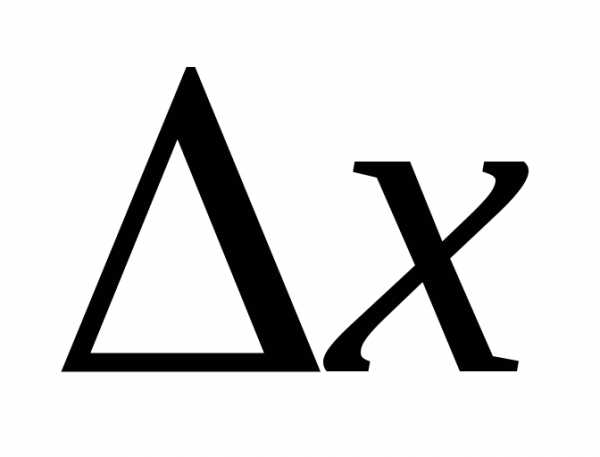 приращение
функции.
приращение
функции.
Определение 2.Точка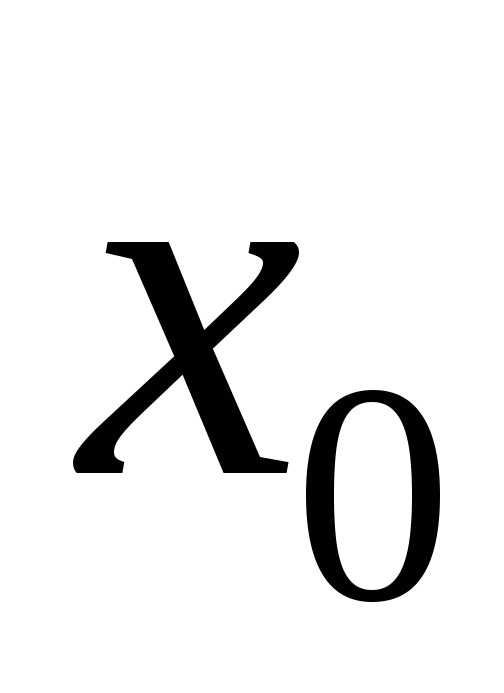
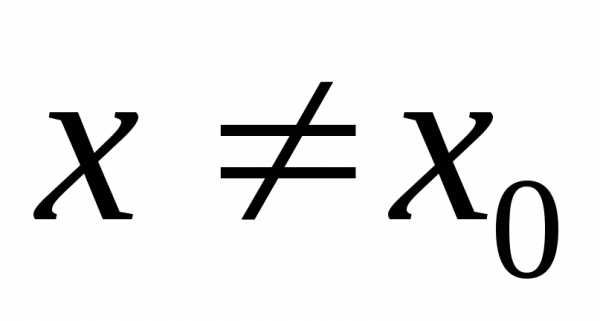 )
выполняется неравенство.
Другими словами
)
выполняется неравенство.
Другими словами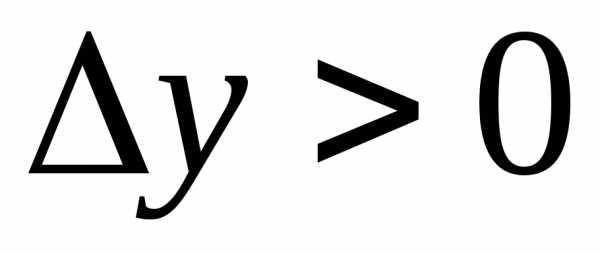 при малых
при малых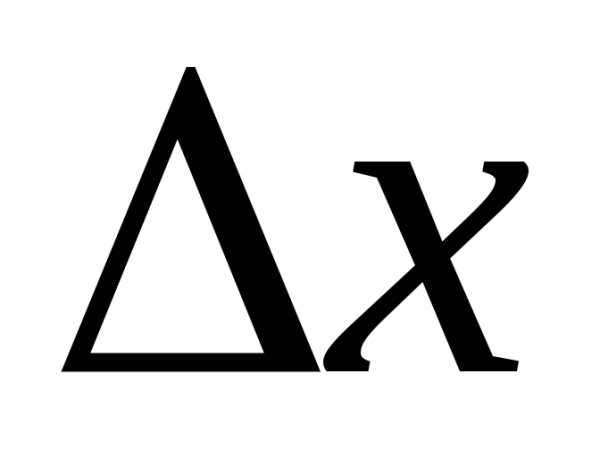 .
. Точки максимума и минимума называются
точками экстремума. Их можно характеризовать
следующим образом: приращение функции
в точке экстремума имеет постоянный
знак, не зависящий от знака 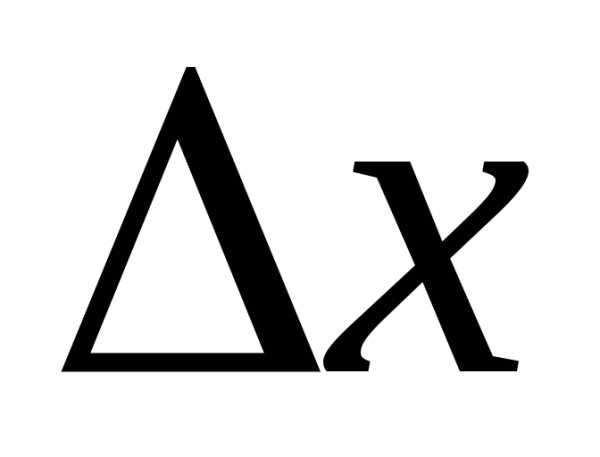 (если
(если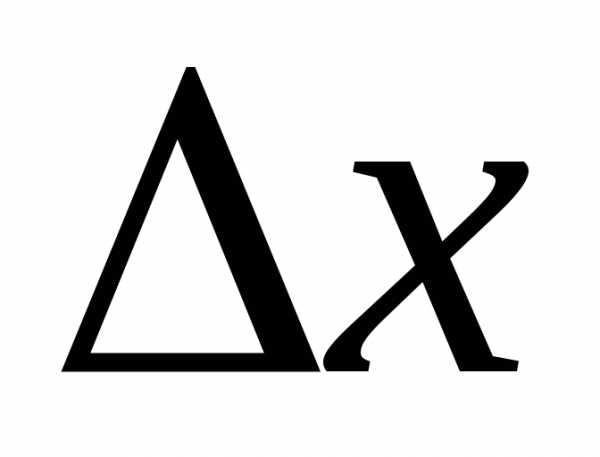 достаточно мало).
достаточно мало).
Теорема Ферма.Если функциядифференцируема в точке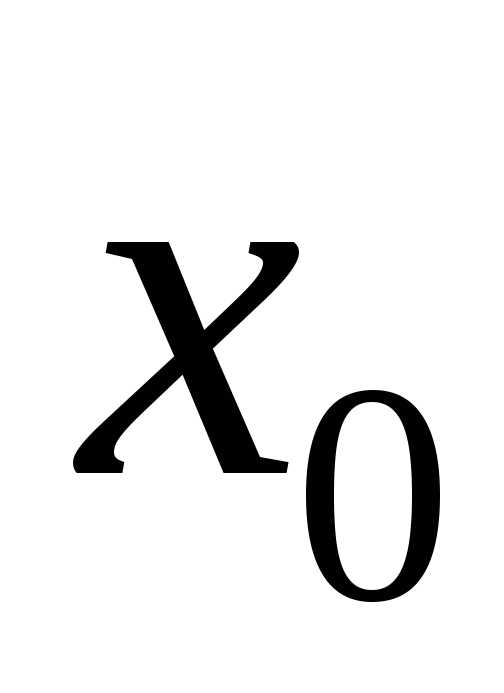 и имеет в этой точке локальный экстремум,
то.
и имеет в этой точке локальный экстремум,
то.
Доказательство.Дифференцируемость означает существование конечного предела
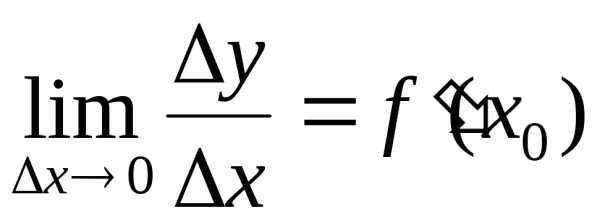 .
.
Для этого предела имеется три возможности: 1) ; 2);
3)
.
Предположим, что.
Тогда для близких к нулю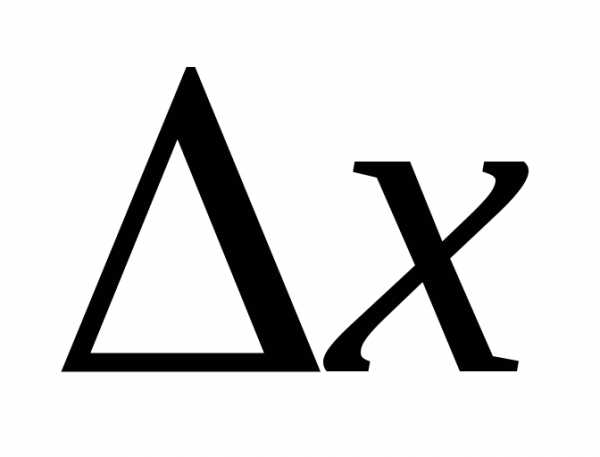 разностное отношение
разностное отношение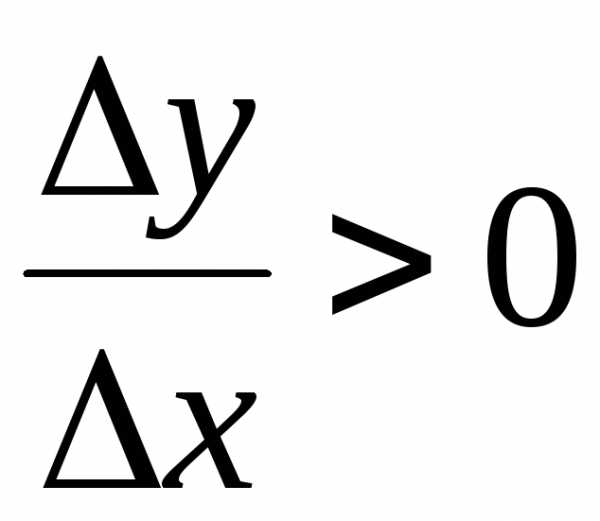 .
Если же,
то и
.
Если же,
то и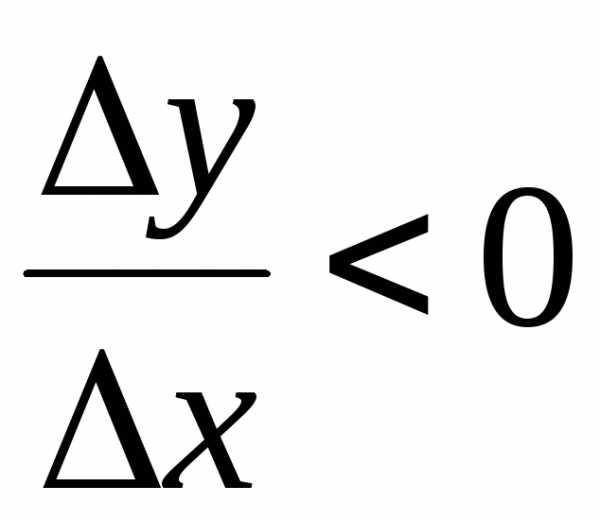 (для малых
(для малых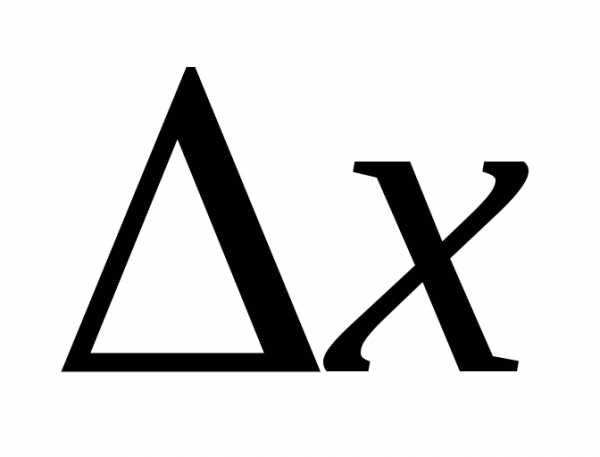 ).
В обоих случаях знак
).
В обоих случаях знак зависит от знака
зависит от знака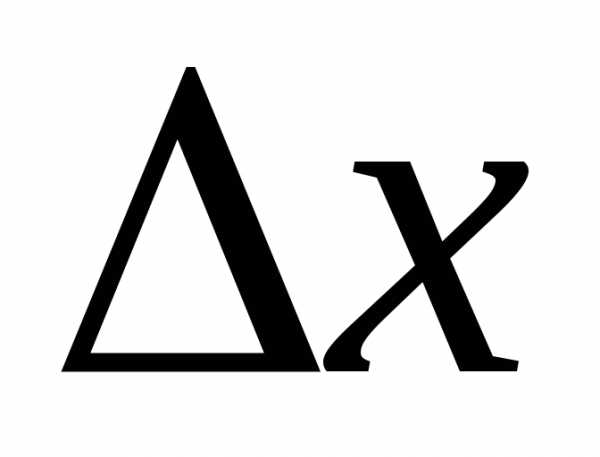 .
Но по условию теоремы
.
Но по условию теоремы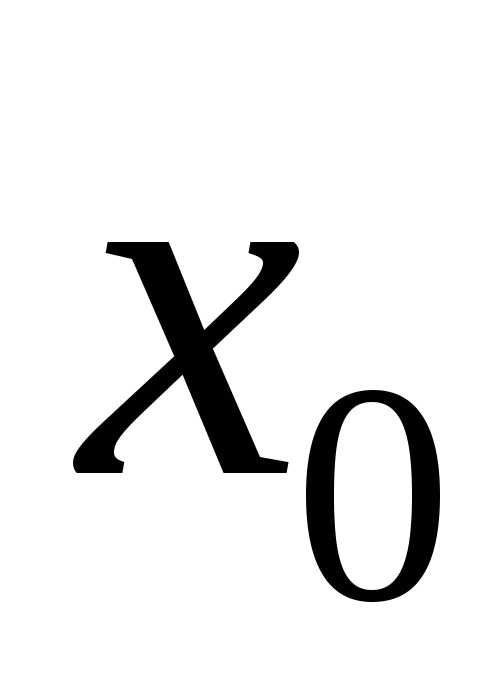 – это точка экстремума, значит, знак
– это точка экстремума, значит, знак
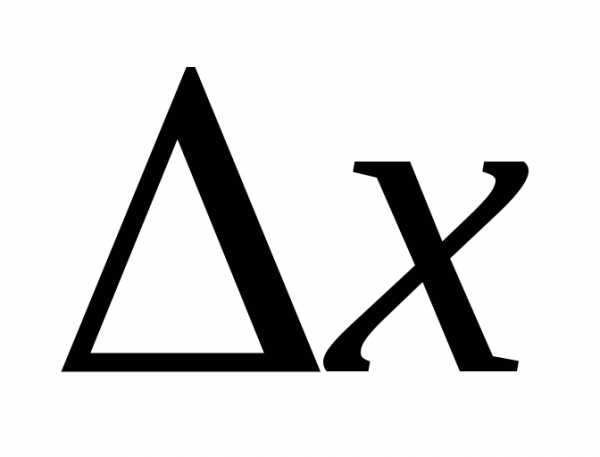 .
Это противоречие означает, что
.
Это противоречие означает, что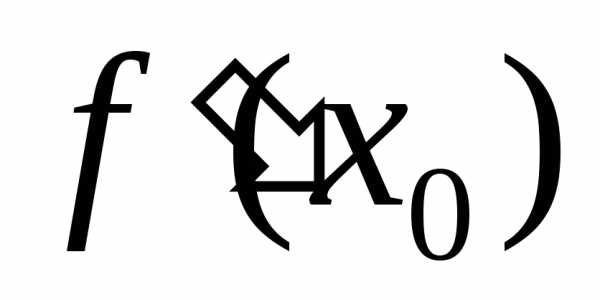 не может быть ни положительным, ни
отрицательным. Остается последняя
возможность:.
не может быть ни положительным, ни
отрицательным. Остается последняя
возможность:.Замечание 1.Эта теорема имеет простой геометрический смысл: если в точке графика функции, которой соответствует экстремум функции, существует касательная к графику, то эта касательная параллельная осиOx.
Замечание 2.Сформулированное
в теореме условиеявляется необходимым, но не достаточным.
Например, функция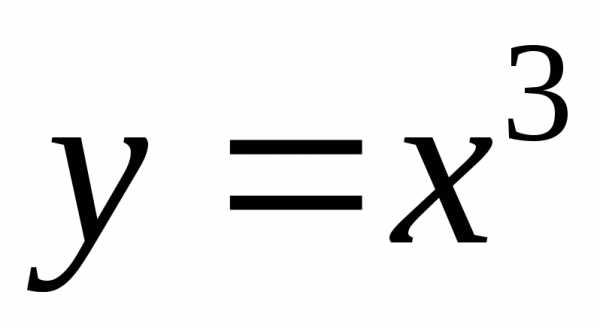 имеет производную,
которая обращается в ноль в точке
имеет производную,
которая обращается в ноль в точке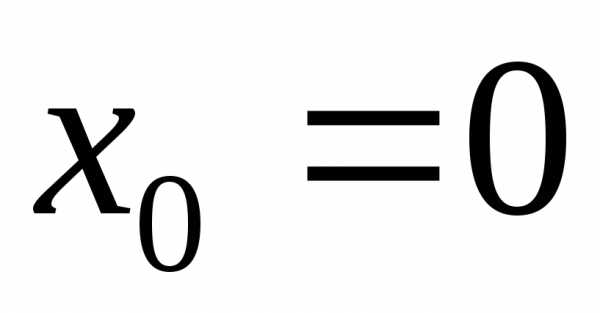 .
Однако,
.
Однако,
.
Выражение в скобках всегда положительно,
как неполный квадрат суммы. Следовательно,
и в точке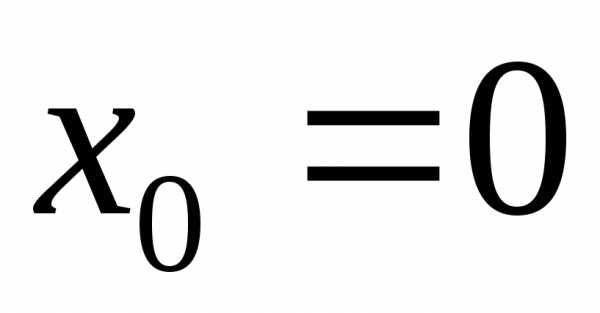
studfiles.net
III Таблица дифференциалов
Так как дифференциал dyлишь множителемdxотличается от производной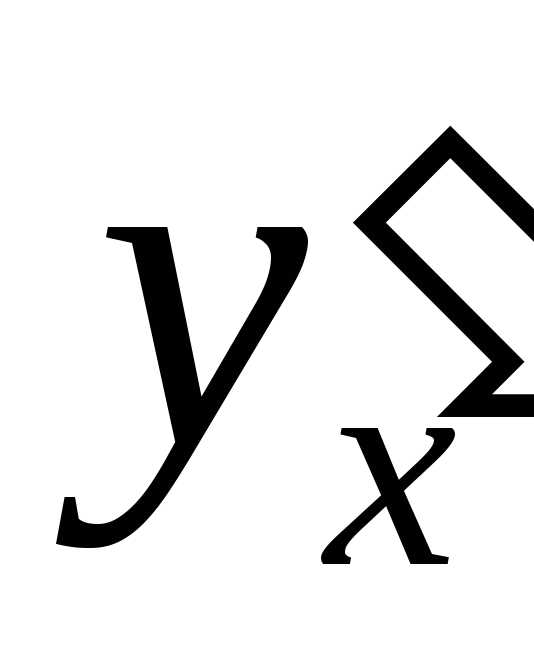 ,
то по таблице производных легко составить
таблицу дифференциалов.
,
то по таблице производных легко составить
таблицу дифференциалов.
1.
,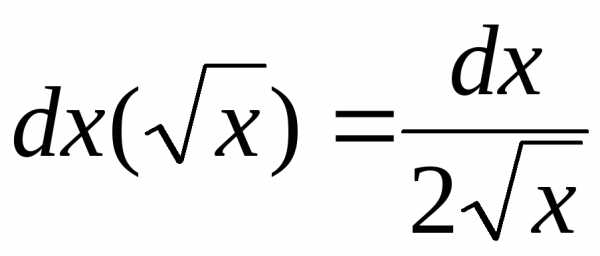 ,
,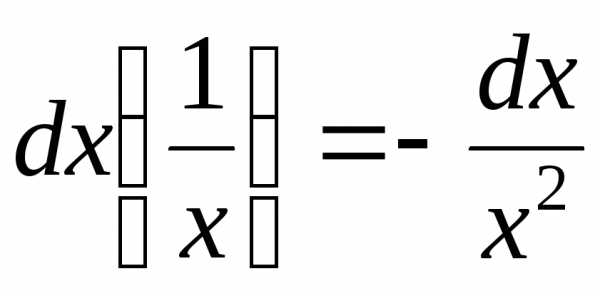 .
.
2. ,.
3. 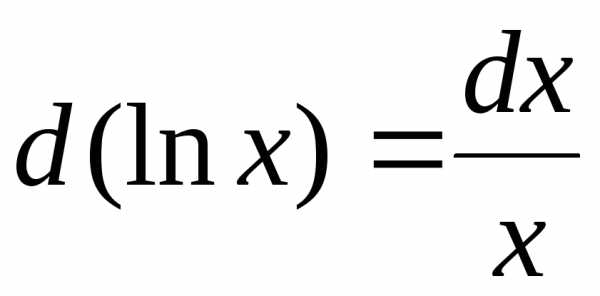 ,
,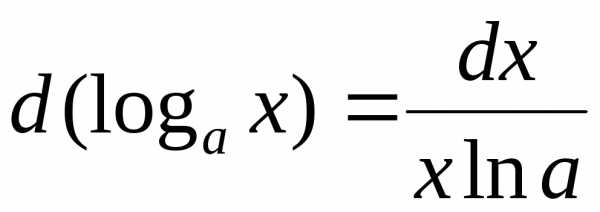
4. . 5..
6. 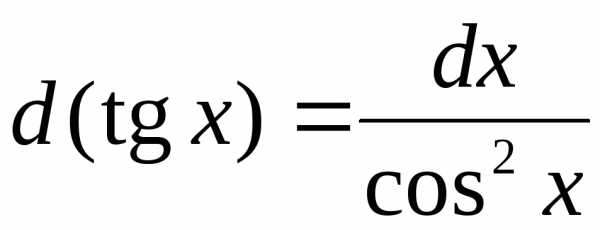 . 7..
. 7..
8. . 9..
10. . 11..
Также легко получить формулы для дифференциалов суммы, разности, произведения и частного функций:
а)
б)
в) 
Отметим, что в таблице дифференциалов переменная xможет быть как независимой, так и некоторой функцией. В таблице же производных (§6)x– это только независимая переменная.
Замечание.Формула для дифференциала
функции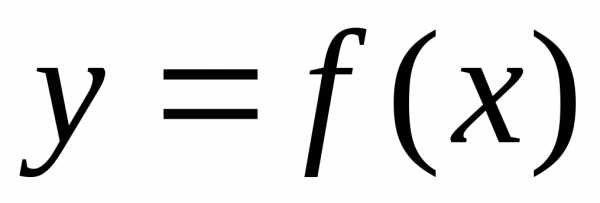 ,
а именно:
,
а именно:
,
позволяет написать формулу, выражающую производную функции через дифференциалы dxиdy:
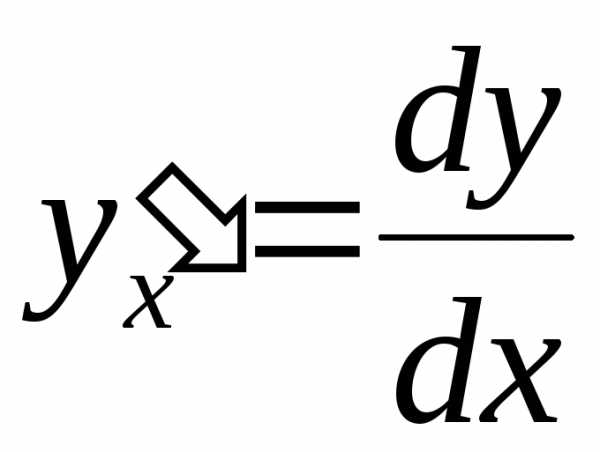 .
.
При этом такая формула сохраняет силу, по какой бы независимой переменной ни были вычислены dxиdy. Эта формула позволяет легко запоминать (но не доказывать!) некоторые правила дифференцирования:
для сложной функции
;
для обратной функции
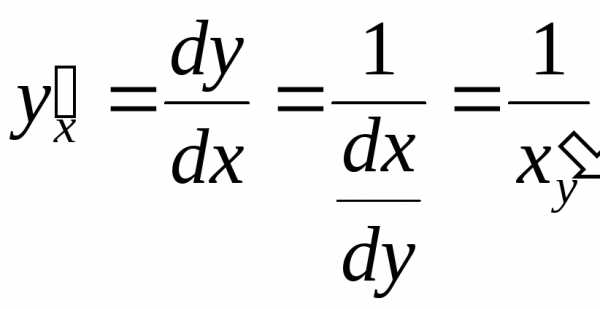 ;
;
для функции, заданной параметрически
.
§8. Производные высших порядков
I Определение и обозначения
Если функция 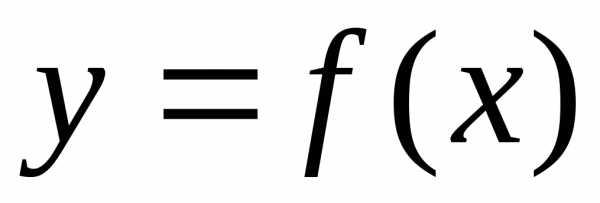 дифференцируема на некотором промежутке,
то её производная
дифференцируема на некотором промежутке,
то её производная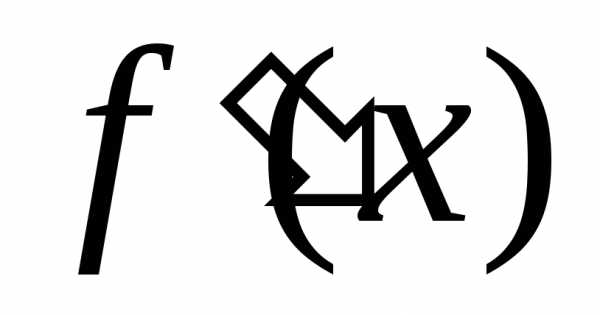 сама является функцией, определенной
на этом промежутке. Следовательно, по
отношению к ней можно ставить вопрос о
существовании и нахождении производной.
Если она существует, то её называют
второй производной (или производной
2гопорядка), и обозначают одним
из символов
сама является функцией, определенной
на этом промежутке. Следовательно, по
отношению к ней можно ставить вопрос о
существовании и нахождении производной.
Если она существует, то её называют
второй производной (или производной
2гопорядка), и обозначают одним
из символов
.
Аналогично, если существует производная
от второй производной, то её называют
третьей производной и обозначают,
например,  .
.
Вообще, производной n-го порядка называют производную от производной (n–1)-го порядка и обозначают. Итак, по определению
.
II Производные некоторых функций
1. y=sinx, y=cosx
Первые производные этих функций и формулы приведенияпозволяют методом математической индукции получить выражения для производныхn-го порядка:
.
2. y=x
Если 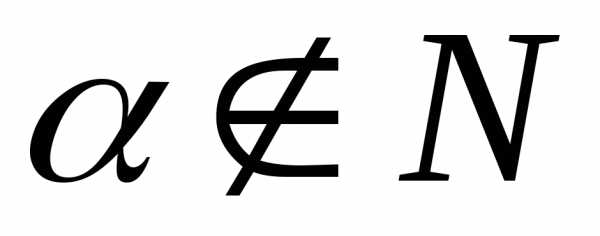 ,
то, последовательно дифференцируя,
получим,,
и вообще:
,
то, последовательно дифференцируя,
получим,,
и вообще:
.
Если же показатель степени натуральный, то:
3. y=ax
, в частности,,.
4. y=lnx
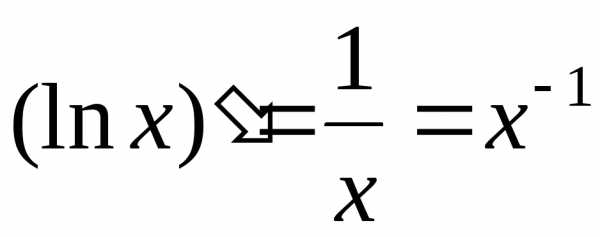 ,
,
.
III Некоторые правила
Очевидно, что и. Для производной
n-го порядка от произведения функций имеется т.н. формула Лейбница. Приведем ее без доказательства:
,
где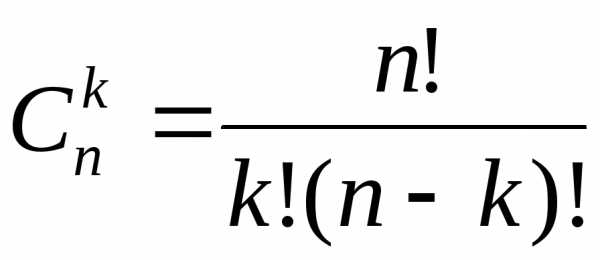 .
.
Заметим, что под производной нулевого порядка принято понимать саму
функцию: 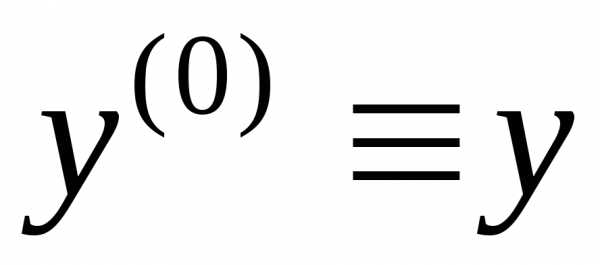 .
.
IV Функция, заданная параметрически
Пусть функция задана параметрическими уравнениями
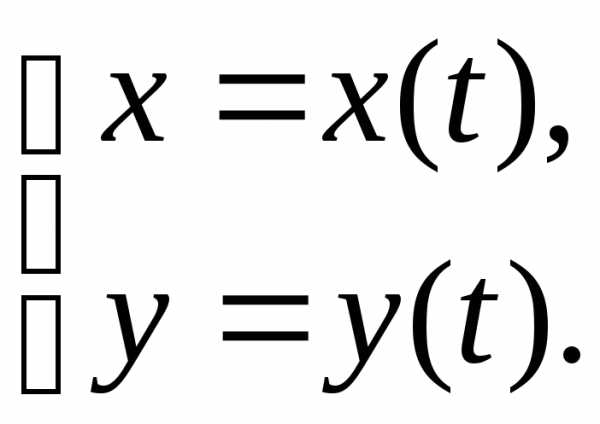
Её первая производная – это также функция, заданная параметрически:
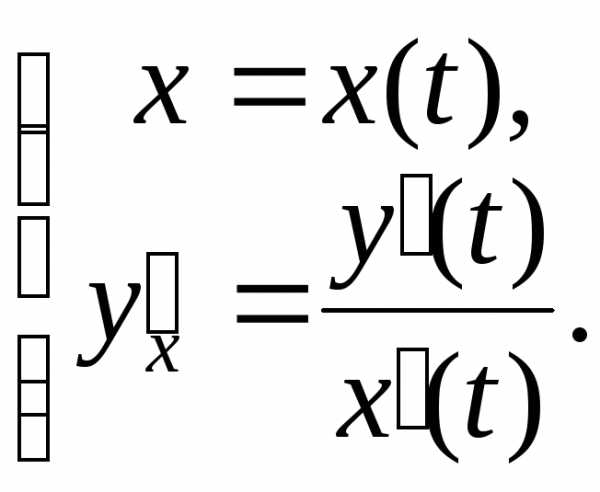
Тогда
Пример.Для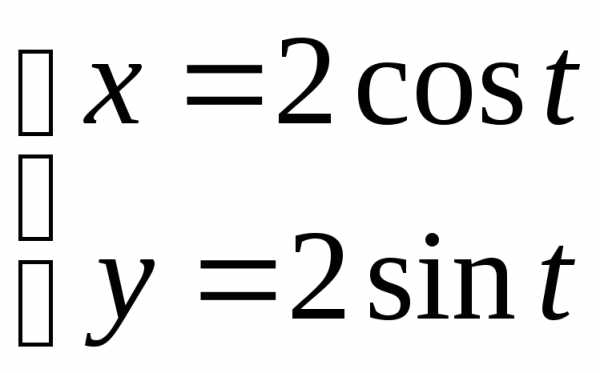 первая производная имеет вид
первая производная имеет вид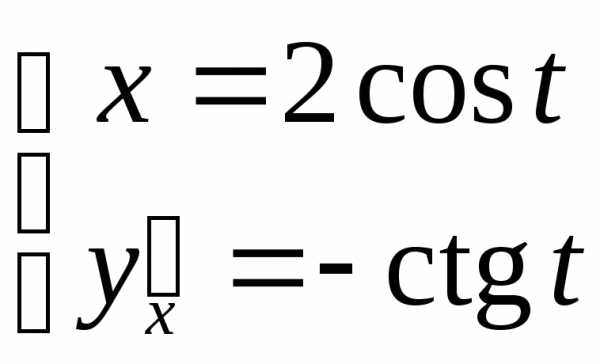 Тогдаи вторая производная такова:
Тогдаи вторая производная такова: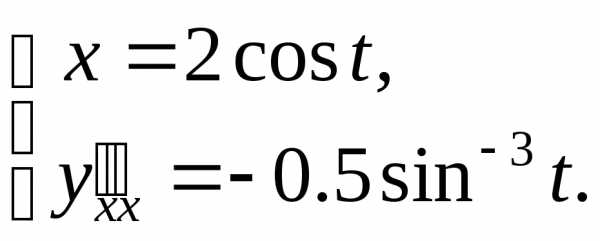
V Функция, заданная неявно
Повторное дифференцирование такой функции покажем на примере:
Тогда по определению:
.
Остается подставить в последнее выражение
значение 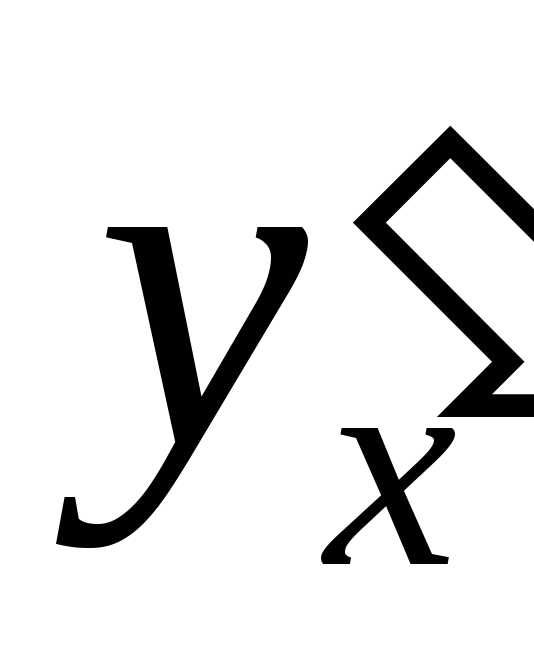 :
:
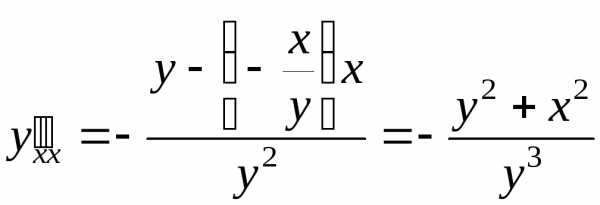 .
.
Полученное выражение можно упростить, используя само уравнение:
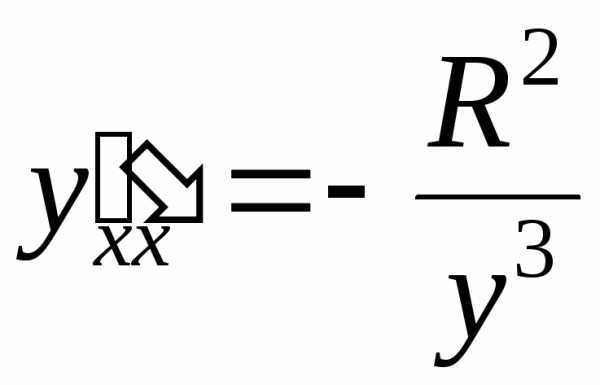 .
.
Тема ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Лекция 10
§1. Необходимое условие экстремума
Рассмотрим функцию
,
определенную на промежутке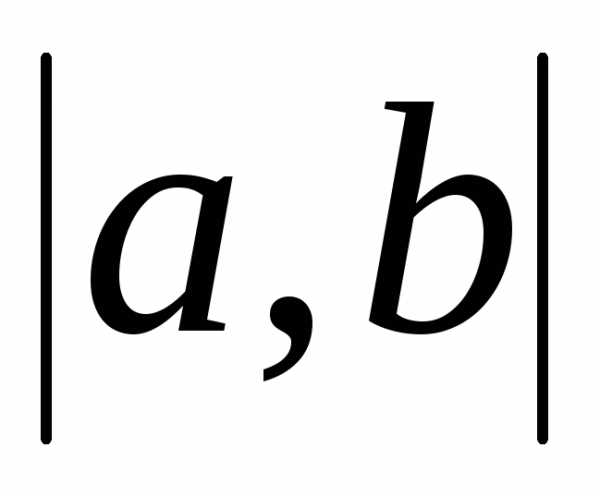 ,
и пусть точка
,
и пусть точка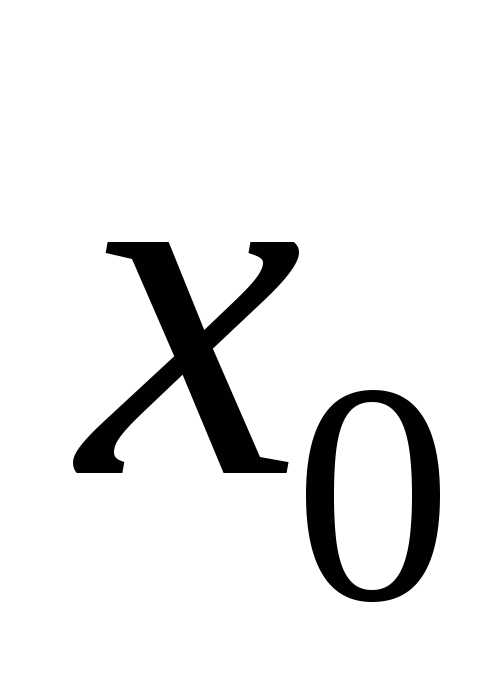 –внутренняяточка промежутка:
–внутренняяточка промежутка: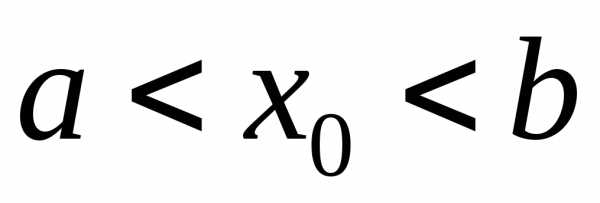 .
.
Определение 1.Точка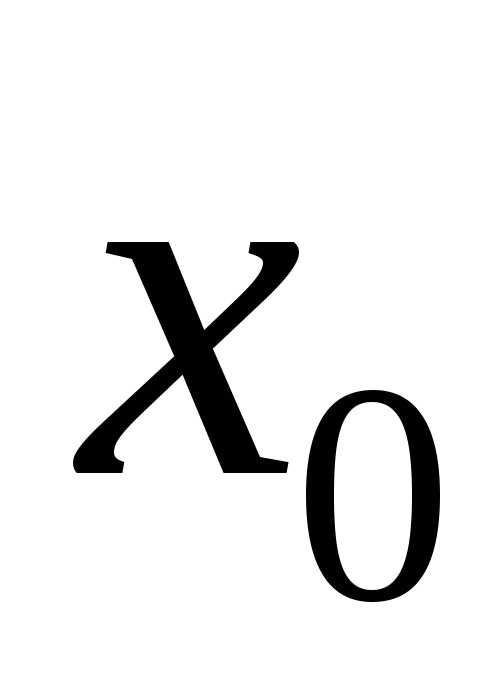 называется точкой (локального) максимума
функции,
если существует окрестность этой точки,
в которой (при
называется точкой (локального) максимума
функции,
если существует окрестность этой точки,
в которой (при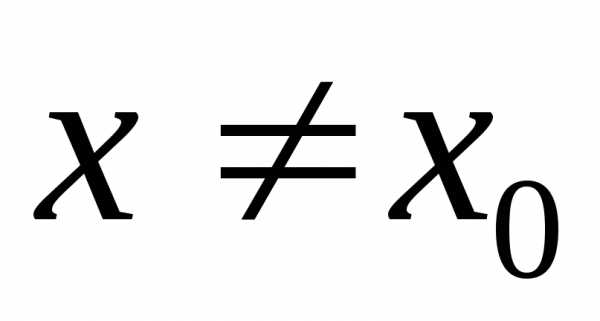 )
выполняется неравенство.
Другими словами для малых приращений
аргумента
)
выполняется неравенство.
Другими словами для малых приращений
аргумента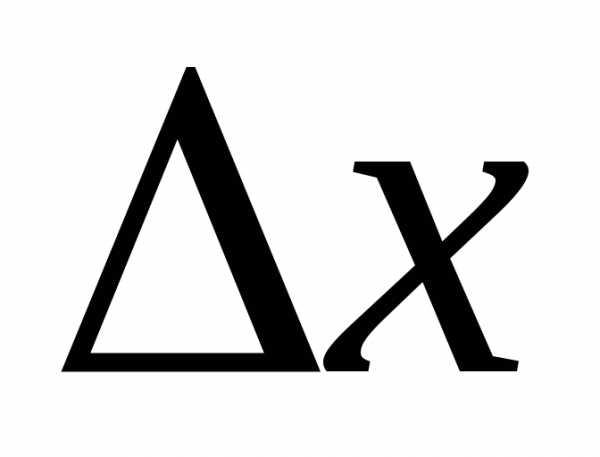 приращение
функции.
приращение
функции.
Определение 2.Точка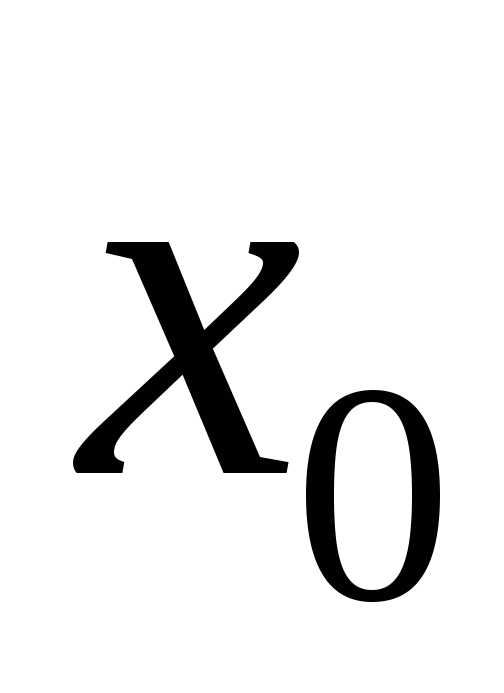 называется точкой (локального) минимума
функции,
если существует окрестность этой точки,
в которой (при
называется точкой (локального) минимума
функции,
если существует окрестность этой точки,
в которой (при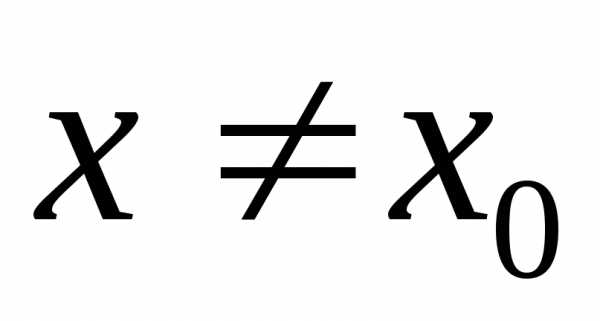 )
выполняется неравенство.
Другими словами
)
выполняется неравенство.
Другими словами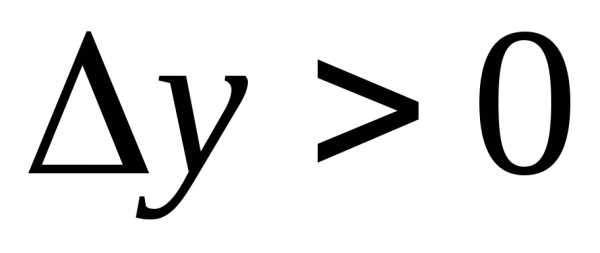 при малых
при малых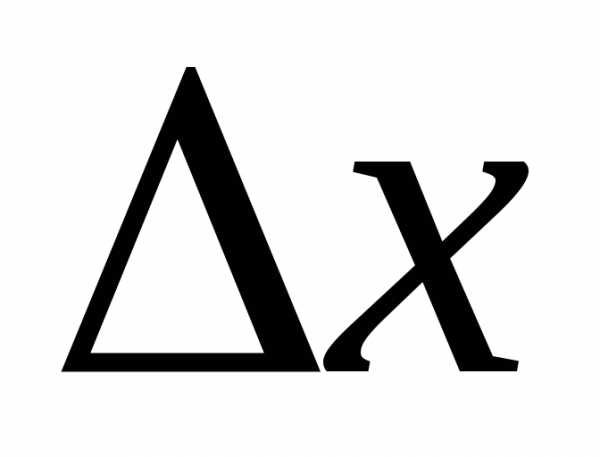 .
.
Точки максимума и минимума называются
точками экстремума. Их можно характеризовать
следующим образом: приращение функции
в точке экстремума имеет постоянный
знак, не зависящий от знака 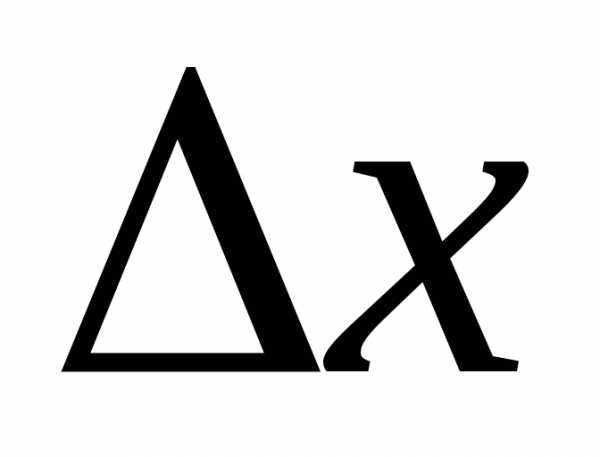 (если
(если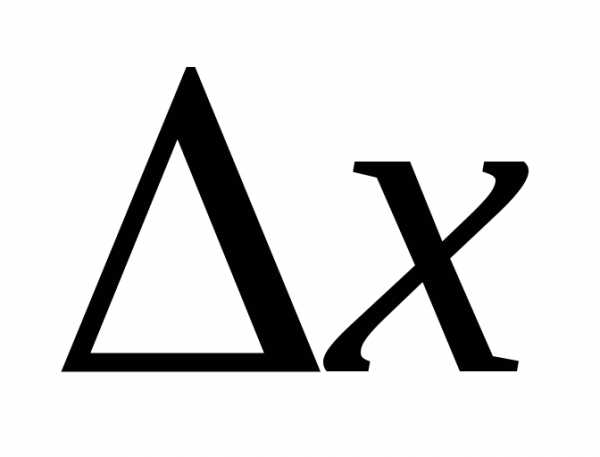 достаточно мало).
достаточно мало).
Теорема Ферма.Если функциядифференцируема в точке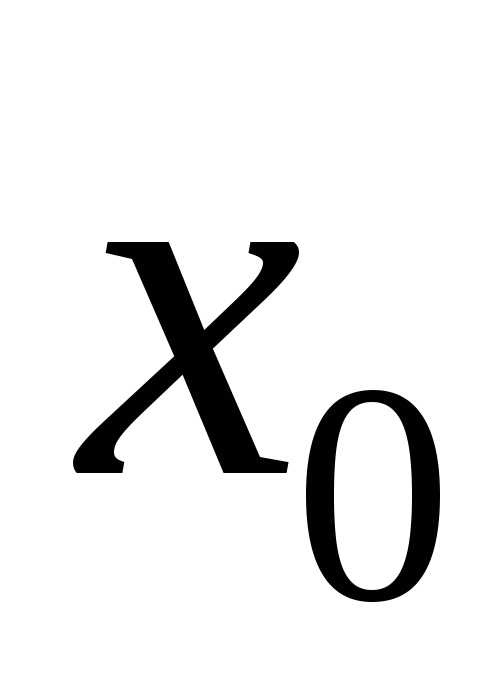 и имеет в этой точке локальный экстремум,
то.
и имеет в этой точке локальный экстремум,
то.
Доказательство.Дифференцируемость означает существование конечного предела
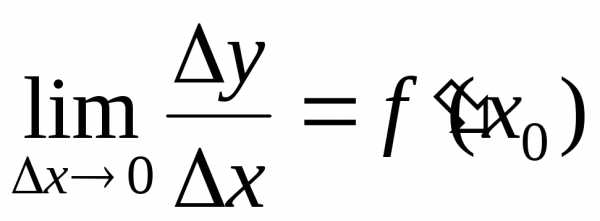 .
.
Для этого предела имеется три возможности: 1) ; 2);
3)
.
Предположим, что.
Тогда для близких к нулю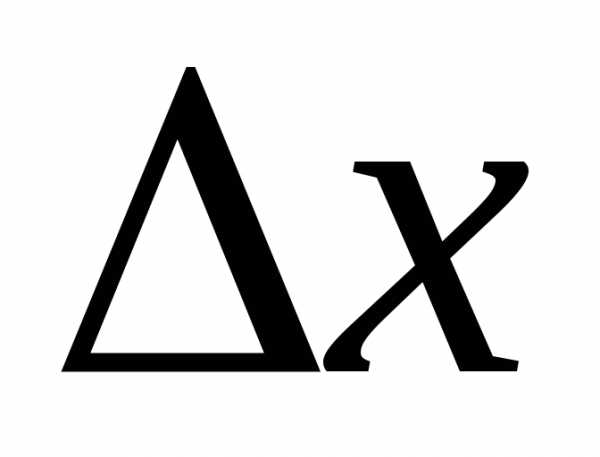 разностное отношение
разностное отношение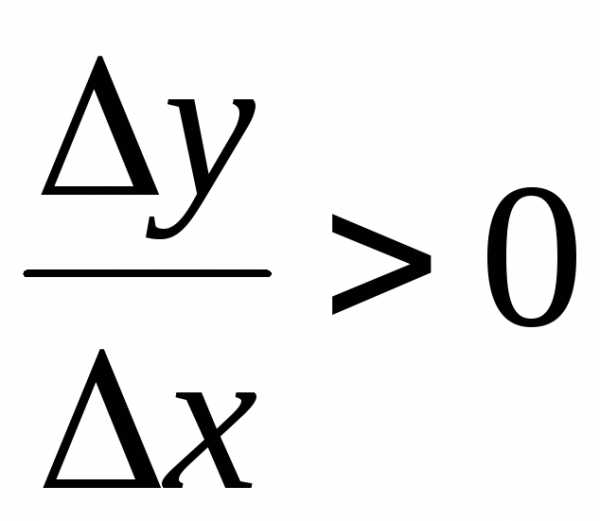 .
Если же,
то и
.
Если же,
то и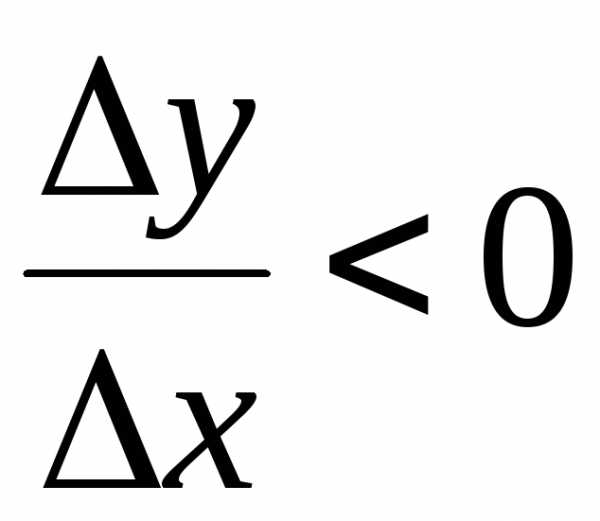 (для малых
(для малых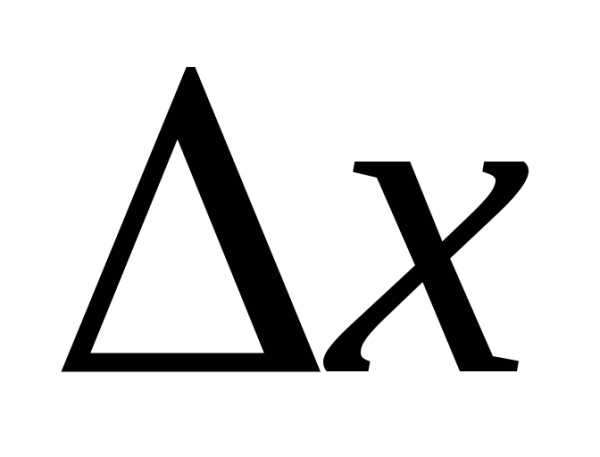 ).
В обоих случаях знак
).
В обоих случаях знак зависит от знака
зависит от знака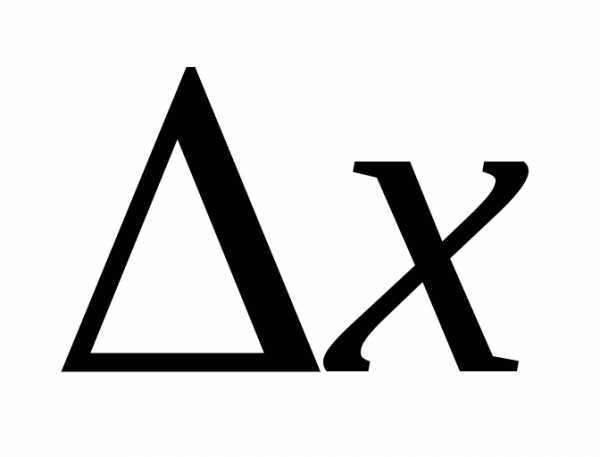 .
Но по условию теоремы
.
Но по условию теоремы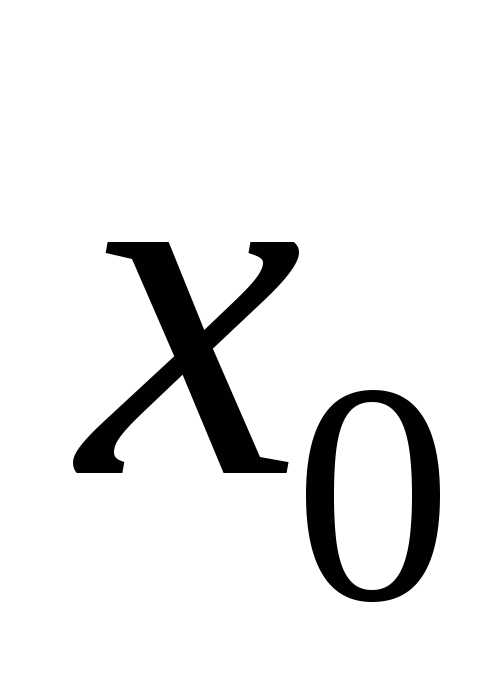 – это точка экстремума, значит, знак
– это точка экстремума, значит, знак не зависит от знака
не зависит от знака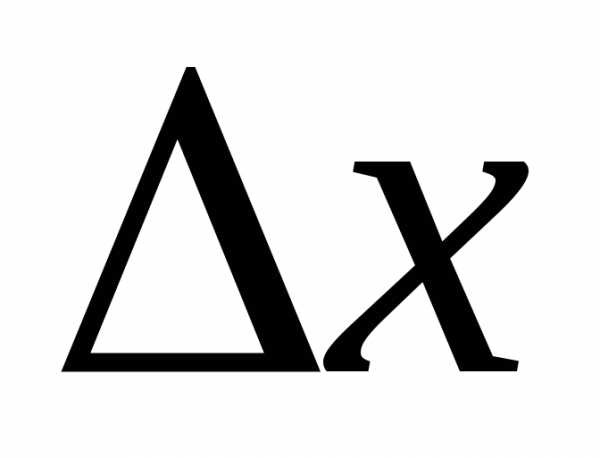 .
Это противоречие означает, что
.
Это противоречие означает, что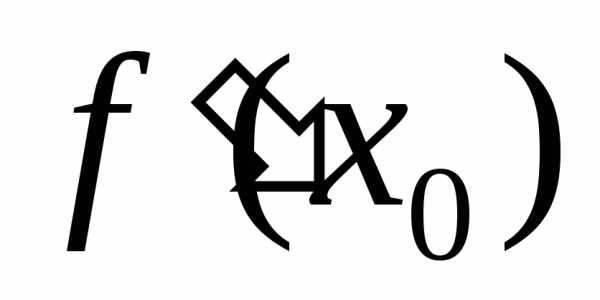 не может быть ни положительным, ни
отрицательным. Остается последняя
возможность:.
не может быть ни положительным, ни
отрицательным. Остается последняя
возможность:.
Замечание 1.Эта теорема имеет простой геометрический смысл: если в точке графика функции, которой соответствует экстремум функции, существует касательная к графику, то эта касательная параллельная осиOx.
Замечание 2.Сформулированное
в теореме условиеявляется необходимым, но не достаточным.
Например, функция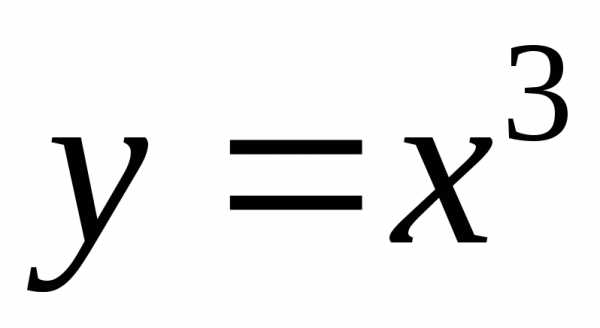 имеет производную
имеет производную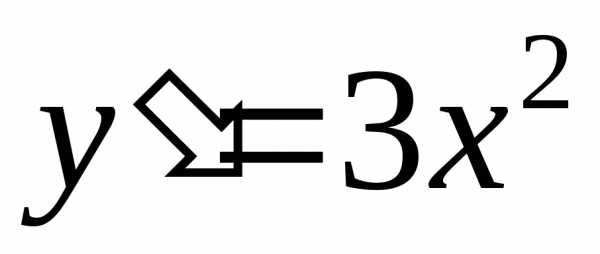 ,
которая обращается в ноль в точке
,
которая обращается в ноль в точке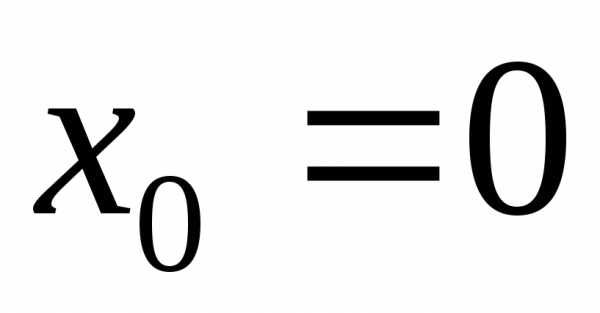 .
Однако,
.
Однако,
.
Выражение в скобках всегда положительно,
как неполный квадрат суммы. Следовательно,
и в точке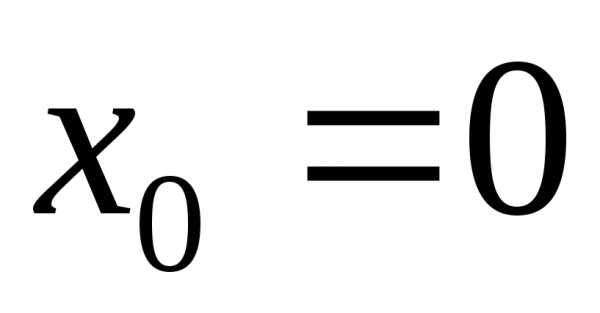 нет экстремума.
нет экстремума.
studfiles.net
Дифференциал функции
Литература.[1], [2], [6], [7], [17].
Понятие дифференциала функции, его геометрический смысл
Пусть функция  дифференцируема на отрезке
дифференцируема на отрезке .
Производная этой функции в некоторой
точке
.
Производная этой функции в некоторой
точке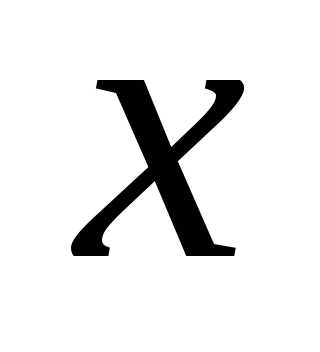 отрезка
отрезка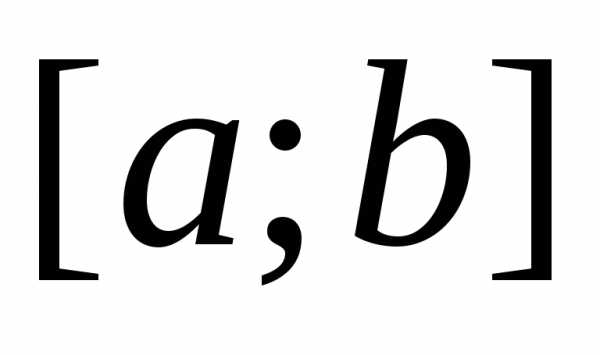 определяется равенством:
определяется равенством: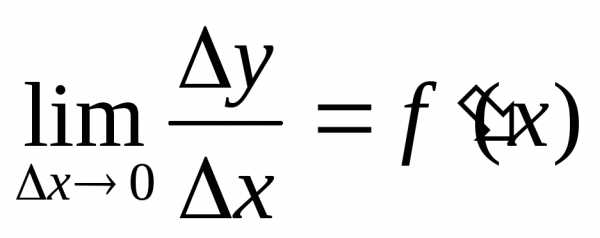 .
Тогда, по теореме о связи функции, её
предела и бесконечно малой функции,
можно записать,
где
.
Тогда, по теореме о связи функции, её
предела и бесконечно малой функции,
можно записать,
где при
при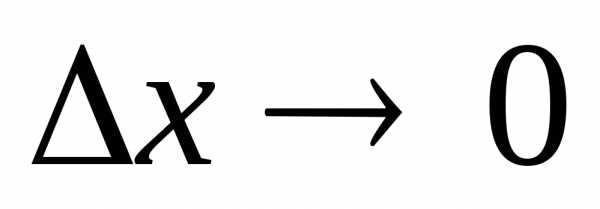 ,
или.
,
или.
Приращение функции  состоит из двух слагаемых, из которых
первое есть так называемая главная
часть приращения, линейная относительно
состоит из двух слагаемых, из которых
первое есть так называемая главная
часть приращения, линейная относительно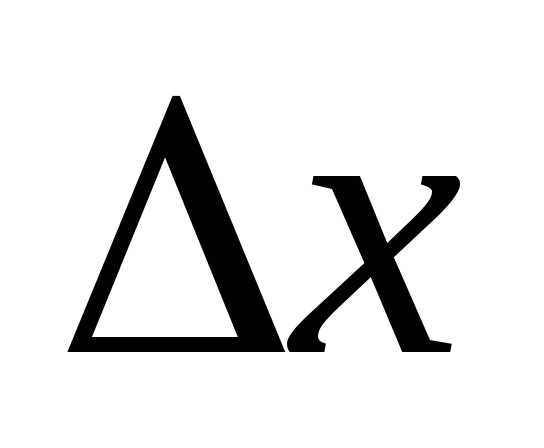 .
.
Дифференциалом функции 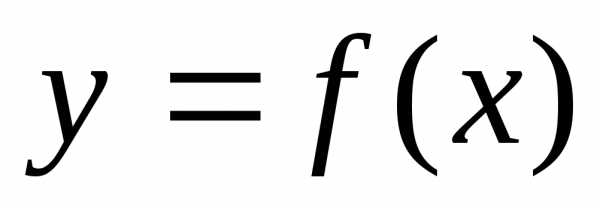 в точке
в точке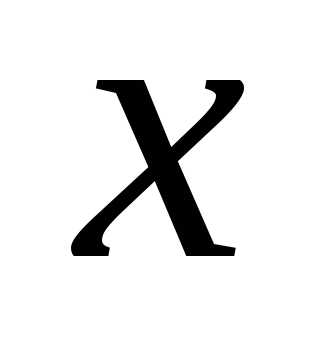 называется главная часть её приращения,
которая равна произведению производной
функции на приращение аргумента, и
обозначается
называется главная часть её приращения,
которая равна произведению производной
функции на приращение аргумента, и
обозначается или
или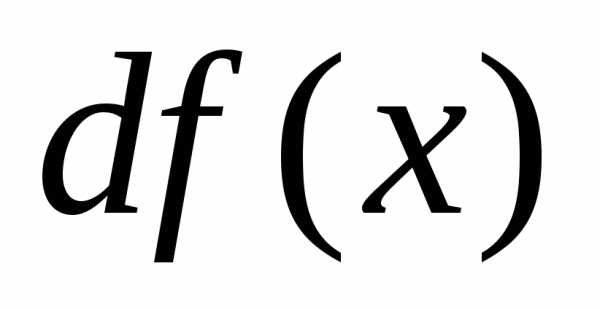 :.
:.
Дифференциал  называют
также дифференциалом первого порядка.
называют
также дифференциалом первого порядка.
Дифференциал независимой переменной
равен приращению этой переменной: 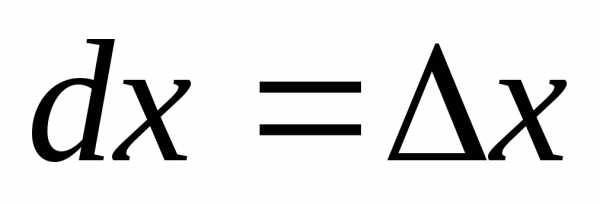 и тогда,
дифференциал функции равен произведению
производной этой функции на дифференциал
независимой переменной.
и тогда,
дифференциал функции равен произведению
производной этой функции на дифференциал
независимой переменной.
Пример 1.Найти дифференциал функции.
Решение:По формуленаходим
.
Основные теоремы о дифференциалах. Таблица дифференциалов.
Теорема 1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяется формулами:
Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточной переменной на дифференциал этой промежуточной переменной
.
Таблица дифференциалов

Применение дифференциала в приближенных вычислениях
.
Пример 2. Вычислить приближенно.
Решение. Рассмотрим функциюf(x)=arctg x.
По формуле имеем:
,
т.е.
.
Так как
,
то при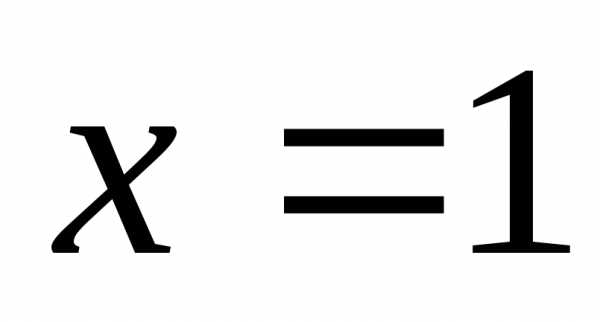 иполучаем:
иполучаем:
.
Вопросы для самопроверки
1.Что называется дифференциалом функции, каков его геометрический смысл?
2. Сформулируйте основные свойства дифференциала функции.
3. Чем отличается дифференциал функции от ее приращения?
4. Укажите формулу для приближенного вычисления значений функции с помощью дифференциала.
5. Что называется дифференциалом второго порядка от данной функции?
Приложения производной
Литература.[1], [2], [6], [7], [17].
Применение производной к вычислению пределов.
Кроме элементарных способов, весьма эффективным средством для нахождения предела функции в тех случаях, когда аргумент неограниченно возрастает или стремится к значению, которое не входит в область определения функции, является правило Лопиталя.
Теорема.Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если он существует или равен бесконечности.
Итак, если имеются неопределенности
вида 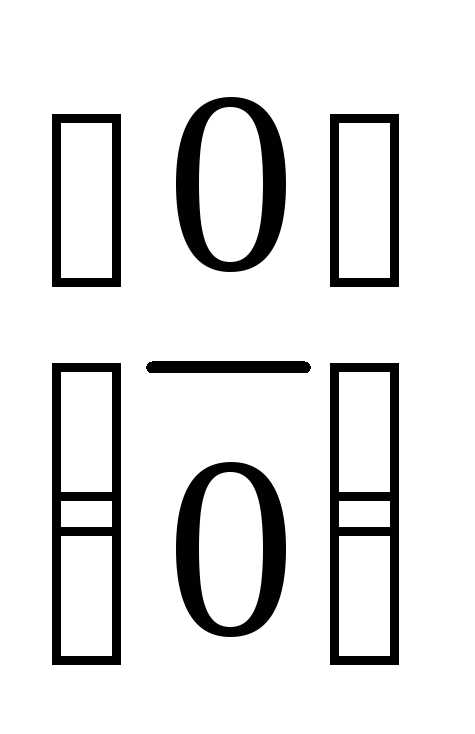 или
или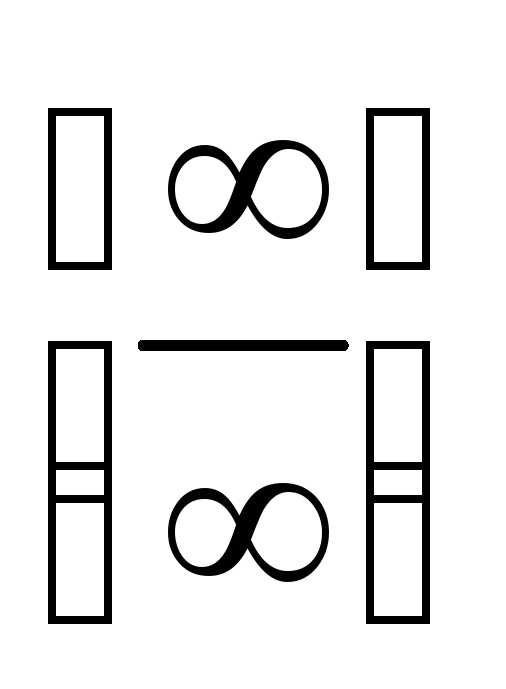 ,
то
,
то
.
Обращаем внимание, что в правой части формулы берется отношение производных, а не производная отношения.
Пример.Найти: а)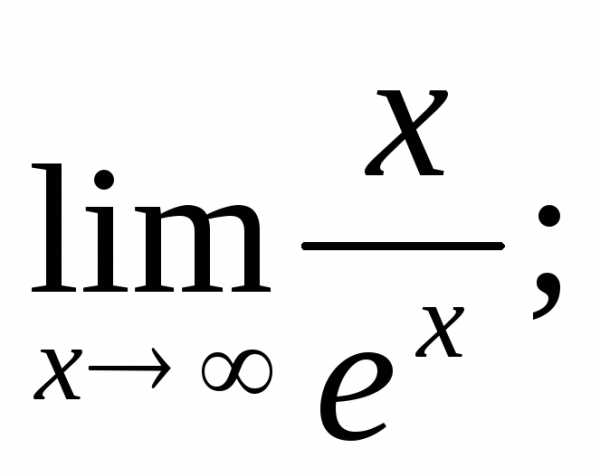 б)
б)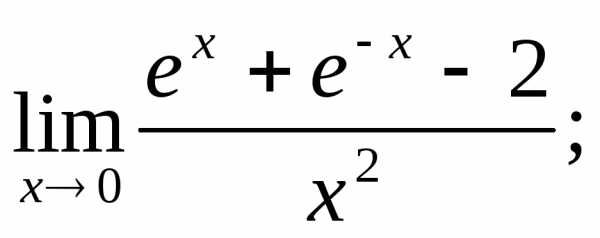 в)
в)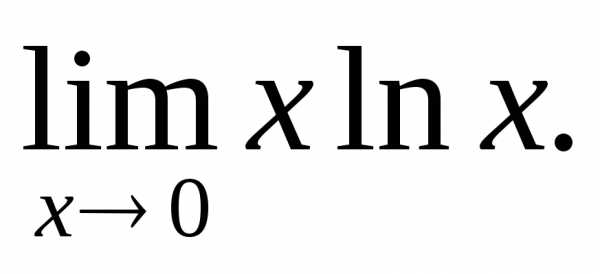
Решение.а) Имеем неопределенность
вида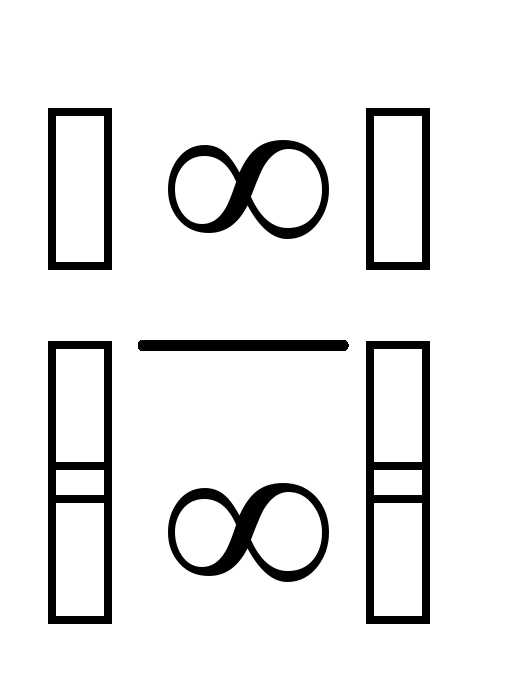 .
Применяя правило Лопиталя, получим:
.
Применяя правило Лопиталя, получим:
б)
Неопределенность вида 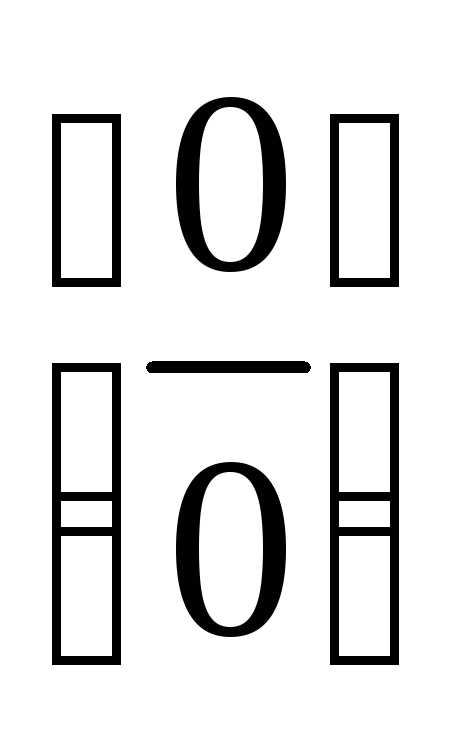 по-прежнему сохраняется. Применим
правило Лопиталя еще раз:
по-прежнему сохраняется. Применим
правило Лопиталя еще раз:
в) Имеем неопределенность вида 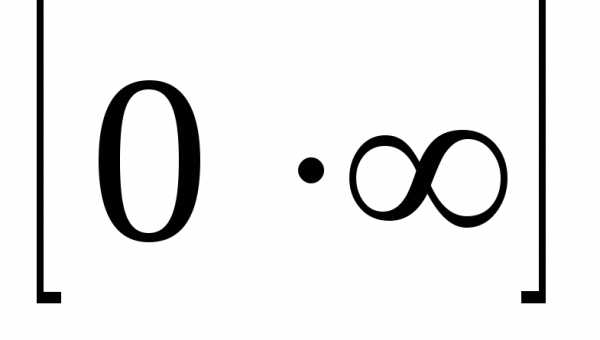 .
Переписываем данное выражение в виде
.
Переписываем данное выражение в виде

получим неопределенность вида 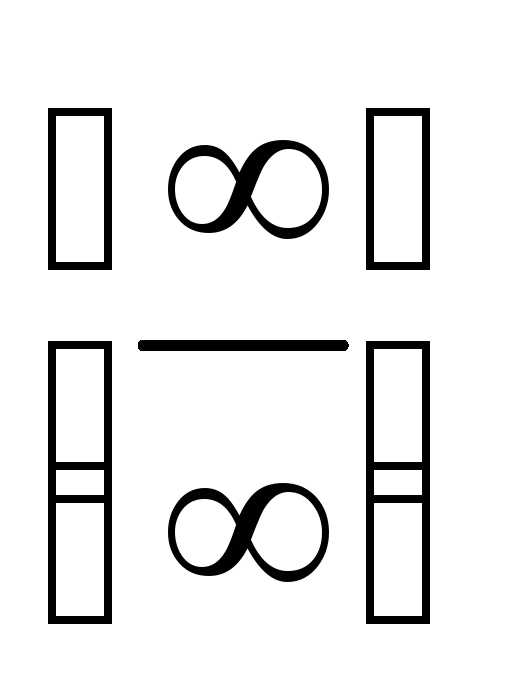 .
Применяя правило Лопиталя, получим
.
Применяя правило Лопиталя, получим
.
Применение производной к исследованию функций Возрастание и убывание функций
При изучении поведения функции в зависимости от изменения независимой переменной обычно предполагается, что во всей области определения функции независимая переменная изменяется монотонно возрастая, т.е. что каждое следующее ее значение больше предыдущего.
Если при этом последовательные значения функции также возрастают, то и функция называется возрастающей, а если они убывают, то и функция называется убывающей.
Некоторые функции во всей своей области определения изменяются монотонно – только возрастают или только убывают (например ).
Многие функции изменяются не монотонно. В одних интервалах изменения независимой переменной они возрастают, а в других интервалах убывают (например, sinx,cosx).
Возрастание и убывание функции 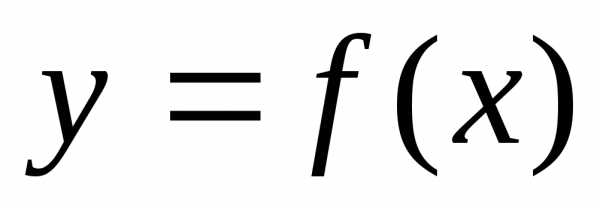 характеризуется значением ее производной
характеризуется значением ее производной :
если в некотором интервале
:
если в некотором интервале >0,
то функция возрастает, а если
>0,
то функция возрастает, а если <0,
то функция убывает в этом интервале.
<0,
то функция убывает в этом интервале.
studfiles.net
III Таблица дифференциалов
Так как дифференциал dyлишь множителемdxотличается от производной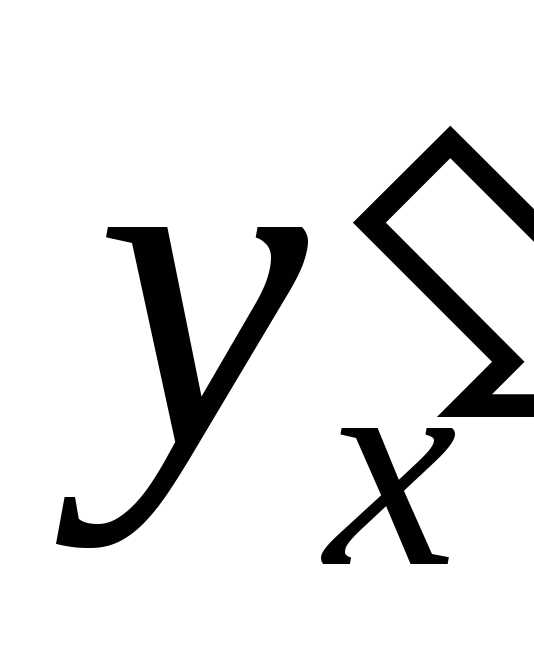 ,
то по таблице производных легко составить
таблицу дифференциалов.
,
то по таблице производных легко составить
таблицу дифференциалов.
1.
,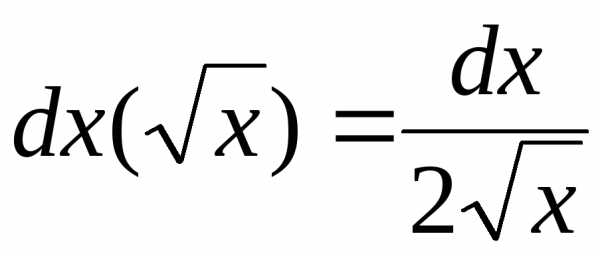 ,
,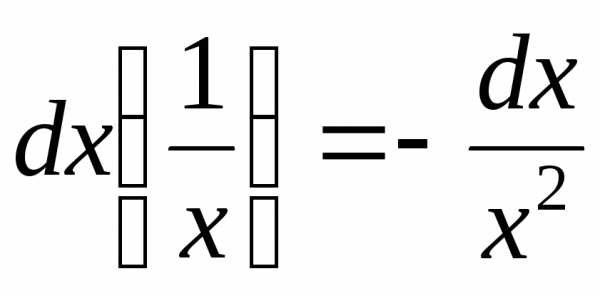 .
.
2. ,.
3. 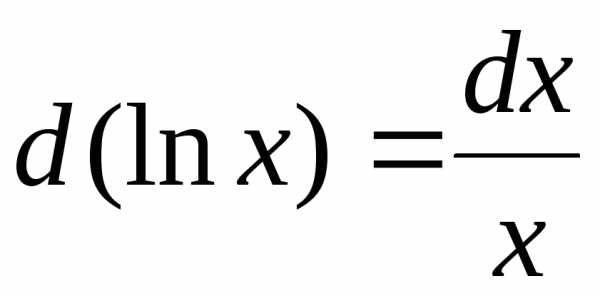 ,
,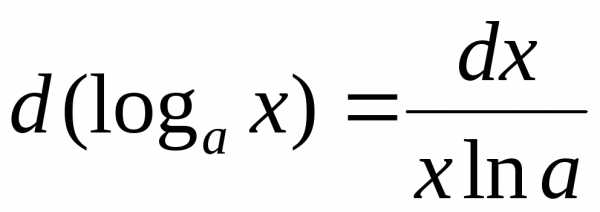 .
.
4. . 5..
6. 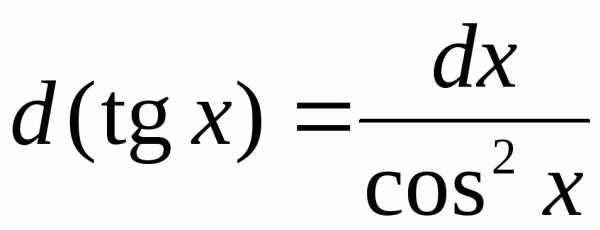 . 7..
. 7..
8. . 9..
10. . 11..
Также легко получить формулы для дифференциалов суммы, разности, произведения и частного функций:
а)
б)
в) 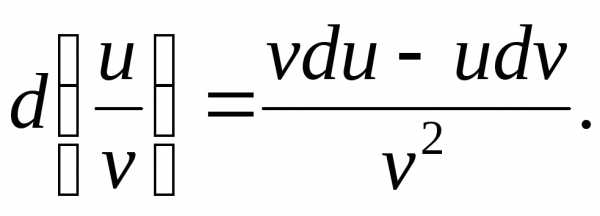
Отметим, что в таблице дифференциалов переменная xможет быть как независимой, так и некоторой функцией. В таблице же производных (§6)x– это только независимая переменная.
Замечание.Формула для дифференциала
функции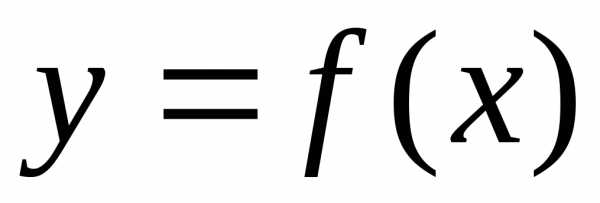 ,
а именно:
,
а именно:
,
позволяет написать формулу, выражающую производную функции через дифференциалы dxиdy:
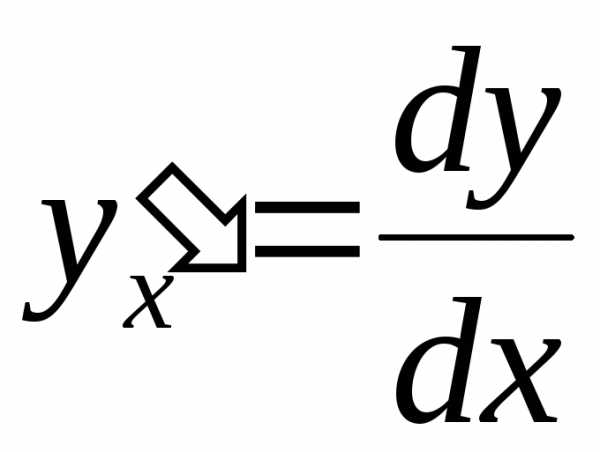 .
.
При этом такая формула сохраняет силу, по какой бы независимой переменной ни были вычислены dxиdy. Эта формула позволяет легко запоминать (но не доказывать!) некоторые правила дифференцирования:
для сложной функции
;
для обратной функции
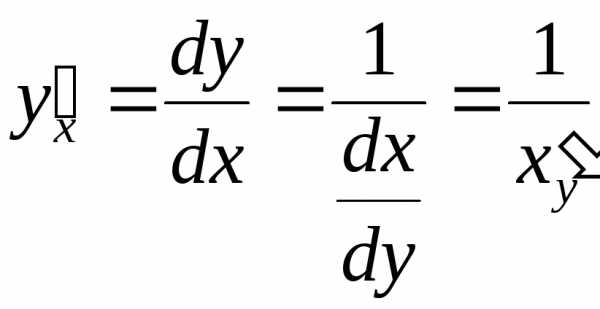 ;
;
для функции, заданной параметрически
.
§8. Производные высших порядков
I Определение и обозначения
Если функция 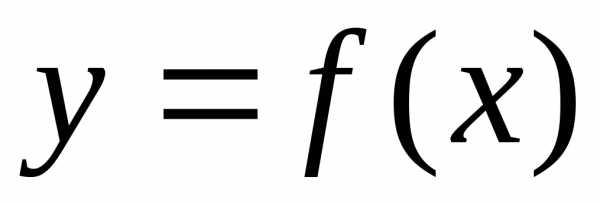 дифференцируема на некотором промежутке,
то её производная
дифференцируема на некотором промежутке,
то её производная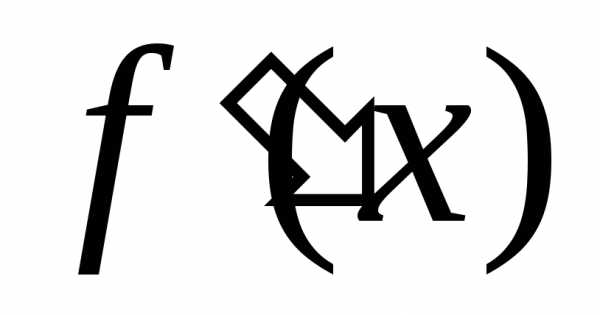 сама является функцией, определенной
на этом промежутке. Следовательно, по
отношению к ней можно ставить вопрос о
существовании и нахождении производной.
Если она существует, то её называют
второй производной (или производной
2гопорядка), и обозначают одним
из символов
сама является функцией, определенной
на этом промежутке. Следовательно, по
отношению к ней можно ставить вопрос о
существовании и нахождении производной.
Если она существует, то её называют
второй производной (или производной
2гопорядка), и обозначают одним
из символов
.
Аналогично, если существует производная
от второй производной, то её называют
третьей производной и обозначают,
например,  .
.
Вообще, производной n-го порядка называют производную от производной (n–1)-го порядка и обозначают. Итак, по определению
.
II Производные некоторых функций
1. y=sinx, y=cosx
Первые производные этих функций и формулы приведенияпозволяют методом математической индукции получить выражения для производныхn-го порядка:
.
2. y=x
Если 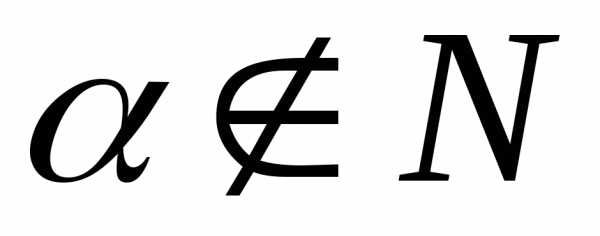 ,
то, последовательно дифференцируя,
получим,,
и вообще:
,
то, последовательно дифференцируя,
получим,,
и вообще:
.
Если же показатель степени натуральный, то:
3. y=ax
, в частности,,.
4. y=lnx
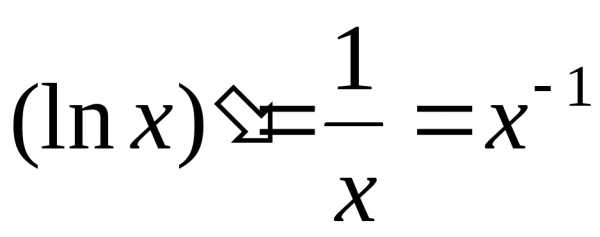 ,
,
.
III Некоторые правила
Очевидно, что и. Для производной
n-го порядка от произведения функций имеется т.н. формула Лейбница. Приведем ее без доказательства:
,
где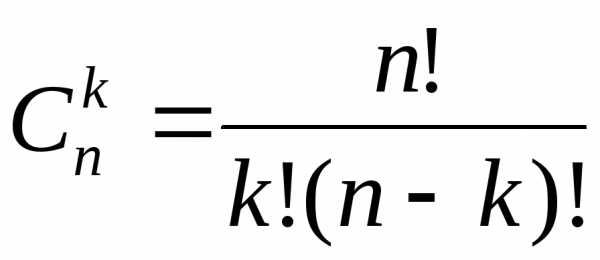 .
.
Заметим, что под производной нулевого порядка принято понимать саму
функцию: 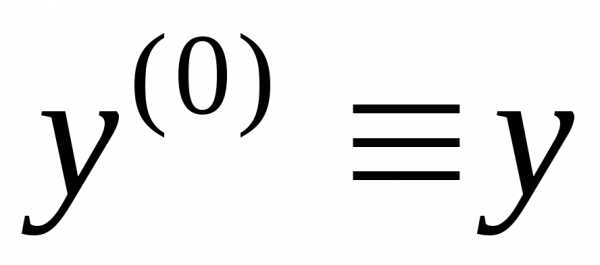 .
.
IV Функция, заданная параметрически
Пусть функция задана параметрическими уравнениями
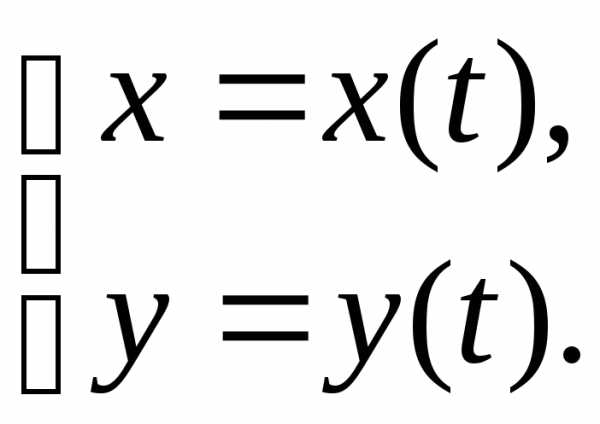
Её первая производная – это также функция, заданная параметрически:
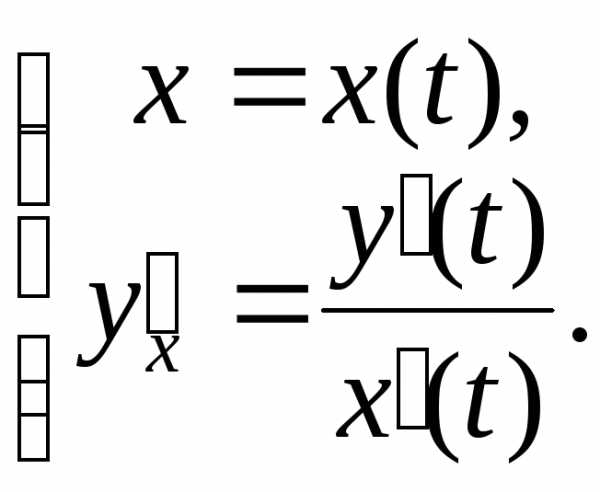
Тогда
Пример.Для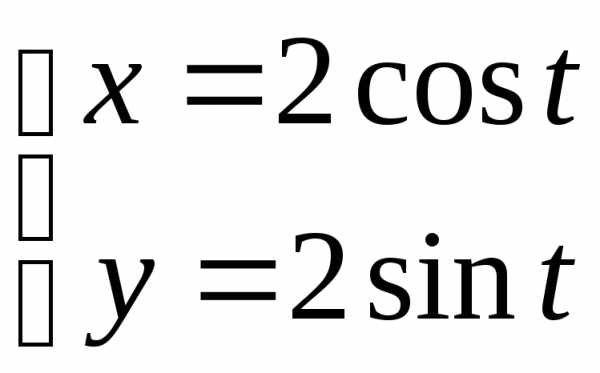 первая производная имеет вид
первая производная имеет вид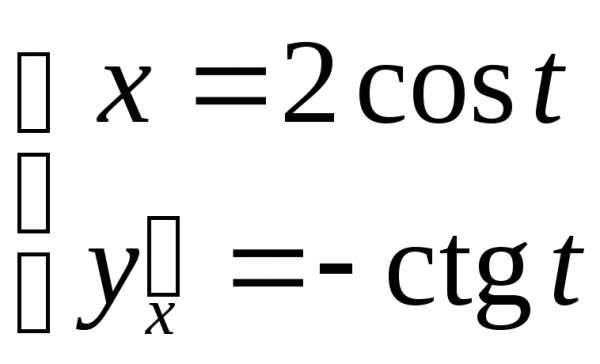 Тогдаи вторая производная такова:
Тогдаи вторая производная такова: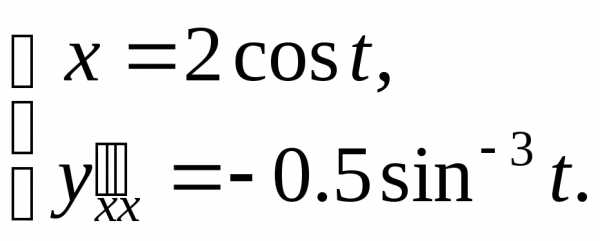
V Функция, заданная неявно
Повторное дифференцирование такой функции покажем на примере:
Тогда по определению:
.
Остается подставить в последнее выражение
значение 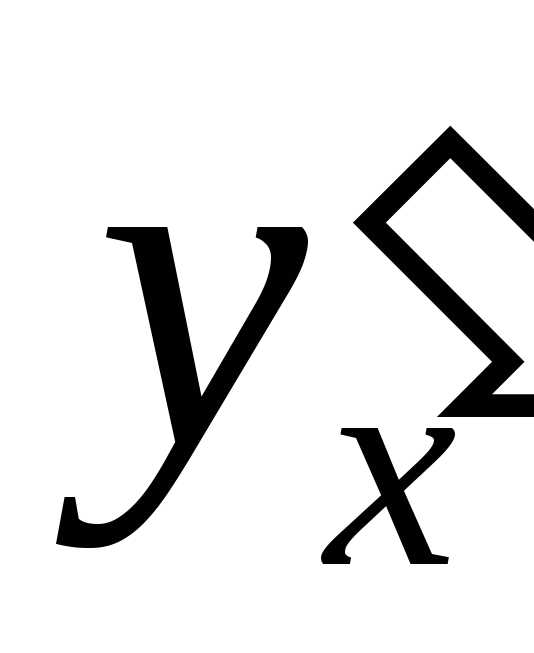 :
:
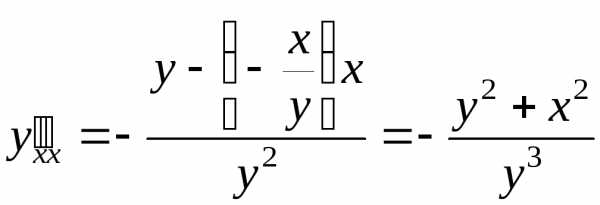 .
.
Полученное выражение можно упростить, используя само уравнение:
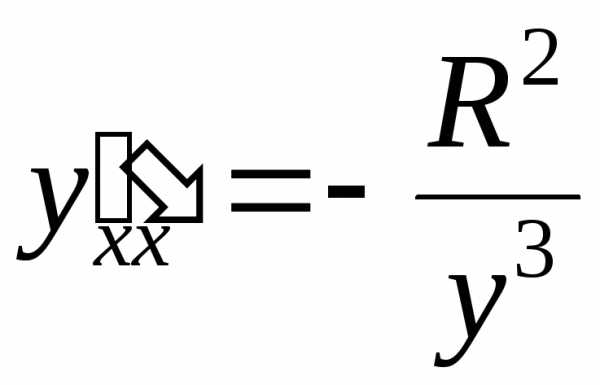 .
.
Тема ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Лекция 10
§1. Необходимое условие экстремума
Рассмотрим функцию
,
определенную на промежутке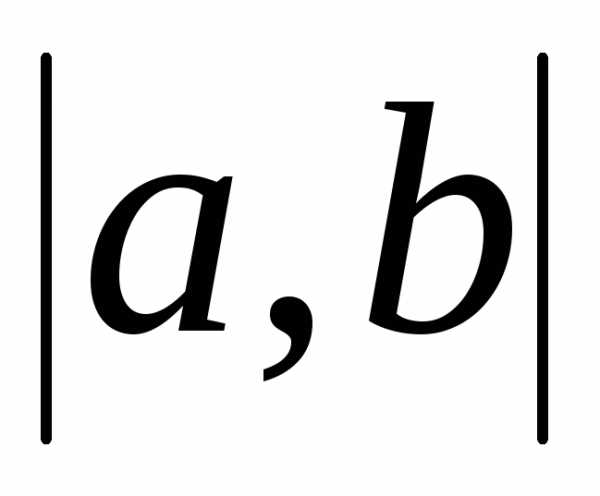 ,
и пусть точка
,
и пусть точка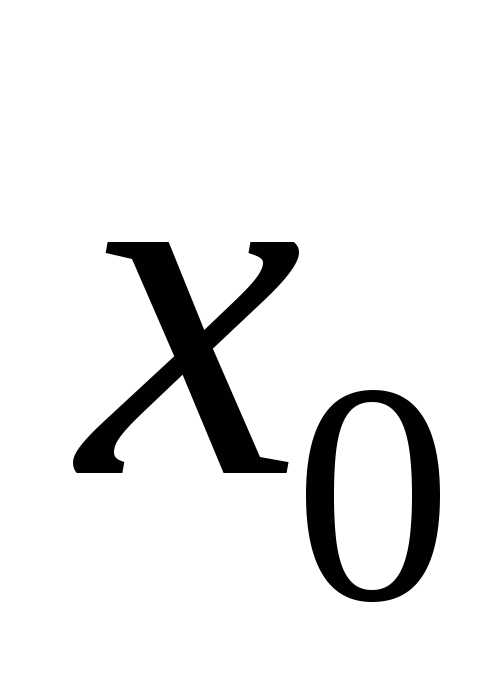 –внутренняяточка промежутка:
–внутренняяточка промежутка: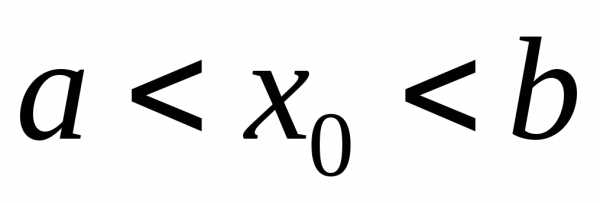 .
.
Определение 1.Точка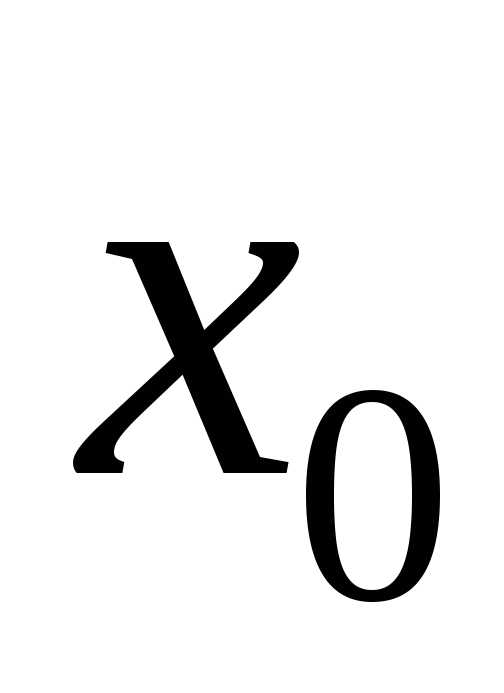 называется точкой (локального) максимума
функции,
если существует окрестность этой точки,
в которой (при
называется точкой (локального) максимума
функции,
если существует окрестность этой точки,
в которой (при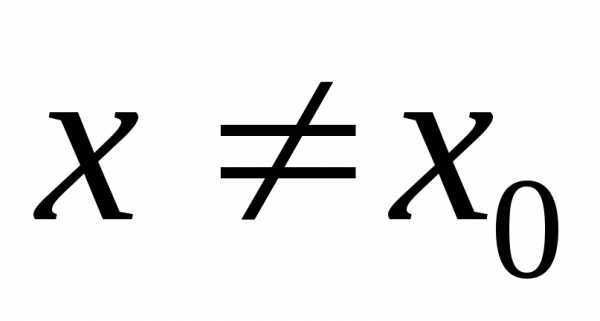 )
выполняется неравенство.
Другими словами для малых приращений
аргумента
)
выполняется неравенство.
Другими словами для малых приращений
аргумента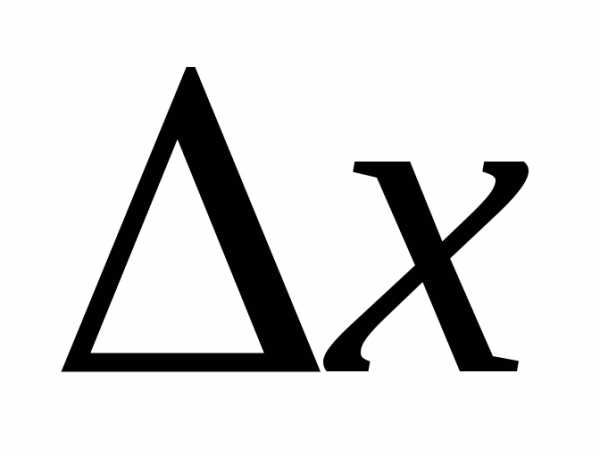 приращение
функции.
приращение
функции.
Определение 2.Точка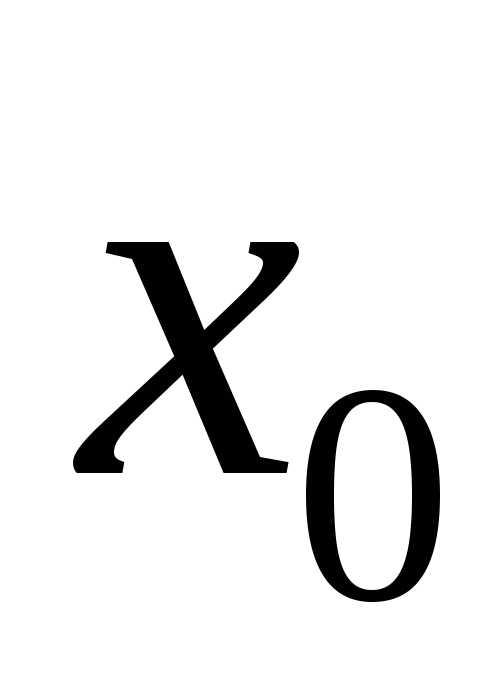 называется точкой (локального) минимума
функции,
если существует окрестность этой точки,
в которой (при
называется точкой (локального) минимума
функции,
если существует окрестность этой точки,
в которой (при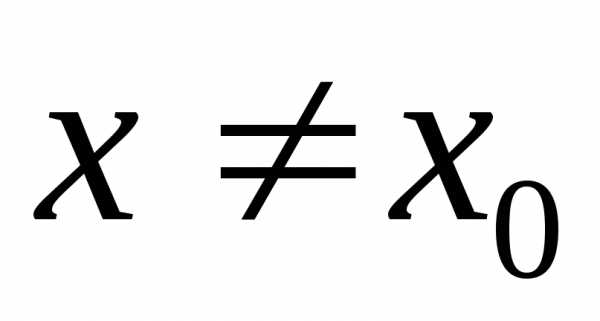 )
выполняется неравенство.
Другими словами
)
выполняется неравенство.
Другими словами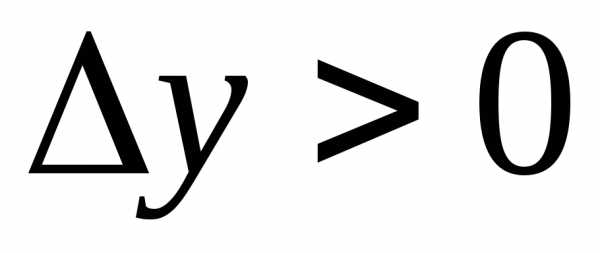 при малых
при малых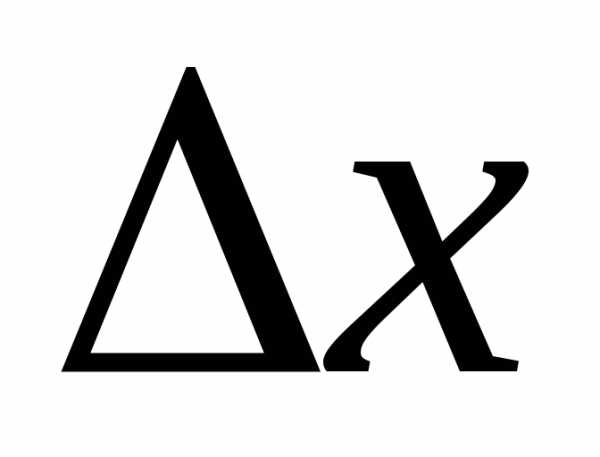 .
.
Точки максимума и минимума называются
точками экстремума. Их можно характеризовать
следующим образом: приращение функции
в точке экстремума имеет постоянный
знак, не зависящий от знака 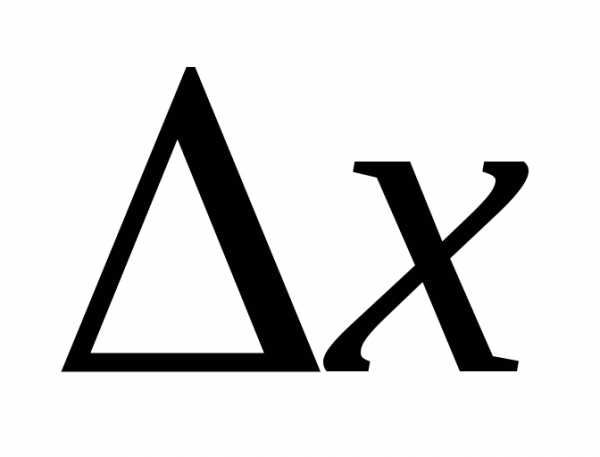 (если
(если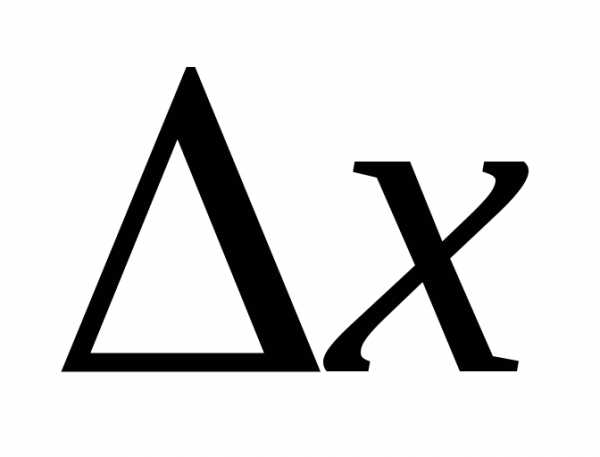 достаточно мало).
достаточно мало).
Теорема Ферма.Если функциядифференцируема в точке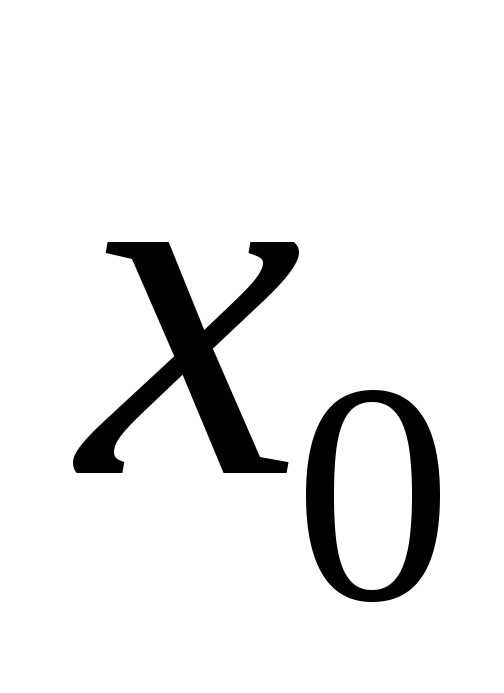 и имеет в этой точке локальный экстремум,
то.
и имеет в этой точке локальный экстремум,
то.
Доказательство.Дифференцируемость означает существование конечного предела
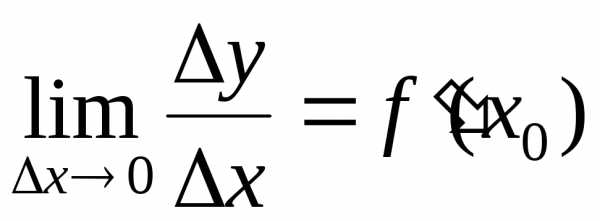 .
.
Для этого предела имеется три возможности: 1) ; 2);
3)
.
Предположим, что.
Тогда для близких к нулю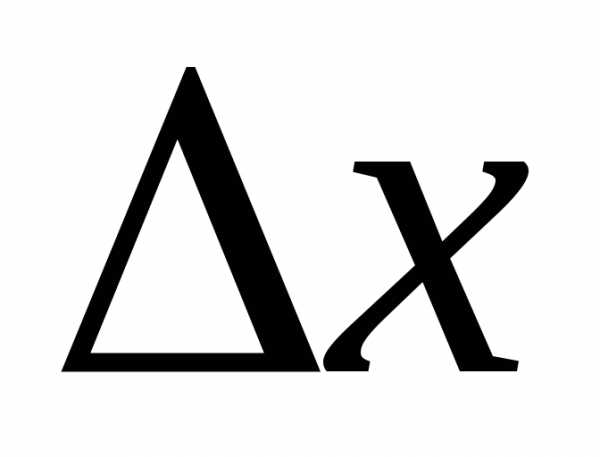 разностное отношение
разностное отношение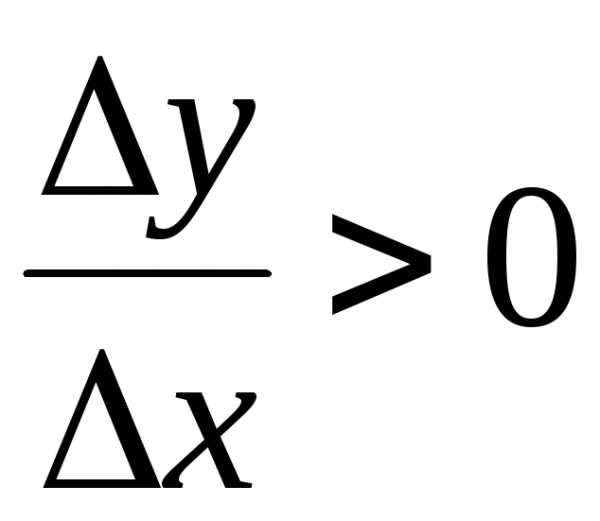 .
Если же,
то и
.
Если же,
то и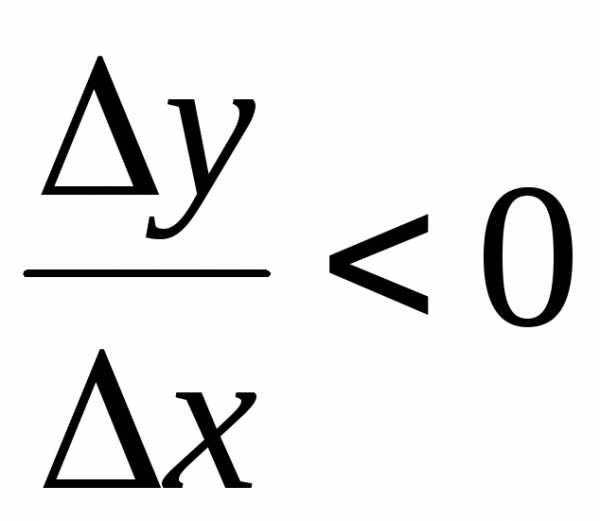 (для малых
(для малых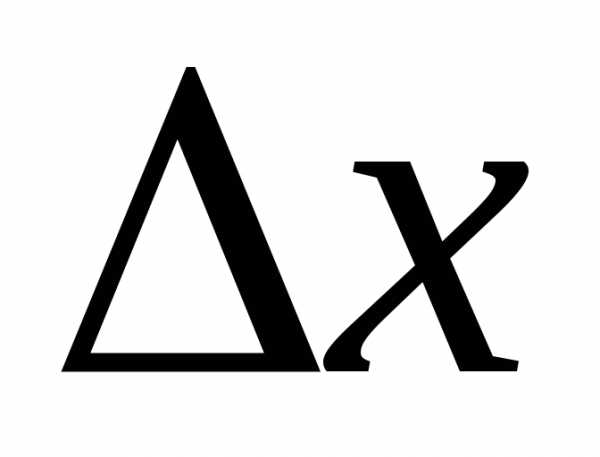 ).
В обоих случаях знак
).
В обоих случаях знак зависит от знака
зависит от знака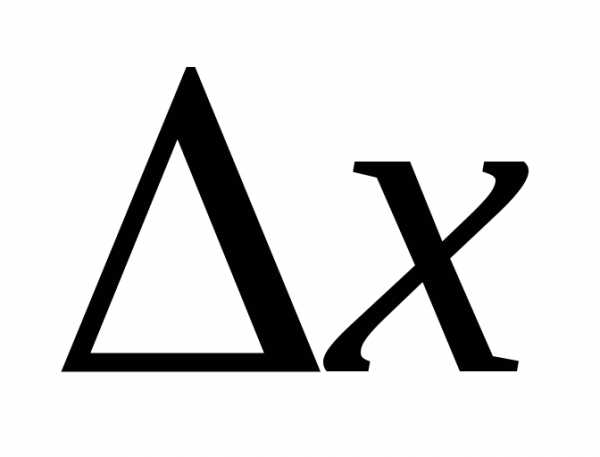 .
Но по условию теоремы
.
Но по условию теоремы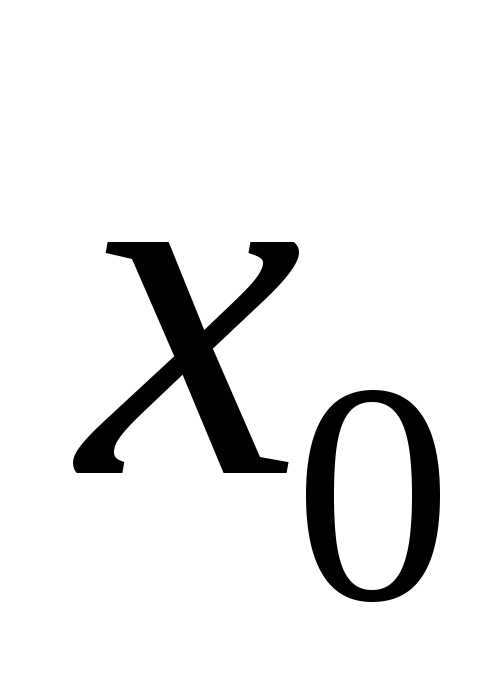 – это точка экстремума, значит, знак
– это точка экстремума, значит, знак не зависит от знака
не зависит от знака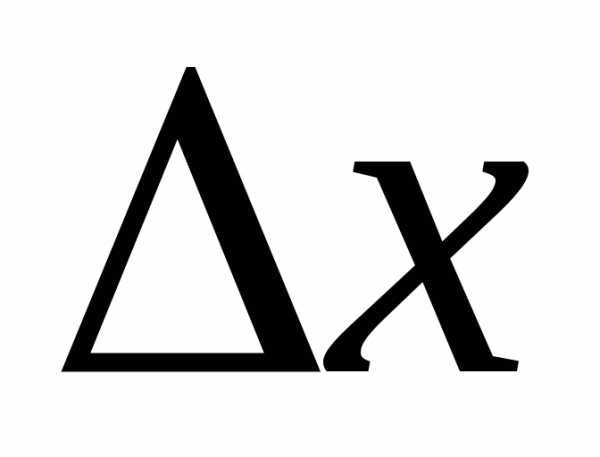 .
Это противоречие означает, что
.
Это противоречие означает, что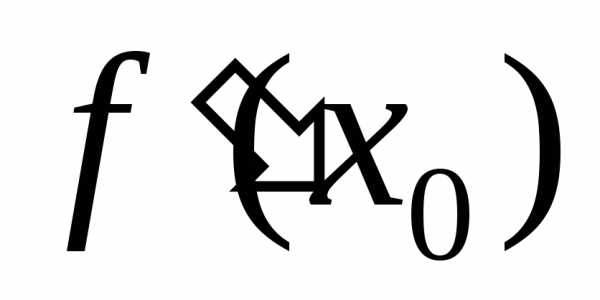 не может быть ни положительным, ни
отрицательным. Остается последняя
возможность:.
не может быть ни положительным, ни
отрицательным. Остается последняя
возможность:.
Замечание 1.Эта теорема имеет простой геометрический смысл: если в точке графика функции, которой соответствует экстремум функции, существует касательная к графику, то эта касательная параллельная осиOx.
Замечание 2.Сформулированное
в теореме условиеявляется необходимым, но не достаточным.
Например, функция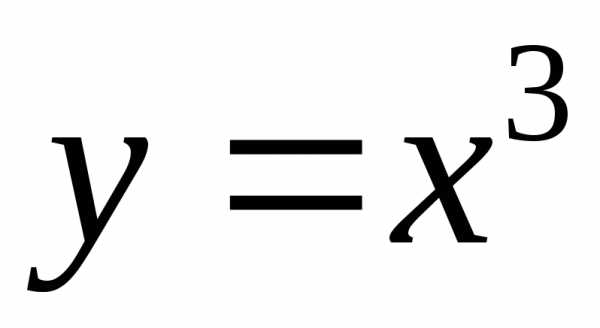 имеет производную
имеет производную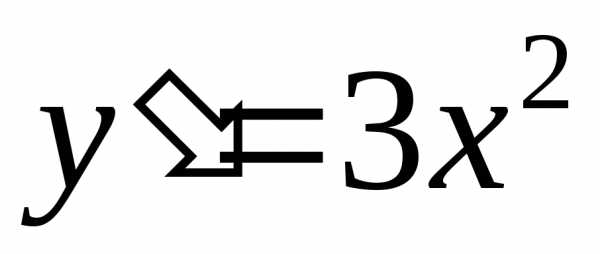 ,
которая обращается в ноль в точке
,
которая обращается в ноль в точке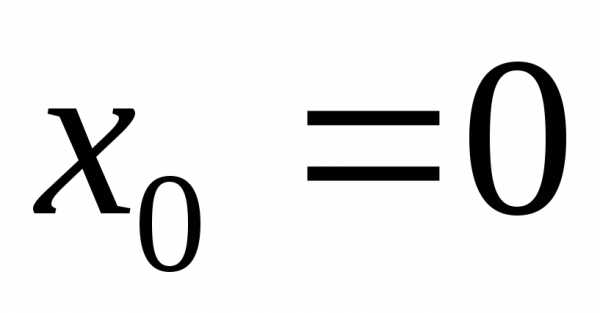 .
Однако,
.
Однако,
.
Выражение в скобках всегда положительно,
как неполный квадрат суммы. Следовательно,
и в точке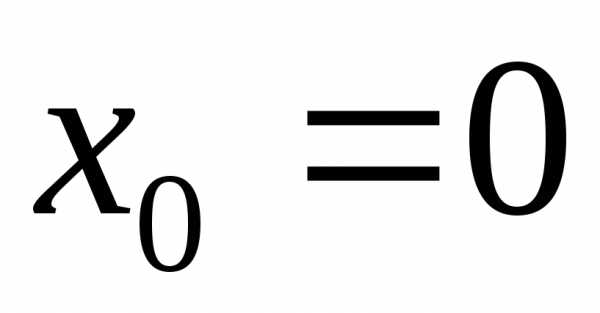 нет экстремума.
нет экстремума.
studfiles.net
6.9. Таблица производных и дифференциалов.
Соберём полученные в разделах 6.2, 6.3, 6.5 выражения для производных и следующие из них выражения для дифференциалов в одну таблицу:
№ | y(x) | y’(x) | dy | № | y(x) | y’(x) | dy | |
1 | y = C | 0 | 0 | 10 |
|
| ||
2 | у = ха | a ха-1 | a ха-1dx | 11 |
|
| ||
3 | | | 12 |
|
| |||
3a |
|
|
| 14 |
|
| ||
4 |
|
| 15 | | | |||
4a |
|
|
| 16 |
|
|
| |
5 | | | 17 |
|
| |||
6 | | 18 |
|
| ||||
7 |
|
| 19 |
|
|
| ||
8 |
|
| 20 |
|
|
| ||
9 |
|
| 21 |
|
|
|
6.10. Производные функций, заданных параметрически и неявно.
6.10.1.
Производные функций, заданных
параметрически. Пусть зависимость у от х задана через параметр t:
,
обе эти функции дифференцируемы, и для
первой из них существует обратная
функция 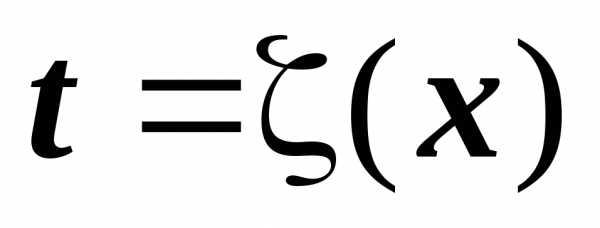 .
Тогда явная зависимость у от х выражается формулой.
Находим производную: .
Здесь мы воспользовались результатами
разделов 6.5.5.
Производная сложной функции и 6.3. Производная
обратной функции. То же выражение можно получить из 6.8.2.
Инвариантности формы первого дифференциала:
.
Тогда явная зависимость у от х выражается формулой.
Находим производную: .
Здесь мы воспользовались результатами
разделов 6.5.5.
Производная сложной функции и 6.3. Производная
обратной функции. То же выражение можно получить из 6.8.2.
Инвариантности формы первого дифференциала: 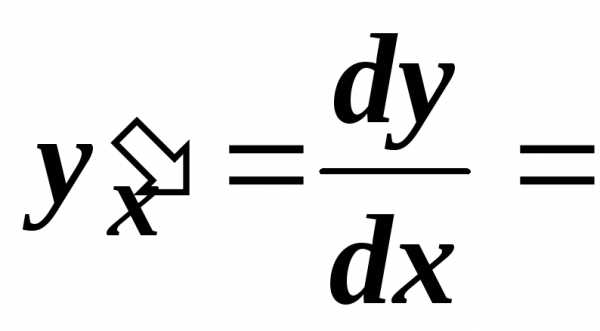 .
.
Примеры:
. Тогда . В этом примере легко получить явную зависимость у от х: . Подставим сюда зависимость х от t: . Как и следовало ожидать, получен тот же результат.
 .
Тогда
.
Тогда  .
.
6.10.2. Производные функций, заданных неявно. Неявным заданием зависимости у от х называется уравнение вида F(x,y) = 0, связывающее эти две переменные. Общая формула для y‘(x), следующая из неявного уравнения F(x,y) = 0, включает в себя частные производные, которые мы будем изучать позже; пока приведём несколько примеров, показывающих, как найти производную y‘(x) из неявного уравнения.
1. . Дифференцируем это равенство по х, учитывая зависимость у от х (применяя правило дифференцирования сложной функции: ):
.
Легко понять, что при этом всегда
получится уравнение, линейное относительно y‘(x),
которое без труда решается:  .
Производная найдена, она совпадает с
полученной в предыдущем разделе (с
учётом явного выражения ).
.
Производная найдена, она совпадает с
полученной в предыдущем разделе (с
учётом явного выражения ).
2. . Дифференцируем по х, учитывая зависимость у от х:
.
Решаем это уравнение относительно y‘: .
6.11. Производные и дифференциалы высших порядков.
6.11.1. Производные
высших порядков. Формула Лейбница. Пусть
функция имеет производную y‘(x)
в каждой точке интервала (а,b).
Функция y‘(x)
тоже может иметь производную в некоторых
точках этого интервала. Производная
функции y‘(x)
называется второй производной (или
производной второго порядка) функции
и обозначается . Функция y»(x)
тоже может иметь производную, которая
называется третьей
производной (или производной третьего
порядка) функции
и обозначается .
Вообще n-ой
производной (или производной n-ого
порядка) функции
называется производная от производной n-1-го
порядка (обозначения: 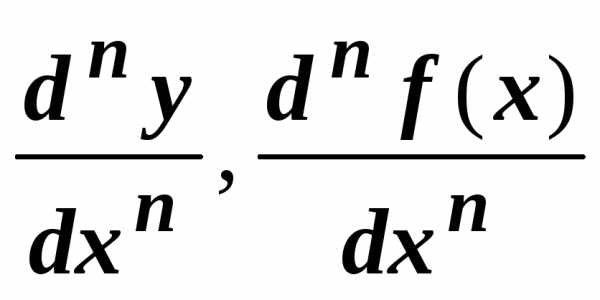 ).
).
Производные высших
порядков последовательно вычисляются
по уже известным формулам и правилам.
Пусть, например, 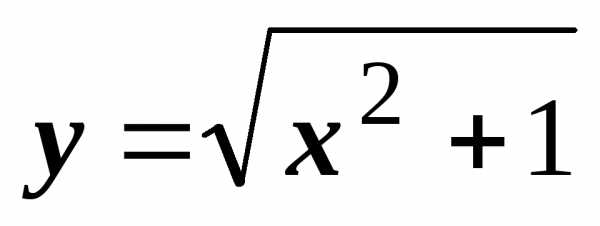 .
Тогда
.
Тогда 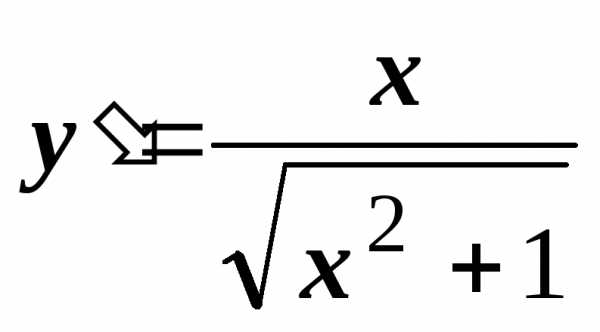 ,
,
, и т.д. В некоторых случаях можно получить
общее выражение для n-ой
производной функции: пусть
,
,
, и т.д. В некоторых случаях можно получить
общее выражение для n-ой
производной функции: пусть 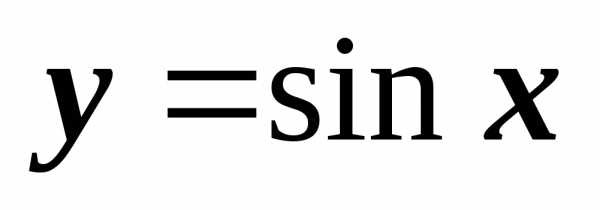 .
Тогда
, , ,
и вообще
.
Аналогичную формулу можно получить для
косинуса. Другой пример:
.
Тогда
, , ,
и вообще
.
Аналогичную формулу можно получить для
косинуса. Другой пример: 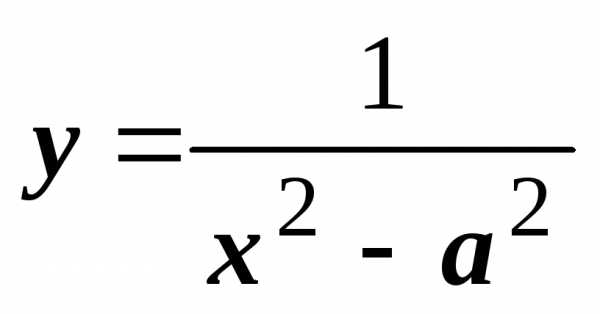 .
Если представить эту функцию в виде
,
то
,,
и вообще
.
.
Если представить эту функцию в виде
,
то
,,
и вообще
.
Для высших производных произведения функций справедлива формула Лейбница:
. Эта формула внешне похожа на формулу бинома Ньютона и, также как формула бинома Ньютона, может быть доказана методом математической индукции. Для низших производных:
; ; .
6.11.2. Дифференциалы высших порядков также определяются индуктивно: дифференциалом второго порядка (или вторым дифференциалом) функции называется дифференциал от её первого дифференциала; дифференциалом третьего порядка называется дифференциал от второго дифференциала; и вообще, дифференциалом n-го порядка функции называется дифференциал от её n-1-го дифференциала. При вычислении высших дифференциалов необходимо учитывать, что дифференциал независимой переменной — произвольная и независимая от х величина, которая при дифференцировании рассматривается как постоянная. Поэтому ; ; …., .
6.11.3. Неинвариантность формы старших дифференциалов относительно замены переменной. В разделе 6.8.2. Инвариантность формы первого дифференциала мы доказали, что независимо от того, является ли х независимой переменной, или сама эта переменная х является функцией другой переменной t, формула для нахождения дифференциала первого порядка одна и та же: dy = y‘dx. Покажем, что уже второй дифференциал этим свойством не обладает. Если х — независимая переменная, то d 2y = y«dx2. Если x = (t), то d 2y = d(dу) = d(y‘хdx) =
= d(y‘х)dx + y‘хd(dx). Для первого слагаемого вследствие инвариантности формы первого дифференциала d(y‘х) = y«ххdx, для второго d(dx) = d 2x, поэтому окончательно d 2y = y«ххdx2+ y‘хd 2x, что отличается от случая независимой переменной. Причина этого понятна: если х независимая переменная, то при нахождении второго дифференциала dx рассматривается как независимая от x константа; в случае x = (t) дифференциал dx определяется дифференциалом dt.
6.11.4. Старшие производные функции, заданной параметрически. В разделе 6.10.1. Производные функций, заданных параметрически, для первой производной функции
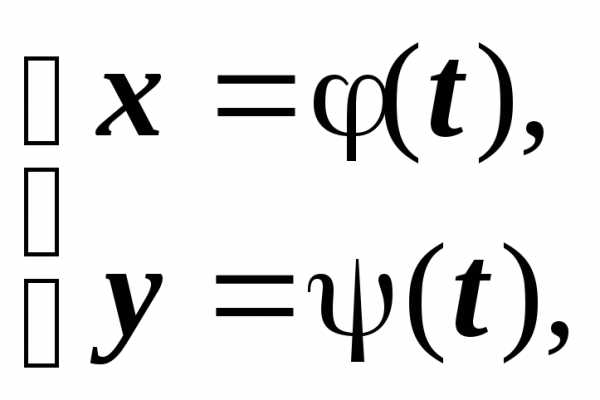 была получена
формула
была получена
формула 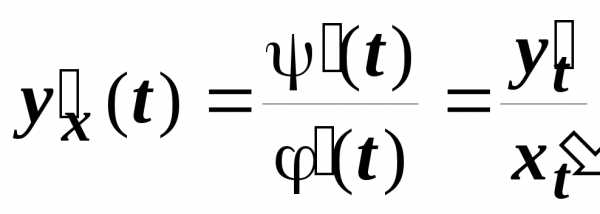 . Если применить
эту формулу к функции
. Если применить
эту формулу к функции
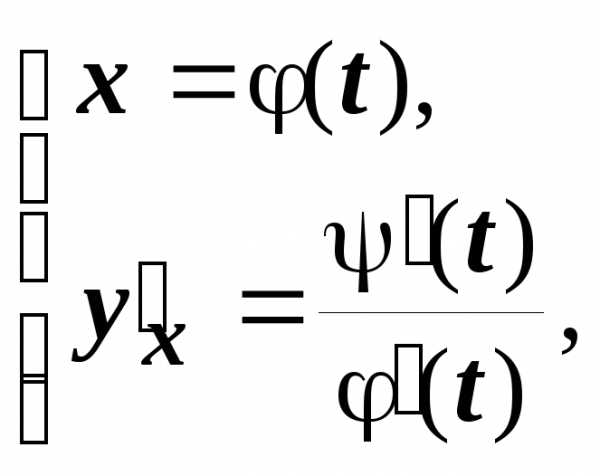 то получим:
;
аналогично, применяя ту же формулу ко
второй производной
то получим:
;
аналогично, применяя ту же формулу ко
второй производной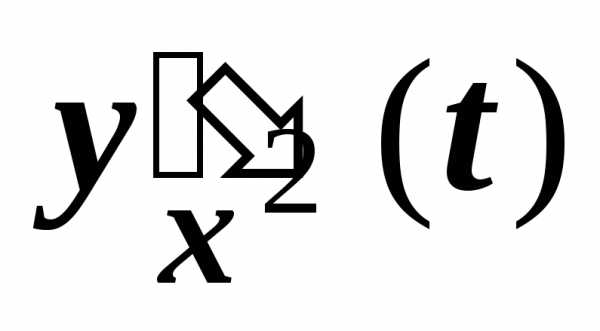 ,
получим выражение для третьей производной,
и т.д. Так, для функции
мы получили .
Найдем вторую производную: .
,
получим выражение для третьей производной,
и т.д. Так, для функции
мы получили .
Найдем вторую производную: .
6.11.5. Старшие
производные функции, заданной неявно, находятся последовательно, в соответствии
с определением старших производных.
Так, для неявно заданной зависимости у от х мы получили 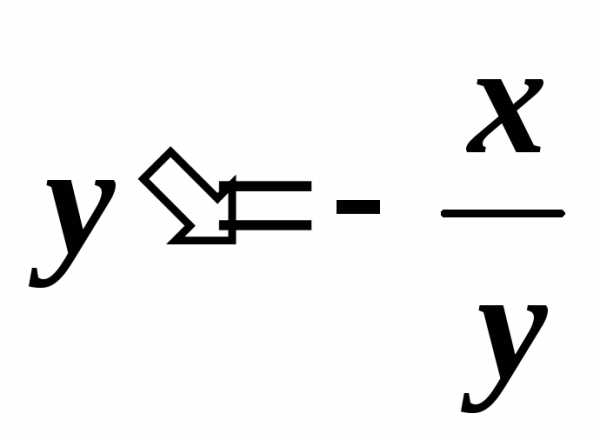 .
Найдём вторую производную: .
Дальше можно найти третью и т.д.
производные.
.
Найдём вторую производную: .
Дальше можно найти третью и т.д.
производные.
67
studfiles.net
Формулы дифференцирования функций
Далее разобраны основные правила и формулы дифференцирования функций:
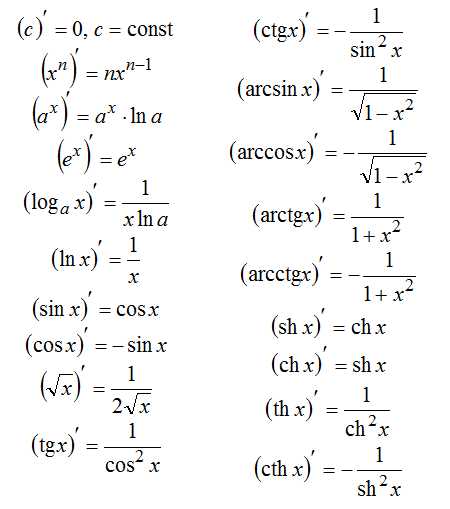
Правила дифференцирования:
Константу можно выносить за знак производной:
Производная суммы равна сумме производных:
Производная произведения равна сумме произведений производной первого слагаемого на второе и первого слагаемого на производную второго:
Производная частного находится по формуле:
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Правила дифференцирования производной
К основным правилам дифференцирования относят:
1. Вынесение постоянного множителя за знак производной:
То есть константу можно выносить за знак производной.
2. Производная суммы, производная разности:
Производная суммы двух функций равна сумме производных от каждой из них.
Замечание. Это правило распространяется и на большее число функций.
Производная разности
равна разности производных от каждой из них.
3. Производная произведения:
Производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
4. Производная дроби (производная частного двух функций):
Итак, производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com

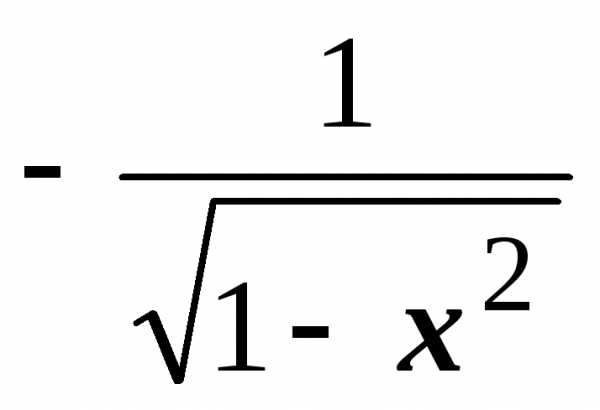
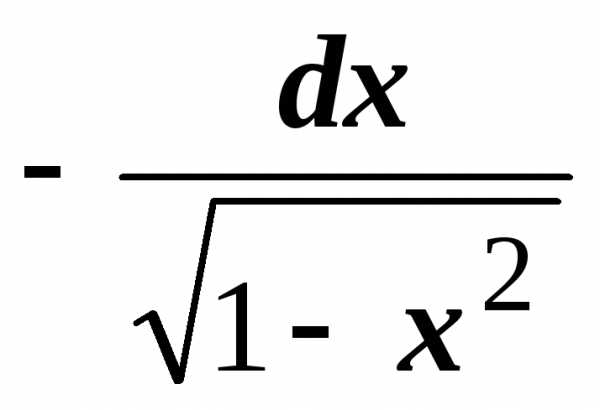
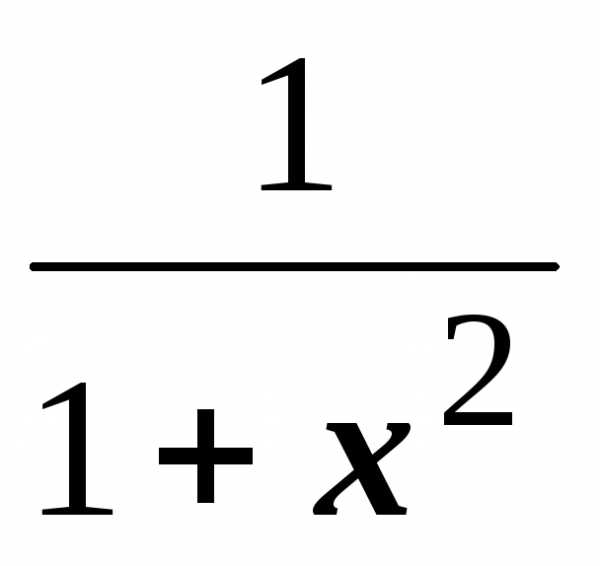
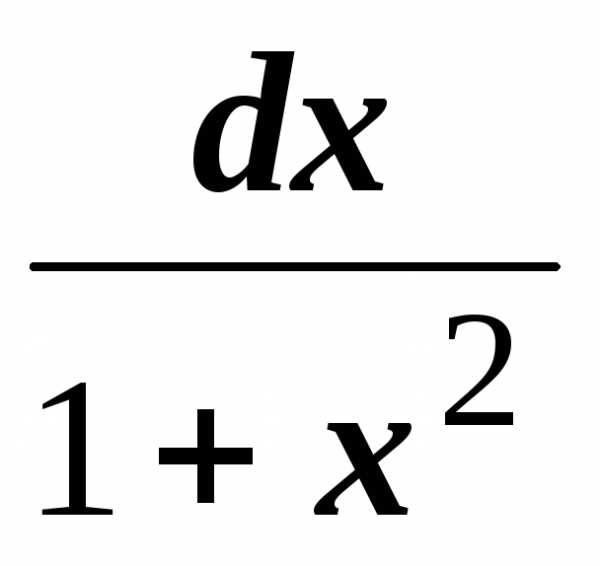
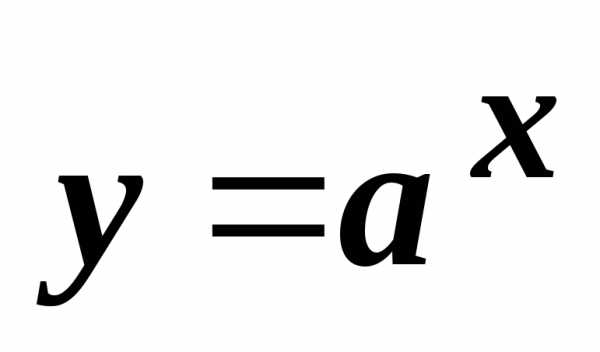
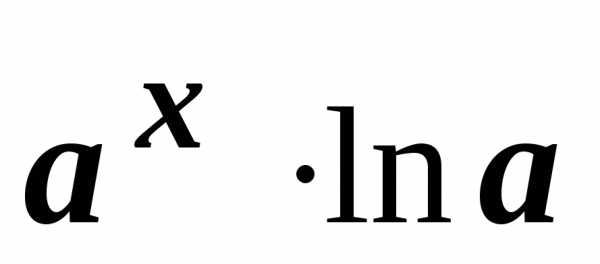
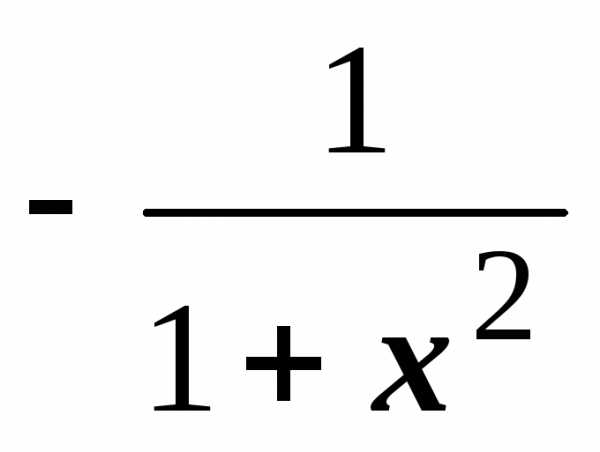
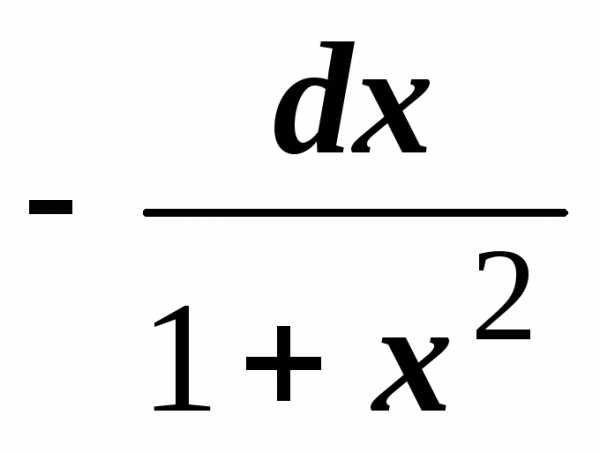
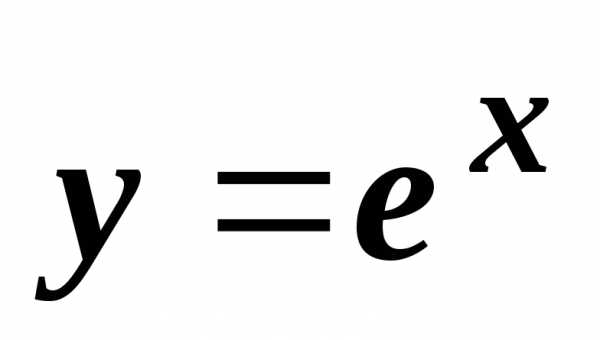
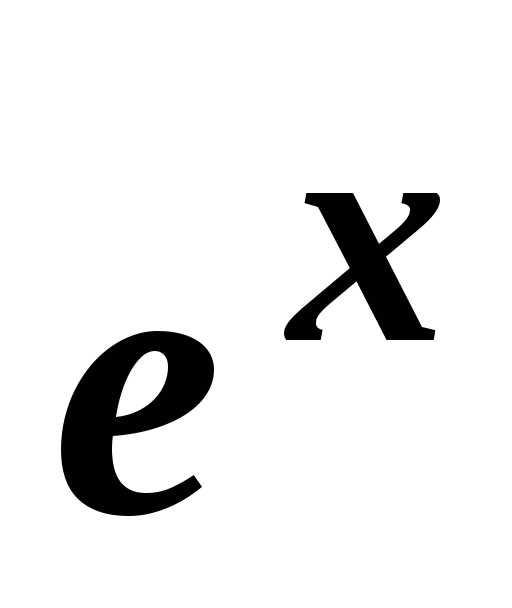
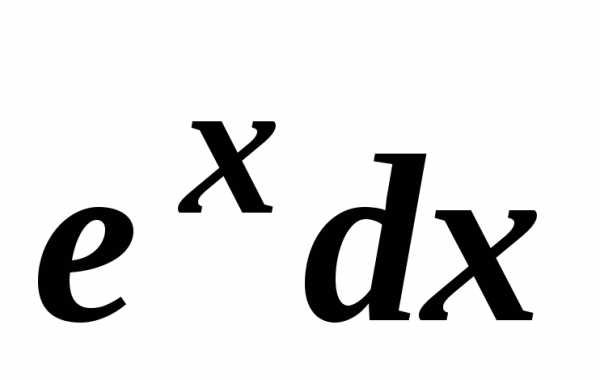
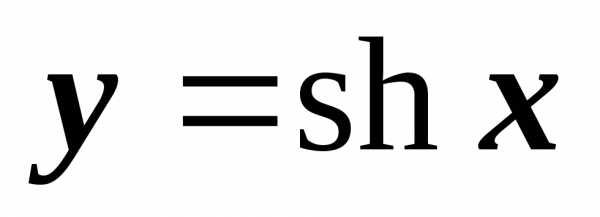
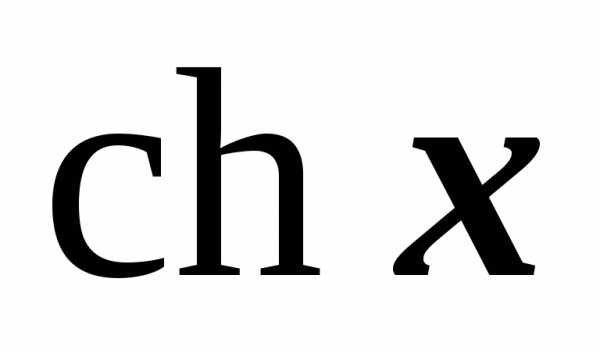
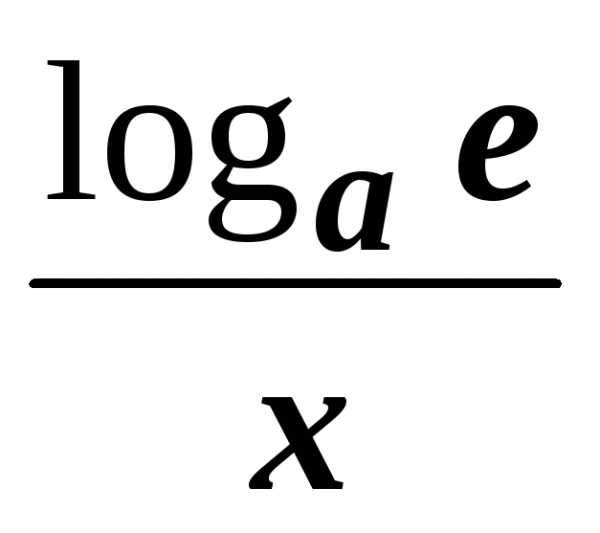
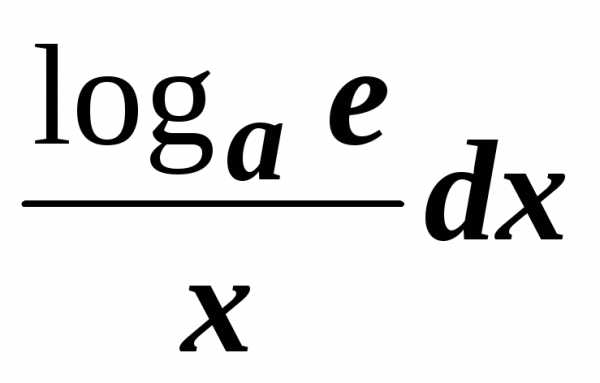
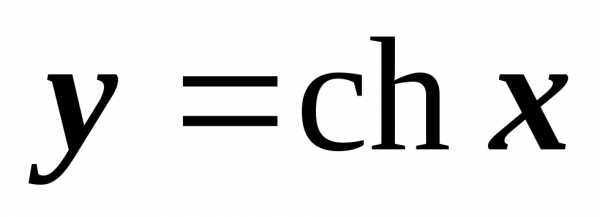
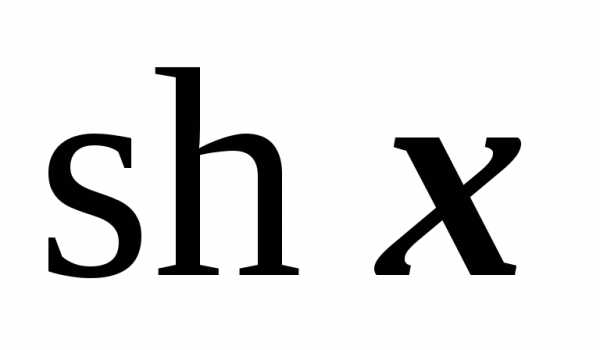
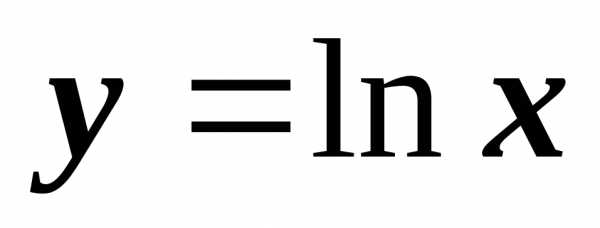
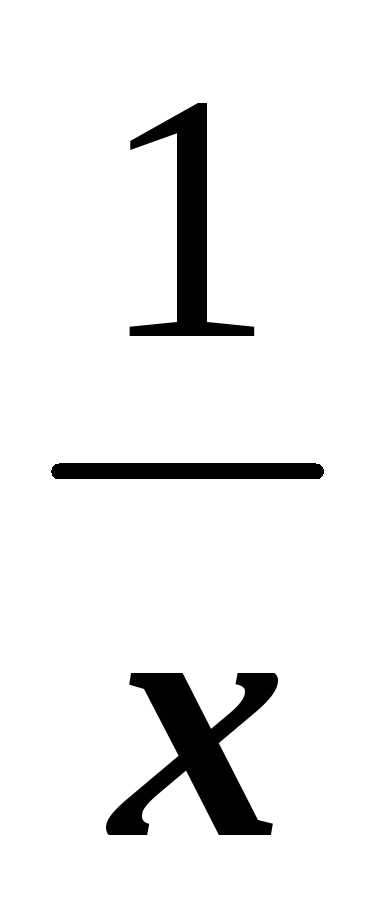
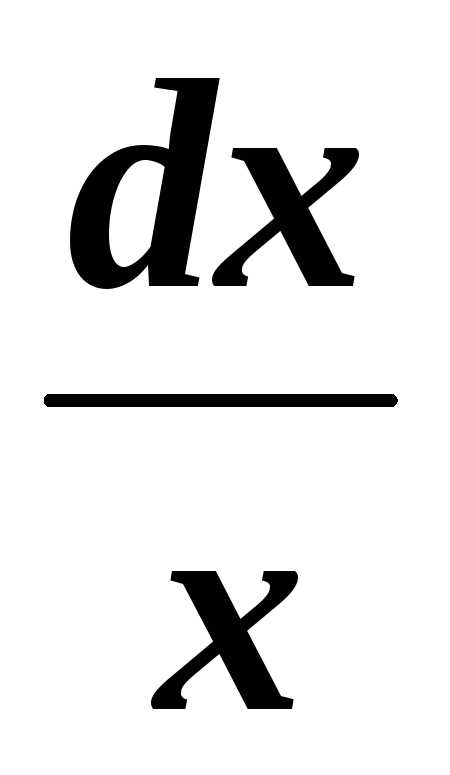
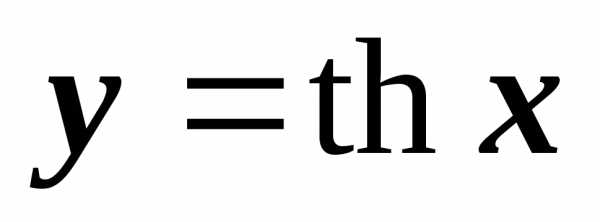
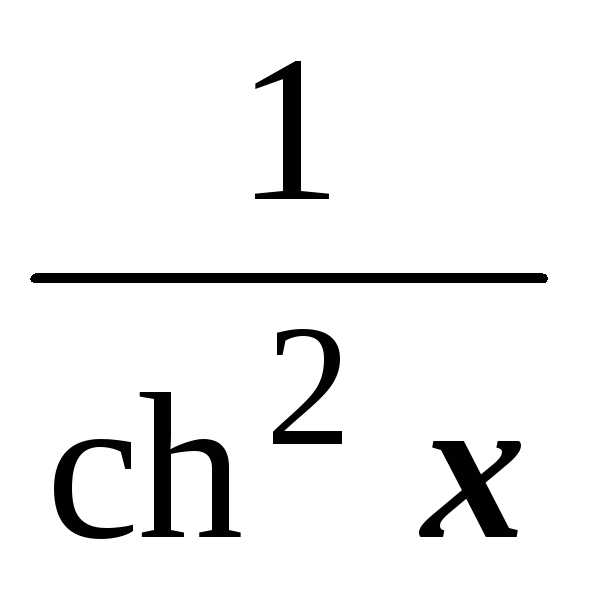
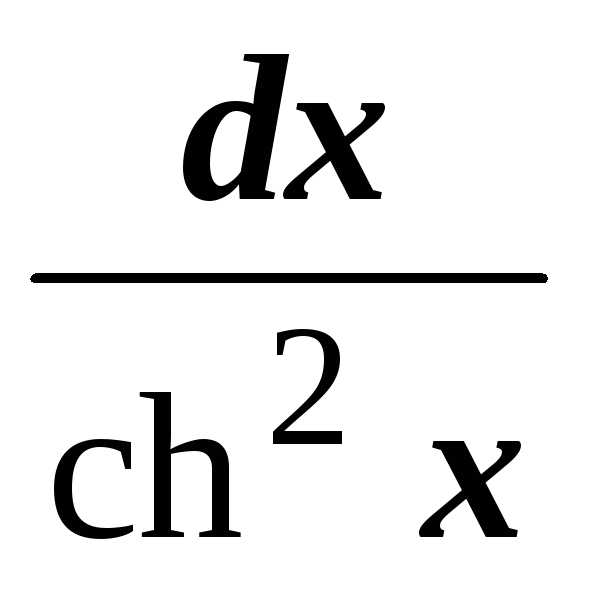
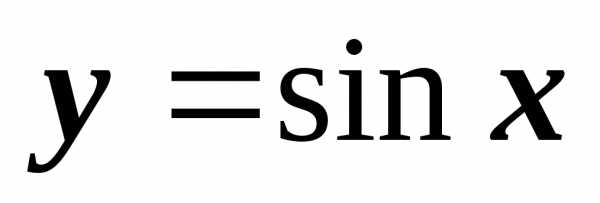

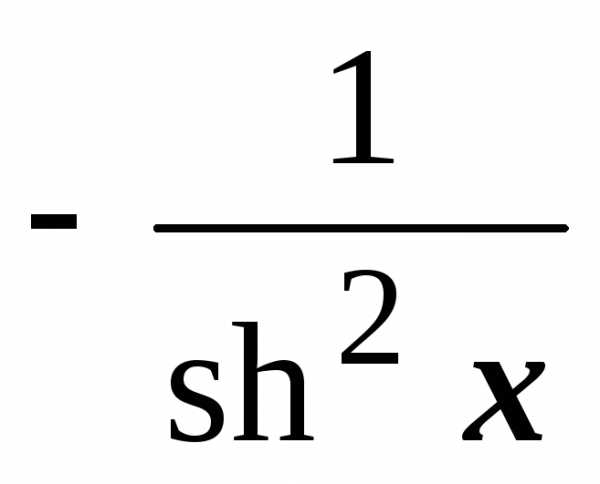
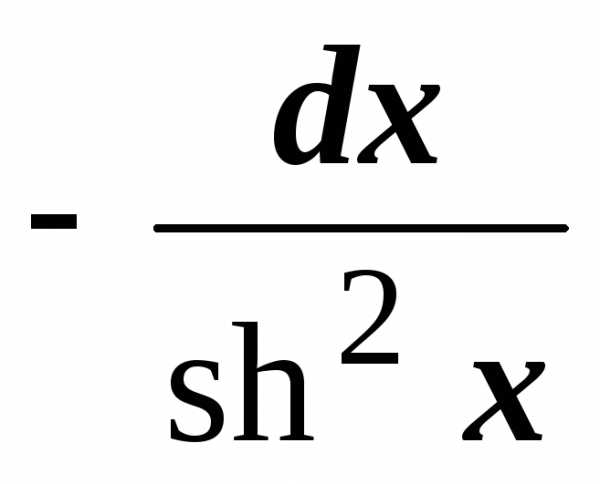
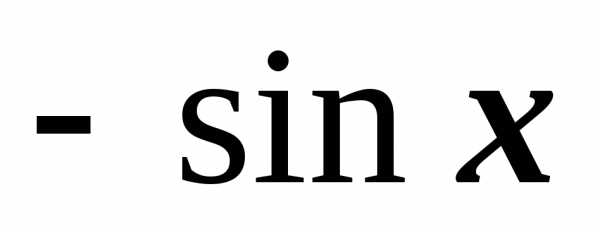
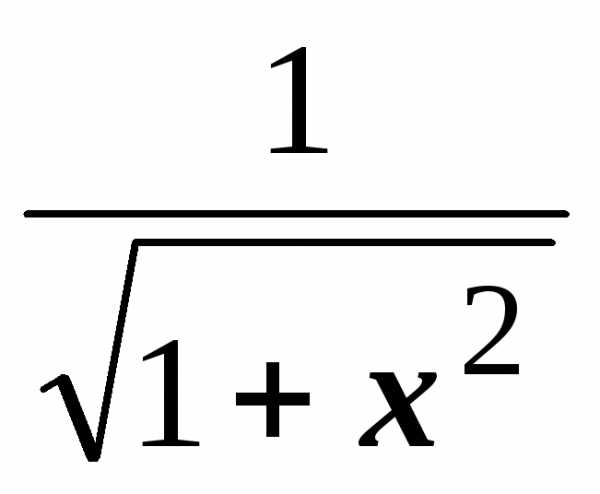
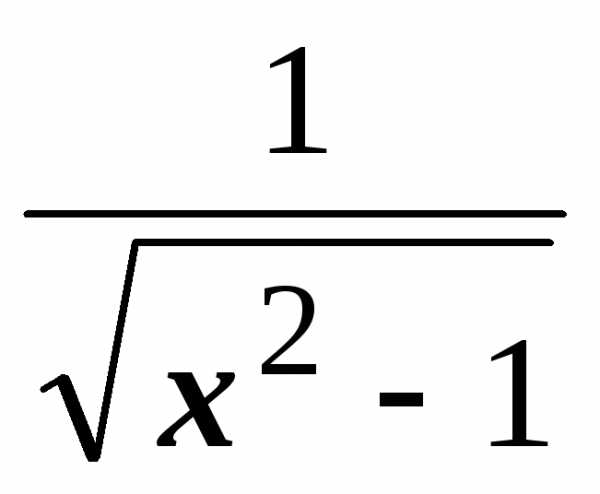
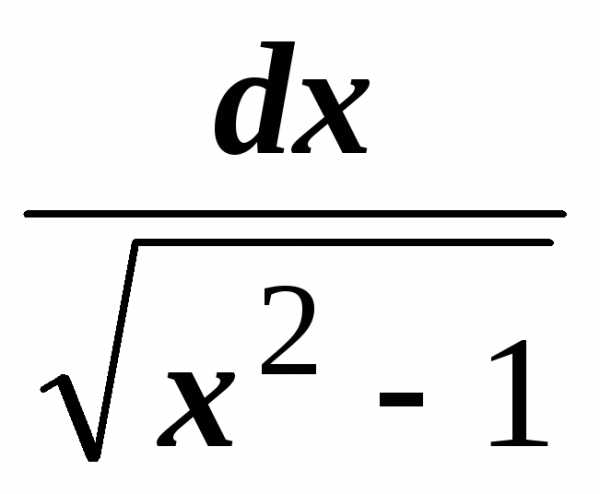

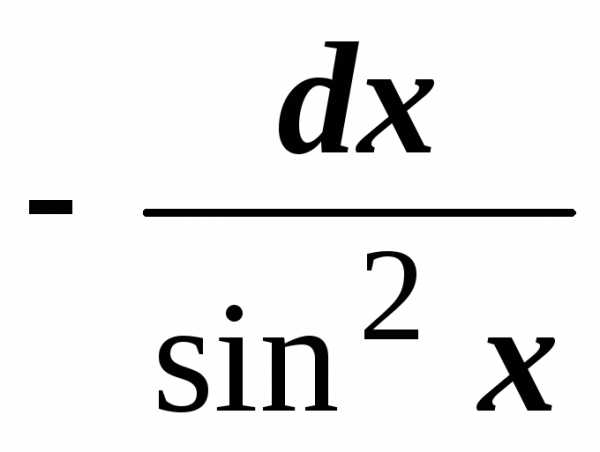

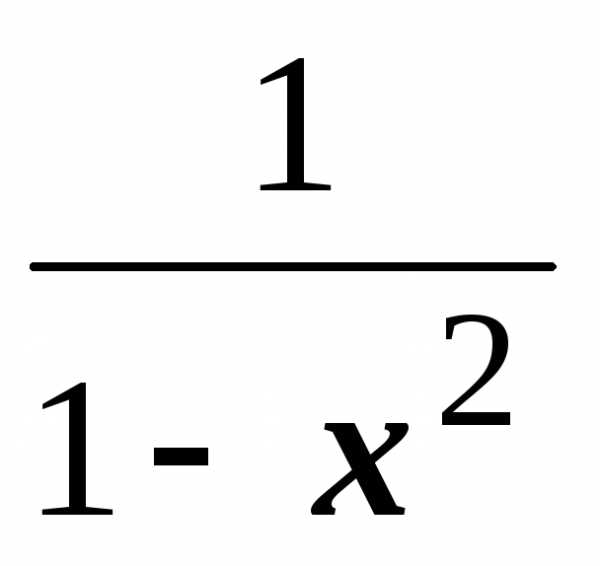
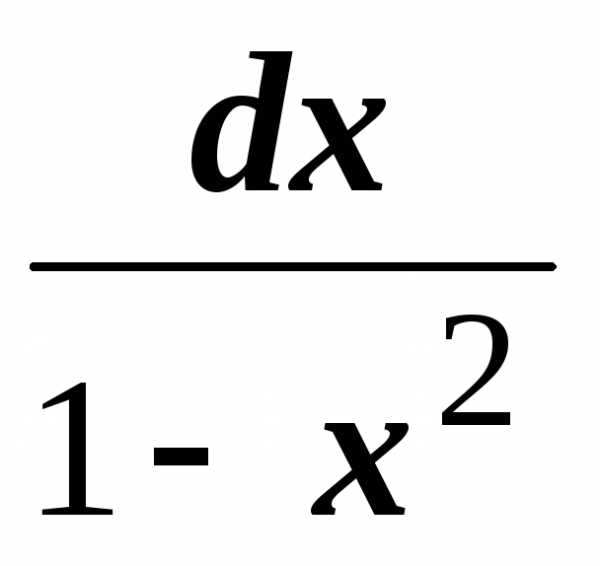
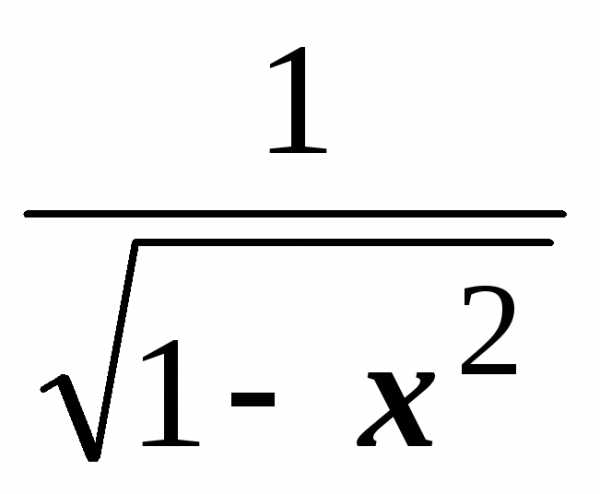
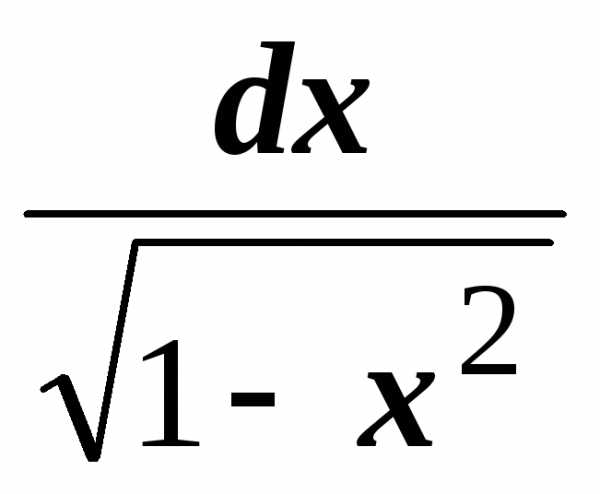
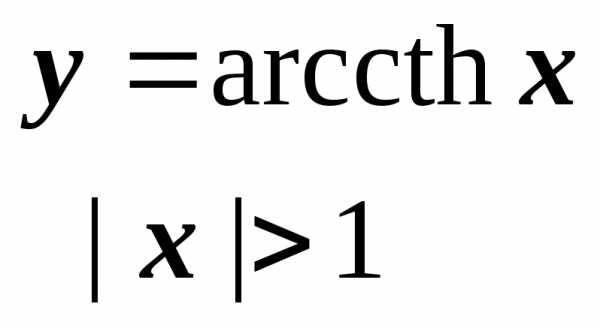
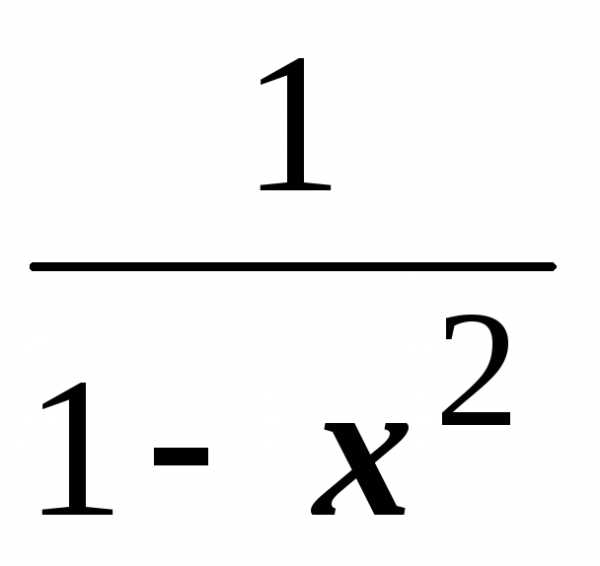
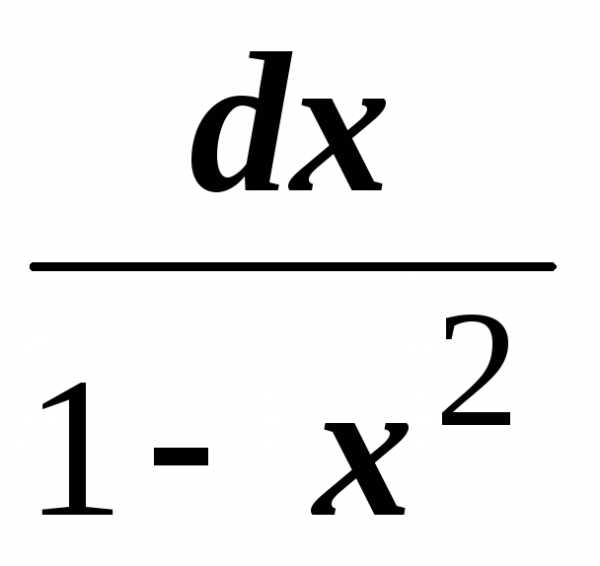
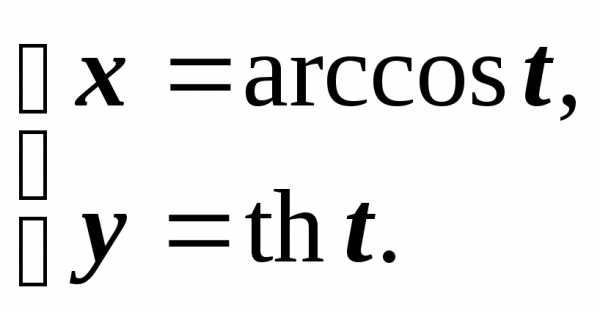 .
Тогда
.
Тогда 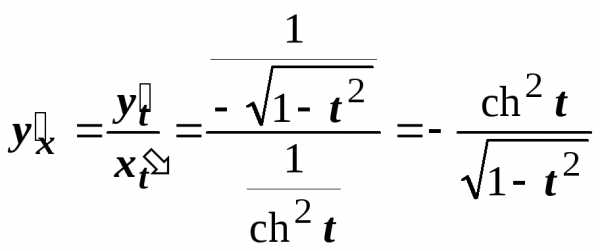 .
.