Что такое уклон линии: § 13. Уклон линии. Определение уклонов по горизонталям. Определение высот точек, лежащих между горизонталями

Как посчитать уклон в процентах

Тема 10. ЗАДАЧИ, РЕШАЕМЫЕ ПО КАРТАМ (ПЛАНАМ) С ПОМОЩЬЮ ГОРИЗОНТАЛЕЙ

10.1. Определение высот течек на карте

Если точка расположена на горизонтали, то ее высоту устанавливают по высоте этой горизонтали. Высоту (отметку) точки, расположенной между горизонталями (рис. 10.1, а), можно определить, если через нее провести линию ab по кратчайшему расстоянию между горизонталями.

Рис. 10.1. Определение отметки точки

Величины d и Δd измеряют на карте, а высота сечения рельефа подписана под масштабом карты.

10.2. Определение уклона линии

Пусть линия местности AB (рис. 10.2) наклонена к горизонту АС под углом v. Тангенс этого угла называют уклоном линиии обозначают буквой i:

,

т. е. уклон линии равен отношению превышения hк горизонтальному проложению S.

Рис. 10.2. Схема определения уклона линии

Пример. Если h = 1 м, a S =20 м, то i = 1/20 = 0,05

Уклон i = 0,05 показывает, что линия местности повышается или понижается на 5 см через каждый 1 м или на 5 м через каждые 100 м горизонтального расстояния S.
Если превышение положительное (+h), то уклон положителен (линия направлена вверх на подъем), а когда превышение отрицательное (-h) – уклон отрицателен и линия направлена вниз на спуск.

Уклон линии численно можно рассматривать как превышение, приходящееся на единицу горизонтального расстояния.

Измерив на карте длину заложения(расстояние между двумя соседними горизонталями по заданному направлению) и зная высоту сечения, можно найти уклон линии. Уклон обычно выражают в процентах или промилле (промилле – это тысячная часть целого или 1/10 процента).

Пример. Измеренное по карте заложение d= 29 м. Высота сечения h = 1 м.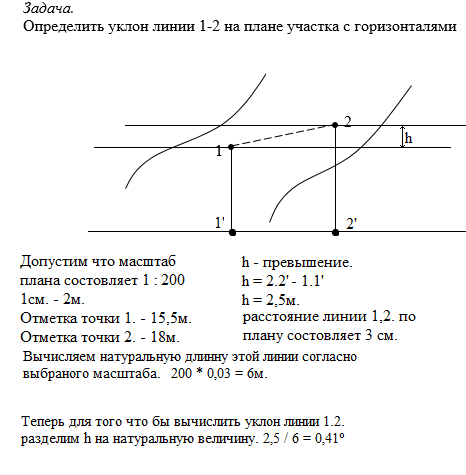 Найти уклон линии.
i = 1/29 = 0,034
или, выразив уклон в процентах, получим i = 3,4%.
3,4% означает, что разница высот в начале и конце 100 метрового горизонтального участка составляет 3,4 м.
Если умножить 3,4% на 10, получим величину уклона в промилле (‰)
3,4% × 10 = 34‰
Уклон 34‰ означает, что разность высот в начале и конце горизонтального участка длиной 1 000 м составит 34 м.

Символ ‰ можно ввести на компьютере с помощью Alt-0137: при включённом NumLock, удерживая левый Alt, набрать на цифровом блоке клавиатуры 0137.

Если вычислить тангенс угла по четырехзначным математическим таблицам Брадиса (таблица 10.1), то получим наклон линии градусах.

Например, из таблицы 10.1 по величине 0,034 находим значение угла наклона 1º58′ (используем интерполяцию).

Обратите внимание на то, что наклон линии выражается в градусах, а уклон в процентах или в промилле!

10.

3. Определение крутизны ската
Рис. 10.3. Графики заложения:
а – для углов наклона; б – для уклонов

При работе с картой или планом угол наклона либо уклон определяют, пользуясь графиками, которые помещают под южной рамкой топографических карт и планов. Для этого с карты раствором циркуля-измерителя берут заложения между двумя горизонталями по данному скату, затем по графику находят то место, где расстояние между кривой и горизонтальной прямой равно этому заложению. Для найденной таким образом ординаты определяют значение ν или i по горизонтальной прямой (на приведенных графиках отмечено звездочками: ν = 1º15′; i = 0,025 = 25%).
График заложений может быть использован только для работы на карте (плане) лишь того масштаба и такой высоты сечения рельефа, для которых он построен.

Например, для карты масштаба 1 : 25 000

10.4. Построение профиля местности по данным топографической карты

Профиль — это вертикальный разрез рельефа местности по заданному направлению. Построение профиля по направлению АВ показано на рис. 10.4.
Порядок построения профиля
1. Прочертить карандашом на карте профильную линию АВ, направление которой задано.
2. Оценить максимальную и минимальную высоту по линии профиля.
H_max = 86,7 м; Н_min = 56,5 м. Разность – 30,2 м. Если разность высот округлить в большую сторону, получаем 7 интервалов по 5 м.
3. Задать горизонтальный и вертикальный масштабы профиля.
Горизонтальной линией профиля является ось расстояний, вертикальной линией – ось высот.

Рис. 10.4. Построение профиля местности по карте

Обычно горизонтальный масштаб профиля равен масштабу топографической карты, по которой он строится, а вертикальный масштаб принимают в 10 раз крупнее горизонтального. Например, масштаб карты 1:50 000. Следовательно, горизонтальный масштаб профиля равен 1:50 000, а вертикальный масштаб – 1:5 000. В некоторых случаях, для большей наглядности, применяют более крупные масштабы высот, либо укрупняют и горизонтальный масштаб. В любом случае для основания масштаба рекомендуется выбирать числа: 1; 2; 2,5; 5 (1:1000, 1:200, 1:50 и т.п.). В нашем примере горизонтали проведены через 5 м. Если взять высоту профиля (без надписей) 7 см, то получим вертикальный масштаб 1:500 (в 1 см 5 м).
4. Построить горизонтальную и вертикальную оси координат профиля и оцифровать их в соответствии с выбранными горизонтальным и вертикальным масштабами.
Вертикальная координатная ось – шкала высот начинается с абсолютной отметки, выбранной для основания профиля, так называемой линии (точки) условного горизонта. Ее значение должно быть меньше минимальной абсолютной отметки по линии профиля и выражено круглым числом. В зависимости от выбранной точки условного горизонта оцифровывают остальные деления шкалы высот. Работа по построению профиля упрощается, если оцифровка шкалы высот совпадает со значениями отметок горизонталей на карте.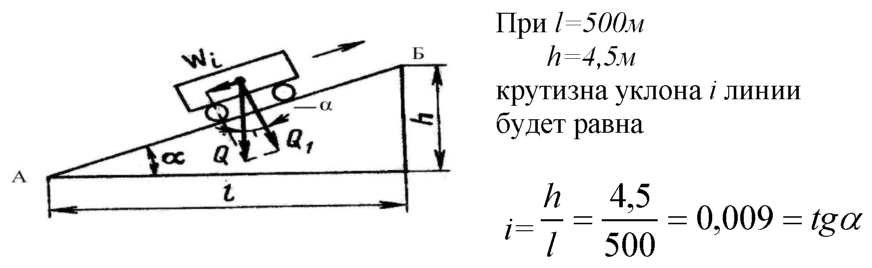 Условный горизонт на рис. 10.4 равен 50 м.
На горизонтальной оси отложить отрезки, соответствующие пересечениям горизонталей с профильной линией, а также точек пересечения линии профиля с объектами ситуации (дорогами, линиями связи, объектами гидрографии, границами лесов и т.п.). Для этого можно воспользоваться полоской бумаги, на которую вначале с карты переносят характерные точки, а затем с полоски бумаги эти точки переносят на горизонтальную линию профиля.
5. Из отмеченных точек на горизонтальной оси восстановить перпендикуляры, соответствующие их абсолютным высотам. Полученные точки соединить плавной линией.
В некоторых случаях на профильной линии можно определить высоты дополнительных точек. Если, например, точка находится между горизонталями, то ее высоту легко найти интерполированием заложения.
При пересечении лощины (хребта) дополнительную точку определяют на линии водослива (водораздела) также методом интерполирования.
При пересечении седловины для точки седловины принимают, что она находится на половине высоты сечения рельефа от ближайшей к ней горизонтали.
Для точки 16, находящейся рядом с вершиной горы, определение высоты связано с построением однородного отрезка ав. В этом случае превышение точки в по отношению к вершине горы будет отрицательным:
h_в = 85,0 — 87,8 = -2,8 м
Длина отрезка ав равна 26 мм, отрезка от точки а до точки №16 – 10 мм. Из пропорции находим, что
ав = -2,8 м (10 мм / 26 мм) = -1,1 м
Следовательно, высота точки №16 будет равна
Н₁₆ = 87,8 — 1,1 = 86,7 м
Если высоты точек профиля определяют дополнительно, то их значения записывают в скобках.
Характерными точками рельефа и ситуации являются точки перегибов рельефа, линии водоразделов и водосливов (тальвеги), седловины, вершины гор (холмов), дна котловин (ям), пересечения с объектами линейного типа, гидрографией, а также и другие точки, представляющие интерес для исполнителя.

10.5. Построение на карте (плане) линии заданного уклона

Задача построения линии заданного уклона часто встречается в практике при проектировании трассы дороги, трубопровода и т. д. Определение положения такой линии может производиться на топографических картах и планах.
Рассмотрим задачу нанесения на топографическую карту (план) линии заданного уклона на следующем примере. Допустим, что из точки М (рис. 10.5) на топографической карте с высотой сечения рельефа 5 м требуется провести кратчайшую ломаную линию по направлению к точке N так, чтобы уклоны отдельных участков ее не превышали 5 %. Тогда подъем или спуск (превышение) вдоль линии допускается не более 1 м на каждые 20 м или 5 м на 100 м горизонтального расстояния.

Рис. 10.5. Схема поиска линии заданного уклона

Так как горизонтали проведены на плане через 5 м, то при соблюдении требования 5% уклона расстояние между смежными горизонталями должно быть 100 м. Поэтому, взяв в раствор циркуля-измерителя по масштабу плана 100 м, засекаем этим раствором циркуля из точки М горизонталь с высотой 35 м в двух точках с и е. Из этих точек тем же раствором 100 м засекаем точки на горизонтали с высотой 40 м. Если этот прием продолжим далее, то получим два варианта положения на плане линии заданного уклона MсN и MeN. Вариант MсN извилистее и длиннее, направление MeNменее извилисто, короче по длине и может быть принято за окончательное.

10.6. Определение границы водосборной площади и площади затопления

Водосборной площадью называется территория, с которой вода атмосферных осадков стекает к данному пункту водосбора. На рис. 10.6 обозначена плотина АВ на горизонтали с высотой 185 м с зеркалом воды (обозначено штриховкой). Требуется показать на плане границу площади, с которой вода атмосферных осадков стекает к плотине.

Рис. 10.6. Схема определения границ водосборной площади

Граница водосборной площади показана пунктиром, который проходит по водораздельным линиям CDMEF. Для этого сначала в верховье лощины находят середину седловины М и вершины холмов, примыкающих к ней. От водоразделов к плотине граница проходит перпендикулярно горизонталям.
По карте определяют также площадь затопления – территорию, которую заливает вода в результате строительства искусственного водоема. Работа начинается с нанесения на карту положения плотины с учетом отметки уровня воды в будущем водоеме. Условие будет выполнено, если на месте возведения плотины соединить на противоположных склонах водотока одноименные горизонтали с заданной высотой. Площадь затопления ограничится горизонталью, замыкаемой плотиной (рис. 10.7).

Рис. 10.7. Определение водосборной площади и площади затопления по карте

Если отметки горизонталей не соответствуют уровню будущего водоема, то для определения его контура методом интерполяции находят точки с заданной высотой, которые затем соединяют кривой. Следует обратить внимание на особенности оконтуривания водосборной площади реки и водоема: для реки граница замыкается в ее устье, для водоема – на концах плотины.

10.7. Построение орографической схемы рельефа местности

Орографическая (греч. oros гора и grapho пишу, описываю) схема является одним из видов носителей информации о местности. Это изображение местности с прорисовкой хребтов и долин. По таким схемам легко ориентироваться в горах.
Орографическая схема рельефа местности получается в результате проведения по карте линий водоразделов и тальвегов. Водоразделы проходят по точкам, от которых линии скатов расходятся в разные стороны, тальвеги – по точкам, в которых линии скатов сходятся (рис. 10.8,a). Размещаются такие точки в местах наибольшей кривизны горизонталей.

Рис. 10.8. Положение водоразделов и тальвегов, определяемое по горизонталям (а) и образуемая ими орографическая схема (б)

10.8. Определение формы ската

Скаты могут иметь равномерную (постоянную) кривизну, тогда форма (экспозиция) такого ската называется ровной; промежутки между горизонталями (заложения) здесь будут одинаковыми.

Рис. 10.9. Формы скатов

Но чаще можно встретить скаты, крутизна которых меняется. Если крутизна по направлению спуска увеличивается (заложения уменьшаются), то такой скат называют выпуклым, и, наоборот, при уменьшении крутизны по направлению спуска скат называют вогнутым. На волнистых склонах чередуются выпуклые и вогнутые участки; эти скаты имеют горизонтали, расположенные на различном удалении одна от другой.

Вопросы и задания для самоконтроля

1. Как определить абсолютную высоту точки и превышение?
2. Как провести на карте водораздельную линию и тальвег?
3. Как установить (определить) границы площади водосбора?
4. Что такое профиль местности и как его построить?
5. Как определить среднюю высоту бассейна?
6. Как определить средний уклон бассейна?
7. Как определить объем бассейна?
8. Как определить форму ската с помощью горизонталей?

Почему крутизна склонов измеряется в процентах, и зачем водителям это нужно

Наверняка вы уже ни раз встречали предупреждающие дорожные знаки 1. 13, он же «Крутой спуск», и 1.14 (соответственно, «Крутой подъем»). И кто-то из водителей точно обратил внимание, что уклон обозначен не в привычных градусах, а в процентах. Градусы – они же и при температуре, и в спиртном. Родные, понятные. Зачем все усложнять? Настало время разобраться с этим недоразумением и узнать, как автомобилистам может помочь данная информация при езде.

Представьте ситуацию: едете вы за городом и встречаете перед собой дорожный знак, предупреждающий водителей о том, что впереди подъем с крутизной уклона в 10%. Как на картинке выше. В голове сразу: 10% – это вообще сколько? Но если мы скажем, что это почти 6 градусов, вам разве станет от этого понятнее?

Тут важно понимать, что дорога постоянно меняет угол своего наклона, поэтому определить этот показатель в градусах будет сложновато. Зато уклон дороги в процентах – легко! Это то количество метров, на которое проезжая часть опустится или поднимется через 100 метров пути. То есть в нашем случае, проехав 1 километр по дороге с крутизной уклона в 10%, вы поднимитесь на 100 метров относительно первоначальной точки. Если вспоминать школьный курс тригонометрии, то цифра на дорожном знаке – это тангенс угла наклона проезжей части, выраженный в процентах. Впрочем, не заморачивайтесь: за вас уже давно все подсчитали, а вам нужно просто научиться этими данными пользоваться.

Зачем нужно знать крутизну склона?

Оказывается, тангенс угла наклона равняется коэффициенту сцепления с дорожным покрытием. Если вы едете по сухому асфальту, этот показатель составляет около 0,7 (при условии, что у вас не «лысая» резина). Пошел дождь – коэффициент сцепления с мокрой дорогой сразу упал до 0,5. А если дело происходит поздней осенью, и после ливня «удачно» подморозило, то асфальт превращается в настоящий каток. И тут уже коэффициент сцепления с проезжей частью снижается до минимума – менее 0,1. Что это значит в нашей ситуации, когда мы поднимаемся в горку с крутизной уклона в 10%, или 0,1?

Вы должны понимать, что, если вы остановитесь на склоне, то, в лучшем случае, не сможете тронуться, чтобы продолжить путь, в худшем – автомобиль с легкостью покатится обратно. И никакой водительский опыт или даже самая лучшая шипованная резина не помогут автомобилю остановиться, пока он не скатится с горы. Потому что с дорогой колеса практически ничего не связывает. Именно поэтому Правила дорожного движения (п. 11.7 ПДД) принуждают спускающихся со склона водителей уступать встречному поднимающемуся в гору потоку (даже, если препятствие расположено на их половине дороги).

Чем опасен затяжной спуск

Съезд с крутой горы – не менее опасное мероприятие. Во время длительного спуска, когда вы беспрерывно давите на педаль тормоза, в автомобиле могут перегреться и отказать тормоза. Чтобы этого не случилось, советуем научиться «гасить скорость» при помощи двигателя, постепенно снижая передачи. Чем круче спуск, тем ниже должна быть передача. Об особенностях торможения двигателем мы подробно писали в нашем блоге ранее.

Кстати, многие не обращают особого внимания на знаки «Крутой спуск» или «Крутой подъем». Особенно, когда там указан небольшой процент крутизны склона. Напрасно. Нередко случается, что в условиях плохой погоды (например, в снегопад, туман или когда темно) автомобилист может попросту не заметить небольшие, но затяжные спуски или подъемы. А именно на них чаще всего и перегреваются тормоза. Так что знаки не пропускаем. Стали бы чиновники тратить деньги из местного бюджета, если бы данный отрезок дороги не представлял никакой опасности?

Разница в знаках

Ну и напоследок расскажем о том, как отличить спуск и подъем на знаках. Конечно, чаще всего можно понять, что перед тобой чисто визуально. Но не всегда. Погода вносит коррективы, и в сильный снегопад небольшой длительный спуск можно запросто не заметить, а тормозная система автомобиля заметит. Так что в плохую погоду стоит особенно внимательно смотреть на знаки, установленные на обочине.

Отличить спуск от подъема на дорожных знаках вам поможет левая рука. Направьте ладонь по наклонной линии, над которой написана крутизна склона в процентах. Если пальцы будут направлены вниз, значит перед вами крутой спуск, если вверх, то значит вам предстоит забираться в гору.

К счастью, наибольшие продольные уклоны на автомобильных дорогах России не превышают 6-7% на равнинной и холмистой местности и 9-10% в горах. Конечно, в приморских городах есть дороги с довольно серьезными склонами, крутизна которых превышает все имеющиеся нормативы. Но мы-то теперь знаем, где опасность, а значит преодолеем даже самые крутые подъемы и спуски. Удачи на дорогах!

Адаптация пандусов для МГН

Калькулятор для пандуса

В соответствии с приказом Минстроя России №750/пр от 21 октября 2015 г. «Об утверждении изменений №1 к СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» «При проектировании реконструируемых, подлежащих капитальному ремонту и приспосабливаемых существующих зданий и сооружений уклон пандуса принимается в интервале от 1:20 (5%) до 1:12 (8%)».

Введите параметры будущего пандуса, исходя из данных объекта. Параметры необходимо вводить в милиметрах. Нажмите кнопку «рассчитать». Длина наклонной площадки в рассчитывается в милиметрах. Также Вы получите рекомендации относительно параметров, которые у Вас получились.

Основным действующим нормативным документом для определения уклона пандуса и его длины в РФ является СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения»

При высоте марша до 800 мм — мах угол 2,86°
При высоте марша до 200 мм — мах угол 5,71°
Для временных конструкций
при высоте марша до 800 мм — мах угол 4,76°

Пандус – это устройство для адаптации социально-значимых объектов и открытых пространств: вход в здание, сопровождение лестницы, пешеходный переход и т.д. Пандус необходим, чтобы сделать жизнь маломобильных групп населения комфортнее: пожилые люди, с коляской или тяжелой поклажей, с костылями после травм, инвалиды-колясочники.

Активное развитие и продвижение федеральной программы «Доступная среда» сподвигло многие организации установить пандусы на входной группе. Однако зачастую это делается либо для галочки, либо организациями, не владеющими навыками и знаниями существующих нормативов. Поэтому не всегда готовое изделие соответствует государственным стандартам. Как результат — недоступность для людей с ограничениями.

Нормативы для пандусов 2018

По нормативам СП 59.13330.2016 (с учетом вступивших в силу изменений 15 Мая 2017 года) пандус должен иметь следующие характеристики:

Список документации, рекомендуемой к ознакомлению:

СНиП 35-01-2001 содержит предписания по адаптации жилых домов и социально-значимых объектов для маломобильных групп населения. А так же конкретные ограничения по установке и параметрам пандусов.
ГОСТ Р 51261-99 содержит технические требования к стационарным опорным устройствам.
СП 30-102-99 содержит требования к входной площадке.
СП 59.13330.2012 содержит предписания по доступности зданий и сооружений для маломобильных групп населения

Угол наклона пандуса не должен превышать уклон в отношении 1:20 (5%). В данном случае очень часто проценты путают с градусами. В результате чего подъем /спуск получается в разы выше. Угол наклона — это соотношение длины к высоте подъема.

Справка! В ряде некоторых случаев допускается небольшое увеличение угла наклона пандуса:

• При временном сооружении пандуса (ремонте или реконструкции здания). Если его высота не превышает 0,5 м, а промежуток между площадками не более 6 м, уклон может быть 8% или 1:12
• Если высота подъема не достигает 0,2 м, уклон допустим в пропорции 1:10 (10%).
• Длина непрерывного движения марша пандуса не должна превышать 9,0 м, далее необходимо организовывать разворотную площадку или площадку отдыха.
• Длина горизонтальной площадки прямого пандуса должна быть не менее 1,5 м.
• Пандусы должны иметь двухстороннее ограждение с поручнями на высоте 0,9 и 0,7 м.
• Поверхность пандуса должна быть нескользкой текстурой.
• Поверхность марша пандуса должна визуально контрастировать с горизонтальной поверхностью в начале и конце пандуса.

Запомните! При перепаде высоты от трех метров, вместо пандусов применяются подъемные устройства. В данном случае наличие пандуса будет бесполезным и недоступным для инвалида-колясочника.

Поручни для пандуса

— В начале и конце поручни должны быть длиннее на 300 мм и иметь закруглённую форму.

— Верхний поручень расположен на высоте 900 мм.

— Расстояние между поручнями 900-1000 мм.

— Перила должны быть круглого сечения с диаметром от 30 до 50 мм.

— Начало и конец маркируются предупредительными полосами.

— Нижний поручень должен быть на расстоянии 700 мм.

— При высоте пандуса более 0,45 м необходимо наличие бортиков высотой не менее 0,05 м.

— Покрытие пандуса должно обладать противоскользящим эффектом.

— Минимальное расстояние от гладкой стены 45 мм, от неровной 60 мм.

— Поручни с внутренней стороны не должны прерываться.

— Поручни изготавливаются из металла и устанавливаются с обеих сторон наклонной площадки.

Если пандус изначально соответствует всем строительным параметрам, то его можно оснастить необходимыми дополнительными устройствами при их отсутствии:

• Опорными поручнями. Расстояние между поручнями пандуса одностороннего движения должно быть в пределах 0,9-1,0 м, чтобы инвалид-колясочник мог на них подтянуться. Также для удобства и безопасности хвата поручни должны иметь закругленную форму и выступать на 300 мм от края.
• Контрастной тактильной разметкой (для незрячих и слабовидящих людей). Разметкой следует обозначать сами поручни и подстилающую поверхность. С внутренней стороны поручней можно приклеить тактильные наклейки для обозначения начала и конца препятствия.

Если пандус изначально не соответствует конструкторским параметрам в соответствии со сводами правил, то его следует демонтировать, а на его месте организовать доступный пандус.

НАШЕ ПРЕИМУЩЕСТВО — ДОЛГОЛЕТНИЙ ОПЫТ и КАЧЕСТВО!

Выбор и расчет угла уклона крыши

Наклон крыши и его значение при строительстве домов

Проезжая мимо населенных пунктов, мы часто рассматриваем крыши домов и построек. Одни похожи на крутые склоны Эльбруса, другие — на покатые спуски дальневосточных сопок. Почему же перекрытия имеют такой разный наклон? Уклон кровли способствует быстрому удалению атмосферных осадков с территории сооружения и измеряется углом между плоскостью ската крыши и плоскостью горизонта. Чем больше величина угла ската, тем круче крыша, и наоборот, с его уменьшением крыша становится более покатистая или пологая, пока не перейдет в горизонтальную. Этот угол профессионалы архитектурного строительства измеряют градусами (º), процентами (%) или числовым соотношением. Если угол очень маленький, тогда используют измерение в промилле (сотых долях процента). Для справки: 1º — 1,7%; 1% — 34′ 20″.

Наклон любой крыши является очень важным элементом. Его величина вычисляется в зависимости от климата и применяемого кровельного материала.

Наклон плоскости любой части крыши является очень важным элементом при домостроении, и его величина выбирается в зависимости от климата и применяемого кровельного материала. Он влияет на ее надежность, герметичность, на возможность водоотвода, а значит, и на долговечность здания в целом. Для правильного выбора материала кровли, а также для расчета его расхода, высоты сооружения нужно знать, как посчитать уклон кровли.

Виды крыш и выбор их материала

Виды формы крыш.

Для каждого здания уклон крыши рассчитывается индивидуально.

Различают 4 вида крыш:

• высокие;
• скатные;
• пологие;
• плоские.

Плоские перекрытия не являются абсолютно горизонтальными, а имеют угол наклона, но он не менее 3º, при этом крыша обустраивается специальными водоотводными воронками с уклоном стенок около 1,5º.

При эксплуатации на поверхность кровли оказывает давление ветер, поэтому высокие более подвержены этому воздействию, а с очень пологих крыш ураган может сорвать кровельное покрытие.

Угол наклона крыши зависит от материала, выбранного для кровли, а также плоскости ската.

С увеличением размера угла наклона от 11º до 45º это давление усиливается почти в 5 раз. Учитывая ветровые нагрузки, на местностях с несильными ветрами этот размер выбирают в пределах 35-40º, а там, где скорость движения воздушных масс высока, — 15-25º.

Следует отметить, что при больших значениях угла наклона плоскости перекрытия (около 50º) зимой снег будет съезжать с нее под собственным весом, сводя к нулю его давление на кровлю.

От крутизны плоскости ската зависит выбор материала, а иногда и количество его слоев при укладке.

Диаграмма связывает минимальный наклон крыши с кровельным материалом и помогает в выборе при необходимости и того, и другого. Вертикальная шкала обозначает уклон в процентах, дуговидная — в градусах, на полках указано соотношение высоты к заложению. Материал условно сгруппирован по своим технико-экономическим свойствам в 11 категорий.

Практика показывает, что рулонные материалы применяют для накрытия кровель с уклоном 0-25% (0-10% — трехслойное покрытие, 10-25% — однослойное покрытие, но материал должен быть с посыпкой). Асбестоцементный шифер укладывают на крышах с наклоном до 28%, стальные листы — до 29%, черепица — более 33%.

Вычисление угла ската к горизонту

Его можно просто измерить уклономером, который являет собой планку с рамкой с маятником со стрелкой, показывающей градусную величину. Но на сегодняшний день этот прибор уже неактуален, поскольку есть много капельных и электронных уклономеров с намного большей точностью измерения и удобством пользования.

При отсутствии в распоряжении геодезических устройств для измерения существует простой математический метод, позволяющий относительно точно посчитать угол наклона стропил. Для этого используется рулетка и отвес. От конька до перекрытия здания опускается отвес и измеряется высота h. Затем от точки, в которой отвес касался перекрытия под коньком, измеряем расстояние до нижней точки ската — заложение l.

Угол наклона крыши зависит от выбранного для кровли материала.

Угол наклона ската i равен отношению высоты конька к заложению (при одинаковых единицах измерения) і = h:l. При этом уклон выражен соотношением, которое показывает, на какую высоту поднимается кровля на протяжении единицы заложения (на сколько метров будет поднят верхний край крыши на одном метре горизонтального перекрытия). Чтобы посчитать этот же уклон в процентах, умножаем полученное соотношение на 100%. Если же нужно знать эту величину в градусах, переводим ее с помощью таблицы.

Для примера: высота кровли h = 3,0 м, длина заложения l=6,5 м. Тогда і = h:l = 3,0:6,5 = 1:2,17. Это пример измерения уклона соотношением. і = 3,0:6,5 = 0,4615. В процентном измерении это значение вычисляется умножением его на 100%: і = 0,4615. 100% = 46,15%. Для определения угла в градусах переводим по таблице и получаем 25º. Если есть нужда в более точном градусном значении, тогда из полученного соотношения, применяя калькулятор или специальные таблицы, вычисляем котангенс, который будет равен 24,78º.

Следует отметить, что уклон в 100% — это когда высота кровли равна заложению, то есть соответствует соотношению 1:1 или углу наклона в 45º. Но не следует думать, что процентная величина уклона и его градусная величина имеют прямую зависимость. Ведь уклон в процентах — это значение тангенса угла при нижней точке ската, умноженное на 100%, а график тангенса (тангенсоида) никогда не был прямой линией. И если 100% — это 45º, то 50% — это не 22,5º, а около 27º (точнее 26,56º).

Практическое применение результатов вычисления

Кроме того что угол уклона позволяет выбрать материал кровли, он необходим при промежуточных вычислениях в процессе строительства дома. Зная значения угла в процентах, можно посчитать высоту конька. Для этого заложение умножаем на уклон h = l х і = 6,5 х 0,46 = 2,99 м. Либо зная уклон и высоту, можно посчитать расстояние до нижней точки ската l = h : і = 3,0 : 0,46 = 6,52 м. Точность полученных линейных размеров зависит от точности измерений и вычислений. В данном случае невысокая точность вычислений (до сотых) дает расхождение в пределах 1-2 см. Измерение угла ската кровли в процентах намного удобнее при строительстве крыши, чем в градусах.

Уклон линии. Графики заложений

Уклон i линии – отношение превышения h к заложению линии d (рис. 5.22). Уклон – мера крутизны ската.

Например, h = 1 м, d = 20 м. i = 1/20 = 0,05.

Уклоны выражаются в процентах i = 5% или в промиллях i = 50 ‰. Чем больше d, тем меньше крутизна <.

                                                                      уклон линии ;                   (5.1)    

                                                                      крутизна ската <.   

Рис. 5.22. Уклон линии

График заложений по уклонам

График строится по формуле ,

где h – константа для данной карты; i – задается.

Пример: Масштаб 1:10 000, h = 1 м, i = 0,001 (табл. 5.2). Подставляя в формулу, получим  = 1000 м, что на карте  масштаба 1:10 000 составляет 10 см.

                                                                                                    Таблица 5.2

h, м	1	1	1	1	1	1
i ‰	0,001	0,002	0,003	0,004	0,005	0,006
d, м	1000	500	333	250	200	167
на карте, см	10	5	3,33	2,5	2,0	1,67

Рис. 5.23. График заложений по уклонам

График заложений по углам

  График строится по формуле ,

где h – константа для данной карты;

   < – задается.

Пример: Масштаб 1:10 000, h = 2,5 м (табл. 5.3). Для < = 0°30r; d = 2,5 · ctg 0°30r = 286,5 м, что на карте составляет 2,86 см и т.д. для углов 1°, 2°, 3°… 10°.

                                                                                                                Таблица 5.3

h, м	2,5	2,5	2,5	2,5	2,5	2,5	2,5
<, град.	0°30r	1°	2°	3°	5°	…	10°
ctg <	114.59	57.29	28.64	19.08	11.43	…	5.67
d, м	286.47	143.22	71.59	47.70	28.58	…	14.18
На карте, см	2,86	1,43	0,72	0,48	0,29	…	0,14

Рис. 5.24. График заложений по углам

Задачи, решаемые по карте

Рис. 5.25 Фрагмент топографической карты

Задачи, которые можно решать по карте, следующие:

1. Определение по карте географических координат т. а (рис. 5.25):

т. а   г. Малиновская     j = 54°40¢21²;

                                                                              l = 18°05¢03².

2. Определение по карте прямоугольных координат т. б (см. рис. 5.25):

т. б   т.148,1                  х = 6065 300 м;

                                                                             у = 4312 800 м.   

3. Определение направления аб (см. рис. 5.25): 

a = 60°;

А = a + g = 60° + (-2°22¢) = 57°38¢;

А_м = А — d = 57°38¢ — (6°12¢ + 1°02¢) = 50°24¢.

4. Определение крутизны ската по линии а – б (табл. 5.4): n₁ = 1,8° и т.д.

                                                                                             

                                                                                              Таблица 5.4

№	1	2	3	4	5	6
n	1,8°	1,6°	1,6°	0,40°	0,50°	1,2°

      

5. Построение линии заданного уклона (рис. 5.26):

i = h : d; d = h : i; h = 2,5 м; i = 0,035; d = 2,5 : 0,035 = 71 м.

Для масштаба 1: 10000: в 1 см – 100 м;   

                                                х см — 71 м;   х = 0,71 см или » 7 мм.

  Раствором циркуля в 7 мм (или более) шагают от горизонтали до горизонтали, выбирая наиболее рациональный ход:

    

                        

Рис. 5.26. Построение линии заданного уклона

    

6. Построение продольного профиля по линии а – б (рис. 5.27):

Рис. 5.27.  Продольный профиль

7. Определение расстояния аб (см. рис. 5.25): d = 1053 м.

Тема 6. Плановые и высотные геодезические сети

Государственная геодезическая сеть – совокупность пунктов с известными координатами (х, у) и высотой (Н), равномерно расположенных на всей территории страны.

Плановая геодезическая сеть

Методы, схемы, точность и плотность пунктов при создании сети

— триангуляция (рис. 6.1) применяется в открытой местности:

Рис. 6.1. Триангуляция

— полигонометрия (рис. 6.2) применяется в закрытой местности:

Рис. 6.2. Полигонометрия

— трилатерация (рис. 6.3) применяется в особых случаях и выполняется по особой программе:

Рис. 6.3. Трилатерация

Точность сетей:  

— главное геодезическое обоснование 1 – 4 классов;

— сети сгущения 1 и 2 р.;

— съемочное обоснование.

Плотность пунктов:

— для съемок в масштабах 1:10 000 и 1: 25 000 — 1 пункт на 50 – 60 км²;

— для 1:5 000 — 1 пункт на 20 – 30 км²;

— для 1:2 000 — 1 пункт на 5 – 15 км².

— для крупномасштабных съемок в застроенной территории — 4 пункта на 1 км²;

                                                           в незастроенной территории — 1 пункт на 1 км²;

Для уменьшения продольного и поперечного сдвига ряда сети выполняют базисные и астрономические измерения широты j, долготы l и азимута а (рис. 6.4).

Типы знаков и типы центров

Для обеспечения видимости между геодезическими пунктами над центрами устанавливают различные типы знаков, конструкция и высота которых зависят от физико-географических условий местности, а также целесообразности применения материалов, дающих наибольший экономический эффект.

                    сигнал                пирамида             насадка         надстройка на здании

Рис. 6.5. Типы знаков

Для сохранности геодезических пунктов на длительное время, возможности их дальнейшего использования и исходя из физико-географических условий местности, глубины промерзания почвы, наличия зданий и сооружений закладывают центры различных типов. Существует специальный альбом типов центров.

          фундаментальный              грунтовый            стенной  стенная      временный

                    репер                              репер                   репер      марка            репер

Рис. 6.6. Типы центров

Высотная геодезическая сеть

Высотная (нивелирная) геодезическая сеть предназначена для создания единой системы высот на территории государства, для решения научных и прикладных задач. В настоящее время наряду с традиционными методами нивелирования применяются современные методы определения высотного положения геодезических пунктов с помощью спутниковых и лазерных приборов, что позволяет сократить время и средства на выполнение данной работы.

Не удается найти страницу | Autodesk Knowledge Network

(* {{l10n_strings.REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}}*

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}  

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings.LANGUAGE}} {{$select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.AUTHOR}}  

{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}

Определение крутизны ската по графику заложения. Проектирование линий заданного уклона 2

    Скачать с Depositfiles 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Горно-геологический факультет

Кафедра геоинформатики и геодезии

Отчёт

По курсу «Геодезия»

По лабораторной работе №6

Тема: «Определение крутизны ската по графику заложения. Проектирование линий заданного уклона»

 

 

Выполнила:

Ст. гр. ГКЗ-11

Проверил:

Асс. каф.

Шморгун Е. И.

Донецк 2011

                                 Определение крутизны ската по графику заложений

       Крутизной ската называется угол наклона ската к горизонтальной плоскости. Чем больше угол, тем круче скат. Величина угла наклона ската ν вычисляется по формуле:

ν = arctg 

где  — высота сечения рельефа, м,

 – заложение, м.

     Заложением называется расстояние на карте между двумя соседними горизонталями; чем круче скат, тем меньше заложение.

     Чтобы избежать расчетов при определении крутизны скатов по карет, на практике часто пользуются специальными графиками, называемыми графиками заложений. График заложений представляет собой график функции d=h*ctgν, абсциссами которого являются значения углов наклона, начиная с 0°30′, а ординатами – значения заложений, соответствующих этим углам наклона и выраженных в масштабе карты.

     Для определения крутизны ската раствором циркуля берут с карты соответствующее значение и переносят его на график заложений так, чтобы отрезок АВ оказался параллельным вертикальным линиям графика, а одна ножка циркуля располагалась на горизонтальной линии графика, другая ножка – на кривой заложений.

     Значение крутизны ската определяют, пользуясь оцифровкой горизонтальной шкалы графика.

Крутизна ската ν = 1°4′

 

 

Проектирование линии заданного уклона.

     При проектировании автомобильных и железных дорог, каналов, различных инженерных коммуникаций возникает задача построения на карте трассы будущего сооружения с заданным уклоном.

     Пусть на карте масштаба 1:10 000 требуется наметить трассу автомобильной дороги между точками Т8 и Т2, чтобы уклон ее на всем протяжении не превышал

і=0,07. Высота сечения рельефа на карте h=2,5 м.

     Для решения задачи рассчитывают величину заложения, соответствующую заданному уклону і=0,07и высоте сечения рельефа на карте h=2,5 м:

d=  =  = 35,7 м.

     затем выражают заложение в масштабе карты:

 =  =  = 0,004 м = 4 мм.

     Величину заложения  можно определить также по графику заложений, для чего надо определить угол наклона ν, соответствующий заданному уклону i, и раствором циркуля измерить заложение для этого угла наклона.

     Построение трассы между точками Т8 и Т2 осуществляется следующим образом. Раствором циркуля, равным заложению = 4 мм. Из точки Т8 засекают соседнюю горизонталь и получают точку 1. Из точки 1 тем же раствором циркуля засекают следующую горизонталь, получая точку 2, и т.д. соединив полученные точки, проводят линию с заданным уклоном.

     Во многих случаях рельеф местности позволяет наметить не один, а несколько вариантов трассы, из которых выбирается наиболее приемлемый по технико-экономическим соображениям. Так, например, из двух вариантов трассы, проведенной примерно в одинаковых условиях, будет выбран вариант с меньшей длиной проектируемой трассы.

     При построении линии трассы на карте может оказаться, что из какой-либо точки трассы раствор циркуля не достигает следующей горизонтали, т.е. рассчитанное заложение  меньше фактического расстояния между двумя соседними горизонталями. Это означает, что на данном участке трассы уклон ската меньше заданного, и при проектировании дорог расценивается как положительный фактор. В этом случае следует данный участок трассы провести по кратчайшему расстоянию между горизонталями по направлению к конечной точке.

    Скачать с Depositfiles 

Уклон и Конусность • ChertimVam.Ru

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.

Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

Уклон — линия — Большая Энциклопедия Нефти и Газа, статья, страница 4

Уклон — линия

Cтраница 4

Если дифференциальный манометр установлен ниже сужающего устройства, для удаления конденсата из соединительных линий необходимо предусмотреть специальные устройства ( отстойные сосуды), устанавливаемые в самой низкой точке линии. Уклоны линий должны обеспечивать свободный слив конденсата к этим устройствам. При измерении расхода запыленного газа или воздуха соединительные линии подключают через специальные приспособления, позволяющие избежать засорения линий и обеспечить продувку линий сжатым воздухом.  [46]

Величина уклона указывается над изображаемой наклонной линией. Если уклон линии на чертеже выражен нечетко, то его направление указывается стрелкой.  [48]

В первую очередь в ведомость вписываем все известные величины: расходы, длины участков и отметки поверхности земли. Затем выбираем уклоны линий и диаметры труб с таким расчетом, чтобы наполнение труб не превышало установленного нормами. Отметки равняем по поверхности воды, так как абсолютная величина наполнения h на каждом последующем участке возрастает.  [49]

По взаиморасположению горизонталей можно судить о том, где склоны, возвышения или щеки котловины имеют больший или меньший уклон, называемый крутизной. Крутизна, так же как и уклон линии или плоскости, измеряется тангенсом угла наклона ската к горизонтальной плоскости. Принято говорить о крутизне ската в данной точке, так как в разных точках топографической поверхности он обычно различен.  [50]

Устранение уклона сводится к тому, чтобы установить сегменты подпятника строго горизонтально. Наклон сегментов подпятника под углом а вызывает уклон линии валов к вертикали под таким же углом. Поэтому определять и устранять уклон линии вала нужно после того, как зеркало пяты установлено перпендикулярно валу.  [51]

Со шпинделем связана шестеренка е, приводящая в движение через шестеренку ж винт з, по к-рому ходит перо и; перемещения этого пера пропорциональны числам оборотов, сделанных шпинделем. Явление затупления сверла сказывается во внезапном изменении уклона линии, напр, на линиях а и г фиг.  [52]

Износу воздушной кабельной линия способствуют: а) уклоны линии, б) более сильные колебания температуры в результате непосредственного атмосферного воздействия и в) вибрация, особенно скачкообразное движение обледеневшего кабеля. Сплавы применяются также в случае обычных конструкций линий с несущим тросом и кольцами, когда оболочка должна обладать сопротивлением про-резанию кольцами.  [53]

Линейные смотровые колодцы, устраиваемые на прямых участках канализационной сети, предназначены для периодического осмотра и прочистки канализационной сети. Кроме того, линейные колодцы устраивают во всех местах изменения уклона линии или диаметра трубопровода и в местах изменения направления трассы сети.  [55]

В самом деле, если на местности передвигаться по линии АВ от точки А к точке В, то последовательно будут пройдены точки с перечисленными выше целыми отметками. Величину dl можно вычислить по формуле ( 3), приведенной в § 3, если известен уклон линии АВ. Поскольку точки А и В заданы на плане, горизонтальное расстояние между ними d АВ можно определить по масштабу чертежа; иногда d известно из результатов измерений на местности. Превышение h точки В над точкой А вычисляют как разность заданных отметок этих точек.  [56]

При измерении расхода газа необходимо исключить попадание конденсата из основного трубопровода в соединительные линии, а также обеспечить удаление конденсата, выделившегося в линиях. Для этого соединительные линии подключают к верхней половине сужающего устройства, установленного на горизонтальном или наклонном трубопроводе с уклоном линий в сторону трубопровода; дифманометр устанавливают выше сужающего устройства. Соединительные линии на всем протяжении по возможности должны иметь односторонний непрерывный уклон.  [58]

Плюсовая и минусовая линии должны находиться в одинаковых температурных условиях. Соединительные линии должны быть проложены вертикально или с уклоном к горизонтали не менее 1: 10, при этом желательно, чтобы на всем протяжении уклон линии был направлен в одну сторону.  [59]

Страницы:      1    2    3    4    5

Уклоны. Теория — на уровне глаз — ЖЖ

Как было сказано ранее, по одному из определений уклон это тангенс угла. С большим интересом узнал, что он равен коэффициенту сцепления. Вот тут и начинает прояснятся тайный смысл предупреждающих дорожных знаков 1.13 и 1.14 (крутой спуск / подъём).

Коэффициентом сцепления называется отношение двух сил – силы, необходимой для сдвига машины с заблокированными колесами, и силы тяжести, прижимающей машину к дороге. Так мы легко можем получить коэффициенты сцепления для сухого асфальта – 7000/10000 = 0,7, для грязной дороги – 3000/10000 = 0,3, и для льда – 1000/10000 = 0,1.
Например, автомобиль, стоящий на сухом асфальтированном уклоне с коэффициентом сцепления 0,7, начнет сползать вниз, если тангенс угла наклона при этом будет равен 70% (это уклон около 35 градусов, вряд ли вы когда-нибудь встретите такой). Но, кроме дорог, существуют улочки старых городов, особенно приморских, с углами наклона, существенно превышающими всевозможные нормативы. [2]

И в чём практическая ценность этой информации? Вот в чём: если на дворе гололёд, то на дороге с уклоном в 10% и более остановившаяся машина не удержится, будет скатываться.
К тому же, «при движении в сырую погоду вниз по асфальтированному уклону крутизной 20% эффективность торможения падает наполовину. И очень часто вам придется двигаться по мокрому льду с коэффициентом сцепления 0,1 и менее. А это значит, что вы должны внимательно отслеживать предупреждающие дорожные знаки 1.13 и 1.14. Их устанавливают, когда тангенс угла уклона приближается к 10%. Если вы пренебрежете этими знаками и остановитесь на подъеме, то в лучшем случае – не сможете сдвинуться с места. А уж если затормозите на спуске, машину может занести. Старайтесь тормозить двигателем на длительных спусках.» [2]
Вот о чём предупреждают знаки.

Кстати, есть знаки и меньше 10%, поэтому стало интересно в каких случаях их устанавливают.
ГОСТ Р 52289-2004 «Правила применения дорожных знаков, разметки, светофоров, дорожных ограждений и направляющих устройств», п. 5.2.16:
4% — если длина участка дороги на спуске или подъёме больше 600 метров при данном уклоне.
5% если больше 450 метров
6% если больше 350 метров
7% если больше 300 метров
8% (и более) если больше 270 метров.
Там же указаны и другие случаи, как например расстояние видимости, но сейчас они нас не интересуют.

Причины: почему проценты?

При рассмотрении темы уклонов всегда возникает вопрос, а почему уклон измеряют в процентах, а не в привычных градусах? По этому поводу слышал несколько версий:

а) Карты
Так проще вычислять уклон рельефа на карте или на строительном плане. Рельеф на картах обозначается линиями — горизонталями. Это замкнутая линия, которая получается если мысленно сделать сечение на какой-либо высоте и посмотреть сверху. Проще это представить если вспомнить линию уреза воды реки или водоёма, это тоже своего рода горизонталь.
Горизонтали, т.е. горизонтальные сечения, проводятся через определённое постоянное расстояние по высоте, о чём указывается в примечаниях. Зная высоту сечения горизонталей и определив на карте расстояние между ними можно получить уклон. Чем ближе друг к другу на карте изображены горизонтали, тем рельеф круче.

б) Погрешность
Построить угол, заданный в градусах, так сказать «в натуре» на строительной площадке, задача не из простых, а построить точно и вовсе запредельная. Небольшие величины уклона в градусах имеют вид десятичных дробей, а ведь погрешность даже в 1° на 10 метров длины даст ошибочные 17 сантиметров высоты. Так же, проценты величина относительная, и потому уклон, выраженный в процентах, можно построить имея в распоряжении только рулетку (или иной инструмент для измерения длинны) и уровень.

в) Неравномерность
Дорога, на протяжении всего спуска (подъёма), имеет неравномерный уклон. В каждый отдельный момент угол разный, и поэтому проще посчитать сколько составляет горизонтальная длинна участка спуска (подъёма), и на сколько изменилась высота относительно начала спуска (подъёма).

seyfulmulyukov.livejournal.com / 1avtorul.ru

Все эти версии вполне имеют право на жизнь. Общим для них является то, что для нахождения величины уклона используются меры длинны, которые всегда есть под рукой, а это практично. Что касается дорожных знаков, то более правдоподобной выглядит третья версия (неравномерность уклона), а для строительства дорог вторая (погрешность построений).
Есть ещё Международная Конвенция о дорожных знаках и сигналах за 1968 год, и Европейское соглашение 1971 года, дополняющее эту Конвенцию, по которой на предупреждающих знаках крутизна уклонов и подъемов указывается в процентах. [3]

Что стоит за цифрами, например 1/12 или 10%, много это или мало, как это выглядит и где применяется, рассмотрим в следующий раз на примерах из жизни.

---

Использованные материалы

1. Словари и энциклопедии на Академике © Академик
2. Материалы сайта «Школа жизни» © Shkolazhizni.ru
3. Википедия © Wikipedia
—

Как использовать формулу наклона и найти наклон прямой, положительный, отрицательный или неопределенный.

Разные слова, та же формула

Первый пример

Наклон линии , проходящей через точку (1, 2) и точку (4, 3), равен $$ \ frac {1} {3} $$.

Помните: разница значений y указывается в числителе формулы, а разница значений x — в знаменателе формулы.

Может ли любая точка быть $$ (x_1, y_1) $$?

Есть только один способ узнать!

Теперь давайте используем точку (4, 3) как $$ x_1, y_1 $$, и, как видите, наклон упрощается до того же значения: $ \ boxed {\ frac {1} {3}} $.

балл (4, 3) как $$ (x_1, y_1) $$

$$ slope = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} = \ frac {3-2} {4-1} = \ frac {1} {3} $$

балл (1, 2) как $$ (x_1, y_1) $$

$$ slope = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} = \ frac {2-3} {1-4} = \ frac {-1} {- 3} = \ frac {1} {3} $$

Ответ: не имеет значения, какую точку поставить первой.Вы можете начать с (4, 3) или с (1, 2), и в любом случае вы закончите с тем же самым номером! $$ \ frac {1} {3} $$

Пример 2 наклона линии A

Наклон линии , проходящей через точки (3, 4) и (5, 1), равен $$ — \ frac {3} {2} $$, потому что каждый раз, когда линия понижается на 3 (изменение y или подъем) линия переместится вправо (разбег) на 2.

Видеоурок на уклоне линии

Наклон вертикальной и горизонтальной линий

Наклон вертикальной линии не определен

Это потому, что любая вертикальная линия имеет нулевое значение $$ \ Delta x $$ или «пробег».Всякий раз, когда знаменателем дроби является ноль, в данном случае дроби, представляющей наклон прямой, дробь не определена. На рисунке ниже показана вертикальная линия (x = 1).

Наклон горизонтальной линии равен нулю

Это потому, что любая горизонтальная линия имеет нулевое значение $$ \ Delta y $$ или «подъем». Следовательно, независимо от того, что это за прогон (при условии, что он «не равен нулю!»), Дробь, представляющая наклон, имеет ноль в числителе.Следовательно, наклон должен быть равен нулю. Ниже изображена горизонтальная линия — вы можете видеть, что она не имеет никакого «подъема».

Есть ли у двух точек на линии одинаковый наклон?

Ответ: Да, и это важный момент, о котором следует помнить при вычислении наклона.

Каждая линия имеет постоянный наклон.Другими словами, наклон линии никогда не меняется. Эта фундаментальная идея означает, что вы можете выбрать любых 2 точек на линии.

Подумайте об идее прямой линии. Если бы наклон линии изменился, то это была бы зигзагообразная линия, а не прямая, как вы можете видеть на картинке выше.

Как вы можете видеть ниже, наклон остается неизменным независимо от того, какие 2 точки вы выбрали.

Наклон прямой

никогда не меняется

Проблема 1

Каков наклон прямой, проходящей через точки (10,3) и (7, 9)?

Покажи ответ

$ \ frac {rise} {run} = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} $

---

Использование $$ \ red {(10,3)} $$ как $$ x_1, y_1 $$

$ \ frac {9- \ red 3} {7- \ red {10}} \\ = \ frac {6} {- 3} \\ = \ в коробке {-2} $

Использование $$ \ red {(7,9)} $$ как $$ x_1, y_1 $$

$ \ frac {3- \ red 9} {10- \ red 7} \\ = \ frac {-6} {3} \\ = \ в коробке {-2} $

Задача 2

Линия проходит через (4, -2) и (4, 3).Какой у него наклон?

Покажи ответ

$ \ frac {rise} {run} = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} $

---

---

Использование $$ \ red {(4,3)} $$ как $$ x_1, y_1 $$

$ = \ frac {-2 — \ red 3} {4- \ red 4} знак равно \ frac {-5} {\ color {красный} {0}} \\ = \ текст {undefined} $

Использование $$ \ red {(4, -2)} $$ как $$ x_1, y_1 $$

$ = \ frac {3- \ red {-2}} {4- \ red 4} знак равно \ frac {5} {\ color {красный} {0}} \\ = \ text {undefined} $

Задача 3

Линия проходит через (2, 10) и (8, 7).Какой у него наклон?

Покажи ответ

$ \ frac {rise} {run} = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} $

---

Использование $$ \ red {(8, 7)} $$ как $$ x_1, y_1 $$

$ \ frac {10 — \ red 7} {2 — \ red 8} \\ = \ frac {3} {- 6} \\ = — \ frac {1} {2} $

Использование $$ \ red {(2,10)} $$ как $$ x_1, y_1 $$

$ \ frac {7 — \ red {10}} {8- \ red 2} \\ = \ frac {-3} {6} \\ = — \ frac {1} {2} $

Задача 4

Линия проходит через (7, 3) и (8, 5).Какой у него наклон?

Покажи ответ

$ \ frac {rise} {run} = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} $

---

Использование $$ \ red {(7,3)} $$ как $$ x_1, y_1 $$

$$ \ frac {5- \ red 3} {8- \ red 7} \\ = \ frac {2} {1} \\ = 2 $$

Использование $$ \ red {(8,5)} $$ как $$ x_1, y_1 $$

$$ \ frac {3- \ red 5} {7- \ red 8} \\ = \ frac {-2} {- 1} \\ = 2 $$

Задача 5

Линия проходит через (12, 11) и (9, 5).Какой у него наклон?

Покажи ответ

$ \ frac {rise} {run} = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} $

---

Использование $$ \ red {(5, 9)} $$ как $$ x_1, y_1 $$

$$ \ frac {11 — \ red 5} {12- \ red 9} \\ = \ frac {6} {3} \\ = 2 $$

Использование $$ \ red {(12, 11)} $$ как $$ x_1, y_1 $$

$$ \ frac {5- \ red {11}} {9- \ red {12}} \\ = \ frac {-6} {- 3} \\ = 2 $$

Задача 6

Каков наклон прямой, проходящей через (4, 2) и (4, 5)?

Покажи ответ

$ \ frac {rise} {run} = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} $

---

Использование $$ \ red {(4,5)} $$ как $$ x_1, y_1 $$

$$ \ frac {2 — \ red 5} {4- \ red 4} \\ = \ frac {-3} {\ color {красный} {0}} \\ = undefined $$

Использование $$ \ red {(4,2)} $$ как $$ x_1, y_1 $$

$$ \ frac {5 — \ red 2} {4- \ red 4} \\ = \ frac {3} {\ color {красный} {0}} \\ = undefined $$

ПРЕДУПРЕЖДЕНИЕ! Можете ли вы уловить ошибку в следующей задаче, которую Дженнифер пыталась найти уклон, который проходит через точки $$ (\ color {blue} {1}, \ color {red} {3}) $$ и $$ (\ color {blue} {2}, \ color {red} {6}) $$.У нее были небольшие проблемы с применением формулы наклона, она пыталась вычислить наклон 3 раза, и она дала 3 разных ответа. Сможете ли вы определить правильный ответ?

Задача

Найдите наклон прямой по двум точкам.

Попытка № 1

$ slope = \ frac {rise} {run} \\ = \ frac {\ color {красный} {y_ {2} -y_ {1}}} {\ color {синий} {x_ {2} -x_ {1}}} знак равно \ frac {6-3} {1-2} \\ = \ frac {3} {- 1} = \ в коробке {-3} $

---

Попытка № 2

$$ slope = \ frac {rise} {run} \\ = \ frac {\ color {красный} {y_ {2} -y_ {1}}} {\ color {синий} {x_ {2} -x_ {1}}} знак равно \ frac {6-3} {2-1} \\ = \ frac {3} {1} \\ = \ в коробке {3} $$

---

Попытка № 3

$$ slope = \ frac {rise} {run} \\ = \ frac {\ color {красный} {y_ {2} -y_ {1}}} {\ color {синий} {x_ {2} -x_ {1}}} \\ = \ frac {2-1} {6-3} \\ = \ в коробке {\ frac {1} {3}} $$

Покажи ответ

Правильный ответ — попытка №2.

В попытке №1 она не всегда использовала очки. В первой попытке она сделала следующее:

$$ \ frac {\ color {red} {y {\ boxed {_2}} — y_ {1}}} {\ color {blue} {x \ boxed {_ {1}} — x_ {2}}} $$

Проблема с попыткой №3 заключалась в изменении подъема и бега вспять.Она поместила значения x в числитель (вверху), а значения y в знаменатель, что, конечно же, противоположно!

$$ \ cancel {\ frac {\ color {blue} {x_ {2} -x_ {1}}} {\ color {red} {y_ {2} -y_ {1}}}} $$

Практика уклона Генератор задач

Вы можете сколько угодно практиковаться в решении такого рода задач с помощью приведенного ниже генератора задачи наклона.

Он будет случайным образом генерировать числа и запрашивать наклон линии, проходящей через эти две точки. Вы можете выбрать, насколько большими будут числа, регулируя уровень сложности.

Отвечать

Создать новую задачу уклона

Как найти наклон прямой

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Калькулятор уклона

Калькулятор уклона определяет уклон или градиент между двумя точками в декартовой системе координат. Наклон — это в основном величина наклона линии, которая может иметь положительное, отрицательное, нулевое или неопределенное значение.Прежде чем мы сможем использовать калькулятор, вероятно, стоит узнать, как найти уклон по формуле уклона. Чтобы найти уравнение прямой для любых данных двух точек, через которые она проходит, используйте наш калькулятор формы пересечения наклона.

Как найти уклон

1. Определите координаты (x₁, y₁) и (x₂, y₂) . Воспользуемся формулой для вычисления наклона прямой, проходящей через точки (3,8) и (-2, 10) .
2. Введите значения в формулу.Это дает нам (10-8) / (- 2-3) .
3. Вычтите значения в скобках, чтобы получить 2 / (- 5) .
4. Упростите дробь, чтобы получить наклон -2/5 .
5. Проверьте результат с помощью калькулятора уклона.

Чтобы найти наклон линии, нам нужны две координаты на линии. Достаточно любых двух координат. В основном мы измеряем величину изменения координаты y, часто известную как подъем , деленную на изменение координаты x, известное как прогон .Вычисления при нахождении наклона просты и включают в себя не что иное, как базовое вычитание и деление.

Формула наклона

наклон = (y₂ - y₁) / (x₂ - x₁)

Обратите внимание, что наклон прямой легко вычисляется вручную с использованием небольших целочисленных координат. Формула становится все более полезной, поскольку координаты принимают большие значения или десятичные значения.

Стоит отметить, что любая горизонтальная линия имеет нулевой градиент, потому что горизонтальная линия имеет те же координаты y.Это приведет к нулю в числителе формулы наклона. С другой стороны, вертикальная линия будет иметь неопределенный наклон, поскольку координаты x всегда будут одинаковыми. Это приведет к ошибке деления на ноль при использовании формулы.

Так же, как наклон может быть вычислен с использованием конечных точек сегмента, также может быть вычислена средняя точка. Средняя точка является важным понятием в геометрии, особенно при вписывании многоугольника внутрь другого многоугольника с его вершинами, касающимися середины сторон большего многоугольника.Это можно получить с помощью калькулятора средней точки или просто взяв среднее значение каждой x-координаты и среднее значение y-координаты, чтобы сформировать новую координату.

Наклон линий важен для определения того, является ли треугольник прямоугольным. Если любые две стороны треугольника имеют наклон, умножающийся на -1, то треугольник является прямоугольным. Вычисления для этого можно выполнить вручную или с помощью калькулятора прямоугольного треугольника. Вы также можете использовать калькулятор расстояний, чтобы вычислить, какая сторона треугольника самая длинная, что помогает определить, какие стороны должны образовывать прямой угол, если треугольник прямой.

Знак перед градиентом, предоставляемый калькулятором наклона, указывает, увеличивается ли линия, уменьшается, постоянная или неопределенная. Если график линии перемещается из нижнего левого угла в верхний правый, он увеличивается и, следовательно, является положительным. Если он уменьшается при движении из верхнего левого угла в нижний правый, то градиент отрицательный.

FAQ

Как найти наклон из уравнения?

Метод для нахождения наклона из уравнения будет варьироваться в зависимости от формы уравнения перед вами.Если уравнение имеет форму y = mx + c, то наклон (или градиент) равен м. Если уравнение не в такой форме, попробуйте переставить уравнение. Чтобы найти градиент других многочленов, вам нужно будет дифференцировать функцию относительно x .

Как рассчитать наклон холма?

1. Используйте карту, чтобы определить расстояние между вершиной и основанием холма по прямой.
2. Используя ту же карту или GPS, найдите высоту между вершиной и основанием холма .Убедитесь, что точки, от которых вы измеряете, такие же, как в шаге 1.
3. Преобразуйте оба измерения в одинаковые единицы. Если вы не уверены, используйте конвертер длины Omni.
4. Разделите разницу в высоте на расстояние между двумя точками.
5. Это число представляет собой уклон холма, если он увеличивается линейно. Если этого не произошло, повторите шаги, но там, где наблюдается заметное изменение наклона.

Как рассчитать длину откоса?

1. Измерьте разницу между вершиной и основанием уклона по отношению к осям x и y.
2. Если вы можете измерить только изменение x, умножьте это значение на градиент, чтобы найти изменение по оси y.
3. Убедитесь, что единицы для обоих значений совпадают.
4. Используйте теорему Пифагора, чтобы найти длину уклона . Возвести в квадрат как изменение x, так и изменение y.
5. Сложите два значения вместе.
6. Найдите квадратный корень из суммы.
7. Это новое значение — длина откоса.

Что такое уклон 1 к 20?

Уклон 1/20 — это уклон, который увеличивается на 1 единицу на каждые 20 единиц, пройденных по горизонтали. .Так, например, пандус длиной 200 футов и высотой 10 футов будет иметь уклон 1/20. Уклон 1/20 эквивалентен уклону 1/20 (как ни странно) и образует угол 2,86 ° между собой и осью x.

Как найти наклон кривой?

Поскольку наклон кривой изменяется в каждой точке, вы можете найти наклон кривой, дифференцируя уравнение относительно x и в полученном уравнении заменяя x на точку, в которой вы хотите найти градиент.

Скорость изменения такая же, как и крутизна?

Скорость изменения графика — это также его наклон , который также совпадает с градиентом. Скорость изменения можно найти, разделив изменение направления y (вертикальное) на изменение направления x (горизонтальное), если, конечно, оба числа находятся в одинаковых единицах. Скорость изменения особенно полезна, если вы хотите предсказать будущее предыдущего значения чего-то , так как при изменении переменной x будет присутствовать соответствующее значение y (и наоборот).

Где вы используете склон в повседневной жизни?

Склоны (или уклоны) имеют множество применений в повседневной жизни . Есть несколько очевидных физических примеров — у каждого холма есть уклон, и чем круче холм, тем больше его уклон . Это может быть полезно, если вы смотрите на карту и хотите найти лучший холм для езды на велосипеде. Вы также, вероятно, спите под наклоном, крышей, которая имеет высоту . Наклон крыши будет меняться в зависимости от стиля и места проживания.Но, что более важно, , если вы когда-нибудь захотите узнать, как что-то меняется со временем, вы построите график с наклоном .

Что такое уклон 10%?

Наклон 10% — это уклон, который увеличивается на 1 единицу на каждые 10 единиц, пройденных по горизонтали. (10%). Например, крыша с уклоном 10% и шириной 20 м будет иметь высоту 2 м. Это то же самое, что и градиент 1/10 , и между линией и осью x образуется угол 5,71 °.

Как найти участок под откосом?

Чтобы найти площадь под уклоном, необходимо проинтегрировать уравнение и вычесть нижнюю границу площади из верхней границы.3.5).

Разделите m на новый номер заказа и поставьте его перед новым x.

Умножьте c на x и добавьте это в новую строку.

Решите эту новую строку дважды: в первой, где x — это верхняя граница области, которую вы хотите найти, и в другой, где x — это нижняя граница.

Вычтите нижнюю границу из верхней.

Поздравьте себя с достижением.

Какой градус уклона 5: 1?

Наклон 5 к 1 — это наклон, который при каждом увеличении на 5 единиц по горизонтали увеличивается на 1 единицу .Число градусов между наклоном 5: 1 и осью x составляет 11,3 °. Это можно найти, сначала вычислив наклон, разделив изменение направления y на изменение направления x, а затем найдя арктангенс угла наклона.

Уклон прямой — Бесплатная справка по математике

Наклон линии — это ее угол или крутизна. Он может быть положительным, если линия наклоняется вверх, если смотреть слева направо, или отрицательным, если линия наклоняется вниз слева направо.

Горизонтальные и вертикальные линии

Горизонтальная линия идеально ровная. У него нет «крутизны», и он не идет ни вверх, ни вниз. Математически мы можем выразить это, сказав, что горизонтальная линия имеет наклон 0 . График ниже имеет наклон 0, и вы можете видеть, что у него нет крутизны или наклона (он плоский!).

Если горизонтальная линия плоская, как насчет вертикальной линии? Этот тип линии идет прямо вверх и вниз, поэтому на самом деле у нее нет определенного наклона, который мы можем измерить.Фактически, истинно вертикальная линия имеет бесконечный наклон и . Вот пример вертикальной линии:

Расчет уклона

Вам может быть любопытно, как мы точно определяем наклон. А slope — это изменение y по сравнению с изменением x . Это означает, что если у вас есть две точки на линии, \ ((0,0) \) и \ ((2,2) \), наклон может рассчитывается так:

$$ \ frac {\ text {изменение y}} {\ text {изменение x}} = \ frac {y_2-y_1} {x_2-x_1} = \ frac {2-0} {2-0} = 1 $$

Вот что мы сделали:

1. Найдите две точки на прямой
2. Найдите координаты первой точки \ ((x_1, y_1) \) и координаты второй точки \ ((x_2, y_2) \)
3. Подключитесь к приведенной выше формуле или просто определите изменение y и разделите на изменение x.

Как построить линию с заданным наклоном

Теперь, когда мы знаем, как рассчитать уклон, мы должны выяснить, как построить линию. Линия часто пишется с пересечением наклона form, y = mx + b, где m — наклон, а b — точка пересечения с y. Y-пересечение — это точка, в которой линия пересекает ось Y. Если задано y = 2x + 0, тогда линия имеет наклон 2 и точку пересечения оси y , равную 0, равную 0. Поскольку точка пересечения оси y равна 0, мы знаем одну точку (0,0).Так как наклон равен 2 или 2/1, мы должны подниматься на 2 на каждые 1, когда идем направо. Строка выглядит так:

Как Вы можете видеть, что линия поднимается на 2 балла за каждый 1 балл, который она проходит справа, что означает, что изменение y равно 2, когда изменение x равно 1. Наклон = 2. Для получения дополнительной информации, пожалуйста, просмотрите наш урок. на графических линиях.

Сводка

Наклон прямой — это изменение y, деленное на изменение x между двумя точками. Это также величина, на которую линия «поднимается» на каждую правильную точку.Некоторые называют это «подъем через бег». В любом случае, имея два очка, вы всегда можете найти наклон прямой с помощью этой быстрой формулы.

Виды уклонов трассы

Как правило, существует три (3) типа наклона линии: положительный, отрицательный и нулевой. Четвертый вариант немного противоречивый.

1. Положительный наклон
2. Отрицательный наклон
3. Нулевой наклон
4. Неопределенный наклон (также известный как бесконечный наклон)

Примечание: Четвертый наклон в списке не считается типом наклона потому что это случай вертикальной линии, где линия параллельна оси y, и у нее нет движения вдоль оси x.Другими словами, вертикальная линия идет вверх и вниз; следовательно, у него вообще нет крутизны.

Это также называется неопределенной крутизной, потому что знаменатель равен нулю. Помните концепцию уклона как подъема через бег. Рост (числитель) описывает изменение \ large {y}, которое символически записывается как \ color {blue} \ Delta \, y. Между тем, серия (знаменатель) описывает изменение \ large {x}, которое записывается как \ color {red} \ Delta \, x.

В случае неопределенного наклона значение числителя или \ color {blue} \ Delta \, y является ненулевым целым числом, а знаменатель или \ color {red} \ Delta \, x равно \ large {0 }.Таким образом, имеем:

---

Узнайте, как мистер Пигги может помочь нам запомнить концепции различных видов наклонов прямой.

---

Положительный наклон

Положительный наклон означает, что линия увеличивается, если смотреть слева направо.

Как видите, мистеру Пигги трудно подниматься наверх, поскольку подъем в гору требует дополнительных усилий.

---

Отрицательный наклон

Отрицательный наклон означает, что линия уменьшается, если смотреть слева направо.

Благодаря силе тяжести мистеру Пигги определенно нравится спуск, потому что ему нужно меньше усилий, чтобы спуститься.

---

Нулевой наклон

Нулевой наклон означает, что линия не увеличивается и не уменьшается, если смотреть слева направо, и наоборот. Проще говоря, наклон горизонтальной линии равен нулю, \ large0.

Мистер Пигги может продемонстрировать свои навыки бега на этом ровном месте.

---

Неопределенный уклон или бесконечный уклон

Неопределенный или бесконечный наклон означает, что линия не движется ни влево, ни вправо, как в случае вертикальной линии.Наклон вертикальной линии равен + \, \ infty или — \, \ infty.

В этой ситуации мистера Пигги ждет бесконечное «падение» всей его жизни!

---

Возможно, вас заинтересует:

Формула уклона

Форма линии наклона-пересечения

Форма прямой-наклонной линии

Каков наклон вертикальной линии?

«Каков наклон вертикальной линии?» — это частый вопрос, когда вы начинаете анализировать графики и линейные уравнения.Чтобы ответить на этот вопрос, давайте вернемся к основному определению.

Уклон определяется как крутизна, уклон или уклон линии. Это также определяется как изменение значения y («рост») по сравнению с изменением значения x («бег»). Формула наклона:

Поиск наклона

Обычно в линейном уравнении наклон линии легче всего вычислить, поместив уравнение линии в форму пересечения наклона или в формате y = mx + b (в отличие от стандартной формы).

Здесь переменная м представляет уклон.У вас может быть положительный или отрицательный наклон в зависимости от его значения.

Формула для горизонтальной линии (например, y = -1) соответствует форме пересечения наклона, всего без и м x . Значит, у него нет наклона!

Однако формулы для вертикальных линий (например, x = 4) не могут быть представлены в форме пересечения наклона. Чуть позже мы покажем вам, почему это так.

Какой наклон горизонтальной линии?

Наклон горизонтальной линии равен 0, потому что линия вообще не поднимается.Другими словами, для любых двух точек на прямой изменение значения y всегда будет равно 0.

Какой наклон вертикальной линии?

Наклон вертикальной линии не определен. Это потому, что для горизонтальной линии изменение значения x всегда будет равно 0. Вы можете выяснить это, вычислив горизонтальную разницу между двумя координатами x. Запомните формулу наклона:

С вертикальной линией нижний знаменатель равен 0.Однако деления на 0 в математике не существует! Даже если разница в координате y может измениться, деление любого числа на изменение координаты x, 0, приведет к неопределенному наклону.

Помните формулу наклона

При построении линейных уравнений помните, что м , уклон, вычисляется путем нахождения вертикального изменения между двумя точками, деленного на горизонтальное изменение между этими двумя точками.

Однако помните об этих двух уникальных случаях: горизонтальные линии имеют наклон 0, потому что вертикальное изменение равно 0.Вертикальные линии имеют неопределенный наклон, потому что горизонтальное изменение равно 0 — вы не можете разделить число на 0.

Дополнительные домашние задания по математике

Уклон прямой

Наклон прямой является мерой крутизны и направления невертикальной линии. Когда линия поднимается слева направо, наклон — положительное число. На рисунке 1 (а) показана линия с положительным наклоном. Когда линия идет слева направо, наклон — отрицательное число. На рис. 1 (б) показана линия с отрицательным наклоном.Угол наклона оси x или любой линии, параллельной оси x , равен нулю. На рисунке 1 (c) показана линия с нулевым наклоном. Ось y или любая линия, параллельная оси y , не имеет определенного наклона. На рисунке 1 (d) показана линия с неопределенным наклоном.

Рисунок 1 Различные варианты наклона линии.

Если м представляет наклон линии, а A и B — точки с координатами ( x _l , y ₁ ) и ( x ₂ , y ₂ ) соответственно, то наклон линии, проходящей через A и B , определяется по следующей формуле.

A и B не могут быть точками на вертикальной линии, поэтому x ₁ и x ₂ не могут быть равны друг другу. lf x ₁ = x ₂ , тогда линия вертикальная и наклон не определен.

Пример 1: Используйте рисунок, чтобы найти наклоны линий a, b, c и d.

Рисунок 2 Нахождение наклонов конкретных линий.

а. (a) Линия и проходит через точки (−7, 2) и (−3, 4).

г. (b) Линия b проходит через точки (2, 4) и (6, −2).

г. (c) Линия c параллельна оси x . Следовательно, м = 0.

г. (d) Линия d параллельна оси y . Следовательно, линия d имеет неопределенный наклон.

Пример 2: Линия проходит через (−5, 8) с наклоном 2/3.Если другая точка на этой линии имеет координаты ( x , 12), найдите x.

.

No related posts.