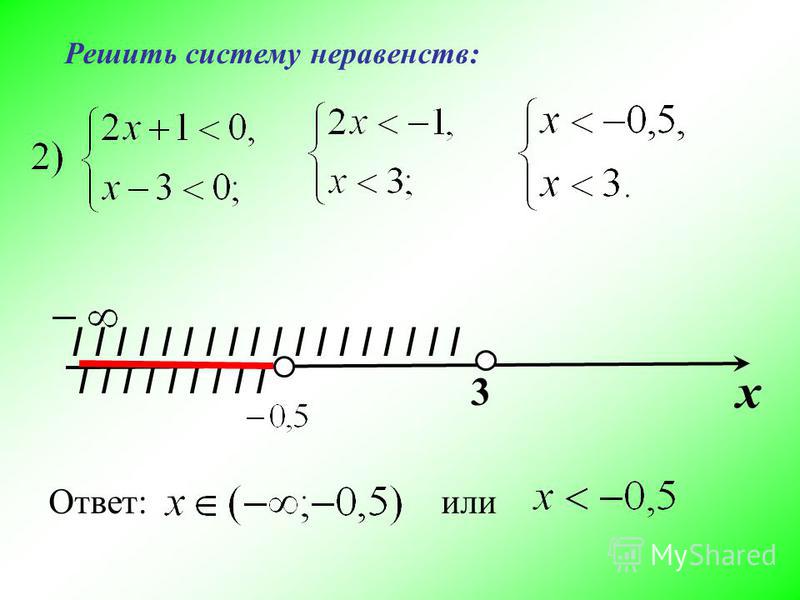
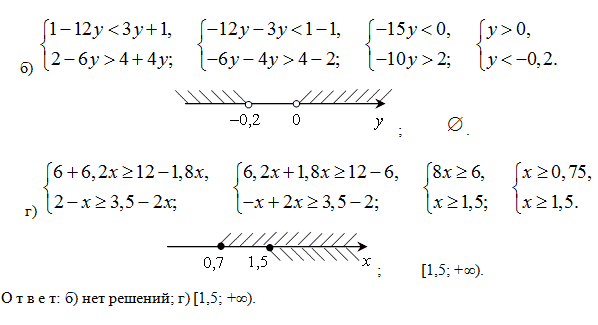Как решать систему неравенств 8 класс
Поможем понять и полюбить математику
Начать учиться
Начиная с 8 класса, задачи с системой неравенств появляются так часто, что проще выучить тему, чем списывать у соседа. В этой статье сделаем это и, наконец, выдохнем.
Основные понятия
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Числовое неравенство — в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Типы неравенств
Строгие — используют только больше (>) или меньше (<)
- a < b — это значит, что a меньше, чем b.

- a > b — это значит, что a больше, чем b.
- a > b и b < a означают одно и тоже, то есть равносильны.
Нестрогие — используют сравнения ≥ (больше или равно) или ≤ (меньше или равно)
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
Другие типы
- a ≠ b — означает, что a не равно b.
- a ≫ b — означает, что a намного больше, чем b.
- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Система неравенств
Чтобы щелкать задачки, нам пригодятся свойства числовых неравенств. Вот они:
Вот они:
Если а > b , то b < а. Также наоборот: а < b, то b > а.
Если а > b и b > c, то а > c. И также если а < b и b < c, то а < c.
Если а > b, то а + c > b+ c (и а – c > b – c).
Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям можно прибавлять или вычитать одну и ту же величину.
Если а > b и c > d, то а + c > b + d.
Если а < b и c < d, то а + c < b + d.
Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять, т.к. возможны исключения. Например, если из 12 > 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а > b и c < d, то а – c > b – d.
Если а < b и c > d, то а – c < b – d.
Из одного неравенства можно почленно вычесть другое противоположного смысла, оставляя знак того, из которого вычиталось.
Если а > b, m — положительное число, то mа > mb и
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
.
Если же а > b, n — отрицательное число, то nа < nb иОбе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.
Если а > b и c > d, где а, b, c, d > 0, то аc > bd.
Если а < b и c < d, где а, b, c, d > 0, то аc < bd.
Неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствием является: если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2. На множестве положительных чисел обе части можно возвести в квадрат.
- Если а > b, где а, b > 0, то .
Если а < b , то .
Таблица числовых промежутков
Полезна тем, что с ее помощью удобно записывать множество решений.
Неравенство | Графическое решение | Форма записи ответа |
x < c | x ∈ (−∞; c) | |
x ≤ c | x ∈ (−∞; c] | |
x > c | x ∈ (c; +∞) | |
x ≥ c | x ∈ (c; +∞) |
Еще один важный шаг — запись ответа.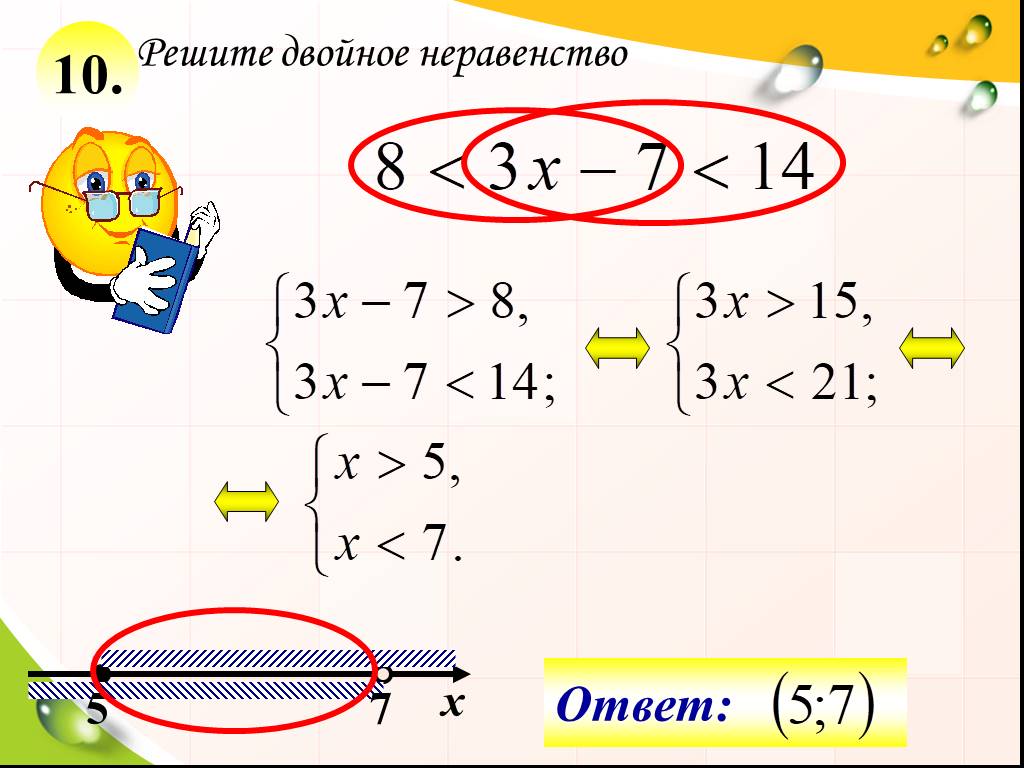 Вот, как правильно это делать:
Вот, как правильно это делать:
- Если знак строгий (>, <), точка на оси будет не закрашена, а скобка — круглой.
- Если знак нестрогий (≥, ≤), точка на оси будет закрашена, а скобка — квадратной.
- Скобка, рядом со знаком бесконечности всегда круглая.
Решение системы неравенств
Линейное неравенство — то, в котором неизвестное представлено в первой степени. Для его решения нужно, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице. Алгоритм решения:
1. Раскрыть скобки, перенести неизвестное в левую часть, числа в правую и привести подобные слагаемые. Получится одно из следующих видов:
- ax < b,
- ax ≤ b,
- ax > b,
- ax ≥ b.

2. Если получилось ax ≤ b.Для его решения необходимо поделить левую и правую часть на коэффициент перед неизвестным a.
Если a < 0, то знак меняется на противоположный.
Получаем x ≥ ba.
4. Записываем ответ как он есть или в соответствии с таблицей числовых промежутков.
Решим пример
3 * (2 − x) > 18
Как решаем
Ответ: x < −4 или в числовом промежутке x ∈ (−∞; −4). |
И еще один
Как решаем
Ответ: х < – 2. |
Последний, чтобы разобраться наверняка
Как решаем
Ответ: числовой промежуток x ∈ (– 2; 0]. |
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
239.8K
Как найти периметр треугольника
К следующей статье
185.8K
Сложение дробей: теория и практика
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
§ Как решать системы неравенств
Прежде чем перейти к разбору темы «Как решать
систему линейных неравенств» обязательно внимательно изучите
урок «Как решать неравенства».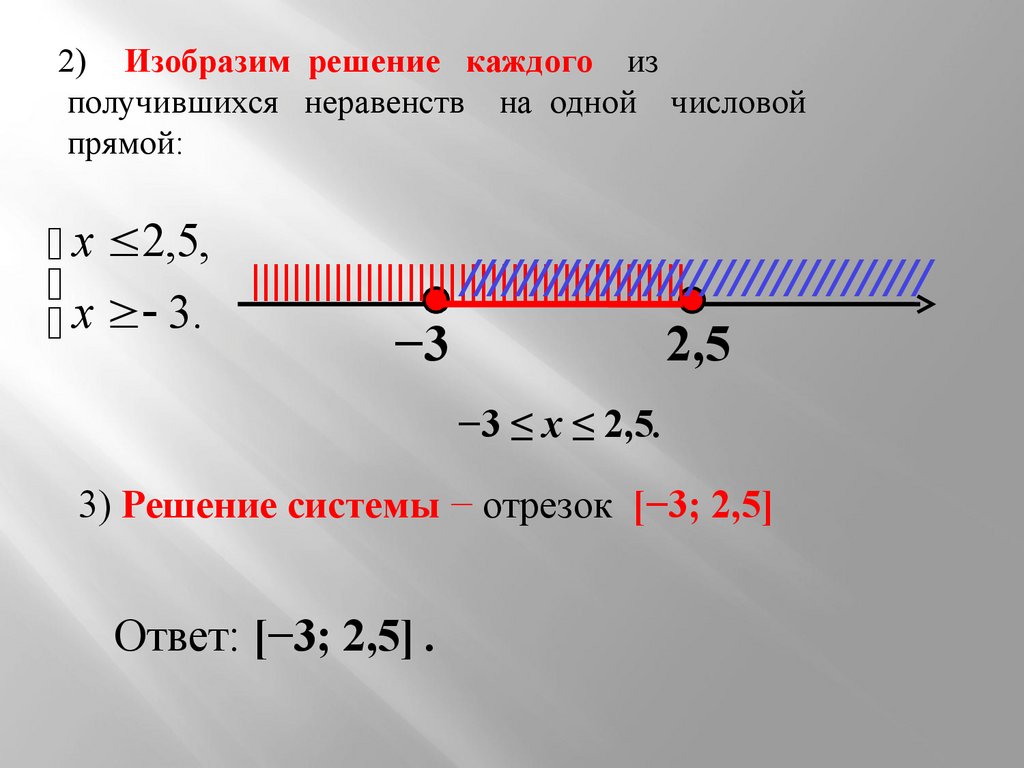
Важно!
Системой неравенств называют два или более неравенства, которые объединены фигурной скобкой.
Рассмотрим пример системы неравенств.
| x > 2 | |
| x > 5 |
Как видно на примере выше, систему неравенств легко определить по фигурной скобке.
Запомните!
Чтобы решить систему неравенств нужно:
- решить отдельно каждое неравенство;
- сравнить полученные решения каждого неравенства и получить общий ответ системы.
Вернемся к нашему примеру системы неравенств.
| x > 2 | |
| x > 5 |
Так как оба неравенства в системе уже решены и представляют собою готовый ответ, то
сразу переходим к поиску общего решения всей системы.
Для этого проведем две числовые оси (для каждого из неравенств свою). На осях заштрихуем результат решения неравенств.
Важно!
Числовые оси с решениями нужно располагать друг под другом.
Числа на осях отмечают в порядке возрастания. То есть число «2» будет находиться левее «5».
|
После того как мы построили числовые оси с решениями неравенств, необходимо провести через отмеченные на осях числа перпендикулярные прямые.
Запомните!
При проведении прямых через точки на осях соблюдают следующие правила:
- если точка не входит в область решения («пустая» точка), то рисуют пунктирную линию;
- если точка входит в область решения («заполненная» точка), то рисуют
сплошную линию.

Проведем прямые через числовые точки на осях.
Для определения ответа найдем те области решения, которые удовлетворяют ответам обоим неравенствам. Другими словами, те области, где в обоих случаях области решений заштрихованы.
Исходя из полученного анализа, мы получаем, что решением системы неравенств будет «x > 5». Запишем полученный ответ.
|
Ответ: x > 5
Рассмотрим другой пример системы неравенств.
| x | |
| x ≥ − 2 |
Так как неравенства в системе снова представляют собой готовые ответы — сразу перейдем к поиску общего
решения системы неравенств.
Нарисуем числовые оси для каждого неравенства и отметим на них решения. Проведем через каждое отмеченное число на осях прямую по правилам, описанным выше.
|
Выберем те области решений, которые удовлетворяют обоим неравенствам.
Как видно на рисунке выше, область решений, которая подходит для обоих неравенств, находится между числами «−2» и «0».
Когда область решений находится между двумя числами, принято записывать ответ с помощью двойного неравенства.
|
Ответ: −2 ≤ x
Запомните!
Запись двойного неравенства используют, когда интервал решения системы неравенств лежит между числами.
Знаки сравнения («
Числа записываются в том же порядке, что они расположены на оси.
Другие примеры решения систем неравенств
В отличии от примеров выше, как правило, в системах неравенств перед поиском общего решения всей системы необходимо предварительно решить каждое из неравенств.
Рассмотрим и решим систему, где неравенства требуют предварительного решения.
Решим линейные неравенства по правилам, описанным в уроке «Решение линейных неравенств». Затем найдем общий ответ системы.
| 5(x + 1) − x > 2x + 2 | |
| 4(x + 1) − 2 ≤ 2(2x + 1) − x |
| 5x + 5 − x > 2x + 2 | |
| 4x + 4 − 2 ≤ 4x + 2 − x |
| 5x − x + 5 > 2x + 2 | |
| 4x + 4 − 2 ≤ 4x + 2 − x |
| 4x + 5 > 2x + 2 | |
| 4x + 2 ≤ 3x + 2 |
| 4x − 2x > 2 − 5 | |
| 4x − 3x ≤ 2 − 2 |
| 2x > −3 | (:2) | |
| x ≤ 0 |
| 2x (:2) > −3 (:2) | |
| x ≤ 0 |
| x > − | |
| x ≤ 0 |
|
Ответ: −1
При решении систем неравенств, в которых есть неравенства, содержащие пропорцию, используем
правило пропорции.
| 5(x + 1) ≤ 3(x + 3) + 1 | ||||
|
| 5x + 5 ≤ 3x + 9 + 1 | |
| (2x − 1) · 2 ≤ (x + 1) · 7 |
| 5x − 3x ≤ 10 − 5 | |
| 4x − 2 ≤ 7x + 7 |
| 2x ≤ 5 | |
| 4x − 7x ≤ 7 + 2 |
| 2x ≤ 5 | (:2) | |
| − 3x ≤ 9 | (:−3) |
| 2x (:2) ≤ 5 (:2) | |
| − 3x (:−3) ≥ 9 (:−3) |
| x ≤ | |
| x ≥ −3 |
|
Ответ: −3 ≤ x ≤ 2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
| Отправить |
Системы уравнений и неравенств — Решение систем с тремя переменными
Три уравнения. Три неизвестные переменные. Если они не будут найдены вовремя, мировые запасы Silly Putty сгорят. Только один человек может найти их вовремя, и она только что заболела. О-о.
В качестве нашего лучшего агента Shmoop вы должны научиться решать системы уравнений с тремя переменными и спасать глупую замазку мира, что довольно близко к спасению самого мира.
К счастью, для решения системы с тремя переменными используются те же методы, что и с двумя переменными, — нам просто нужно попасть в эту лох более одного раза. Иногда будет проще использовать исключение, иногда быстрая замена решает проблему в один миг, а иногда оба метода объединяются для решения проблемы, а затем вместе борются с преступностью.
Типы ответов, которые мы можем найти, тоже одинаковы: может быть ноль, одно или бесконечное количество решений.
Быстро в тренировочную комнату. Да-на-нана-на-на.
Проблема выборки
Решить систему уравнений:
x + 2 Y -3 Z = -3
2 x + Y + Z = -2 2 + Z = -2 2
9000 2 9000 2 9000 2 9000 2
9000 2 9000 2 9000 2
9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 + . x – y + 4 z = 4
Будь начеку, Шмупер. Мы можем начать эту проблему либо с замены, либо с исключения. На этот раз мы собираемся использовать исключение. Когда у нас есть три уравнения, мы можем складывать или вычитать только два уравнения за раз. Мы не можем жонглировать так много сразу.
Воспользуемся третьим уравнением, чтобы избавиться от y в первом и втором уравнениях. Например, давайте добавим:
Например, давайте добавим:
2 x + y + z = -2
2 x — y + 4 z = 4
. Это дает нам 9004
(2 (2 (2002 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2002 (2002 (2002 (2002 (2002 (2 (2 (2 (2 (2001 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 (2 x + 2 x ) + ( Y — Y ) + ( Z + 4 Z ) = (-2 + 4)
4 x + 5 Z = 2
Небольшое умножение в третьем уравнении поможет нам исключить другие y из первого уравнения.
x + 2 y – 3 z = -3
2(2 x – y + 4 z 4) Проверьте это.
x + 2 Y -3 Z = -3
4 x -2 Y + 8 Z = 8
Теперь мы можем добавить EM, как босс.
( x + 4 x ) + (2 y – 2 y ) + (-3 z + 8 z ) = (-3 + 9001 9 х +
90 5 z = 5 Теперь у нас есть система уравнений с двумя переменными, точно такая же, как когда-то давно. Две секции назад.
Две секции назад.
4 x + 5 z = 2
5 x + 5 z = 5
Помни свое обучение, секретный агент. Хотя подстановка часто полезна, когда мы работаем только с двумя переменными, в этом случае мы можем исключить z из этих уравнений путем умножения 4 x + 5 z = 2 на -1.
-4 x -5 Z = -2
5 x + 5 Z = 5
Добавление двух уравнений вместе, мы получаем:
x = 3
Отлично. Теперь мы к чему-то пришли; не уверен, где, хотя. Мы можем подставить x = 3 в любое из наших предыдущих уравнений. Мы рекомендуем один из них без y , чтобы мы могли решить за з .
4 x + 5 Z = 2
4 (3) + 5 Z = 2
12 + 5 Z = 2
5 Z = -10
Z 5 Z = -10 Z = -2 Теперь вернем все это домой, подставив x = 3 и z = -2 в одно из трех исходных уравнений. 3 + 2 у – 3(-2) = -3 2 у + 9= -3 2 y = -12 y = -6 Мы нашли единственное решение, поэтому это упорядоченная тройка в виде (3, -6, -2). Это означает, что есть одна точка, где встречаются все самолеты (например, аэропорт). Однако это не единственный возможный результат для системы из трех уравнений. Иногда решений не будет, потому что по крайней мере две плоскости параллельны друг другу. Решите систему уравнений. x + 3 y + 2 z = -1 2 x + 6 y + 4 z = 3 2 x + 2 y – 3 z = 9 Хорошо, как начать? Ну, а начнем с начала, а когда дойдем до конца, остановимся. Да, это дельный совет. Мы можем использовать первое уравнение, чтобы исключить x из нашей системы, умножив на -2. -2( x + 3 y + 2 z = -1) -2 x – 6 y – 4 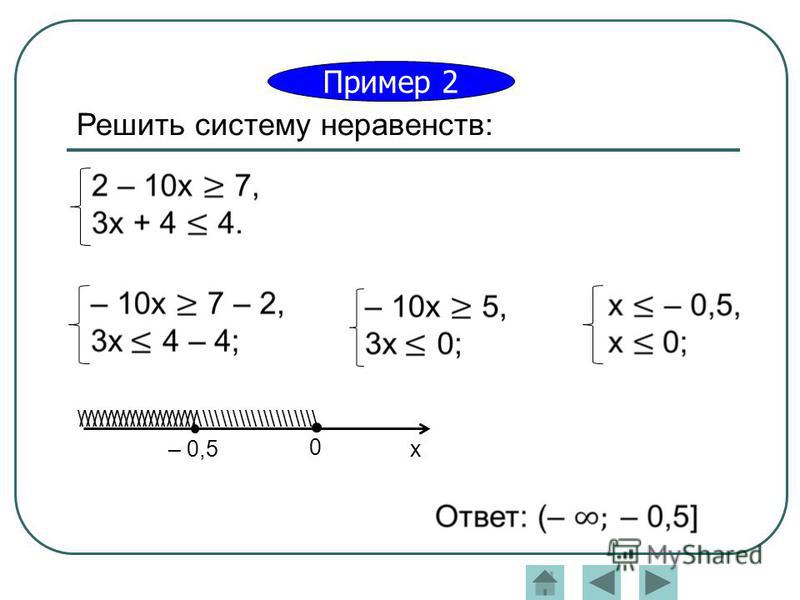 Возьмем x + 2 y – 3 z = -3.
Возьмем x + 2 y – 3 z = -3. Пример задачи
 Это кажется нам хорошим началом.
Это кажется нам хорошим началом.
-2 x -6 Y -4 Z = 2
2 x + 6 y + 4 z = 3
( — 2 x + 2 x ) + (-6 y + 6 y ) + (-4 z + 4 z ) = (2 + 3)
Дополнительные способности Shmoop — активировать:
0 = 5
Э-э, что? Это не правильно. Наши силы Шмуп сломали математику? Нет, просто нет решений, удовлетворяющих этим уравнениям. Нет никакой точки, которая, если подставить ее в эти уравнения, даст 0 = 5.
Таков наш ответ: решения нет. Наши три плоскости не все пересекаются. Может быть, у двоих из них есть, но у третьего уже были планы на обед. Может быть, все трое и встречаются, но никогда одновременно. Системы без решений должны лучше координировать свои графики.
Системы без решений должны лучше координировать свои графики.
Пример задачи
Решите эту систему линейных уравнений.
3 x + 2 Y -2 Z = -2
6 x + 4 Y -4 Z = -4
5 x – y y y y + 5 x – y y + 5 x – y y 5 x — = -4 5 x — От какой переменной мы можем попытаться избавиться в первую очередь? Какой метод будет работать лучше всего? Кто из участников выиграет American Idol в этом году? Коэффициенты y и z в третьем уравнении можно использовать для исключения любой переменной. Одно из них также можно было бы использовать в качестве замены, но с этими 5 x вместе с коэффициентами в первых двух уравнениях у нас на руках была бы большая мешанина чисел. Обычно мы любим устраивать беспорядок, но только не во время решения математических задач. Итак, мы решили добавить: 3 x + 2 y – 2 z = -2 2(5 x – Это устранит y … и z ! Н-м-повезло. 3 x + 2 Y -2 Z = -2 10 x -2 y + 2 Z = 2 , который дает нам: (3 x 99 , который дает нам: (3 x 9 : (3 x = 2 . + 10 x ) + (2 Y -2 Y ) + (-2 Z + 2 Z ) = (-2 + 2) 13 x = 0 x. = 0 Великолепное начало. Мы можем все упростить, подставив 0 вместо x в наших исходных уравнениях. 2 Y -2 Z = -2 4 Y -4 Z = -4 — Y + Z = 1 Запомните метод оборотной? Мы делаем. Мы как слон или жесткий диск компьютера — мы никогда не забываем. y = z – 1 А теперь подставьте z – 1 вместо y в первом уравнении. 2( z – 1) – 2 z = -2 2 z – 2 – 2 z = -2 0 = 0 0 = 0 Бззз! Неправильный. Мы показали, что х и х имеют бесконечное количество общих решений, но мы уже знаем, что х = 0, помните? Даже если бы мы этого не сделали, нам все равно нужно было бы выяснить, что такое x . Когда у нас были бесконечные двумерные решения, это означало, что обе линии были абсолютно одинаковыми. Сейчас мы находимся в трехмерном пространстве и работаем с тремя плоскостями. У нас может быть бесконечное количество решений, при этом все три плоскости не должны быть одинаковыми; они могут просто разделить линию между собой. Что это за линия? Это y = z – 1. Любое решение системы уравнений должно удовлетворять x = 0 и y = z – 1. уравнения с тремя переменными, секретный агент Shmoop. Мир и его запасы Silly Putty теперь в ваших руках. Удачи. Решение систем равенств и неравенств и многое другое
Проблемы Системы уравнений Определим линейную систему двух уравнений с двумя неизвестными как топор + по = с дх + еу = е Геометрия линейной системы 2 на 2 состоит из двух линий. Если
прямые параллельны (одинаковый наклон), то они не будут пересекаться. В противном случае
решение линейной системы 2 на 2 является точкой пересечения. Ликвидация Один из способов решения систем линейных уравнений называется подстановкой . Пошаговый метод: Шаг 1: Расположите уравнения так, чтобы переменные были выровнены
вверх вертикально. Шаг 2: Выберите переменную, которую проще всего исключить и умножить
оба уравнения разными числами, так что коэффициенты этой переменной
одинаковы. Шаг 3: Вычтите два уравнения. Шаг 4: Решите систему с одной переменной. Шаг 5: Подставьте это значение обратно в любое уравнение, чтобы найти
другое уравнение. Шаг 6: Перечитайте вопрос и снова вставьте свои ответы в
проверять. Пример Решать 2x
= 3 года + 3 4x — 5 лет
= 7 Решение 2x — 3г
= 3 4x — 5 лет
= 7 Умножьте первое уравнение на 2. 4х — 6у = 6 4х — 5у = 7 -у
= -1 После
вычитание уравнений. у = 1 4x — 5(1)
= 7 Подстановка
1 для у
во втором уравнении. 4x
= 12 Икс
= 3 Ответ (3,1) Мы видим, что 2(3) = 3(1) + 3 4(3) — 5(1)
= 7 Упражнения Решать: у = 5x — 5 3x + 4y = 26 у = 4x + 2 8x — 2y = -3 Замена Есть и второй способ решения таких систем. Пошаговый метод Шаг 1: Вычислите одну переменную явно через другую.
Вставьте это уравнение в рамку. Шаг 2: Подставьте это в другое уравнение. Шаг 3: Решите, что получится. Шаг 4: Подставьте этот результат в выражение в поле. Шаг 5: Проверьте решение. Пример Решить х — 2у = 2 3х — 5у = 7 Решение Мы можем манипулировать первым уравнением, чтобы получить x с помощью
сам. х
= 2 + 2y 3(2 + 2г) — 5г
= 7 Подстановка в
второе уравнение. 6+ 6 лет — 5 лет
= 7 6 + у
= 7 у = 1 х = 2 + 2 (1) = 4
Подключаемся к уравнению с шага 1. Решение (4,1) Проверяем: 4 — 2(1)
= 2 3(4) — 5(1)
= 7 Упражнения Решить методом подстановки. 3x + y = 5 2x — 3y = -4 5x — 4y = 2 8x + 5y = 26 Решение систем неравенств В прошлый раз мы решали неравенства. Пример Изобразите систему неравенств: 3x + у > 12 3x + 2г < 15 у > 2 Решение Мы рисуем Т-таблицы, чтобы отобразить две линии. Обратите внимание, что последние два
линии горизонтальны. 3x + у = 12 Решаем систему два на два, чтобы найти координаты пересечения. у
= 12–3 x 3x + 2(12
— 3x)
= 15 3x +
24 — 6х
= 15 -3x
= -9 Икс
= 3 Подключение обратно у =
12 —
3(3) = 3 Следовательно, точка (3,3) является точкой
пересечение. График показан ниже. Упражнения: График: х — у > 2 у — х >
-1 3x + 2 года > 15 х > 3 Решение проблем Пример Сколько граммов чистого золота и сколько граммов
сплав, который на 55% состоит из золота, следует переплавить вместе, чтобы получить 72 г
сплава
это 65% золота? Позволять х =
грамм чистого золота у =
грамм сплава. Затем х + у =
72 и х + 0,55 г =
0,65(72) = 46,8 Следовательно х =
72-й (72 — лет) + 0,55 лет
= 46,8 72 —
0,45 г = 46,8 -0,45 г = -25,2 у = 56 Решение дает у = 56 Теперь поместите это в «коробочное» уравнение, чтобы найти x.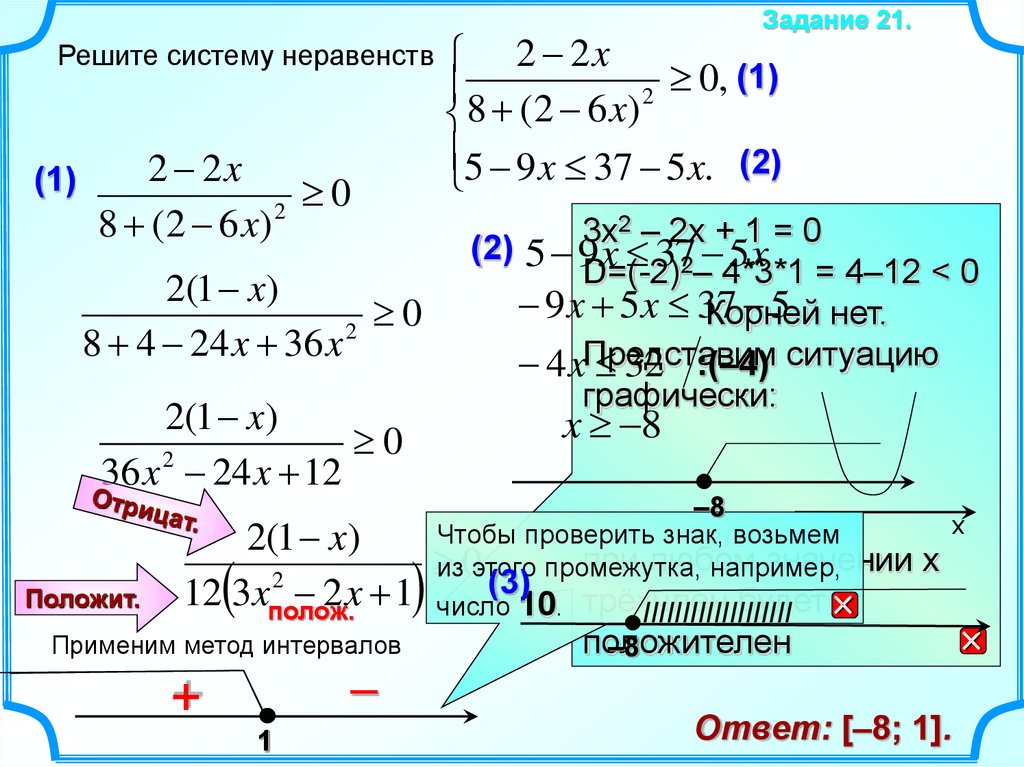
8 y0019 + z = 1)  Как насчет того, чтобы заменить наш путь к решению? Сначала найдите y в третьем уравнении.
Как насчет того, чтобы заменить наш путь к решению? Сначала найдите y в третьем уравнении.
Решение систем равенств и неравенств и других текстовых задач


 Мы называем этот альтернативный способ заменой .
Мы называем этот альтернативный способ заменой .
и 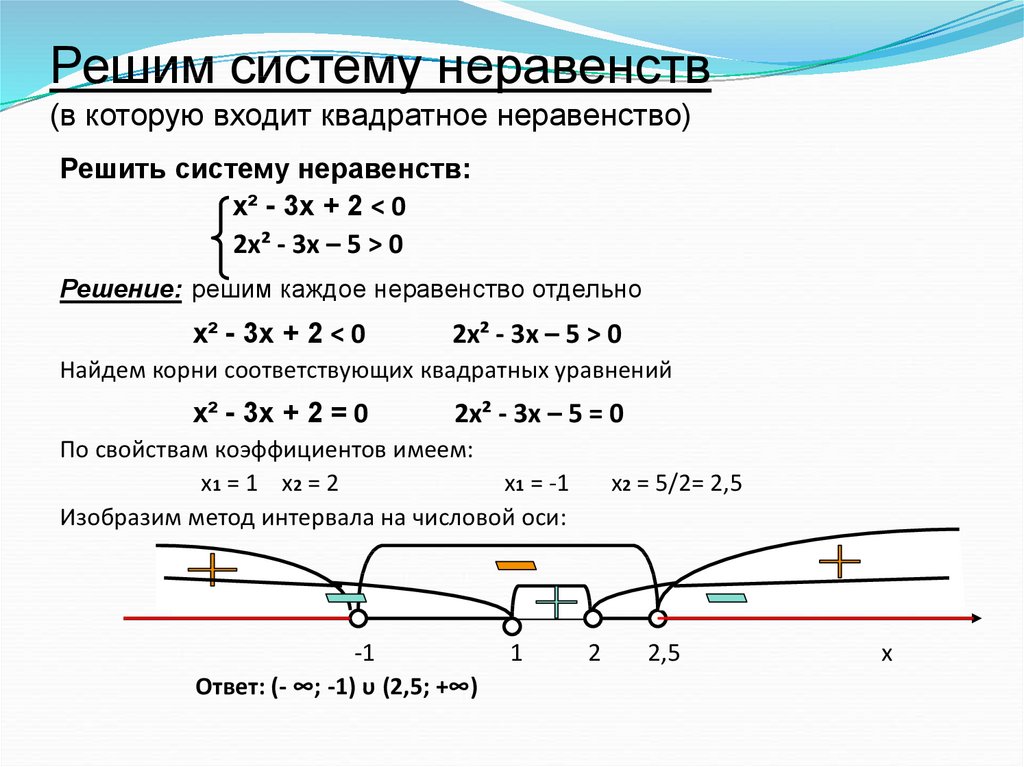 Если у нас есть система неравенств,
мы выполняем те же шаги, за исключением того, что на этот раз мы рисуем все неравенства
и взять пересечение определенных областей.
Если у нас есть система неравенств,
мы выполняем те же шаги, за исключением того, что на этот раз мы рисуем все неравенства
и взять пересечение определенных областей. х у 0 12 4 0
3x + 2 года
= 15 х г 0 7,5 5 0 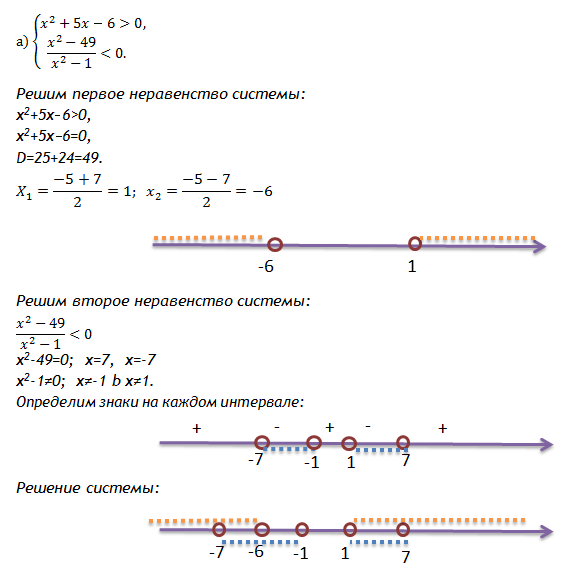



 Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.