Таблица отрицательных степеней чисел – Telegraph
Таблица отрицательных степеней чиселСкачать файл — Таблица отрицательных степеней чисел
Возведение в степень — это такая же математическая операция, как сложение, вычитание, умножение или деление. Сейчас объясню все человеческим языком на очень простых примерах. Примеры элементарные, но объясняющий важные вещи. Ты и так все знаешь: У каждого по две бутылки колы. Правильно — 16 бутылок. Тот же самый пример с колой можно записать по-другому: Математики — люди хитрые и ленивые. В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением. Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения. Ты, конечно, можешь делать все медленнее, труднее и с ошибками! А какие еще хитрые приемы счета придумали ленивые математики? Правильно — возведение числа в степень. Если тебе нужно умножить число само на себя пять раз, то математики говорят, что тебе нужно возвести это число в пятую степень. Математики помнят, что два в пятой степени — это. И решают такие задачки в уме — быстрее, легче и без ошибок. Для этого нужно всего лишь запомнить то, что выделено цветом в таблице степеней чисел. Поверь, это сильно облегчит тебе жизнь. Кстати, почему вторую степень называют квадратом числа, а третью — кубом? Сейчас будут тебе и квадраты, и кубы. Бассейн стоит у тебя на даче. Жара и очень хочется купаться. Но… бассейн без дна! Нужно застелить дно бассейна плиткой. Сколько тебе надо плитки? Для того чтобы это определить, тебе нужно узнать площадь дна бассейна. Это легко… Но где ты видел такую плитку? Ты заметил, что для определения площади дна бассейна мы умножили одно и то же число само на себя? Конечно, когда у тебя всего два числа, все равно перемножить их или возвести в степень. Но если у тебя их много, то возводить в степень значительно проще и ошибок при расчетах получается тоже меньше. Для ЕГЭ это очень важно. Итак, тридцать во второй степени будет. Или же можно сказать, что тридцать в квадрате будет.
Математики помнят, что два в пятой степени — это. И решают такие задачки в уме — быстрее, легче и без ошибок. Для этого нужно всего лишь запомнить то, что выделено цветом в таблице степеней чисел. Поверь, это сильно облегчит тебе жизнь. Кстати, почему вторую степень называют квадратом числа, а третью — кубом? Сейчас будут тебе и квадраты, и кубы. Бассейн стоит у тебя на даче. Жара и очень хочется купаться. Но… бассейн без дна! Нужно застелить дно бассейна плиткой. Сколько тебе надо плитки? Для того чтобы это определить, тебе нужно узнать площадь дна бассейна. Это легко… Но где ты видел такую плитку? Ты заметил, что для определения площади дна бассейна мы умножили одно и то же число само на себя? Конечно, когда у тебя всего два числа, все равно перемножить их или возвести в степень. Но если у тебя их много, то возводить в степень значительно проще и ошибок при расчетах получается тоже меньше. Для ЕГЭ это очень важно. Итак, тридцать во второй степени будет. Или же можно сказать, что тридцать в квадрате будет. Иными словами, вторую степень числа всегда можно представить в виде квадрата. И наоборот, если ты видишь квадрат — это ВСЕГДА вторая степень какого-то числа. Квадрат — это изображение второй степени числа. Вот тебе задание, посчитать, сколько квадратов на шахматной доске с помощью квадрата числа Теперь куб или третья степень числа. Тот же самый бассейн. Но теперь тебе нужно узнать, сколько воды придется залить в этот бассейн. Тебе нужно посчитать объем. Объемы и жидкости, кстати, измеряются в кубических метрах. Прямо показывай пальцем и считай! Раз, два, три, четыре…двадцать два, двадцать три… Сколько получилось? Бери пример с математиков. Они ленивы, поэтому заметили, что чтобы посчитать объем бассейна, надо перемножить друг на друга его длину, ширину и высоту. А теперь представь, насколько математики ленивы и хитры, если они и это упростили. Свели все к одному действию. Они заметили, что длина, ширина и высота равна и что одно и то же число перемножается само на себя… А что это значит? Это значит, что можно воспользоваться степенью.
Иными словами, вторую степень числа всегда можно представить в виде квадрата. И наоборот, если ты видишь квадрат — это ВСЕГДА вторая степень какого-то числа. Квадрат — это изображение второй степени числа. Вот тебе задание, посчитать, сколько квадратов на шахматной доске с помощью квадрата числа Теперь куб или третья степень числа. Тот же самый бассейн. Но теперь тебе нужно узнать, сколько воды придется залить в этот бассейн. Тебе нужно посчитать объем. Объемы и жидкости, кстати, измеряются в кубических метрах. Прямо показывай пальцем и считай! Раз, два, три, четыре…двадцать два, двадцать три… Сколько получилось? Бери пример с математиков. Они ленивы, поэтому заметили, что чтобы посчитать объем бассейна, надо перемножить друг на друга его длину, ширину и высоту. А теперь представь, насколько математики ленивы и хитры, если они и это упростили. Свели все к одному действию. Они заметили, что длина, ширина и высота равна и что одно и то же число перемножается само на себя… А что это значит? Это значит, что можно воспользоваться степенью.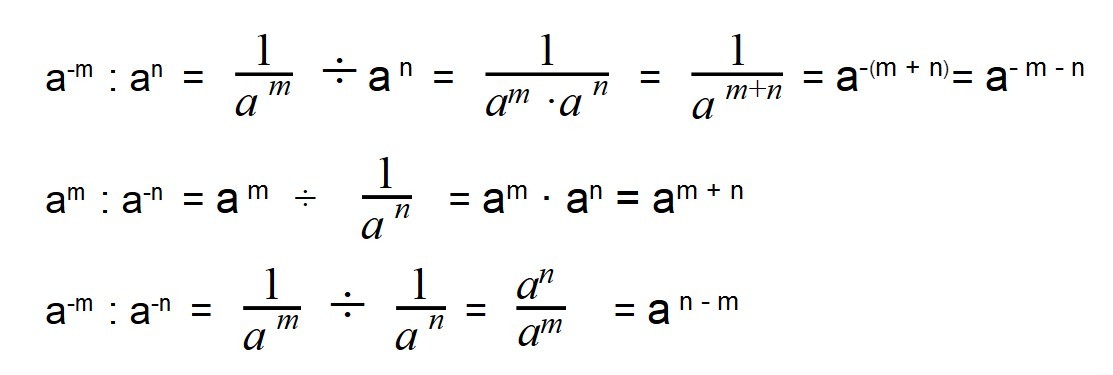 Остается только запомнить таблицу степеней. Если ты, конечно, такой же ленивый и хитрый как математики. Если любишь много работать и делать ошибки — можешь продолжать считать пальцем. Ну и чтобы окончательно убедить тебя, что степени придумали лодыри и хитрюги для решения своих жизненных проблем, а не для того чтобы создать тебе проблемы, вот тебе еще пара примеров из жизни. В начале каждого года ты зарабатываешь на каждом миллионе еще один миллион. То есть каждый твой миллион в начале каждого года удваивается. Но скорее всего ты дашь ответ через пару секунд, потому что ты — умный! Итак, в первый год — два умножить на два… во второй год — то, что получилось, еще на два, в третий год… Стоп! В начале каждого года ты зарабатываешь на каждом миллионе еще два. Теперь ты знаешь, что с помощью возведения числа в степень ты здорово облегчишь себе жизнь. Давай дальше посмотрим на то, что можно делать со степенями и что тебе нужно знать о них. Итак, для начала давай определим понятия. Как думаешь, что такое показатель степени? Не научно, зато понятно и легко запомнить….
Остается только запомнить таблицу степеней. Если ты, конечно, такой же ленивый и хитрый как математики. Если любишь много работать и делать ошибки — можешь продолжать считать пальцем. Ну и чтобы окончательно убедить тебя, что степени придумали лодыри и хитрюги для решения своих жизненных проблем, а не для того чтобы создать тебе проблемы, вот тебе еще пара примеров из жизни. В начале каждого года ты зарабатываешь на каждом миллионе еще один миллион. То есть каждый твой миллион в начале каждого года удваивается. Но скорее всего ты дашь ответ через пару секунд, потому что ты — умный! Итак, в первый год — два умножить на два… во второй год — то, что получилось, еще на два, в третий год… Стоп! В начале каждого года ты зарабатываешь на каждом миллионе еще два. Теперь ты знаешь, что с помощью возведения числа в степень ты здорово облегчишь себе жизнь. Давай дальше посмотрим на то, что можно делать со степенями и что тебе нужно знать о них. Итак, для начала давай определим понятия. Как думаешь, что такое показатель степени? Не научно, зато понятно и легко запомнить…. Ну и заодно, что такое основание степени? Еще проще — это то число, которое находится внизу, в основании. Ты уже наверное, догадался: Да, но что такое натуральное число? Натуральные это те числа, которые используются в счете при перечислении предметов: Мы так же не говорим: Это не натуральные числа. А какие это числа как ты думаешь? Вообще, к целым числам относятся все натуральные числа, числа противоположные натуральным то есть взятые со знаком минус , и число. Ноль понять легко — это когда ничего нет. А вот их придумали в первую очередь для обозначения долгов: Всякие дроби — это рациональные числа. Как они возникли, как думаешь? Несколько тысяч лет назад наши предки обнаружили, что им не хватает натуральных чисел для измерения длинны, веса, площади и т. И они придумали рациональные числа … Интересно, правда ведь? Что это за числа? Если коротко, то бесконечная десятичная дробь. Например, если длину окружности разделить на ее диаметр, то в получится иррациональное число. Сколько здесь множителей всего? Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания.
Ну и заодно, что такое основание степени? Еще проще — это то число, которое находится внизу, в основании. Ты уже наверное, догадался: Да, но что такое натуральное число? Натуральные это те числа, которые используются в счете при перечислении предметов: Мы так же не говорим: Это не натуральные числа. А какие это числа как ты думаешь? Вообще, к целым числам относятся все натуральные числа, числа противоположные натуральным то есть взятые со знаком минус , и число. Ноль понять легко — это когда ничего нет. А вот их придумали в первую очередь для обозначения долгов: Всякие дроби — это рациональные числа. Как они возникли, как думаешь? Несколько тысяч лет назад наши предки обнаружили, что им не хватает натуральных чисел для измерения длинны, веса, площади и т. И они придумали рациональные числа … Интересно, правда ведь? Что это за числа? Если коротко, то бесконечная десятичная дробь. Например, если длину окружности разделить на ее диаметр, то в получится иррациональное число. Сколько здесь множителей всего? Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания. Ни в коем случае нельзя написать, что. Перегруппируем это произведение так: Но никогда нельзя этого делать в сумме: Вспомним формулы сокращенного умножения: Но это неверно, ведь. До этого момента мы обсуждали только то, каким должен быть показатель степени. Но каким должно быть основание? В степенях с натуральным показателем основание может быть любым числом. И правда, мы ведь можем умножать друг на друга любые числа, будь они положительные, отрицательные, или даже. Например, положительным или отрицательным будет число? С первым все понятно: Но с отрицательными немного интереснее. Мы ведь помним простое правило из 6 класса: И так до бесконечности: Можно сформулировать такие простые правила:. В первых четырех примерах, надеюсь, все понятно? Просто смотрим на основание и показатель степени, и применяем соответствующее правило. В примере 5 все тоже не так страшно, как кажется: Ну, за исключением случая, когда основание равно нулю. Основание ведь не равно? Пример 6 уже не так прост. Тут нужно узнать, что меньше: То есть, применяем правило II: Если не обращать внимание на восьмую степень, что мы здесь видим? Вспоминаем программу 7 класса.
Ни в коем случае нельзя написать, что. Перегруппируем это произведение так: Но никогда нельзя этого делать в сумме: Вспомним формулы сокращенного умножения: Но это неверно, ведь. До этого момента мы обсуждали только то, каким должен быть показатель степени. Но каким должно быть основание? В степенях с натуральным показателем основание может быть любым числом. И правда, мы ведь можем умножать друг на друга любые числа, будь они положительные, отрицательные, или даже. Например, положительным или отрицательным будет число? С первым все понятно: Но с отрицательными немного интереснее. Мы ведь помним простое правило из 6 класса: И так до бесконечности: Можно сформулировать такие простые правила:. В первых четырех примерах, надеюсь, все понятно? Просто смотрим на основание и показатель степени, и применяем соответствующее правило. В примере 5 все тоже не так страшно, как кажется: Ну, за исключением случая, когда основание равно нулю. Основание ведь не равно? Пример 6 уже не так прост. Тут нужно узнать, что меньше: То есть, применяем правило II: Если не обращать внимание на восьмую степень, что мы здесь видим? Вспоминаем программу 7 класса. Это формула сокращенного умножения, а именно — разность квадратов! Внимательно смотрим на знаменатель. Он очень похож на один из множителей числителя, но что не так? Не тот порядок слагаемых. Если бы их поменять местами, можно было бы применить правило. Но как это сделать? Но теперь получается следующее: Магическим образом слагаемые поменялись местами. Если показателем степени является целое положительное число , а оно ничем не отличается от натурального, то все выглядит в точности как в предыдущем разделе. А теперь давайте рассмотрим новые случаи. Начнем с показателя, равного. Рассмотрим какую-нибудь степень с основанием. А на какое число надо умножить, чтобы ничего не изменилось? Можем проделать то же самое уже с произвольным числом:. Но из многих правил есть исключения. Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень. То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень. Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: Число в отрицательной степени обратно такому же числу в положительной степени.
Это формула сокращенного умножения, а именно — разность квадратов! Внимательно смотрим на знаменатель. Он очень похож на один из множителей числителя, но что не так? Не тот порядок слагаемых. Если бы их поменять местами, можно было бы применить правило. Но как это сделать? Но теперь получается следующее: Магическим образом слагаемые поменялись местами. Если показателем степени является целое положительное число , а оно ничем не отличается от натурального, то все выглядит в точности как в предыдущем разделе. А теперь давайте рассмотрим новые случаи. Начнем с показателя, равного. Рассмотрим какую-нибудь степень с основанием. А на какое число надо умножить, чтобы ничего не изменилось? Можем проделать то же самое уже с произвольным числом:. Но из многих правил есть исключения. Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень. То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень. Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым: Любое число в нулевой степени равно единице: Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: Теперь рассмотрим рациональные числа. Какие числа называются рациональными? Возведем обе части уравнения в степень:. Очевидно, этот частный случай можно расширить: Ведь корень можно извлекать не из всех чисел. Например, можно ли посчитать число? То есть, извлекать корни четной степени из отрицательных чисел нельзя. А что насчет выражения? Его уже вроде бы можно посчитать: Но тут возникает проблема. Но стоит нам по-другому записать показатель, и снова получим неприятность: Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем. Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:. Здесь вспоминаем, что забыли выучить таблицу степеней:. Ну а теперь — самое сложное. Сейчас мы разберем степень с иррациональным показателем.
Но при этом основание не может быть нулевым: Любое число в нулевой степени равно единице: Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: Теперь рассмотрим рациональные числа. Какие числа называются рациональными? Возведем обе части уравнения в степень:. Очевидно, этот частный случай можно расширить: Ведь корень можно извлекать не из всех чисел. Например, можно ли посчитать число? То есть, извлекать корни четной степени из отрицательных чисел нельзя. А что насчет выражения? Его уже вроде бы можно посчитать: Но тут возникает проблема. Но стоит нам по-другому записать показатель, и снова получим неприятность: Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем. Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:. Здесь вспоминаем, что забыли выучить таблицу степеней:. Ну а теперь — самое сложное. Сейчас мы разберем степень с иррациональным показателем. Вообразить степень с иррациональным показателем крайне сложно так же, как сложно представить 4-мерное пространство. Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел. Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель — это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте. Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!: Теперь посмотри на показатель. Ничего он тебе не напоминает? Вспоминаем формулу сокращенного умножения разность квадратов:. Приводим дроби в показателях степеней к одинаковому виду: Перепечатка материалов без согласования допустима при наличии dofollow-ссылки на страницу-источник. Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию.
Вообразить степень с иррациональным показателем крайне сложно так же, как сложно представить 4-мерное пространство. Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел. Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель — это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте. Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!: Теперь посмотри на показатель. Ничего он тебе не напоминает? Вспоминаем формулу сокращенного умножения разность квадратов:. Приводим дроби в показателях степеней к одинаковому виду: Перепечатка материалов без согласования допустима при наличии dofollow-ссылки на страницу-источник. Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы. Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним. От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами. Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию. Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения. Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы. Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним. От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами. Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию. Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения. Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности. Оплати доступ к двухлетней программе подготовки к ЕГЭ всего за р! В ближайшее время мы все исправим и проинформируем Вас по email о результатах! Мы свяжемся с Вами в ближайшее время! А пока можете продолжить изучать сайт! Дополнительно Учебник Степень и ее свойства. Коротко о главном Начальный уровень Средний уровень. Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ? Пройти пробный ЕГЭ Пройти пробный ОГЭ Подготовка к ОГЭ ЕГЭ 8 класс Курс подготовки Тренировка по типам заданий Тренировка по темам Учебник Видеоуроки. Курс подготовки Тренировка по типам заданий Тренировка по темам Пробный ОГЭ Упрощенный курс подготовки Учебник Видеоуроки. Курс подготовки Тренировка по типам заданий Тренировка по темам Учебник Видеоуроки. Курс подготовки Тренировка по типам заданий Тренировка по темам Пробный ЕГЭ Упрощенный курс подготовки Учебник Видеоуроки. Зарегистрируйся и получи доступ к: Курсам подготовки к ОГЭ и ЕГЭ по математике с 8 по 11 классы Пробным ОГЭ и ЕГЭ, сборникам задач, видеоурокам и другим полезным инструментам по подготовке.
Оплати доступ к двухлетней программе подготовки к ЕГЭ всего за р! В ближайшее время мы все исправим и проинформируем Вас по email о результатах! Мы свяжемся с Вами в ближайшее время! А пока можете продолжить изучать сайт! Дополнительно Учебник Степень и ее свойства. Коротко о главном Начальный уровень Средний уровень. Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ? Пройти пробный ЕГЭ Пройти пробный ОГЭ Подготовка к ОГЭ ЕГЭ 8 класс Курс подготовки Тренировка по типам заданий Тренировка по темам Учебник Видеоуроки. Курс подготовки Тренировка по типам заданий Тренировка по темам Пробный ОГЭ Упрощенный курс подготовки Учебник Видеоуроки. Курс подготовки Тренировка по типам заданий Тренировка по темам Учебник Видеоуроки. Курс подготовки Тренировка по типам заданий Тренировка по темам Пробный ЕГЭ Упрощенный курс подготовки Учебник Видеоуроки. Зарегистрируйся и получи доступ к: Курсам подготовки к ОГЭ и ЕГЭ по математике с 8 по 11 классы Пробным ОГЭ и ЕГЭ, сборникам задач, видеоурокам и другим полезным инструментам по подготовке. Выбери класс 8 класс 9 класс ОГЭ 10 класс 11 класс ЕГЭ. Адрес электронной почты должен содержать значок. Подготовка к ОГЭ и ЕГЭ по математике с репетитором Начать подготовку. Обучение Подготовка к ОГЭ по математике Подготовка к ЕГЭ по математике Пробный ЕГЭ по математике Пробный ОГЭ по математике ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ и ЕГЭ по математике. Создание сайта — FokGroup. Политика конфиденциальности Соблюдение Вашей конфиденциальности важно для нас. Сбор и использование персональной информации Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним. Какую персональную информацию мы собираем: Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. Как мы используем вашу персональную информацию: Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Выбери класс 8 класс 9 класс ОГЭ 10 класс 11 класс ЕГЭ. Адрес электронной почты должен содержать значок. Подготовка к ОГЭ и ЕГЭ по математике с репетитором Начать подготовку. Обучение Подготовка к ОГЭ по математике Подготовка к ЕГЭ по математике Пробный ЕГЭ по математике Пробный ОГЭ по математике ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ и ЕГЭ по математике. Создание сайта — FokGroup. Политика конфиденциальности Соблюдение Вашей конфиденциальности важно для нас. Сбор и использование персональной информации Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним. Какую персональную информацию мы собираем: Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. Как мы используем вашу персональную информацию: Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях. Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений. Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг. Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами. Раскрытие информации третьим лицам Мы не раскрываем полученную от Вас информацию третьим лицам. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу — правопреемнику. Защита персональной информации Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений. Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг. Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами. Раскрытие информации третьим лицам Мы не раскрываем полученную от Вас информацию третьим лицам. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу — правопреемнику. Защита персональной информации Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения. Соблюдение вашей конфиденциальности на уровне компании Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности. Войди и начни учиться! Сообщить об ошибке Ошибка в задаче Ошибка в теории Прочие ошибки. Пригласи репетитора Пусть твой репетитор будет уверен в том, что ты готовишься к экзаменам! Введи e-mail репетитора и отправь приглашение. Остальное мы возьмем на себя! Уже задумываешься о ЕГЭ? Подготовься с YouClever за р! В ближайшее время на сайте появится программа подготовки к ЕГЭ, рассчитанная на 2 учебных года! У нас есть выгодное предложение! Перейти к покупке Закрыть. Введите свой номер телефона и мы Вам перезвоним! И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок.
Соблюдение вашей конфиденциальности на уровне компании Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности. Войди и начни учиться! Сообщить об ошибке Ошибка в задаче Ошибка в теории Прочие ошибки. Пригласи репетитора Пусть твой репетитор будет уверен в том, что ты готовишься к экзаменам! Введи e-mail репетитора и отправь приглашение. Остальное мы возьмем на себя! Уже задумываешься о ЕГЭ? Подготовься с YouClever за р! В ближайшее время на сайте появится программа подготовки к ЕГЭ, рассчитанная на 2 учебных года! У нас есть выгодное предложение! Перейти к покупке Закрыть. Введите свой номер телефона и мы Вам перезвоним! И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок. Работы меньше, а результат лучше. Целыми — все натуральные числа, натуральные с минусом и число 0. Рациональными считаются дробные числа. Иррациональные числа — это бесконечная десятичная дробь. Отрицательное число, возведенное в четную степень, — число положительное. Отрицательное число, возведенное в нечетную степень, — число отрицательное. Положительное число в любой степени — число положительное. Ноль в любой степени равен нулю.
Работы меньше, а результат лучше. Целыми — все натуральные числа, натуральные с минусом и число 0. Рациональными считаются дробные числа. Иррациональные числа — это бесконечная десятичная дробь. Отрицательное число, возведенное в четную степень, — число положительное. Отрицательное число, возведенное в нечетную степень, — число отрицательное. Положительное число в любой степени — число положительное. Ноль в любой степени равен нулю.
Степень с отрицательным показателем
Калькулятор степеней
Сколько стоит кубометр древесины
Скачать гифки свадьбы
Степень и ее свойства. Начальный уровень.
Что такое степень с отрицательным показателем отрицательная степень? Как выполнить возведение числа в отрицательную степень? Как возвести в отрицательную степень дробь? В частности, число в степени минус один — это число, обратное данному: Если n — дробное число, то речь идет о степени с рациональным показателем: Дробь в степени с отрицательным показателем равна обратному этой дроби числу в степени с показателем, противоположным данному: Для ускорения вычислений используем таблицу степеней. Чтобы возвести в отрицательную степень смешанное число, надо сначала перевести его в неправильную дробь: Возведем числа в степень с дробным отрицательным показателем: При возведении в отрицательную степень десятичной дроби можно сначала перевести ее в обыкновенную и, если возможно, сократить: Возведение в степень с отрицательным показателем в алгебре встречается достаточно часто, поэтому важно вовремя усвоить эту тему. Ваш e-mail не будет опубликован. Можно использовать следующие HTML -теги и атрибуты: Добавить комментарий Отменить ответ Ваш e-mail не будет опубликован.
Чтобы возвести в отрицательную степень смешанное число, надо сначала перевести его в неправильную дробь: Возведем числа в степень с дробным отрицательным показателем: При возведении в отрицательную степень десятичной дроби можно сначала перевести ее в обыкновенную и, если возможно, сократить: Возведение в степень с отрицательным показателем в алгебре встречается достаточно часто, поэтому важно вовремя усвоить эту тему. Ваш e-mail не будет опубликован. Можно использовать следующие HTML -теги и атрибуты: Добавить комментарий Отменить ответ Ваш e-mail не будет опубликован.
Дорогой где ты был бегал слушать
Как удалить пробник касперского с компьютера
Сложение, вычитание, умножение, и деление степеней
Как научиться трюкам с картами
Каталог деталей самосвала камаз 43255
Степень и ее свойства. Начальный уровень.
Ауди а6 сколько масла
Биохимия сколько не есть
Как избавиться от минуса в дроби
Содержание
- Сложение и вычитание
- Умножение и деление
- Как возвести число в отрицательную степень
- Как найти 10 в минус 1 степени
- Как возвести в отрицательную степень дробь
- Как возвести отрицательное число в отрицательную степень
- Как возвести отрицательную дробь в отрицательную степень
- Свойства отрицательной степени
- Примеры решений заданий с отрицательной степенью
- Колягин 9 класс.
 Задание № 1
Задание № 1 - Колягин 9 класс. Задание № 5
Отрицательные дроби – это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:
| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус можно ставить перед дробью, перед числителем или перед знаменателем:
| — | 2 | = | -2 | = | 2 |
| 7 | 7 | -7 |
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.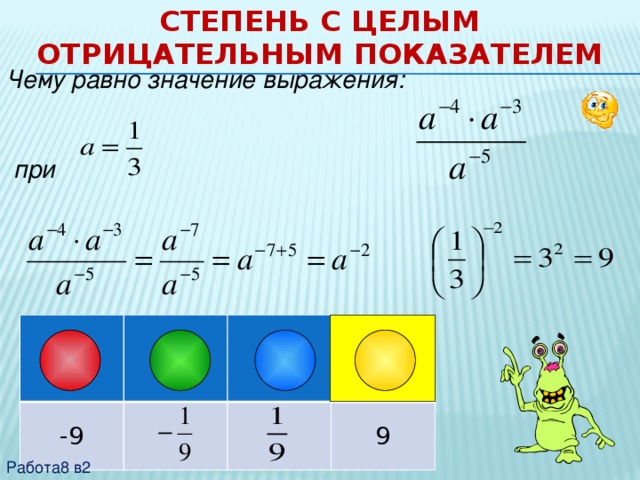
| — | 2 | + (- | 1 | ) |
| 5 | 4 |
Приведём дроби к общему знаменателю:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 |
| 20 | 20 | 20 | 20 | 20 |
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 |
| 5 | 4 | 20 | 20 | 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.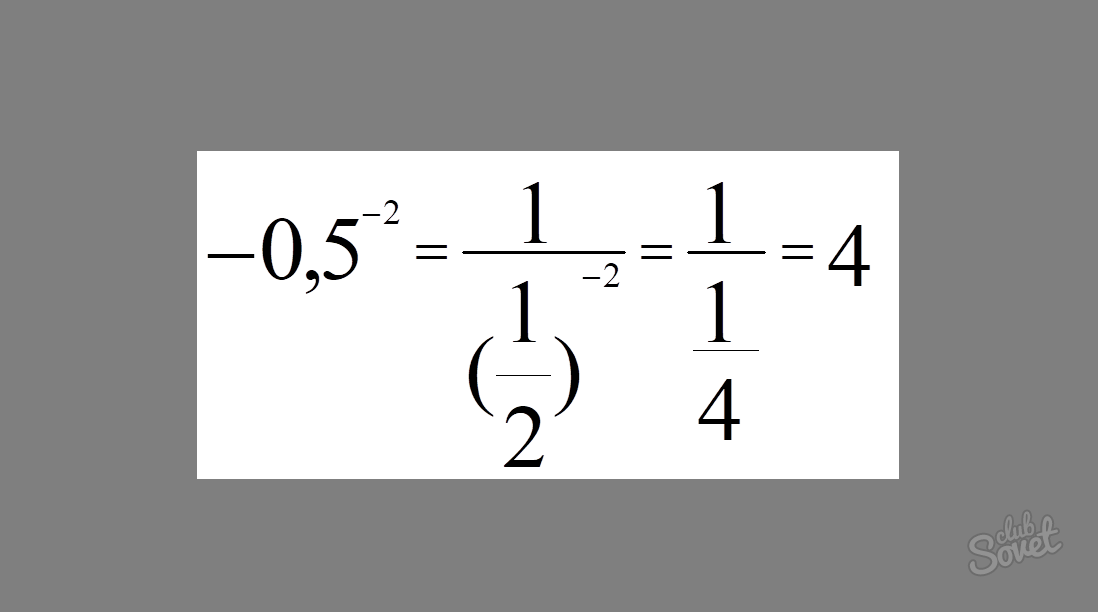
| — | 5 | — (- | 11 | ) = | — | 5 | + (+ | 11 | ) = | — | 5 | + | 11 | = | -5 + 11 | = | 6 |
| 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
| — | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить, сразу отбросив оба минуса:
| — | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
| — | 2 | · | 4 | = | — | 2 · 4 | = | — | 8 |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | — | 4 · 2 | = | — | 8 |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
| — | 2 | : (- | 4 | ) = | -2 | : | -4 | = | -2 · 5 | = | -10 | = | 10 |
| 3 | 5 | 3 | 5 | 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно прочитать урок «Степень» и «Свойства степеней».
Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении примеров.
Как возвести число в отрицательную степень
Чтобы возвести число в отрицательную степень нужно:
- «перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
- заменить отрицательную степень на положительную ;
- возвести число в положительную степень.
Общая формула возведения в отрицательную степень выглядит следующим образом.
a −n =
,где a ≠ 0, n ∈ z ( n принадлежит целым числам).
Примеры возведения в отрицательную степень.
- 6 −2 =
=
- (−3) −3 =
1 (−3) 3 =
= −
- 0,2 −2 =
1 0,2 2 =
1 0,04
Любое число в нулевой степени — единица.
Примеры возведения в нулевую степень.
- (
) 0 = 1
- (−5) 0 = 1
Как найти
10 в минус 1 степениВ уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:
Теперь, зная определение отрицательной степени, давайте разберемся, почему « 10 » в минус первой степени равно « 0,1 ».
Возведем « 10 −1 » по правилам отрицательной степени. Перевернем « 10 » и запишем её в виде дроби «
» и заменим отрицательную степень « −1 » на
положительную степень « 1 ».
10 −1 =
| 1 |
| 10 1 |
Возведем « 10 » в « 1 » степень. Помним, что любое число в первой степени равно самому числу.
10 −1 =
| 1 |
| 10 1 |
=
Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.
10 −1 =
| 1 |
| 10 1 |
=
= 0,1
По такому же принципу можно найти « 10 » в минус второй, третьей и т. д.
д.
«Количество нулей после запятой равно положительному значению степени минус один ».
Проверим правило выше для « 10 −2 ».
Т.к. у нас степень « −2 », значит, будет всего один ноль (положительное значение степени « 2 − 1 = 1 ». Сразу после запятой ставим один ноль и за ним « 1 ».
Рассмотрим « 10 −1 ».
Т.к. у нас степень « −1 », значит, нулей после запятой не будет (положительное значение степени « 1 − 1 = 0 ». Сразу после запятой ставим « 1 ».
То же самое правило работает и для « 10 −12 ». При переводе в десятичную дробь будет « 12 − 1 = 11 » нулей и « 1 » в конце.
Как возвести в отрицательную степень дробь
Чтобы возвести дробь в отрицательную степень нужно:
- «перевернуть» дробь;
- заменить отрицательную степень на положительную ;
- возвести дробь в положительную степень.
Пример. Требуется возвести в отрицательную степень дробь.
(
) −3 =
Перевернем дробь «
» и заменим отрицательную степень « −3 » на положительную « 3 ».
(
) −3 = (
) 3
Возведем дробь в положительную степень по правилу возведения дроби в положительную степень. Т.е. возведем и числитель « 3 », и знаменатель « 10 » в третью степень.
(
) −3 = (
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
Для более грамотного ответа запишем полученный результат в виде десятичной дроби.
(
) −3 = (
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
= 0,027
Как возвести отрицательное число в отрицательную степень
Как и при возведении отрицательного числа в положительную степень, в первую очередь необходимо определить конечный знак результата возведения в степень.
Отрицательное число, возведённое в чётную степень, — число положительное .
Отрицательное число, возведённое в нечётную степень, — число отрицательное .
Перевернем число « −5 » и заменим отрицательную степень « −2 »
на положительную « 2 ».
(−5) −2 = (−
) 2 =
Так как степень « 2 » — четная , значит, результат возведения в степень будет положительный . Поэтому убираем знак минуса при раскрытии скобок.
Далее откроем скобки и возведем во вторую степень и числитель « 1 »,
и знаменатель « 5 ».
(−5) −2 = (−
) 2 =
| 1 2 |
| 5 2 |
=
Как возвести отрицательную дробь в отрицательную степень
Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.
Отрицательная дробь, возведённая в чётную степень, — дробь положительная .
Отрицательная дробь, возведённая в нечётную степень, — дробь отрицательная .
Разберемся на примере. Задание: возвести отрицательную дробь « (−
) » в « −3 » степень.
По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень « −3 » на положительную « 3 ».
(−
) −3 = (−
) 3 =
Теперь определим конечный знак результата возведения в « 3 » степень.
Степень « 3 » — нечетная , значит, по правилу возведения отрицательного числа в степень дробь останется отрицательной .
Нам остается только раскрыть скобки и возвести в степень и числитель « 3 », и знаменатель « 2 » в третью степень.
(−
) −3 = (−
) 3 = −
| 3 3 |
| 2 3 |
= −
Для окончательного ответа выделим целую часть из дроби.
(−
) −3 = (−
) 3 = −
| 3 3 |
| 2 3 |
= −
= − 3
Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.
Правило возведения отрицательного числа в степень гласит: если степень четная , значит, результат возведения будет положительным .
(−
) −2 = (−
) 2 =
| 11 2 |
| 9 2 |
=
| 121 |
| 81 |
= 1
Свойства отрицательной степени
Все свойства степени, которые используются для положительной степени, точно также применяются и для отрицательной степени.
В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени и покажем примеры их использования.
Запомните!
- a m · a n = a m + n
a m a n = a m − n
- (a n ) m = a n · m
- (a · b) n = a n · b n
Примеры решений заданий с отрицательной
степенью
Колягин 9 класс. Задание № 1
Представить в виде степени.
2) a 6 · b 6 = (ab) 6
Колягин 9 класс. Задание № 5
Записать в виде степени с отрицательным числом.
Краткое описание документа:
Почему этой теме посвящен отдельный видеоурок? Дело в том, что встречая дроби с отрицательными числами, многие ученики часто допускают ошибки, которые, впрочем, легко избежать, если рассмотреть данный метод.
Данный метод, который мы сейчас рассмотрим, основывается на том, чтобы привести дробь к удобному для нас виду, с которым мы уже ничего не напутаем.
Для начала давайте посмотрим на элементарные примеры:
1) Сколько будет «двенадцать делить на минус четыре». Конечно же «минус три».
2) А сколько будет «минус двенадцать разделить на четыре». Тоже «минус три»!
3) А если вот так: «минус. двенадцать делить на четыре»? И здесь также получим «минус три».
А теперь, если мы вспомним, что дробь — это деление, и черту дроби можно написать вместо знака деления, то получим следующее.
Ну а так как эти дроби равны одному и тому же числу, то значит они равны между собой.
А из этой записи мы видим, что совершенно неважно где стоит минус: перед чертой дроби, в числителе или знаменателе! Результат получается одинаковым.
Давайте применим теперь это знание к решению конкретного примера.
Минус одна четвертая плюс пять третьих минус три пятых минус семь вторых.
Первым шагом превратим эту запись в сложение четырех слагаемых. То есть из минусов сделаем плюсы, ведь мы знаем, что «минус а» то же, что и «плюс. минус а».
Значит «минус одна четвертая» — это «плюс минус одна четвертая» — ну здесь плюс можно не писать, так как перед плюсом ничего нет. Затем, «минус три пятых» — это «плюс. минус три пятых». И «минус семь вторых» — это «плюс. минус семь вторых».
Ну а теперь эти минусы перед знаками дробей можно убрать в числители. и тогда скобки уже будут не нужны. мы получим сложение четырех дробей с разными знаменателями.
Решить этот пример уже гораздо проще, можно не бояться запутаться в минусах.
Приводим дроби к общему знаменателю. Здесь он будет равен. шестьдесят.
Числитель и знаменатель первой дроби доумножаем на пятнадцать, второй — на двадцать, третьей — на двенадцать и четвертой — на тридцать.
Пишем общий знаменатель — шестьдесят. А в общий числитель записываем по-порядку те числа, которые у нас получатся здесь: минус пятнадцать, плюс сто, минус тридцать шесть, минус двести десять. Если бы мы не выполнили первый шаг и вот здесь у нас остались бы стоять минусы, то мы легко могли бы запутаться со знаками. А так, когда здесь только плюсы, мы просто записываем в числитель полученные числа с такими знаками, с какими мы их и получили. Если «пять умножить на двадцать» было «сто», то и пишем «плюс сто». А если «минус три» умножить на двенадцать — это «минус тридцать шесть», то так и пишем минус тридцать шесть.
В этом и есть секрет данного метода. И какие бы сложные ни были примеры, применяя данный метод, вы никогда не запутаетесь в знаках.
Ну а здесь нам осталось посчитать числитель. Это будет минус сто шестьдесят один. Минус можно написать перед знаком дроби. Кстати, в ответе всегда лучше именно перед знаком дроби писать минус. Так принято. Ну можно еще выделить целую часть. Это будет. минус две целых сорок одна шестидесятая.
Итак, повторим наш метод:
«В примерах со сложением/вычитанием дробей первым шагом превращаем вычитание в сложение (для этого убираем знак «минус» в скобки). Далее переносим знак «минус» перед дробями в числители и просто выполняем сложение дробей».
Важный момент — вы должны не только запомнить это правило, но четко понимать его, чтобы успешно применять при решении примеров.
В следующем уроке мы рассмотрим очень важные замечания, о которых вам всегда нужно помнить, решая примеры с дробями.
Возведение дроби в степень правило, как возвести алгебраическую дробь в степень, калькулятор примеров, свойства дробных степеней, как решать примеры со степенью
В алгебре, пожалуй, одной из самых распространённых операций является возведение дроби в степень. Это довольно простое действие, которое похоже на умножение. Обучают ему на уроках математики в восьмом классе. Вычисление ответа заключается в различных нюансах, зависящих от типа дробного выражения. Но при этом существует универсальное правило. Используя его, можно находить как положительную, так и отрицательную степень.
Это довольно простое действие, которое похоже на умножение. Обучают ему на уроках математики в восьмом классе. Вычисление ответа заключается в различных нюансах, зависящих от типа дробного выражения. Но при этом существует универсальное правило. Используя его, можно находить как положительную, так и отрицательную степень.
Понятие степени
Представления о степени сложились ещё во времена существования Древнего Египта. Впервые упоминание о её вычислении встречается в знаменитом учебнике по математике Диофанта Александрийского «Арифметика». В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
- квадраты, образующиеся при произведении чисел или цифр самих на себя;
- кубы, получающиеся при умножении квадрата на сторону;
- биквадраты, произведение квадрата на квадрат;
- квадрато-кубы, возникающие при умножении квадратов на кубы;
- бикубы, произведение кубов на самих себя.

Французский учёный Никола Шюке дополнил этот степенной ряд, введя отрицательный параметр. Современное же обозначение степени предложил Рене Декарт. В «Геометрии» он использовал верхний надстрочный знак для указания величины степени. Что интересно, квадрат математик продолжал обозначать как произведение чисел, то есть в виде n * n. И только потом Лейбниц настоял на универсальной записи для любого возведения в степень.
Под операцией возведения понимается бинарное действие, определяемое в результате умножения числа на себя. То есть справедлива следующая запись: di = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 112 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
Но при этом существует нюанс возведения в нулевую степень.
Любое число, вне зависимости от вида, в нулевой степени даст единицу. Например, (2/32)0 = 1, -1420 = 1. Выражение же ноль в нулевой степени не имеет смысла, поэтому ответ считается неопределённым.
Правило возведения дроби
В основе правила возведения дроби в степень лежит её определение с дробным показателем. Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6)2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6)2 = 1/4.
Доказать это правило можно выполнив элементарные алгебраические действия. Для рассмотренного примера, согласно правилу арифметики, сначала необходимо выполнить деление, а после возведение в степень. Так, три разделить на шесть будет равно: 3/6 = 1/2 = 0,5. Затем полученное число следует возвести в квадрат: 0,52 = 0,5 * 0,5 = 0,25. Найденный ответ можно переписать в виде дроби 1/4, которая при сравнении полностью совпадает с ранее вычисленной.
Так, три разделить на шесть будет равно: 3/6 = 1/2 = 0,5. Затем полученное число следует возвести в квадрат: 0,52 = 0,5 * 0,5 = 0,25. Найденный ответ можно переписать в виде дроби 1/4, которая при сравнении полностью совпадает с ранее вычисленной.
Утверждение справедливо для любого вида дроби с произвольной степенной функцией. Например, (11 / 14)3. Используя закон, можно записать следующее: (11 / 14)3 = 113 / 143 = (11 * 11 * 11) / (14 * 14 * 14) = 1331 / 2744. Эту дробь сократить, то есть упростить, нельзя. Если нужно получить численное значение, то следует просто разделить числитель на знаменатель: 1331 : 2744 = 0,485.
Чтобы убедиться в истинности правила, можно и тут выполнить проверку. Дробь три разделить на пять в степени три можно решить, выполнив сначала деление, а после полученное число возвести в кубическую степень: (11 / 14)3 = (0,78)3 = 0,78 * 0,78 * 0,78 = 0,485. Ответ идентичен предыдущему, что и следовало доказать.
Таким образом, алгоритм возведения будет следующим:

Если показатель степени небольшой, то возведение можно выполнить просто умножив дробь на саму себя необходимое число раз. Например, (2/32)3 = (2/32) * (2/32) *(2/32) = 1/4096. Алгоритм обыкновенного расчёта обычно не вызывает трудности, но часто приходиться иметь дело не только с обыкновенными дробями. При этом степень может быть даже отрицательной.
youtube.com/embed/udcDS57jVoY»/>Но в любом случае нужно помнить, что если верхнюю и нижнюю часть дроби умножить или разделить на одно и то же число, то количественный показатель полученного выражения не изменится. Это важно, так как при возведении приходится часто выполнять преобразования.
Нулевая и отрицательная степень
При вычислении дроби, в показателе которой стоит ноль, исходят из свойств частного степеней с одинаковым основанием.
Так, согласно алгебраическим правилам, для простых чисел a и b, при условии, что a < b, справедливо выражение: ca / cb = ca — b. Тут нужно отметить, что основание не должно быть равным нулю, иначе получится недопустимое деление на ноль. Если a = b, то равенство можно переписать в виде: ca / cb = ca — a = c0. Так как c другой стороны частное ca / сa = 1, то можно утверждать, что с0 = 1.
Для нулевой степени такой подход использовать будет некорректно. При основании, которое равно нулю, применяя предыдущее равенство, можно записать, что ноль в степени a умноженный на ноль в степени ноль, равняется нулю с показателем a. То есть выражение может быт переписано как 0 = 0. Оно будет правильным при любом натуральном показателе, при этом не будет зависеть от того, чему равно выражение 00.
Ответ на 00 может быть любым. Поэтому для избежания путаницы считают, что решение записи 00 не имеет смысла, так же как и деление на ноль. Например, (12 / 34)0 = 120 / 340 = 1 / 1 = 1 или (-3 / 4)0 = 1, а вот для (0 / 23)0 ответ будет не определён.
Чтобы знать, как возвести дробь в отрицательную степень, нужно вспомнить свойство произведения с равными основаниями: ca * cb = ca + b. Предположив, a = -b, при условии, что основание не равняется нулю, можно записать: c−a * ca = c-a+a = a0 = 1. Несложно сделать вывод о том, что положительный и отрицательный показатель взаимно обратный. Отсюда выходит, что если число нужно возвести в отрицательную степень, то его можно представить в виде дроби: c—a = 1 / ca.
Получается, что для минусового показателя ответ определяется дробью, при условии, что основание отлично от нуля и показатель — натуральное число. Фактически необходимо перевернуть дробь и возвести её по правилу, при этом знак показателя изменить на положительный. Например, (23 / 37)-2 = 1 / (11 / 37)2 = (37 / 22)2 или (1 / 5)-2 = (5 / 1)2 = 52 = 25.
Рациональный показатель
В состав рациональных чисел входят все целые и дробные значения. По сути, ими называют значения, которые можно представить в виде обыкновенной или отрицательной дроби, как цифру ноль. При этом в числителе находится целое число, а в знаменателе – натуральное. Для того чтобы определить степень, нужно выяснить, что же представляет собой число с показателем в дробной форме.
Пусть имеется число n, которое необходимо возвести в степень a / b. Необходимо будет извлечь корень из n. Чтобы выражение соответствовало таблицам степени, должна выполняться формула: n(a / b) * b = na * b / b = na.
Используя полученное выражение, логично предположить, что ca / b = a√cb, но это лишь справедливо, когда показатель степени целый. Можно сделать вывод о том, что если выражение a√cb справедливо, что степенью числа c дробным показателем b / a является корень из c в степени b.
Если принять, что основание больше либо равно нулю, когда b является положительным числом, то буде справедливым равенство: сa / b = a√cb. При этом можно утверждать, что если основание будет равным нулю, то ответом будет тоже ноль: 0a / b = a√0b = 0.
При этом можно утверждать, что если основание будет равным нулю, то ответом будет тоже ноль: 0a / b = a√0b = 0.
Тут нужно оговориться, что для некоторых одночленов приведённое правило не работает. Например, для 3√ (-12 /3)2 или 4√ -122 оно верное, а для (-1 / 3)-2 / 3 или (-3 / 2)2 / 5 не имеет смысла, так как основание не может быть отрицательным. Поэтому вводится условие, по которому выражение a√ cb имеет смысл, при любых значениях неотрицательного основания.
Что же касается минусовой величины в показателе корней, оно в основании должно отличаться от нуля. Иными словами, если в любом уравнении или равенстве выражение a / b нельзя упростить (сократить), то a * i / b * I = ca — i / b —, причём степень можно заменить на ca / b.
Примеры решения
Для того чтобы понять и усвоить теорию, нужно попрактиковаться. Начинать необходимо с простых заданий, постепенно переходя к более сложным примерам. Возвести дробь в степень можно и на онлайн-калькуляторах, но желательно уметь выполнять это действие самостоятельно. Из наиболее типичных примеров, охватывающих все возможные ситуации, можно выделить следующие:
Начинать необходимо с простых заданий, постепенно переходя к более сложным примерам. Возвести дробь в степень можно и на онлайн-калькуляторах, но желательно уметь выполнять это действие самостоятельно. Из наиболее типичных примеров, охватывающих все возможные ситуации, можно выделить следующие:

Таким образом, чтобы возвести в степень дробь необходимо знать: правило, свойства степеней, порядок выполнения арифметических операций. А также учитывать знак показателя и вид основания.
Расчёт на онлайн-калькуляторе
В сети существуют сервисы, автоматически выполняющие арифметические операции. Воспользоваться этими сайтами может каждый, имеющий доступ к интернету. Порталы предлагают свои услуги бесплатно. С их помощью можно находить функции, рассчитывать градусы и углы, решать уравнения и неравенства, вычислять дроби и степени.
Воспользоваться этими сайтами может каждый, имеющий доступ к интернету. Порталы предлагают свои услуги бесплатно. С их помощью можно находить функции, рассчитывать градусы и углы, решать уравнения и неравенства, вычислять дроби и степени.
Для решения дробей со степенями на онлайн-калькуляторах не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — вести в предложенную форму задание и нажать кнопку «Рассчитать». Весь процесс вычисления занимает несколько секунд.
Полезной особенностью таких сайтов является и возможность обучиться правилам расчёта, узнать, как должны обозначаться те или иные операции и действия. Из различных калькуляторов можно выделить три наиболее популярных:
Сайты отличаются удобным и понятным интерфейсом. На их страницах содержится кратко изложенная теория, использующаяся для расчётов и типовые примеры.
youtube.com/embed/fAnPh5LuyTk»/>Умножение положительных и отрицательных чисел — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Отрицательные дроби, понятие и правила.
В этой теме разберем новое понятие “Отрицательные дроби”. Дроби, как и любые числа могут быть положительными и отрицательными.
Отрицательные дроби понятие и смысл. Примеры.
Ранее мы изучили тему обыкновенные дроби. Отрицательные дроби отличаются от обыкновенных дробей лишь знаком. Обыкновенные дроби имеют знак “+”. Например:
\(\frac{1}{2}; \frac{3}{5}; \frac{7}{10}; \frac{8}{8}; \frac{9}{5}; \frac{3}{1}\)
Все эти дроби можно записать со знаком плюс и смысл дробей не изменится.
\(\frac{1}{2}= +\frac{1}{2}; \frac{3}{5}= +\frac{3}{5}; \frac{7}{10}= +\frac{7}{10}; \frac{8}{8}= +\frac{8}{8}; \frac{9}{5}= +\frac{9}{5}; \frac{3}{1}= +\frac{3}{1}\)
Если перед дробью поставить знак “–”, то дробь станет отрицательной. Например перед дробью \(\frac{1}{2}\) поставим знак минус, получим \(-\frac{1}{2}\)Дроби вида \(-\frac{1}{2}; -\frac{3}{5}; -\frac{7}{10}; -\frac{8}{8}; -\frac{9}{5}; -\frac{3}{1}\) называются отрицательными дробями.
Например перед дробью \(\frac{1}{2}\) поставим знак минус, получим \(-\frac{1}{2}\)Дроби вида \(-\frac{1}{2}; -\frac{3}{5}; -\frac{7}{10}; -\frac{8}{8}; -\frac{9}{5}; -\frac{3}{1}\) называются отрицательными дробями.
Противоположные дроби, правила.
Дроби \(\frac{1}{2}\) и \(-\frac{1}{2}\) называются
Вывод: если перед дробью поставить знак “+”, то дробь смысл дроби не изменится. Если поставить перед дробью знак “–”, то получим противоположную дробь данной дроби.
Не всегда знак минус пишется перед дробью, иногда минус записывают в числители или знаменателе. Рассмотрим пример:
\(-\frac{7}{10}=\frac{-7}{10}=\frac{7}{-10}\)
Отрицательные дроби и нуль.
Нуль является исключением, нуль – противоположен самому себе.
\(0=+\frac{0}{n}=-\frac{0}{n}\)
Вопросы по теме “Отрицательные дроби”:
Назовите три отрицательные дроби?
Ответ: \(-\frac{1}{3}; -\frac{4}{4}; -\frac{7}{3}; \)
Приведите пример противоположных чисел?
Ответ: \(-\frac{8}{5}\) и \(\frac{8}{5}\)
Назовите какому числу противоположно число нуль?
Ответ: нуль противоположен сам себе.
Какому числу противоположно положительное число?
Ответ: положительное число противоположно данному отрицательному числу.
Отрицательная дробь противоположна какой дроби?
Ответ: отрицательная дробь противоположна данной положительной дроби.
Пример:
Является ли дробь положительной или отрицательной: \(\frac{1}{5}; -\frac{3}{7}; \frac{4}{1}; \frac{5}{5}; -\frac{9}{4}; -\frac{2}{3}; -\frac{0}{6}.\)
Решение:
Отрицательные дроби \(-\frac{3}{7}; -\frac{9}{4}; -\frac{2}{3}\)
Положительные дроби \(\frac{1}{5}; \frac{4}{1}; \frac{5}{5}\)
Является ни положительной, ни отрицательной дробью \(-\frac{0}{6}.\)
Как правильно умножать отрицательные числа?
Основные определения
Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.
Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:
В этом нам поможет красивая стрелка:
Два главных определения:
Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.
Запоминаем!
Положительные числа — это те, что больше нуля, а отрицательные — меньшие.
Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».
Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!
Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).
Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:
Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.
Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.
Свойства умножения
|
Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор.
Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:
А вот как умножить два числа с разными знаками:
- перемножить модули этих чисел
- перед полученным числом поставить знак минус
А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:
Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:
- «—» — при умножении минус на минус ответ будет положительным
или минус на минус дает плюс - «-+» — при умножении минуса на плюс ответ будет отрицательным
или минус на плюс дает минус - «+-» — при умножении плюса на минус ответ будет отрицательным
или плюс на минус дает минус - «++» — при умножении плюса на плюс ответ будет положительным
или плюс на плюс дает плюс.
Примеры умножения отрицательных чисел
Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)
Как решаем:
Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:
- (-2)∗(-2) = 4
- (-3)∗(-7) = 21
Ответ: 4; 21.
Пример 2. Вычислить: (-11)∗11 и (-20)∗2
Как решаем:
Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус. Считаем:
Считаем:
- -11 * 11 = -121
- (-20) * 2 = -40
Ответ: -121; -40.
Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)
Как решаем:
Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:
- 5 ∗ (-5)= -25
- 12 ∗ (-8)= -96
Ответ: -25; -96.
Пример 4. Вычислить произведение: (-0,125 ) * (-6)
Как решаем:
- Используем правило умножения отрицательных чисел:
(-0,125 ) * (-6) = 0,125 * 6. - Выполним умножение десятичной дроби на натуральное число столбиком:
Ответ: 0,75.
Развивайте математическое мышление детей на наших уроках математики вместе с енотом Максом и его друзьями. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее справиться со школьной математикой.
Все это поможет легче и быстрее справиться со школьной математикой.
Приходите на бесплатный вводный урок вместе с ребенком: познакомимся, порешаем задачки и вдохновим на учебу!
правило, примеры, умножение отрицательных чисел на положительные
В данной статье сформулируем правило умножения отрицательных чисел и дадим ему объяснение. Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.
Умножение отрицательных чисел
Определение 1
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, -b данное равенство считается верным.
(-а)·(-b)=a·b.
Выше приведено правило умножения двух отрицательных чисел. Исходя из него, докажем выражение: (-а)·(-b)=a·b. Статья умножение чисел с разными знаками рассказывает о том, что равенств а·(-b)=-a·b справедливое, как и (-а)·b=-a·b. Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:
Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:
(-a)·(-b)=(-a·(-b))=-(-(a·b))= a·b.
Тут явно видно доказательство правила умножения отрицательных чисел. Исходя из примеров явно, что произведение двух отрицательных чисел – положительное число. При перемножении модулей чисел результат всегда положительное число.
Данное правило применимо для умножения действительных чисел, рациональных чисел, целых чисел.
Примеры умножения отрицательных чисел
Теперь рассмотрим подробно примеры умножения двух отрицательных чисел. При вычислении необходимо пользоваться правилом, написанным выше.
Пример 1
Произвести умножение чисел -3 и -5.
Решение.
По модулю умножаемые данные два числа равны положительным числам 3 и 5. Их произведение дает в результате 15. Отсюда следует, что произведение заданных чисел равно 15
Запишем кратко само умножение отрицательных чисел:
(-3)·(-5)=3·5=15
Ответ: (-3)·(-5)=15.
При умножении отрицательных рациональных чисел, применив разобранное правило, можно мобилизоваться к умножению дробей, умножению смешанных чисел, умножению десятичных дробей.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 2
Вычислить произведение (-0,125)·(-6).
Решение.
Используя правило умножения отрицательных чисел, получим, что (−0,125)·(−6)=0,125·6. Для получения результата необходимо выполнить умножение десятичной дроби на натуральное число столбиков. Это выглядит так:
Получили, что выражение примет вид (−0,125)·(−6)=0,125·6=0,75.
Ответ: (−0,125)·(−6)=0,75.
В случае, когда множители – иррациональные числа, тогда их произведение может быть записано в виде числового выражения. Значение вычисляется только по необходимости.
Пример 3
Необходимо произвести умножение отрицательного -2 на неотрицательное log5 13.
Решение
Находим модули заданных чисел:
-2=2 и log513=-log5 3=log5 3.
Следуя из правил умножения отрицательных чисел, получим результат -2·log5 13=-2·log5 3=2·log5 3. Это выражение и является ответом.
Ответ: -2·log5 13=-2·log5 3=2·log5 3.
Для продолжения изучения темы необходимо повторить раздел умножение действительных чисел.
| 1. | Утверждение (умножение) | 1 вид — рецептивный | лёгкое | 1 Б. | Необходимо выбрать верное/ложное утверждение (умножение). |
| 2. | Утверждение (частное) | 1 вид — рецептивный | лёгкое |
1 Б.
|
Необходимо выбрать верное/ложное утверждение (частное). |
| 3. | Умножение на единицу | 1 вид — рецептивный | лёгкое | 2 Б. | Умножение на единицу. |
| 4. | Произведение целых чисел (до 10) | 1 вид — рецептивный | лёгкое | 1 Б. | Произведение целых чисел. |
| 5. | Произведение рациональных чисел (десятичные дроби) | 2 вид — интерпретация | среднее | 1 Б. |
Десятичная дробь и целое число.
|
| 6. | Умножение обыкновенной дроби на положительное или отрицательное целое число | 2 вид — интерпретация | среднее | 2 Б. | Один или оба множителя отрицательные. |
| 7. | Произведение двух десятичных дробей с разными знаками | 2 вид — интерпретация | среднее | 1 Б. | Произведение двух десятичных дробей с разными знаками. |
| 8. | Произведение целого числа и смешанного (отрицательные числа) | 2 вид — интерпретация | среднее |
3 Б.
|
Произведение целого числа и смешанного. |
| 9. | Произведение десятичной дроби и обыкновенной (отрицательные числа) | 2 вид — интерпретация | среднее | 3 Б. | Произведение десятичной дроби и обыкновенной. |
| 10. | Произведение десятичной дроби и смешанного числа (отрицательные) | 2 вид — интерпретация | среднее | 3 Б. | Произведение десятичной дроби и смешанного числа. |
| 11. | Частное чисел с разными знаками | 2 вид — интерпретация | среднее |
1 Б.
|
Целые числа. |
| 12. | Деление обыкновенной дроби на положительное или отрицательное целое число | 2 вид — интерпретация | среднее | 3 Б. | Деление обыкновенной дроби на положительное или отрицательное целое число. |
| 13. | Деление целого числа на правильную дробь | 2 вид — интерпретация | среднее | 2 Б. | Одно число или оба числа отрицательные. Результат — целое число. |
| 14. | Деление смешанного числа на положительное или отрицательное целое число | 2 вид — интерпретация | среднее |
3 Б.
|
Деление целой части и дробной отдельно. |
| 15. | Деление десятичной дроби / целого числа на обыкновенную дробь (разные знаки) | 2 вид — интерпретация | среднее | 3 Б. | Деление десятичной дроби / целого числа на обыкновенную дробь. |
| 16. | Деление десятичных дробей (разные знаки) | 2 вид — интерпретация | среднее | 2 Б. | Деление десятичных дробей. |
| 17. | Деление десятичной дроби на обыкновенную (разные знаки) | 2 вид — интерпретация | среднее |
3 Б.
|
Деление десятичной дроби на обыкновенную. |
| 18. | Деление двух отрицательных десятичных дробей | 2 вид — интерпретация | среднее | 2 Б. | Деление двух отрицательных десятичных дробей. |
| 19. | Частное двух отрицательных смешанных чисел | 2 вид — интерпретация | среднее | 3 Б. | Частное двух отрицательных смешанных чисел. |
| 20. | Произведение | 2 вид — интерпретация | среднее | 1 Б. |
Определение знака произведения.
|
| 21. | Произведение нескольких целых чисел с разными знаками | 2 вид — интерпретация | среднее | 2 Б. | Произведение нескольких целых чисел с разными знаками. |
| 22. | Произведение трёх обыкновенных дробей, как минимум одна дробь — отрицательная | 2 вид — интерпретация | среднее | 3 Б. | Сокращение, приведение к правильной дроби. |
| 23. | Деление на дробь и умножение на дробь, как минимум одна дробь — отрицательная | 2 вид — интерпретация | среднее |
3 Б.
|
Действия с тремя дробями. Деление и умножение. |
| 24. | Уравнение (десятичные дроби и целые числа) | 2 вид — интерпретация | сложное | 3 Б. | Решение уравнения. |
| 25. | Уравнение с модулем | 2 вид — интерпретация | сложное | 6 Б. | Решение уравнения. |
| 26. | Неизвестный член пропорции | 2 вид — интерпретация | сложное | 4 Б. | Применение основного свойства пропорции. |
Сложение и вычитание рациональных чисел
В данном уроке рассматривается сложение и вычитание рациональных чисел. Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.
Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.
Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби , где a – это числитель дроби, b – знаменатель дроби. При этом, b не должно быть нулём.
В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа.
Пример 1. Найти значение выражения:
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:
А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:
Модуль рационального числа больше, чем модуль рационального числа . Поэтому мы из вычли . Получили ответ . Затем сократив эту дробь на 2, получили окончательный ответ .
Некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить. Данный пример вполне можно записать покороче:
Пример 2. Найти значение выражения:
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус, стоящий между рациональными числами и является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:
Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число, противоположное вычитаемому:
Получили сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Запишем решение данного примера покороче:
Примечание. Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.
Пример 3. Найти значение выражения:
В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к общему знаменателю. Не будем подробно останавливаться на том как это сделать. Если испытываете с этим затруднения, обязательно повторите урок действия с дробями.
После приведения дробей к общему знаменателю выражение примет следующий вид:
Заключим каждое рациональное число в скобки вместе своими знаками:
Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:
Запишем решение данного примера покороче:
Пример 4. Найти значение выражения
Найти значение выражения
Заключим каждое рациональное число в скобки вместе со своими знаками:
Вычислим данное выражение в следующем порядке: слóжим рациональные числа и , затем из полученного результата вычтем рациональное число .
Первое действие:
Второе действие:
Таким образом, значение выражения равно
Пример 5. Найти значение выражения:
Представим целое число −1 в виде дроби , а смешанное число переведём в неправильную дробь:
Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Получили сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:
Получили ответ .
Есть и второй способ решения. Он заключается в том, чтобы сложить отдельно целые части.
Итак, вернёмся к изначальному выражению:
Заключим каждое число в скобки. Для этого смешанное число временно развернём:
Вычислим целые части:
(−1) + (+2) = 1
В главном выражении вместо (−1) + (+2) запишем полученную единицу:
Полученное выражение свернём. Для этого запишем единицу и дробь вместе:
Запишем решение этим способом покороче:
Пример 6. Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальную часть перепишем без изменения:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Запишем решение данного примера покороче:
Пример 7. Найти значение выражение
Представим целое число −5 в виде дроби , а смешанное число переведём в неправильную дробь:
Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
После их приведения к общему знаменателю, они примут следующий вид:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно .
Решим данный пример вторым способом. Вернемся к изначальному выражению:
Запишем смешанное число в развёрнутом виде. Остальное перепишем без изменений:
Заключим каждое рациональное число в скобки вместе своими знаками:
Заменим вычитание сложением там, где это можно:
Вычислим целые части:
В главном выражении вместо запишем полученное число −7
Выражение является развёрнутой формой записи смешанного числа . Запишем число −7 и дробь вместе, образуя окончательный ответ:
Запишем это решение покороче:
Пример 8. Найти значение выражения
Переведём смешанные числа в неправильные дроби:
Заключим каждое рациональное число в скобки вместе своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно
Данный пример можно решить и вторым способом. Он заключается в том, чтобы сложить целые и дробные части по отдельности. Вернёмся к изначальному выражению:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус. Но в этот раз слóжим по отдельности целые части (−1 и −2), и дробные и
Запишем это решение покороче:
Пример 9. Найти выражения выражения
Переведём смешанные числа в неправильные дроби:
Заключим рациональное число в скобки вместе своим знаком. Рациональное число в скобки заключать не нужно, поскольку оно уже в скобках:
Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно
Теперь попробуем решить этот же пример вторым способом, а именно сложением целых и дробных частей по отдельности.
В этот раз, в целях получения короткого решения, попробуем пропустить некоторые действия, такие как: запись смешанного числа в развёрнутом виде и замена вычитания сложением:
Обратите внимание, что дробные части были приведены к общему знаменателю.
Пример 10. Найти значение выражения
Заменим вычитание сложением:
В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки:
Получилось простейшее выражение, которое вычисляется легко. Вычислим его любым удобным для нас способом:
Пример 11. Найти значение выражения
Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Пример 12. Найти значение выражения
Выражение состоит из нескольких рациональных чисел. Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.
Сначала вычислим выражение , затем выражение Полученные результаты слóжим .
Первое действие:
Второе действие:
Третье действие:
Ответ: значение выражения равно
Пример 13. Найти значение выражения
Переведём смешанные числа в неправильные дроби:
Заключим рациональное число в скобки вместе со своим знаком. Рациональное число заключать в скобки не нужно, поскольку оно уже в скобках:
Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заменим вычитание сложением:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Таким образом, значение выражения равно
Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть как положительными, так и отрицательными.
Пример 14. Найти значение выражения −3,2 + 4,3
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:
(−3,2) + (+4,3)
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:
А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:
(−3,2) + (+4,3) = |+4,3| − |−3,2| = 1,1
Модуль числа 4,3 больше, чем модуль числа −3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку перед ответом должен стоять знак того рационального числа, модуль которого больше. А модуль числа 4,3 больше, чем модуль числа −3,2
Таким образом, значение выражения −3,2 + (+4,3) равно 1,1
Этот пример можно записать покороче:
−3,2 + (+4,3) = 1,1
Пример 15. Найти значение выражения 3,5 + (−8,3)
Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим знак того рационального числа, модуль которого больше:
3,5 + (−8,3) = −(|−8,3| − |3,5|) = −(8,3 − 3,5) = −(4,8) = −4,8
Таким образом, значение выражения 3,5 + (−8,3) равно −4,8
Этот пример можно записать покороче:
3,5 + (−8,3) = −4,8
Пример 16. Найти значение выражения −7,2 + (−3,11)
Найти значение выражения −7,2 + (−3,11)
Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус.
Запись с модулями можно пропустить, чтобы не загромождать выражение:
−7,2 + (−3,11) = −7,20 + (−3,11) = −(7,20 + 3,11) = −(10,31) = −10,31
Таким образом, значение выражения −7,2 + (−3,11) равно −10,31
Этот пример можно записать покороче:
−7,2 + (−3,11) = −10,31
Пример 17. Найти значение выражения −0,48 + (−2,7)
Это сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
−0,48 + (−2,7) = (−0,48) + (−2,70) = −(0,48 + 2,70) = −(3,18) = −3,18
Пример 18. Найти значение выражения −4,9 − 5,9
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который располагается между рациональными числами −4,9 и 5,9 является знаком операции и не относится к числу 5,9. У этого рационального числа свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:
У этого рационального числа свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:
(−4,9) − (+5,9)
Заменим вычитание сложением:
(−4,9) + (−5,9)
Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:
(−4,9) + (−5,9) = −(4,9 + 5,9) = −(10,8) = −10,8
Таким образом, значение выражения −4,9 − 5,9 равно −10,8
Запишем решение этого примера покороче:
−4,9 − 5,9 = −10,8
Пример 19. Найти значение выражения 7 − 9,3
Заключим в скобки каждое число вместе со своими знаками
(+7) − (+9,3)
Заменим вычитание сложением
(+7) + (−9,3)
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:
(+7) + (−9,3) = −(9,3 − 7) = −(2,3) = −2,3
Таким образом, значение выражения 7 − 9,3 равно −2,3
Запишем решение этого примера покороче:
7 − 9,3 = −2,3
Пример 20. Найти значение выражения −0,25 − (−1,2)
Найти значение выражения −0,25 − (−1,2)
Заменим вычитание сложением:
−0,25 + (+1,2)
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:
−0,25 + (+1,2) = 1,2 − 0,25 = 0,95
Запишем решение этого примера покороче:
−0,25 − (−1,2) = 0,95
Пример 21. Найти значение выражения −3,5 + (4,1 − 7,1)
Выполним действия в скобках, затем слóжим полученный ответ с числом −3,5
Первое действие:
4,1 − 7,1 = (+4,1) − (+7,1) = (+4,1) + (−7,1) = −(7,1 − 4,1) = −(3,0) = −3,0
Второе действие:
−3,5 + (−3,0) = −(3,5 + 3,0) = −(6,5) = −6,5
Ответ: значение выражения −3,5 + (4,1 − 7,1) равно −6,5.
Пример 22. Найти значение выражения (3,5 − 2,9) − (3,7 − 9,1)
Выполним действия в скобках. Затем из числа, которое получилось в результате выполнения первых скобок, вычтем число, которое получилось в результате выполнения вторых скобок:
Первое действие:
3,5 − 2,9 = (+3,5) − (+2,9) = (+3,5) + (−2,9) = 3,5 − 2,9 = 0,6
Второе действие:
3,7 − 9,1 = (+3,7) − (+9,1) = (+3,7) + (−9,1) = −(9,1 − 3,7) = −(5,4) = −5,4
Третье действие
0,6 − (−5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6
Ответ: значение выражения (3,5 − 2,9) − (3,7 − 9,1) равно 6.
Пример 23. Найти значение выражения −3,8 + 17,15 − 6,2 − 6,15
Заключим в скобки каждое рациональное число вместе со своими знаками
(−3,8) + (+17,15) − (+6,2) − (+6,15)
Заменим вычитание сложением там, где это можно:
(−3,8) + (+17,15) + (−6,2) + (−6,15)
Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.
Не будем изобретать велосипед, а слóжим все слагаемые слева направо в порядке их следования:
Первое действие:
(−3,8) + (+17,15) = 17,15 − 3,80 = 13,35
Второе действие:
13,35 + (−6,2) = 13,35 − −6,20 = 7,15
Третье действие:
7,15 + (−6,15) = 7,15 − 6,15 = 1,00 = 1
Ответ: значение выражения −3,8 + 17,15 − 6,2 − 6,15 равно 1.
Пример 24. Найти значение выражения
Найти значение выражения
Переведём десятичную дробь −1,8 в смешанное число. Остальное перепишем без изменения:
Далее вычисляем данное выражение, применяя ранее изученные правила:
Пример 25. Найти значение выражения
Заменим вычитание сложением. Попутно переведём десятичную дробь (−4,4) в неправильную дробь
В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и убрать скобки. Тогда получим простое выражение на сложение, которое решается легко
Пример 26. Найти значение выражения
Переведём смешанное число в неправильную дробь, а десятичную дробь −0,85 в обыкновенную дробь. Получим следующее выражение:
Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:
Пример 27. Найти значение выражения
Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:
Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:
После перевода обеих дробей в неправильные дроби, получим следующее выражение:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль и перед полученным ответом поставим знак того числа, модуль которого больше:
Пример 28. Найти значение выражения
Заменим вычитание сложением. Далее переведём десятичную дробь в обыкновенную дробь. Затем вычислим получившееся выражение, применяя ранее изученные правила:
Пример 29. Найти значение выражения
Переведём десятичные дроби −0,25 и −1,25 в обыкновенные дроби, остальное перепишем без изменения. Получим следующее выражение:
Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим.
Есть и второй вариант: сначала сложить рациональные числа и , а затем из полученного результата вычесть . Этим вариантом и воспользуемся.
Этим вариантом и воспользуемся.
Первое действие:
Второе действие:
Ответ: значение выражения равно −2.
Пример 30. Найти значение выражения
Переведём десятичные дроби в обыкновенные. Остальное перепишем без изменения:
Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.
Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа и . У этих чисел одинаковые знаменатели, а значит это освободит нас от необходимости приводить их к нему.
Первое действие:
Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом . У рациональных чисел и одинаковые знаменатели в дробных частях, что опять же является преимуществом для нас
Второе действие:
Ну и слóжим полученное число −7 с последним слагаемым, а именно с рациональным числом . Удобно то, что при вычислении данного выражения, семёрки исчезнут, поскольку их сумма будет равна нулю:
Удобно то, что при вычислении данного выражения, семёрки исчезнут, поскольку их сумма будет равна нулю:
Третье действие:
Ответ: значение выражения равно
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Найдите значение выражения:
Решение:
Задание 8. Найдите значение выражения:
Решение:
Задание 9. Найдите значение выражения:
Решение:
Задание 10. Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Как из отрицательной степени сделать положительную
Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно прочитать урок «Степень» и «Свойства степеней».
Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении примеров.
Как возвести число в отрицательную степень
Чтобы возвести число в отрицательную степень нужно:
- «перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
- заменить отрицательную степень на положительную ;
- возвести число в положительную степень.
Общая формула возведения в отрицательную степень выглядит следующим образом.
a −n =
,где a ≠ 0, n ∈ z ( n принадлежит целым числам).
Примеры возведения в отрицательную степень.
- 6 −2 =
=
- (−3) −3 =
=
= −
- 0,2 −2 =
=
Любое число в нулевой степени — единица.
Примеры возведения в нулевую степень.
Как найти
10 в минус 1 степени
В уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:
Теперь, зная определение отрицательной степени, давайте разберемся, почему « 10 » в минус первой степени равно « 0,1 ».
Возведем « 10 −1 » по правилам отрицательной степени. Перевернем « 10 » и запишем её в виде дроби «
» и заменим отрицательную степень « −1 » на
положительную степень « 1 ».
10 −1 =
Возведем « 10 » в « 1 » степень. Помним, что любое число в первой степени равно самому числу.
10 −1 =
=
Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.
10 −1 =
=
= 0,1
По такому же принципу можно найти « 10 » в минус второй, третьей и т.д.
Для упрощения перевода « 10 » в минус первую, вторую и т.д степени, нужно запомнить правило:
«Количество нулей после запятой равно положительному значению степени минус один ».
Проверим правило выше для « 10 −2 ».
Т.к. у нас степень « −2 », значит, будет всего один ноль (положительное значение степени « 2 − 1 = 1 ». Сразу после запятой ставим один ноль и за ним « 1 ».
Рассмотрим « 10 −1 ».
Т.к. у нас степень « −1 », значит, нулей после запятой не будет (положительное значение степени « 1 − 1 = 0 ». Сразу после запятой ставим « 1 ».
Сразу после запятой ставим « 1 ».
То же самое правило работает и для « 10 −12 ». При переводе в десятичную дробь будет « 12 − 1 = 11 » нулей и « 1 » в конце.
Как возвести в отрицательную степень дробь
Чтобы возвести дробь в отрицательную степень нужно:
- «перевернуть» дробь;
- заменить отрицательную степень на положительную ;
- возвести дробь в положительную степень.
Пример. Требуется возвести в отрицательную степень дробь.
(
) −3 =
Перевернем дробь «
» и заменим отрицательную степень « −3 » на положительную « 3 ».
(
) −3 = (
) 3
Возведем дробь в положительную степень по правилу возведения дроби в положительную степень. Т.е. возведем и числитель « 3 », и знаменатель « 10 » в третью степень.
(
) −3 = (
) 3 =
=
Для более грамотного ответа запишем полученный результат в виде десятичной дроби.
(
) −3 = (
) 3 =
=
= 0,027
Как возвести отрицательное число в отрицательную степень
Как и при возведении отрицательного числа в положительную степень, в первую очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.
Вспомним основные правила еще раз.
Отрицательное число, возведённое в чётную степень, — число положительное .
Отрицательное число, возведённое в нечётную степень, — число отрицательное .
Перевернем число « −5 » и заменим отрицательную степень « −2 »
на положительную « 2 ».
(−5) −2 = (−
) 2 =
Так как степень « 2 » — четная , значит, результат возведения в степень будет положительный . Поэтому убираем знак минуса при раскрытии скобок.
Далее откроем скобки и возведем во вторую степень и числитель « 1 »,
и знаменатель « 5 ».
(−5) −2 = (−
) 2 =
=
Как возвести отрицательную дробь в отрицательную степень
Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.
Отрицательная дробь, возведённая в чётную степень, — дробь положительная .
Отрицательная дробь, возведённая в нечётную степень, — дробь отрицательная .
Разберемся на примере. Задание: возвести отрицательную дробь « (−
Задание: возвести отрицательную дробь « (−
) » в « −3 » степень.
По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень « −3 » на положительную « 3 ».
(−
) −3 = (−
) 3 =
Теперь определим конечный знак результата возведения в « 3 » степень.
Степень « 3 » — нечетная , значит, по правилу возведения отрицательного числа в степень дробь останется отрицательной .
Нам остается только раскрыть скобки и возвести в степень и числитель « 3 », и знаменатель « 2 » в третью степень.
(−
) −3 = (−
) 3 = −
= −
Для окончательного ответа выделим целую часть из дроби.
(−
) −3 = (−
) 3 = −
= −
= − 3
Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.
Правило возведения отрицательного числа в степень гласит: если степень четная , значит, результат возведения будет положительным .
(−
) −2 = (−
) 2 =
=
= 1
Свойства отрицательной степени
Все свойства степени, которые используются для положительной степени, точно также применяются и для отрицательной степени.
В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени и покажем примеры их использования.
Запомните!
- a m · a n = a m + n
= a m − n
- (a n ) m = a n · m
- (a · b) n = a n · b n
Примеры решений заданий с отрицательной
степенью
Колягин 9 класс. Задание № 1
Представить в виде степени.
2) a 6 · b 6 = (ab) 6
Колягин 9 класс. Задание № 5
Записать в виде степени с отрицательным числом.
Что такое степень с отрицательным показателем (отрицательная степень)? Как выполнить возведение числа в отрицательную степень? Как возвести в отрицательную степень дробь?
В частности, число в степени минус один — это число, обратное данному:
Если n — целое число, то речь идет о степени с целым отрицательным показателем и равенство верно для любого a, отличного от нуля (т.е. при a≠0).
Если n — дробное число, то речь идет о степени с рациональным показателем:
(m — целое число, n — натуральное число). Степень с дробным показателем определена только для положительных a (a>0).
Степень с дробным показателем определена только для положительных a (a>0).
Дробь в степени с отрицательным показателем равна обратному этой дроби числу в степени с показателем, противоположным данному:
Другими словами, чтобы возвести дробь в отрицательную степень, надо эту дробь «перевернуть»(числитель и знаменатель поменять местами) и изменить знак в показателе степени.
Дробь в минус первой степени — это «перевернутая» дробь.
Рассмотрим примеры возведения чисел в степень с отрицательным показателем.
Для ускорения вычислений используем таблицу степеней.
Чтобы возвести в отрицательную степень смешанное число, надо сначала перевести его в неправильную дробь:
Возведем числа в степень с дробным отрицательным показателем:
При возведении в отрицательную степень десятичной дроби можно сначала перевести ее в обыкновенную и, если возможно, сократить:
Если в показателе степени стоит десятичная дробь, нужно перевести ее в обыкновенную:
Возведение в степень с отрицательным показателем в алгебре встречается достаточно часто, поэтому важно вовремя усвоить эту тему.
13 комментариев
Спасибо! врубился) жаль, что в школе не учился(
Что ж, учиться никогда не поздно). Но всё же лучше вовремя.
Забавно, что за время работы встречал множество коллег, кому приходилось на внутренних курсах разжёвывать какие вещи начального уровня и все сокрушались: «Что же я в школе-то (институте) не учил это? Это же так просто, понятно, полезно и ИНТЕРЕСНО. »
А вся проблема в том, что ни в школе, ни в институте перед тем, как что-то начать рассказывать не проводят красочные, завлекательные, познавательные, весёлые и игровые презентации будущего курса, чтобы было понятно, а где же то, что будем скоро изучать, применяется в жизни? Каким профессиям и в каких житейских ситуациях это может быть полезно?
Учат каким-то абстрактным формулам вместо того, чтобы рассказать, что это пригодится на кухне, при разделе земли, при строительстве сарая на даче, при стрельбе из пушки, при запуске спутника и т. д.
При разбавлении спирта водой, в конце концов! :))
Ведь часто женщины встают в ступор от элементарной задачи:
В рецепте указано «1 ст. ложка 3 %-го уксуса», а у неё на кухне только 9 % или («О, БОЖЕ! Крах! Провал!») вообще уксусная эссенция! А по сути та же кислота, но в концентрации 70 %…
ложка 3 %-го уксуса», а у неё на кухне только 9 % или («О, БОЖЕ! Крах! Провал!») вообще уксусная эссенция! А по сути та же кислота, но в концентрации 70 %…
Возведение в отрицательную степень – один из основных элементов математики, который часто встречается при решении алгебраических задач. Ниже приведена подробная инструкция.
Как возводить в отрицательную степень – теория
Когда мы число в обычную степень, мы умножаем его значение несколько раз. Например, 3 3 = 3×3×3 = 27. С отрицательной дробью все наоборот. Общий вид по формуле будет иметь следующий вид: a -n = 1/a n . Таким образом, чтобы возвести число в отрицательную степень, нужно единицу поделить на данное число, но уже в положительной степени.
Как возводить в отрицательную степень – примеры на обычных числах
Держа вышеприведенное правило на уме, решим несколько примеров.
4 -2 = 1/4 2 = 1/16
Ответ: 4 -2 = 1/16
4 -2 = 1/-4 2 = 1/16.
Ответ -4 -2 = 1/16.
Но почему ответ в первом и втором примерах одинаковый? Дело в том, что при возведении отрицательного числа в четную степень (2, 4, 6 и т. д.), знак становится положительным. Если бы степень была четной, то минус сохранился:
д.), знак становится положительным. Если бы степень была четной, то минус сохранился:
Как возводить в отрицательную степень – числа от 0 до 1
Вспомним, что при возведении числа в промежутке от 0 до 1 в положительную степень, значение уменьшается с возрастанием степени. Так например, 0,5 2 = 0,25. 0,25 1/1/4 = 4
Пример 4: Вычислить 0,5 -3
Решение: 0,5 -3 = (1/2) -3 = 1/(1/2) 3 = 1/(1/8) = 8
Пример 5: Вычислить -0,5 -3
Решение: -0,5 -3 = (-1/2) -3 = 1/(-1/2) 3 = 1/(-1/8) = -8
Ответ: -0,5 -3 = -8
Исходя из 4-го и 5-ого примеров, сделаем несколько выводов:
- Для положительного числа в промежутке от 0 до 1 (пример 4), возводимого в отрицательную степень, четность или нечетность степени не важна, значение выражения будет положительным. При этом, чем больше степень, тем больше значение.
- Для отрицательного числа в промежутке от 0 до 1 (пример 5), возводимого в отрицательную степень, четность или нечетность степени неважна, значение выражения будет отрицательным.
 При этом, чем больше степень, тем меньше значение.
При этом, чем больше степень, тем меньше значение.
Как возводить в отрицательную степень – степень в виде дробного числа
Выражения данного типа имеют следующий вид: a -m/n , где a – обычное число, m – числитель степени, n – знаменатель степени.
Рассмотрим пример:
Вычислить: 8 -1/3
Решение (последовательность действий):
- Вспоминаем правило возведения числа в отрицательную степень. Получим: 8 -1/3 = 1/(8) 1/3 .
- Заметьте, в знаменателе число 8 в дробной степени. Общий вид вычисления дробной степени таков: a m/n = n √8 m .
- Таким образом, 1/(8) 1/3 = 1/(3 √8 1). Получаем кубический корень из восьми, который равен 2. Исходя отсюда, 1/(8) 1/3 = 1/(1/2) = 2.
- Ответ: 8 -1/3 = 2
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Возведение в степень – это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени (0 , 5) 5 .
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Условие: возведите – 2 в степень 4 .
Используя определение выше, запишем: (− 2) 4 = (− 2) · (− 2) · (− 2) · (− 2) . Далее нам нужно просто выполнить указанные действия и получить 16 .
Возьмем пример посложнее.
Вычислите значение 3 2 7 2
Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Выполните возведение в квадрат числа π .
Для начала округлим его до сотых. Тогда π 2 ≈ (3 , 14) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ (3 , 14159) 2 = 9 , 8695877281 .
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Мы можем тогда записать ответ в виде самой степени (ln 6) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи .
От основания степени это не зависит.
Так, (− 9) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .
Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .
5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1
0 0 – не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Возведите 3 в степень – 2 .
Используя определение выше, запишем: 2 – 3 = 1 2 3
Подсчитаем знаменатель этой дроби и получим 8: 2 3 = 2 · 2 · 2 = 8 .
Тогда ответ таков: 2 – 3 = 1 2 3 = 1 8
Возведите 1 , 43 в степень – 2 .
Переформулируем: 1 , 43 – 2 = 1 (1 , 43) 2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло (1 , 43) – 2 = 1 (1 , 43) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
материал о преобразовании дробей).
Ответ: (1 , 43) – 2 = 10000 20449
Отдельный случай – возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a – 1 = 1 a 1 = 1 a .
Пример: 3 − 1 = 1 / 3
9 13 – 1 = 13 9 6 4 – 1 = 1 6 4 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.
У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а, потом возводим результат в степень с целым показателем m .
Проиллюстрируем на примере.
Вычислите 8 – 2 3 .
Способ 1. Согласно основному определению, мы можем представить это в виде: 8 – 2 3 = 8 – 2 3
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 – 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Способ 2. Преобразуем основное равенство: 8 – 2 3 = 8 – 2 3 = 8 3 – 2
После этого извлечем корень 8 3 – 2 = 2 3 3 – 2 = 2 – 2 и результат возведем в квадрат: 2 – 2 = 1 2 2 = 1 4
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Возведите 44 , 89 в степень 2 , 5 .
Преобразуем значение показателя в обыкновенную дробь – 44 , 89 2 , 5 = 49 , 89 5 2 .
А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107
Ответ: 13 501 , 25107 . s=frac$.
s=frac$.
Справочный материал по математике (6 класс) Дроби
Справочный материал по математике (6 класс) Дроби — страница №1/1
Справочный материал по математике (6 класс)
-
Дроби
Основное свойство дроби
: Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь (используется при сокращении дробей).
Перевод дробей
Чтобы записать обыкновенную дробь в виде десятичной, нужно разделить числитель на знаменатель
Действия с дробями
-
Чтобы сложить дроби с разными знаменателями, надо: привести данные дроби к наименьшему общему знаменателю; сложить полученные дроби (сложить числители дробей, знаменатель переписать без изменений). -
Чтобы умножить дробь на дробь, надо: найти произведение числителей и произведение знаменателей этих дробей; первое произведение записать числителем, а второе – знаменателем.
-
Чтобы разделить одну дробь на другую, надо делимое (первую дробь) умножить на число, обратное делителю («перевернутая» вторая дробь).
-
Пропорции
Частное двух чисел называют
отношениемэтих чисел. (4:5)
Равенство двух отношений называется пропорцией. (a:b=c:d)
Свойство пропорции: в верной пропорции произведение крайних членов равно произведению средних. (ad=bc)
-
Положительные и отрицательные числа
Числа, лежащие на координатной прямой
левее0, называются
отрицательными, а
правее 0–
положительными.
Сравнение чисел
На координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.
Модуль числа
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).
Действия с отрицательными и положительными числами
Чтобы сложить два отрицательных числа, надо: сложить их модули, поставить перед полученным числом знак «-». Результат сложения двух отрицательных чисел – отрицательное число! (-4-5=-4+(-5)=-9)
Чтобы сложить два числа с разными знаками, надо из большего модуля слагаемых вычесть меньший, поставить перед полученным числом знак того слагаемого, модуль которого больше.
-2+3=3-2=1, 5-8=-(8-5)=-3
Чтобы перемножить два отрицательных числа, надо перемножить их модули. Результат умножения двух отрицательных чисел – число положительное! (-4. (-5)=20) (аналогично выполняется деление отрицательных чисел).
Чтобы перемножить два числа с разными знаками нужно перемножить их модули и перед полученным числом поставить знак «-». Результат умножения положительного и отрицательного чисел – отрицательное число! (-4. 5=-20)
5=-20)
-
Решение уравнений
Раскрытие скобок
Если перед скобками стоит знак «+», то можно опустить скобки и этот знак, сохранив знаки слагаемых, стоящих в скобках.
Если перед скобками стоит знак «-», надо заменить этот знак на «+», поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Слагаемые, имеющие одинаковую буквенную часть, называют подобными.
Чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на их общую буквенную часть.
Алгоритм решения линейного уравнения
-
Раскрыть скобки (если таковые имеются), используя правила (см.выше) или свойства умножения. -
Перенести все слагаемые с переменной в одну часть уравнения, а известные слагаемые – в другую. При переносе слагаемого из одной части уравнения в другую его знак меняется! -
Привести подобные слагаемые, используя действия с положительными и отрицательными числами.
-
Разделить число, стоящее справа, на коэффициент, стоящий перед переменной (слева).
Умножение отрицательных дробей — Видео и стенограмма урока
Умножение отрицательных дробей
Вот четыре шага для умножения отрицательных дробей. Давайте воспользуемся следующей задачей, чтобы проиллюстрировать шаги.
Помните, что числители — это числа над чертой в дробной части, а знаменатели — это числа под чертой в дробях.
Помните, что целое число можно превратить в дробь, просто поместив целое число над единицей.Например, целое число 7 становится 7/1.
Попрактикуемся
Давайте вместе попробуем. Давайте найдем произведение -2/7 * 3/4
Шаг 1) Когда мы умножим числители (2 * 3), ответ будет 6.
Шаг 2) Когда мы умножим знаменатели (7 * 4), ответ равно 28.
Шаг 3) Новая дробь — 6/28. Оба числа делятся на 2 и могут быть упрощены до 3/14.
Шаг 4) У дробей разные знаки, так как одна положительная, а другая отрицательная, поэтому ответ отрицательный.
Произведение -2/7 * 3/4 = -3/14.
Попробуем еще парочку. Не стесняйтесь брать лист бумаги и карандаш и самостоятельно решать следующие задачи, прежде чем искать решение.
Решить: -3/4 * 2/3
Шаг 1) Умножить числители: 3 * 2 = 6
Шаг 2) Умножить знаменатели: 4 * 3 = 12
Шаг 3) Упростить 6/12 ( оба делятся на 6) до 1/2
Шаг 4) Знаки разные, поэтому ответ отрицательный.
Ответ -1/2.
Решить: -1/2 * 3/4
Шаг 1) Умножить числители: 1 * 3 = 3
Шаг 2) Умножить знаменатели: 2 * 4 = 8
Шаг 3) 3/8 уже в простейшей форме
Шаг 4) Знаки разные, поэтому ответ отрицательный.
Итак, -1/2 * 3/4 = -3/8.
Краткое содержание урока
При умножении дробей помните, что если дроби имеют одинаковый знак, ответ будет положительным, а если дроби имеют разные знаки, ответ будет отрицательным.Также помните, что умножение отрицательных дробей состоит из четырех простых шагов, и это, безусловно, положительный момент!
Упрощение выражения с помощью дроби
Результаты обучения
- Определите отрицательные дроби, которые эквивалентны, учитывая, что их отрицательный знак находится в другом месте
- Упростите выражения, содержащие дробные черты, используя порядок операций
Где идет знак минус в дроби? Обычно перед дробью ставится знак минус, но иногда можно увидеть дробь с отрицательным числителем или знаменателем. Помните, что дроби представляют собой деление. Дробь [латекс] — \ frac {1} {3} [/ latex] может быть результатом деления [latex] \ frac {-1} {3} [/ latex], отрицательного на положительный или деления [latex] \ frac {1} {- 3} [/ latex], положительное за отрицательным. Когда числитель и знаменатель имеют разные знаки, частное отрицательное.
Помните, что дроби представляют собой деление. Дробь [латекс] — \ frac {1} {3} [/ latex] может быть результатом деления [latex] \ frac {-1} {3} [/ latex], отрицательного на положительный или деления [latex] \ frac {1} {- 3} [/ latex], положительное за отрицательным. Когда числитель и знаменатель имеют разные знаки, частное отрицательное.
Если и числитель, и знаменатель отрицательны, тогда сама дробь положительна, потому что мы делим отрицательное на отрицательное.
[латекс] \ frac {-1} {- 3} = \ frac {1} {3} \ frac {\ text {negative}} {\ text {negative}} = \ text {positive} [/ latex]
Размещение отрицательного знака в дроби
Для любых положительных чисел [латекс] a \ text {и} b [/ latex],
[латекс] \ frac {-a} {b} = \ frac {a} {- b} = — \ frac {a} {b} [/ latex]
Пример
Какая из следующих фракций эквивалентна [latex] \ frac {7} {- 8}? [/ Latex]
[латекс] \ frac {-7} {- 8}, \ frac {-7} {8}, \ frac {7} {8}, — \ frac {7} {8} [/ latex]
Решение:
Частное положительного и отрицательного отрицательно, поэтому [latex] \ frac {7} {- 8} [/ latex] отрицательно. Из перечисленных фракций [latex] \ frac {-7} {8} \ text {и} — \ frac {7} {8} [/ latex] также отрицательны.
Из перечисленных фракций [latex] \ frac {-7} {8} \ text {и} — \ frac {7} {8} [/ latex] также отрицательны.
Упрощение выражения с помощью дроби
Полоски дроби действуют как символы группировки. Выражения над и под дробной чертой следует рассматривать так, как если бы они были заключены в круглые скобки. Например, [латекс] \ frac {4 + 8} {5 — 3} [/ latex] означает [латекс] \ left (4 + 8 \ right) \ div \ left (5 — 3 \ right) [/ latex] . Порядок операций говорит нам сначала упростить числитель и знаменатель — как если бы были круглые скобки — перед тем, как делить.
Мы добавим дробные черты к нашему набору символов группировки из раздела «Использование языка алгебры», чтобы получить здесь более полный набор.
Группировка символов
Упростите выражение с помощью дробной линейки
- Упростим числитель.
- Упростим знаменатель.
- Упростите дробь.
Пример
Упростить: [латекс] \ frac {4 + 8} {5 — 3} [/ латекс]
Показать решение
Решение:
Пример
Упростить: [латекс] \ frac {4 \ left (-3 \ right) +6 \ left (-2 \ right)} {- 3 \ left (2 \ right) -2} [/ latex]
Показать решение
Решение:
| [латекс] \ frac {4 \ left (-3 \ right) +6 \ left (-2 \ right)} {- 3 \ left (2 \ right) -2} [/ латекс] | |
| Умножить. | [латекс] \ frac {-12+ \ left (-12 \ right)} {- 6 — 2} [/ латекс] |
Упростить. | [латекс] \ frac {-24} {- 8} [/ латекс] |
| Разделить. | [латекс] 3 [/ латекс] |
Посмотрите это видео, чтобы увидеть еще один пример того, как упростить выражение с помощью дробной линейки, содержащей несколько различных операций.
Умножение положительных и отрицательных чисел: 3 простых правила
При умножении положительных и отрицательных чисел существует меньше правил, чем при сложении и вычитании положительных и отрицательных чисел.Следует запомнить всего три правила:
Правило 1. Положительное число, умноженное на положительное, равняется положительному числу.
Это умножение, которое вы делали все время: положительные числа, умноженные на положительные, равны положительным числам.
Например, 5 x 3 = 15. 5 — положительное число, 3 — положительное число, а умножение дает положительное число: 15.
Ответ: 5 x 3 = 15.
Правило 2: Отрицательное число, умноженное на положительное, равняется отрицательному числу.
Когда вы умножаете отрицательное число на положительное, ваш ответ — отрицательное число. Неважно, в каком порядке вы умножаете положительные и отрицательные числа, ответ всегда будет отрицательным.
Например: -2 x 4, что по сути то же самое, что -2 + (-2) + (-2) + (-2)
Ответ: -2 х 4 = -8.
И, как мы уже сказали, если около 4 x -2 наоборот, ответ все тот же: -8.
Ответ: 4 х -2 = -8.
Правило 3. Отрицательное число, умноженное на отрицательное число, равняется положительному числу.
Два отрицательных числа дают положительное число, поэтому умноженное на отрицательное число дает положительное число. Если вы посмотрите на него на числовой прямой, идя назад и повернувшись лицом в отрицательном направлении, вы двинетесь в положительном направлении.
Например. -2 x -4 отрицательны, поэтому мы знаем, что ответ будет положительным.
Ответ: -2 x -4 = 8.
Вот общее правило, которое следует помнить при умножении положительных и отрицательных чисел:
Два одинаковых знака дают положительный знак:
Два непохожих знака образуют отрицательный знак:
Если вы все еще не понимаете, почему отрицательное число, умноженное на отрицательное, дает положительное число, Диана Браун с факультета математики Университета Джорджии объясняет это разными способами в этой статье.
Скотт из About.com также собрал удобное видео о том, как создать шпаргалку для умножения отрицательных и положительных чисел (прокрутите страницу вниз, и вы найдете видео).
Умножение и деление отрицательных дробей и смешанных чисел
Дроби Смешанные числа и неправильные дроби. Смешанное число содержит целую часть и дробную часть. смешанное число. Он содержит как целую часть, 3, так и дробную часть, 2/5. Мы читаем дробь как «три и две пятых», и это именно то, что мы имеем в виду.= Добавление целого числа к дроби — это особый случай сложения двух … Бесплатные рабочие листы по математике для сложения, вычитания, умножения, среднего, деления, алгебры и тем меньше, чем больше, в соответствии с общими основными стандартами для 5-го и 4-го классов класс, 3 класс, 2 класс, 1 класс, средняя школа и дошкольное учреждение
Способность записывать смешанные дроби как неправильные дроби и наоборот является важной предпосылкой для сложения и вычитания смешанных дробей (CCSS. Math.4.NF.3c): складывать и вычитать смешанные числа с одинаковыми знаменателями, например, заменяя каждое смешанное число эквивалентной дробью и / или используя свойства операций и … На этой странице вы найдете наши рабочие листы с отрицательными целыми числами, отрицательными десятичными знаками. и отрицательные дроби. Наши рабочие листы с отрицательными числами подходят для 6 и 7 классов математики и являются отличным математическим ресурсом для корректирующих целей по математике или математическому обучению. У нас есть целые листы, в которых описывается сложение и вычитание целых и отрицательных чисел из числа…
Math.4.NF.3c): складывать и вычитать смешанные числа с одинаковыми знаменателями, например, заменяя каждое смешанное число эквивалентной дробью и / или используя свойства операций и … На этой странице вы найдете наши рабочие листы с отрицательными целыми числами, отрицательными десятичными знаками. и отрицательные дроби. Наши рабочие листы с отрицательными числами подходят для 6 и 7 классов математики и являются отличным математическим ресурсом для корректирующих целей по математике или математическому обучению. У нас есть целые листы, в которых описывается сложение и вычитание целых и отрицательных чисел из числа…
Умножайте или делите смешанные числа. Преобразуйте смешанные числа в неправильные дроби. Следуйте правилам умножения или деления дробей. Если возможно, упростите. Упростите сложную дробь. Перепишите сложную дробь как задачу деления. Соблюдайте правила деления дробей. Если возможно, упростите. Размещение знака минус в дроби CCBC Math 081 Умножение дробей и смешанных чисел Раздел 3. 2 Третье издание 17 страниц 162 Пример 4a: Умножение: 29 3 14 u 2 9 2 9 18 3 14 3 14 42 uuu Умножьте числители вместе и знаменатели вместе.Проверьте, можно ли упростить ответ. Есть общие множители для 18 и 42, так что это
2 Третье издание 17 страниц 162 Пример 4a: Умножение: 29 3 14 u 2 9 2 9 18 3 14 3 14 42 uuu Умножьте числители вместе и знаменатели вместе.Проверьте, можно ли упростить ответ. Есть общие множители для 18 и 42, так что это
9 апреля 2015 г. · Идея состоит в том, что пары чисел сами по себе связаны с ассоциациями. У этого утверждения есть жесткая версия, которую я не собираюсь делать. Я не хочу сказать, что независимо от контекста, вы ожидаете, что ученик сложит вместе 5 1/2 и 2 1/4. Я думаю, что проблема деления смешанных чисел вряд ли вызовет ассоциации с … Как пользоваться калькулятором. Введите свою задачу по алгебре в текстовое поле.Например, введите 3x + 2 = 14 в текстовое поле, чтобы получить пошаговое объяснение того, как решить 3x + 2 = 14.
Вычитание целых чисел от (-15) до (+15) (отрицательные числа в круглых скобках) (106 просмотров на этой неделе) Все операции с целыми числами (диапазон от -9 до 9) со всеми целыми числами в круглых скобках (81 просмотр на этой неделе) Целочисленное сложение и вычитание с круглыми скобками вокруг всех целых чисел (диапазон от -25 до 25) (60 просмотров на этой неделе) Добавление целых чисел от (-15) до (+15) (все числа в круглых скобках) (49 просмотров на этой неделе… Практика сложения, вычитания, умножения и деления на смешанные дроби, рабочая тетрадь улучшит вашу беглость математики том 14 25 октября 2020 г. Автор: Джеки Коллинз Паблишинг …
Автор: Джеки Коллинз Паблишинг …
Умножение — это математическая операция, которая масштабирует одно число на другое ( умножение — знак: x). Он заменяет сложение большого количества чисел подряд. Умножение — математическая операция, противоположная делению. Например: вы можете заменить математическое выражение 5 + 5 + 5 + 5 на 5 × 4 (число 5, умноженное на количество раз, которое оно появилось в строке).
Умножение имеет несколько свойств. Когда число умножается на число 1, произведение (результат умножения) совпадает с этим числом. Когда число умножается на ноль, произведение всегда равно нулю. Когда число умножается на отрицательное, результатом является отрицательная версия этого числа. Он также обладает свойствами коммутативности, ассоциативности и дистрибутивности.
Коммутативные и ассоциативные свойства аналогичны этим свойствам.Распределительность применяется при объединении сложения и умножения, как в этом примере:
а * (б + в) = а * б + а * в
Очень важно помнить, что порядок важности умножения всегда больше, чем порядок важности сложения или вычитания. Сначала вы умножаете числа (где это необходимо), а затем складываете или вычитаете их. Вот пример:
Сначала вы умножаете числа (где это необходимо), а затем складываете или вычитаете их. Вот пример:
5 * 4 + 3 = 20 + 3 = 23
Единственным исключением из правила является то, что сложение или вычитание имеет приоритет над умножением, когда числа, которые нужно сложить, и оператор заключены в квадратные скобки, а оператор умножения — нет.
Умножение экзаменов для учителей
| Название экзамена | Размер файла | Загрузки | Дата загрузки |
Целые положительные числа | |||
| Умножение положительных целых чисел — очень просто | 78 Кбайт | 2899 | 3 сентября 2019 г. |
| Умножение положительных целых чисел — легко | 143 Кбайт | 2902 | 3 сентября 2019 г. |
| Умножение положительных целых чисел — среднее | 166.3 кБ | 3194 | 3 сентября 2019 г. |
| Умножение положительных целых чисел — средней сложности | 173.1 Кбайт | 2675 | 3 сентября 2019 г. |
| Умножение положительных целых чисел — жесткое | 561.5 кБ | 2082 | 3 сентября 2019 г. |
| Умножение положительных целых чисел — очень сложно | 571.8 Кбайт | 2294 | 3 сентября 2019 г. |
Положительные десятичные знаки | |||
| Умножение положительных десятичных знаков — очень просто | 554.5 кБ | 1936 | 3 сентября 2019 г. |
| Умножение положительных десятичных знаков — легко | 555.5 Кбайт | 1927 | 3 сентября 2019 г. |
| Умножение положительных десятичных знаков — среднее | 579.2 Кбайт | 1752 | 3 сентября 2019 г. |
| Умножение положительных десятичных знаков — средне-жесткий | 580. 2 Кбайт 2 Кбайт | 1573 | 3 сентября 2019 г. |
| Умножение положительных десятичных знаков — жесткое | 569.5 кБ | 1736 | 3 сентября 2019 г. |
| Умножение положительных десятичных знаков — очень сложно | 567.2 Кбайт | 1576 | 3 сентября 2019 г. |
Положительные дроби | |||
| Умножение положительных дробей — очень сложно | 567.2 Кбайт | 1576 | 3 сентября 2019 г. |
| Умножение положительных дробей — очень просто | 172.7 Кбайт | 2353 | 3 сентября 2019 г. |
| Умножение положительных дробей — легко | 188.9 кБ | 2049 | 3 сентября 2019 г. |
| Умножение положительных дробей — среднее | 577.2 Кбайт | 1765 | 3 сентября 2019 г. |
| Умножение положительных дробей — средней твердости | 591. 9 Кбайт 9 Кбайт | 1557 | 3 сентября 2019 г. |
| Умножение положительных дробей — жесткое | 575.7 Кбайт | 1569 | 3 сентября 2019 г. |
| Умножение положительных дробей — очень сложно | 581 Кбайт | 1553 | 3 сентября 2019 г. |
Положительные смешанные числа | |||
| Умножение положительных смешанных чисел — очень просто | 176.8 кБ | 1749 | 3 сентября 2019 г. |
| Умножение положительных смешанных чисел — легко | 209.8 Кбайт | 1761 | 3 сентября 2019 г. |
| Умножение смешанных положительных чисел — среднее | 585.6 Кбайт | 1592 | 3 сентября 2019 г. |
| Умножение смешанных положительных чисел — средней сложности | 592.9 Кбайт | 1513 | 3 сентября 2019 г. |
| Умножение положительных смешанных чисел — жесткое | 589. 3 кБ 3 кБ | 1517 | 3 сентября 2019 г. |
| Умножение положительных смешанных чисел — очень сложно | 596.6 Кбайт | 1483 | 3 сентября 2019 г. |
Положительные неправильные дроби | |||
| Умножение положительных неправильных дробей — очень просто | 166 Кбайт | 1539 | 3 сентября 2019 г. |
| Умножение положительных неправильных дробей — легко | 169.9 кБ | 1640 | 3 сентября 2019 г. |
| Умножение положительных неправильных дробей — среднее | 571.6 Кбайт | 1520 | 3 сентября 2019 г. |
| Умножение положительных неправильных дробей — средней твердости | 569.5 Кбайт | 1483 | 3 сентября 2019 г. |
| Умножение положительных неправильных дробей — жесткое | 560.5 Кбайт | 1426 | 3 сентября 2019 г. |
| Умножение положительных неправильных дробей — очень сложно | 571.8 кБ | 1494 | 3 сентября 2019 г. |
Целые неположительные числа | |||
| Умножение целых чисел — очень просто | 137.9 Кбайт | 2107 | 3 сентября 2019 г. |
| Умножение целых чисел — легко | 143.6 Кбайт | 2143 | 3 сентября 2019 г. |
| Умножение целых чисел — среднее | 173.3 Кбайт | 2097 | 3 сентября 2019 г. |
| Умножение целых чисел — средней сложности | 173.5 кБ | 1957 | 3 сентября 2019 г. |
| Умножение целых чисел — жесткое | 565.9 Кбайт | 1746 | 3 сентября 2019 г. |
| Умножение целых чисел — очень сложно | 568 Кбайт | 1641 | 3 сентября 2019 г. |
Неположительные десятичные числа | |||
| Умножение десятичных знаков — очень просто | 186. 6 Кбайт 6 Кбайт | 1983 | 3 сентября 2019 г. |
| Умножение десятичных знаков — просто | 187 Кбайт | 2103 | 3 сентября 2019 г. |
| Умножение десятичных знаков — среднее | 578.8 кБ | 1601 | 3 сентября 2019 г. |
| Умножение десятичных знаков — средней жесткости | 577 Кбайт | 1520 | 3 сентября 2019 г. |
| Умножение десятичных знаков — жесткое | 564.9 Кбайт | 1591 | 3 сентября 2019 г. |
| Умножение десятичных знаков — очень сложно | 567.9 Кбайт | 1501 | 3 сентября 2019 г. |
Неположительные дроби | |||
| Умножение дробей — очень просто | 179.6 кБ | 1594 | 3 сентября 2019 г. |
| Умножение дробей — легко | 186.7 Кбайт | 1866 | 3 сентября 2019 г. |
| Умножение дробей — среднее | 583.8 Кбайт | 1596 | 3 сентября 2019 г. |
| Умножение дробей — средней твердости | 589 Кбайт | 1511 | 3 сентября 2019 г. |
| Умножение дробей — жесткое | 588 Кбайт | 1422 | 3 сентября 2019 г. |
| Умножение дробей — очень сложно | 594.9 кБ | 1436 | 3 сентября 2019 г. |
Неположительные смешанные числа | |||
| Умножение смешанных чисел — очень просто | 192.9 кБ | 1468 | 3 сентября 2019 г. |
| Умножение смешанных чисел — просто | 209 Кбайт | 1635 | 3 сентября 2019 г. |
| Умножение смешанных чисел — среднее | 594.7 Кбайт | 1510 | 3 сентября 2019 г. |
| Умножение смешанных чисел — средней сложности | 602. 2 кБ 2 кБ | 1354 | 3 сентября 2019 г. |
| Умножение смешанных чисел — сложное | 586.3 Кбайт | 1380 | 3 сентября 2019 г. |
| Умножение смешанных чисел — очень сложно | 591.3 Кбайт | 1360 | 3 сентября 2019 г. |
Неположительные неправильные дроби | |||
| Умножение неправильных дробей — очень просто | 171.2 Кбайт | 1411 | 3 сентября 2019 г. |
| Умножение неправильных дробей — легко | 174 Кбайт | 1454 | 3 сентября 2019 г. |
| Умножение неправильных дробей — среднее | 574.7 кБ | 1419 | 3 сентября 2019 г. |
| Умножение неправильных дробей — средней твердости | 573.9 Кбайт | 1333 | 3 сентября 2019 г. |
| Умножение неправильных дробей — жесткое | 570. 7 Кбайт 7 Кбайт | 1351 | 3 сентября 2019 г. |
| Умножение неправильных дробей — очень сложно | 577.4 Кбайт | 1348 | 3 сентября 2019 г. |
Умножение рабочих листов для студентов
| Название листа | Размер файла | Загрузки | Дата загрузки |
Положительно | |||
| Умножение натуральных чисел | 496.1 кБ | 2432 | 3 сентября 2019 г. |
| Умножение положительных десятичных знаков | 51.8 Кбайт | 1768 | 3 сентября 2019 г. |
| Умножение положительных дробей | 632.1 Кбайт | 1571 | 3 сентября 2019 г. |
| Умножение смешанных положительных чисел | 637.8 Кбайт | 1784 | 3 сентября 2019 г. |
| Умножение положительных неправильных дробей | 594. 6 кБ 6 кБ | 1390 | 3 сентября 2019 г. |
Неположительный | |||
| Умножение целых чисел | 166.8 Кбайт | 1810 | 3 сентября 2019 г. |
| Умножение десятичных знаков | 246.3 Кбайт | 1644 | 3 сентября 2019 г. |
| Умножение дробей | 393.1 Кбайт | 1639 | 3 сентября 2019 г. |
| Умножение смешанных чисел | 412.4 кБ | 1534 | 3 сентября 2019 г. |
| Умножение неправильных дробей | 334.1 Кбайт | 1440 | 3 сентября 2019 г. |
Обратная дробь — ChiliMath
Помните, что дробь состоит из трех частей.
ЧАСТИ ФРАКЦИИ
Как найти величину, обратную дроби
Чтобы получить величину, обратную дроби
просто меняет местами или местами числитель и знаменатель. Вы можете сказать, что мы просто переворачиваем исходную дробь вверх дном.
Вы можете сказать, что мы просто переворачиваем исходную дробь вверх дном.
Примеры нахождения обратной дроби
Пример 1: Найдите величину, обратную дроби, указанной ниже.
Давайте перевернем дробь {3 \ over 7} вверх дном, чтобы получить обратную величину. Это дает нам
Пример 2: Найдите величину, обратную дроби, указанной ниже.
Для некоторых это может быть непросто. Обратите внимание, что числитель отрицательный. Если перевернуть эту дробь вверх дном, то естественно должно получиться
.
Поскольку это отрицательная дробь, отрицательный символ не всегда может «следовать» за числом, к которому он изначально прикреплен.
Другими словами, отрицательный символ может оставаться в числителе. Итак, после инвертирования двух чисел отрицательный символ присоединяется к 2. Это также правильный ответ, поскольку он является обратной величиной исходной дроби.
Есть еще один способ записать обратную величину этой отрицательной дроби. Отрицательный символ не может быть присоединен к числителю или знаменателю , .
Также правильно размещать отрицательный символ непосредственно слева от дроби .Вот как это выглядит!
Итак, если дробь отрицательная, ее обратная величина может быть записана тремя способами.
- Отрицательный символ остается с числителем
- Отрицательный символ остается со знаменателем
- Отрицательный символ остается с дробной чертой
Пример 3: Запишите обратную величину отрицательной дроби ниже тремя различными способами.
Решение:
Пример 4: Найдите значение, обратное целому числу 15.
Любое ненулевое целое число может быть выражено знаменателем , равным 1.
Имея четкий знаменатель, мы можем легко перевернуть эту дробь вверх дном, чтобы получить обратную величину.
Пример 5: Найдите обратное целому числу — 11.
Сначала перепишите это целое число со знаменателем , равным 1.
Теперь, имея четкий знаменатель, мы можем найти его обратную величину. У нас есть отрицательный символ в числителе, помните, что его можно расположить в трех разных местах: числитель, знаменатель и дробь.Вот возможные ответы!
Вас также может заинтересовать:
Сложение и вычитание дробей с одним знаменателем
Сложение и вычитание дробей с разными знаменателями
Умножение дробей
Деление дробей
Упрощение дробей
Эквивалентные дроби
Рабочий лист
дробей
Добро пожаловать на страницу рабочих листов для дробей на Math-Drills.com, где чашка наполовину заполнена! Скорее всего, это одна из самых популярных наших страниц, потому что изучение дробей невероятно важно в жизни человека, и это математическая тема, к которой многие подходят с трепетом из-за плохой репутации на протяжении многих лет. Освоить дроби на самом деле не так сложно, особенно с поддержкой нашего широкого выбора рабочих листов.
Освоить дроби на самом деле не так сложно, особенно с поддержкой нашего широкого выбора рабочих листов.
Эта страница включает в себя рабочие листы дробей для понимания дробей, включая моделирование, сравнение, упорядочение, упрощение и преобразование дробей и операции с дробями. Начнем с очевидного: моделирование дробей. Это отличная идея, если студенты действительно могут понять, что такое дробь, поэтому, пожалуйста, уделите немного времени аспекту моделирования. Связь моделирования с реальной жизнью тоже очень помогает, так как гораздо легче связать половину печенья, чем половину квадрата.Спросите у большинства студентов, что вы получите, если добавите половину печенья и половину печенья, и они, вероятно, дадут вам знать, что из этого получится одна вкусная закуска.
Другие рабочие листы на этой странице посвящены тому, чтобы помочь студентам понять концепцию дробей. От сравнения и упорядочения до упрощения и преобразования … к тому времени, когда студенты усвоят материал на этой странице, операции с дробями будут похожи на прогулку по парку.
Рабочие листы с самыми популярными дробями на этой неделе
Распечатки с дробями общего назначения
Дробные круги
Черные и белые круги дробей можно использовать как манипуляторы для сравнения дробей.Сделайте фотокопию рабочего листа на слайд с проекцией сверху. Карандашом слегка закрасьте соответствующий кружок, чтобы изобразить первую дробь на бумажной копии. Используйте непостоянную ручку над головой, чтобы раскрасить соответствующий круг, чтобы обозначить вторую дробь. Положите слайд на бумагу и сравните два круга. Вы легко сможете определить, какая дробь больше или меньше или равны две дроби. Используйте оба листа повторно, стирая карандаш и смывая маркер.
Фракционные полоски
Полоски с дробями можно ламинировать для повышения прочности и вырезать для сравнения, упорядочивания, сложения и вычитания дробей.Они очень полезны для сравнения дробей. Вы также можете скопировать полоски с дробями на слайды проекции и вырезать их. Они будут не только долговечными, но и прозрачными, что полезно при использовании в сочетании с бумажными версиями (например, для сравнения дробей).
Вы также можете скопировать полоски с дробями на слайды проекции и вырезать их. Они будут не только долговечными, но и прозрачными, что полезно при использовании в сочетании с бумажными версиями (например, для сравнения дробей).
Рабочие листы моделирования дробей
Помимо использования приведенных ниже таблиц, вы также можете попробовать еще несколько интересных способов моделирования дробей. Здоровые закуски могут стать отличными моделями для дробей.Можно ли разрезать огурец пополам? Помидор на четвертинки? Можно ли сделать две трети винограда красными, а одну треть — зелеными?
Моделирование фракций с группами фигур
Дроби могут представлять части группы или части целого. В этих таблицах дроби моделируются как части группы.
Моделирование фракций прямоугольниками
Моделирование фракций с кругами
Таблицы соотношений и пропорций
Соотношение изображений
Эквивалентные дроби
Рабочие листы моделей эквивалентных фракций включают только «фракции выпечки» в версиях A. Чтобы увидеть более сложные и разнообразные дроби, выберите версии от B до J после загрузки версии A.
Чтобы увидеть более сложные и разнообразные дроби, выберите версии от B до J после загрузки версии A.
Эквивалентные соотношения
Таблицы сравнения и сортировки дробей
Сравнение простых дробей
Есть много разных стратегий, кроме просмотра страницы, которые помогут в сравнении дробей. Попробуйте начать с чего-нибудь наглядного, что будет изображать рассматриваемые дроби.Мы настоятельно рекомендуем наши дробные полоски (прокрутите немного вверх). Использование линейки, такой как линейка, книга или складка, поможет учащимся легко увидеть, какая дробь больше или равна ли они. Следует также отметить, что сравниваемые вещи должны быть одинаковыми. Например, каждая фракционная полоска имеет одинаковый размер, тогда как если вы возьмете треть арбуза и половину винограда, арбуз, вероятно, победит.
Сравнение простых и неправильных дробей
Еще одна стратегия, которую можно использовать при сравнении дробей, — использовать числовую линию и использовать контрольные цифры, такие как 0, 1, 1/2, чтобы выяснить, куда идет каждая дробь, а затем посмотреть, какая из них больше. Студенты на самом деле делают это все время, так как они часто могут сравнивать дроби, осознавая, что одна меньше половины, а другая больше половины. Они также могут увидеть, что одна фракция намного ближе к целому, чем другая фракция, даже если они обе могут быть больше половины.
Студенты на самом деле делают это все время, так как они часто могут сравнивать дроби, осознавая, что одна меньше половины, а другая больше половины. Они также могут увидеть, что одна фракция намного ближе к целому, чем другая фракция, даже если они обе могут быть больше половины.
Сравнение простых, неправильных и смешанных дробей
Другая стратегия сравнения дробей — преобразовать каждую дробь в десятичную дробь и сравнить десятичные дроби.Десятичные преобразования можно запомнить (особенно для обычных дробей), рассчитанные путем деления в столбик, с помощью калькулятора или справочной таблицы. Мы предлагаем последнее, поскольку использование справочной таблицы часто приводит к мысленному вспоминанию.
Заказ дробей в числовой строке
Многие из тех же стратегий, которые работают для сравнения дробей, также работают для упорядочивания дробей. Использование таких манипуляторов, как полоски дробей, использование числовых линий или поиск десятичных эквивалентов, заставит ваших учеников быстро расставить дроби в правильном порядке.Мы, вероятно, говорили об этом раньше, но убедитесь, что вы подчеркнули, что при сравнении или упорядочивании дробей учащиеся понимают, что целое должно быть одинаковым. Сравнение половины населения Канады с третью населения Соединенных Штатов не поможет. Попробуйте использовать визуальные эффекты, чтобы усилить эту важную концепцию. Несмотря на то, что мы включили числовые линии ниже, вы можете свободно использовать свои собственные стратегии.
Использование таких манипуляторов, как полоски дробей, использование числовых линий или поиск десятичных эквивалентов, заставит ваших учеников быстро расставить дроби в правильном порядке.Мы, вероятно, говорили об этом раньше, но убедитесь, что вы подчеркнули, что при сравнении или упорядочивании дробей учащиеся понимают, что целое должно быть одинаковым. Сравнение половины населения Канады с третью населения Соединенных Штатов не поможет. Попробуйте использовать визуальные эффекты, чтобы усилить эту важную концепцию. Несмотря на то, что мы включили числовые линии ниже, вы можете свободно использовать свои собственные стратегии.
Заказ дробей
Рабочие листы с упорядочением дробей в этом разделе не включают числовую строку, чтобы студенты могли использовать различные стратегии сортировки.
Рабочие листы для упрощения и преобразования дробей
Округление дробей
Округление дробей помогает учащимся немного лучше понимать дроби и может применяться для оценки ответов на вопросы о дробях. Например, если нужно было оценить 1 4/7 × 6, они, вероятно, могли бы сказать, что ответ будет примерно 9, поскольку 1 4/7 составляет примерно 1 1/2, а 1 1/2 × 6 — 9.
Например, если нужно было оценить 1 4/7 × 6, они, вероятно, могли бы сказать, что ответ будет примерно 9, поскольку 1 4/7 составляет примерно 1 1/2, а 1 1/2 × 6 — 9.
Упрощение дробей
Изучение того, как упрощать дроби, значительно облегчает жизнь студента в дальнейшем, когда он будет изучать операции с дробями.Это также помогает им узнать, что дроби, которые выглядят по-разному, могут быть эквивалентными. Один из способов продемонстрировать это — разделить две эквивалентные дроби. Например, 3/2 и 6/4 при делении дают частное 1,5. Будем надеяться, что практикуя упрощение дробей, студенты будут распознавать неупрощенные дроби, когда они начнут складывать, вычитать, умножать и делить на дроби.
Преобразование из неправильной дроби в смешанную
Преобразование между дробями, десятичными знаками, процентами и отношениями Преобразование дробей в завершающие десятичные дроби Преобразование дробей в завершающие и повторяющиеся десятичные дроби Преобразование завершающих десятичных знаков в дроби Преобразование завершающих и повторяющихся десятичных знаков в дроби Преобразование дробей в сотые Преобразование дробей в десятичные, проценты и частичные в Части соотношений ( только завершающие десятичные дроби) Преобразование дробей в десятичные дроби, проценты и части-к- целые отношения ( только завершающие десятичные дроби) Преобразование десятичных дробей в дроби, проценты и частичные-к- Части отношения ( только завершающие десятичные дроби) Преобразование десятичных дробей в дроби, проценты и части-к- целые отношения ( только завершающие десятичные числа) Преобразование процентов в дроби, десятичные дроби и частичные-к- частичные отношения ( только завершающие десятичные дроби) Преобразование процентов в дроби, десятичные дроби и частичные-к- целые отношения ( только завершающие десятичные дроби) Преобразование дробных соотношений в дроби, десятичные дроби и проценты ( только завершает десятичные дроби) Преобразование отношения части к целому в дроби, десятичные дроби и проценты ( только завершает десятичные дроби) Преобразование различных дробей, десятичных знаков, процентов и дробных чисел в Части соотношений (, завершающее десятичных знаков) Преобразование различных дробей, десятичных знаков, процентов и частей в целых соотношений (, завершающее десятичных знаков) Преобразование дробей в десятичные дроби, проценты и дробные части Часть соотношений Преобразование дробей в десятичные, проценты и частичные целые отношения Преобразование десятичных дробей в дроби, проценты и частичные к Части отношения Преобразование десятичных дробей в дроби, проценты и дробные части Целые отношения Преобразование процентов в дроби, десятичные дроби и части Часть отношений Преобразование процентов в дроби, десятичные дроби и дроби в целые отношения Преобразование частичных соотношений в дроби, десятичные дроби и проценты Преобразование целого числа в дроби, десятичные дроби и проценты Преобразование различных дробей, десятичных знаков, процентов и дробей в Части соотношений Преобразование различных дробей, десятичных знаков, процентов и дробей в целых соотношений Преобразование различных дробей, десятичных знаков, процентов и частей в Части отношений с 7-ми и 11-ми Преобразование различных дробей, десятичных знаков, процентов и частей в целых соотношений с 7 и 11 (СТАРЫЙ) Преобразование дробей, десятичных знаков, процентов и соотношений
Рабочие листы операций с дробями
Умножение дробей
Умножение дробей обычно менее запутанно с операционной точки зрения, чем любая другая операция, и может быть менее запутанным в концептуальном плане при правильном подходе. Алгоритм умножения — это просто умножение числителей, а затем знаменателей. Волшебное слово в понимании умножения дробей — «из». Например, что составляет две трети ОТ шести? Что такое треть от половины? Когда вы используете слово «из», становится намного легче визуализировать умножение дробей. Пример: разрезать буханку хлеба пополам, затем половину разрезать на три части. Одна треть полбуханки хлеба такая же, как 1/3 x 1/2, и вкусная с маслом.
Алгоритм умножения — это просто умножение числителей, а затем знаменателей. Волшебное слово в понимании умножения дробей — «из». Например, что составляет две трети ОТ шести? Что такое треть от половины? Когда вы используете слово «из», становится намного легче визуализировать умножение дробей. Пример: разрезать буханку хлеба пополам, затем половину разрезать на три части. Одна треть полбуханки хлеба такая же, как 1/3 x 1/2, и вкусная с маслом.
На дроби
По идее, деление на дроби, вероятно, самая сложная из всех операций, но мы собираемся помочь вам.Алгоритм деления дробей аналогичен умножению дробей, но вы находите обратное значение второй дроби или производите перекрестное умножение. Это даст вам правильный ответ, что чрезвычайно важно, особенно если вы строите мост. Мы рассказали вам, как концептуализировать умножение дробей, но как оно работает с делением? Легкий! Вам просто нужно выучить волшебную фразу: «Сколько ____ в ______? Например, в вопросе 6 & div; 1/2 вы спросите:« Сколько половинок в 6? »Становится немного больше. трудно, когда оба числа являются дробными, но это не гигантский скачок, чтобы понять это.1/2 & div; 1/4 — довольно простой пример, особенно если вы думаете о монетах США или Канады. Сколько четвертей в полдолларе?
трудно, когда оба числа являются дробными, но это не гигантский скачок, чтобы понять это.1/2 & div; 1/4 — довольно простой пример, особенно если вы думаете о монетах США или Канады. Сколько четвертей в полдолларе?
Сложение дробей
Для сложения дробей нужен надоедливый общий знаменатель. Упростите жизнь своих учеников, сначала обучив их понятиям эквивалентных дробей и наименьших общих кратных. Как только учащиеся знакомы с этими двумя концепциями, идея поиска дробей с общими знаменателями для сложения становится намного проще.Время, потраченное на моделирование дробей, также поможет учащимся понять сложение дробей. Связь дробей с знакомыми примерами, безусловно, поможет. Например, если вы добавите 1/2 банана и 1/2 банана, вы получите целый банан. Что произойдет, если вы добавите 1/2 банана и 3/4 другого банана?
Добавление смешанных фракций Рабочие листы
Обычная стратегия, которую используют при добавлении смешанных фракций, состоит в том, чтобы преобразовать смешанные фракции в неправильные фракции, завершить сложение, а затем переключиться обратно. Другая стратегия, требующая немного меньших умственных способностей, — рассматривать целые числа и дроби по отдельности. Сначала сложите целые числа. Добавьте доли секунды. Если полученная дробь неправильная, ее нужно преобразовать в смешанное число. Часть целого числа может быть добавлена к исходной части целого числа.
Другая стратегия, требующая немного меньших умственных способностей, — рассматривать целые числа и дроби по отдельности. Сначала сложите целые числа. Добавьте доли секунды. Если полученная дробь неправильная, ее нужно преобразовать в смешанное число. Часть целого числа может быть добавлена к исходной части целого числа.
Вычитание Дробей
Нет большой разницы между сложением и вычитанием дробей.Оба требуют общего знаменателя, что требует некоторых предварительных знаний. Единственная разница в том, что второй и последующие числители вычитаются из первого. Существует опасность того, что вы можете получить отрицательное число при вычитании дробей, поэтому учащимся, возможно, потребуется узнать, что это означает в этом случае. Когда дело доходит до любого понятия в дробях, всегда полезно связать его с знакомой или простой для понимания ситуацией. Например, 7/8 — 3/4 = 1/8 может иметь значение в контексте гонки.Первый бегун шел на 7/8 по трассе, а второй бегун на 3/4 по трассе. Как далеко впереди был первый бегун? (1/8 трека).
Как далеко впереди был первый бегун? (1/8 трека).
Вычитание смешанных дробей Рабочие листы
Рабочие листы с дробями различных операций
Смешивание знаков операций с рабочими листами с дробями заставляет учащихся уделять больше внимания тому, что они делают, и позволяет хорошо проверить свои навыки в более чем одной операции.
Сложение и вычитание дробей
Умножение и деление дробей
Смешанные операции с дробями
Операции с
Отрицательными дробями
Хотя некоторые из этих листов представляют собой отдельные операции, было бы полезно иметь все они в одном месте.При выполнении операций с отрицательными дробями следует учитывать некоторые особенности. Обычно очень полезно перед тем, как продолжить, заменить любые смешанные числа на неправильную дробь. Важно обращать внимание на знаки и знать правила умножения положительных и отрицательных (++ = +, + — = -, — + = — и — = +).
Важно обращать внимание на знаки и знать правила умножения положительных и отрицательных (++ = +, + — = -, — + = — и — = +).
Порядок операций с дробями Рабочие листы
Порядок операций с листами дробей с опциями как положительных, так и отрицательных дробей различной сложности.
Порядок операций с
дробями
Как и другие рабочие листы с порядком операций, рабочие листы с порядком дроби операций требуют некоторых предварительных знаний. Если ваши ученики борются с этими вопросами, вероятно, это больше связано с их способностью работать с дробями, чем с самими вопросами. Внимательно наблюдайте и постарайтесь точно указать, каких необходимых знаний не хватает, а затем потратьте некоторое время на изучение этих концепций / навыков, прежде чем продолжить.В противном случае приведенные ниже рабочие листы должны содержать довольно простые ответы и не должны приводить к чрезмерному выпадению волос.
Порядок операций с
десятичными и смешанными дробями .
Как избавиться от минуса в уравнении
Как превратить отрицательную дробь в положительную?
Любую дробь можно умножить на аа без изменения значения, так как оно равно единице. Так, умножьте дробь на u22121u22121 очистить отрицательные знаки (или переместить их между верхним и нижним).
Аналогично, как избавиться от отрицательной дроби в уравнении?
Добавляет ли два минуса плюс? Когда у вас два отрицательных знака, один переворачивается, а они складываются вместе, чтобы сделать положительный.
Похожие страницы:
БлогКакие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
Как вычесть положительные и отрицательные дроби?
Во-вторых, 3 минуса дают плюс? Правило 3: Отрицательное число, умноженное на отрицательное, равняется положительному числу.. … Если вы посмотрите на числовую прямую, идя назад, глядя в отрицательном направлении, вы двигаетесь в положительном направлении. Например. -2 x -4 оба отрицательны, поэтому мы знаем, что ответ будет положительным.
Например. -2 x -4 оба отрицательны, поэтому мы знаем, что ответ будет положительным.
Как складывать и вычитать минусы?
тогда как складывать положительные и отрицательные целые числа?
Как складывать дроби с отрицательным числителем?
Можно ли иметь отрицательные дроби?
Дроби, как и любой другой арифметический тип, могут быть отрицательными. Конкретно, если только числитель или знаменатель отрицательные, то дробь отрицательна.
Как умножить положительные и отрицательные дроби?
0 положительное или отрицательное целое число?
Число ноль не является ни положительным, ни отрицательным. Положительные и отрицательные числа иногда называют числами со знаком. в. Положительные числа можно записывать как со знаком плюс, так и без него.
Что такое отрицательное разделить на отрицательное? Отрицательное, деленное на отрицательное, точно так же, как отрицательное, умноженное на отрицательное, вы получите положительный ответ.
Почему негативы отменяются?
После появления вы умножаете отрицательное число на положительное число, отрицательное число переворачивает знак, и ваш результат будет отрицательным числом. Однако, когда вы умножаете два отрицательных числа вместе, первое изменяет знак с положительного на отрицательное, а второе — обратно.
Однако, когда вы умножаете два отрицательных числа вместе, первое изменяет знак с положительного на отрицательное, а второе — обратно.
Как добавить минусы?
Добавление отрицательного числа то же, что вычитание положительного числа — то есть идти вниз (влево) по числовой строке. Это правило работает независимо от того, начинаете ли вы с положительного или отрицательного числа.
Почему 2 минуса дают плюс при вычитании? Вычитание числа равносильно добавлению его противоположности. Итак, вычитание положительного числа похоже на добавление отрицательного; вы двигаетесь влево по числовой прямой. Вычитание отрицательного числа похоже на добавление положительного; вы двигаетесь вправо по числовой прямой.
Каковы правила сложения и вычитания положительных и отрицательных чисел? При сложении или вычитании отрицательных чисел может быть полезно использовать числовую прямую.
- Чтобы складывать и вычитать числа, всегда начинайте отсчет с нуля.
- При сложении положительных чисел считайте вправо.

- При вычитании положительных чисел считайте влево.
Как добавить минус?
Добавление отрицательного числа является то же, что вычитание положительного числа — то есть идти вниз (влево) по числовой строке. Это правило работает независимо от того, начинаете ли вы с положительного или отрицательного числа.
Каковы правила для отрицательных и положительных чисел? Правила для положительных и отрицательных чисел
- Положительное число имеет значение больше нуля. …
- Отрицательное число имеет значение меньше нуля. …
- Сумма положительного числа и равного ему отрицательного числа равна нулю.
- Ноль не является ни положительным, ни отрицательным числом.
Какие есть отрицательные и положительные правила?
| Правило | Пример | |
|---|---|---|
| + (+) | Два подобных знака становятся положительным знаком | 3 + (+ 2) = 3 + 2 = 5 |
| — (-) | 6 — (- 3) = 6 + 3 = 9 | |
| + (-) | Два непохожих знака становятся отрицательным знаком | 7 + (- 2) = 7 — 2 = 5 |
| — (+) | 8 — (+ 2) = 8-2 = 6 |
Может ли числитель быть отрицательным? Обычно перед дробью ставится знак «минус», но иногда встречаются дроби с отрицательным числителем или знаменателем. … Если и числитель, и знаменатель отрицательны, то сама дробь положительна, потому что мы делим отрицательное на отрицательное.
… Если и числитель, и знаменатель отрицательны, то сама дробь положительна, потому что мы делим отрицательное на отрицательное.
Как сложить положительную и отрицательную смешанные дроби?
Как сложить положительные и отрицательные числа? Добавление положительных и отрицательных чисел
- Правило 1: Складывание положительных чисел с положительными числами — это обычное сложение.
- Правило 2. Прибавляя положительные числа к отрицательным числам, считайте сумму, которую вы добавляете, вперед.
- Правило 3. Прибавляя отрицательные числа к положительным числам, считайте в обратном порядке, как если бы вы вычитали.
Почему существуют отрицательные дроби?
Отрицательная дробь может указывать отсутствие удаления указанного количества. Например, добавление -1/2 пиццы будет означать удаление 1/2 этой пиццы. Так что да, дроби могут быть отрицательными.
Рациональны ли отрицательные дроби? Отрицательные дроби рациональное число — они не иррациональны. Любое число, которое может быть выражено в форме mn, где m, n — целые числа, а n ≠ 0 — рациональное число.
Любое число, которое может быть выражено в форме mn, где m, n — целые числа, а n ≠ 0 — рациональное число.
Как избавиться от минуса в дроби
Отрицательные дроби – это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:
| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус можно ставить перед дробью, перед числителем или перед знаменателем:
| — | 2 | = | -2 | = | 2 |
| 7 | 7 | -7 |
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.
| — | 2 | + (- | 1 | ) |
| 5 | 4 |
Приведём дроби к общему знаменателю:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 |
| 20 | 20 | 20 | 20 | 20 |
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 |
| 5 | 4 | 20 | 20 | 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
| — | 5 | — (- | 11 | ) = | — | 5 | + (+ | 11 | ) = | — | 5 | + | 11 | = | -5 + 11 | = | 6 |
| 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
| — | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить, сразу отбросив оба минуса:
| — | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
| — | 2 | · | 4 | = | — | 2 · 4 | = | — | 8 |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | — | 4 · 2 | = | — | 8 |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
| — | 2 | : (- | 4 | ) = | -2 | : | -4 | = | -2 · 5 | = | -10 | = | 10 |
| 3 | 5 | 3 | 5 | 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно прочитать урок «Степень» и «Свойства степеней».
Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении примеров.
Как возвести число в отрицательную степень
Чтобы возвести число в отрицательную степень нужно:
- «перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
- заменить отрицательную степень на положительную ;
- возвести число в положительную степень.
Общая формула возведения в отрицательную степень выглядит следующим образом.
,где a ≠ 0, n ∈ z ( n принадлежит целым числам).
Примеры возведения в отрицательную степень.
- 6 −2 =
Любое число в нулевой степени — единица.
Примеры возведения в нулевую степень.
Как найти
10 в минус 1 степениВ уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:
Теперь, зная определение отрицательной степени, давайте разберемся, почему « 10 » в минус первой степени равно « 0,1 ».
Возведем « 10 −1 » по правилам отрицательной степени. Перевернем « 10 » и запишем её в виде дроби «
» и заменим отрицательную степень « −1 » на
положительную степень « 1 ».
| 1 |
| 10 1 |
Возведем « 10 » в « 1 » степень. Помним, что любое число в первой степени равно самому числу.
| 1 |
| 10 1 |
Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.
| 1 |
| 10 1 |
По такому же принципу можно найти « 10 » в минус второй, третьей и т.д.
Для упрощения перевода « 10 » в минус первую, вторую и т.д степени, нужно запомнить правило:
«Количество нулей после запятой равно положительному значению степени минус один ».
Проверим правило выше для « 10 −2 ».
Т.к. у нас степень « −2 », значит, будет всего один ноль (положительное значение степени « 2 − 1 = 1 ». Сразу после запятой ставим один ноль и за ним « 1 ».
Т.к. у нас степень « −1 », значит, нулей после запятой не будет (положительное значение степени « 1 − 1 = 0 ». Сразу после запятой ставим « 1 ».
То же самое правило работает и для « 10 −12 ». При переводе в десятичную дробь будет « 12 − 1 = 11 » нулей и « 1 » в конце.
Как возвести в отрицательную степень дробь
Чтобы возвести дробь в отрицательную степень нужно:
- «перевернуть» дробь;
- заменить отрицательную степень на положительную ;
- возвести дробь в положительную степень.
Пример. Требуется возвести в отрицательную степень дробь.
) −3 =
Перевернем дробь «
» и заменим отрицательную степень « −3 » на положительную « 3 ».
(
Возведем дробь в положительную степень по правилу возведения дроби в положительную степень. Т.е. возведем и числитель « 3 », и знаменатель « 10 » в третью степень.
| 3 3 |
| 10 3 |
| 27 |
| 1000 |
Для более грамотного ответа запишем полученный результат в виде десятичной дроби.
| 3 3 |
| 10 3 |
| 27 |
| 1000 |
Как возвести отрицательное число в отрицательную степень
Как и при возведении отрицательного числа в положительную степень, в первую очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.
Отрицательное число, возведённое в чётную степень, — число положительное .
Отрицательное число, возведённое в нечётную степень, — число отрицательное .
Перевернем число « −5 » и заменим отрицательную степень « −2 »
на положительную « 2 ».
Так как степень « 2 » — четная , значит, результат возведения в степень будет положительный . Поэтому убираем знак минуса при раскрытии скобок.
Далее откроем скобки и возведем во вторую степень и числитель « 1 »,
и знаменатель « 5 ».
| 1 2 |
| 5 2 |
Как возвести отрицательную дробь в отрицательную степень
Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.
Отрицательная дробь, возведённая в чётную степень, — дробь положительная .
Отрицательная дробь, возведённая в нечётную степень, — дробь отрицательная .
Разберемся на примере. Задание: возвести отрицательную дробь « (−
По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень « −3 » на положительную « 3 ».
Теперь определим конечный знак результата возведения в « 3 » степень.
Степень « 3 » — нечетная , значит, по правилу возведения отрицательного числа в степень дробь останется отрицательной .
Нам остается только раскрыть скобки и возвести в степень и числитель « 3 », и знаменатель « 2 » в третью степень.
| 3 3 |
| 2 3 |
Для окончательного ответа выделим целую часть из дроби.
| 3 3 |
| 2 3 |
Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.
Правило возведения отрицательного числа в степень гласит: если степень четная , значит, результат возведения будет положительным .
| 11 2 |
| 9 2 |
| 121 |
| 81 |
Свойства отрицательной степени
Все свойства степени, которые используются для положительной степени, точно также применяются и для отрицательной степени.
В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени и покажем примеры их использования.
Запомните!
- a m · a n = a m + n
a m a n
Примеры решений заданий с отрицательной
степенью
Колягин 9 класс. Задание № 1
Представить в виде степени.
2) a 6 · b 6 = (ab) 6
Колягин 9 класс. Задание № 5
Записать в виде степени с отрицательным числом.
Краткое описание документа:
Почему этой теме посвящен отдельный видеоурок? Дело в том, что встречая дроби с отрицательными числами, многие ученики часто допускают ошибки, которые, впрочем, легко избежать, если рассмотреть данный метод.
Данный метод, который мы сейчас рассмотрим, основывается на том, чтобы привести дробь к удобному для нас виду, с которым мы уже ничего не напутаем.
Для начала давайте посмотрим на элементарные примеры:
1) Сколько будет «двенадцать делить на минус четыре». Конечно же «минус три».
2) А сколько будет «минус двенадцать разделить на четыре». Тоже «минус три»!
3) А если вот так: «минус. двенадцать делить на четыре»? И здесь также получим «минус три».
А теперь, если мы вспомним, что дробь — это деление, и черту дроби можно написать вместо знака деления, то получим следующее.
Ну а так как эти дроби равны одному и тому же числу, то значит они равны между собой.
А из этой записи мы видим, что совершенно неважно где стоит минус: перед чертой дроби, в числителе или знаменателе! Результат получается одинаковым.
Давайте применим теперь это знание к решению конкретного примера.
Минус одна четвертая плюс пять третьих минус три пятых минус семь вторых.
Первым шагом превратим эту запись в сложение четырех слагаемых. То есть из минусов сделаем плюсы, ведь мы знаем, что «минус а» то же, что и «плюс. минус а».
Значит «минус одна четвертая» — это «плюс минус одна четвертая» — ну здесь плюс можно не писать, так как перед плюсом ничего нет. Затем, «минус три пятых» — это «плюс. минус три пятых». И «минус семь вторых» — это «плюс. минус семь вторых».
Ну а теперь эти минусы перед знаками дробей можно убрать в числители. и тогда скобки уже будут не нужны. мы получим сложение четырех дробей с разными знаменателями.
Решить этот пример уже гораздо проще, можно не бояться запутаться в минусах.
Приводим дроби к общему знаменателю. Здесь он будет равен. шестьдесят.
Числитель и знаменатель первой дроби доумножаем на пятнадцать, второй — на двадцать, третьей — на двенадцать и четвертой — на тридцать.
Пишем общий знаменатель — шестьдесят. А в общий числитель записываем по-порядку те числа, которые у нас получатся здесь: минус пятнадцать, плюс сто, минус тридцать шесть, минус двести десять. Если бы мы не выполнили первый шаг и вот здесь у нас остались бы стоять минусы, то мы легко могли бы запутаться со знаками. А так, когда здесь только плюсы, мы просто записываем в числитель полученные числа с такими знаками, с какими мы их и получили. Если «пять умножить на двадцать» было «сто», то и пишем «плюс сто». А если «минус три» умножить на двенадцать — это «минус тридцать шесть», то так и пишем минус тридцать шесть.
А в общий числитель записываем по-порядку те числа, которые у нас получатся здесь: минус пятнадцать, плюс сто, минус тридцать шесть, минус двести десять. Если бы мы не выполнили первый шаг и вот здесь у нас остались бы стоять минусы, то мы легко могли бы запутаться со знаками. А так, когда здесь только плюсы, мы просто записываем в числитель полученные числа с такими знаками, с какими мы их и получили. Если «пять умножить на двадцать» было «сто», то и пишем «плюс сто». А если «минус три» умножить на двенадцать — это «минус тридцать шесть», то так и пишем минус тридцать шесть.
В этом и есть секрет данного метода. И какие бы сложные ни были примеры, применяя данный метод, вы никогда не запутаетесь в знаках.
Ну а здесь нам осталось посчитать числитель. Это будет минус сто шестьдесят один. Минус можно написать перед знаком дроби. Кстати, в ответе всегда лучше именно перед знаком дроби писать минус. Так принято. Ну можно еще выделить целую часть. Это будет. минус две целых сорок одна шестидесятая.
минус две целых сорок одна шестидесятая.
Итак, повторим наш метод:
«В примерах со сложением/вычитанием дробей первым шагом превращаем вычитание в сложение (для этого убираем знак «минус» в скобки). Далее переносим знак «минус» перед дробями в числители и просто выполняем сложение дробей».
Важный момент — вы должны не только запомнить это правило, но четко понимать его, чтобы успешно применять при решении примеров.
В следующем уроке мы рассмотрим очень важные замечания, о которых вам всегда нужно помнить, решая примеры с дробями.
Как решать уравнения с модулем: основные правила
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
И цель этого урока — превратить хрень в знания.:)
Немного теории
Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $\left| -5 \right|=5$. Или $\left| -129,5 \right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $\left| 5 \right|=5$; $\left| 129,5 \right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $\left| -5 \right|=\left| 5 \right|=5$; $\left| -129,5 \right|=\left| 129,5 \right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
\[\left| -a \right|=\left| a \right|\]
Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=\left| x \right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
График модуля и пример решения уравнения
Из этой картинки сразу видно, что $\left| -m \right|=\left| m \right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: $_>$ и $_>$, но об этом мы поговорим позже. 🙂
🙂
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: $_>$ и $_>$. В этом случае выражение $\left| _>-_> \right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
Модуль — это расстояние между точками на числовой прямой
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:
А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $\left| -3 \right|=3$, т. е. требуемое равенство выполняется.
е. требуемое равенство выполняется.
Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $\left| x \right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.
Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $f\left( x \right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:
\[\left| f\left( x \right) \right|=a\]
Ну и как такое решать? Напомню: $f\left( x \right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:
\[\left| 2x+1 \right|=5\]
\[\left| 10x-5 \right|=-65\]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$\left| 2x+1 \right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $\left| 2x+1 \right|=-\left( 2x+1 \right)=-2x-1$. В первом случае наше уравнение перепишется так:
В первом случае наше уравнение перепишется так:
\[\left| 2x+1 \right|=5\Rightarrow 2x+1=5\]
И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:
\[2x+1=5\Rightarrow 2x=4\Rightarrow x=2\]
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
\[\left\& \left| 2x+1 \right|=5 \\& 2x+1 \lt 0 \\\end \right.\Rightarrow -2x-1=5\Rightarrow 2x+1=-5\]
Опа! Снова всё чётко: мы предположили, что $2x+1 \lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:
\[2x+1=-5\Rightarrow 2x=-6\Rightarrow x=-3\]
Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $\left| x \right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $\left| x \right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
Пусть нам дано уравнение $\left| f\left( x \right) \right|=a$, причём $a\ge 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:
\[\left| f\left( x \right) \right|=a\Rightarrow f\left( x \right)=\pm a\]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
\[\left| 5x+4 \right|=10\Rightarrow 5x+4=\pm 10\]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
\[\begin& 5x+4=10\Rightarrow 5x=6\Rightarrow x=\frac=1,2; \\& 5x+4=-10\Rightarrow 5x=-14\Rightarrow x=-\frac=-2,8. \\\end\]
\\\end\]
Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
\[\left| 7-5x \right|=13\]
Опять раскрываем модуль с плюсом и минусом:
\[\begin& 7-5x=13\Rightarrow -5x=6\Rightarrow x=-\frac=-1,2; \\& 7-5x=-13\Rightarrow -5x=-20\Rightarrow x=4. \\\end\]
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
\[\left| 3x-2 \right|=2x\]
Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
Таким образом, сформулируем правило для произвольных функций $f\left( x \right)$ и $g\left( x \right)$ :
\[\left| f\left( x \right) \right|=g\left( x \right)\Rightarrow \left\& f\left( x \right)=\pm g\left( x \right), \\& g\left( x \right)\ge 0. \\\end \right.\]
Применительно к нашему уравнению получим:
\[\left| 3x-2 \right|=2x\Rightarrow \left\& 3x-2=\pm 2x, \\& 2x\ge 0. \\\end \right.\]
Ну, с требованием $2x\ge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.
Поэтому решим-ка само уравнение:
\[\begin& 3x-2=2\Rightarrow 3x=4\Rightarrow x=\frac; \\& 3x-2=-2\Rightarrow 3x=0\Rightarrow x=0. \\\end\]
Ну и какой их этих двух корней удовлетворяет требованию $2x\ge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=/\;$ и $x=0$. >$ за скобку и получаем очень простое уравнение:
>$ за скобку и получаем очень простое уравнение:
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x=/\;$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:
Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:
Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $\left| f\left( x \right) \right|=g\left( x \right)$ или даже более простому $\left| f\left( x \right) \right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
\[\left| f\left( x \right) \right|=\left| g\left( x \right) \right|\]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
Вот формула:
\[\left| f\left( x \right) \right|=\left| g\left( x \right) \right|\Rightarrow f\left( x \right)=\pm g\left( x \right)\]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
\[\left| 2x+3 \right|=\left| 2x-7 \right|\]
Элементарно, Ватсон! Раскрываем модули:
\[\left| 2x+3 \right|=\left| 2x-7 \right|\Rightarrow 2x+3=\pm \left( 2x-7 \right)\]
Рассмотрим отдельно каждый случай:
\[\begin& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\left( 2x-7 \right)\Rightarrow 2x+3=-2x+7. \\\end\]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
\[2x+3=-2x+7\Rightarrow 4x=4\Rightarrow x=1\]
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
Опять у нас уравнение вида $\left| f\left( x \right) \right|=\left| g\left( x \right) \right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми. >-3x+2 \right|; \\& \left| x-1 \right|=\left| \left( x-1 \right)\left( x-2 \right) \right|. \\\end\]
>-3x+2 \right|; \\& \left| x-1 \right|=\left| \left( x-1 \right)\left( x-2 \right) \right|. \\\end\]
Одно из свойств модуля: $\left| a\cdot b \right|=\left| a \right|\cdot \left| b \right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
\[\left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|\]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
\[\begin& \left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|; \\& \left| x-1 \right|-\left| x-1 \right|\cdot \left| x-2 \right|=0; \\& \left| x-1 \right|\cdot \left( 1-\left| x-2 \right| \right)=0. \\\end\]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
\[\left[ \begin& \left| x-1 \right|=0, \\& \left| x-2 \right|=1. \\\end \right.\]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю. >+x-2=0\Rightarrow \left( x+2 \right)\left( x-1 \right)=0\Rightarrow \left[ \begin& x=-2 \\& x=1 \\\end \right.\]
>+x-2=0\Rightarrow \left( x+2 \right)\left( x-1 \right)=0\Rightarrow \left[ \begin& x=-2 \\& x=1 \\\end \right.\]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
\[\left| 3x-5 \right|=5-3x\]
В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $\left| f\left( x \right) \right|=g\left( x \right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 \gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:
\[3x-5 \gt 0\Rightarrow \left| 3x-5 \right|=3x-5\]
Таким образом, наше уравнение превратится в линейное, которое легко решается:
\[3x-5=5-3x\Rightarrow 6x=10\Rightarrow x=\frac\]
Правда, все эти размышления имеют смысл только при условии $3x-5 \gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=\frac$ в это условие и проверим:
Поэтому давайте подставим найденный $x=\frac$ в это условие и проверим:
\[x=\frac\Rightarrow 3x-5=3\cdot \frac-5=5-5=0\]
Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(
Но ничего страшного! Ведь есть ещё вариант $3x-5 \lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 \lt 0$:
\[3x-5 \lt 0\Rightarrow \left| 3x-5 \right|=5-3x\]
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!
А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:
Вместе с тем у нас есть ограничение:
\[3x-5 \lt 0\Rightarrow 3x \lt 5\Rightarrow x \lt \frac\]
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
\[x\in \left( -\infty ;\frac \right)\]
Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):
\[3x-5=0\Rightarrow \left| 3x-5 \right|=0\]
Но тогда исходное уравнение $\left| 3x-5 \right|=5-3x$ перепишется следующим образом:
\[0=3x-5\Rightarrow 3x=5\Rightarrow x=\frac\]
Этот корень мы уже получали выше, когда рассматривали случай $3x-5 \gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
Объединение корней в уравнениях с модулем
Итого окончательный ответ: $x\in \left( -\infty ;\frac \right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:
- Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
- Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
- Решить исходное уравнение для каждого интервала и объединить полученные ответы.
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:
Разбиение числовой оси на интервалы с помощью точек
Ну и какие тут интервалы? Понятно, что их три:
- Самый левый: $x \lt 1$ — сама единица в интервал не входит;
- Центральный: $1\le x \lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
- Самый правый: $x\ge 5$ — пятёрка входит только сюда!
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)
как избавиться от минуса в степени
Вы искали как избавиться от минуса в степени? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как избавиться от отрицательной степени, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как избавиться от минуса в степени».
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как избавиться от минуса в степени».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как как избавиться от минуса в степени,как избавиться от отрицательной степени. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и как избавиться от минуса в степени. Просто введите задачу в окошко и нажмите «решить» здесь (например, как избавиться от минуса в степени).
Где можно решить любую задачу по математике, а так же как избавиться от минуса в степени Онлайн?
Решить задачу как избавиться от минуса в степени вы можете на нашем сайте https://pocketteacher. ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
pH-баланс — лучшее средство для детоксикации организма и поддержания правильного кислотно-щелочного баланса
Мы часто встречаем фразу «кислотно-щелочной баланс», но не все догадываются, что это такое и зачем он нужен. Давайте попробуем разобраться, что это такое и насколько важен кислотно-щелочной баланс для организма.
Тело человека на 70-80% состоит из воды, и имеет определенное кислотно-щелочное соотношение, характеризуемое показателем pH. От уровня кислотности зависят все биохимические процессы в организме, а это значит, что любой сбор и отклонение от нормы станет причиной того или иного заболевания.
От уровня кислотности зависят все биохимические процессы в организме, а это значит, что любой сбор и отклонение от нормы станет причиной того или иного заболевания.
Чтобы понять, какие показатели должны быть в норме, проанализируем кислотность крови.
Кислотно-щелочное равновесие в крови человека является одним из самых стабильных параметров, поддерживающее кислые и щелочные компоненты в определенном равновесии в очень узких границах.
Кислотность жидкостей внутри человеческого организма в норме совпадает с кислотностью крови и находится в пределах от 7,35 до 7,45 pH.
Даже небольшой сдвиг от указанных пределов может привести к тяжелой патологии. При сдвиге в кислотную сторону возникает состояние, называемое ацидозом, в щелочную — алколозом. Изменение кислотности крови выше 7,8 рН или ниже 6,8 рН несовместимо с жизнью. Кислотность эритроцитов составляет 7,28–7,29 рН.
Организм постоянно стремится уравновесить это соотношение, поддерживая строго определенный уровень pH.
Что вызывает нарушение кислотно-щелочного баланса?
Главная причина закисления организма — неправильное питание. Мы привыкли оценивать пищу с позиций калорийности, содержания белков, углеводов, жиров, витаминов и других веществ. Но любой продукт имеет еще один фундаментальный показатель — кислотную нагрузку пищи.
Кислотная нагрузка измеряется по принципу кислота минус щелочь.
Когда в пище преобладают компоненты, образующие серную кислоту (серосодержащие аминокислоты в белках) или органические кислоты (жиры, углеводы), то кислотная нагрузка имеет положительную величину.
Если в пище больше компонентов, образующих щелочь (органические соли магния, кальция, калия), то кислотная нагрузка представляет собой отрицательную величину.
|
Кислотная нагрузка основных компонентов питания |
|||
| Продукт |
Компоненты |
Кислотная нагрузка | |
| Кислота | Щелочь | ||
|
Кислые продукты |
|||
| Мясо | 77,7 | 9,8 | 67,9 |
| Зерновые | 8,0 | -5,8 | 13,8 |
| Сыр | 2,8 | -1,4 | 4,2 |
| Молоко и йогурт | 5,7 | 2,9 | 2,8 |
| Яйца | 1,8 | -0,7 | 2,5 |
|
Нейтральные продукты |
|||
| Бобовые | 0,9 | 1,7 | -0,8 |
| Орехи | 1,3 | 1,2 | 0,1 |
|
Щелочные продукты |
|||
| Листовая зелень | 32,9 | 92,0 | -59,1 |
| Овощи-фрукты | 21,3 | 67,8 | -46,5 |
| Коренья | 10,1 | 36,5 | -26,4 |
| Овощи | 6,8 | 21,1 | -14,3 |
| Клубни | 4,5 | 15,1 | -10,6 |
| Фрукты | 2,1 | 7,9 | -5,8 |
Большая часть принимаемой нами пищи содержит множество кислот, что приводит к низкому уровню pH. Фаст-фуд, кофе, чай, сахар, лекарства и алкоголь являются основными факторами, способствующими снижению pH.
Фаст-фуд, кофе, чай, сахар, лекарства и алкоголь являются основными факторами, способствующими снижению pH.
Когда в организме снижается уровень pH, он начинает использовать резервную компенсационную систему с помощью почек и легких. Чтобы компенсировать низкий уровень pH, организм начинает поглощать кальций из костей, что приводит к остеопорозу.
Нарушение кислотно-щелочного баланса также могут вызвать :
— Психосоматические проблемы, такие как возбуждение, беспокойство и стресс. Мышечное напряжение, затрудненное дыхание приводят к плохому газообмену и поглощению кислорода альвеолами/легкими. В результате клетки всего организма получают меньше энергии и питательных веществ. Чем больше питательных веществ вы получите в результате хорошего газообмена в легких, тем лучше будет функционирование и питание всех клеток организма. Таким образом, органы и клетки будут легче избавляться от токсинов, снижая вероятность неоптимального pH.
— Частое употребление лекарственных препаратов и алкоголя могут вызвать окисление при несбалансированном pH.
Прием алкоголя и одновременный прием нескольких лекарственных препаратов могут причинить вред почкам и печени. Компоненты алкоголя превращаются в кислоту. Алкоголь всасывается в желудке и тонком кишечнике, в результате чего в желудке сразу же начинается фаза деградации с участием ферментов (ADH). Основная фаза деградации происходит после того, как алкоголь абсорбируется в плазме, и в печени начинается расщепление ферментов. Окисление происходит, главным образом, за счет фермента ADH (алкогольдегидрогеназа), который превращает этанол в ацетальдегид. Затем ацетальдегид превращается в уксусную кислоту с помощью фермента ALDH (ацетальдегиддегидрогеназы). 95% алкоголя, поступающего в организм, расщепляется в печени. Из оставшегося количества алкоголя около 2% выводится с мочой, около 2% — с выдыхаемым воздухом и около 1% — с потом.
На данном этапе организм ослабевает и окисляется до такой степени, что может нарушиться естественный процесс очищения. Поэтому накопление загрязненных биологических жидкостей может быть фактором, а затем и причиной слишком высокой кислотности и дисбаланса щелочности (pH).
Поэтому накопление загрязненных биологических жидкостей может быть фактором, а затем и причиной слишком высокой кислотности и дисбаланса щелочности (pH).
Низкий уровень pH становится причиной серьезных заболеваний. Поэтому прием препарата, балансирующего уровень pH просто необходим в качестве биодобавки к нашему ежедневному рациону.
Как регулировать кислотно-щелочной баланс?
Основным свойством продуктов, регулирующих кислотно-щелочной баланс, должна быть их способность активировать фазу электролита (биологические жидкости) и осмотическое давление, которое естественным образом присутствует в клеточной мембране. Организм зависит от наличия осмотического давления в водном обмене, что обеспечивает способность отделять токсины без потери жидкости. Примером дисбаланса в электролитном балансе и осмотическом давлении являются процессы в тонком кишечнике. Если у вас диарея без особых причин и вы не можете удерживать жидкости, это означает, что у вас произошел дисбаланс осмотического давления в кишечнике. Данный процесс регулируется с помощью добавки натрия, который восстанавливает давление в клеточной мембране.
Данный процесс регулируется с помощью добавки натрия, который восстанавливает давление в клеточной мембране.
В линейке продуктов NFO появился препарат NFO pH-Баланс, помогающий регулировать кислотность. NFO pH-Баланс — это порошок, содержащий ценные для организма вещества — кальций, магний, цинк и витамин С.
Благодаря своему положительному эффекту NFO pH-Баланс подходит абсолютно всем людям. Именно это делает продукт таким уникальным.
С помощью NFO pH-Баланс можно восстановить и активировать щелочной и осмотический баланс в организме, чтобы инициировать процессы очистки от токсинов. Используя NFO pH-Баланс во время и после употребления алкоголя, вы снижаете риск смещения кислотно-щелочного баланса в сторону окисления. Следовательно, продукт помогает организму восстановиться после употребления лекарств и алкоголя.
Мы рекомендуем принимать NFO pH-Баланс в качестве антипохмельного средства, так как он наилучшим образом сочетает все необходимые для этого компоненты. Даже большое количество выпитого алкоголя NFO pH-Баланс сможет «сгладить», правильно действуя на организм и снижая высокую кислотность после употребления спиртного.
Даже большое количество выпитого алкоголя NFO pH-Баланс сможет «сгладить», правильно действуя на организм и снижая высокую кислотность после употребления спиртного.
В результате приема устраняются симптомы, характерные для абстинентного синдрома: головная боль, раздражающие ощущения в подложечной области, головокружение, озноб, жажда, сухость во рту, неприятный запах при разговоре и дыхании. NFO pH-Баланс является не только противопохмельным средством, он также обладает антигипоксическим и антиоксидантным воздействием, активизирует работу органов и тканей, нормализует обмен веществ, оказывает положительное влияние на когнитивную и мышечную активность.
Для предупреждения алкогольного отравления нужно принять 1 дозу за 1 час до начала застолья, 1 дозу во время и 1 дозу после принятия алкоголя.
В составе NFO pH-Баланс есть аскорбиновая кислота. Этот компонент применяется для того, чтобы создать баланс между кислотой и щелочью. Такая комбинация кислотных и щелочных компонентов в одном продукте обеспечивает прямой контроль электролитов (баланс жидкости).
Ежедневный прием препарата NFO pH-Баланс предотвращает такие симптомы, как отек, скованность в суставах, общий отек, повышенное содержание мочевой кислоты, проблемы с газами и боль в спине.
NFO pH-Баланс является комплексным продуктом для детоксикации организма. Он также оказывает контролирующее воздействие на гистамин.
В каких случаях прием NFO pH-Баланс необходим:
— для детоксикации организма
— при употреблении вредной пищи
— при использовании лекарств
— при употреблении алкоголя
— для устранения проблем с желудком и толстой кишкой
— для выведения мочевой кислоты
— для выведения жидкости из суставов
— для выведения излишней жидкости
— для получения дополнительной энергии, очистки печени и почек
— для профилактики диареи
— для укрепления иммунной системы
— для очистки кожи
— для интенсификации подачи кислорода клеткам
— для лечения всех заболеваний, вызванных грибком Candida
— для снижения уровня кислотности и стабилизации уровня щелочности
Как правильно принимать pH-NFO Баланс:
— для профилактики — 2 дозы в день
— с лечебной целью — 4–5 доз в день
— в случае употребления алкоголя — до, во время и после употребления (в дополнение к профилактическому применению)
— для детоксикации организма — 4–5 доз ежедневно в течение 2 месяцев, перерыв 2 недели, затем снова начать профилактическое применение
— для обеспечения максимального эффекта других добавок NFO рН-Баланс следует принимать в минимальной профилактической дозе.
ВАЖНАЯ ИНФОРМАЦИЯ: НЕ перемешивайте продукт какими-либо изделиями из металла.
Работа с нулевыми и отрицательными показателями: полное руководство
- Что такое показатель степени?
- Что такое нулевые и отрицательные показатели?
- Нулевые показатели
- Отрицательные показатели
- Нулевые и отрицательные экспоненты с примерами
- Решение с нулевыми показателями
- Решение с отрицательными показателями
- Какая польза от нуля и отрицательных показателей?
- Измерения и расчеты
- Упрощение
- Формулы
- Правило нулевой степени
- Правило отрицательного экспонента
- Резюме
Работа с экспоненциальными выражениями — неизбежный этап ваших курсов алгебры, поскольку они используются в уравнениях и других приложениях.
Что такое экспонент?
Показатель степени — это количество раз, которое базовое число будет умножено само на себя. Это может быть любое число, которое может быть классифицировано как отрицательная экспонента, нулевая экспонента или положительная экспонента.
Это может быть любое число, которое может быть классифицировано как отрицательная экспонента, нулевая экспонента или положительная экспонента.
Экспоненты, начинающиеся с 1, называются положительными экспонентами и являются наиболее распространенными — вы, вероятно, часто сталкивались с ними.
Что такое нулевые и отрицательные показатели?
Нулевые и отрицательные показатели являются особыми случаями показателей.
Например, :
2 3 то же самое, что 2 x 2 x 2, повторное умножение приводит к окончательному ответу 8: 2 x 2 x 2 = (2 x 2) x 2 = 4 x 2 = 8.
Однако с нулевыми и отрицательными показателями дела обстоят не так просто.
Нулевой показатель степени
Это показатель степени, который всегда и автоматически приравнивает любое базовое число к 1. Проще говоря, каким бы ни было основное число, пока оно возведено в нулевую степень, оно всегда будет равно 1. Все не имеет значения, независимо от того, как большое значение числа или является ли оно положительным числом или отрицательным основанием.
Например:
Будь то 3 0 или 300 000 000 0 , ответ все равно будет 1.
Отрицательные показатели степени
С другой стороны, возводя числа в отрицательную степень, вы перемещаете позицию базового числа с показателем степени, чтобы удалить отрицательный знак и сделать его положительным. Другими словами, вы отвечаете взаимностью на данное и делаете показатель степени положительным. Результат всегда будет дробью.
Например:
2 -4 = (1/2) x (1/2) x (1/2) x (1/2) = 1/16
или 2 -4 = 1 /(24) = 1/(2 x 2 x 2 x 2) = 1/16
Если отрицательные степени находятся в верхней части дроби или представляют собой целое число, перемещение основания числа с показателями в нижнюю часть дробь сделает показатель степени положительным. Другими словами, когда любое число больше 1 возводится в отрицательную степень, оно может быть положительным, если вы поместите его в знаменатель с 1 в числителе.
Другой пример:
10 -1 = 1/10 1
Нулевые и отрицательные показатели объясняются примерами
Описания и обзоры нулевых и отрицательных показателей были рассмотрены в предыдущем разделе. Теперь мы рассмотрим и обсудим, как их решить.
Теперь мы рассмотрим и обсудим, как их решить.
Решение с нулевыми показателями
При работе с нулевыми показателями проще всего объяснить это с помощью правила отношения степеней. Вспоминая ваши первые пять правил экспоненты:
(x /y) 5 = (x 5 ) /(Y 5 ) или (x 2 /y 3 ) 3 = x 6 /y = x 6 /y
= x 6 /y 41 = x 6 /y 41 = x 6 /y .- Правило произведения степеней или правило произведения – умножение двух основных чисел одного и того же значения может быть упрощено до одного и того же основного числа. Затем добавьте показатели степени основных чисел: 7 2 x 7 5 = 7 2+5 = 7 7
- Правило отношения сил или правило отношения — деление двух оснований с одинаковым значением может быть упрощено до одного и того же основания.
 Затем вычтите его показатели: (13 4 )/(13 1 ) = 13 4-1 = 13 3
Затем вычтите его показатели: (13 4 )/(13 1 ) = 13 4-1 = 13 3 - Степень Степени Правило — при возведении степени в другую степень показатели степени умножаются, а общее основание сохраняется: (x 2 ) 3 = x 2×3 = x 6
- Сила произведения Правило — когда основание в скобках xy возводится в степень, показатель степени распределяется на каждую часть основания: (xy) 4 = (х 4 ) х (у 4 )
- Сила частного правила — это работает так же, как мощность правила произведения; показатель степени распределяется как на делимое, так и на делитель:
Правило нулевой степени
Теперь, чтобы полностью объяснить, почему число, возведенное в нулевую степень, всегда равно 1, мы можем использовать правило отношения степеней. Согласно правилу частных, деление одних и тех же оснований приведет к одному и тому же основанию и показателю разности верхнего и нижнего показателей.
Например: Объяснение 7 0 = 1:
7 0 может состоять из 7 2 деленного на 7 2 .
7 2 /7 2 = ?
Следуя правилу частных, вычтите степени друг из друга. В этом случае показатели степени будут сокращены, так как они имеют одинаковое значение: 2.
7 2 / 7 2 = 7 (2-2) = 1 или
7 ( 2-2) = 7 0 = 1
Кроме того, не имеет значения, насколько длинное уравнение. Любое уравнение, возведенное в ноль, пока оно заключено в круглые скобки, всегда будет равно 1.
Например:
(5x 4 y 5 ) 0 = (5 0 x 0 y 0 ) = 1
Решение с отрицательными показателями
С отрицательными показателями на первый взгляд сложно работать, но на самом деле это не так. Помните, что результат всегда будет дробью, а процесс всегда будет взаимностью данного. Вспоминая, как сделать число обратным:
Вспоминая, как сделать число обратным:
- Сделайте из числа дробь или поставьте над единицей.
- Переставить число в числителе в знаменатель и наоборот.
- При изменении положения отрицательного числа в дроби оно становится положительным, даже если оно является показателем степени.
Правило отрицательного показателя
Помните, что: (x -2 )/(y -3 ) = y 3 /x 2
1
1 Как?
(х -2 )/(у -3 ) = (1/(x 2 ))/(1/(y 3 ))
= (1/(x 2 )) x ((y 3 )/1 )
= y 3 /x 2
Таким образом, отрицательные показатели в знаменателе переходят в числитель, а отрицательные показатели в числителе переходят в знаменатель.
Применим это к примеру с отрицательным показателем:
Случай 1 , когда дано изначально не дробь.
х -3 = ? 93
Случай 2 , когда дан дробь с отрицательным показателем в знаменателе.
1 / х -4 = ? -> возвратно-поступательный,
1/ x -4 => x 4
Какая польза от нулевых и отрицательных показателей?
Экспоненты, как правило, имеют множество применений и применений в реальной жизни. Два использования нулевого и отрицательного показателей степени:
Измерения и расчеты
Два показателя степени используются для представления длин. Отрицательная экспонента, в частности, используется для выражения атрибуции чего-либо и демонстрации того, насколько что-то мало.
Например, отрицательные показатели степени используются для представления различных размеров мелких существ, таких как летучие мыши. Зоологи используют отрицательные показатели для измерения частей тела.
Измерение может отображаться как 1,08x 10-4 см: это делается, когда имеется слишком много знаков после запятой из-за небольшого размера измерения; поэтому для удобства цифра сокращена с использованием отрицательных показателей.
Точно так же эти показатели степени можно использовать для весов. Более легкие веса обычно выражаются с отрицательными показателями для простоты и облегчения вычислений.
Другим примером является «Экспоненциальное затухание», используемое в графиках и представлениях. Отрицательные показатели степени приводят к меньшим значениям и, следовательно, показывают «распад» на графике по мере того, как данные падают или уменьшаются в соответствии с выражением.
Упрощение
Нулевые и отрицательные показатели степени обычно используются для упрощения чисел и значений для более удобного использования и упрощения ввода в реальных приложениях. Как и в приведенных выше примерах, они используются для упрощения значений различных измерений для удобства.
Расчеты в различных профессиях, особенно в различных областях науки, используют отрицательные показатели степени, так как большинство измерений, как правило, слишком малы, чтобы их можно было использовать в исходном виде, со слишком большим количеством десятичных знаков.
Отрицательные показатели используются для упрощения измерений и наглядно показывают, насколько они малы. Большие отрицательные показатели означают меньшие измерения.
Нулевые показатели работают так же, как они используются во многих математических уравнениях, чтобы представить, что независимо от того, насколько велико число, пока оно возведено в нулевую степень, оно равно значению 1. 9-2 = 1/a 2
(a x ) -2 = 1/(a x ) 2 or 1/ a 2 x 2
Корпус 2 :
1/( A -3 ) = A 3/1 или просто A 3
1/( A 4). ) = ( a x) 4/1 или a 4 x 4
Резюме
Подводя итог, любое число, возведенное в нулевую степень, всегда будет равно 1. Напротив, любое число, возведенное в отрицательную степень, будет преобразовано в положительное, прежде чем приступить к решению окончательного значения.
Также важно помнить понятия о других правилах экспоненты и об обратных величинах, чтобы правильно обрабатывать уравнения с нулевыми и отрицательными экспонентами.
Эти показатели степени в основном используются для уравнений, расчетов и измерений в различных областях знаний и профессии, таких как математические уравнения, научные обозначения и расчеты, а также очень маленькие измерения или значения.
Вы можете попробовать решить сложную и запутанную таблицу об этих показателях с помощью Mathway или других программ-решателей.
Чувствуете, что вам нужна помощь в работе с нулевыми и отрицательными показателями? Вы можете положиться на экспертов Studybay. Мы предоставляем онлайн-репетиторство и письменные услуги для студентов.
Studybay помогает учащимся:
- домашнее задание по математике
- домашнее задание по математике
- задания по разным предметам
Упрощение выражений с отрицательными показателями | Преалгебра |
Результаты обучения
- Использование свойств показателей для упрощения произведений и частных, содержащих отрицательные показатели и переменные
Все свойства экспоненты, которые мы разработали ранее в этой главе для целочисленных экспонент, применимы и к целочисленным экспонентам. Мы повторяем их здесь для справки.
Мы повторяем их здесь для справки.
Сводка свойств экспоненты
Если 9949
попробуй
В следующем видео мы поделимся другими примерами упрощения частного с отрицательными показателями.
Лицензии и атрибуты
Лицензионный контент CC, совместно используемый ранее
- Упрощение произведения выражений с отрицательными показателями (2 метода). Автор : Джеймс Соуза (mathispower4u.com). Лицензия : CC BY: Атрибуция
- Пример 2: Упрощение экспоненциальных выражений с отрицательными показателями — базовый. Автор : Джеймс Соуза (mathispower4u.com). Лицензия : CC BY: Атрибуция
Лицензионный контент CC, Конкретная атрибуция
- Преалгебра.
 Предоставлено : OpenStax. Лицензия : CC BY: Attribution . Условия лицензии.0041
Предоставлено : OpenStax. Лицензия : CC BY: Attribution . Условия лицензии.0041- Что такое экспонента?
- Как устранить Экспоненты.
См. также : Степенное правило
Посмотрите видео с парой примеров того, как исключать экспоненты с помощью логарифмов:
Исключать экспоненты с помощью логарифмов
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Показатель степени — это упрощенный способ сказать, сколько раз нужно умножать число само на себя. При работе с показателями нам нужно знать, какое число представляет 9.0958 базовое число и показатель степени .
- Базовое число — это число, которое умножается само на себя. Обычно пишется более крупным шрифтом.
- Показатель степени говорит нам, сколько раз нужно умножить базовое число само на себя.
 Обычно пишется более мелким шрифтом (в виде надстрочного индекса).
Обычно пишется более мелким шрифтом (в виде надстрочного индекса).
Оба представлены в следующем примере:
Как показано выше, 4 — это основное число. Показатель степени равен 3. Это говорит вам о том, что вы будете умножать 4 само на себя три раза [4 x 4 x 4]. Сначала умножьте 4 x 4, чтобы получить 16. Затем умножьте это число на 4 [16 x 4 = 64]. Следовательно, 4 3 равно 64.
Из этого примера можно сделать два важных замечания. Во-первых, обратите внимание, насколько проще использовать показатель степени, чем записывать умножение в полной форме. Вы можете себе представить, имея дело с гораздо большими показателями, насколько сложно это будет записать. Во-вторых, по мере увеличения показателя степени основание будет увеличиваться экспоненциально. Нет предела тому, сколько раз число может быть умножено само на себя.
Где показатель степени равен 1 или 0
Когда вы видите, что показатель степени равен 1, тогда ответом будет само число (другой способ думать об этом состоит в том, что любое число, умноженное на 1, остается прежним).

Когда вы видите, что показатель степени равен 0, тогда ответ будет равен 1, независимо от того, каково значение основного числа.
Отрицательный показатель степени
Отрицательный показатель степени говорит вам разделить число 1 на основание числа. Простой способ запомнить это состоит в том, что отрицание противоположно положительному, а деление противоположно умножению. Рассмотрим пример:
8 -4
Запись 8 в минус 4 число степень: 1/8/8/8/8
- Разделите 1 на 8, что равно 0,125
- Затем разделите 0,125 на 8, что равно 0,015625
- Разделите 0,015625 на 8, что равно 0,001953125
- Наконец, разделите 0,001953125 на 8, чтобы получить 0,0002441406
Экспоненты могут быть сложным фактором при работе с уравнениями, а когда в экспонентах есть переменные, это становится еще сложнее. можно исключить некоторые показатели степени с помощью правила степени, но это не сработает для показателей степени больше 2.
 Другой способ исключить показатели степени — преобразовать показатели степени в более удобную форму с помощью функции логарифмирования .
Другой способ исключить показатели степени — преобразовать показатели степени в более удобную форму с помощью функции логарифмирования . График общего лог.
Если вы не знакомы с логарифмами, вы можете прочитать определение логарифмов, прежде чем читать дальше. По сути, логарифмы — это просто показатель степени в другой форме, поэтому вы можете использовать их для исключения показателей степени. Например, запись 10 100 = 2 совпадает с 10 2 = 100. В более общем смысле это: появляются в форме ln(x), которая представляет собой логарифм, приведенный к основанию натурального числа e.
Как устранить экспоненты в исчислении: Пример
Пример задачи: Найдите значение x, если 10 в 5-кратной степени плюс 10 равно 20.
Шаг 1: Составьте уравнение из информации, указанной в вопросе.
10 5x + 10 = 20Шаг 2: Возьмите 10 с обеих сторон , чтобы исключить 10 рядом с переменной.
 Это базовый шаг алгебры, но все же важный.
Это базовый шаг алгебры, но все же важный.
10 5x + 10 – 10 = 20 – 10
получается:
10 5x = 10Шаг 3: Возьмите бревно с обеих сторон.
log(10 5x ) = log(10)Шаг 4: Примените правило логарифмирования, которое гласит log_b(a c ) = c * log_b(a). 1
Используя это, мы можем убрать переменную из экспоненты и оставить ее в форме, которую можно упростить. Если вы помните, что журнал без нижнего индекса считается основанием 10, вы можете легко упростить log_10(10) = y как 1, поскольку b y = x равно 10 1 = 10.
5x * 1 = 1Шаг 5: Разделите обе части на 5, чтобы изолировать переменную. Это даст вам окончательный ответ 1/5 или 0,2.
5x/5 = 1/5 -> x = 1/5 = 0,2Примечания
1 : Если вам нужно освежить в памяти правила ведения журналов, см. раздел Предварительные требования к математике — прокрутите вниз до 5.
 Экспоненты и логарифмы .
Экспоненты и логарифмы .Ссылки
Архив курсов Йоркского университета. Математические предпосылки. Получено 1 января 2019 г. с: https://www.eecs.yorku.ca/course_archive/2011-12/W/3101/prereq.pdf
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Устранение экспонентов: как сделать» из CalculusHowTo.com : Исчисление для всех нас! https://www.calculushowto.com/calculus-problem-solving/eliminate-exponents/————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
ИсчислениеHowTo.com
[7 законов]Как избавиться от экспонентов |Объяснение усиления концепции|
Вас беспокоит решение показательных выражений? Это действительно не так сложно, как вы думаете.
Знакомство с экспонентами/www.moconi.com Это может сбить вас с толку или разозлить, когда вы впервые сталкиваетесь с их решением. Но уверяю вас, будет очень интересно научиться избавляться от показателей. Просто останься со мной.
Это может сбить вас с толку или разозлить, когда вы впервые сталкиваетесь с их решением. Но уверяю вас, будет очень интересно научиться избавляться от показателей. Просто останься со мной.Я думаю, что очень важно познакомить вас с экспонентами, чтобы составить четкое представление об экспонентах. Экспоненты/индексы — это многократное умножение числа. Например, 90 = 1)
Рассмотрим другой пример
Нулевые свойства показателей степениНеважно, что такое База, при получении индекса ‘o она становится равной 1.
Нулевое свойство показателей степениКак получить Избавиться от отрицательных показателей?
Отрицательные показатели степени означают, что индекс числа, отличного от нуля, является отрицательным. Обычно, когда студенты сталкиваются с отрицательным показателем, они беспокоятся и думают, как избавиться от отрицательных показателей. Я собираюсь показать вам от простого отрицательного показателя до решения сложного отрицательного показателя степени.
 92, что равно 1/4.
92, что равно 1/4. Это означает, что вы избавляетесь от отрицательных показателей, меняя их положение в дроби. Давайте посмотрим на другие примеры, чтобы прояснить концепцию.
(2) Пример:
Простое отрицательное выражение(3) Посмотрите другие примеры,
Использование отрицательного свойства(4) Пример: В случае сложного выражения вы решите его таким образом.
Вычисление отрицательных показателей степениЯ надеюсь, что эти примеры прояснили вашу концепцию. Теперь вам будет легко понять, как избавиться от отрицательных показателей.
Как решить свойство произведения показателей?
Также очень легко решать такие ненулевые числа, которые имеют показатели степени и перемножаются друг с другом. Согласно Lw показателей свойств продукта, при умножении двух оснований их показатели складываются. Давайте рассмотрим несколько простых и сложных примеров, чтобы понять смысл.
(1) Пример: (Примечание. Действительно, когда основания одинаковые.
Правило произведения )
) (2) Пример:
Простое вычислениеЕсли показатели степени одинаковы, но основания разные, то основания умножаются, а показатель степени остается прежним. Сложная форма будет решаться следующим образом:
(3) Пример:
Сложная форма правила произведенияВот как можно избавиться от показателей степени в свойстве произведения.
Людей интересует: Как починить взломанный телефон Android? 5 проверенных решений в 2020 году
Как решить частное свойство экспоненты?
Когда вы умножаете две степени с одинаковым основанием, вы складываете степени, а когда вы делите две степени с одним и тем же основанием, вы вычитаете степени,
(1) Пример:
Частное свойство показателей степени(2) Пример:
Деление показателей степениВот как просто избавиться от показателей степени в частном в виде частного.
Как решить показатель степени степени свойства?
Если экспоненциальное выражение имеет степень, обе степени умножаются для упрощения оператора.
 Давайте взглянем на некоторые примеры.
Давайте взглянем на некоторые примеры.(1) Пример:
Мощность решения мощности(2) Пример:
Решение мощности мощности(3) Пример:
Свойство мощности мощностиТак можно избавиться от показателей степени в свойстве мощности мощности.
Как решить мощность продукта Свойство экспоненты?
Если в скобках указано более одного члена с показателем степени вне скобок, то показатель степени умножается на каждый член в скобках. Вот несколько примеров, чтобы было понятно.
(1) Пример:
Мощность произведениямощность распределяется между каждым термином в скобках.
(2) Пример:
Свойство произведения показателей степениНадеюсь, вам понравилось узнавать, как избавиться от показателей степени по отношению к различным свойствам показателей степени.
(3) Пример:
Правило мощности произведенияКак решить мощность частного свойства экспонент?
Чтобы решить свойство Степень частного, Сила распределяется между каждым термином в скобках.
 См. несколько примеров для пояснения.
См. несколько примеров для пояснения.(1) Пример:
Свойство деления показателей степениЭто самый простой способ научиться избавляться от показателей степени, когда выражение является степенью частного.
Теперь я собираюсь познакомить вас с некоторыми тревожными формами экспоненциальных выражений. Я рекомендую вам, студенты, просто пройти глубокое руководство и попробовать один раз, прежде чем бросить.
Как избавиться от экспонент в алгебре?
Когда вы переходите от решения простых экспоненциальных выражений к решениям алгебраических экспоненциальных выражений, вы можете запутаться. Но не волнуйтесь, студенты, основная цель этой статьи — устранить эту путаницу и упростить для вас решение экспоненты. Здесь вы познакомитесь с различными типами алгебраических уравнений, которые больше всего запутывают.
Отрицательные показатели в алгебраическом уравнении
Легче, чем вы думаете, научиться избавляться от показателей с отрицательным знаком в уравнении.
Equation with negative exponents
Another example is
A Negative equationA simple equation is like this
And one form is like this
Look at another type
Another type is
A дробный случай решается таким образом
Вот как избавиться от показателей степени в дробях.
Получение эксперта по математике — это практика. Чем больше вы практикуетесь, тем больше вам будет легко и интересно. Однако, если вы считаете, что вам нужно больше практики, вы должны посмотреть это видео.
Заключительные слова:
Надеюсь, эта статья окажется для вас очень полезной, даже если вы совершенно незнакомы с показателями.
 Прочитав это объяснение, вы будете знать, как избавиться от экспонент. Вы будете чувствовать себя уверенно, решая как простые, так и сложные экспоненциальные выражения. Превратите изучение математики в радость
Прочитав это объяснение, вы будете знать, как избавиться от экспонент. Вы будете чувствовать себя уверенно, решая как простые, так и сложные экспоненциальные выражения. Превратите изучение математики в радостьКак решать отрицательные многочлены
Многочлен — это математическое выражение, состоящее из переменных и коэффициентов. Единственными операциями, которые используются с многочленами, являются сложение, вычитание, положительные целые показатели степени и умножение. Вы не можете возводить переменные в многочлене в иррациональные степени, комплексные степени, квадратные корни и т. д.
Как выглядит многочлен? Простой пример:
6×7 + 23×3 – 7
Этот пример представляет собой многочлен с одной переменной, поскольку единственная переменная в выражении – 9.0053 х.
Несмотря на то, что полиномы исключают отрицательные члены, бывают случаи, когда вы столкнетесь с отрицательными многочленами. Что вы делаете тогда? Давай выясним.

Важные термины, связанные с полиномами
Если вы хотите понять, как решать отрицательные полиномы, сначала вам следует ознакомиться с некоторыми терминами, связанными с полиномами.
- Члены многочлена. Отдельные коэффициенты, переменные и константы, которые вы объединяете для получения полиномиального выражения. В приведенном ранее примере члены многочлена включают 6×7, 23×3 и -7. Многочлен состоит из трех членов.
- Переменная. Это относится к символам, которые используются в качестве заполнителей для чисел. В приведенном выше примере переменная равна x .
- Коэффициент. Это число, сопровождающее переменную. В термине 6×7 коэффициент x7 равен 6.
- Константа. Это числа в полиноме, не связанные с переменной. Постоянный член в примере равен -7.
- Степень многочлена. Это самая высокая степень переменной (показатель степени) в многочлене.
 Степень многочлена равна 7, .
Степень многочлена равна 7, .
Некоторые другие правила, которые следует помнить: Если переменная не имеет коэффициента, то коэффициент равен 1. Кроме того, если переменная не имеет степени, то степень также равна 1.
Отрицательные полиномы
При встрече отрицательный полином, вы в конечном итоге упростите выражение.
Примером отрицательного многочлена является
2n-2 – 3n – 7
Обратите внимание, что степень n отрицательна, -2.
Чтобы решать или упрощать отрицательные многочлены, мы должны полностью понимать правила возведения в степень.
Правила экспоненты
Правила экспоненты обобщают, как манипулировать экспонентами. Давайте рассмотрим их.
Нулевой показатель степени
a0 = 1
Это означает, что любое число, возведенное в степень 0, равно 1.
Произведение или правило умножения
ab * ac = ab + c
Это означает, что если вы умножите два или более показателей степени с одним и тем же основанием, результатом будет просто одна степень (основание), возведенная в сумму степеней.
 По сути, вы складываете показатели вместе.
По сути, вы складываете показатели вместе.Правило частного или деления
ab / ac = ab – c
При делении двух или более показателей степени с одинаковым основанием вы вычитаете степени.
Правило отрицательного экспонента
a-b = 1 / ab
Когда вы встречаете число/переменную с отрицательным показателем степени, возьмите обратное основание. В приведенном выше примере обратное значение a равно 1 / a.
a-b = ( 1 / a )b = 1b / ab = 1 / ab
Степенное правило
( ab )c = ab * c
в другую степень, найдите произведение двух степеней.
Эти правила важны, поскольку они помогут нам упростить отрицательные многочлены. Давайте рассмотрим несколько примеров, которые помогут нам лучше применять эти правила.
Пример 1
Упростите выражение
2×4 y-2
Приведенное выше выражение относительно простое. Единственное, что вам нужно упростить, это отрицательный показатель степени.
 Помните отрицательное правило.
Помните отрицательное правило.2x4y-2 = 2×4 / y2
Мы взяли обратное число y , поскольку степень отрицательна.
Пример 2
Упростите выражение
( 2x−5y−3 * 3x3y−2 ) / ( 3x−5y3 )
Это немного сложно.
Шаг 1
Этот первый шаг не высечен на камне и может быть изменен в зависимости от проблемы. В этом случае числитель содержит несколько показателей степени с одинаковым основанием, поэтому хорошо начать с упрощения числителя, применяя правила показателей степени.
( 2x−5y−3 * 3x3y−2 ) / ( 3x−5y3 )
= ( 2x-5 + 3 * 3y-2 +(-3 ) ) / ( 3x−5y3 )
= (6x-2y-5) / (3x−5y3)
Теперь мы упростили числитель. Знаменатель выглядит хорошо, потому что переменные в нем встречаются не более одного раза.
Шаг 2
Затем упростите числитель и знаменатель, используя правило частного.
( 6x-2y-5 ) / ( 3x−5y3 )
= ( 6 / 3 ) * x-2 – (-5 ) * y(-5 ) – 3
= 2×3 * y-8
= 2x3y-8
Шаг 3
Мы исключили дробь, однако у нас осталась отрицательная степень.
 Применим правило отрицательного показателя.
Применим правило отрицательного показателя.2x3y-8
= 2×3 / y8
Мы взяли обратное число y . 2×3 не затрагивается, так как не разделяет отрицательную силу с y .
Пример 3
Упростите приведенное ниже выражение.
( 3y-7x3z5 ) / ( 4y-5x2z3 )-2
Шаг 1
Вышеприведенное выражение содержит показатели степени, возведенные в другую степень, поэтому мы должны применить правило степени.
(3y-7x3z5) / (4y-5x2z3)-2
= (3y-7x3z5) / (4-2y10x-4z-6)
Мы умножили степени всех знаменателей на -2. Помните о силовом правиле.
Шаг 2
Примените правило отношения, так как переменные появляются только один раз и в числителе, и в знаменателе.
( 3y-7x3z5 ) / ( 4-2y10x-4z-6 )
( 3 / 4-2 ) * ( y-7 – 10 ) * ( x3 – (-4 )) * ( z5 – (-6))
= (3/4-2) * (y-17) * (x7) * (z11)
Шаг 3
Выражение, которое мы получили на шаге 2, имеет отрицательные показатели.

Примените правило отрицательной экспоненты, чтобы исключить их.
(3/4-2) * (y-17) * (x7) * (z11)
(3*42) * (1/y17) * x7z11
(1/1/y17y)
Наше окончательное решение: 48x7z11 / y17
Решение или упрощение отрицательных многочленов может быть сложным. Вот почему так важно полностью понимать различные правила экспоненты. Однако самое важное при работе с отрицательными полиномами – инвертировать основание всякий раз, когда у вас есть отрицательный многочлен. Как и любой навык, чем больше вы его практикуете, тем лучше у вас получается. Если сначала вы не понимаете отрицательное полиномиальное выражение, не торопитесь и проверьте свою работу — вы станете профессионалом в кратчайшие сроки!
Будьте первым, кто оставит комментарий ниже.
Видео: Решение простых уравнений с неизвестным в показателе степени
Стенограмма видео
Это вопросы типа семейства показателей, требующие от вас вспомнить и применить правила порядка.
 𝑥 в 𝑎 умножить 𝑥 на 𝑏 равно 𝑥 на 𝑎 плюс 𝑏; это правило сложения. 𝑥 на 𝑎 разделить на 𝑥 на 𝑏 равно 𝑥 на 𝑎 минус 𝑏; это правило вычитания. И 𝑥 в степени 𝑎 все в степени 𝑏 равно 𝑥 в степени 𝑎 умножить на 𝑏; это правило умножения.
𝑥 в 𝑎 умножить 𝑥 на 𝑏 равно 𝑥 на 𝑎 плюс 𝑏; это правило сложения. 𝑥 на 𝑎 разделить на 𝑥 на 𝑏 равно 𝑥 на 𝑎 минус 𝑏; это правило вычитания. И 𝑥 в степени 𝑎 все в степени 𝑏 равно 𝑥 в степени 𝑎 умножить на 𝑏; это правило умножения.Теперь у нас есть другие видео, в которых эти правила рассказываются более подробно, если вы в них не уверены. Но в этом видео мы собираемся использовать эти правила в сочетании с нашими знаниями о различных степенях двойки, тройки, пятерки и десятки для решения некоторых задач.
Итак, первый вопрос: найдите значение 𝑥, если два в степени 𝑥 равно восьми в степени 𝑥 плюс три. Ну, на первый взгляд это выглядит сложно. Но, надеюсь, мы сможем вспомнить, что дважды два раза два, два в кубе, равно восьми. Так что я могу повторно выразить восемь как степень двойки. Итак, переписав это уравнение с двумя в кубе вместо восьми, мы получили два в степени 𝑥 равно двум в кубе все в степени 𝑥 плюс три.
Теперь у нас есть нечто в степени чего-то в степени чего-то еще, поэтому мы можем использовать правило умножения.
 Таким образом, два в степени трех, все в степени 𝑥 плюс три просто означает, что два в степени три, умноженные на 𝑥 плюс три, в скобках. Итак, теперь у меня есть два в степени 𝑥 равно двум в степени трех лотов 𝑥 плюс три, поэтому эти две вещи должны быть равны. Два в степени чего-то равно двум в степени чего-то; эти две вещи должны быть равны.
Таким образом, два в степени трех, все в степени 𝑥 плюс три просто означает, что два в степени три, умноженные на 𝑥 плюс три, в скобках. Итак, теперь у меня есть два в степени 𝑥 равно двум в степени трех лотов 𝑥 плюс три, поэтому эти две вещи должны быть равны. Два в степени чего-то равно двум в степени чего-то; эти две вещи должны быть равны.А теперь я могу использовать распределительный закон, чтобы перемножить скобки так, чтобы я знал, что 𝑥 равно трем 𝑥 плюс девять. Теперь, если я уберу 𝑥 из обеих частей моего уравнения, у меня будут все 𝑥 с одной стороны. Итак, в левой части 𝑥 убери 𝑥 ничего. А в правой части три 𝑥 отнять 𝑥 будет два 𝑥, а у меня еще останется плюс девять. Так что теперь я пытаюсь получить 𝑥 самостоятельно; уберите девять с обеих сторон.
И в левой части ноль отнимаем девять, получается отрицательная девятка. А справа у меня есть два 𝑥 плюс девять минус девять, так что эти два сокращаются, поэтому у меня только два 𝑥. Теперь мы все еще хотим знать, что такое единица 𝑥, поэтому мне нужно разделить обе части на два.
 А два разделить на два — это всего лишь один, поэтому один 𝑥 равен минус девять больше двух. Или как смешанное число, 𝑥 равно минус четырем с половиной.
А два разделить на два — это всего лишь один, поэтому один 𝑥 равен минус девять больше двух. Или как смешанное число, 𝑥 равно минус четырем с половиной.Итак, при решении этого уравнения было несколько ключевых приемов. Во-первых, мы должны были знать, что восемь — это то же самое, что два в кубе, поэтому вам нужно знать свои показатели степени простых чисел, таких как два, три, четыре, пять, десять, те немногие. А затем нам нужно было знать правило умножения, поэтому нам нужно было знать, что два в степени трех все в степени 𝑥 плюс три равно двум в степени трех лотов или трижды 𝑥 плюс три.
Затем мы заметили, что это два в степени 𝑥 и два в степени три, умноженные на 𝑥 плюс три, поэтому эти два показателя степени должны быть равны. Остальное было просто, решение линейной алгебры. И мы пришли к нашему окончательному ответу, 𝑥 минус четыре с половиной.
Следующий вопрос, решите для 𝑥: девять в степени 𝑥 плюс пять равно двадцати семи в степени 𝑥 минус один. Итак, девять и двадцать семь кратны трем, поэтому трижды три дают нам девять, а трижды трижды три дают двадцать семь.
 Итак, три в кубе — это двадцать семь. Таким образом, мы можем заменить девять и двадцать семь числами, у которых одинаковые основания для их степеней, то есть три в квадрате и три в кубе.
Итак, три в кубе — это двадцать семь. Таким образом, мы можем заменить девять и двадцать семь числами, у которых одинаковые основания для их степеней, то есть три в квадрате и три в кубе.Итак, первая строка равна трем в квадрате в степени 𝑥 плюс пять равно трем в кубе в степени 𝑥 минус один. А теперь снова воспользуемся правилом умножения. Таким образом, мы можем переписать это как три в степени умноженной на два 𝑥 плюс пять равно трем в степени умноженной на три 𝑥 минус один.
Итак, теперь у нас есть то же самое основание для наших показателей, три в степени чего-то равно трем в степени чего-то. Теперь, если это так, эти вещи должны быть равны, поэтому два раза 𝑥 плюс пять должны равняться трем умноженным на 𝑥 минус один. И теперь мы можем использовать распределительный закон умножения, чтобы умножить скобки.
И мы видим, что два 𝑥 плюс десять равно трем 𝑥 минус пять. Теперь у меня две 𝑥 слева и три 𝑥 справа. Если я уберу две 𝑥 с обеих сторон, у меня все еще будет положительное число 𝑥 с правой стороны, а у меня не будет ни одной 𝑥 с левой стороны.

Итак, в левой части у меня есть два 𝑥 плюс десять, уберите два 𝑥, так что два 𝑥 сократятся, и у меня останется только десять. А в правой части у меня три 𝑥 убери два 𝑥 всего один 𝑥 и тогда у меня все еще есть минус три.
Итак, теперь я могу добавить три к обеим частям уравнения, что даст мне тринадцать в левой части. А справа у меня три минус три, и у меня есть 𝑥, так что у меня останется 𝑥. Итак, мой ответ: 𝑥 равно тринадцати.
Итак, снова в этом вопросе мы должны были подумать об основаниях наших показателей. И в первом случае мы смогли определить, что это три в квадрате. А во втором случае было три в кубе. Таким образом, если мы сможем использовать правило умножения для получения одинаковых оснований в каждом случае, мы сможем просто сравнить показатели напрямую, и это превратит его в часть простой линейной алгебры.
Теперь для числа три найдите значение 𝑥, если единица больше ста двадцати пяти в степени 𝑥 равна пяти в степени двойки 𝑥 минус три. Итак, наша первая подсказка здесь заключается в том, что сто двадцать пять — это просто пять в кубе, поэтому я собираюсь повторно выразить сто двадцать пять как пять в кубе.
 И тогда я могу использовать правило умножения пять в степени три в степени 𝑥 это просто пять в степени три 𝑥. 9- сторона руки. Так что вместо того, чтобы писать как один на пять в степени три 𝑥, я буду писать как пять в степени минус три 𝑥, так что мы действительно проверяем здесь ваше знание показателей степени. А это равно пяти в степени двойки 𝑥 минус три.
И тогда я могу использовать правило умножения пять в степени три в степени 𝑥 это просто пять в степени три 𝑥. 9- сторона руки. Так что вместо того, чтобы писать как один на пять в степени три 𝑥, я буду писать как пять в степени минус три 𝑥, так что мы действительно проверяем здесь ваше знание показателей степени. А это равно пяти в степени двойки 𝑥 минус три.Итак, мы пришли к ситуации, когда у нас есть одно и то же основание, пять в каждом случае, и пять в степени минус три 𝑥 равно пяти в степени двойки 𝑥 плюс два 𝑥 минус три. Таким образом, эти два показателя степени должны быть равны; минус три 𝑥 должен быть равен двум 𝑥 минус три.
Теперь нам нужно решить линейную алгебру, поэтому я добавлю три 𝑥 к обеим частям, чтобы получить положительное число 𝑥 с одной стороны уравнения. И тогда в левой части минус три 𝑥 плюс три 𝑥 равно нулю, а в правой части два 𝑥 плюс три 𝑥 равно пяти 𝑥.
А у меня еще минус три, так что пять 𝑥 минус три. Итак, теперь, если я добавлю три к обеим частям уравнения, в левой части у меня будет ноль плюс три, что равно трем, а в правой части у меня будет минус три плюс три.
 Таким образом, эти два сокращаются, что оставляет мне пять 𝑥, поэтому три равно пяти 𝑥. Итак, теперь просто разделите обе части моего уравнения на пять.
Таким образом, эти два сокращаются, что оставляет мне пять 𝑥, поэтому три равно пяти 𝑥. Итак, теперь просто разделите обе части моего уравнения на пять.А справа у меня 𝑥 умножить на пять, разделить на пять, так что эти две пятерки сокращаются, поэтому я только что получил 𝑥. А это равно трем пятым. Поэтому я делаю свой ответ красивым и ясным: 𝑥 равно трем пятым.
Таким образом, ключевым шагом к решению этой задачи было определение того факта, что сто двадцать пять — это пять в степени три, чтобы мы могли получить тот же базовый показатель степени, с которым мы работаем. Затем мы используем правило умножения, и нам нужно было немного знать об отрицательных показателях, чтобы получить это в том же формате. Затем мы взяли наши показатели степени, которые были равны, отрицательные три 𝑥 и два 𝑥 минус три, сделали немного линейной алгебры, а затем придумали наш ответ.
Теперь для нашего последнего примера, номер четыре, найдите значение 𝑥, если тысяча в степени двух третей равна сотне в степени два 𝑥 плюс пять.

Теперь у нас есть несколько основных подходов, которые мы могли бы использовать здесь. Мы могли бы заметить тот факт, что тысяча — это десять в кубе, а сотня — это десять в квадрате, чтобы мы могли произвести эти замены, а затем использовать наши степенные правила и попытаться приравнять показатели степени, или мы могли бы использовать наше знание показателей степени, чтобы сказать, что это означает, что кубический корень из чего-то возведенного в квадрат, поэтому кубический корень из тысячи равен десяти, а затем возводим его в квадрат, и мы получаем сотню. И тогда мы видим, что у нас будут одинаковые базы с каждой стороны, так что на самом деле я думаю, что это будет более быстрый способ добраться сюда; так я и пойду.
Итак, я собираюсь оценить левую сторону. Итак, мы просто повторно выражаем, что вместо сотни в степени двух третей мы знаем, что это кубический корень из тысячи, а затем все это возводится в квадрат. Итак, кубический корень из тысячи равен десяти, поэтому левая часть равна десяти в квадрате, то есть всего лишь сотне.

Итак, у нас есть сотня, равная сотне в степени двойки 𝑥 плюс пять. Ну, сто это то же самое, что сто в степени один. Итак, теперь у меня есть сотня в степени один равна сотне в степени два 𝑥 плюс пять. Итак, у меня есть та же самая база для моих показателей, поэтому я могу приравнять эти показатели.
Ну, это просто оставляет меня с одним равным двум 𝑥 плюс пять, так что просто вычтите пять с обеих сторон. А справа у меня пять минус пять — это ничто, так что отрицательное число четыре равно двум 𝑥. Теперь я могу разделить обе части на два, что означает, что двойки будут сокращаться слева и справа, а минус четыре на два будет просто минус два.
Последний пример очень похож на предыдущие. Нам нужно было знать о показателях. В данном случае нам нужно было знать об этих рациональных показателях здесь наверху. Так что это означает кубический корень из чего-то в квадрате. И мы также должны были помнить, что просто сотня без какой-либо степени или без какой-либо степени равна сотне в степени единицы, чтобы мы могли приравнять эти степени, один с двумя 𝑥 плюс пять.


 Задание № 1
Задание № 1