Как найти синус угла в треугольнике непрямоугольном
Как найти синус угла в треугольнике? Не в прямоугольном, в любом
Если рассматриваемый треугольник является прямоугольным, то можно использовать базовое определение тригонометрической функции синуса для острых углов. По определению синусом угла называют соотношение длины катета, лежащего напротив этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла α, лежащего напротив катета А, определяйте по формуле α=А/С, а синус угла β, лежащего напротив катета В — по формуле β=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, так как угол, лежащий напротив гипотенузы всегда равен 90°, а его синус всегда равен единице.
2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).
Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).
3
Воспользуйтесь для нахождения синуса угла двумя разными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в другой — длины двух сторон и синус угла между ними. Так как результаты их будут равны, то из тождества можно выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С)) . А вторую формулу можно написать так: S=А*В*sin(γ). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего напротив стороны С: sin(γ)= ¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С) /(А*В)) . Синусы двух других углов можно найти по аналогичным формулам.
Как находить синус угла
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией.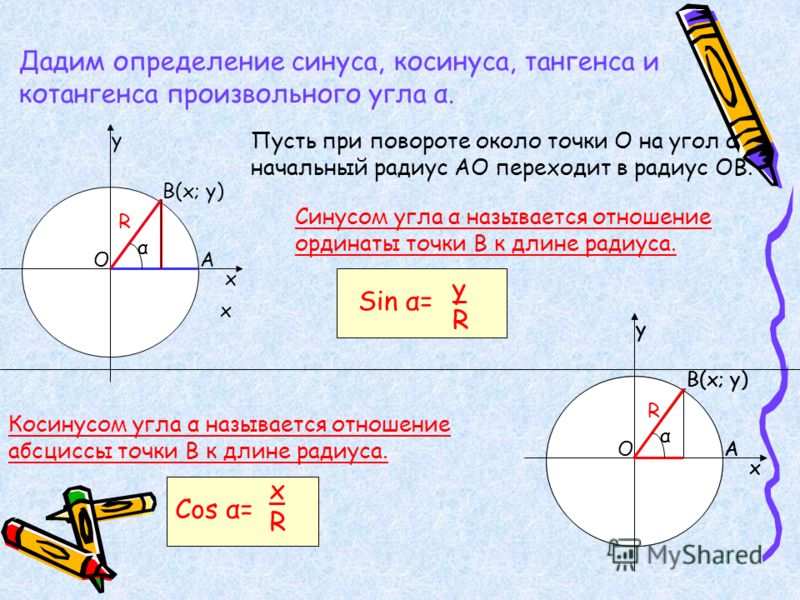 Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий.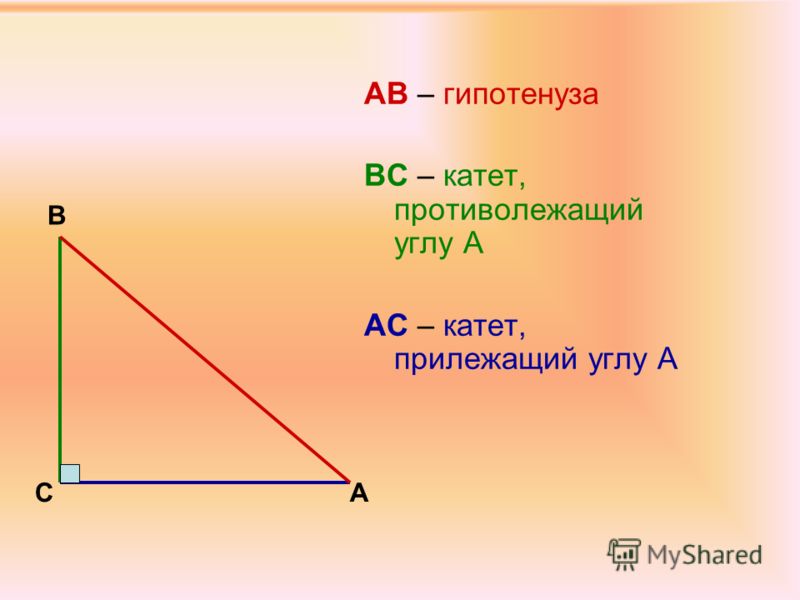 Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1.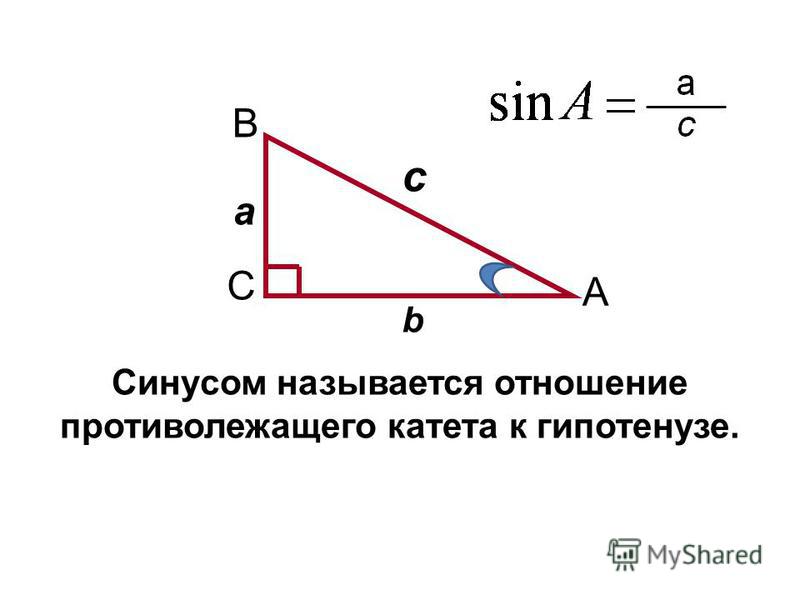 Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.
Что такое синус, косинус и тангенс в НЕ прямоугольном треугольнике? P.S. я имею в виду не формулы синуса, косинуса и тангенса, а именно определение. Что они из себя представляют? В прямоугольном треугольнике знаю, что синус — отношение противолежащего катета к гипотенузе и т.п., а вот не в прямоугольном?
Синус (sin) – это одна из прямых тригонометрических функций. Находить синус угла в произвольном треугольнике проще всего с использованием теоремы косинусов (cos): квадрат длины любой стороны равен сумме квадратов длин двух других сторон за минусом их удвоенного произведения на косинус угла между ними.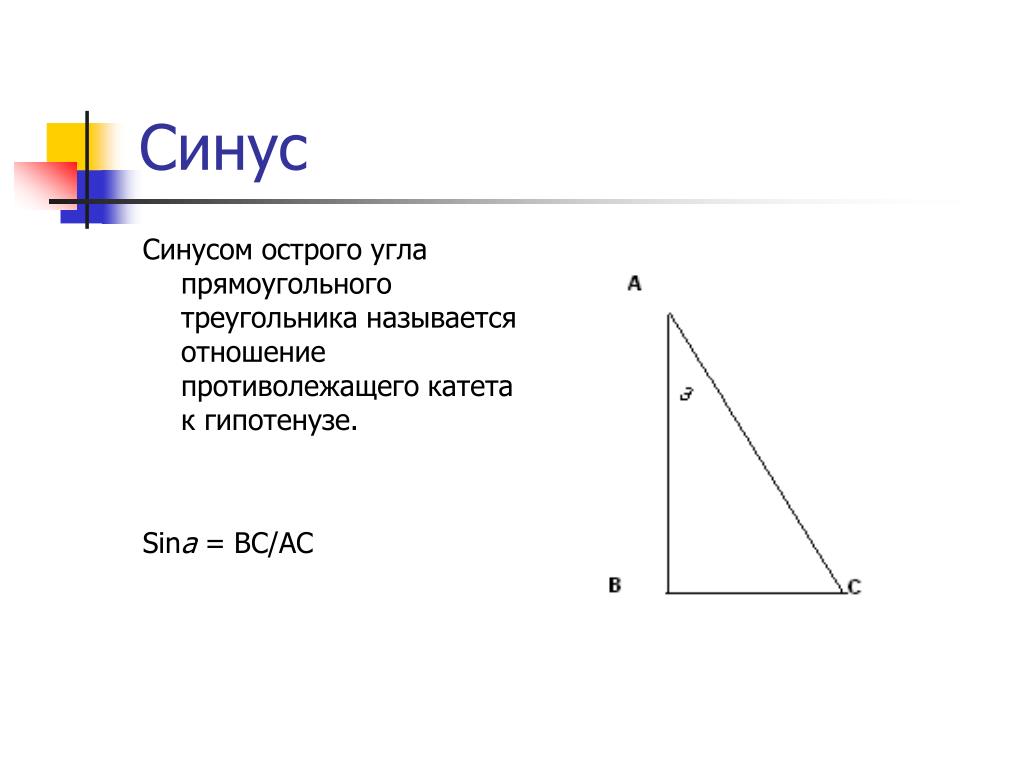
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Чему равен синус угла в прямоугольном треугольнике. Что такое синус и косинус. Выражения через комплексные числа
Отношение противолежащего катета к гипотенузе называют синусом острого угла прямоугольного треугольника.
\sin \alpha = \frac{a}{c}
Косинус острого угла прямоугольного треугольника
Отношение близлежащего катета к гипотенузе называют косинусом острого угла прямоугольного треугольника.
\cos \alpha = \frac{b}{c}
Тангенс острого угла прямоугольного треугольника
Отношение противолежащего катета к близлежащему катету называют тангенсом острого угла прямоугольного треугольника.
tg \alpha = \frac{a}{b}
Котангенс острого угла прямоугольного треугольника
Отношение близлежащего катета к противолежащему катету называют котангенсом острого угла прямоугольного треугольника.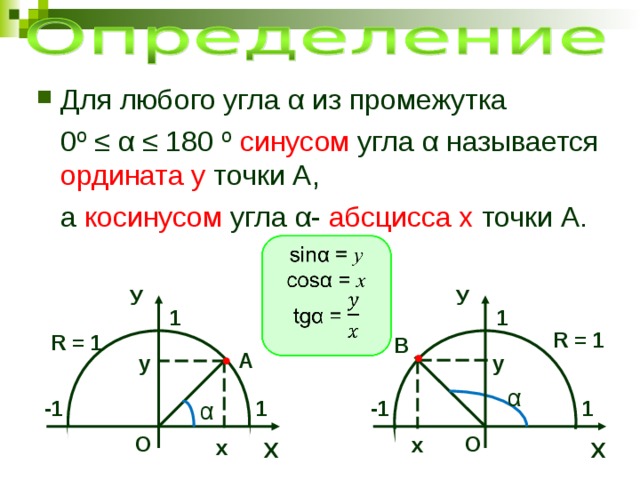
ctg \alpha = \frac{b}{a}
Синус произвольного угла
Ордината точки на единичной окружности , которой соответствует угол \alpha называют синусом произвольного угла поворота \alpha .
\sin \alpha=y
Косинус произвольного угла
Абсцисса точки на единичной окружности, которой соответствует угол \alpha называют
\cos \alpha=x
Тангенс произвольного угла
Отношение синуса произвольного угла поворота \alpha к его косинусу называют тангенсом произвольного угла поворота \alpha .
tg \alpha = y_{A}
tg \alpha = \frac{\sin \alpha}{\cos \alpha}
Котангенс произвольного угла
Отношение косинуса произвольного угла поворота \alpha к его синусу называют котангенсом произвольного угла поворота \alpha .
ctg \alpha =x_{A}
ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
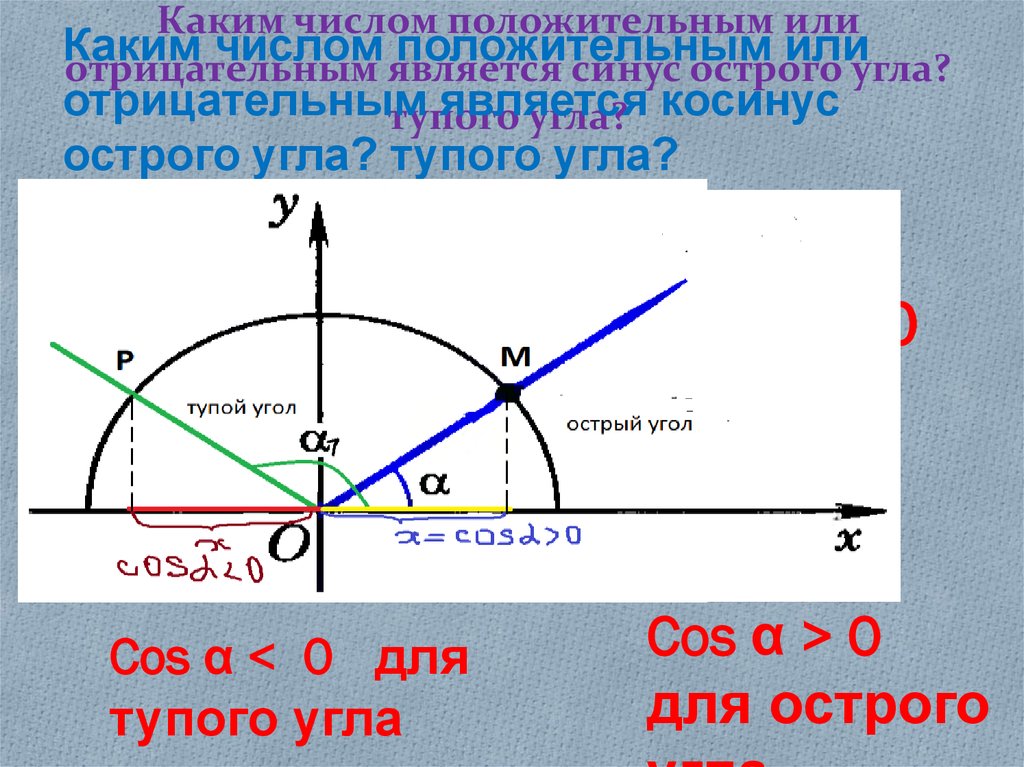
Пример нахождения произвольного угла
Если \alpha — некоторый угол AOM , где M — точка единичной окружности, то
\sin \alpha=y_{M}
, \cos \alpha=x_{M}
, tg \alpha=\frac{y_{M}}{x_{M}}
, ctg \alpha=\frac{x_{M}}{y_{M}}
. {\circ}\left(2\pi\right)
{\circ}\left(2\pi\right)
Синус острого угла α прямоугольного треугольника – это отношение противолежащего
катета к гипотенузе.
Обозначается так: sin α.
Косинус острого угла α прямоугольного треугольника – это отношение прилежащего
катета к гипотенузе.
Обозначается так: cos α.
Тангенс острого угла α – это отношение противолежащего катета к прилежащему катету.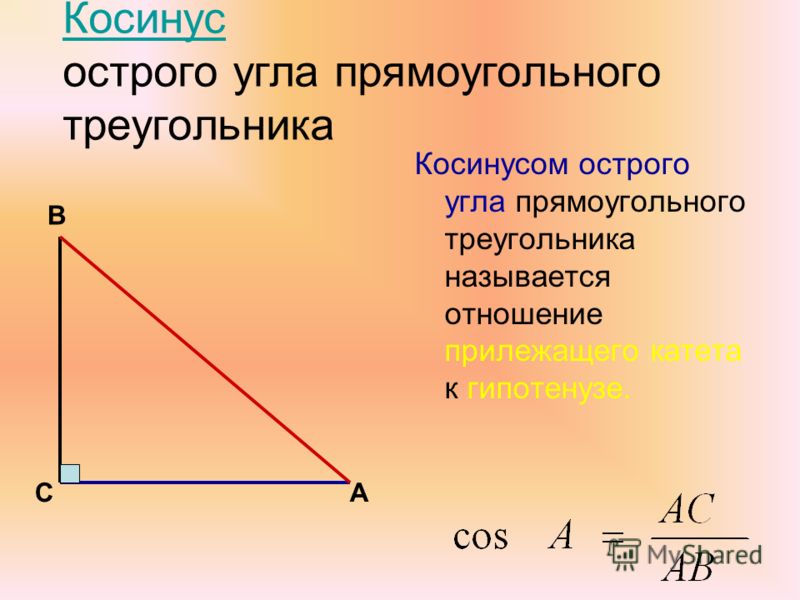
Обозначается так: tg α.
Котангенс острого угла α – это отношение прилежащего катета к противолежащему.
Обозначается так: ctg α.
Синус, косинус, тангенс и котангенс угла зависят только от величины угла.
Правила:
Основные тригонометрические тождества в прямоугольном треугольнике:
(α – острый угол, противолежащий катету b и прилежащий к катету a . Сторона с – гипотенуза. β – второй острый угол).
b | sin 2 α + cos 2 α = 1 | |
a | 1 | |
b | 1 | |
a | 1 1 | |
sin α |
При возрастании острого угла sin α и tg α возрастают, а cos α убывает.
Для любого острого угла α:
sin (90° – α) = cos α
cos (90° – α) = sin α
Пример-пояснение :
Пусть в прямоугольном треугольнике АВС
АВ = 6,
ВС = 3,
угол А = 30º.
Выясним синус угла А и косинус угла В.
Решение .
1) Сначала находим величину угла В. Тут все просто: так как в прямоугольном треугольнике сумма острых углов равна 90º, то угол В = 60º:
В = 90º – 30º = 60º.
2) Вычислим sin A. Мы знаем, что синус равен отношению противолежащего катета к гипотенузе. Для угла А противолежащим катетом является сторона ВС. Итак:
BC 3 1
sin A = — = — = —
AB 6 2
3) Теперь вычислим cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла В прилежащим катетом является все та же сторона ВС. Это значит, что нам снова надо разделить ВС на АВ – то есть совершить те же действия, что и при вычислении синуса угла А:
BC 3 1
cos B = — = — = —
AB 6 2
В итоге получается:
sin A = cos B = 1/2.
sin 30º = cos 60º = 1/2.
Из этого следует, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла – и наоборот. Именно это и означают наши две формулы:
sin (90° – α) = cos α
cos (90° – α) = sin α
Убедимся в этом еще раз:
1) Пусть α = 60º. Подставив значение α в формулу синуса, получим:
sin (90º – 60º) = cos 60º.
sin 30º = cos 60º.
2) Пусть α = 30º. Подставив значение α в формулу косинуса, получим:
cos (90° – 30º) = sin 30º.
cos 60° = sin 30º.
(Подробнее о тригонометрии — см.раздел Алгебра)
В этой статье мы покажем, как даются определения синуса, косинуса, тангенса и котангенса угла и числа в тригонометрии . Здесь же мы поговорим об обозначениях, приведем примеры записей, дадим графические иллюстрации. В заключение проведем параллель между определениями синуса, косинуса, тангенса и котангенса в тригонометрии и геометрии.
Навигация по странице.
Определение синуса, косинуса, тангенса и котангенса
Проследим за тем, как формируются представление о синусе, косинусе, тангенсе и котангенсе в школьном курсе математики. На уроках геометрии дается определение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. А позже изучается тригонометрия, где говорится о синусе, косинусе, тангенсе и котангенсе угла поворота и числа. Приведем все эти определения, приведем примеры и дадим необходимые комментарии.
На уроках геометрии дается определение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. А позже изучается тригонометрия, где говорится о синусе, косинусе, тангенсе и котангенсе угла поворота и числа. Приведем все эти определения, приведем примеры и дадим необходимые комментарии.
Острого угла в прямоугольном треугольнике
Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки.
Определение.
Синус острого угла в прямоугольном треугольнике
Определение.
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
Определение.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Определение.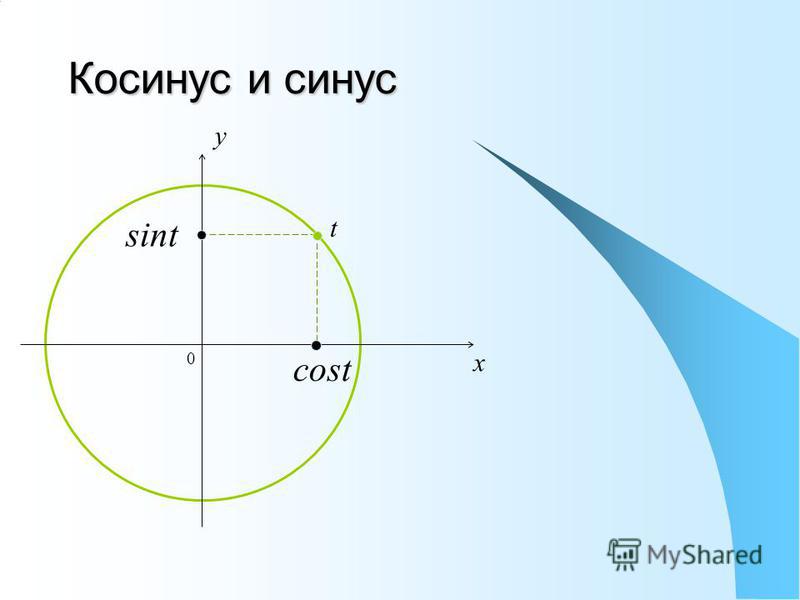
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.
Там же вводятся обозначения синуса, косинуса, тангенса и котангенса – sin , cos , tg и ctg соответственно.
Например, если АВС – прямоугольный треугольник с прямым углом С , то синус острого угла A равен отношению противолежащего катета BC к гипотенузе AB , то есть, sin∠A=BC/AB .
Эти определения позволяют вычислять значения синуса, косинуса, тангенса и котангенса острого угла по известным длинам сторон прямоугольного треугольника, а также по известным значениям синуса, косинуса, тангенса, котангенса и длине одной из сторон находить длины других сторон. Например, если бы мы знали, что в прямоугольном треугольнике катет AC равен 3 , а гипотенуза AB равна 7 , то мы могли бы вычислить значение косинуса острого угла A по определению: cos∠A=AC/AB=3/7 .
Угла поворота
В тригонометрии на угол начинают смотреть более широко — вводят понятие угла поворота . Величина угла поворота, в отличие от острого угла, не ограничена рамками от 0
до 90
градусов, угол поворота в градусах (и в радианах) может выражаться каким угодно действительным числом от −∞
до +∞
.
Величина угла поворота, в отличие от острого угла, не ограничена рамками от 0
до 90
градусов, угол поворота в градусах (и в радианах) может выражаться каким угодно действительным числом от −∞
до +∞
.
В этом свете дают определения синуса, косинуса, тангенса и котангенса уже не острого угла, а угла произвольной величины — угла поворота. Они даются через координаты x и y точки A 1 , в которую переходит так называемая начальная точка A(1, 0) после ее поворота на угол α вокруг точки O – начала прямоугольной декартовой системы координат и центра единичной окружности .
Определение.
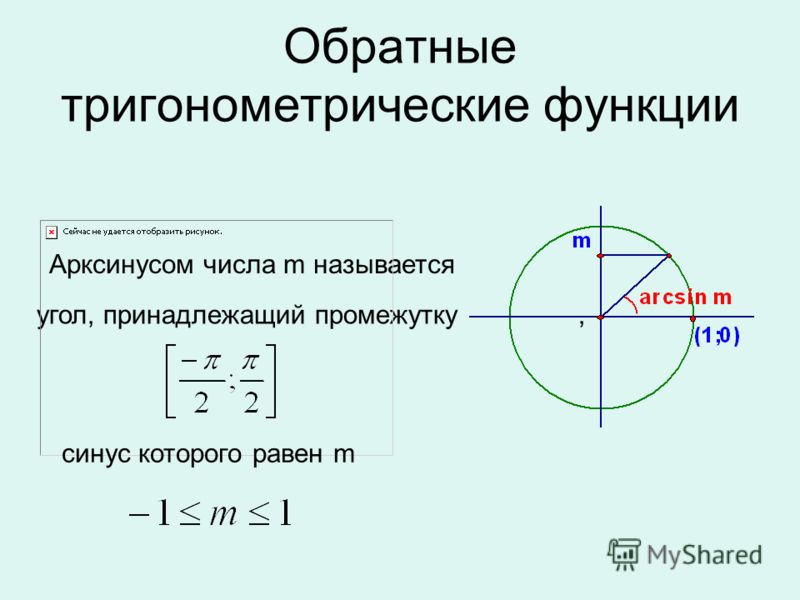
Синус угла поворота α — это ордината точки A 1 , то есть, sinα=y .
Определение.
Косинусом угла поворота α называют абсциссу точки A 1 , то есть, cosα=x .
Определение.
Тангенс угла поворота α — это отношение ординаты точки A 1 к ее абсциссе, то есть, tgα=y/x .
Определение.
Котангенсом угла поворота α
называют отношение абсциссы точки A 1
к ее ординате, то есть, ctgα=x/y
.
Синус и косинус определены для любого угла α , так как мы всегда можем определить абсциссу и ординату точки, которая получается в результате поворота начальной точки на угол α . А тангенс и котангенс определены не для любого угла. Тангенс не определен для таких углов α , при которых начальная точка переходит в точку с нулевой абсциссой (0, 1) или (0, −1) , а это имеет место при углах 90°+180°·k , k∈Z (π/2+π·k рад). Действительно, при таких углах поворота выражение tgα=y/x не имеет смысла, так как в нем присутствует деление на нуль. Что же касается котангенса, то он не определен для таких углов α , при которых начальная точка переходит к в точку с нулевой ординатой (1, 0) или (−1, 0) , а это имеет место для углов 180°·k , k∈Z (π·k рад).
Итак, синус и косинус определены для любых углов поворота, тангенс определен для всех углов, кроме 90°+180°·k , k∈Z (π/2+π·k рад), а котангенс – для всех углов, кроме 180°·k , k∈Z (π·k рад).
В определениях фигурируют уже известные нам обозначения sin
, cos
, tg
и ctg
, они используются и для обозначения синуса, косинуса, тангенса и котангенса угла поворота (иногда можно встретить обозначения tan
и cot
, отвечающие тангенсу и котангенсу).
В заключение этого пункта стоит заметить, что в разговоре про синус, косинус, тангенс и котангенс угла поворота часто опускают словосочетание «угол поворота» или слово «поворота». То есть, вместо фразы «синус угла поворота альфа» обычно используют фразу «синус угла альфа» или еще короче – «синус альфа». Это же касается и косинуса, и тангенса, и котангенса.
Также скажем, что определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике согласуются с только что данными определениями синуса, косинуса, тангенса и котангенса угла поворота величиной от 0 до 90 градусов. Это мы обоснуем .
Числа
Определение.
Синусом, косинусом, тангенсом и котангенсом числа t
называют число, равное синусу, косинусу, тангенсу и котангенсу угла поворота в t
радианов соответственно.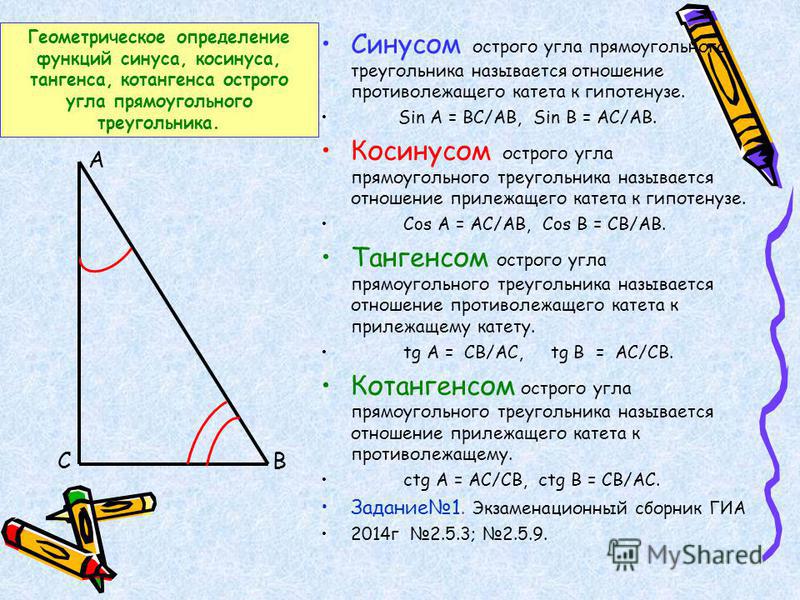
Например, косинус числа 8·π по определению есть число, равное косинусу угла в 8·π рад. А косинус угла в 8·π рад равен единице, поэтому, косинус числа 8·π равен 1 .
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Он состоит в том, что каждому действительному числу t ставится в соответствие точка единичной окружности с центром в начале прямоугольной системы координат, и синус, косинус, тангенс и котангенс определяются через координаты этой точки. Остановимся на этом подробнее.
Покажем, как устанавливается соответствие между действительными числами и точками окружности:
- числу 0 ставится в соответствие начальная точка A(1, 0) ;
- положительному числу t ставится в соответствие точка единичной окружности, в которую мы попадем, если будем двигаться по окружности из начальной точки в направлении против часовой стрелки и пройдем путь длиной t ;
- отрицательному числу t
ставится в соответствие точка единичной окружности, в которую мы попадем, если будем двигаться по окружности из начальной точки в направлении по часовой стрелке и пройдем путь длиной |t|
.

Теперь переходим к определениями синуса, косинуса, тангенса и котангенса числа t . Допустим, что числу t соответствует точка окружности A 1 (x, y) (например, числу &pi/2; отвечает точка A 1 (0, 1) ).
Определение.
Синусом числа t называют ординату точки единичной окружности, соответствующей числу t , то есть, sint=y .
Определение.
Косинусом числа t называют абсциссу точки единичной окружности, отвечающей числу t , то есть, cost=x .
Определение.
Тангенсом числа t называют отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t , то есть, tgt=y/x . В другой равносильной формулировке тангенс числа t – это отношение синуса этого числа к косинусу, то есть, tgt=sint/cost .
Определение.
Котангенсом числа t
называют отношение абсциссы к ординате точки единичной окружности, соответствующей числу t
, то есть, ctgt=x/y
. Другая формулировка такова: тангенс числа t
– это отношение косинуса числа t
к синусу числа t
: ctgt=cost/sint
.
Здесь отметим, что только что данные определения согласуются с определением, данным в начале этого пункта. Действительно, точка единичной окружности, соответствующая числу t , совпадает с точкой, полученной в результате поворота начальной точки на угол в t радианов.
Еще стоит прояснить такой момент. Допустим, перед нами запись sin3 . Как понять, о синусе числа 3 или о синусе угла поворота в 3 радиана идет речь? Обычно это ясно из контекста, в противном случае это скорее всего не имеет принципиального значения.
Тригонометрические функции углового и числового аргумента
Согласно данным в предыдущем пункте определениям, каждому углу поворота α
соответствуют вполне определенное значение sinα
, как и значение cosα
. Кроме того, всем углам поворота, отличным от 90°+180°·k
, k∈Z
(π/2+π·k
рад) отвечают значения tgα
, а отличным от 180°·k
, k∈Z
(π·k
рад) – значения ctgα
. Поэтому sinα
, cosα
, tgα
и ctgα
— это функции угла α
. Другими словами – это функции углового аргумента.
Аналогично можно говорить и про функции синус, косинус, тангенс и котангенс числового аргумента. Действительно, каждому действительному числу t отвечает вполне определенное значение sint , как и cost . Кроме того, всем числам, отличным от π/2+π·k , k∈Z соответствуют значения tgt , а числам π·k , k∈Z — значения ctgt .
Функции синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями .
Из контекста обычно понятно, с тригонометрическими функциями углового аргумента или числового аргумента мы имеем дело. В противном случае мы можем считать независимую переменную как мерой угла (угловым аргументом), так и числовым аргументом.
Однако, в школе в основном изучаются числовые функции, то есть, функции, аргументы которых, как и соответствующие им значения функции, являются числами. Поэтому, если речь идет именно о функциях, то целесообразно считать тригонометрические функции функциями числовых аргументов.
Связь определений из геометрии и тригонометрии
Если рассматривать угол поворота α
величиной от 0
до 90
градусов, то данные в контексте тригонометрии определения синуса, косинуса, тангенса и котангенса угла поворота полностью согласуются с определениями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике, которые даются в курсе геометрии.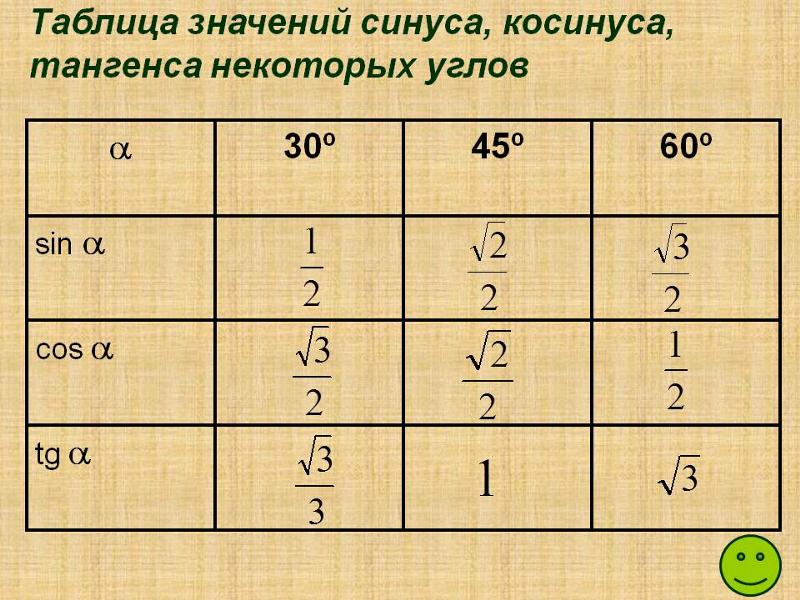 Обоснуем это.
Обоснуем это.
Изобразим в прямоугольной декартовой системе координат Oxy единичную окружность. Отметим начальную точку A(1, 0) . Повернем ее на угол α величиной от 0 до 90 градусов, получим точку A 1 (x, y) . Опустим из точки А 1 на ось Ox перпендикуляр A 1 H .
Легко видеть, что в прямоугольном треугольнике угол A 1 OH
равен углу поворота α
, длина прилежащего к этому углу катета OH
равна абсциссе точки A 1
, то есть, |OH|=x
, длина противолежащего к углу катета A 1 H
равна ординате точки A 1
, то есть, |A 1 H|=y
, а длина гипотенузы OA 1
равна единице, так как она является радиусом единичной окружности. Тогда по определению из геометрии синус острого угла α
в прямоугольном треугольнике A 1 OH
равен отношению противолежащего катета к гипотенузе, то есть, sinα=|A 1 H|/|OA 1 |=y/1=y
. А по определению из тригонометрии синус угла поворота α
равен ординате точки A 1
, то есть, sinα=y
. Отсюда видно, что определение синуса острого угла в прямоугольном треугольнике эквивалентно определению синуса угла поворота α
при α
от 0
до 90
градусов.
Аналогично можно показать, что и определения косинуса, тангенса и котангенса острого угла α согласуются с определениями косинуса, тангенса и котангенса угла поворота α .
Список литературы.
- Геометрия. 7-9 классы : учеб. для общеобразоват. учреждений / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. — 20-е изд. М.: Просвещение, 2010. — 384 с.: ил. — ISBN 978-5-09-023915-8.
- Погорелов А. В. Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений/ А. В. Погорелов. — 2-е изд — М.: Просвещение, 2001. — 224 с.: ил. — ISBN 5-09-010803-X.
- Алгебра и элементарные функции : Учебное пособие для учащихся 9 класса средней школы / Е. С. Кочетков, Е. С. Кочеткова; Под редакцией доктора физико-математических наук О. Н. Головина.- 4-е изд. М.: Просвещение, 1969.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.
 : ил.- ISBN 5-09-002727-7
: ил.- ISBN 5-09-002727-7 - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Мордкович А. Г. Алгебра и начала анализа. 10 класс. В 2 ч. Ч. 1: учебник для общеобразовательных учреждений (профильный уровень)/ А. Г. Мордкович, П. В. Семенов. — 4-е изд., доп. — М.: Мнемозина, 2007. — 424 с.: ил. ISBN 978-5-346-00792-0.
- Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни /[Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. — 3-е изд. — И.: Просвещение, 2010.- 368 с.: ил.- ISBN 978-5-09-022771-1.
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В.
 А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла.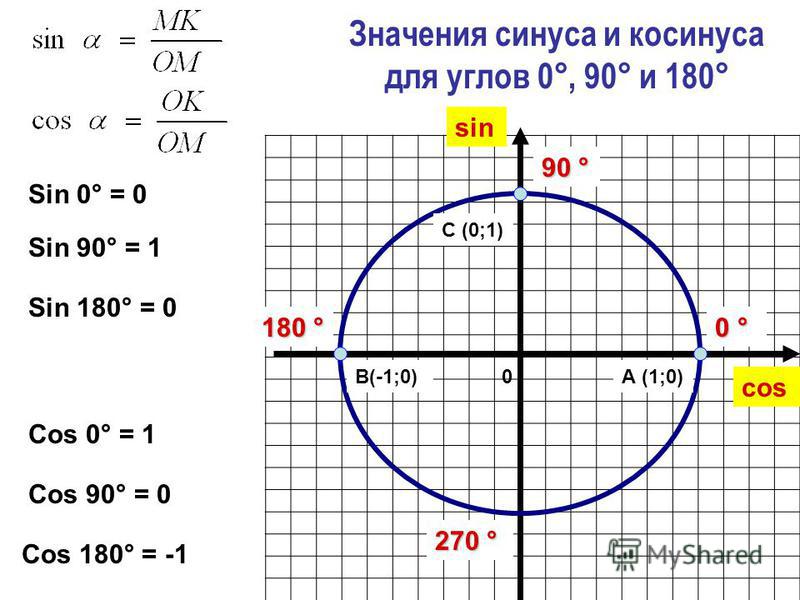 Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.
Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.
Лекция: Синус, косинус, тангенс, котангенс произвольного угла
Синус, косинус произвольного угла
Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом. Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР , который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ . Так как окружность имеет радиус, равный единице, то ОР = R = 1 .
Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР , который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ . Так как окружность имеет радиус, равный единице, то ОР = R = 1 .
Если с точки Р опустить перпендикуляр на ось ОХ , то получим прямоугольный треугольник с гипотенузой, равной единице.
Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным , если же он двигается против движения часовой стрелки — положительным .
Синусом угла ОР , является ордината точки Р вектора на окружности.
То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.
Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе, получим, что
А так как R = 1 , то sin(α) = y 0 .
В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой — отрицательное.
Косинусом угла данной окружности, образованного радиусом-вектором ОР , является абсцисса точки Р вектора на окружности.
То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.
Косинус произвольного угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе, получим, что
А так как R = 1 , то cos(α) = x 0 .
В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей — отрицательное.
Тангенсом произвольного угла считается отношение синуса к косинусу.
Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.
Расчет объемной теплоты сгорания газа
Электропроводность воды, или что такое кондуктометрия
Синус и косинус острого угла презентация, доклад
Синус и косинус острого угла
Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе. Синус угла А обозначается sin A.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе. Косинус угла А обозначается cos A.
Косинус угла А обозначается cos A.
По определению,
Тангенс и котангенс острого угла
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к прилежащему.Тангенс угла А обозначается tg A.
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к противолежащему. Котангенс угла А обозначается сtg A.
По определению,
Тригонометрические функции
Синус, косинус, тангенс и котангенс называют тригонометрическими функциями острого угла.
Из определения тригонометрических функций следует:
1) катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего угла;
2) катет прямоугольного треугольника равен произведению гипотенузы на косинус прилежащего угла;
3) катет прямоугольного треугольника равен произведению второго катета на тангенс противолежащего угла;
4) катет прямоугольного треугольника равен произведению второго катета на котангенс прилежащего угла.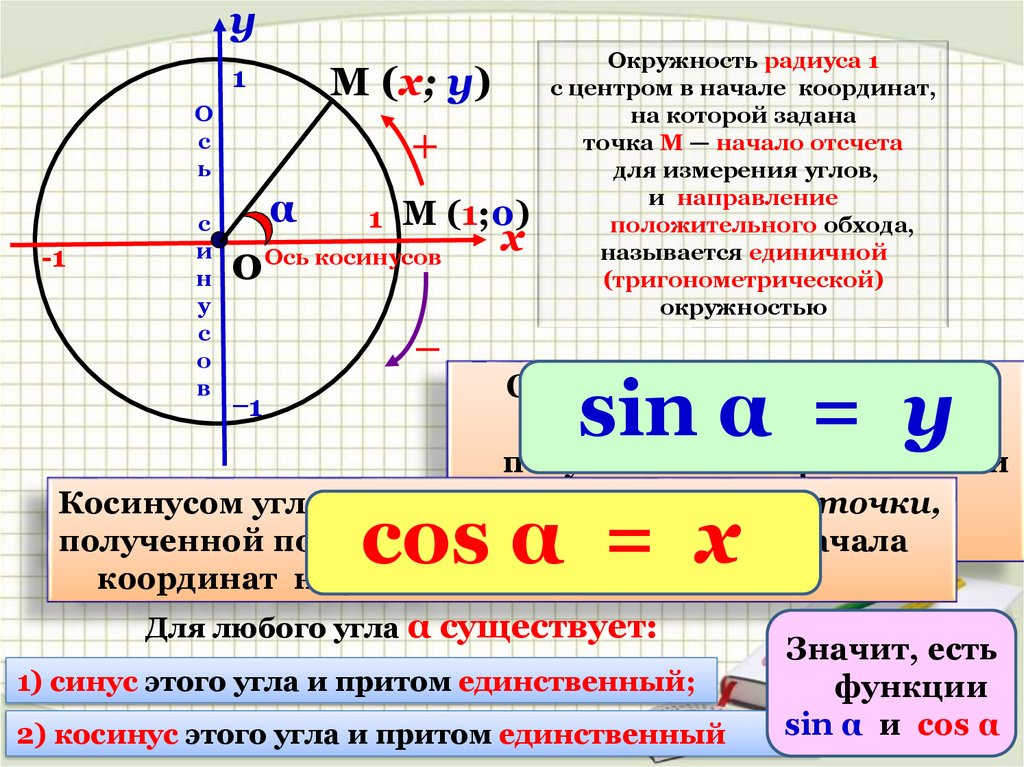
Вопрос 1
Что называется синусом острого угла прямоугольного треугольника?
Ответ: Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе.
Вопрос 2
Как обозначается синус угла A?
Ответ: Синус угла А обозначается sin A.
Вопрос 3
Что называется косинусом острого угла прямоугольного треугольника?
Ответ: Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.
Вопрос 4
Как обозначается косинус угла A?
Ответ: Косинус угла А обозначается cos A.
Вопрос 5
Что называется тангенсом острого угла прямоугольного треугольника?
Ответ: Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к прилежащему.
Вопрос 6
Как обозначается тангенс угла A?
Ответ: Тангенс угла А обозначается tg A.
Вопрос 7
Что называется котангенсом острого угла прямоугольного треугольника?
Ответ: Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к противолежащему.
Вопрос 8
Как обозначается котангенс угла A?
Ответ: Котангенс угла А обозначается ctg A.
Вопрос 9
Что называется тригонометрическими функциями острого угла?
Ответ: Тригонометрическими функциями острого угла называются синус, косинус, тангенс и котангенс.
Вопрос 10
Чему равен катет, лежащий против угла в 30о?
Ответ: Катет, лежащий против угла в 30о равен половине гипотенузы.
Упражнение 1
Найдите значения тригонометрических функций угла в 30о.
Упражнение 2
Найдите значения тригонометрических функций угла в 45о.
Упражнение 3
Найдите значения тригонометрических функций угла в 60о.
Упражнение 4
Найдите значения тригонометрических функций угла AOB, изображенного на рисунке.
Упражнение 5
Найдите значения тригонометрических функций угла AOB, изображенного на рисунке.
Упражнение 6
Найдите значения тригонометрических функций угла AOB, изображенного на рисунке.
Упражнение 7
Найдите значения тригонометрических функций угла AOB, изображенного на рисунке.
Упражнение 8
Найдите значения тригонометрических функций угла AOB, изображенного на рисунке.
Упражнение 9
На клетчатой бумаге изобразите угол, тангенс которого равен: а) 1; б) 0,5; в) 2; г) 3.
Упражнение 10
От луча OA отложите угол, тангенс которого равен: а) 1/2; б) 1/3; в) 2.
Упражнение 11
Может ли синус (косинус) угла быть равен ?
Ответ: Нет, значения синуса и косинуса меньше единицы.
Упражнение 12
Может ли тангенс (котангенс) угла быть равен ?
Ответ: Да.
Упражнение 13
Катеты прямоугольного треугольника равны 12 см и 5 см.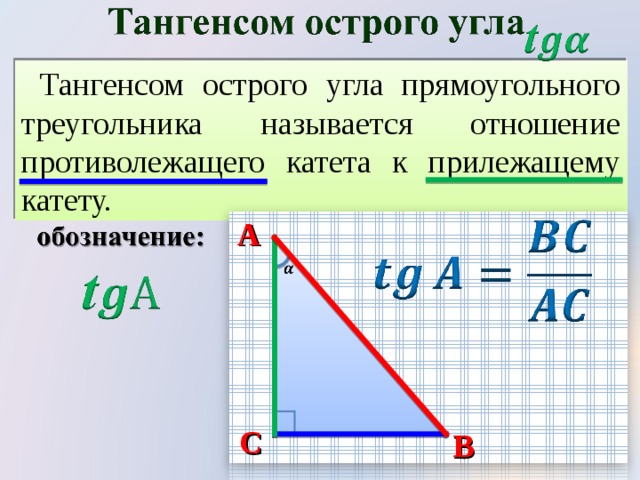 Найдите все тригонометрические функции его меньшего угла A.
Найдите все тригонометрические функции его меньшего угла A.
Упражнение 14
В треугольнике ABC угол C равен 90о, CH – высота, AC = 5, AH = 4. Найдите:
а) sin B;
б) cos B.
Ответ: а) 0,8.
б) 0,6.
Упражнение 15
В треугольнике ABC угол C равен 90о, CH – высота, BC = 5, BH = 3. Найдите:
а) sin A;
б) cos A.
Ответ: а) 0,6;
б) 0,8.
Упражнение 16
В треугольнике ABC угол C равен 90о, AC = 5, высота CH равна 3. Найдите sin B.
Ответ: 0,8.
Упражнение 17
В треугольнике ABC угол C равен 90о, BC = 5, высота CH равна 4. Найдите sin A.
Ответ: 0,6.
Упражнение 18
Высота, проведенная к основанию равнобедренного треугольника, равна 8 см, основание равно 12 см. Найдите синус и косинус угла A при основании треугольника.
Найдите синус и косинус угла A при основании треугольника.
Упражнение 19
В треугольнике ABC AC = BC = 5, AB = 8. Найдите tg A.
Ответ: 0,75.
Упражнение 20
В треугольнике ABC AC = BC, AB = 5, высота AH равна 4. Найдите sin A.
Ответ: 0,8.
Упражнение 21
В треугольнике ABC AC = BC, AB = 5, высота AH равна 4. Найдите cos A.
Ответ: 0,6.
Упражнение 22
В треугольнике ABC AC = BC, AB = 5, AH – высота, BH = 3. Найдите cos A.
Ответ: 0,6.
Упражнение 23
В треугольнике ABC AC = BC, AH – высота, sin A = 0,8. Найдите косинус угла BAH.
Ответ: 0,8.
Упражнение 24
В треугольнике ABC AC = BC, AH – высота, sin A = 0,8. Найдите синус угла BAH.
Ответ: 0,6.
Упражнение 25
В треугольнике ABC AB = BC, AC = 10, CH – высота, AH = 8. Найдите sin C.
Ответ: 0,6.
Упражнение 26
В треугольнике ABC AB = BC, CH — высота, sin C = 0,4. Найдите косинус угла ACH.
Ответ: 0,4.
Упражнение 27*
Найдите синус угла в 18о.
Упражнение 28*
Найдите синус угла в 54о.
Упражнение 29*
Найдите косинус угла в 18о.
Упражнение 30*
Найдите косинус угла в 54о.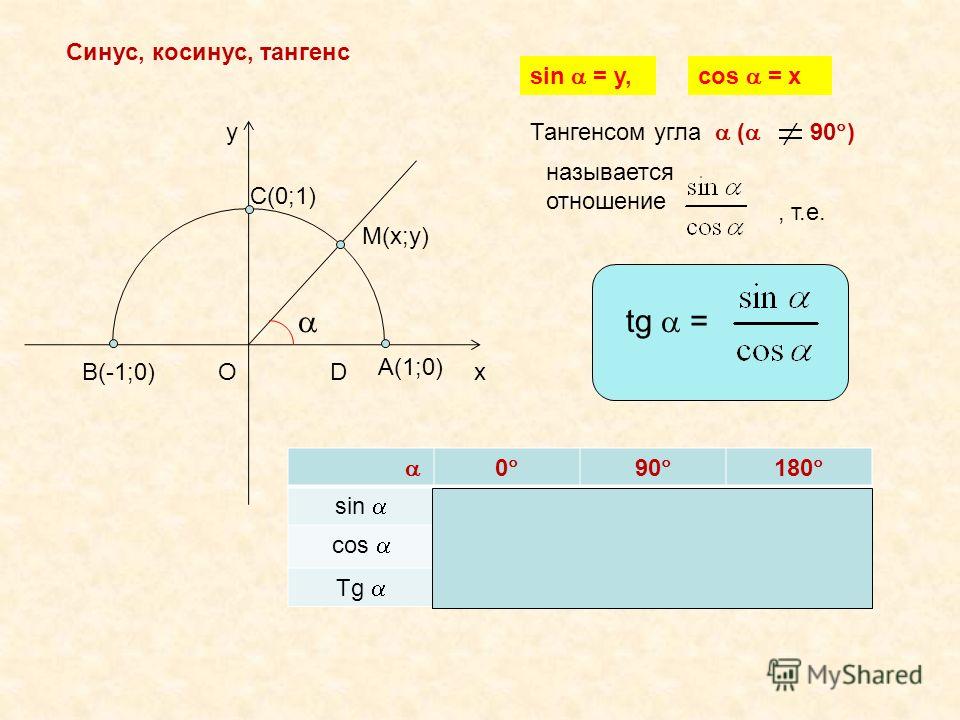
Упражнение 31
Ответ: 37о.
Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. Под каким углом к направлению на запад он должен идти, чтобы вернуться домой? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических функций.)
Упражнение 32
Ответ: 37о.
Грибник, войдя в лес, в течение двух часов шел в направлении на север, а затем с той же скоростью в течение полутора часов – на восток. Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических функций.)
Упражнение 33
Ответ: 14о.
Маятник AB длиной 50 см отклонили от положения равновесия на расстояние CD, равное 12 см.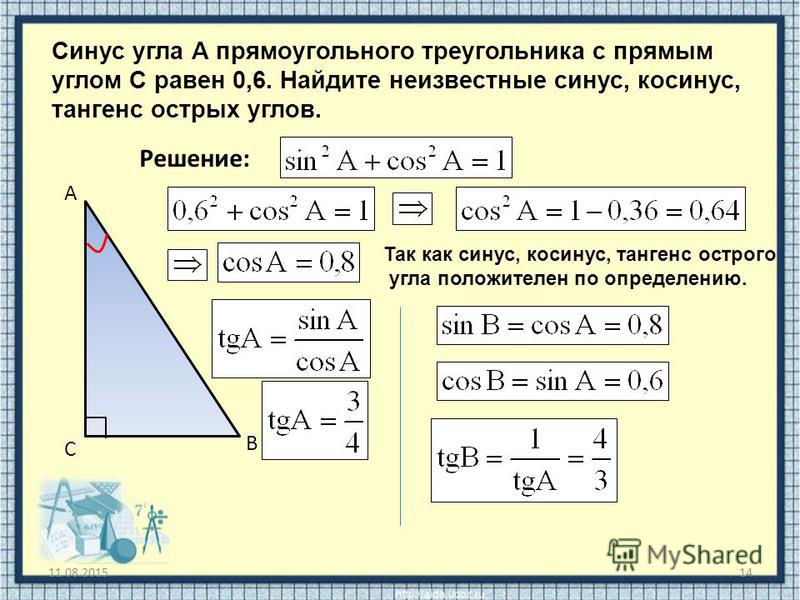 Используя таблицу тригонометрических функций, найдите угол, который образует новое положение AC маятника с положением равновесия AB
Используя таблицу тригонометрических функций, найдите угол, который образует новое положение AC маятника с положением равновесия AB
Упражнение 34
Ответ: 2о.
Горная железная дорога поднимается на 1 м на каждые 30 м пути. Используя таблицу тригонометрических функций, найдите угол подъема в градусах. В ответе укажите приближенное значение, выражаемое целым числом градусов.
Упражнение 35
Ответ: 5о.
Человек, пройдя вверх по склону холма 1000 м, поднялся на 90 м над плоскостью основания холма. Используя таблицу тригонометрических функций, найдите (в среднем) угол наклона холма в градусах. В ответе укажите приближенное значение, выражаемое целым числом градусов.
Упражнение 36
Ответ: 2о.
Использую таблицу тригонометрических функций, найдите приближенное значение угла, под которым виден столб высотой 3 м, находящийся от наблюдателя на расстоянии 100 м.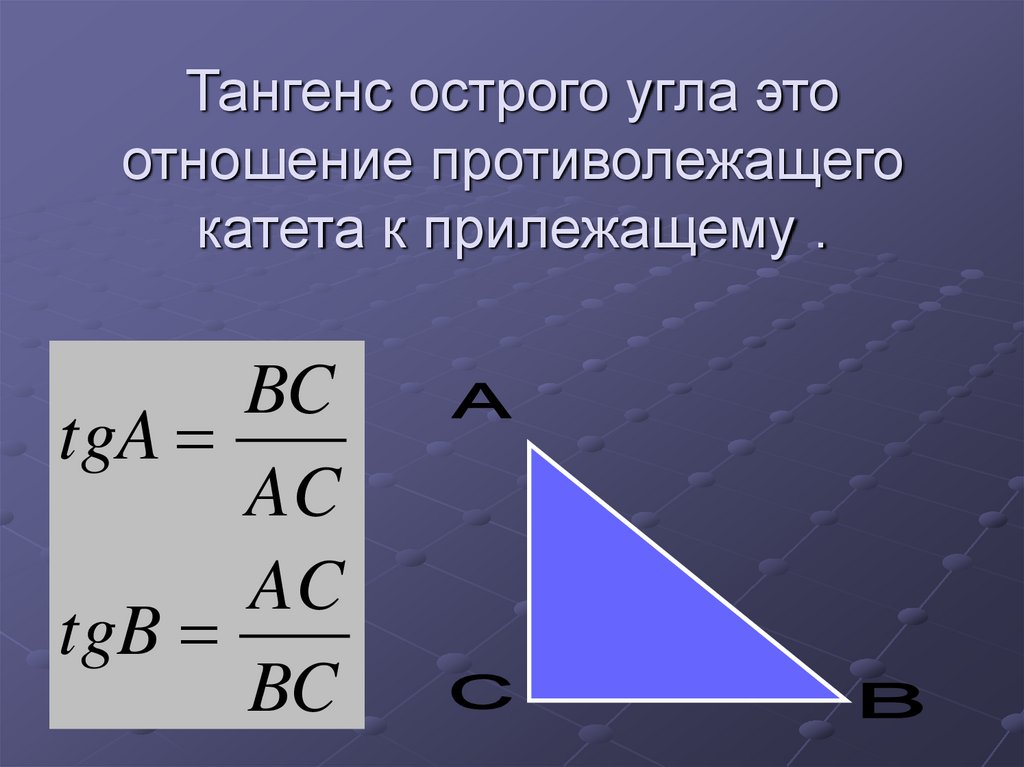 В ответе укажите целое число градусов.
В ответе укажите целое число градусов.
Упражнение 37
Ответ: 50о.
Высота башни главного здания МГУ имени М.В. Ломоносова равна 240 м. Под каким углом видна эта башня с расстояния 200 м? В ответе укажите приближенное значение, равное целому числу градусов.
Упражнение 38
Ответ: 15о.
Высота Останкинской телевизионной башни – 540 м. Используя таблицу тригонометрических функций, найдите угол в градусах, под которым видна башня с расстояния 2000 м.
Упражнение 39
Ответ: 34о.
Строение высоты 30 м бросает тень длиной 45 м. Используя таблицу тригонометрических функций, найдите угол наклона солнечных лучей. В ответе укажите приближенное значение, выражаемое целым числом градусов.
Упражнение 40
Ответ: 64о.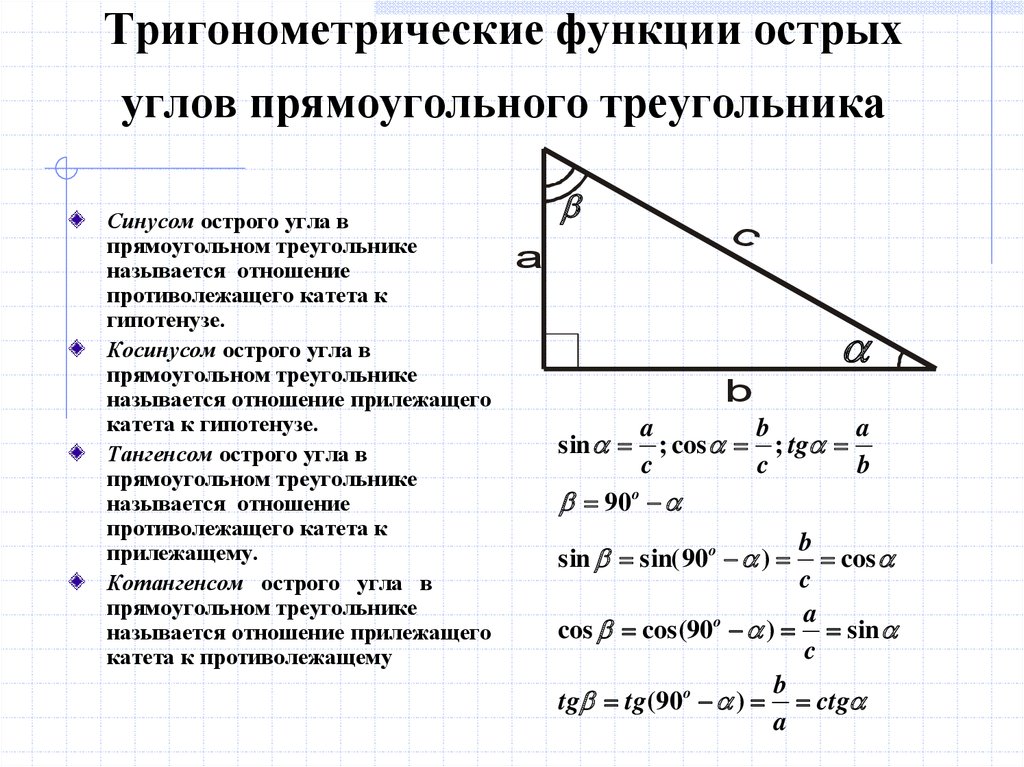
Используя таблицу тригонометрических функций, найдите угол наклона солнечных лучей, если длина тени стоящего человека в два раза меньше его роста. В ответе укажите приближенное значение, выражаемое целым числом градусов.
Упражнение 41
Ответ: 31о.
Лестница имеет ступеньки, ширина которых равна 30 см, а высота – 18 см. Используя таблицу тригонометрических функций, найдите угол подъема лестницы. В ответе укажите приближенное значение, выражаемое целым числом градусов.
Упражнение 42
Ответ: 53о.
Ширина дачного домика равна 6 м, ширина одного ската его двускатной крыши равна 5 м. Используя таблицу тригонометрических функций, найдите угол между стропилами крыши и потолком.
Упражнение 43
Ответ: 37о.
Ширина футбольных ворот равна 8 ярдам. Расстояние от 11-метровой отметки до линии ворот равно 12 ярдам. Найдите угол, под которым видны ворота с 11-метровой отметки. В ответе укажите целое число градусов.
Расстояние от 11-метровой отметки до линии ворот равно 12 ярдам. Найдите угол, под которым видны ворота с 11-метровой отметки. В ответе укажите целое число градусов.
Таблица тригонометрических функций
Скачать презентацию
Синус, косинус и тангенс острого угла прямоугольного треугольника — Студопедия
Поделись
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный . Другими словами, половина развернутого угла.
Острый угол — меньший .
Тупой угол — больший . Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой.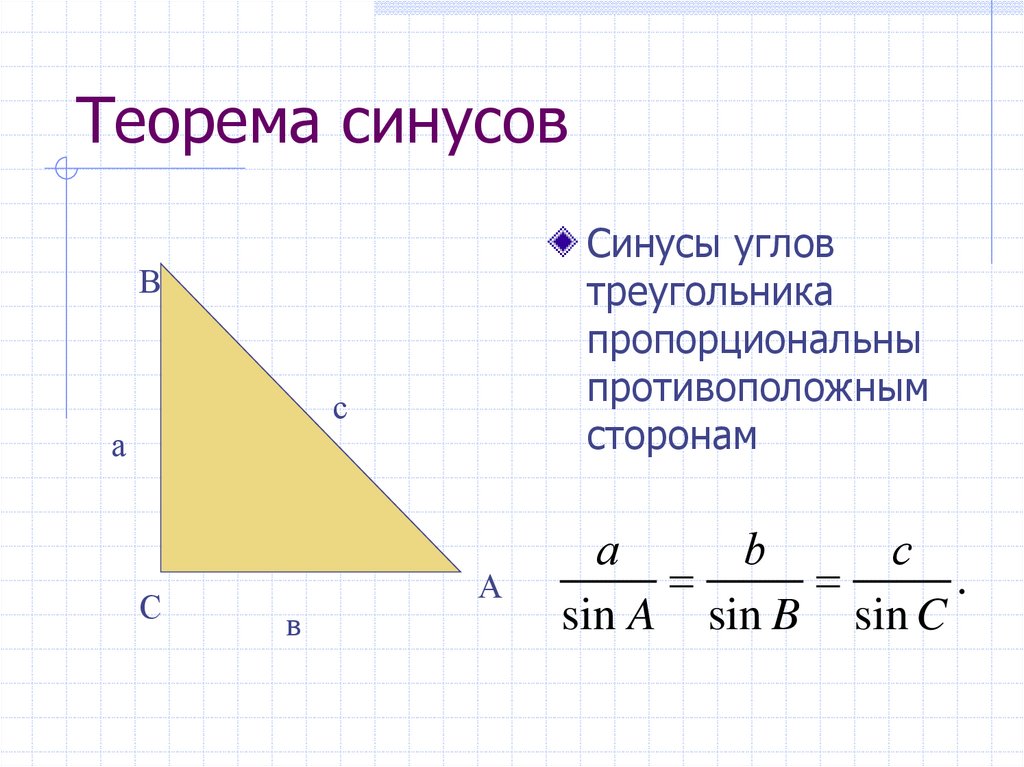 Так, сторона, лежащая напротив угла , обозначается .
Так, сторона, лежащая напротив угла , обозначается .
Угол обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты— стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
1. Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
2. С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет будет прилежащим.
Получаем, что . Иными словами, .
3. Возьмем теорему Пифагора: . Поделим обе части на :
Мы получили основное тригонометрическое тождество:
Таким образом, зная синус угла, мы можем найти его косинус, и наоборот.
4. Поделив обе части основного тригонометрического тождества на , получим:
Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус.
Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна.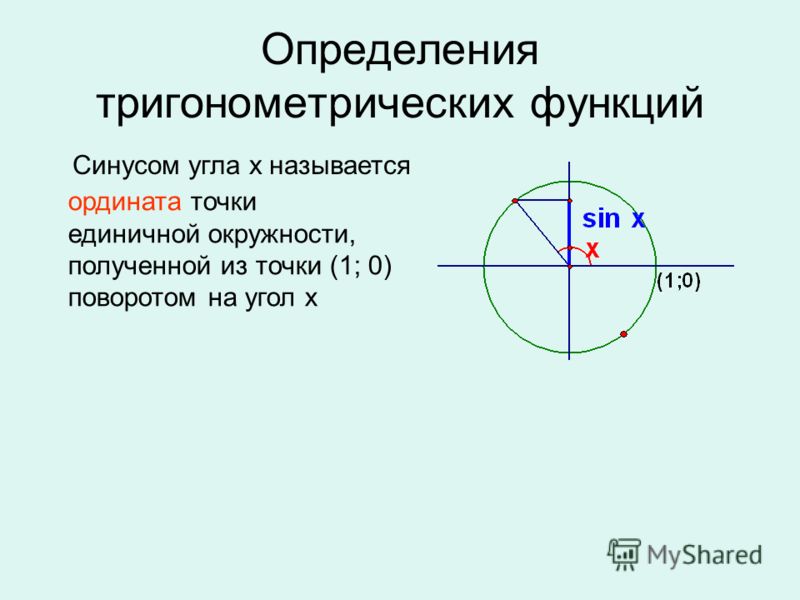
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике угол равен , . Найдите .
Задача решается за четыре секунды.
Поскольку , имеем: .
2. В треугольнике угол равен , , . Найдите .
Имеем:
Отсюда
Теперь находим по теореме Пифагора:
Задача решена.
Часто в задачах встречаются треугольники с углами , и или с углами , и . Основные соотношения для них запоминайте наизусть!
Для треугольника с углами , и катет, лежащий напротив угла в , равен половине гипотенузы.
Треугольник с углами , и — равнобедренный. В нем гипотенуза в раз больше катета.
Соотношения в прямоугольном треугольнике — определение и вычисление с формулами и примерами решения
Содержание:
Пусть в прямоугольном треугольнике гипотенуза равна с, один из острых углов равен
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:
Пример:
Угол К в равен 90° (рис. 7).
Тогда:
Для угла N катет МК — противолежащий, а катет NK — прилежащий (см. рис. 7, с. 11). Поэтому согласно определениям получаем:
Можно заметить, что синус острого угла а прямоугольного треугольника и косинус другого острого угла этого треугольника, содержащего равны, т. е. . Так же Например,
е. . Так же Например,
А теперь выполните Тест 1 и Тест 2.
Значение синуса острого угла, а также косинуса, тангенса и котангенса зависит только от величины угла и не зависит от размеров и расположения прямоугольного треугольника с указанным острым углом.
Это следует из того, что прямоугольные треугольники с равным острым углом подобны, а у подобных треугольников соответствующие стороны пропорциональны. Так, в (рис. 8)
Рассмотрим прямоугольный треугольник АВС, у которого (рис. 9). Так как катет, лежащий против угла в 30°, равен половине гипотенузы, то АВ = 2. По теореме Пифагора
Тогда:
Так как (см. рис. 9), то
Рассмотрим равнобедренный прямоугольный треугольник АВС, у которого (рис. 10). По теореме Пифагора
Тогда:
Составим таблицу значений синусов, косинусов, тангенсов и котангенсов для углов 30°, 45° и 60°.
Значения синуса, косинуса, тангенса и котангенса данного угла можно приближенно находить при помощи специальных тригонометрических таблиц* либо калькулятора.
Например, с помощью калькулятора, компьютера или мобильного телефона (смартфона) находим: sin45° = 0,707106… . Приближенное значение тригонометрических функций при решении задач будем брать с округлением до четырех знаков после запятой: sin45° = 0,7071.
Итак, точное значение sin 45° равно . а приближенное — 0,7071.
Таблицы и калькулятор также позволяют находить величину острого угла по значению синуса, косинуса или тангенса. Например, найдем острый угол, синус которого равен 0,4175. Выбрав на компьютере вид калькулятора «инженерный», далее «градусы», нужно ввести последовательно . На экране появится ответ: 24,676… . Округлим его до десятых долей градуса и получим 24,7°. Учитывая, что 1° содержит 60 угловых минут, получим: 0,7° = 0,7 • 60′ = 42′. Искомый угол, синус которого 0,4175, приближенно равен 24°42′.
Искомый угол, синус которого 0,4175, приближенно равен 24°42′.
А теперь выполните Тест 3.
Синус, косинус, тангенс и котангенс являются функциями угла, так как каждому острому углу соответствует единственное значение синуса, косинуса, тангенса и котангенса. Они называются тригонометрическими функциями и записываются так:
Поскольку в прямоугольном треугольнике катет меньше гипотенузы, то для острого угла справедливо: следовательно синус и косинус острого угла положительны и меньше 1.
Тангенс и котангенс острого угла могут принимать любое положительное значение. Например, tg85° ~ 11,4.
С увеличением острого угла синус и тангенс возрастают, а косинус и котангенс убывают (рис. 11), то есть если то
но (cm. c. 28, задачу 2*). Это гарантирует, что синус (косинус, тангенс и котангенс) острого угла определяют этот угол однозначно.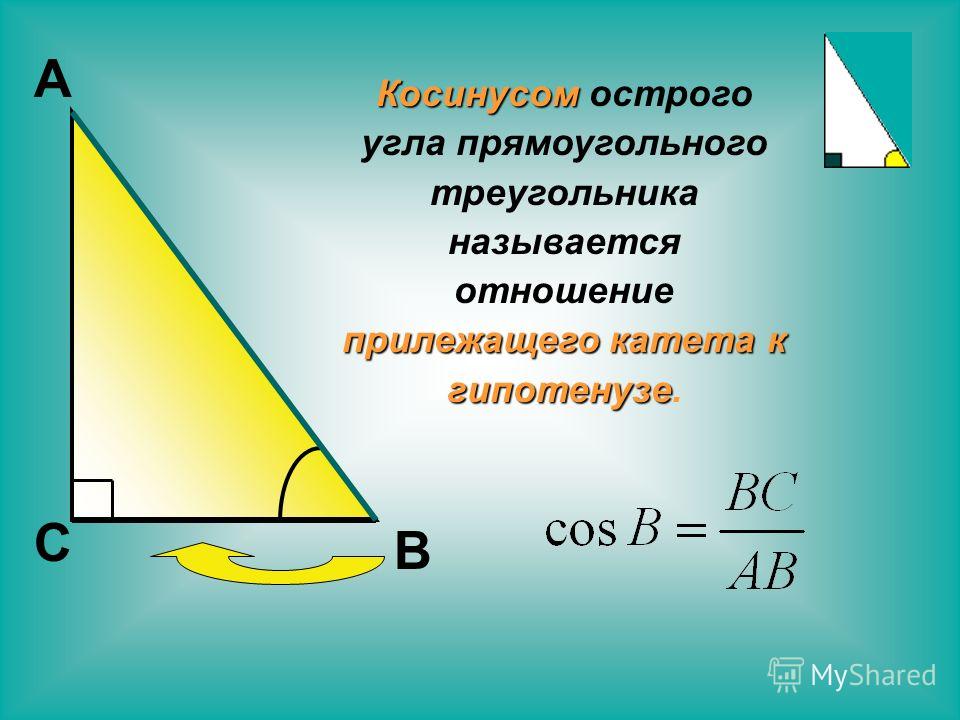
В прямоугольном треугольнике АВС, где , катет ВС равен 8 см, гипотенуза АВ равна 17 см. Найти косинус угла А (рис. 12).
Решение:
По теореме Пифагора найдем катет (см). Косинус острого угла прямоугольного треугольника равен от ношению прилежащего катета к гипотенузе. Тогда
Ответ:
Пример №2Гипотенуза АВ прямоугольного треугольника АВС равна 20 см, (рис. 13). Найти площадь треугольника.
Решение:
Так как Обозначим По теореме Пифагора Тогда ВС = 4 • 4 = 16(см),
Ответ: 96
Пример №3При помощи циркуля и линейки построить угол, синус которого равен
Решение:
Идея решения. Построим прямоугольный треугольник с катетом, равным 4 единицы, и гипотенузой, равной 5 единиц. Синус угла, противолежащего указанному катету, будет равен
Построение.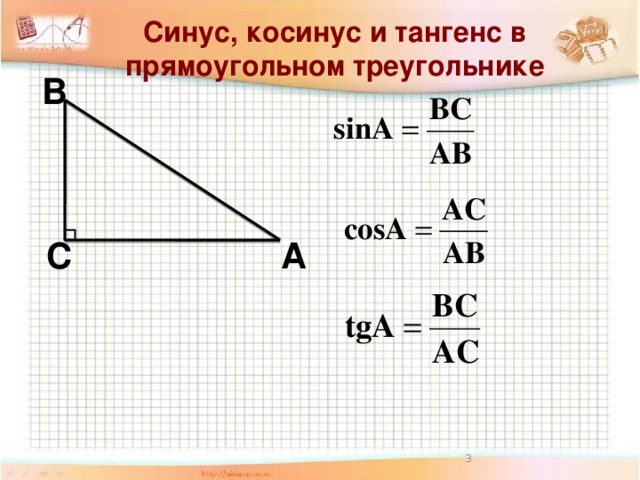 1) Строим прямой угол С (рис. 14), для чего проводим произвольную прямую отмечаем на ней точку С и строим прямую проходящую через точку С перпендикулярно прямой (вспомните по рисунку алгоритм построения). 2) На прямой от точки С откладываем последовательно четыре равных отрезка. Получаем отрезок ВС, который содержит 4 единицы. 3) Строим окружность с центром в точке В радиусом, равным пяти единицам. В пересечении этой окружности и прямой получаем точку А.
1) Строим прямой угол С (рис. 14), для чего проводим произвольную прямую отмечаем на ней точку С и строим прямую проходящую через точку С перпендикулярно прямой (вспомните по рисунку алгоритм построения). 2) На прямой от точки С откладываем последовательно четыре равных отрезка. Получаем отрезок ВС, который содержит 4 единицы. 3) Строим окружность с центром в точке В радиусом, равным пяти единицам. В пересечении этой окружности и прямой получаем точку А.
Угол ВАС — искомый.
Доказательство:
Из находим
Алгоритм решения прямоугольного треугольникаПод решением прямоугольного треугольника понимают нахождение его неизвестных сторон и углов по некоторым элементам, определяющим этот треугольник. Рассмотрим три задачи:
- нахождение катета по гипотенузе и острому углу;
- нахождение катета по другому катету и острому углу;
- нахождение гипотенузы по катету и острому углу.

Гипотенуза прямоугольного треугольника равна 6, острый угол равен 32° (рис. 23). Найти катет, прилежащий к данному углу. Ответ округлить до 0,1.
Решение:
Примем длину искомого катета за
Ответ: 5,1.
Пример №5Катет прямоугольного треугольника равен 2,5, а прилежащий к нему угол равен 68° (рис. 24). Найти другой катет. Ответ округлить до 0,1.
Решение:
Примем длину неизвестного катета за
Ответ: 6,2.
Пример №6Катет прямоугольного треугольника равен 4,2, противолежащий ему угол равен 29° (рис. 25). Найти гипотенузу треугольника. Ответ округлить до 0,1.
Решение:
Примем длину гипотенузы за
Ответ: 8,7.
Правила решения прямоугольного треугольникаПреобразуем формулы синуса, косинуса, тангенса и котангенса и запишем результаты для треугольника на рисунке 26:
Удобно пользоваться следующими правилами:
- Катет равен гипотенузе, умноженной на синус противолежащего или на косинус прилежащего угла (рис.
 27, а).
27, а). - Гипотенуза равна катету, деленному на синус противолежащего или на косинус прилежащего угла (рис. 27, б).
- Катет равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к первому катету угла (рис. 27, в).
В известно: (рис. 28).
Полезно запомнить!
Если в прямоугольном треугольнике с углом 30° (или 60°) дан меньший катет а, то больший
катет (рис. 29, а). А если дан больший катет то меньший катет (рис. 29, б).
Если в прямоугольном треугольнике с углом 45° дан катет а,
то гипотенуза (рис. 30, а), а если дана гипотенуза с, то катет (рис. 30, б).
Пример №8В прямоугольном треугольнике АВС известно: — высота, проведенная к гипотенузе (рис. 31). Найти проекцию НВ катета ВС на гипотенузу.
31). Найти проекцию НВ катета ВС на гипотенузу.
Решение:
Заметим, что так как эти углы дополняют Из Из
Ответ:
Пример №9В равнобедренной трапеции ABCD меньшее основание ВС равно 7, боковая сторона АВ равна 10, sinA = 0,8. Найти площадь трапеции.
Решение:
Площадь трапеции находится по формуле Найдем большее основание и высоту трапеции. Проведем в трапеции высоты ВН и СК (рис. 32). Так как НВСК — прямоугольник (все углы — прямые), то НК = ВС = 7. Из равенства прямоугольных треугольников АНВ и DKC (по катету и гипотенузе) АН = KD. Из прямоугольного треугольника АНВ находим: откуда АН = 6 (пифагорова тройка 6, 8, 10). Тогда
Ответ: 104.
Тригонометрические формулыИспользуя формулы где и — катеты, с — гипотенуза прямоугольного треугольника, можно получить формулы, связывающие значения тригонометрических функций острого угла.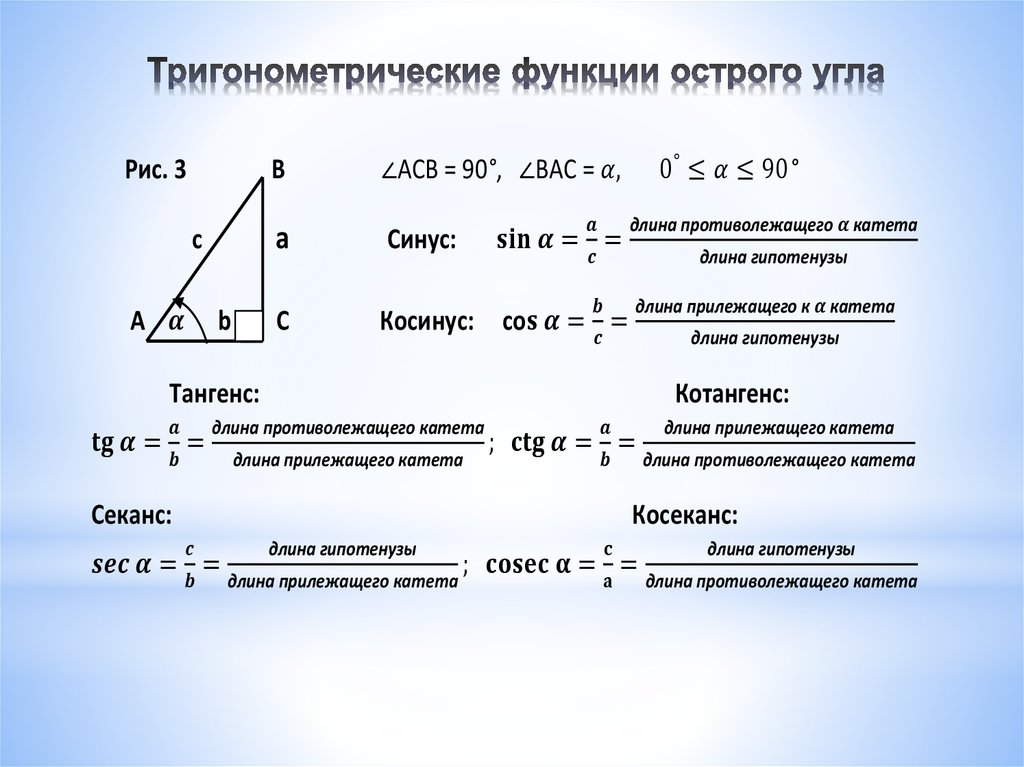
1. Основное тригонометрическое тождество
Доказательство:
По теореме Пифагора
Тогда
Следствие:
Так как синус и косинус острого угла а положительны, то
2. Выражение тангенса и котангенса через синус и косинус
Доказательство:
a) б)
Следствие:
Проверим справедливость основного тригонометрического тождества.
Верно ли, например, что Да, это верно, так как
3. Основная задача
Дано: — острый угол.
Найти:
Решение:
Способ 1. Используем основное тригонометрическое тождество: Так как косинус острого угла больше нуля, то откуда
Способ 2. Изобразим прямоугольный треугольник с катетом 5 и гипотенузой 13 (рис. 41). Синус угла, противолежащего данному катету, равен Поэтому этот угол равен По теореме Пифагора другой катет равен Тогда
Способ 3.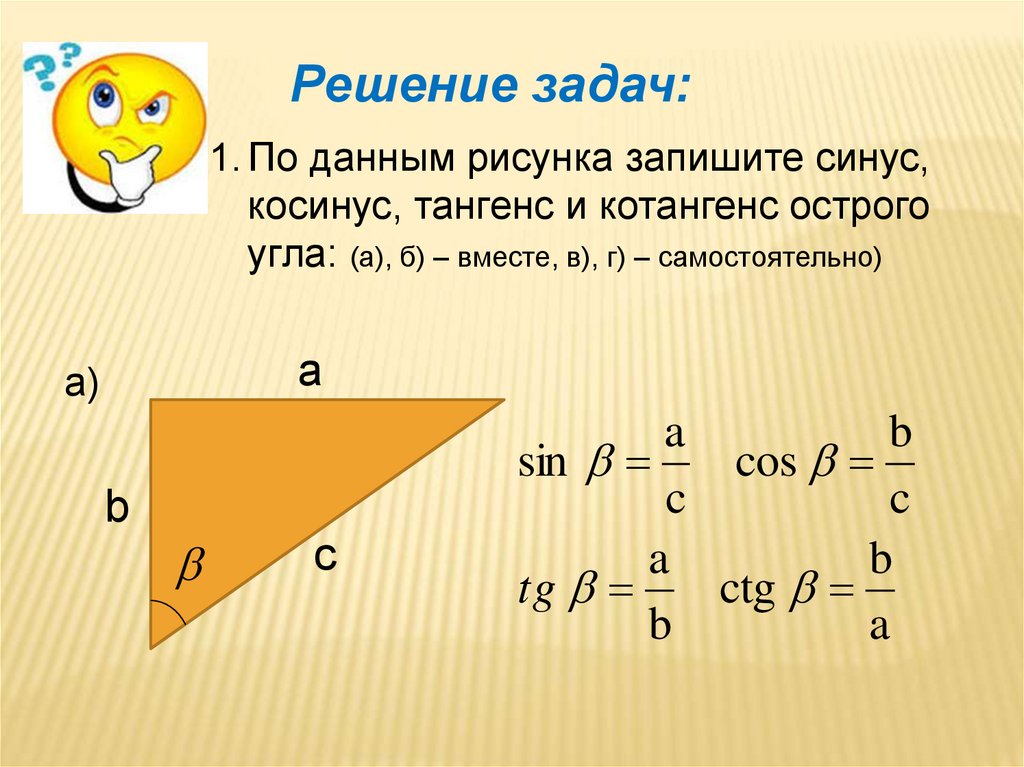 Пусть катет, противолежащий углу равен 5х, тогда гипотенуза равна По теореме Пифагора прилежащий катет равен Отсюда
Пусть катет, противолежащий углу равен 5х, тогда гипотенуза равна По теореме Пифагора прилежащий катет равен Отсюда
Ответ:
Пример №10В параллелограмме ABCD (рис. 42) сторона ВС = 50 см, высота ВК = 30 см, . Найти периметр параллелограмма.
Решение:
Из треугольника АВК находим: Из основного тригонометрического тождества следует: (так как угол А — острый, то sinA > 0). Тогда (см )
Ответ: 168 см.
Доказать, что при увеличении угла от 0° до 90°:
а) синус угла увеличивается от 0 до 1, а косинус — уменьшается от 1 до 0;
б) тангенс угла увеличивается от О до бесконечности.
Решение:
а) Рассмотрим прямоугольные треугольники с гипотенузой, равной 1. Для этого опишем радиусом ОМ, равным 1, четверть окружности — дугу МК (рис. 43). Пусть Опустим из точки А перпендикуляр АВ на ОМ. Тогда При повороте радиуса ОМ вокруг центра О против часовой стрелки, начиная от ОМ и заканчивая ОК, угол будет увеличиваться от 0° до 90° (образуя указанные на чертеже углы: и т. д.). Величина катета АВ, противолежащего углу будет увеличиваться от 0 до 1. А величина катета ОВ, наоборот, будет уменьшаться от 1 до 0. Таким образом, при увеличении угла от 0° до 90° его синус увеличивается от 0 до 1, а косинус уменьшается от 1 до 0.
43). Пусть Опустим из точки А перпендикуляр АВ на ОМ. Тогда При повороте радиуса ОМ вокруг центра О против часовой стрелки, начиная от ОМ и заканчивая ОК, угол будет увеличиваться от 0° до 90° (образуя указанные на чертеже углы: и т. д.). Величина катета АВ, противолежащего углу будет увеличиваться от 0 до 1. А величина катета ОВ, наоборот, будет уменьшаться от 1 до 0. Таким образом, при увеличении угла от 0° до 90° его синус увеличивается от 0 до 1, а косинус уменьшается от 1 до 0.
Из формулы также следует (учитывая положительность синуса и косинуса острого угла), что с увеличением синуса от 0 до 1 косинус уменьшается от 1 до 0.
б) Для определения изменения тангенса угла удобно рассматривать треугольники, у которых прилежащий катет не изменяется и остается равным 1, а противолежащий катет изменяется. Рассмотрим прямоугольный треугольник АОМ, у которого отрезок ОМ = 1, (рис. 44). По определению Угол станем изменять, перемещая точку А по прямой MN, начиная от точки М и проходя через точки и т. д. При этом угол и его тангенс начнут возрастать. Таким образом, когда угол при движении точки А вверх будет стремиться к углу КОМ, равному 90°, то тангенс этого угла будет неограниченно возрастать.
44). По определению Угол станем изменять, перемещая точку А по прямой MN, начиная от точки М и проходя через точки и т. д. При этом угол и его тангенс начнут возрастать. Таким образом, когда угол при движении точки А вверх будет стремиться к углу КОМ, равному 90°, то тангенс этого угла будет неограниченно возрастать.
К такому же выводу можно прийти, рассматривая формулу При увеличении угла от 0° до 90° числитель дроби будет увеличиваться от 0 до 1, а знаменатель — уменьшаться от 1 до 0, значит, вся дробь будет увеличиваться от 0 до бесконечности. Таким образом, при увеличении угла от 0° до 90° его тангенс увеличивается от 0 до бесконечности.
В основании прямоугольного параллелепипеда лежит квадрат, диагональ которого см. Диагональ боковой грани составляет с ребром основания угол (рис. 46). Найдите объем параллелепипеда.
Решение:
Объем прямоугольного параллелепипеда находится по формуле , где а, b и с — его измерения. Так как ABCD — квадрат, то . Из прямоугольного треугольника находим . Искомый объем .
Так как ABCD — квадрат, то . Из прямоугольного треугольника находим . Искомый объем .
Ответ: 576 см3.
1. Определение значений для любого угла а от 0° до 180°
Ранее мы дали определения синуса, косинуса, тангенса и котангенса острого угла через отношение сторон прямоугольного треугольника. Сделаем теперь это для углов от 0° до 180°.
Рассмотрим полуокружность с центром в начале координат и радиусом, равным 1 (рис. 48). От положительной полуоси против часовой стрелки отложим острый угол сторона которого пересекает полуокружность в точке . Из прямоугольного треугольника OMN, где ОМ = 1, ON = х, MN = у, получаем: то есть синус, косинус,
тангенс и котангенс острого угла а выражаются через координаты точки Точно так же определяются значения и для любого угла а из промежутка Таким образом, синусом угла а называется ордината косинусом — абсцисса тангенсом — отношение ординаты к абсциссе а котангенсом — отношение абсциссы к ординате точки М единичной полуокружности.
Например, для тупого (рис. 48), где получим:
Для любого положения точки на единичной полуокружности верно равенство (докажите самостоятельно). Поэтому для углов где верно основное тригонометрическое тождество
Также верны тождества:
Пусть откуда (рис. 49). Так как по гипотенузе и острому углу, то Точки имеют координаты: и Тогда то есть для углов от 0° до 180° справедливы равенства:
Можно пользоваться следующим правилом:
Синус тупого угла равен синусу смежного с ним острого угла.
Косинус тупого угла равен косинусу смежного с ним острого угла, взятому со знаком «минус».
Пример 1.
Разделив почленно равенство на равенство а затем наоборот, получим равенства:
Можно пользоваться следующим правилом:
Тангенс (котангенс) тупого угла равен тангенсу (котангенсу) смежного с ним острого угла, взятому со знаком «минус».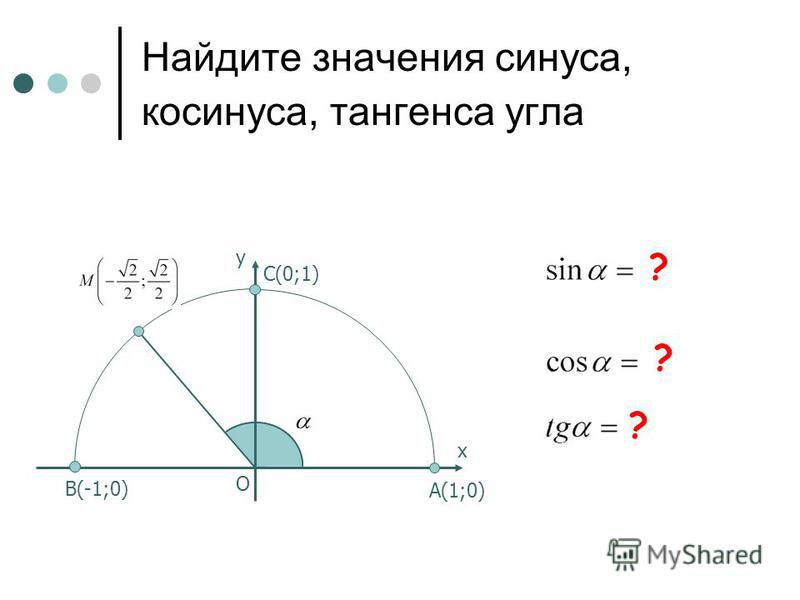
Пример 2.
Указанные формулы и правила позволяют находить значения тригонометрических функций тупого угла через значения тригонометрических функций острого угла, который дополняет данный тупой угол до 180°: синусы углов, дополняющих друг друга до 180°, равны между собой, а косинусы, тангенсы и котангенсы — противоположны. Так как синус, косинус, тангенс и котангенс острого угла положительные, то синус тупого угла положительный, а косинус, тангенс и котангенс — отрицательные.
Если луч ОМ совпадет с лучом (рис. 50), то будем считать, что Тогда:
а) значение не определено, так как деление на нуль невозможно;
б) значение не определено, так как деление на нуль невозможно; в) значение не определено, так как деление на нуль невозможно.
Поскольку проекции радиуса, равного 1, на оси координат меньше либо равны 1, то для углов справедливы неравенства:
Найти если — тупой угол.
Решение:
Способ 1. Так как то Поскольку угол — тупой, то его косинус отрицательный. Поэтому Тогда
Способ 2. Синус острого угла смежного с данным тупым углом равен также Построим прямоугольный треугольник со сторонами 3, 4 и 5 (рис. 52). В нем Так как косинусы смежных углов противоположны, то . Аналогично,
Ответ:
Формулы площади треугольника и площади параллелограммаТригонометрические функции позволяют получить формулы для вычисления площади треугольника и площади параллелограмма. Сформулируем их в виде двух теорем.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними, т. е.
Доказательство:
Пусть в треугольнике — острый, — высота (рис. 56, а).
Из прямоугольного треугольника Тогда
Если угол тупой (рис. 56, то — острый. Из прямоугольного треугольника АКС следует, что Так как то
Если то — прямоугольный с катетами Учитывая, что получим:
Теорема доказана.
Теорема. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними, т. е.
Используя рисунок 57, докажите эту теорему самостоятельно.
Замечание. Если то параллелограмм является прямоугольником. Его площадь так как Таким образом, формула площади прямоугольника — частный случай формулы площади параллелограмма
Известно, что слово «синус» в переводе с латинского имеет множество значений: изгиб, дуга, пазуха, бухта, впадина, залив, хорда, забота и нежная любовь. При помощи Интернета выясните:
а) какое из значений подходит к математическому понятию «синуса»;
б) какие из значений относятся к медицине и почему насморк врачи иногда называют синуситом.
Пример №14Дан параллелограмм ABCD, площадь которого 40 см2, а периметр 36 см. Найти стороны параллелограмма, если его угол D равен 150° (рис. 58).
Решение:
Полупериметр параллелограмма равен 18 см. Если см, то см.
Если см, то см.
Тогда
Так как то
По условию Составим и решим уравнение: По теореме Виета (обратной) — корни.
Если CD = 8 см, то AD = 10 см, если CD = 10 см, то AD = 8 см.
Ответ: 8 см, 10 см.
Доказать, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними, т.е.
Доказательство:
Пусть диагонали и четырехугольника ABCD (рис. 59) пересекаются в точке О, Докажем, что
Обозначим Заметим, что как вертикальные, по свойству смежных углов. Поэтому По формуле площади треугольника у получим:
Утверждение доказано
Если для положительных чисел выполняется пропорция то число называется средним пропорциональным чисел а и с (между числами а и с).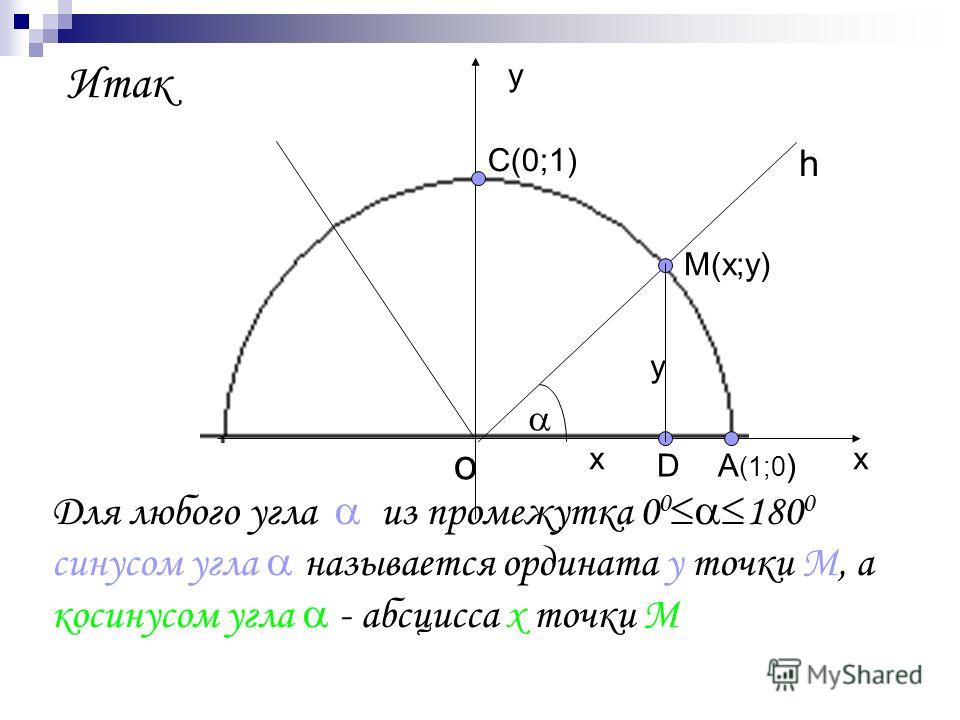 Из указанной пропорции откуда В такой форме записи число еще называют средним геометрическим чисел а и с.
Из указанной пропорции откуда В такой форме записи число еще называют средним геометрическим чисел а и с.
Число 4 является средним пропорциональным, или средним геометрическим чисел 2 и 8, так как = или
В прямоугольном треугольнике АВС, где , проведем высоту СК (рис. 61). Отрезок АК является проекцией катета АС на гипотенузу, а отрезок ВК — проекцией катета ВС на гипотенузу. Катеты, гипотенуза, высота и проекции катетов на гипотенузу связаны отношениями, которые мы сформулируем в виде следующей теоремы.
Теорема (о среднем пропорциональном в прямоугольном треугольнике).
а) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу, т. е. (см. рис. 61).
б) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу, т.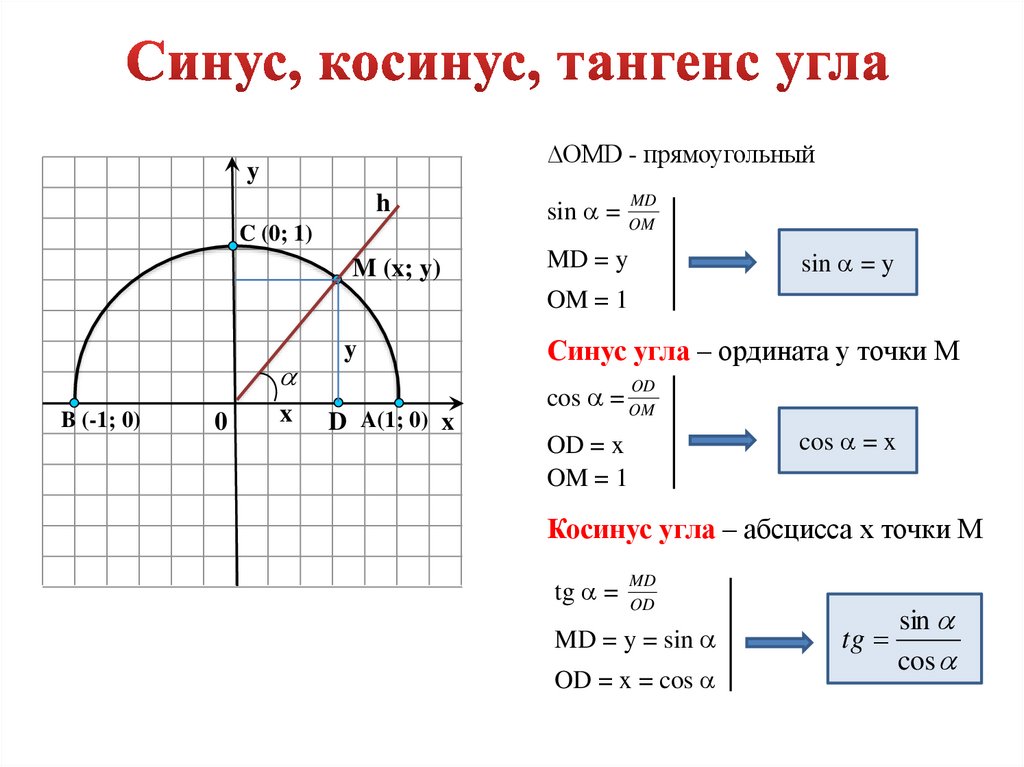 е.
е.
Доказательство:
а)3аметим, что если то (эти углы дополняют до 90°) (рис. 62). Из из Отсюда
б) Из , из откуда
Аналогично доказывается, что Теорема доказана.
Обозначив катеты гипотенузу с, высоту проекции катетов на гипотенузу (рис. 63), получим следующие формулы:
Пример №17Найти площадь прямоугольного треугольника, если проекции катетов на гипотенузу равны 2 см и 8 см.
Решение:
Пусть СН — высота прямоугольного треугольника АВС АН = 2 см — проекция катета АС на гипотенузу, НВ = 8 см —
проекция катета СВ на гипотенузу (рис. 64). Так как высота СН есть среднее геометрическое между проекциями катетов на гипотенузу, то
Ответ: 20 см2.
Пример №18В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота см, АК = 12 см (рис.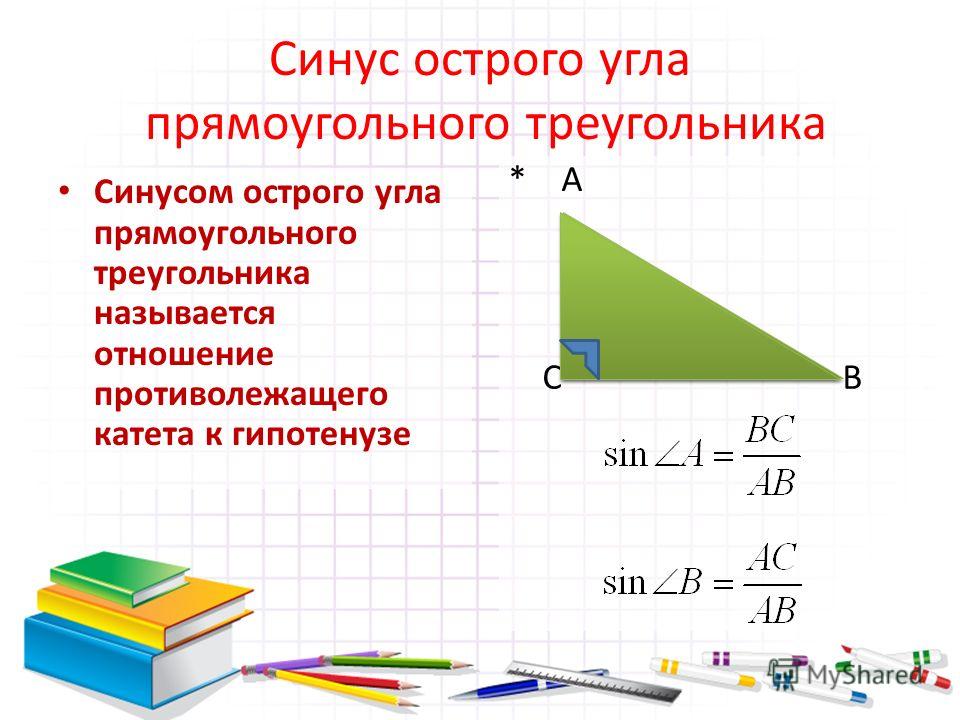 65). Найти гипотенузу АВ.
65). Найти гипотенузу АВ.
Решение:
Пусть см, тогда см.
Катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу. Поэтому т. е. По теореме Виета (обратной) По смыслу задачи Значит, КВ = 3 см, АВ = 15 см.
Ответ: 15 см.
При помощи циркуля и линейки построить отрезок, равный среднему геометрическому отрезков т и п .
Решение:
Пусть даны отрезки т и п . Необходимо построить отрезок
Построение.
1) На произвольной прямой откладываем данные отрезки:
2) На отрезке АВ как на диаметре строим полуокружность, для чего находим середину О отрезка АВ, откуда ОА — радиус данной окружности.
3) Из точки К восстанавливаем перпендикуляр к прямой АВ до пересечения с полуокружностью в точке М (рис. 66).
66).
Отрезок — среднее пропорциональное отрезков
Доказательство:
— прямой как вписанный угол, опирающийся на диаметр. В прямоугольном треугольнике АМВ высота МК является средним пропорциональным проекций катетов AM и МВ на гипотенузу
Повторение*
В 8-м классе мы доказали следующую теорему:
Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков се кущей, соединяющих данную точку и точки пересечения секущей с окружностью, т. е. (рис. 70).
Как видим, отрезок является средним пропорциональным между отрезками секущей. Глядя на рисунок 70, вспомните идею доказательства теоремы.
Теорема о площадях треугольников с общим (равным) угломПлощади треугольников, имеющих общий угол (или равный угол), относятся как произведения сторон, заключающих этот угол (рис.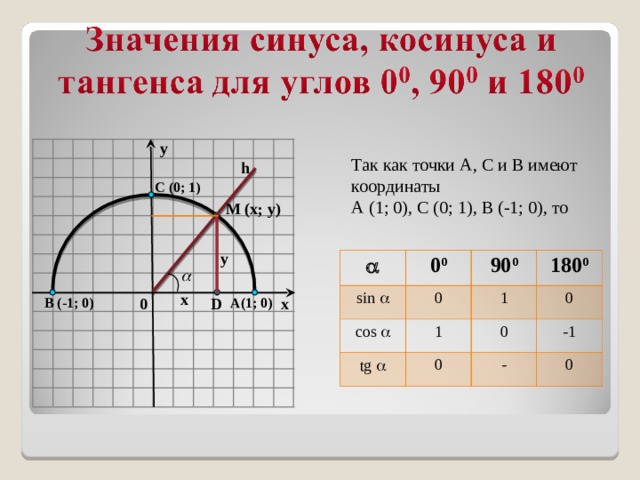 75),
75),
т.е.
Доказательство:
Следствие: Верно:
Пример №20Площадь треугольника АВС равна 16, АК : КС = 3 :1 , AM : МВ = 1 :2 (рис. 76). Найти
Решение:
Способ 1. По следствию из теоремы о площадях треугольников с общим углом получаем:
Способ 2.
Ответ: 4.
Теорема МенелаяЕсли дан треугольник АВС и прямая пересекает стороны ВС, АВ и продолжение стороны АС в точках соответственно (рис. 79), то
Доказательство:
Проведем отрезок Так как и (по двум углам), то и Перемножив почленно указанные пропорции, получим
откуда
Замечание. При составлении произведения трех отношений теоремы Менелая можно начинать с любой из шести точек (трех вершин треугольника и трех точек пересечения прямой с прямыми, содержащими стороны треугольника) и двигаться по контуру либо по часовой, либо против часовой стрелки. При этом вершины треугольника и точки пересечения должны чередоваться.
При этом вершины треугольника и точки пересечения должны чередоваться.
В треугольнике АВС на сторонах АВ и АС взяты соответственно точки М и К, такие, что AM : МВ = 2 :1 , АК : КС = 3 :2 . Отрезки СМ и ВК пересекаются в точке О. Найти ВО : ОК.
Решение:
Способ 1 (теорема Менелая). Рассмотрим (рис. 80). Прямая пересекает две его стороны АВ и ВК соответственно в точках М и О и продолжение третьей стороны АК в точке С. По теореме Менелая откуда
Способ 2 (теорема Фалеса обобщенная). Проведем (рис. 81). По теореме Фалеса Тогда АЕ — три части, ЕМ — две части, AM — пять частей, откуда
Но Отсюда Для
по теореме Фалеса
Ответ:
Пример №22
Дан равнобедренный треугольник АВС (АВ = ВС), площадь которого равна 80. Точка К делит высоту ВН в отношении 1 : 3, считая от основания. Прямая АК пересекает сторону ВС в точке М. Найти площадь четырехугольника НКМС (рис. 82).
Прямая АК пересекает сторону ВС в точке М. Найти площадь четырехугольника НКМС (рис. 82).
Решение:
1) (ВН — высота и медиана треугольника АВС).
2) Применим теорему Менелая к треугольнику НВС.
Прямая AM пересекает его стороны ВН и ВС соответственно в точках К и М и продолжение стороны НС в точке Тогда Откуда
3)
4)
Ответ: 22.
Неравенство КошиСреднее арифметическое двух неотрицательных чисел больше либо равно их среднему геометрическому, т. е.
Например, Действительно,
Алгебраическое доказательство указанного неравенства таково. Рассмотрим разность левой и правой частей неравенства Получим: Так как при всех допустимых , то Следовательно, неравенство верно.
Неравенство где называется неравенством Коши по имени известного французского математика и часто используется при решении олимпиадных задач.
Приведем геометрическое доказательство указанного неравенства. Изобразим окружность с диаметром АВ и центром в точке О (рис. 87). На диаметре возьмем точку К (для определенности левее центра О). Пусть Из точки К восстановим перпендикуляр КС, где точка С принадлежит окружности. Проведем радиус ОС. Так как вписанный угол, опирающийся на диаметр, прямой, то прямоугольный, СК — его высота, проведенная к гипотенузе. По теореме о среднем пропорциональном в прямоугольном треугольнике . Но радиус ОС равен половине диаметра АВ, т. е. . В катет меньше гипотенузы, т. е. так как катет меньше гипотенузы. Отсюда
Равенство левой и правой частей неравенства достигается, когда точка К совпадает с точкой О и становится равнобедренным и прямоугольным. Поэтому справедливо неравенство т. е
ЗАПОМИНАЕМ
2. Значения тригонометрических функций углов 30 45°, 60°:
3. Тригонометрические формулы (тождества):
Тригонометрические формулы (тождества):
Примеры:
4. Формулы площади треугольника и параллелограмма:
5. Среднее пропорциональное в прямоугольном треугольнике:
Синус, косинус и тангенс острого угла прямоугольного треугольника
Урок 25. Геометрия 8 класс ФГОС
На этом уроке мы повторим основные элементы прямоугольного треугольника. Введем понятие прилежащего и противолежащего катетов. Познакомимся с синусом, косинусом и тангенсом, понятиями, которые связывают острый угол прямоугольного треугольника с катетами и гипотенузой этого треугольника. Выведем две формулы для нахождения тангенса острого угла прямоугольного треугольника. Докажем основное тригонометрическое тождество. Подробно рассмотрим примеры, в которых надо найти синусы, косинусы и тангенсы острых углов прямоугольного треугольника.
Конспект урока «Синус, косинус и тангенс острого угла прямоугольного треугольника»
На этом уроке мы
познакомимся с синусом, косинусом и тангенсом, понятиями, которые связывают
острый угол прямоугольного треугольника с катетами и гипотенузой этого
треугольника.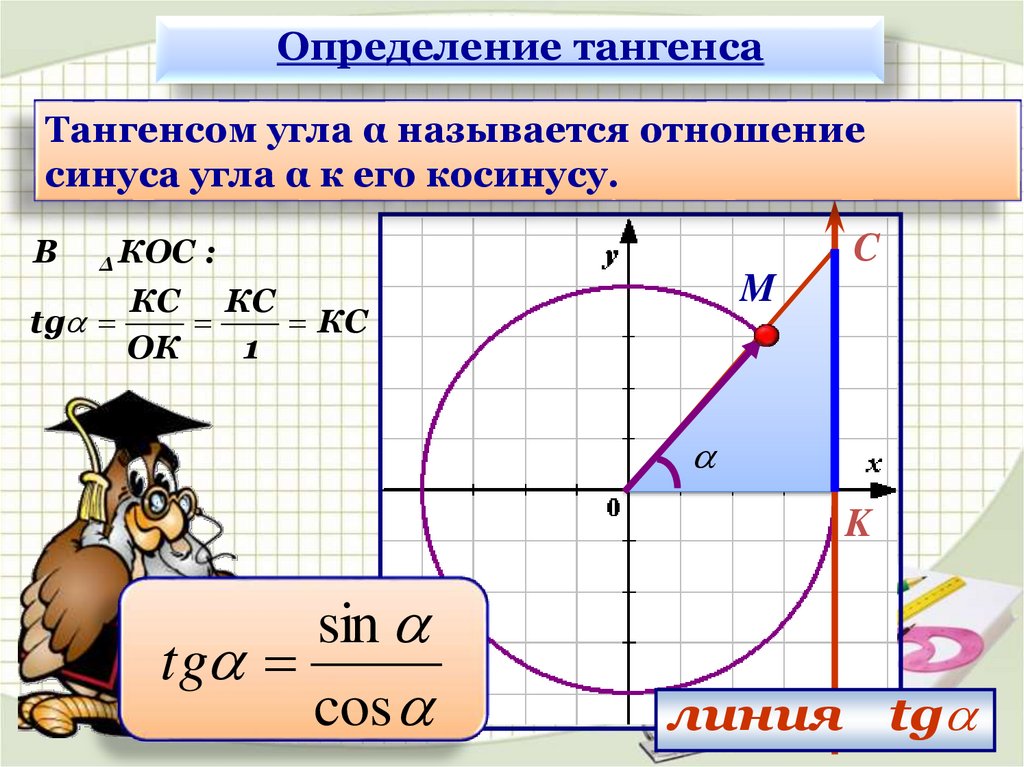
Прежде всего, давайте повторим основные сведения о прямоугольном треугольнике. Пусть нам дан прямоугольный треугольник ABC. Вершина C, угол С= 90º – прямой, гипотенуза с. Вершина А, угол α — острый, катет a. Вершина B, угол β — острый, катет b.
Напомним, что сумма углов треугольника равна 180º, значит, сумма острых углов прямоугольного треугольника равна 90º. Мы знаем, что стороны прямоугольного треугольника связаны между собой теоремой Пифагора.
Катет, BC является противолежащим для угла А, катет AC является прилежащим для угла А. Аналогично, катет AC является противолежащим для угла B, катет BC является прилежащим для угла B.
А теперь давайте подумаем, а можно ли связать между собой стороны и углы прямоугольного треугольника?
Давайте, посмотрим на два прямоугольных треугольника с острыми углами 30º и 60º.
И давайте,
попробуем найти отношение катета, противолежащего углу в тридцать градусов к
гипотенузе одного и второго треугольника.
Мы видим, что это отношение одинаково в обоих треугольниках.
Теперь давайте найдем отношение катета, прилежащего к углу в тридцать градусов. И опять получили одинаковые отношения.
;
Теперь давайте найдем отношение противолежащего катета к прилежащему. И снова у нас получились одинаковые отношения.
;
Теперь давайте, рассмотрим два прямоугольных равнобедренных треугольника. Острые углы этих треугольников равны по 45º. Находя для них такие же отношения, получим, что и в этом случае эти отношения для обоих треугольников равны.
= ;
= ;
;
Учеными было сделано предположение, что эти отношения не зависят от величины сторон прямоугольного треугольника, а зависят от величины острых углов прямоугольного треугольника. Для этих отношений были введены специальные названия и обозначения.
Определение: синусом
острого угла прямоугольного треугольника называется отношение противолежащего
катета к гипотенузе.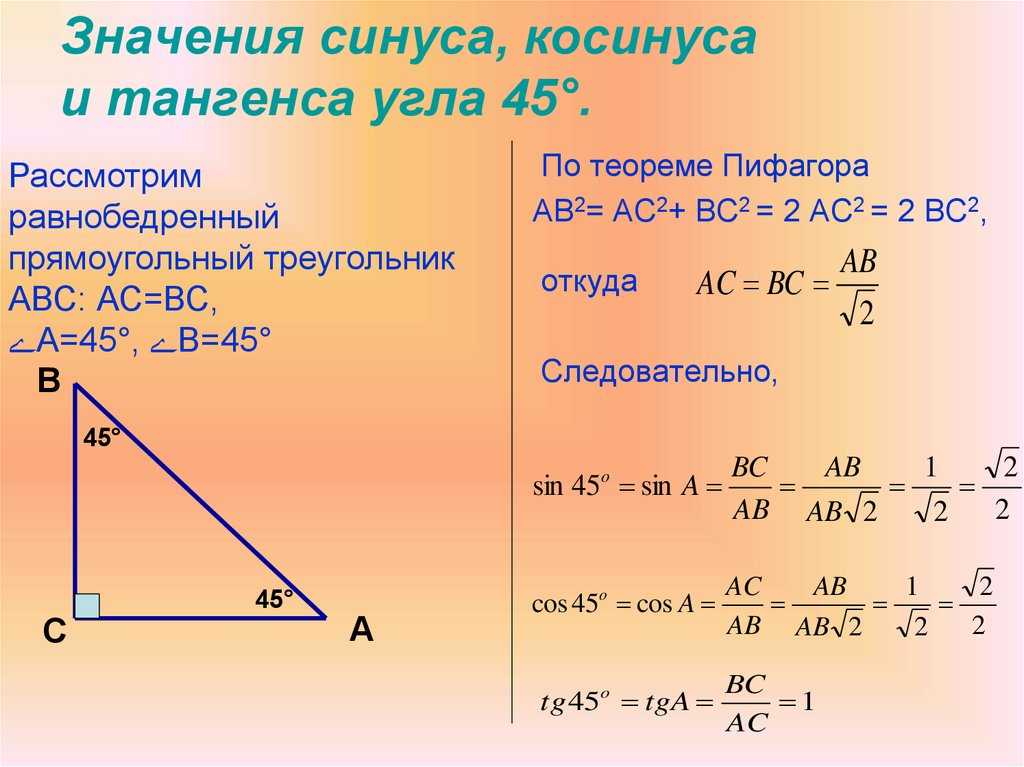
Определение: косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Определение: тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Теперь давайте попробуем найти отношение синуса угла α к косинусу того же угла.
; ;
Сравним полученную формулу с формулой тангенса угла α и увидим, что можно записать, что тангенс угла альфа равен отношению синуса угла альфа к косинусу угла альфа.;
Задача. Найти треугольника с прямым углом , если см, см.
Решение.
(см)
Ответ: .
Из определения синуса,
Из определения
тангенса угла А можно получить формулу, которая связывает два катета
прямоугольного треугольника. Получим, что катет a равен
произведению катета b на тангенс противолежащего угла.
Получим, что катет a равен
произведению катета b на тангенс противолежащего угла.
Задача. Пусть в прямоугольном треугольнике, один из катетов равен см, а противолежащий угол равен . Выразить второй катет, противолежащий ему угол и гипотенузу через известный катет и угол, и найти их значение.
Решение.
Ответ: .
Теперь давайте докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
Пусть нам даны два
прямоугольных треугольника ABC и A1B1C1 с прямыми
углами C и C1 и
равными острыми углами А и A1. Очевидно, что
углы B и B1 также
будут равны. То есть наши треугольники подобны по первому признаку подобия
(если два угла одного треугольника соответственно равны двум углам другого треугольника,
то такие треугольники подобны).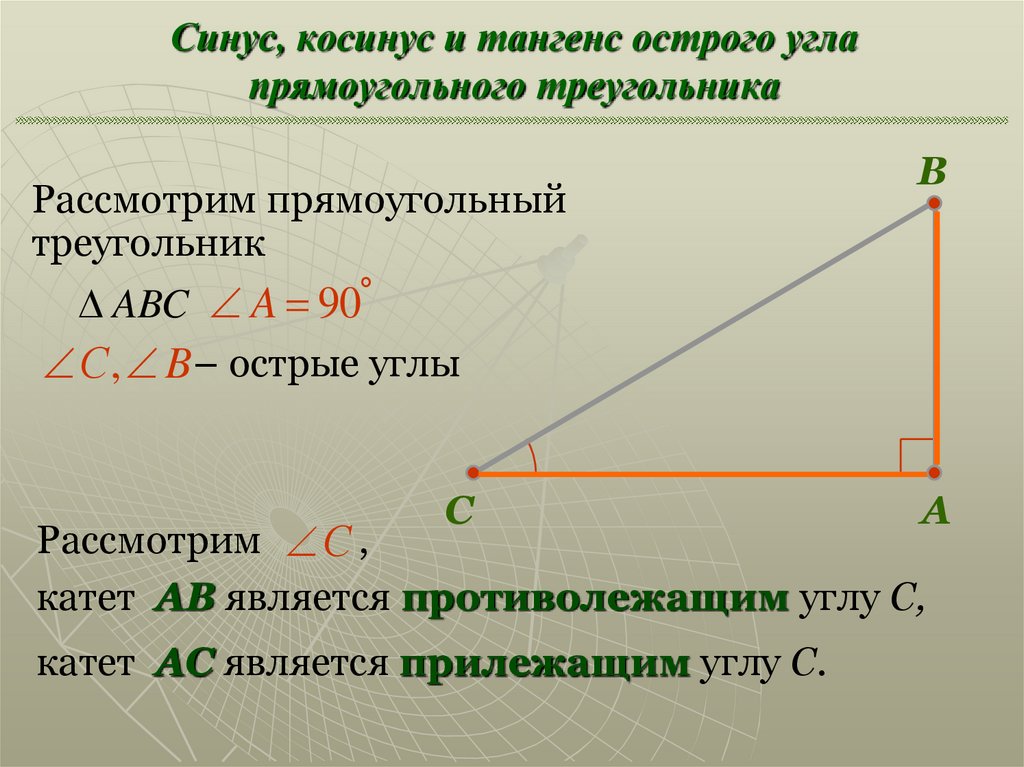
Значит, справедливы равенства
Из этих равенств несложно вывести равенство отношения а эти отношения есть ничто иное как синус угла А и синус угла A1. То есть можно записать, что .
Аналогично, можно вывести равенство отношения то есть равенство . А раз равны синусы и косинусы, то из формулы , получим, что . Таким образом, наше утверждение доказано.
Теперь, давайте попробуем доказать справедливость равенства:
Рассмотрим прямоугольный треугольник ABC.
Таким образом, справедливость равенства доказана.
Это равенство называют основным тригонометрическим тождеством. Синус, косинус, тангенс – тригонометрические функции.
Слово «тригонометрия»
происходит от греческих слов «треугольники» и «измеряю».
«Тригонометрия» — раздел математики, в котором изучают тригонометрические
функции и их использование в геометрии.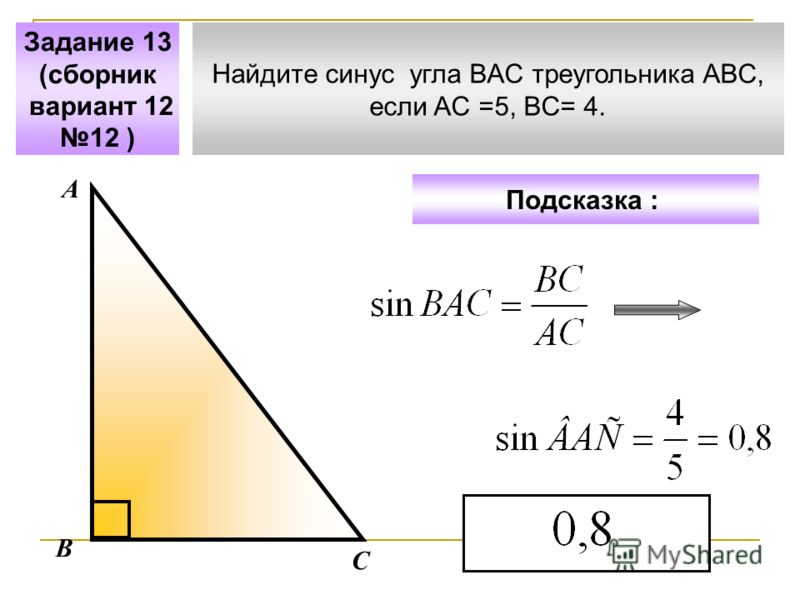
Задача. Найти если .
Решение
или
Ответ: .
Повторим главное:
синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе;
косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе;
тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему;
Синус и косинус одного и того же угла связаны между собой основным тригонометрическим тождеством.
Предыдущий урок 24 О подобии произвольных фигур
Следующий урок 26 Значения синуса, косинуса и тангенса для углов 30, 45 и 60
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 8 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Синус угла – формулы и примеры
Синус угла – это функция, относящаяся к сторонам прямоугольного треугольника.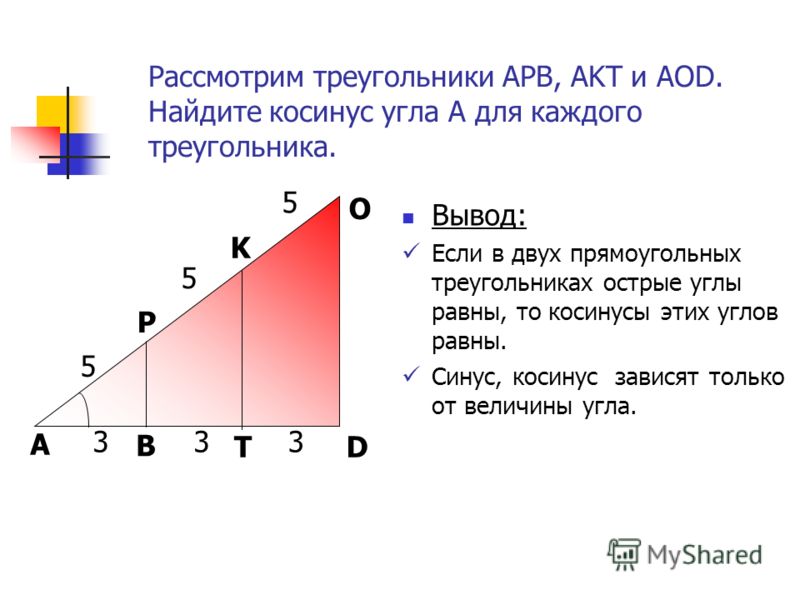 В частности, синус находится путем деления стороны, противоположной углу, на гипотенузу треугольника. Вне треугольника функцию синуса можно использовать для нахождения компонента y вектора, имеющего любой угол. Синус также эквивалентен косинусу дополнительного угла.
В частности, синус находится путем деления стороны, противоположной углу, на гипотенузу треугольника. Вне треугольника функцию синуса можно использовать для нахождения компонента y вектора, имеющего любой угол. Синус также эквивалентен косинусу дополнительного угла.
Здесь мы более подробно узнаем о синусе углов. Мы узнаем, как узнать синус важных углов, и решим некоторые практические задачи.
ТРИГОНОМЕТРИЯ
Актуально для …
Изучение синуса угла на примерах.
См. примеры
Содержание
ТРИГОНОМЕТРИЯ
Актуально для …
Изучение синуса угла на примерах.
См. примеры
Определение синуса угла
Синус угла определяется с помощью прямоугольного треугольника. Когда у нас есть прямоугольный треугольник, синус равен длине стороны, противоположной углу, деленной на длину гипотенузы треугольника.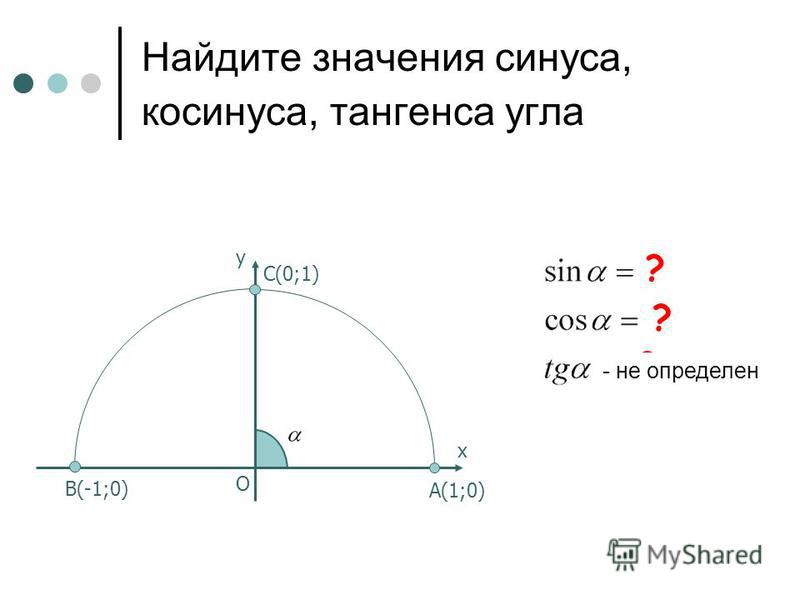 9{\circ}-\theta)$
9{\circ}-\theta)$
В радианах имеем:
$latex \sin(\theta)=\cos(\frac{\pi}{2}-\theta)$
Синусы в прямоугольных треугольниках
Мы можем определить функцию синуса, используя следующий прямоугольный треугольник с прямым углом C.
Обычно мы используем строчные буквы для обозначения сторон треугольников и заглавные буквы для обозначения соответствующих углов. Например, сторона a — это сторона, противоположная углу A, сторона b — это сторона, противоположная углу B, а сторона 9.0003 c является стороной, противоположной углу C.
У всех треугольников внутренние углы в сумме составляют 180°. Мы знаем, что угол C равен 90°, поэтому мы знаем, что углы A и B должны составлять в сумме 90° (дополнительные углы).
Следовательно, мы можем вывести, что синус угла A равен косинусу угла B. Синус угла прямоугольного треугольника равен противолежащему катету, деленному на гипотенузу:
| $latex \ sin=\frac{\text{напротив}}{\text{гипотенуза}}$ |
Используя это, мы имеем отношения $latex \sin(A)=\frac{a}{c}$ y $latex \sin(B)=\frac{b}{c}$ в треугольнике выше. 2}$. Однако в случае 45°-45°-9{\circ})=\frac{\sqrt{3}}{2}$.
2}$. Однако в случае 45°-45°-9{\circ})=\frac{\sqrt{3}}{2}$.
| Degrees | Radians | Sine |
| 90° | $latex \frac{\pi}{2}$ | 1 |
| 60° | $ латекс \frac{\pi}{3}$ | $латекс \frac{\sqrt{3}}{2}$ |
| 45° | $латекс \frac{\pi}{4}$ | $латекс \frac{\sqrt{2}}{2}$ |
| 30° | $латекс \frac{\pi}{6}$ | $ LaTex \ FRAC {1} {2} $ |
| 0 ° | 0 | 0 |
СТАРЬ СЕЙЧАС: Исследование наших дополнительных ресурсов по математике
SIN
Следующие примеры решаются с использованием того, что мы узнали о синусе угла.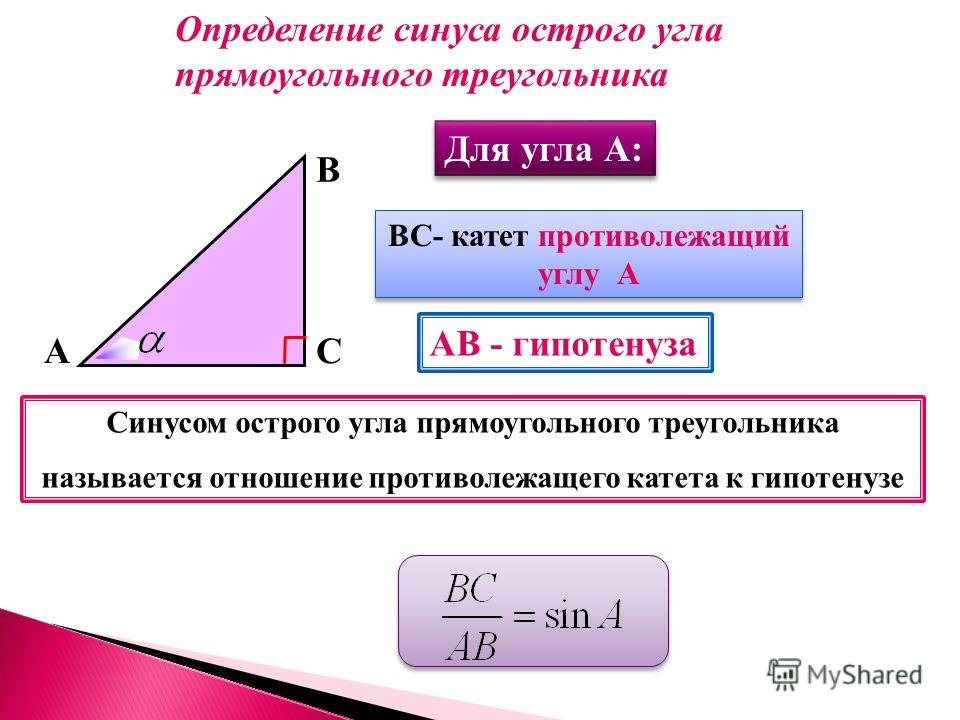 Каждый пример имеет свое решение, но рекомендуется попробовать решить проблемы самостоятельно, прежде чем искать решение.
Каждый пример имеет свое решение, но рекомендуется попробовать решить проблемы самостоятельно, прежде чем искать решение.
Если $латекс \cos(A) = 0,25$ и $латекс а=5$, каково значение c ?
Решение
Мы используем прямоугольный треугольник выше, чтобы получить правильные отношения. Следовательно, мы можем использовать уравнение $latex \sin(A) = \frac{a}{c}$. Используя это уравнение с заданными значениями и решая для c, , мы получаем:
$latex \cos(A)=\frac{a}{c}$
$latex 0.25=\frac{5}{c} $
$латекс c=\frac{5}{0,25}$
$латекс c=20$
Значение гипотенузы равно 20.
ПРИМЕР 2Имеем $latex b=8$ и $latex \sin(B) = \frac{1}{4}$. Каково значение c ?
Решение
Если мы воспользуемся приведенным выше прямоугольным треугольником, мы получим уравнение $latex \cos(B) = \frac{b}{c}$. Поэтому мы используем это уравнение вместе с заданными значениями и находим c :
$latex \cos(B)=\frac{b}{c}$
$latex \frac{1}{4}= \frac{8}{c}$
$латекс c=4(8)$ 9{-1}}=33,8$°
Угол B равен 33,8°.
→ Калькулятор синуса (градусы и радианы)
Синус угла – Практические задачи
Используйте то, что вы узнали о синусе угла, для решения следующих практических задач. Выберите ответ и проверьте его, чтобы убедиться, что вы получили правильный ответ.
Если у нас есть $latex a=4$ и $latex \sin(A)=0.3$, каково значение c?
Выберите ответ
$латекс c=11,3$
$латекс c=12,3$
$латекс c=13,3$
$latex c=14.3$
Если у нас есть $latex b=10$ и $latex \cos(B)=\frac{1}{3}$, каково значение c?
Выберите ответ
$латекс c=20$
$латекс c=25$
$латекс c=28$
$latex c=30$
Если у нас есть $latex a=4$ и $latex c=7$, каково значение A?
Выберите ответ
$латекс A=32,3$°
$латекс A=34,8$°
$латекс A=37,9$°
$latex A=41.4$°
См. также
Хотите узнать больше о синусе угла? Взгляните на эти страницы:
- Калькулятор синуса (градусы и радианы)
- График синуса с примерами
- Период функции синуса – формулы и примеры
- Амплитуда функции синуса – формулы и примеры
Изучение математики с нашими дополнительными ресурсами в разных темах
УЗНАТЬ БОЛЬШЕ
сообщить об этом объявлении
Math Scene — Тригонометрия синуса, косинуса и тангенса
Math Scene — Тригонометрия синуса, косинуса и тангенса — Урок 1 2008 Расмус Эхф | Печать |
Урок 1
ABC — прямоугольный треугольник
Угол А
составляет 30 градусов.
|
а – это символ стороны, противоположной углу A
b — это символ стороны, противоположной углу B
c – это символ стороны, противоположной углу C
Подобные треугольники треугольники, у которых все углы одного треугольника равны углам другого другой треугольник
Эти два треугольника похожи. Отношение двух сторон в одном треугольнике равно отношение соответствующих сторон другого треугольника. |
Использование обозначений в приведенных выше треугольниках получаем следующее:
Коэффициент зависит на величину угла.
Тангенс
Отношение, называемое тангенсом (tan)
острого угла в прямоугольном треугольнике определяется как отношение
между стороной, противоположной углу, и стороной, прилегающей к углу. |
Пример 1 Найти угол А
Первый Тан А = 3 / 4 = 0,75 |
Нам нужно используйте обратную функцию для tan, tan -1 , найти угол. Эта функция находится на той же клавише калькулятора, что и загар. функция (сменный загар).
Мы используем следующая последовательность команд:
сдвиг — желтовато-коричневый -1 0,75 = 37
Попробуйте следующее на калькуляторе, чтобы увидеть разницу между загаром и загаром -1 :
угол → отношение соотношение → угол
желтовато-коричневый 37 = 0,75 tan -1 0,75 = 37
Пример 2 Найти боковая б
тан 37 = 4 / б тан 37 б = 4 0,75 б = 4 б=5,3 |
Старший
Синус (грех)
острый угол прямоугольного треугольника – это отношение
сторона, противоположная углу и гипотенузе треугольника. |
Пример 3 Найдите угол А, дающий ответ с точностью до градуса.
sin A = 3 / 5 = 0,6 дает <А = 37 Сдвиг sin -1 0,6 = 37 |
Пример 4 Найдите сторону а.
грех 37 = a / 5 а = Грех 37 5 а = 3 |
Косинус
Косинус (cos) острый угол в прямоугольном треугольнике — это отношение стороны рядом с углом и гипотенузой треугольника. |
Пример 5 Используйте функцию косинуса, чтобы найти угол A, дающий ответ на ближайший угол.
 степень.
степень. cos A = 4 / 5 = 0,8 дает Сдвиг cos -1 0,8 = 37 |
Пример 6 Найдите сторону б.
соз 37 = б / 5 б = Кос 37 5 б = 4 |
некоторые значения для sin, cos и tan.
| грех 80 = 0,98 | соз 80 = 0,17 | желтовато-коричневый 80 = 5,67 |
| грех 60 = 0,87 | соз 60 = 0,5 | желтовато-коричневый 60 = 1,73 |
| грех 30 = 0,5 | соз 30 = 0,87 | желтовато-коричневый 30 = 0,58 |
| грех 10 = 0,17 | соз 10 = 0,98 | желтовато-коричневый 10 = 0,18 |
Практикуйте эти методы, а затем
викторина по тригонометрии 1 (грех, косинус и загар).
синусов
Синус — это половина хорды. Точнее, синус угла равен половине хорды удвоенного угла.
Схема лука и стрелРассмотрим угол BAD на этом рисунке и предположим, что AB имеет единичную длину. Пусть точка C будет основанием перпендикуляра, опущенного из B на линию AD. Тогда синус угла BAD определяется как длина прямой BC, и записывается как sin BAD. Вы можете удвоить угол BAD , чтобы получить угол BAE, и хорда угла BAE равна BE. Таким образом, синус BC угла BAD составляет половину хорды BE угла BAE, , а угол BAE вдвое больше угла BAD. Следовательно, как сказано выше, синус угла равен половине хорды удвоенного угла.
Смысл этого в том, чтобы показать, что синусы так сложно понять. (Ой, это описка! Я хотел написать «, а не , все это сложно понять».)
Значение слова «синус»
Санскритское слово для половины аккорда было джья-ардха, , которое иногда сокращалось до джива. Это было переведено на арабский язык как jiba, и написано по-арабски просто с двумя согласными jb, гласных не пишутся. Позже латинские переводчики выбрали слово sinus для перевода jb , думая, что это слово арабское.0308 jaib, , что означало грудь, и sinus имели два значения: грудь и залив. В английском языке sinus было импортировано как «sine».
Это было переведено на арабский язык как jiba, и написано по-арабски просто с двумя согласными jb, гласных не пишутся. Позже латинские переводчики выбрали слово sinus для перевода jb , думая, что это слово арабское.0308 jaib, , что означало грудь, и sinus имели два значения: грудь и залив. В английском языке sinus было импортировано как «sine».
История этого слова для синуса интересна тем, что следует по пути тригонометрии из Индии через арабский язык из Багдада через Испанию в Западную Европу на латинском языке, а затем в современные языки, такие как английский и остальной мир. .
Синусы и прямоугольные треугольники
Мы можем использовать свойства подобных треугольников, чтобы связать синусы с прямоугольными треугольниками. На рисунке выше треугольник ABC представляет собой прямоугольный треугольник с прямым углом C и гипотенузой длины 1.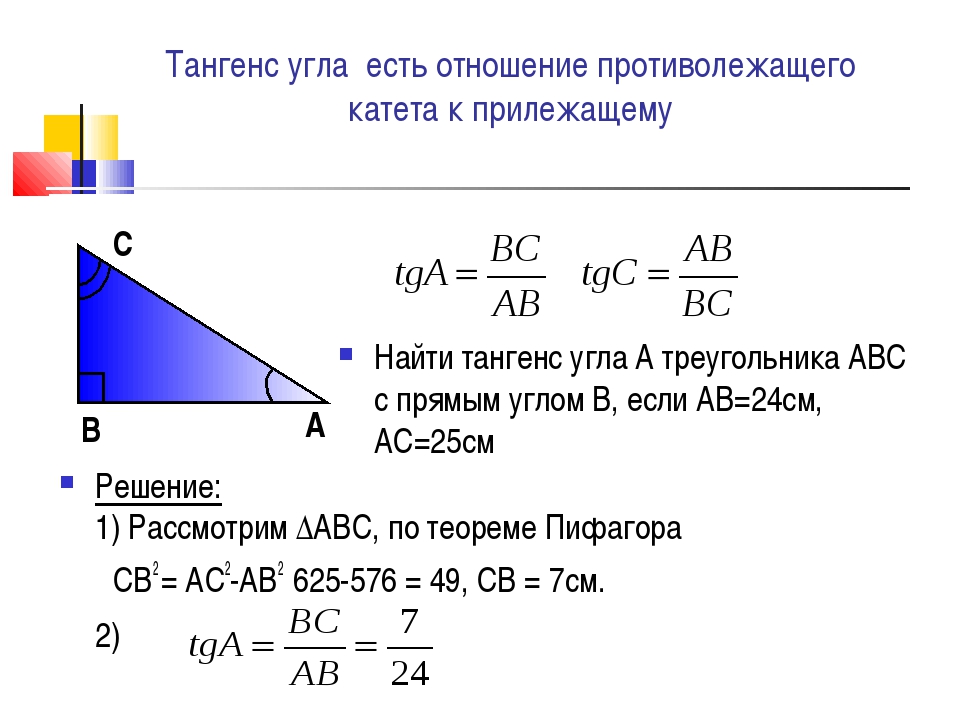 Рассмотрим аналогичный прямоугольный треугольник AB’C’ с гипотенузой произвольной длины. веб-браузер с поддержкой Java, вы можете перетаскивать точки B’ , чтобы изменить размер прямоугольного треугольника AB’C’. )
Рассмотрим аналогичный прямоугольный треугольник AB’C’ с гипотенузой произвольной длины. веб-браузер с поддержкой Java, вы можете перетаскивать точки B’ , чтобы изменить размер прямоугольного треугольника AB’C’. )
Поскольку треугольники подобны, отношение BC к AB равно отношению B’C’ к AB’. Но AB равно 1. Следовательно,
но до н.э. = sin A, так
Этот результат легче всего запомнить, поскольку синус угла в прямоугольном треугольнике равен противолежащему катету, деленному на гипотенузу:
Стандартное обозначение прямоугольного треугольника
Какое-то время мы будем рассматривать в основном прямоугольные треугольники, поэтому было бы полезно использовать стандартные обозначения для углов и сторон этих треугольников.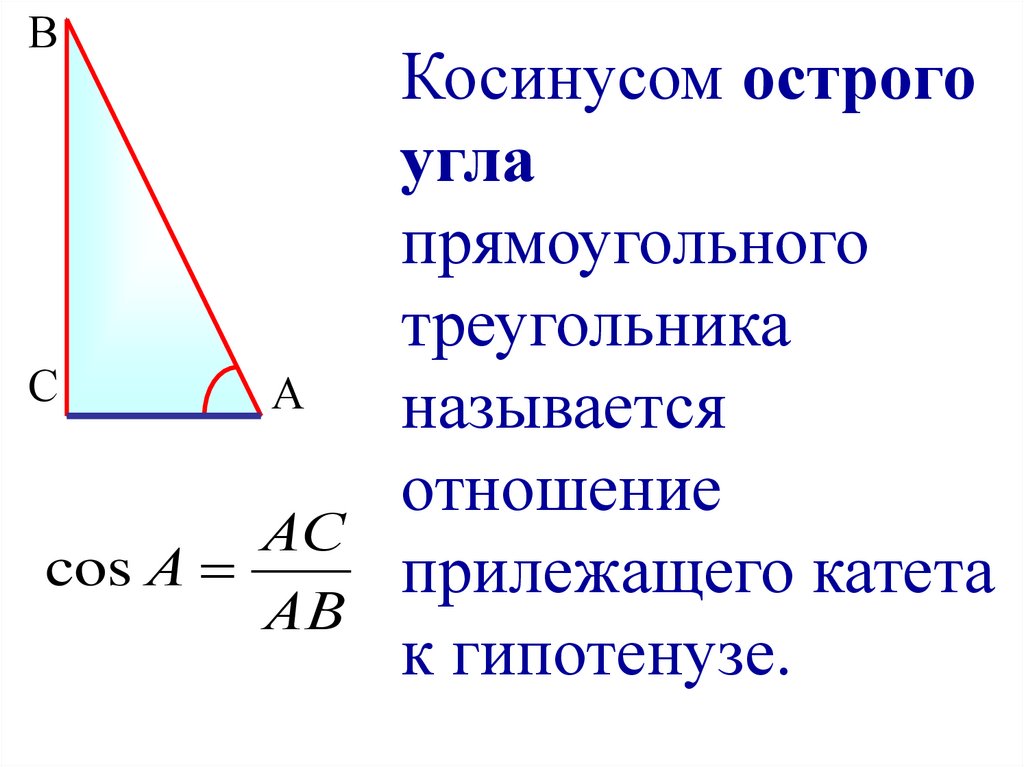
Рассмотрим прямоугольный треугольник ABC с прямым углом C. Обычно мы будем использовать букву a для обозначения стороны, противоположной углу A, букву b для обозначения стороны, противоположной углу В, и буквой с для обозначения стороны, противолежащей углу С, то есть гипотенузе.
При таком обозначении sin A = a/c, и sin B = b/c.
Далее мы рассмотрим косинусы. Косинусы — это просто синусы дополнительного угла. Отсюда и название «косинус» («ко» — первые две буквы слова «дополнение»). Для треугольника ABC , потому что A просто sin Б.
Упражнения
28. В прямоугольном треугольнике гипотенуза c = 15 дюймов, а синус одного угла A, равен sin = A 90 209 . Найдите а, сторону, противоположную А, и найдите b, оставшуюся сторону.
44. В прямоугольном треугольнике B = 55° 30′, а b = 6,05. Найти c и a.
191. Если высота фронтона крыши составляет 22,5 фута, а длина стропил 30 футов 8 дюймов, под каким углом наклоняются стропила и какой ширины фронтон у основания?
194. Верх лестницы длиной 50 футов упирается в здание на высоте 43 фута от земли. Под каким углом наклонена лестница и каково расстояние ее основания от стены?
Подсказки
28. Гипотенуза c равно 15″. Поскольку sin A = a/c, , следовательно, a = c sin A. Это дает вам a. и и с
44. Поскольку sin B = b/c, можно определить c. Когда у вас есть b и c, , вы можете определить a по теореме Пифагора.
191. Фронтон ABD крыши представляет собой равнобедренный треугольник, основание которого равно ширине дома, а две равные наклонные стороны — стропила на конце крыши. Если опустить перпендикуляр из вершины B треугольника, вы получите два конгруэнтных прямоугольных треугольника, ABC и DBC. Поскольку вы знаете две стороны прямоугольного треугольника ABC, , вы можете вычислить третью, используя теорему Пифагора. Вы можете использовать синусы для определения угла наклона, так как sin A = BC/AB = 22,5’/30’8″ = 0,7337. Чтобы найти угол A, , вам понадобится так называемый арксинус 0,7337.
Если опустить перпендикуляр из вершины B треугольника, вы получите два конгруэнтных прямоугольных треугольника, ABC и DBC. Поскольку вы знаете две стороны прямоугольного треугольника ABC, , вы можете вычислить третью, используя теорему Пифагора. Вы можете использовать синусы для определения угла наклона, так как sin A = BC/AB = 22,5’/30’8″ = 0,7337. Чтобы найти угол A, , вам понадобится так называемый арксинус 0,7337.
Функция арксинуса обратна функции синуса, и ваш калькулятор может их вычислить. Обычно на калькуляторе есть кнопка с надписью «inv» или «arc», которую вы нажимаете перед нажатием кнопки «sin». Тогда у вас будет угол. Ваш калькулятор, вероятно, может быть установлен либо в градусный режим, либо в радианный режим. Если он установлен в градусный режим, вы получите угол в градусах; и если он установлен в радианном режиме, то вы получите угол в радианах. Всегда знайте, в каком режиме установлен ваш калькулятор.
194. Нарисуйте треугольник ABC , как указано выше. Вы знаете гипотенузу с и вертикальную сторону а. Расстояние b можно найти по теореме Пифагора. Просто возьмите квадратный корень из c 2 – a 2 . С помощью синусов можно найти наклон, то есть угол А, . Вы знаете, что sin A = a/c = 43/50 = 0,86. Как и в задаче 191, используйте arcsin, чтобы найти угол А.
Ответы
28. a = c sin A = 15 (2/5) = 6 дюймов.
b 2 = c 2 – a 2 = 189, поэтому b = 13,7 дюйма.
44. c = b /sin B = 6,05/sin 55°30′ = 7,34.
a = 4,16.
191. Угол A равен 0,824 радиана или 47,2° = 47°12′. Ширина фронтона 41,7 фута = 41 фут 8 дюймов.
194.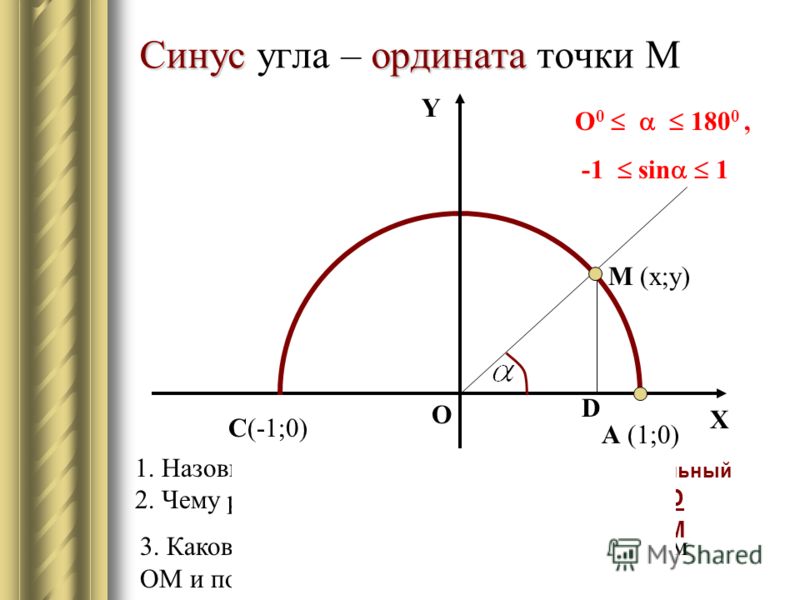 Так как c 2 – a 2 = 651, следовательно, расстояние b равно квадратному корню, а именно 25,5 футов.
Так как c 2 – a 2 = 651, следовательно, расстояние b равно квадратному корню, а именно 25,5 футов.
Теперь sin A = 0,86, поэтому A составляет 1,035 радиана, или
около 59,32° = 59°20′.
Геометрия: коэффициент синуса
Функция тангенса исследовала значения отношения двух катетов прямоугольного треугольника. Также можно взять отношение длины одного катета к длине гипотенузы. У тебя две ноги, так какую использовать?
В прямоугольном треугольнике у каждого угла есть противолежащая сторона и прилежащая сторона. И всегда есть гипотенуза. Не забывайте про гипотенузу. Если вы работаете с противоположной стороной и гипотенузой, вы имеете дело с отношением синусов. Синус угла есть отношение длины противолежащего катета к длине гипотенузы.
Твердые факты
В прямоугольном треугольнике синус угла равен отношению длины противоположной стороны к длине гипотенузы.
Давайте воспользуемся теоремой Пифагора, чтобы исследовать некоторые свойства соотношения синусов. Дан прямоугольный треугольник (подобный показанному на рис. 20.4), пусть длины треугольника равны a, b и c, где a — длина стороны, противоположной A, b — длина стороны, противоположной B, и с — длина стороны, противоположной С (и длина гипотенузы). Тогда теорема Пифагора говорит вам, что 2 + б 2 = с 2 . Синус А (который будет записан как sin А) есть отношение длины стороны, противоположной А, к длине гипотенузы; sin A = a / c . Так как a c, sin A 1 (единственный способ, при котором sinA = 1, если a = c, но тогда получился бы странный треугольник!), отношение синусов не может быть больше 1.
Рис. 20.4 Прямоугольный треугольник с длинами сторон a и b и длину гипотенузы c.
Если вам дан прямоугольный треугольник и вы знаете тангенс угла, вы можете найти синус угла, применив теорему Пифагора.
- Пример 2 : Предположим , что угол прямоугольного треугольника имеет отношение тангенса 5 / 12 . Найдите отношение синусов этого угла.
- Решение : Рисунок 20.5 поможет вам визуализировать происходящее.
- Вам известно, что tan A = 5 / 12 , поэтому a = 5 и b = 12. Вы можете использовать теорему Пифагора, чтобы найти длину гипотенузы:
- c 2 = a 2 + б 2
- c 2 = 5 2 + 12 2 = 25 + 144 = 169
- c = 13
Касательная линия для прямого угла
Letine. Определение отношения синуса — это отношение длины противоположной стороны к длине гипотенузы. Итак, длина стороны, противоположной C , равна длины гипотенузы, поэтому sin C = c / c = 1 Потому что C — прямой угол, мС = 90º , поэтому sin 90º = 1 .
Рисунок 20.5 Прямоугольный треугольник с загаром A = 5 / 12 .
Теперь, когда вы знаете длину гипотенузы, нужно просто найти отношение синусов этого угла (это отношение длины стороны, противоположной углу, к длине гипотенузы):
- sin A = 5 / 13
Этот расчет работает в обе стороны. Зная отношение синусов угла треугольника, можно найти отношение тангенсов угла.
- Пример 3 : Если прямоугольный треугольник имеет угол с отношением синусов 4 / 5 , найдите отношение тангенсов этого угла.
- Решение . Давайте посмотрим на рисунок 20.6. Для того, чтобы найти отношение тангенсов угла, нужно знать длину стороны, противолежащей углу, и длину стороны, примыкающей к углу. Поскольку отношение синусов равно 3 / 5 , длина стороны, противоположной углу, равна 3, а длина гипотенузы равна 5.
 Используя теорему Пифагора, вы можете найти длину стороны, прилегающей к углу:
Используя теорему Пифагора, вы можете найти длину стороны, прилегающей к углу: - a 2 + b 2 = c 2
- 3 2 + b 2 = 5 2
- 9 + b 2 = 25
- b 2 = 16
- b = 4
Таким образом, отношение тангенсов равно 3 / 4 .
Рис. 20.6 Прямоугольный треугольник, угол которого имеет отношение синусов 3 / 5 .
Теорема Пифагора будет использоваться в этом разделе так часто, что вы будете знать ее как свои пять пальцев к тому времени, как вы закончите этот раздел!
Выдержки из Полное руководство идиота по геометрии © 2004 Дениз Сечеи, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
- Геометрия: отношение косинусов
Предварительное исчисление по алгебре — Что на самом деле означают синус, тангенс, кос?
Я думаю, что историческая причина путаницы связана с отображением тригонометрических функций в полярной форме, а не в прямоугольной. В прямоугольной форме справедливо следующее утверждение. $$ \theta \quad =\quad x $$ (Где смысл этого равенства в том, что мы пусть мера угла на единичной окружности представляет собой прямоугольное расстояние вдоль оси x или область, прямоугольной функции.) Но в полярной форме это неверно, и $\theta$ означает нечто иное, а именно, используется для определения исходного угла от нуля радиан, не расстояние по оси $x$ . Таким образом, значение $\theta$ или $x$ зависит от того, как вы строите график в двумерной плоскости, т.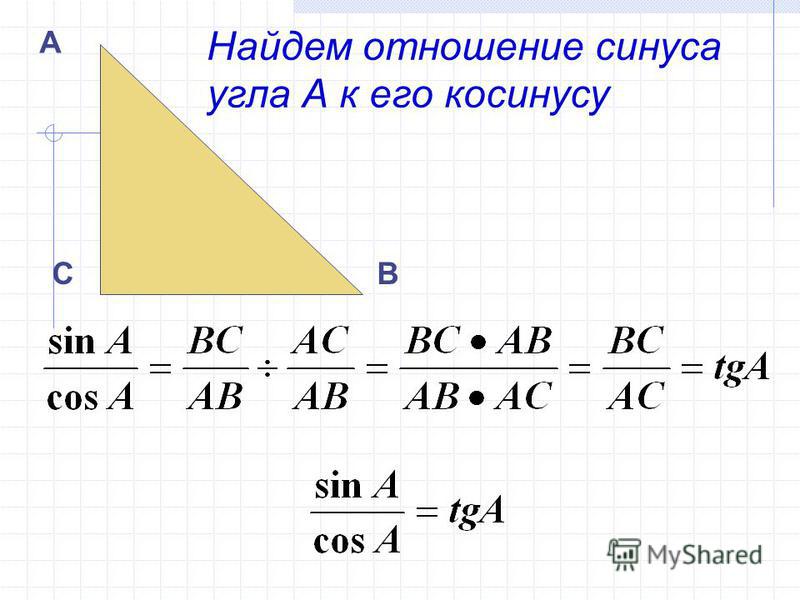 е. полярный или прямоугольный график. В полярном методе смысл прямоугольной пары координат $$(x,y)$$ состоит в том, что это положение аналогично паре координат, определяемой направленным расстоянием от начала координат для некоторой меры $\theta$, с абсциссой, или значением $x$ пары прямоугольных координат, определяемым как $$x=r\cdot \cos(\theta)$$, и ординатой, или значением $y$ пары прямоугольных координат, определяемым по $$y=r\cdot \sin(\theta )$$
е. полярный или прямоугольный график. В полярном методе смысл прямоугольной пары координат $$(x,y)$$ состоит в том, что это положение аналогично паре координат, определяемой направленным расстоянием от начала координат для некоторой меры $\theta$, с абсциссой, или значением $x$ пары прямоугольных координат, определяемым как $$x=r\cdot \cos(\theta)$$, и ординатой, или значением $y$ пары прямоугольных координат, определяемым по $$y=r\cdot \sin(\theta )$$
Таким образом, в полярном методе мы представляем пару координат или точку на плоскости, используя другое значение $\theta$, а именно, как входное значение угла от начала координат в терминах $r$, определяемых как функция от $\theta$, поэтому мы обычно называем каждую пару координат на плоскости следующим образом: $$(r,\theta )$$
формы, то мы пусть : $$ \theta \quad =\quad x $$ (где $\theta$ теперь понимается как прямоугольное расстояние вдоль оси $x$ или область определения прямоугольной функции .) Таким образом, вместо того, чтобы представлять угловую меру от нуля радиан, угол тета теперь представляет собой расстояние по оси $x$ от начала координат. Кроме того, в случае родительской функции, полученной из единичной окружности, поскольку: $$r=1$$ мы можем построить следующую функциональную машину одной переменной для прямоугольного графика: $$ r\cdot \sin(\theta ) =y $$ И это интуитивно понятно, потому что ордината, или переменная y, оказывается удобно изолированной. И поскольку мы очень привыкли к тому, что y является функцией x, имеет смысл записать это как: $$[r\cdot \sin(\theta )=y=f(x)=\sin(x)]\ quad \Longleftrightarrow \quad \theta =x\quad \cap \quad r=1$$ Но становится менее очевидным, когда мы строим функциональную машину для прямоугольного графика для косинуса, который, когда мы умножаем обе стороны в вашем примере на r: $$r\cdot \cos(\theta )=x$$ И это странно, потому что, хотя прямоугольная и полярная графики относятся к одним и тем же двумерным плоскостям, в приведенном ниже утверждении x используется двумя разными способами. Сначала рассмотрим логически эквивалентное утверждение: $$ [r\cdot \cos(\theta )=x=f(x)=\cos(x)]\quad \Longleftrightarrow \quad \theta =x\quad \cap \ quad r=1 $$ Проблема в том, что в формуле преобразования полярная/прямоугольная мы определяем $x$ как значение абсцисс для полярного представления координаты, но теперь, когда мы переключаемся на прямоугольную форму графика, мы используем $x$ в качестве входной переменной для представления тета.
Кроме того, в случае родительской функции, полученной из единичной окружности, поскольку: $$r=1$$ мы можем построить следующую функциональную машину одной переменной для прямоугольного графика: $$ r\cdot \sin(\theta ) =y $$ И это интуитивно понятно, потому что ордината, или переменная y, оказывается удобно изолированной. И поскольку мы очень привыкли к тому, что y является функцией x, имеет смысл записать это как: $$[r\cdot \sin(\theta )=y=f(x)=\sin(x)]\ quad \Longleftrightarrow \quad \theta =x\quad \cap \quad r=1$$ Но становится менее очевидным, когда мы строим функциональную машину для прямоугольного графика для косинуса, который, когда мы умножаем обе стороны в вашем примере на r: $$r\cdot \cos(\theta )=x$$ И это странно, потому что, хотя прямоугольная и полярная графики относятся к одним и тем же двумерным плоскостям, в приведенном ниже утверждении x используется двумя разными способами. Сначала рассмотрим логически эквивалентное утверждение: $$ [r\cdot \cos(\theta )=x=f(x)=\cos(x)]\quad \Longleftrightarrow \quad \theta =x\quad \cap \ quad r=1 $$ Проблема в том, что в формуле преобразования полярная/прямоугольная мы определяем $x$ как значение абсцисс для полярного представления координаты, но теперь, когда мы переключаемся на прямоугольную форму графика, мы используем $x$ в качестве входной переменной для представления тета. Короче говоря, мы используем $x$ двумя разными способами. (Точно так же мы используем $y$ двумя разными способами.) По сути, мы заменяем полярное использование $x$ на прямоугольную ординату, или $y$, и мы заменяем полярное использование тета в приведенном выше примере. оператор с прямоугольным использованием $x$ в качестве независимой переменной. Эту двусмысленность можно устранить, если мы заменим наш обычный способ записи отношений в полярной форме фиктивными переменными. Вот почему некоторые учителя предпочитают использовать противоположные, смежные и т. д. вместо $x$ и $y$, потому что мы используем их по-разному, когда строим функциональные машины. Чтобы устранить смешение, просто используйте phi для формулы полярной абсциссы, что даст: $$ [r\cdot \cos(\theta )=\varphi =f(x)= \cos(x)]\quad \Longleftrightarrow \quad \ theta =x\quad \cap \quad r=1 $$ Таким образом, оба тригонометрических отношения были преобразованы в функции от $x$. Давайте проясним, какие $x$ мы имеем в виду!? Что ж, в этом случае мы имеем в виду $x$ как независимую переменную, а не вывод по абсциссе направленного расстояния полярного представления.
Короче говоря, мы используем $x$ двумя разными способами. (Точно так же мы используем $y$ двумя разными способами.) По сути, мы заменяем полярное использование $x$ на прямоугольную ординату, или $y$, и мы заменяем полярное использование тета в приведенном выше примере. оператор с прямоугольным использованием $x$ в качестве независимой переменной. Эту двусмысленность можно устранить, если мы заменим наш обычный способ записи отношений в полярной форме фиктивными переменными. Вот почему некоторые учителя предпочитают использовать противоположные, смежные и т. д. вместо $x$ и $y$, потому что мы используем их по-разному, когда строим функциональные машины. Чтобы устранить смешение, просто используйте phi для формулы полярной абсциссы, что даст: $$ [r\cdot \cos(\theta )=\varphi =f(x)= \cos(x)]\quad \Longleftrightarrow \quad \ theta =x\quad \cap \quad r=1 $$ Таким образом, оба тригонометрических отношения были преобразованы в функции от $x$. Давайте проясним, какие $x$ мы имеем в виду!? Что ж, в этом случае мы имеем в виду $x$ как независимую переменную, а не вывод по абсциссе направленного расстояния полярного представления. То же самое можно математически вывести для всех других функций. Опять же, может быть полезно заменить ваши исходные отношения фиктивными переменными, которые определены как абсцисса и ордината, чтобы не смешивать использование $x$ в первом случае, который используется как абсцисса, с $x$ в машина функций, которая для косинуса имеет два разных использования, как описано выше. Таким образом, используя фиктивные переменные, очевидное множественное использование и значение $x$ удаляются. Это ответ на ваши первые три вопроса. Правильное понимание этого также проливает свет на тот факт, что даже при построении синуса и других функций мы все еще совершаем то же самое математическое тщеславие переключения между использованием переменных $x$ и $y$ в полярном методе, что и отличаются от использования переменных $x$ и $y$ в прямоугольном методе. Чтобы было ясно, это использование, и мы по-прежнему строим график в двумерной координатной плоскости в обоих случаях.
То же самое можно математически вывести для всех других функций. Опять же, может быть полезно заменить ваши исходные отношения фиктивными переменными, которые определены как абсцисса и ордината, чтобы не смешивать использование $x$ в первом случае, который используется как абсцисса, с $x$ в машина функций, которая для косинуса имеет два разных использования, как описано выше. Таким образом, используя фиктивные переменные, очевидное множественное использование и значение $x$ удаляются. Это ответ на ваши первые три вопроса. Правильное понимание этого также проливает свет на тот факт, что даже при построении синуса и других функций мы все еще совершаем то же самое математическое тщеславие переключения между использованием переменных $x$ и $y$ в полярном методе, что и отличаются от использования переменных $x$ и $y$ в прямоугольном методе. Чтобы было ясно, это использование, и мы по-прежнему строим график в двумерной координатной плоскости в обоих случаях.
Ваш следующий вопрос: как связаны синус и $x$, косинус и $x$ и т. д. Не зря тригонометрические функции называются трансцендентными. Отношения трансцендентны. Это означает, что нельзя использовать базовую арифметику, т. е. сложение, вычитание, умножение или деление, чтобы решить, например: $$ \cos(30) $$. В древности это тщательно измерялось итерациями по единичному кругу. В результате были разработаны таблицы, особенно в случае птолемеевской астрономии. Позже, когда было разработано исчисление, бесконечные ряды использовались для более точной аппроксимации этих трансцендентных величин, и теперь они все вместе называются рядами Тейлора, которые представляют собой ряды Маклорена, центр которых не находится в 0. Таким образом, взаимосвязь является символической и что синус «угла» измеряется ординатой единичного треугольника определенного тэта или угла. Точно так же косинус «угла» измеряется абсциссой единичного треугольника определенного тета или угла. И так далее для остальных…
д. Не зря тригонометрические функции называются трансцендентными. Отношения трансцендентны. Это означает, что нельзя использовать базовую арифметику, т. е. сложение, вычитание, умножение или деление, чтобы решить, например: $$ \cos(30) $$. В древности это тщательно измерялось итерациями по единичному кругу. В результате были разработаны таблицы, особенно в случае птолемеевской астрономии. Позже, когда было разработано исчисление, бесконечные ряды использовались для более точной аппроксимации этих трансцендентных величин, и теперь они все вместе называются рядами Тейлора, которые представляют собой ряды Маклорена, центр которых не находится в 0. Таким образом, взаимосвязь является символической и что синус «угла» измеряется ординатой единичного треугольника определенного тэта или угла. Точно так же косинус «угла» измеряется абсциссой единичного треугольника определенного тета или угла. И так далее для остальных…
Затем вы дополнительно спрашиваете, что означает обратная функция и почему мы можем ее написать. Во-первых, в ответ на то, почему мы можем написать это, следует отметить, что каждая машина тригонометрических функций требует другого домена и ограничения диапазона, чтобы быть функцией в первую очередь. Вот почему некоторые сторонники предпочитают писать «дуга» перед функцией, а не использовать отрицательный верхний индекс, который для некоторых подразумевает, что существует совершенная обратная функция без ограничений. Теперь, если вы спрашиваете более широко, почему можно строить обратные функции, я бы либо уступил теоретику, либо предложил бы проще, что иногда известно отношение, но нужен угол, а иногда известен угол, но нужно отношение . Возьмем ранний анализ движения планет, воздушный шар, расчет расстояния до веревки воздушного змея, определение расстояния траектории с помощью параметрических триггерных функций и т. д., конечно, в настоящее время все это ограничено двумя измерениями.
Во-первых, в ответ на то, почему мы можем написать это, следует отметить, что каждая машина тригонометрических функций требует другого домена и ограничения диапазона, чтобы быть функцией в первую очередь. Вот почему некоторые сторонники предпочитают писать «дуга» перед функцией, а не использовать отрицательный верхний индекс, который для некоторых подразумевает, что существует совершенная обратная функция без ограничений. Теперь, если вы спрашиваете более широко, почему можно строить обратные функции, я бы либо уступил теоретику, либо предложил бы проще, что иногда известно отношение, но нужен угол, а иногда известен угол, но нужно отношение . Возьмем ранний анализ движения планет, воздушный шар, расчет расстояния до веревки воздушного змея, определение расстояния траектории с помощью параметрических триггерных функций и т. д., конечно, в настоящее время все это ограничено двумя измерениями.
Тогда ответ на ваш вопрос о значении обратной функции — это просто логическая обратная или арксинус «отношения (с $r=1$)», измеряемого определенной тетой в единичном треугольнике конкретная ордината или значение y.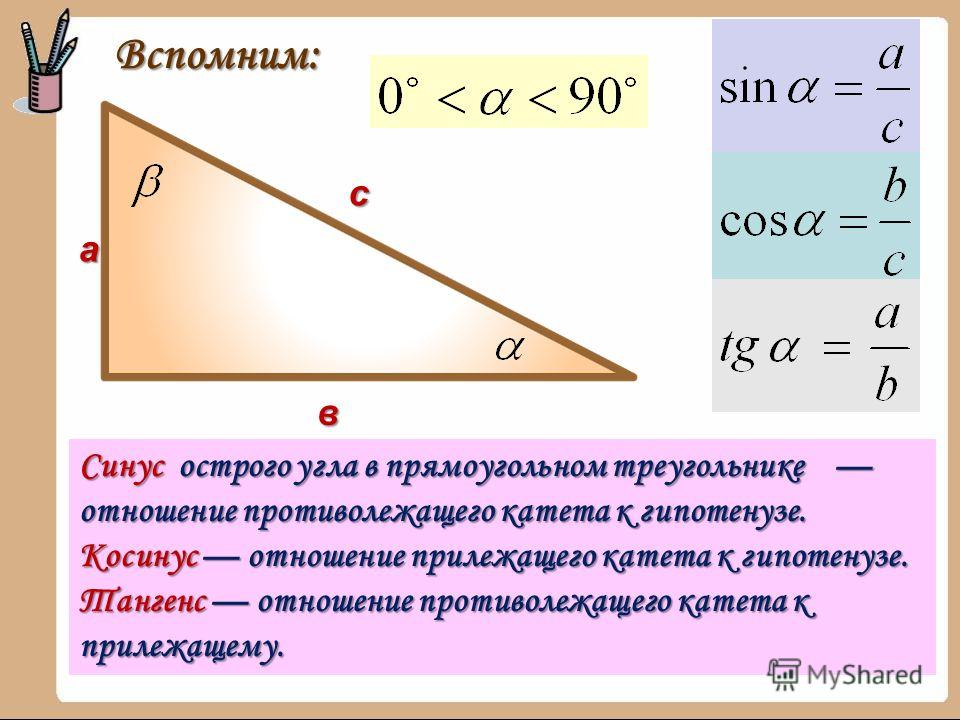 Точно так же арккосинус «отношения (с $ r = 1 $)» измеряется определенной тетой на единичном треугольнике определенной абсциссы или значением $ x $. Это просто логическая обратная функция и значение вышеуказанных машин тригонометрических функций (включая необходимые ограниченные области и диапазоны). Кроме того, они оба трансцендентны и требуют либо итераций, либо измерений, приводящих к таблицам, либо требуют аппроксимации трансцендентных значений с помощью так называемых рядов Тейлора, которые представляют собой ряды Маклорена, центр которых не находится в 0. Эта последняя часть отвечает на то, что обратная функция означает.
Точно так же арккосинус «отношения (с $ r = 1 $)» измеряется определенной тетой на единичном треугольнике определенной абсциссы или значением $ x $. Это просто логическая обратная функция и значение вышеуказанных машин тригонометрических функций (включая необходимые ограниченные области и диапазоны). Кроме того, они оба трансцендентны и требуют либо итераций, либо измерений, приводящих к таблицам, либо требуют аппроксимации трансцендентных значений с помощью так называемых рядов Тейлора, которые представляют собой ряды Маклорена, центр которых не находится в 0. Эта последняя часть отвечает на то, что обратная функция означает.
Как работают синус, косинус и тангенс?
МАТЕМАТИКА — Геометрия
Задумывались ли вы когда-нибудь…
- Что такое тригонометрия?
- Что такое синус, косинус и тангенс?
- Как найти синус, косинус и тангенс?
Теги:
Просмотреть все теги
- Математика,
- Геометрия,
- Тригонометрия,
- Функция,
- Синус,
- Косинус,
- Тангенс,
- Треугольник,
- Прямоугольный треугольник,
- Формула,
- Угол,
- Гипотенуза
Сегодняшнее чудо дня было вдохновлено Саем.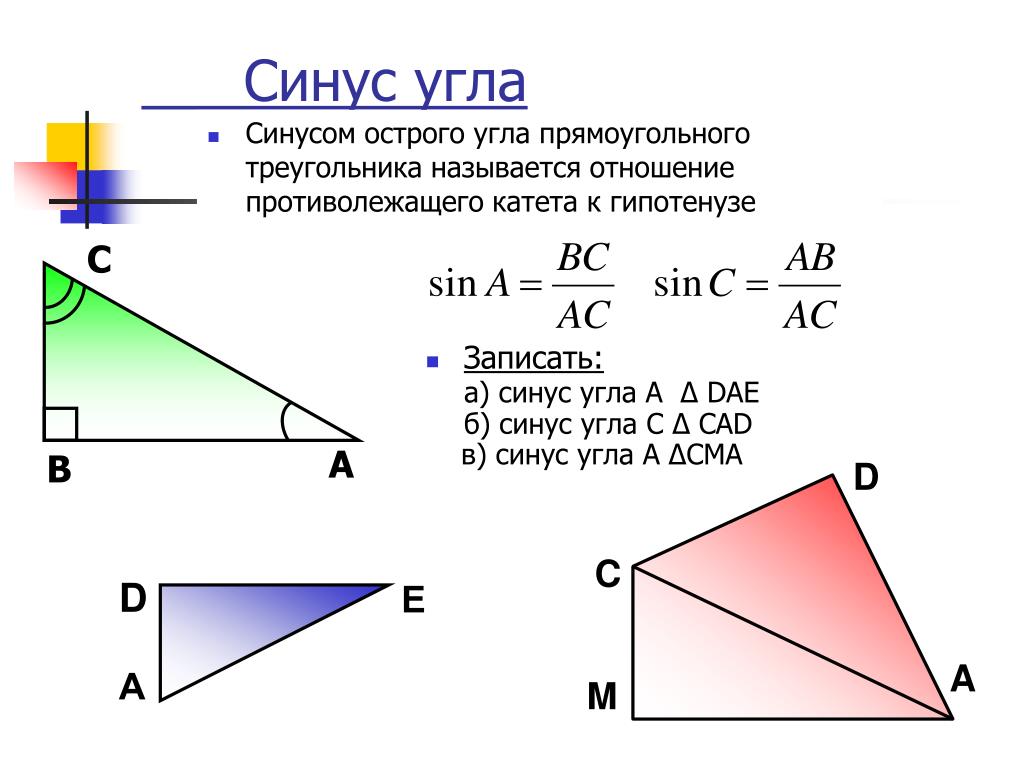 Sai Wonders , “ Как работают синус, косинус и тангенс? ”Спасибо, что ДУМАЕТЕ вместе с нами, Сай!
Sai Wonders , “ Как работают синус, косинус и тангенс? ”Спасибо, что ДУМАЕТЕ вместе с нами, Сай!
Многие из наших чудесных друзей уже знают о теореме Пифагора. Возможно, они читали о треугольнике Паскаля. Они могут даже знать другие типы треугольников. Сегодня нас интересует еще одна тема, связанная с треугольниками. О чем мы говорим? Синус, косинус и тангенс, конечно!
Что такое синус, косинус и тангенс? Это три основные функции в тригонометрии. Возможно, вы уже слышали о них на уроках математики. Тригонометрия связана с геометрией и другими разделами математики. Это может помочь нам лучше понять связи между сторонами и углами прямоугольников.
Синус, косинус и тангенс важны для изучения прямоугольных треугольников. Вы когда-нибудь видели такой треугольник? Если да, то вы знаете, что один из трех его углов всегда равен 90° (прямой угол). Два других угла могут иметь любые измерения, если сумма всех трех углов составляет 180°.
Как математики находят синус, косинус и тангенс? Начнем с одного из непрямых углов прямоугольного треугольника. Обычно они обозначают этот угол как тета (Θ). Затем они обозначают три стороны треугольника.
Сторона треугольника, расположенная непосредственно напротив прямого угла, называется гипотенузой. Это самая длинная сторона треугольника. Сторона напротив теты называется «противоположной». Это довольно легко запомнить — это на противоположной стороне от тета-угла! Наконец, сторона, которая касается теты, но не является гипотенузой, называется «прилегающей».
Правильное обозначение сторон очень важно при нахождении синуса, косинуса и тангенса. Это потому, что у каждого есть формула, которая делит длину одной стороны на длину другой. Вот формулы для поиска каждой из этих функций:
SINE θ = противоположность ÷ гипотенуза
косинус θ = прилегающая ÷ гипотеновая
Tangence θ vanposite ÷ rasten
- .
 формулы могут показаться трудными для запоминания. Тем не менее, запоминание полезной мнемоники может помочь. При нахождении синуса, косинуса и тангенса просто помните SOHCATOA (sō-kŭ-tō-ŭ). В этом примере S, C и T обозначают синус, косинус и тангенс. O, A и H обозначают противоположность, смежность и гипотенузу.
формулы могут показаться трудными для запоминания. Тем не менее, запоминание полезной мнемоники может помочь. При нахождении синуса, косинуса и тангенса просто помните SOHCATOA (sō-kŭ-tō-ŭ). В этом примере S, C и T обозначают синус, косинус и тангенс. O, A и H обозначают противоположность, смежность и гипотенузу.Запомнив SOHCATOA, вы сможете правильно писать формулы для синуса, косинуса и тангенса. Затем просто введите правильные числа, и все готово! Чтобы найти эти функции, нужно запомнить формулы и использовать правильные измерения сторон. Многие люди считают полезным пометить треугольник перед тем, как начать.
Можете ли вы найти синус, косинус и тангенс угла? Мы уверены, что вы можете! Однако поначалу новые математические темы могут быть трудными. С практикой и помощью учителя или друга мы знаем, что скоро вы многое узнаете о тригонометрии!
Common Core, Научные стандарты следующего поколения и Национальный совет по социальным исследованиям.
 »> Стандарты: CCSS.MATH.HSF.TF.A.2, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.L.1, CCRA.L.2, CCRA .L.3, CCRA.L.6, CCRA.W.2, CCRA.W.4, CCRA.W.9, CCRA.W.10, CCRA.SL.1, CCRA.SL.2
»> Стандарты: CCSS.MATH.HSF.TF.A.2, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.L.1, CCRA.L.2, CCRA .L.3, CCRA.L.6, CCRA.W.2, CCRA.W.4, CCRA.W.9, CCRA.W.10, CCRA.SL.1, CCRA.SL.2Интересно, что дальше?
Сегодняшнее чудо дня обычно выходит только ночью.
Попробуйте
Готовы продолжать учиться? Проверьте действия ниже с помощью друга или члена семьи!
- Узнайте больше о синусе, косинусе и тангенсе, а также посмотрите полезные диаграммы на веб-сайте Math Is Fun. Помогло ли это вам глубже понять эти функции? Обобщите то, что вы узнали сегодня, для друга или члена семьи.
- Теперь, когда у вас есть мнемосхема, которая поможет вам запомнить формулы синуса, косинуса и тангенса, сделайте плакат, который поможет другим запомнить. Используйте мнемонику SOHCAHTOA и включите любые изображения или диаграммы, которые, по вашему мнению, помогут вашим друзьям или членам семьи научиться находить эти функции.
 Не забудьте также указать правильные формулы!
Не забудьте также указать правильные формулы! - Чувствуете себя хитрым? Узнайте больше о геометрических фигурах и проявите творческий подход, создавая свои собственные! Вы можете попробовать сделать некоторые фигуры самостоятельно или следовать этому видео, чтобы научиться создавать трехмерные фигуры, используя только бумагу и ножницы. Убедитесь, что взрослый помогает вам, и получайте удовольствие, создавая свои фигуры.
Wonder Sources
- https://www.khanacademy.org/math/geometry-home/right-triangles-topic/intro-to-the-trig-ratios-geo/v/basic-trigonometry
- https ://www.mathsisfun.com/sine-cosine-tangent.html
- https://www.livescience.com/51026-what-is-trigonometry.html
- https://learnersdictionary.com/
Ты понял?
Проверьте свои знанияWonder Words
- ответвления
- углы
- этикетка
- функций
- формулы
- измерений
- тригонометрия
- геометрия
- математики
Примите участие в конкурсе Wonder Word
Оцените это чудо
Поделись этим чудом
×ПОЛУЧАЙТЕ СВОЕ ЧУДО ЕЖЕДНЕВНО
Подпишитесь на Wonderopolis и получайте Wonder of the Day® по электронной почте или SMS
Присоединяйтесь к Buzz
Не пропустите наши специальные предложения, подарки и рекламные акции.


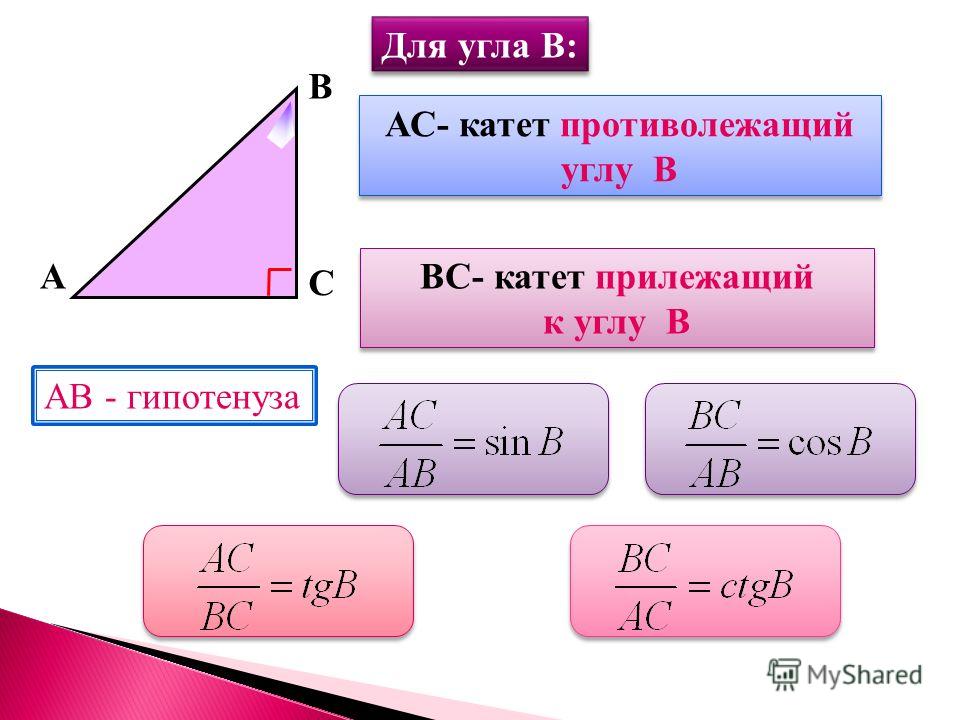
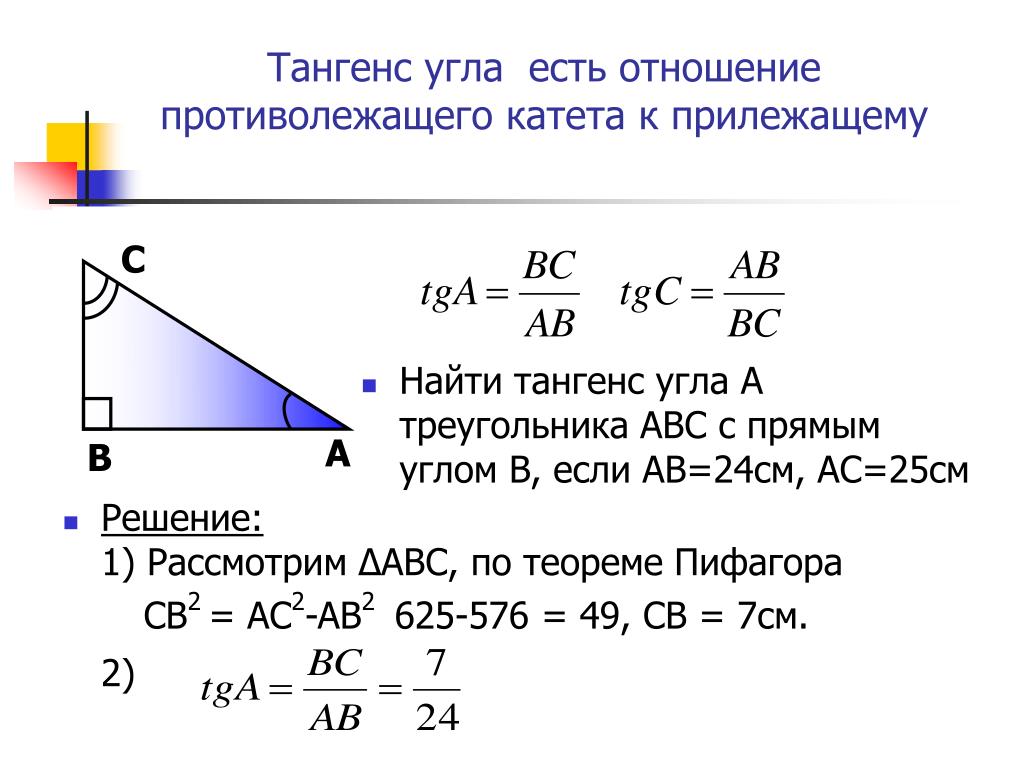 : ил.- ISBN 5-09-002727-7
: ил.- ISBN 5-09-002727-7 А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
 27, а).
27, а).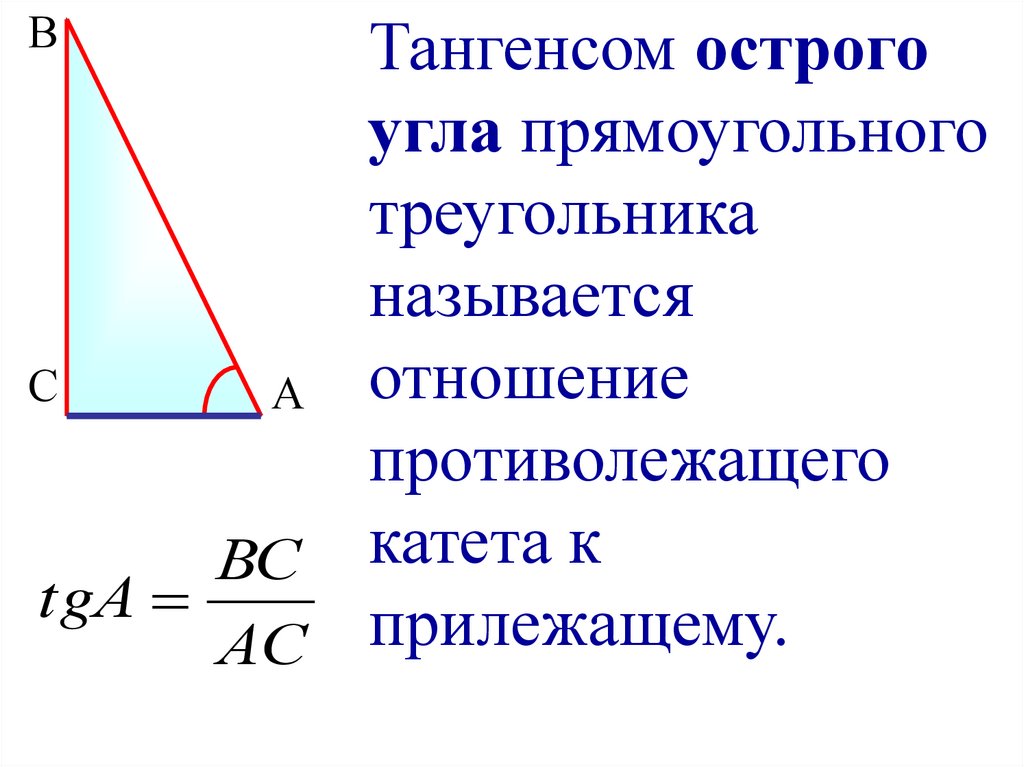 Запишем это как:
Запишем это как:

 Используя теорему Пифагора, вы можете найти длину стороны, прилегающей к углу:
Используя теорему Пифагора, вы можете найти длину стороны, прилегающей к углу: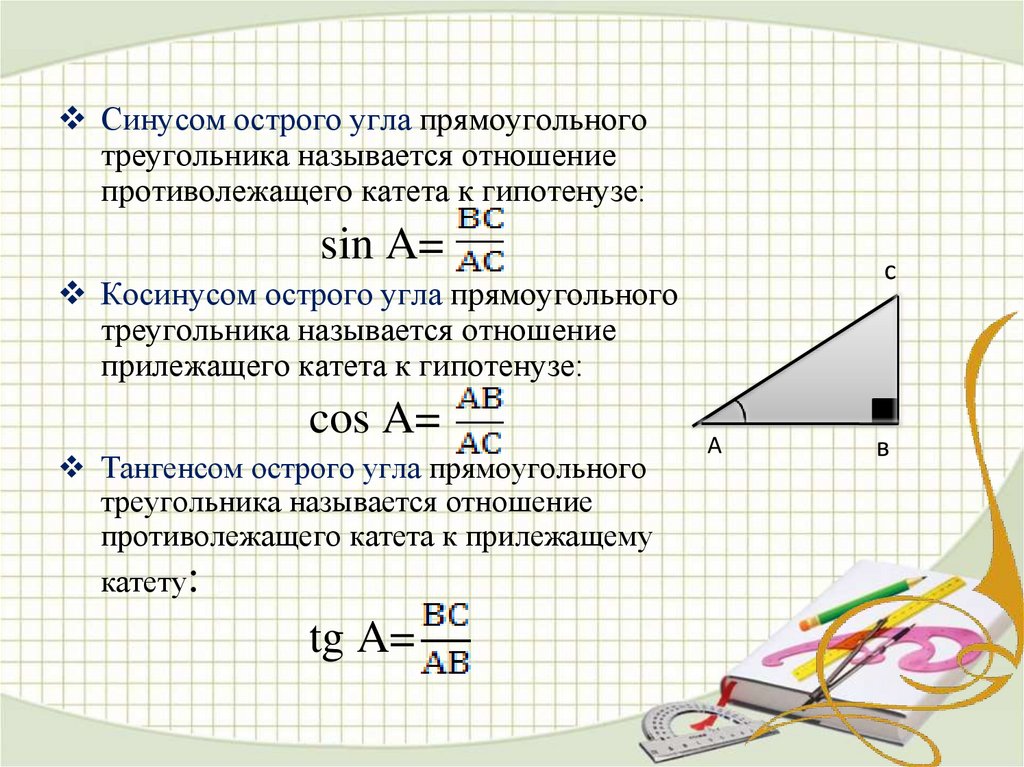 формулы могут показаться трудными для запоминания. Тем не менее, запоминание полезной мнемоники может помочь. При нахождении синуса, косинуса и тангенса просто помните SOHCATOA (sō-kŭ-tō-ŭ). В этом примере S, C и T обозначают синус, косинус и тангенс. O, A и H обозначают противоположность, смежность и гипотенузу.
формулы могут показаться трудными для запоминания. Тем не менее, запоминание полезной мнемоники может помочь. При нахождении синуса, косинуса и тангенса просто помните SOHCATOA (sō-kŭ-tō-ŭ). В этом примере S, C и T обозначают синус, косинус и тангенс. O, A и H обозначают противоположность, смежность и гипотенузу. »> Стандарты: CCSS.MATH.HSF.TF.A.2, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.L.1, CCRA.L.2, CCRA .L.3, CCRA.L.6, CCRA.W.2, CCRA.W.4, CCRA.W.9, CCRA.W.10, CCRA.SL.1, CCRA.SL.2
»> Стандарты: CCSS.MATH.HSF.TF.A.2, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.L.1, CCRA.L.2, CCRA .L.3, CCRA.L.6, CCRA.W.2, CCRA.W.4, CCRA.W.9, CCRA.W.10, CCRA.SL.1, CCRA.SL.2 Не забудьте также указать правильные формулы!
Не забудьте также указать правильные формулы!