Как умножить обратную матрицу на матрицу: Действия с матрицами

Содержание

10. Умножение квадратных матриц одного порядка

Произведение любых двух квадратных матриц одного порядка всегда определено. При умножении двух квадратных матриц n-го порядка получится матрица того же порядка.

Теорема 7. Определитель произведения квадратных матриц одного порядка равен произведению определителей сомножителей.

Доказательство. Пусть А = , В = . Составим

С =

Матрицу С и вычислим её определитель двумя способами. Сначала используем теорему Лапласа, разложив его по первым N Строкам. Получим |С| = |А|×|В|.

Для вычисления вторым способом преобразуем матрицу С, Используя те преобразования, которые не меняют определитель. К (N +1)-му столбцу матрицы С прибавим 1-ый столбец, умноженный на ,

2-ой столбец, умноженный на , … , N-Ый столбец, умноженный на .

Тогда в (N +1)-м столбце на первых N Местах будут стоять элементы первого столбца матрицы А×В, А на остальных местах – нули.

С1 =

Продолжая аналогичные преобразования с (N +2)-м и т. д. столбцами, получим матрицу С1. Здесь Скр – элементы произведения А×В. Очевидно, |С1| = |С|. Определитель матрицы С1 вычислим, разлагая его (по теореме Лапласа) по последним N Строкам. Получим

|С| = (-1)n×(-1)к×|А×В|, где к = 1 + 2 + …+ n + + (n + 1) + … + 2n = (2n + 1 )×n. Так как (2n + 1 )×n + + n = 2(n + 1 ), то |С| = |АВ |. Итак, |АВ | = |А|×|В| (12).

Если |А| ¹ 0, то матрица А Называется Невырожденной, если же |А| = 0, то матрица А Вырожденная. Из теоремы 7 следует, что произведение двух невырожденных квадратных матриц одного порядка есть невырожденная матрица того же порядка, если же одна из матриц вырожденная, то их произведение – тоже вырожденная матрица.

Квадратная матрица Е = называется Единичной матрицей. Легко проверить, что Е×А = А×Е для любой квадратной матрицы А, Имеющей тот же порядок, что и Е. Очевидно, |Е| = 1.

Определение 11. Матрица В Называется Правой Обратной для матрицы А, если В×А= Е И Левой обратной для А, если А×В = Е.

Возникает вопрос, всякая ли квадратная матрица имеет левую или правую обратную матрицу. Если В – левая или правая обратная матрица, то (по теореме 7) |В|×|А| = |А|×|В| = 1, т. е. матрица

А Не может быть вырожденной.

Пусть А Квадратная невырожденная матрица, найдём алгебраические дополнения для всех её элементов. Составим новую матрицу А* следующим образом: алгебраические дополнения элементов К-ой строки матрицы А поставим в К-ый столбец матрицы А*, Т. е. А* = . Матрица А* называется Присоединённой для матрицы А. По правилу умножения матриц и свойствам определителя получаем, что

А×А*= А*×А = = |А|×Е.

Так как |А| ¹ 0, то матрица В = Существует и А×В = В×А = Е, т. е. матрица В является и левой и правой обратной матрицей для матрицы А. Эта матрица называется Обратной матрицей для А и обозначается А-1.

Итак, получили

Теорема 8. Для всякой квадратной невырожденной матрицы существует обратная матрица. Обратная матрица перестановочна с данной матрицей и вычисляется по формуле

А-1= (13)

Пример 4. Найдите обратную матрицу, если А = .

Решение. Найдём |А| = 10 + 12 + 0 – 0 + 4 + 12 = 36.

Составим присоединённую матрицу, для этого вычислим алгебраические дополнения. А11 = = 14, А12 = = — 6, А13 = = 3, А21 == 8, А22 = = 2, А23 = = -1, А31 = = 28, А32 = = 16, А33 = = 11. Используя теорему 8, получим А-1 = .

< Предыдущая		Следующая >

Как умножить матрицу на матрицу?

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Какие матрицы можно умножать?

Умножать матрицы можно тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы. Решение. Так как A=A3×2 , а B=B2×2 , то произведение возможно и результатом операции умножения будет матрица C=C3×2 , а это матрица вида C=(c .

Как умножить вектор на матрицу?

Свойства умножения матрицы на вектор Произведение вектора-строки на произведение матрицы и вектора столбца, равноценно произведению произведения вектора-строки на матрицу и вектора-столбца.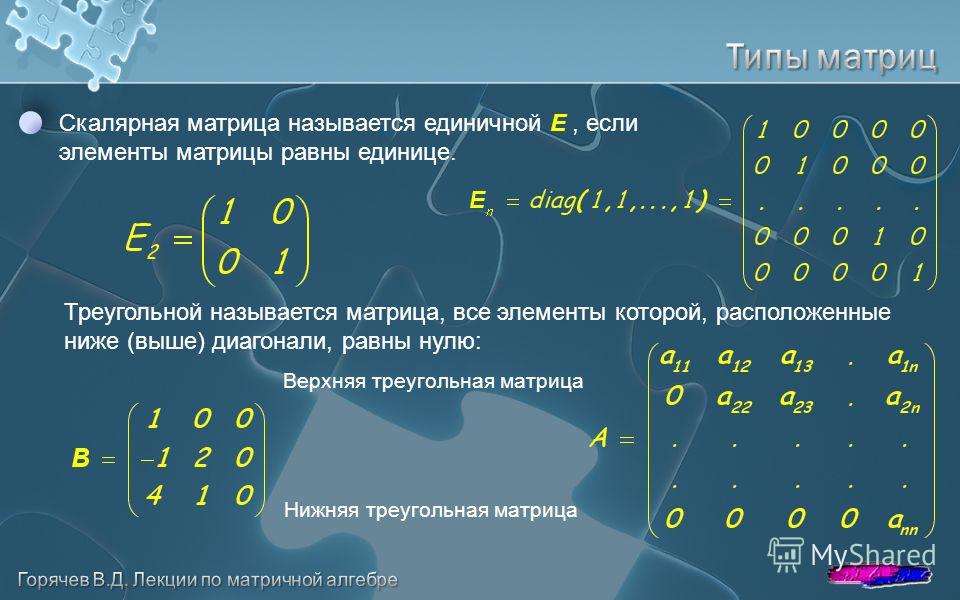

Как умножить строку на матрицу?

Умножение матриц

Умножаем первый элемент первой строки на первый элемент второго столбца.
Умножаем второй элемент первой строки на второй элемент второго столбца.
Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и второго столбца второй матрицы.
Складываем полученные произведения.

Как быстро найти обратную матрицу?

Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Находим определитель матрицы. …
Находим матрицу миноров . …
Находим матрицу алгебраических дополнений . …
Находим транспонированную матрицу алгебраических дополнений . …
Ответ:

Какая матрица не имеет обратной?

Матрица не имеет обратной, если её определитель равен 0. При а=1, а=-8 det(А)=0, те при таких значениях а матрица не имеет обратной.

Какая матрица называется обратной по отношению к матрице А?

Матрица А-1 называется обратной матрицей по отношению к матрице А , если А*А-1 = Е , где Е — единичная матрица n -го порядка. Обратная матрица может существовать только для квадратных матриц.

Что значит обратить матрицу?

Квадратная матрица называется неособенной (или невырожденной, несингулярной), если её определитель не равен нулю, и особенной (или вырожденной, сингулярной), если её определитель равен нулю. … Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.

Что значит т в матрице?

Транспонирование — в линейной алгебре это операция над матрицами в результате которой матрица поворачивается относительно своей главной диагонали. При этом столбцы исходной матрицы становятся строками результирующей.

Как решать уравнения с матрицами?

Для того, чтобы решить матричное уравнение

вида A ⋅ X = B, обе его части следует умножить на обратную к A матрицу слева: . Так как E — единичная матрица, то E ⋅ X = X.

-1

бессмысленно.

Я предполагаю, что вы хотите найти матрицу U так, чтобы

U*a == r

как можно точнее. То есть норма(U*a-r) является наименьшим возможным значением среди всех матриц U?

а=[-0,7398 1,638; 1,4522-4,258; 2,192 5,42];

r=[2,74 1,6; 0 6,9; 0 0];

В справке по / (известной как mrdivide, если посмотреть на саму функцию) мы видим:

>> help /

/ Косая черта или правая матрица деления.

A/B — это матричное деление B на A, что примерно соответствует

тому же A*INV(B) , за исключением того, что оно вычисляется другим способом.

Итак, если бы вы могли инвертировать матрицу, которую вы назвали а, мы бы выполнили вашу задачу как:

U = r/a;

Есть ли у вас желаемое свойство? Да.

norm(U*ar- r)

ans = 9.9301e-16

Как мы видим, норма фактически равна нулю или настолько близка, насколько это возможно в арифметике с плавающей запятой.

г = 3×2

2,7400 1,6000 0 6,9000 0 0

U*a

ans = 3×2

2,7400 1,6000 -0,0000 6,9000 0 0

Матрица U представляет собой матрицу 3×3. так как для того, чтобы размеры матриц соответствовали матричному умножению, он должен иметь этот размер.

U = 3×3

0 0,6593 0,8132 0 -0,8791 0,5824 0 0 0

●

Как видите, U равно 3×3. Вспомните, как вы перемножаете матрицы. Если вы хотите составить произведение U*a, где a равно 3×2, и получить в результате матрицу размера 3×2, то U ДОЛЖНО быть матрицей 3×3.

Произошла ошибка

Не удалось выполнить действие из-за изменений, внесенных на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние.

Выберите веб-сайт

Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .

Вы также можете выбрать веб-сайт из следующего списка:

Европа

Обратитесь в местный офис

Линейная алгебра — интуитивная математика

Ранее мы видели, что произведения матриц и векторов имеют определение, которое можно понять с помощью линза трансформации. А как же деление на матрицу? Единственное интуитивное определение, которое мы можем придумать, может заключаться в делении каждого коэффициента в матрице m×n’ role=»presentation» tabindex=»0″>m×nm×n, но это противоречило бы нашему пониманию умножения, которое определяется на матрицах размера m×role=»presentation» tabindex=»0″>

m×nm×n и n×role=»presentation» tabindex=»0″>n×mn×m , где каждый компонент становится скалярным произведением соответствующей строки и столбца.
Вместо этого мы могли бы подумать о делении с точки зрения умножения. Помните, что умножение любого числа на дробь с числителем 1 — это деление на знаменатель этой дроби. А также напомним, что любая дробь с числителем 1 является обратным умножению на знаменатель, в том смысле, что если мы умножим 1 на знаменатель, умножение на дробь отменит умножение и снова даст 1.
1×a×1a=1
‘ role=»presentation» tabindex=»0″>1×a×1a=11×a×1a=1
Для удобства записи мы обычно называем такие дроби отрицательными показателями степени, поскольку мы можем использовать тот факт, что умножение двух чисел складывает их степени, а сумма 1 и -1 равна нулю.
1×a1×a−1=a0=1
‘ role=»presentation» tabindex=»0″>1×a1×a-1=a0=11×a1×a-1=a0 =1
Обратите внимание, что не у каждого числа есть обратное. В частности, если то, на что мы умножаем, равно нулю, то вы не можете использовать функцию, чтобы получить число обратно, поскольку нуль, умноженный на что-либо, равен нулю. В дробной записи это тоже не имело бы особого смысла:
1×0×10=?
‘ роль=»презентация» tabindex=»0″>1×0×10=?1×0×10=?
В таких случаях мы говорим, что число не имеет обратного, поскольку это было бы то же самое, что деление на ноль.
То же самое можно выразить и для матриц — произведение любой матрицы на обратную (если обратная существует) всегда будет матрицей тождественности, I’ role=»presentation» tabindex=»0″>
II
A& #x2212;1×A=I
‘ role=»presentation» tabindex=»0″>A-1×A=IA-1×A=I
Таким образом, если мы можем найти A−1′ role=»presentation» tabindex=»0″>A-1A-1, то, предварительно умножив на него матрицу, мы фактически разделим на A’ role=»presentation» tabindex =»0″>АА.
Опять же, обратите внимание, что не у каждой матрицы есть обратная. Вспомните, что некоторые преобразования сжимают все пространство в линию или плоскость:
В этом случае было бы невозможно найти матрицу, которая возвращалась бы к нашему исходному пространству, так как все точки в пространстве могли оказаться в том же положении в самолете. Мы также сказали, что, по крайней мере, для этого преобразования 3×3 общий объем равен нулю и, следовательно, определитель равен нулю. Вскоре мы увидим, почему нулевой определитель означает, что обратная форма не может существовать формально.

Теперь для вычисления инверсий. Начнем с случая 2×2. В данном случае я просто приведу формулу, но имейте в виду, что эта формула не является общим или даже рекурсивным определением того, как вычисляется инверсия, а на самом деле является просто сокращением для случая 2×2:
1detA(d& #x2212;b−ca)
‘ role=»presentation» tabindex=»0″>1detA(d-b-ca)1detA(d-b-ca)
Вам простительно думать, что формула была вытащено из ниоткуда, поэтому давайте разобьем его на компоненты, сосредоточившись на примере: матрица, которая масштабируется на 2 в обоих направлениях и вращается против часовой стрелки.
[02−20]
‘ role=»presentation» tabindex=»0″>[02−20][02−20]
Теперь рассмотрим просто умножение преобразованных базисных векторов на переупорядоченную матрицу, которую мы видели ранее. Возвращает ли это нас к стандартным базисным векторам?
[0−220]
‘ role=»presentation» tabindex=»0″>[0-220][0-220]
К сожалению, это не совсем то, что мы хотели. Мы вернулись к нашим базисным векторам, но теперь они в четыре раза больше! Проблема с простой перестановкой матрицы заключается в том, что она не отменяет изменения площади, на самом деле определитель преобразования сохраняется, поэтому, умножая на новую матрицу, мы просто увеличиваем пространство в два раза.
По этой причине для нахождения обратного нам также нужно отменить изменение определителя путем масштабирования на значение, обратное определителю.
10×0−2×−2×(0−220)
‘ role=»presentation» tabindex=»0″>10×0−2×−2× (0-220)10×0-2×-2×(0-220)
14×(0−220)
‘ role=»presentation» tabindex=»0″>14×(0-220 )14×(0−220)
Теперь, если мы это сделаем, преобразование вернет нас к нашим базисным векторам. Обратите внимание: тот факт, что мы умножаем на величину, обратную определителю, означает, что некоторые матрицы по определению необратимы, потому что мы не можем умножать на величину, обратную нулю.
Теперь, если бы этот раздел следовал за другими, он дал бы обобщенную технику для расширения этого знания в несколько измерений. К сожалению, не существует общего механизма для вычисления обратных матриц n×m’ role=»presentation» tabindex=»0″>n×mn×m. Вместо этого мы рассмотрим более алгоритмический подход с использованием элементарных операций со строками.
Вспомним, что с помощью операций с элементарными строками мы смогли взять сложное на вид преобразование и свести его к единичной матрице. Если бы мы могли представить эти операции в виде матрицы, эта матрица была бы обратной исходной матрице.
Рассмотрим то же преобразование 3×3, которое мы сократили по строкам выше:
[1−10−1−10212]
‘ role=»presentation» tabindex=»0″>⎡⎢⎣1−10−1 −10212⎤⎥⎦[1−10−1−10212]
Мы снова сократим его по строкам, но на этот раз применим те же операции к единичной матрице и посмотрим, как это преобразование повлияет на уже преобразованный единичный куб. Итак, рядом:
[1−10−1−10212]’ role=»presentation» tabindex=»0″>⎡⎢⎣1−10−1−10212⎤⎥⎦[1 −10−1−10212][100010001]’ role=»presentation» tabindex=»0″>⎡⎢⎣100010001⎤⎥⎦[100010001]
Сначала вычесть 2 раза первую строку из третьей.
[1−10−1−10032]’ role=»presentation» tabindex=»0″>⎡⎢⎣1−10−1−10032⎤⎥⎦[1−10−1−10032 ][100010−201]’ role=»presentation» tabindex=»0″>⎡⎢⎣100010−201⎤⎥⎦[100010−201]
Теперь вычтите вторую строку из первой.
[200−1−10032]’ role=»presentation» tabindex=»0″>⎡⎢⎣200−1−10032⎤⎥⎦[200−1−10032][1−10010&# x2212;201]’ role=»presentation» tabindex=»0″>⎡⎢⎣1−10010−201⎤⎥⎦[1−10010−201]
Затем добавьте половину первой строки ко второй.
[2000−10032]’ role=»presentation» tabindex=»0″>⎡⎢⎣2000−10032⎤⎥⎦[2000−10032][1−100.50.50−201]’ роль =»presentation» tabindex=»0″>⎡⎢⎣1−100.
No related posts.