Формула суммы в Excel — statanaliz.info
Любое обучение всегда идет от простого к сложному. Когда-то и я не знал, как в Эксель посчитать сумму столбца. Примерно с этого начинали и другие пользователи. Однако все можно изучить, если приложить усилия и выделить время.
В этой статье рассмотрим самые азы, а именно, как в Экселе сплюсовать ячейки , и как автоматически посчитать сумму столбца.
«+» – плюс
«+» – оператор суммирования. Чтобы сплюсовать числа в двух или более ячейках, нужно вначале выделить ячейку для записи суммы, нажать «=», левой кнопкой мыши указать первую ячейку, нажать «+», указать вторую ячейку и т.д., после выделения последней ячейки нажимать Enter. Данная функция является наследием микрокалькуляторов, когда нужно было набирать и плюсовать каждое значение в отдельности.
На мониторе суммирование плюсиком выглядит примерно так:
Если бы мы имели дело с небольшим количеством данных, то на этом обзор можно было бы закончить. Однако на практике обычно имеют дело с большими массивами данных.
Складывать плюсиком будет очень затруднительно. Поэтому существует формула суммы в Эксель, позволяющие несколькими движениями подбить итог у таблицы с сотней строк.
Функция СУММ (SUM) в Excel
СУММ – самая простая и часто используемая функция. Синтаксис очень простой.
СУММ(число1;число2;…)
число1;число2;… – это ссылки на ячейки или на целый диапазон.
Если диапазон суммирования имеет разрывы, то нужные участки следует выделять, удерживая клавишу Ctrl.
Так как функция суммирования используется очень часто, то есть несколько способов ее вызвать. Стандартный вариант – через Мастер функций. Для вызова Мастера функций нужно стать в ячейку (то есть сделать ее активной), где будет прописана формула, затем нажать кнопку fx (слева от строки формул) и выбрать нужную функцию. На рисунке видно, где что нажимать:
Кому такой способ не нравится, в панели инструментов на закладках Главная и Формулы предусмотрена специальная кнопочка — Автосумма.
Использовать автосумму лучше тогда, когда диапазон суммирования является неразрывным, и ячейка для суммирования находится снизу или справа от диапазона суммирования. Иначе придется вручную поправлять диапазон, что не есть большая проблема.
Однако истинные мастера Excel выбирают горячие клавиши. Автосумму можно вызвать комбинацией клавиш Alt + = (Альт и равно). Ниже показано, что происходит на экране при использовании автосуммы: активировали ячейку B21, нажали Alt + = (или кнопку на панели).
Диапазон автоматически выделился – это видно по контуру моргающей рамочки. Формула суммирования появилась как в ячейке, так и в строке формул. Осталось нажать Enter и все – сумма готова. Теперь вы знаете, как в Экселе суммировать столбец или отдельные ячейки.
В видео ниже показан трюк применения автосуммы с помощью горячих клавиш.
Автосумма в Excel» src=»https://www.youtube.com/embed/Pnl8O04CZrE?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Поделиться в социальных сетях:
Статья 6. Особенности осуществления перевода денежных средств по требованию получателя средств \ КонсультантПлюс
Статья 6. Особенности осуществления перевода денежных средств по требованию получателя средств
1. При осуществлении безналичных расчетов в форме перевода денежных средств по требованию получателя средств (прямом дебетовании) оператор по переводу денежных средств на основании договора с плательщиком осуществляет списание денежных средств с банковского счета плательщика с его согласия (акцепта плательщика) по распоряжению получателя средств (далее — требование получателя средств).
2. Право получателя средств предъявлять требования к банковскому счету плательщика должно быть предусмотрено договором между обслуживающим плательщика оператором по переводу денежных средств и плательщиком.
3. Акцепт плательщика может быть дан до поступления требования получателя средств (заранее данный акцепт плательщика) или после его поступления обслуживающему плательщика оператору по переводу денежных средств. Акцепт плательщика может быть дан в договоре между обслуживающим плательщика оператором по переводу денежных средств и плательщиком либо в виде отдельного документа или сообщения.
4. Акцепт плательщика может быть дан в отношении одного или нескольких получателей средств, одного или нескольких требований получателя средств.
5. Требование получателя средств может направляться непосредственно обслуживающему плательщика оператору по переводу денежных средств или через оператора по переводу денежных средств, обслуживающего получателя средств.
6. В случае отсутствия заранее данного акцепта плательщика оператор по переводу денежных средств передает поступившее требование получателя средств для акцепта плательщику не позднее дня, следующего за днем поступления требования получателя средств.
7. Акцепт плательщика должен быть дан в течение пяти рабочих дней, если более короткий срок не предусмотрен договором между оператором по переводу денежных средств и плательщиком.
8. При акцепте плательщика требование получателя средств исполняется в сумме акцепта плательщика.
9. Допускается акцепт плательщика в части суммы требования получателя средств (частичный акцепт плательщика), если иное не предусмотрено договором между оператором по переводу денежных средств и плательщиком.
10. В случае частичного акцепта плательщика оператор по переводу денежных средств обязан указать на это при подтверждении получателю средств исполнения его требования.
11. При отказе плательщика от акцепта или неполучении акцепта в установленный срок требование получателя средств подлежит возврату получателю средств с указанием причины возврата.
12. При поступлении требования получателя средств с заранее данным акцептом плательщика обслуживающий плательщика оператор по переводу денежных средств обязан проверить соответствие требования получателя средств условиям заранее данного акцепта плательщика.
13. При соответствии требования получателя средств условиям заранее данного акцепта плательщика оно исполняется в сумме и в срок, которые предусмотрены условиями заранее данного акцепта плательщика.
14. При несоответствии требования получателя средств условиям заранее данного акцепта плательщика или невозможности их проверки обслуживающий плательщика оператор по переводу денежных средств обязан возвратить требование получателя средств без исполнения, если договором не предусмотрена обязанность обслуживающего плательщика оператора по переводу денежных средств в указанном случае запросить акцепт плательщика.
15. Оператор по переводу денежных средств обязан направить плательщику уведомление об исполнении требования получателя средств не позднее дня, следующего за днем исполнения.
последовательностей и рядов. Для чего в математике используется оператор суммирования?
$\begingroup$
Я достаточно опытен в программировании и знаю, что суммирование в математике похоже на цикл for: он выполняет указанные операции $x$ раз.
Я хочу знать, как это полезно в математике. Я не вижу, какой эффект может дать рекурсивное выполнение операций в математике, который может отличаться от выполнения этого вручную. Почему переменная, которая увеличивается на единицу в каждом цикле, должна это делать? В настоящее время я учусь в 11-м классе, и мой класс еще не затрагивал эту тему, но я видел ее на этом сайте множество раз и хотел бы узнать о ней больше.
- последовательности-и-серии
- обозначения
$\endgroup$
9
$\begingroup$
Во многих формулах операция повторяется снова и снова. Сложение и умножение настолько распространены, что у нас есть соответствующие обозначения суммирования и произведения. Это удобные способы дать компактные выражения для различных формул.
9n i = 1\cdot 2\cdot 3 \cdots n$
Кстати, аналогия с для петель хорошая.
Однако для циклов позволяют повторять множество операций. Обозначения суммирования и произведения гораздо более специализированы (и суммирование, и произведение могут быть вычислены с использованием циклов for ). Кроме того, не все циклы for каждый раз увеличивают индекс на 1. Большинство языков программирования допускают более сложные приращения. Точно так же суммирование и произведение иногда выполняются по множествам (кроме ${1,2,\dots,n}$).
Например: Если $S = \{1,2,4,8\}$, то $\sum\limits_{x \in S} \frac{1}{x} = \frac{1}{1 } + \frac{1}{2} + \frac{1}{4} + \frac{1}{8}$.
В исчислении (часто во втором семестре исчисления) можно узнать о рядах, где вы, по сути, суммируете бесконечные множества [суммирование бесконечных множеств становится немного сложным — возникают проблемы сходимости и проблемы при перетасовке порядка суммирования].
$\endgroup$
3
9nk .
$$
Когда вы попадаете в бесконечные ряды, вы не можете просто выполнять бесконечное количество арифметических операций вручную, поэтому математики (в частности, анализ) разработали так называемый предел, с которым мы можем говорить о бесконечных суммах, и в чтобы сделать это, говоря лаконично , нам нужны обозначения, которые помогают нам обращаться к частичным суммам быстро и легко для понимания. Разложения в ряды широко распространены в любой области математики, основанной на анализе (от дифференциальных уравнений до геометрии, теории чисел, комбинаторики и так далее).
В качестве еще одной практической полезности: иногда слагаемые (добавляемые отдельные количества) имеют шаблон, который нелегко обнаружить в дикой природе, и мы можем избежать препятствий наших читателей, пытающихся выяснить, что представляют собой эти шаблоны, просто написав в нотации суммирования, где каждое из слагаемых может быть записано как явная функция индексной переменной, и угадывать не требуется.
Наконец, суммирование из суммирования громоздко записывать и чрезвычайно трудно анализировать в записи без нотаций, но имеет прямое обозначение и интерпретацию с помощью символа $\sum$. 92}. $$
Это бесконечный ряд обратных величин квадратов всех чисел, взаимно простых с $n$. Набор натуральных чисел, взаимно простых с $n$, можно рассматривать как последовательность, но попытка найти способ перечислить их как $f(1),f(2),\dots$ излишняя и служит только отвлечением от основных понятий. . (Хотя конвергенция — это другой вопрос..)
$\endgroup$
$\begingroup$
«Почему переменная, которая увеличивается на единицу в каждом цикле, должна это делать?» 9к$. Оказывается, есть множества настолько бесконечные, что их нельзя выразить в виде $\{a_1,a_2,\ldots\}$, где для их подсчета используется $1,2,\ldots$. Такое множество называется несчетным (например, действительные числа несчетны).
Это говорит о том, что нам нужно альтернативное определение суммирования суммы по несчетному множеству. Пусть $I$ — некоторое множество и для каждого $\lambda$ в множестве $I$ пусть $\{a_{\lambda}\}$ — некоторый объект. Мы используем обозначение
$$\displaystyle\sum_{\lambda \in I} a_{\lambda}$$ 9+$ представляет собой набор положительных действительных чисел.
Какая польза? Ну, с точки зрения сумм действительных чисел это не очень полезно, так как несчетная сумма положительных действительных чисел всегда равна бесконечности. На самом деле его используют в высшей математике, где мы думаем о таких суммах различных видов объектов, где «сумма» означает не «сложение чисел», а «операцию, которая ведет себя достаточно похоже на сложение, поэтому мы называем это сложением». Объяснение занимает много времени, но если вам действительно нужно название области математики, в которой используются неисчислимые суммы, то я знаю, что это «неразделимые гильбертовы пространства», но я уверен, что их неисчислимо больше!
$\endgroup$
$\begingroup$
Это просто обозначение, позволяющее легко представить, что подразумевается под выражением.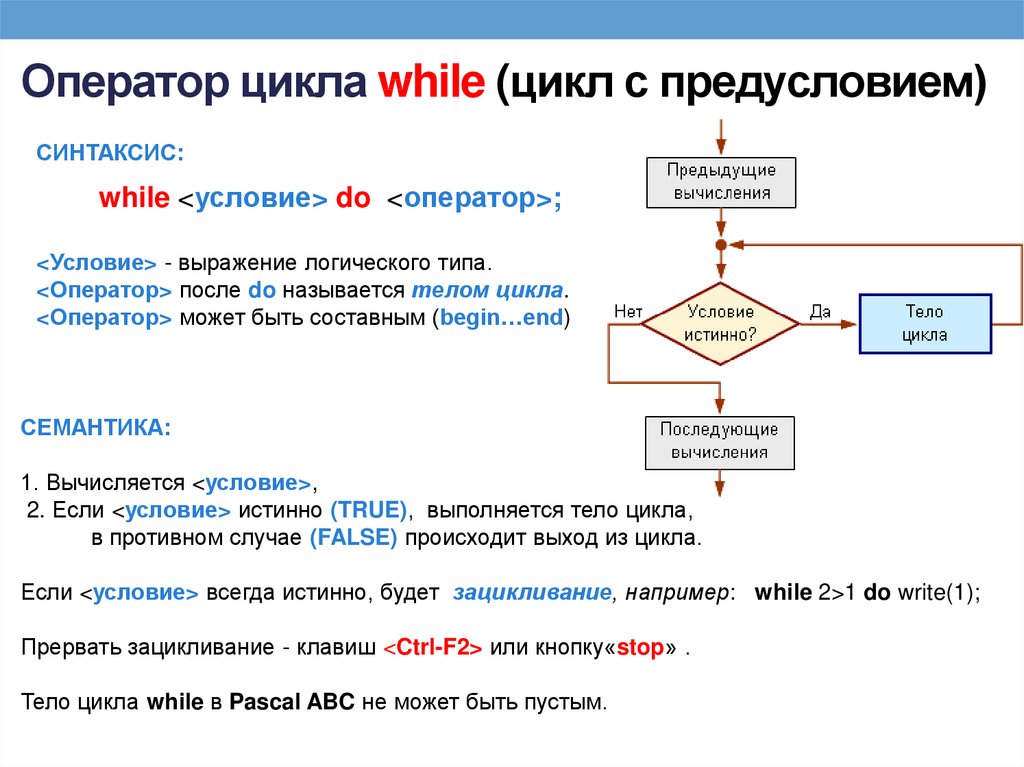
Представьте, что вы хотите сказать $x =$ сумма первых 50 натуральных чисел, тогда вы можете выразить это, сказав $1 + 2 + 3 …. + 50$ или использовать оператор суммирования, в котором $n$ выходит из $1$ до $50$ для удобства. Точно так же есть оператор произведения, который выглядит как пи, но имеет суффиксы, похожие на оператор суммирования, хотя для него может быть лучшее имя.
$\endgroup$
Глава 12 Оператор суммирования
Оператор суммирования , \(\сигма\), является незаменимым элементом статистики, поскольку он используется почти во всех формулах. Большинство студентов впервые столкнутся с ней, когда увидят формулу среднего арифметического. В этой главе я описываю основные правила, которые мы используем при работе с оператором суммирования. Убедитесь, что вы проработали их, чтобы понять, когда и как правило может облегчить вычисления.
12.2 Двойной индекс
В некоторых главах вы встретите двойной индекс \(x_{ij}\).
Например, когда мы строим таблицы непредвиденных обстоятельств с одной категориальной переменной в качестве строк и другой категориальной переменной в качестве столбцов, таблица может выглядеть следующим образом:
Это может быть представлено следующим образом:
Важно отметить, что одна нижний индекс \((i)\) индексирует строку, на которую ссылаются при вычислении, а другой индекс \((j)\) индексирует столбец, на который ссылаются при расчете. 92 \cdots\) суммировать все значения \(x\) и возвести в квадрат \(\sum x\)
