Свойства коллинеарных векторов:
1. Нулевой вектор коллинеарен любому вектору: Если (или ), то (или ).
2. Нулевой вектор одинаково направлен с любым вектором, .
3. Любые два коллинеарных вектора можно отложить на одной прямой.
Достаточно отложить векторы от одной точки.
4. На прямой можно указать всего два направления, следовательно, два вектора, отложенных на ней могут иметь либо одно и то же направление, либо противоположное.
Определение 4.
Векторы и называются противоположными.
Рассмотрим вектор . Отложим его от точки А.
Для вектора = противоположным называется вектор , =–.
Вектор, противоположный , это вектор , т.е. =–(–).
Для нулевого
вектора противоположным является вектор
,
или
=–.
Определение 5.
Ненулевые векторы и называются одинаково направленными (сонаправленными), если лучи АВ и CD одинаково направлены, обозначается символом :
.
Ненулевые векторы и называются противоположно направленными, если лучи АВ и CD противоположно направлены, обозначается символом :
.
3. Абсолютная величина вектора
Определение 6.
Модулем (длиной, абсолютной величиной) вектора называется длина отрезка АВ, обозначается , или АВ.
Длина нулевого вектора равна нулю: .
Определение 7.
Вектор, абсолютная величина которого равна единице, называется единичным.
Единичный вектор обозначается , .
4. Равенство векторов
Определение 8.
Два вектора и называются равными, если выполнены следующие условия:
1) они имеют одинаковое направление, ;
2) абсолютные величины их равны, ||=||.
Из определения следует, что два нулевых вектора всегда равны.
Равенство векторов обладает свойствами, аналогичными свойствам равенства чисел.
Свойства равенства векторов:
1. Рефлексивность: каждый вектор равен самому себе ;
2. Симметричность: .
3. Транзитивность: .
Равенство векторов является отношением эквивалентности.
5. Линейные операции над векторами
Линейными операциями над векторами называются сложение векторов и умножение вектора на действительное число.
5.1. Сложение векторов
Определение 9
(Правило треугольника).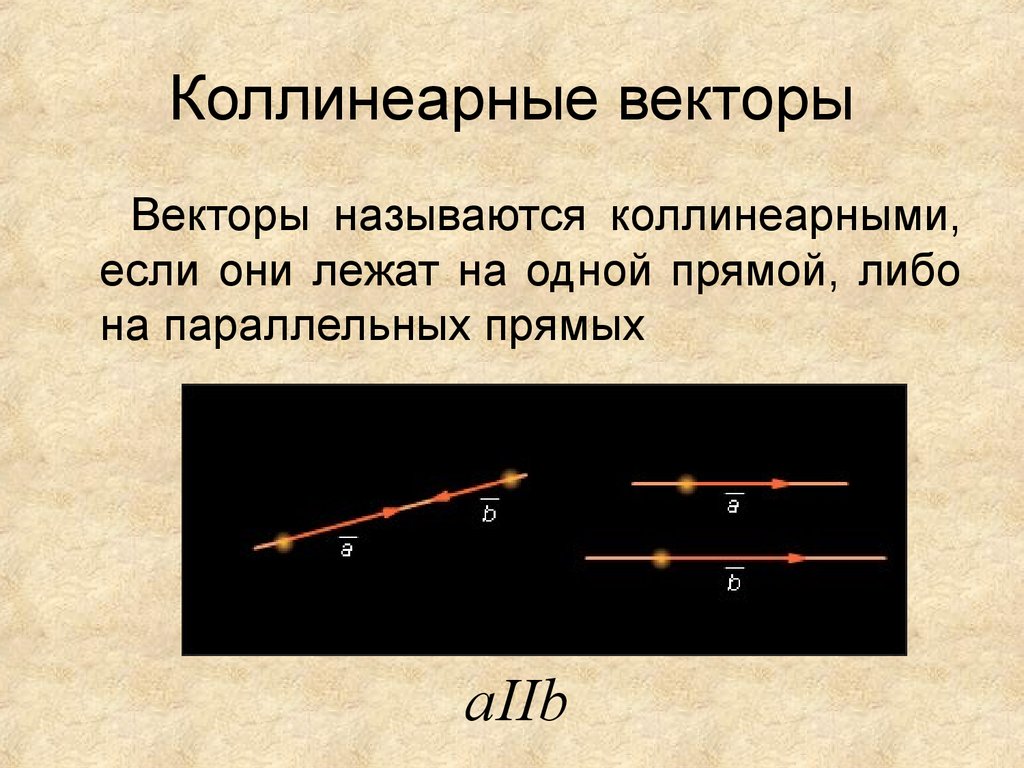
Суммой векторов и , отложенных последовательно, называется вектор , начало которого совпадает с началом первого слагаемого вектора, а конец – с концом второго.
,
(7.1)
Сумма векторов существует и определена однозначно.
Свойства сложения:
1.
С=В
2.
С=В, В=А
3.
С=А
4.
Коммутативность
5.
Ассоциативность
Определение 10 (Правило параллелограмма).
Суммой векторов и , отложенных от общего начала, называется вектор , задаваемый диагональю построенного на них, как на сторонах, параллелограмма, исходящей из их общего начала. Начало вектора суммы совпадает с началом слагаемых векторов, а конец – с противоположным концом диагонали параллелограмма.
Сложение двух скользящих векторов определено лишь в случае, когда прямые,
на которых они расположены, пересекаются.
Тогда каждый из векторов переносится
вдоль своей прямой в точку пересечения
этих прямых, после чего сложение
осуществляется по правилу параллелограмма.
Сложение двух связных (фиксированных) векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Определение 11 (Правило многоугольника).
Суммой n векторов , отложенных последовательно, называется вектор, начало которого совпадает с началом первого слагаемого вектора, а конец – с концом последнего слагаемого вектора.
Как найти вектор, коллинеарный вектору
Содержание статьи
1. Понятие коллинеарности векторов
2. Признак коллинеарности через пропорциональность или как определить коллинеарность векторов по координатам
3. Признаки и свойства коллинеарности векторов через их произведение
Понятие коллинеарности векторов
Чтобы понять, что значит коллинеарные векторы, сперва надо разобраться, что является геометрическим вектором.
Для этого сначала введем понятие отрезка.
Определение 1
Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.
Концами отрезка будем называть точки, которые его ограничивают.
Для введения определения вектора один из концов отрезка назовем его началом.
Определение 2
Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.
Обозначение: $\overline{AB}$ — вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.
Иначе одной маленькой буквой: $\overline{a}$ (рис. 1).
Рисунок 1. Обозначение векторов. Автор24 — интернет-биржа студенческих работ
Определение 3
Нулевым вектором будем называть любую точку, которая принадлежит плоскости.
Обозначение: $\overline{0}$.
Далее рассмотрим, какие векторы называются коллинеарными.
Определение 4
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой.
Кроме того, понятие коллинеарность наблюдается в случается параллельности векторов (рис.2).
Рисунок 2. Коллинеарность векторов. Автор24 — интернет-биржа студенческих работ
Также введем определение векторного произведения, которое будет нам необходимо далее.
Определение 5
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.
Обозначение: $\overline{α}х\overline{β}$.
Чтобы найти векторное произведение, будем пользоваться формулой
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}$
Признак коллинеарности через пропорциональность или как определить коллинеарность векторов по координатам
Теорема 1
Главное условие коллинеарности векторов: чтобы ненулевые векторы были коллинеарны между собой, необходимо, чтобы их соответствующие координаты были пропорциональны друг другу.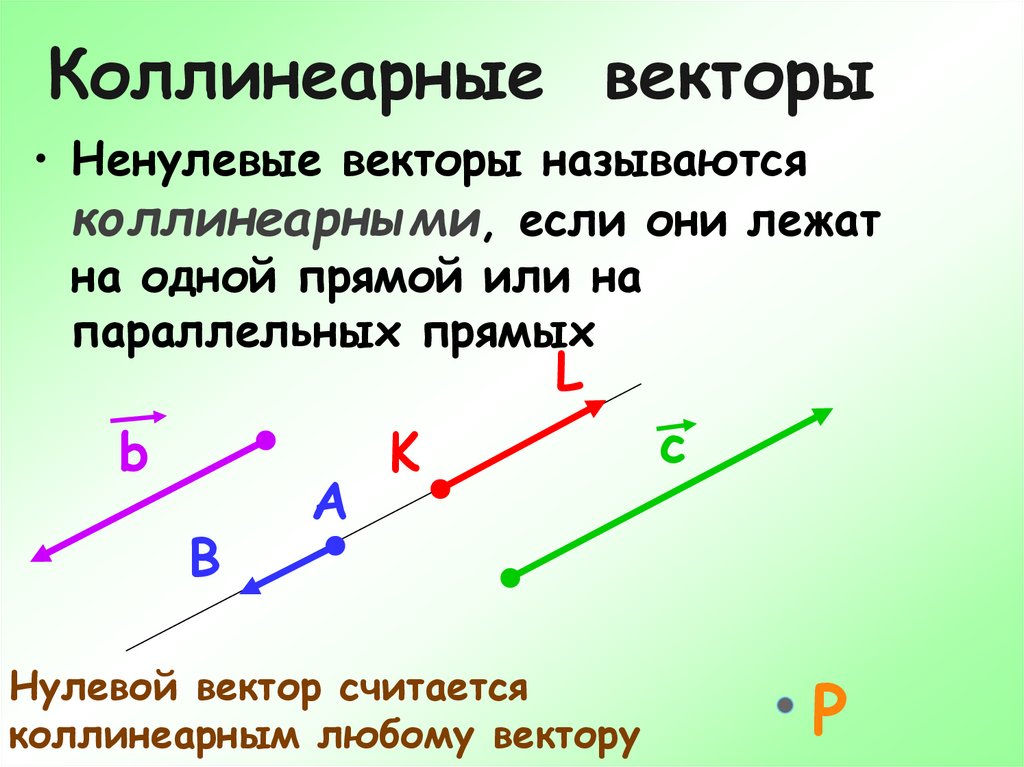
Доказательство.
Необходимость: Пусть нам даны векторы $\overline{α}$ и $\overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать следующие равенства
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Так как векторы $\overline{α}$ и $\overline{β}$ коллинеарны, то они будут либо сонаправленными, либо противоположно направленными. Без ограничения общности, будем считать, что они будут сонаправлены, то есть $\overline{α}↑↑\overline{β}$. Умножим один из этих векторов на действительное, большее нуля, число $r$, так, чтобы длины векторов $r\overline{α}$ и $\overline{β}$ были равны между собой. По определению умножения векторов на число, получим, что $r\overline{α}↑↑\overline{β}$. Но тогда, по определению равенства векторов, получим, что $r\overline{α}=\overline{β}$. Из этого равенства получим, что
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Достаточность: Пусть верны равенства $α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$.
Из данных равенств следует, что $r\overline{α}=\overline{β}$.
Имеются два случая:
$r \lt 0$
В этом случае, по определению умножения вектора на число, получим, что $r\overline{α}↑↓\overline{β}$.
$r >0$
В этом случае получим, что $r\overline{α}↑↑\overline{β}$.
Тогда, в обоих случаях получаем доказательство коллинеарности векторов $\overline{α}$ и $\overline{β}$.
Ответ: теорема доказана.
Пример 1
Как проверить коллинеарность векторов $(3,-1)$ и $(9,-3)$.
Доказательство.
Разложим второй вектор:
$(9,-3)=(3\cdot 3,3\cdot (-1) )=3(3,-1)$
Получаем, что координаты этих векторов пропорциональны друг другу, что, по теореме 1, и доказывает наше утверждение.
Признаки и свойства коллинеарности векторов через их произведение
Теорема 2
Чтобы ненулевые векторы были коллинеарны между собой, необходимо и достаточно, чтобы их векторное произведение было равно нулевому вектору.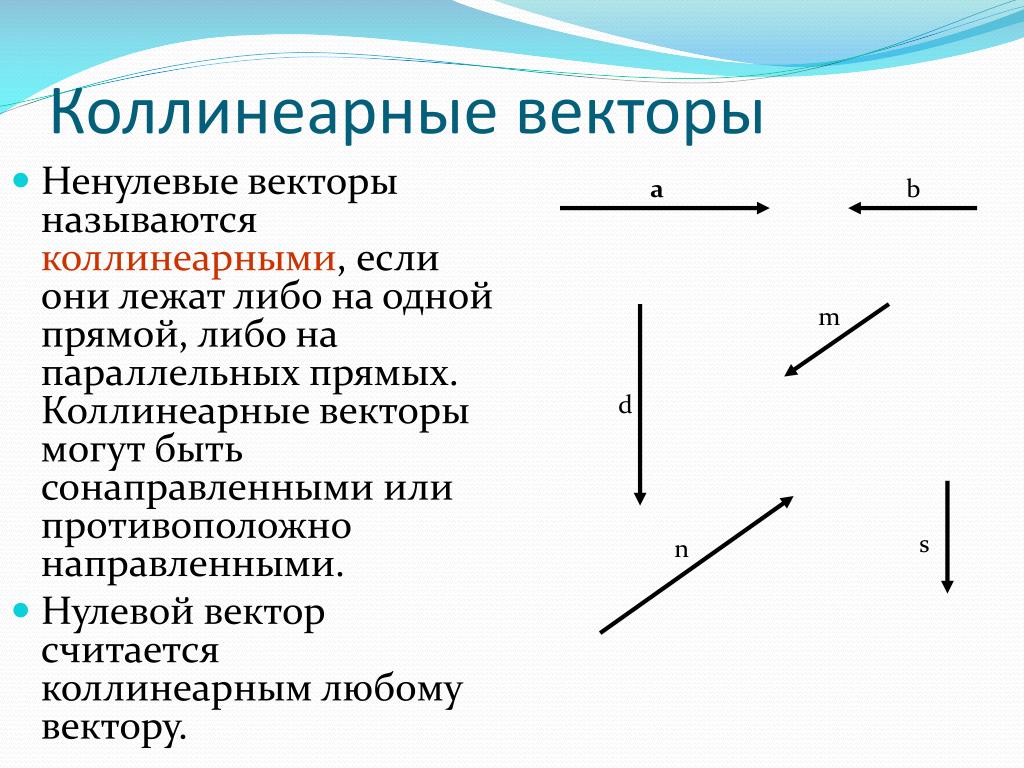
Доказательство.
Необходимость: Пусть нам даны векторы $\overline{α}$ и $\overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать, что $\overline{α}х\overline{β}=\overline{0}$.
Так как векторы коллинеарны, то, по теореме 1, верны равенства
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Найдем $\overline{α}х\overline{β}$ по формуле
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\rβ_1&rβ_2&rβ_3\\β_1&β_2&β_3\end{vmatrix}=r\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\β_1&β_2&β_3\\β_1&β_2&β_3\end{vmatrix}=r\cdot \overline{0}=\overline{0}$
Достаточность: Пусть верно равенство $\overline{α}х\overline{β}=\overline{0}$, докажем, что векторы $\overline{α}$ и $\overline{β}$ коллинеарны.
\circ$. То есть, чтобы они были коллинеарны, векторы должны лежать на одной или параллельных прямых.
Теорема доказана.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 19.07.2022
Выполнение любых типов работ по геометрии
Решение задач по геометрии Контрольная работа на тему теорема синусов и косинусов Реферат по геометрии Отчеты по практике по геометрии Курсовые работы по геометрии Контрольная работа по геометрии Дипломная работа по геометрии
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Значение и условие с примерами и часто задаваемыми вопросами
Что такое коллинеарные векторы? Когда два или более двух векторов параллельны друг другу, независимо от величины или направления, говорят, что векторы коллинеарны.
Векторы задаются как объект, включающий величину плюс направление. Он изображает перемещение объекта из одного места в другое.
Существуют различные типы векторов, а именно: нулевой вектор, единичный вектор, ко-начальный вектор, вектор положения, подобный и отличный вектор, коллинеарный вектор, равный вектор, копланарный вектор, вектор смещения, отрицательный вектор и так далее. В этой статье мы постараемся узнать о коллинеарности векторов, о том, как находить коллинеарные векторы, с примерами, условиями и многим другим.
Что такое коллинеарные векторы? Если рассматривать векторы как прямую линию, то протяженность линии обозначает величину, а указатель на этой линии — направление, в котором движется вектор. Следовательно, мы можем оценить любые два заданных вектора в векторной алгебре как коллинеарные тогда и только тогда, когда эти два вектора либо лежат на одной линии, либо векторы параллельны друг другу в одном / противоположном направлении.
Параллельность векторов указывает на то, что они никогда не встречаются и не пересекаются друг с другом. Рассмотрим изображение ниже, чтобы понять то же самое. Поэтому коллинеарные векторы также известны как параллельные векторы.
Формула коллинеарных векторовВ соответствии с определением теперь мы можем утверждать, что два параллельных вектора являются коллинеарными по той причине, что эти два вектора указывают в одинаковом направлении или в противоположном направлении. Если два вектора представлены как \(\vec{a}=a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\text{ и }\vec{b}=b_1\hat{ i}+b_2\hat{j}+b_3\hat{k}\)
Тогда два вектора коллинеарны тогда и только тогда, когда: \(\frac{b_1}{a_1}=\frac{b_2}{a_2}= \фракция{b_3}{a_3}\)
Условие коллинеарности векторов Двигаясь к тому, как узнать, коллинеарны два вектора или нет, то есть каковы условия коллинеарности двух данных векторов в математике.
Чтобы любые 2 вектора были коллинеарными, они должны удовлетворять указанным ниже условиям.
Условие 1: Два вектора \(\vec{a}\text{ и }\vec{b}\) называются коллинеарными, если существует ненулевой скаляр ‘n’ такой, что:
\(\ vec{b}=n\vec{a}\)
Условие 2: Два вектора \(\vec{a}\text{ и }\vec{b}\) считаются коллинеарными тогда и только тогда, когда пропорции их связанных координат идентичны. То есть, если:
\(\vec{a}=a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\text{ и }\vec{b}=b_1\hat{i }+b_2\hat{j}+b_3\hat{k}\) два вектора:
Тогда
\(b_1\hat{i}+b_2\hat{j}+b_3\hat{k}= n\left(a_1\шляпа{i}+a_2\шляпа{j}+a_3\шляпа{k}\право)\)
\(b_1=na_1\text{,}\ b_2=na_2\text{ и } \ b_3=na_3\)
Условие 2 неверно, если любой из элементов предоставленного вектора аналогичен нулю.
Условие 3: Два вектора \(\vec{a}\text{ и }\vec{b}\) также называются коллинеарными, если их векторное произведение эквивалентно нулевому вектору.
Это если: \(\vec{a}\text{ и }\vec{b}\) два ненулевых вектора. Тогда \(\vec{a}\times\vec{b}=\vec{0}\) тогда и только тогда, когда \(\vec{a}\text{ и }\vec{b}\) параллельны или коллинеарны друг к другу, т. е. \(\vec{a}\times\vec{b}=\vec{0}\Leftrightarrow\vec{a}\text{ || }\vec{b}\).
Условие 3 можно использовать только в трехмерных или пространственных ситуациях
Как доказать, что векторы коллинеарны?Теперь давайте узнаем, как показать, что два вектора коллинеарны, или как доказать коллинеарность векторов. Чтобы два заданных вектора были коллинеарными, мы можем проверить три важных условия, как обсуждалось выше. Давайте возьмем пример, чтобы понять то же самое.
Чтобы проверить коллинеарность, мы можем получить перекрестное произведение между ними, как показано:
Если \(\vec{a}=a_1\шляпа{i}+a_2\шляпа{j}+a_3\шляпа{k}\text{ и }\vec{b}=b_1\шляпа{i}+b_2 \hat{j}+b_3\hat{k}\) — это два вектора. Затем:
\(\vec{a}\times\vec{b}=\begin{vmatrix}i&j&k
a_1&a_2&a_3
b_1&b_2&b_3\end{vmatrix}\)
\(=i\left(a_2b_2-a_3-a_3 \right)-j\left(a_1b_3-a_3b_1\right)+k\left(a_1b_2-a_2b_1\right)\)
\(=i\left(a_2na_3-a_3na_2\right)-j\left(a_1na_3-a_3na_1 \право)+к\лево(а_1на_2-а_2на_1\право)\)
\(\vec{a}\times\vec{b}=i\left(0\right)-j\left(0\right)+k\left(0\right)=\vec{0}\)
Узнайте больше о комплексных числах здесь.
Результат равен нулю, так как разные компоненты вектора одного и того же вектора перпендикулярны друг другу и, следовательно, их произведение равно нулю.
Решенные примеры коллинеарных векторовЗная все о коллинеарных векторах и о том, как доказать их коллинеарность, давайте попрактикуемся в некоторых задачах на коллинеарные вектора для большей ясности.
Решенный Пример 1: Какой из заданных векторов \(\vec{a}\)= {2, 3}, \(\vec{b}\)= {4, 6}, \(\vec{ c}\)= {6, 12} коллинеарны друг другу?
Решение: Для проверки коллинеарности воспользуемся следующим условием:
If \(\vec{a}=a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\text { и }\vec{b}=b_1\шляпа{i}+b_2\шляпа{j}+b_3\шляпа{k}\) тогда:
\(\frac{b_1}{a_1}=\frac{b_2 }{a_2}=\frac{b_3}{a_3}\) для коллинеарности векторов.
Рассмотрим
\(\vec{a}\text{ и }\vec{b}\)
Дано:
\(\vec{a}\)= {2, 3} и \(\vec{b}\ )= {4, 6}
\(\frac{2}{4}=\frac{3}{6}=\frac{1}{2}\)
Следовательно, векторы a и b коллинеарны.
Теперь рассмотрим
\(\vec{a}\text{ и }\vec{c}\)
\(\vec{a}\)= {2, 3} и \(\vec{c }\)= {6, 12}
\(\frac{2}{6}=\frac{3}{12}\Rightarrow\frac{1}{3}\ne\frac{1}{4} \)
Следовательно, векторы а и с неколлинеарны.
Теперь рассмотрим
\(\vec{b}\text{ и }\vec{c}\)
\(\vec{b}\)= {4, 6} и \(\vec{c}\)= { 6, 12}
\(\frac{4}{6}=\frac{6}{12}\Rightarrow\frac{2}{3}\ne\frac{1}{2}\)
Отсюда векторы b и c неколлинеарны.
Узнайте о различных свойствах векторов здесь.
Решено Пример 2: Показать, что векторы \(\vec{a}=\left(3,5,7\right)\text{,}\vec{b}=\left(6,10,14 \справа)\) коллинеарны.
Решение:
Чтобы проверить коллинеарность векторов, применим условия коллинеарности векторов.
Для \(\vec{a}=\left(3,5,7\right)\text{,}\vec{b}=\left(6,10,14\right)\)
\( \frac{3}{6}=\frac{5}{10}=\frac{7}{14}\Rightarrow\frac{1}{2}=\frac{1}{2}=\frac{1 }{2}\)
Следовательно, векторы коллинеарны.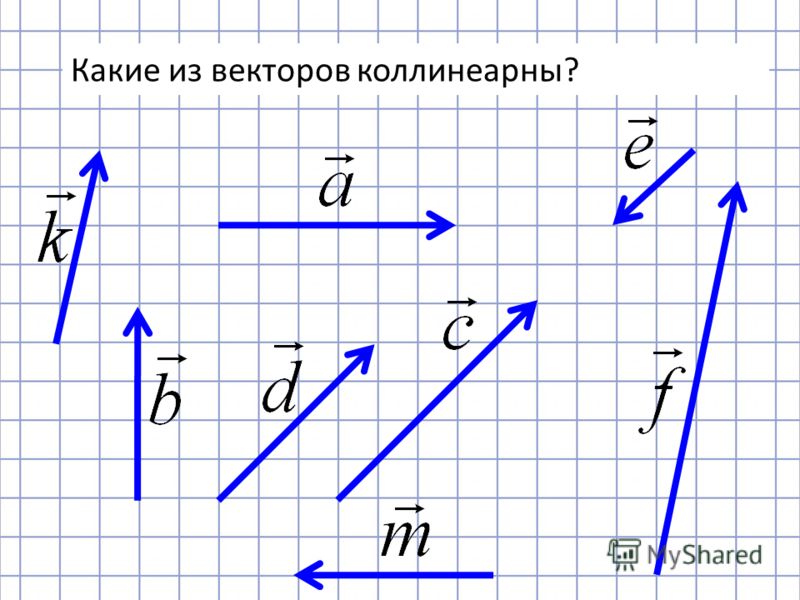
Ознакомьтесь с этой статьей о точечном продукте.
Решенный Пример 3: Определите значение n, при котором векторы \(\vec{a}=\left(2,5\right)\text{ и }\vec{b}=\left(4, n\right)\) коллинеарны.
Решение:
Применяя условие коллинеарности:
\(\frac{b_1}{a_1}=\frac{b_2}{a_2}=\frac{b_3}{a_3}\)
\(\frac{2}{4}=\frac{5} {n}\)
Решите приведенное выше уравнение:
\(n=\frac{5\times4}{2}=\frac{20}{2}=10\)
Мы надеемся, что приведенная выше статья о Коллинеарные векторы полезны для вашего понимания и подготовки к экзаменам. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о коллинеарных векторахВ.1 Что такое вектор?
Ответ 1 Вектор можно интерпретировать как линию с указателем, стремящимся к ее направлению, а ее длина описывает величину вектора.
Q.2 Как мы определяем коллинеарные векторы?
Ответ 2 Когда два или более вектора параллельны друг другу независимо от величины или направления, говорят, что они коллинеарны.
Q.3 Коллинеарны ли параллельные векторы?
Ответ 3 Да, любые два вектора коллинеарны тогда и только тогда, когда эти два вектора либо лежат на одной прямой, либо параллельны друг другу в одном и том же направлении/противоположном направлении. Следовательно, коллинеарные векторы также известны как параллельные векторы.
Q.4 В чем разница между параллельными и коллинеарными векторами?
Отв.4 Параллельные векторы включают одинаковую или параллельную опору. Эти векторы могут иметь одинаковую или неравную величину, а также их направления могут быть одинаковыми или противоположными. Однако два вектора считаются коллинеарными, если они сохраняют одно и то же направление, параллельны или антипараллельны.
Q.5 Что такое неколлинеарные векторы?
Ответ 5 Векторы, параллельные одной и той же прямой, считаются коллинеарными друг другу, а пересекающиеся векторы называются неколлинеарными.
Q.6 Каковы условия коллинеарности векторов?
Ответ 6 Три важных условия коллинеарности векторов: Во-первых, предполагается, что два вектора «p» и «q» являются коллинеарными векторами, если существует скаляр «k» такой, что p = кг Во-вторых, два вектора коллинеарны тогда и только тогда, когда доли их связанных координат эквивалентны. В-третьих, два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
Q.7 Что такое единичный вектор в физике?
Ответ 7 Единичный вектор в физике имеет величину, равную единице, и имеет конкретное направление. Он также распознается как вектор направления.
Скачать публикацию в формате PDF| Дополнение набора: определение, символ, диаграмма Венна, свойства с использованием решенных примеров |
| Обратные функции: изучение определения, действия по поиску, типы, построение графика с использованием примеров! |
| Сложение и вычитание алгебраических выражений: изучите горизонтальный метод и метод столбцов на примерах! |
| Решение линейного дифференциального уравнения: первый и второй порядок DE |
| Теорема де Муавра: выучить формулу, доказать с помощью математической индукции, использовать и решить примеры! |
com11а.4. Векторы положения, расстояния между точками, коллинеарные точки – точка b
Векторы положения
Векторы положения и общие векторы
Вектор состоит из величины и направления: начального или конечного
положение вектора не имеет значения. Например, вектор
$\mathbf{a} = \mathbf{i} + 2 \mathbf{j}$ предполагает перемещение на 1 единицу вдоль
по оси $x$ и 2 единицы по оси $y$.
Неважно, откуда оно начинается:
любое такое движение считается $\mathbf{a}$. На самом деле векторы могут быть
«передвигается» до тех пор, пока мы держим его параллельным и сохраняем его величину.
Когда мы изучаем геометрию (в частности, трехмерную геометрию для нашей программы) часто полезно работать с точками. Мы уже работали с координатами в построении кривых. и может записать, например, координаты точки $A$ как $(1,2,0)$. Пусть начало координат $O$ равно $(0,0,0)$ и, таким образом, иметь вектор $\overrightarrow{OA} = \mathbf{i}+2\mathbf{j}$.
Однако мы «потеряем след» точки $A$, если позволим вектору $\overrightarrow{OA}$ «двигаться».
Чтобы справиться с этим несоответствием, мы называем векторы, которые исходят из начала координат и заканчиваются в точке, вектор положения точки. Этот специальный вектор часто обрабатывается немного иначе, чем общий вектор (направление).
Вектор положения обычно считается «фиксированным», тогда как векторы направления можно «перемещать».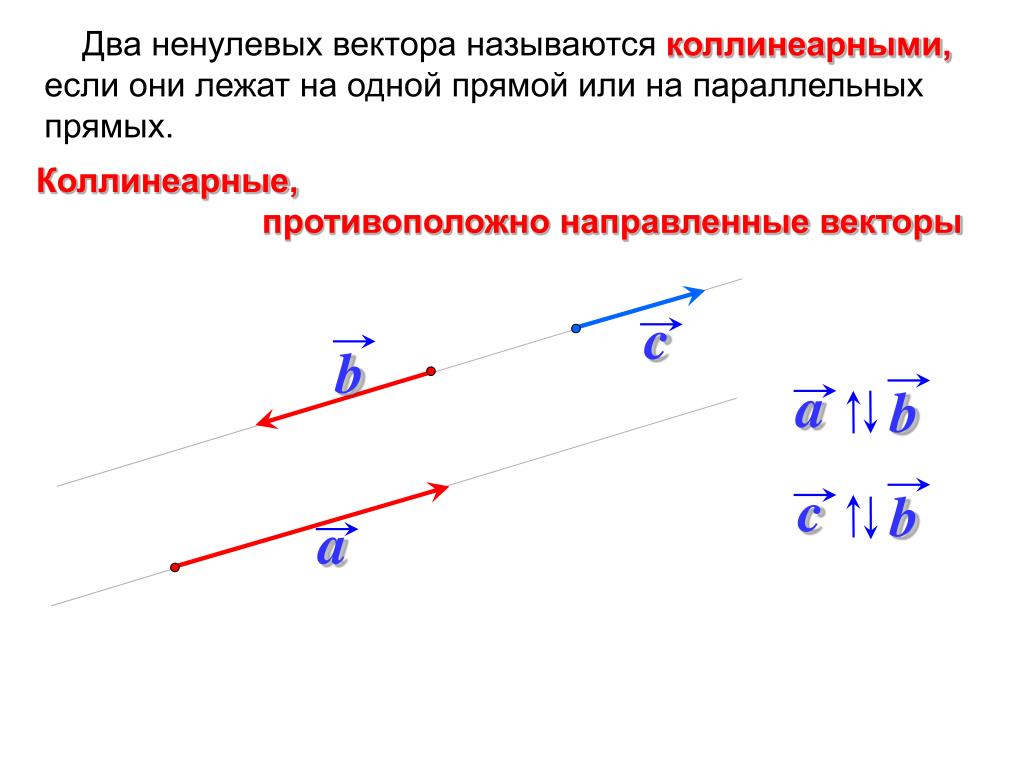
Для нашей программы мы записываем координаты горизонтально, например, $B (1,-3,2)$ и представляем векторы положения в форме вектора-столбца ($\overrightarrow{OB}=\mathbf{b}=\begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix}$). Использование $\mathbf{i},\mathbf{j}$ и $\mathbf{k}$ будет работать для последнего также.
Нас часто интересует формирование вектора, начинающегося с точки $A$ и заканчивающегося точкой $B$. Используя концепции сложения и вычитания векторов, мы получаем $\overrightarrow{AB}=\overrightarrow{AO} + \overrightarrow{OB} = \overrightarrow{OB}-\overrightarrow{OA}$. Это показано на диаграмме ниже.
Эта, казалось бы, тривиальная формула особенно полезна и будет очень часто использоваться в нашей программе, поскольку она позволяет нам перейти от координат/векторов положения к вектору, начинающемуся в одной точке и заканчивающемуся в другой.
Расстояние между точками
Теперь мы знаем, как вычислить $\overrightarrow{AB}$. Чтобы найти расстояние между двумя точками, $A$ и $B$, мы используем величину $\overrightarrow{AB}$,
$\слева | \overrightarrow{AB} \right |$.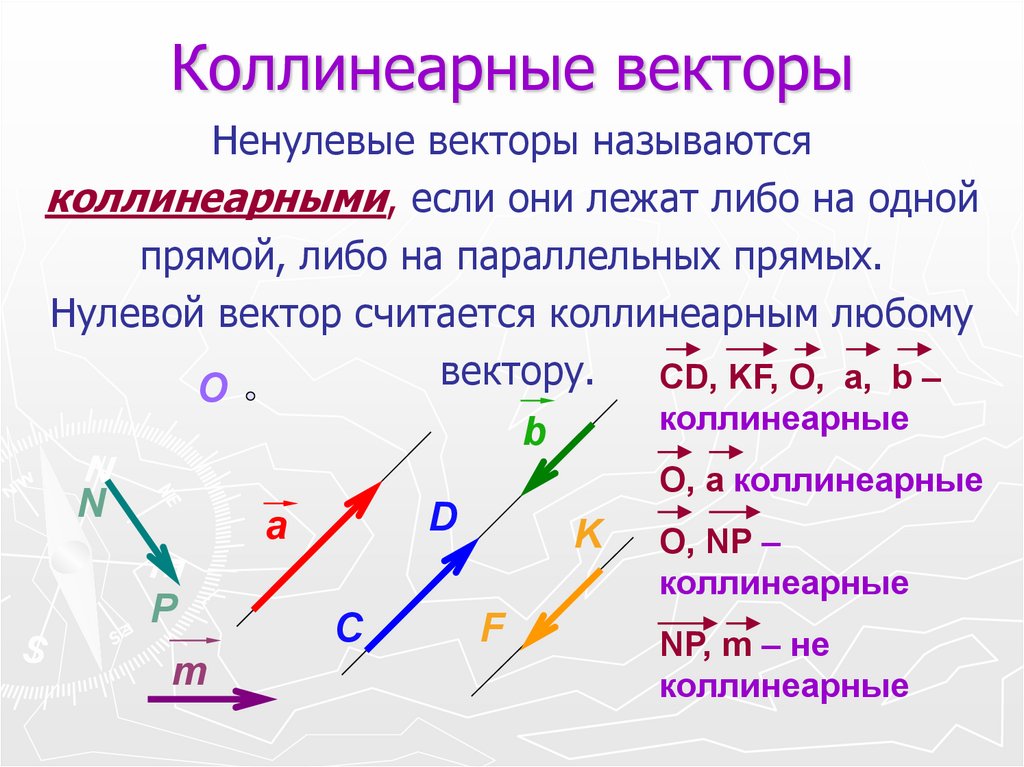
Коллинеарные точки
Иногда нас интересует, лежат ли три точки на одной прямой. Если да, то мы называем их коллинеарными . Чтобы проверить, являются ли 3 точки $A,B$ и $C$ коллинеарны, мы можем образовать векторы $\overrightarrow{AB}$ и $\overrightarrow{AC}$ (допускаются и другие комбинации, такие как $\overrightarrow{BC}$ и $\overrightarrow{CB}$). Если $A,B$ и $C$ коллинеарны, то $\overrightarrow{AB}$ и $\overrightarrow{AC}$ будут параллельны, так что $\overrightarrow{AB}=k\overrightarrow{AC}$.
Обратно, если $\overrightarrow{AB}=k\overrightarrow{AC}$ для некоторого $k \neq 0$, то $\overrightarrow{AB}$ и $\overrightarrow{AC}$ параллельны. Более того, они имеют общую точку $A$, поэтому $A,B$ и $C$ должны лежать на одной прямой.
Решения примеров
1. Даны точки $A(5,-1,3)$ и $B$ с позиционным вектором $\overrightarrow{OB} = \mathbf{i} + 2 \mathbf{j} — 4 \mathbf{k}$, найдите вектор $\overrightarrow{AB}$.
$\overrightarrow{AB} = \overrightarrow{OB} — \overrightarrow{OA} =$ $-4 \mathbf{i} + 3 \mathbf{j} -7\mathbf{k}$.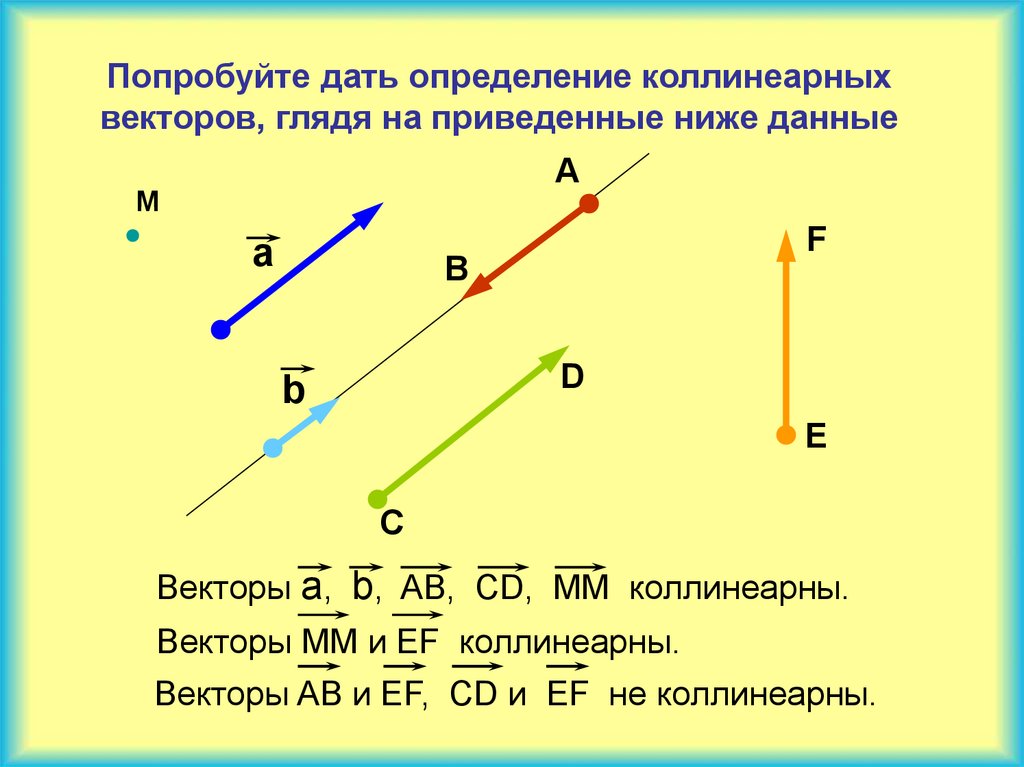
2. Найдите расстояние между $A$ и $B$.
Требуемое расстояние $=|\overrightarrow{AB}| =$ $\sqrt{74}$ единиц.
3. Далее дано, что $C$ имеет координаты $(13,y,17)$. Учитывая, что $A,B$ и $C$ лежат на одной прямой, найдите $y$.
$\overrightarrow{AC} = \overrightarrow{OC}-\overrightarrow{OA} =
\begin{pmatrix} 8 \\ y+1 \\ 14 \end{pmatrix}$.
Поскольку $A,B$ и $C$ коллинеарны, $\overrightarrow{AC} = k \overrightarrow{AB}$ для некоторого $k$.
$\begin{pmatrix} 8 \\ y+1 \\ 14 \end{pmatrix} = k\begin{pmatrix} -4 \\ 3 \\ -7 \end{pmatrix}$.
Следовательно, $k = -2$ и $y+1 = (-2)(-4)$. Это дает $y=7$.
4. Если $D$ имеет координаты $(-3,5,-11)$, покажите, что $A,B$ и $D$ лежат на одной прямой.
$\overrightarrow{AD} = \overrightarrow{OD} — \overrightarrow{OA} = -8\mathbf{i} + 6 \mathbf{j} -14 \mathbf{k}$.
Следовательно, $\overrightarrow{AD} = 2 \overrightarrow{AB}$, поэтому $AD$ параллелен $AB$.